{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 0,
"link": "[](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html)",
"section": ""
}
},
"source": [
"\n",
"*This notebook contains material from [CBE30338](https://jckantor.github.io/CBE30338);\n",
"content is available [on Github](https://github.com/jckantor/CBE30338.git).*\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 0,
"link": "[](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html)",
"section": ""
}
},
"source": [
"\n",
"< [3.6 Second Order Models](https://jckantor.github.io/CBE30338/03.06-Second-Order-Models.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.8 Manometer Models and Dynamics](https://jckantor.github.io/CBE30338/03.08-Manometer-Models-and-Dynamics.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.7 Interacting Tanks](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7-Interacting-Tanks)",
"section": "3.7 Interacting Tanks"
}
},
"source": [
"# 3.7 Interacting Tanks"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.7.1 Problem Statement](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.1-Problem-Statement)",
"section": "3.7.1 Problem Statement"
}
},
"source": [
"## 3.7.1 Problem Statement\n",
"\n",
"The following diagram shows a pair of interacting tanks.\n",
"\n",
"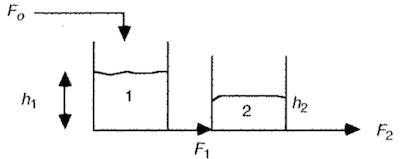\n",
"\n",
"Assume the pressure driven flow into and out of the tanks is linearly proportional to tank levels. The steady state flowrate through the tanks is 3 cubic ft per minute, the steady state heights are 7 and 3 feet, respectively, and a constant cross-sectional area 5 sq. ft. The equations are written as\n",
"\n",
"$$\\begin{align*}\n",
"\\frac{dh_1}{dt} & = \\frac{F_0}{A_1} - \\frac{\\beta_1}{A_1}\\left(h_1-h_2\\right) \\\\\n",
"\\frac{dh_2}{dt} & = \\frac{\\beta_1}{A_2}\\left(h_1-h_2\\right) - \\frac{\\beta_2}{A_2}h_2\n",
"\\end{align*}$$\n",
"\n",
"**a.** Use the problem data to determine values for all constants in the model equations.\n",
"\n",
"**b.** Construct a Phython simulation using `odeint`, and show a plot of the tank levels as function of time starting with an initial condition $h_1(0)=6$ and $h_2(0)$ = 5. Is this an overdamped or underdamped system."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.7.2 Solution](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2-Solution)",
"section": "3.7.2 Solution"
}
},
"source": [
"## 3.7.2 Solution"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.1 Part a. ](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.1-Part-a.)",
"section": "3.7.2.1 Part a. "
}
},
"source": [
"### 3.7.2.1 Part a. \n",
"\n",
"The parameters that need to be determined are $\\beta_1$ and $\\beta_2$. At steady state all of the flows must be identical and\n",
"\n",
"$$\\begin{align*}\n",
"0 & = F_0 - \\beta_1(h_1 - h_2) \\\\\n",
"0 & = \\beta_1(h_1 - h_2) - \\beta_2h_2 \n",
"\\end{align*}$$\n",
"\n",
"Substituting problem data,\n",
"\n",
"$$\\beta_1 = \\frac{F_0}{h_1-h_2} = \\frac{3\\text{ cu.ft./min}}{4\\text{ ft}} = 0.75\\text{ sq.ft./min}$$ \n",
"\n",
"$$\\beta_2 = \\frac{\\beta_1(h_1 - h_2)}{h_2} = \\frac{3\\text{ cu.ft./min}}{3\\text{ ft}} = 1.0\\text{ sq.ft./min}$$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.2 Part b.](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.2-Part-b.)",
"section": "3.7.2.2 Part b."
}
},
"source": [
"### 3.7.2.2 Part b.\n",
"\n",
"The next step is perform a simulation from a specified initial condition. "
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.2 Part b.](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.2-Part-b.)",
"section": "3.7.2.2 Part b."
}
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEKCAYAAAARnO4WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHY5JREFUeJzt3XmcFfWZ7/HP0xvQNLvYIjCCC24oaKNxQ2k17jMak1ei\nozOSxEEzmpiJOrlx5kaTjCZ37kyiyWhyXaJO4thxTYzRiJomBmOURRQEFRWQTRZZTwO9nef+UdXS\nNN2nT/fpOlt9369Xvc6pql/V73ko+znl79SpMndHRESKX0muAxARkexQwRcRiQkVfBGRmFDBFxGJ\nCRV8EZGYUMEXEYmJSAu+mf2Tmb1lZovM7GEz6x9lfyIi0rXICr6ZjQa+Bkxx94lAKXBJVP2JiEhq\nUQ/plAEDzKwMqATWRNyfiIh0oSyqHbv7ajP7D+BDYCcw091ndmxnZjOAGQADBgyoGTt2bK/6SyaT\nlJQUx1cSxZJLseQByiUfFUsekFku77777kZ3H5lWY3ePZAKGAX8ARgLlwK+By1NtU1NT471VX1/f\n623zTbHkUix5uCuXfFQsebhnlgsw19Osy1F+PJ4JLHP3De7eDDwBnBRhfyIikkKUBf9D4AQzqzQz\nA84AlkTYn4iIpBBZwXf3V4HHgPnAwrCvu6PqT0REUovsS1sAd78ZuDnKPkREJD3F8RW3iIh0SwVf\nRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0QkJlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0Qk\nJlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0QkJiIr+GZ2qJktaDdtM7OvR9WfiIikFtkz\nbd39HWAygJmVAquBJ6PqT0REUov0IebtnAG87+4rstSfpCGZdBpbkuxqbv3kdVdLK43Nu5c1tiRp\nbk3SknRawtfWdu9bWn2PdS3JsE2rs2JlI/VbF+FA0h13SDqAk0yGy8J1ePt58LC9d2jrnjonsy6W\n92qb3Ss2bNxF3cp53W9jHbbd8wULG9he7TtfT4f97d2+i/UddtB+uzVrGnlhy8K9cuwqlq5y6zKW\nvsqhQ8cd269Y3sQbLUu7jaPH8XdYv3v7NI9dmvG372fZmhamEb1sFfxLgIez1FcsJJPOtl3NbGpo\n+mTavKOJLTuaSTS2sH1XC4nGFhoaWzqdb2xO0tSa7PO4SkuM0hKjvMRIJlupWL+GEgv+GEoMwMJ5\nKDGjJPyvv6Qk+ANoa2sW/IG0tbG25Sn67uqzwLv7lOh0mz3nGxqSJGgI++l8f23b+Cfzvmdc3azf\nvb3vOd+hu7S32yuX4E1jUwtvbvpojyy63Gdf5bDX9l3F2vn+uvTeu900KAyDK4ybstCP9eaPoUcd\nmFUAa4Aj3X1dJ+tnADMAqqura+rq6nrVTyKRoKqqKpNQ88aGLQl2lVayeVeSTbuczbv8k9fNjUm2\nNzmJ5raz5b0Z0L8MBpRZ8Fpqu9+HrxUlRnkpVJRAefi+vAQqSm2P1/KSsIgblBqUGJSVBIW41KC0\nZPfyUtvzrKqYjolyyQ/tPxASiQaqqgaGy/lk+R7tP9mu8+V7fYDt1V/q5Xv10+V+vdPlbXbs2MHo\n4b07JrW1tfPcfUo6bbNR8C8ErnH3s7prO2XKFJ87d26v+pk1axbTpk3r1ba50Nya5P0NCZauS7B8\nYwPLPm5gxcc7WL6xgY8bmvZoawb7DurHfkMGsN/gfoyo6sfwygqGDwymYQMrGF5ZwbCB5QytrKCy\nvJSSklTnwtlRaMckFeWSf4olD8gsFzNLu+BnY0jnUmI+nLOzqZU3V21h4eqtLFm7nSVrt/He+sQe\nQyr7De7PuH0qOevIalq3fMRpU45ivyH9GTWkPyMH9aO8VFfQikhmIi34ZjYQ+DRwVZT95Jv123fx\n2rJNzFuxmfkrNvPWmm20hOMvIwf14/BRg5k6YR+OGDWYCdWDOGBEJZUVuw/FrFmbmHb0qFyFLyJF\nKtKC7+4NwIgo+8gHTS1J5q7YxEvvbuSP725gydptAPQvL2HSmKHMOPVApowbxtFjhrJPVb8cRysi\ncZWtq3SKzq7mVl56dwPPLFzLC0vWk2hsoazEqDlgGDeefSgnH7wPR+4/WEMxIpI3VPB7wN15ddkm\nHpmzkpmL15FobGFoZTnnHbUfZx5ezYkHjWBQ//Jchyki0ikV/DR8nGjk0Xmr+NWclSzb2MCg/mWc\nf9Qozjt6FCcdNEJn8SJSEFTwU1i+sYF7Z3/Ao3NX0diS5Phxw7m29mDOO2oUAypKcx2eiEiPqOB3\n4p2PtvPjF5fy7KK1lJWU8JljRnPl1PEcUj0o16GJiPSaCn47qzbv4EfPL+WJ11dRVVHG1acdxPST\nxrHv4P65Dk1EJGMq+MCOphbueHEp989eDgb/MPVAvnLaQQwbWJHr0ERE+kzsC/7Mtz7ilqfeYs3W\nXXz22DFcf9YE9h86INdhiYj0udgW/E0NTdz0xEJ+/9ZHHFo9iEcvPYbjxg3PdVgiIpGJZcGvf3s9\nNz72Jtt2NvPNcw7jyqnjdWmliBS9WBX85tYkt/5uCQ/8eTmHVg/iF18+nsNHDc51WCIiWRGbgr9+\n+y6ueWg+c5Zv5osnj+Ob5xxG/3JdSy8i8RGLgv/6h5u5+pfz2LqzmTsumcyFk0fnOiQRkawr+oL/\n/OJ1XPs/89l3cD+e+MrJHLG/hnBEJJ6KuuDXvfYhNz25kKNGD+G+6cfp1sQiEmtFW/Dvful9bnvm\nbU6bMJK7LjuWgf2KNlURkbQUZRW8908fcNszb3PB0aP40Rcm65JLERGKsODfN3sZ//a7JZx/1Chu\n/8JkylTsRUQAKKpq+MjclXzv6cWcO3E/br9ExV5EpL1IK6KZDTWzx8zsbTNbYmYnRtXXwg0t3PTE\nQqYesg93XHKMhnFERDqIekjnDuD37v45M6sAKqPoZNHqrdy5oJFDqgdz12XHUlGmYi8i0lFkBd/M\nhgCnAtMB3L0JaOrrfjY3NPGlB+ZQWW7cP/04PVNWRKQL5u7R7NhsMnA3sBiYBMwDrnP3hg7tZgAz\nAKqrq2vq6up61I+7M3NFC+MHNDKhuqpPYs+1RCJBVVXh51IseYByyUfFkgdklkttbe08d5+SVmN3\nj2QCpgAtwKfC+TuA76Xapqamxnurvr6+19vmm2LJpVjycFcu+ahY8nDPLBdgrqdZl6Mc7F4FrHL3\nV8P5x4BjI+xPRERSiKzgu/tHwEozOzRcdAbB8I6IiORA1FfpfBV4KLxC5wPgixH3JyIiXYi04Lv7\nAoKxfBERyTFdsC4iEhMq+CIiMaGCLyISEyr4IiIxoYIvIhITKvgiIjGhgi8iEhMq+CIiMaGCLyIS\nEyr4IiIxoYIvIhITKvgiIjGhgi8iEhMq+CIiMaGCLyISEyr4IiIxoYIvIhITKvgiIjER6SMOzWw5\nsB1oBVrcXY87FBHJkagfYg5Q6+4bI+3BHbw10i5ERApd4Q/p7NoK99QyevUzuY5ERCSvmbtHt3Oz\nZcBWgiGd/+fud3fSZgYwA6C6urqmrq6ux/1Mfv1bVOxcx5wT7sZLsvE/LdFKJBJUVVXlOoyMFUse\noFzyUbHkAZnlUltbOy/t4XJ3j2wCRoev+wJvAKemal9TU+O98vaz7jcPdl9Q17vt80x9fX2uQ+gT\nxZKHu3LJR8WSh3tmuQBzPc2aHOmQjruvDl/XA08Cx0fS0SFn0VA5Fl6+IxjPFxGRvURW8M1soJkN\nansPnAUsiqSzkhJWjv0MrH8L3nshki5ERApdlGf41cBsM3sDeA34nbv/PqrO1lWfCoP2h9m3R9WF\niEhBi+wbTnf/AJgU1f736q+kHE66Fp67CZa/DONOzlbXIiIFIWXBN7Nj09hHs7sv7KN4MlPzxWAc\nv/5WmP47MMt1RCIieaO7M/w/AnOAVJVzPDCurwLKSEUlTL0env1n+GAWHFSb64hERPJGdwV/jruf\nnqqBmf2hD+PJXM10ePnHwVn+gdN0li8iEkr5pW13xT7dNllV1g9OvQFWzYF3n8t1NCIieSOtq3TM\n7MV0luWNYy6H4QfB89+G1uZcRyMikhdSFnwz629mw4F9zGyYmQ0Pp3HA6GwE2Cul5XDWv8HGd2Du\n/bmORkQkL3R3hn8VMA84LHxtm34D/Fe0oWXo0HNh/Kkw6zbYuTnX0YiI5Fx3BX+Nu48HbnT3A919\nfDhNcvf8LvhmcPZtsHMLzPo/uY5GRCTnuiv43wpfp0ccRzT2OwpqroDX7oa1b+Y6GhGRnOqu4H9s\nZjOB8Wb2VMcpGwFm7IyboXI4/PY6SOohKSISX91dh38+cCzwC+A/ow8nApXD4ezvwxNXwpx74VNX\n5ToiEZGcSFnw3b0J+IuZneTuG7IUU9876nPwxsPw4nfhsPNhyJhcRyQiknXdXZZ5C0CqYt/WJq+Z\nwQU/DO6V/+uvQDKZ64hERLKuuyGdK81sW4r1BlwC3NJnEUVl2Dg457ZgLP/Vn8KJ1+Q6IhGRrOru\nS9t7gEEppqqwTWE49go49Dx44TuwbnGuoxERyaruxvC/k61AssIM/vrH8NMT4bEvwT+8CBUDcx2V\niEhWRPpM27xUNRIuvhs2vB0M7+gZuCISE/Er+AAHnQ6n/wssfBReK5wRKRGRTERe8M2s1MxeN7On\no+6rR065HiacC899C1a8kutoREQi190jDn8CdDnm4e5fS6OP64AlwOCehRaxkhL4zM/gntOh7m/h\nyhdgxEG5jkpEJDLdneHPZc+7ZHacUjKzMQS/1r03szAjMmAoXPZo8GXuLz8LDRtzHZGISGTMe/Cl\npZlVuvuOHrR/DPg+wSWcN7j7BZ20mQHMAKiurq6pq6tLO572EokEVVVVvdp28NZ3mPTGv9IwcBwL\nJn+PZGn/Xu2nr2SSSz4pljxAueSjYskDMsultrZ2nrtPSauxu3c7AScCi4EPw/lJwF3dbHNBWxtg\nGvB0d/3U1NR4b9XX1/d6W3d3X/yU+y1D3R+4wL2xIbN9ZSjjXPJEseThrlzyUbHk4Z5ZLsBcT6OO\nu3vaX9reDpwNfBx+SLwBnNrNNicDf2Nmy4E64HQz+2Wa/WXf4X8NF/0Ulv0pGNNv3pXriERE+lTa\nV+m4+8oOi1Lea9jdv+XuY9x9HMHtF/7g7pf3PMQsmnQJXPhf8EE9/OoyaEp79EpEJO+lW/BXmtlJ\ngJtZuZndQHDlTfE55nL4m5/Aey/CLy6CHZtyHZGISJ9It+BfDVxD8ODy1cDkcD4t7j7LO/nCNm8d\n+/fw+Qdhzetw/7mwdXWuIxIRyVi6Bd/c/TJ3r3b3fd39cnf/ONLIcu2IC+HyJ2DbGrinFla+luuI\nREQykm7Bf9nMZprZl81saKQR5ZPxU+FLz0F5Jdx/Hsx7INcRiYj0WloF390nAP8KHAnMN7OnzSy/\nv4DtK9VHwIx6GH9qcLO131wLTQ25jkpEpMd6cpXOa+7+DeB4YBPwYGRR5ZsBw4Jf5E69Hl7/Jfxs\nKqzu9ofGIiJ5Ja2Cb2aDzewKM3sW+DOwlqDwx0dJKZzxbbjit9CyC+47C2b9AFoacx2ZiEha0j3D\nf4PgypzvuvsEd/+mu8fzFHf8VPjKy3DERTDr+/CzU2D57FxHJSLSrXQL/oHu/k8EhV8GDIPP3Qd/\n+2hwtv/A+fDEVbCl42/TRETyR7oF/wQzWwy8DWBmk8zsrujCKhATzoJ/fBVO+Qa89ST8pAZm/m/Y\nuTnXkYmI7CXKe+nEQ0UlnHkzfHUeTLwY/vwTuGMS/OFW3W5ZRPJKZPfSiZ2hY4MHqlw9G8ZNhZf+\nHX40EZ65ETYvz3V0IiKpn3jVzh730mH3U6yko/0mwiUPwYZ34OUfw9yfB8/NPfhMmPJFOORsKE33\nn11EpO9kci+df4wqqKIw8lC46E647k049UZYtyi47fLtE+H5b8PaN6AHD58REclUWqea7r4RuKz9\nMjP7OsHYvqQyZDSc/i9w2jdh6XPB7RleuRNevgNGHAxHXgyHnQ/7HR08Z1dEJCKZjC18AxX89JWW\nBYX9sPODWy4veQoWPQ4v/d9gvL+qOhj2OeTTlDVryEdE+l4mlcX6LIq4qRwONdODKbE+uPf+0pnw\n9tOw4CFOAVh6BPzViXDAScHrkNG5jVlECl4mBV8D0H2hal+YfGkwtbbAqjksq/8F40vXwpu/grn3\nBe0GjYJRk4Khn1FHB++HjAXT566IpCdlwTez7XRe2A0YEElEcVZaBgecyIpxjYyfNi34AFi3CD58\nJXgYy9o3g/8T8GTQvt/g4HuAfQ4JphGHwD4TYNgBUDEwp6mISP5JWfDdfVC2ApFOlJbB/pODqU3T\nDli/GNYugPVvw8Z3g3v5vPmrPbcdMDz4bcCQsTBkTPg6OviuYOC+UDUy+MDQ/yGIxEZk3w6aWX/g\nJaBf2M9j7n5zVP3FRkUljJkSTO01NcDH78HGpbBlBWxdFdzb5+P34YNZ0JTYe1+l/WDgSBi4TzC0\nVDkC+g+B/kPD186mwVA+EErL9WEhUmCivBykETjd3RPhj7Vmm9mz7v6XCPuMr4qBwbj+qEl7r3OH\nXVuCD4HE+uCWDw3roWEDJDaEr+tg/RLYtQ0at3bfn5UGfZZXQvmATt8funELNPw2+GApLYey8LW0\nH5RWQFlF8NrZ+pKycCoJXq00uEV1SRlYuOyT+bZ1peH79uv0oSTSJrKC7+4OtJ1WloeTvujNBbPg\nDp8DhqXXPtkKjdth19Zw2tLu/TZo3hFMTTuguQGad+75fscmaG5geGIzbJ0PrU27p6yz3R8SZsEr\n1m7eOsx3XB/Mn9DYBAv6p9U2mGfv9W0Xtn3yIZTpPJ3Md7+PozdtglUjIoqhj/bXft1efQQOW7cO\nNj2csk13++i8TTfr+6yf3fMHrtsC06Z1sk3fivSCbzMrBeYBBwN3uvurnbSZAcwAqK6uZtasWb3q\nK5FI9HrbfJOfuQwKp1Apwdf2Kb66TyQSVFVV7V7gjnkLJcnmT15Lki2dLGvGPBlOrUDw2jbf9bo9\n3+9e14q5E5xv+CfvO1u25/rwy3GStJQ3U15WCtBu+e425snwdCaJha/t27bfZk8eru98+e71nS9v\nb/c+Om/Ttt6SrWxb136Ir29iSLf/rv4NOm/bFWdQMsnOrUv2WLbnPvbeprP9pJrfex/db9OZrv9t\nA0NLB2Xnb97dI5+AoUA9MDFVu5qaGu+t+vr6Xm+bb4oll2LJw1255KNiycM9s1yAuZ5mLc7Kb/nd\nfUtY8M/JRn8iIrK3yAq+mY00s6Hh+wHApwkfoCIiItkX5Rj+KODBcBy/BHjE3Z+OsD8REUkhyqt0\n3gSOiWr/IiLSM7ofr4hITKjgi4jEhAq+iEhMqOCLiMSECr6ISEyo4IuIxIQKvohITKjgi4jEhAq+\niEhMqOCLiMSECr6ISEyo4IuIxIQKvohITKjgi4jEhAq+iEhMqOCLiMSECr6ISEyo4IuIxESUDzEf\na2b1ZrbYzN4ys+ui6ktERLoX5UPMW4Dr3X2+mQ0C5pnZ8+6+OMI+RUSkC5Gd4bv7WnefH77fDiwB\nRkfVn4iIpGbuHn0nZuOAl4CJ7r6tw7oZwAyA6urqmrq6ul71kUgkqKqqyizQPFEsuRRLHqBc8lGx\n5AGZ5VJbWzvP3aek1djdI52AKmAecHF3bWtqary36uvre71tvimWXIolD3flko+KJQ/3zHIB5nqa\n9TjSq3TMrBx4HHjI3Z+Isi8REUktyqt0DLgPWOLuP4yqHxERSU+UZ/gnA38HnG5mC8LpvAj7ExGR\nFCK7LNPdZwMW1f5FRKRn9EtbEZGYUMEXEYkJFXwRkZhQwRcRiQkVfBGRmFDBFxGJCRV8EZGYUMEX\nEYkJFXwRkZhQwRcRiQkVfBGRmFDBFxGJCRV8EZGYUMEXEYkJFXwRkZhQwRcRiQkVfBGRmFDBFxGJ\niSgfYv5zM1tvZoui6kNERNIX5Rn+A8A5Ee5fRER6ILKC7+4vAZui2r+IiPSMxvBFRGLC3D26nZuN\nA55294kp2swAZgBUV1fX1NXV9aqvRCJBVVVVr7bNN8WSS7HkAcolHxVLHpBZLrW1tfPcfUpajd09\nsgkYByxKt31NTY33Vn19fa+3zTfFkkux5OGuXPJRseThnlkuwFxPs8ZqSEdEJCaivCzzYeAV4FAz\nW2VmX46qLxER6V5ZVDt290uj2reIiPSchnRERGJCBV9EJCZU8EVEYkIFX0QkJlTwRURiQgVfRCQm\nVPBFRGJCBV9EJCZU8EVEYkIFX0QkJlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0QkJlTw\nRURiQgVfRCQmVPBFRGIi0oJvZueY2Ttm9p6Z/a8o+xIRkdQiK/hmVgrcCZwLHAFcamZHRNWfiIik\nFuUZ/vHAe+7+gbs3AXXAhRH2JyIiKZRFuO/RwMp286uAT3VsZGYzgBnhbMLM3ullf/sAG3u5bb4p\nllyKJQ9QLvmoWPKAzHI5IN2GURb8tLj73cDdme7HzOa6+5Q+CCnniiWXYskDlEs+KpY8IHu5RDmk\nsxoY225+TLhMRERyIMqCPwc4xMzGm1kFcAnwVIT9iYhICpEN6bh7i5ldCzwHlAI/d/e3ouqPPhgW\nyiPFkkux5AHKJR8VSx6QpVzM3bPRj4iI5Jh+aSsiEhMq+CIiMVHwBb+Ybt9gZsvNbKGZLTCzubmO\npyfM7Odmtt7MFrVbNtzMnjezpeHrsFzGmK4ucrnFzFaHx2aBmZ2XyxjTYWZjzazezBab2Vtmdl24\nvOCOS4pcCvG49Dez18zsjTCX74TLIz8uBT2GH96+4V3g0wQ/7JoDXOrui3MaWC+Z2XJgirsX3I9J\nzOxUIAH8t7tPDJf9O7DJ3X8QfhgPc/dv5jLOdHSRyy1Awt3/I5ex9YSZjQJGuft8MxsEzAMuAqZT\nYMclRS6fp/COiwED3T1hZuXAbOA64GIiPi6Ffoav2zfkCXd/CdjUYfGFwIPh+wcJ/kDzXhe5FBx3\nX+vu88P324ElBL+AL7jjkiKXguOBRDhbHk5OFo5LoRf8zm7fUJD/EYQceMHM5oW3nCh01e6+Nnz/\nEVCdy2D6wFfN7M1wyCfvh0HaM7NxwDHAqxT4cemQCxTgcTGzUjNbAKwHnnf3rByXQi/4xeYUd59M\ncIfRa8KhhaLgwdhh4Y4fwk+BA4HJwFrgP3MbTvrMrAp4HPi6u29rv67QjksnuRTkcXH31vBvfQxw\nvJlN7LA+kuNS6AW/qG7f4O6rw9f1wJMEQ1aFbF049to2Brs+x/H0mruvC/9Ik8A9FMixCceIHwce\ncvcnwsUFeVw6y6VQj0sbd98C1APnkIXjUugFv2hu32BmA8MvozCzgcBZwKLUW+W9p4ArwvdXAL/J\nYSwZaftDDH2GAjg24ZeD9wFL3P2H7VYV3HHpKpcCPS4jzWxo+H4AwUUnb5OF41LQV+kAhJdh3c7u\n2zfcmuOQesXMDiQ4q4fglhf/U0i5mNnDwDSC27yuA24Gfg08AvwVsAL4vLvn/ZehXeQyjWDYwIHl\nwFXtxlvzkpmdAvwJWAgkw8U3EYx9F9RxSZHLpRTecTma4EvZUoKT7kfc/btmNoKIj0vBF3wREUlP\noQ/piIhImlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFXwqWmY1od1vcjzrcJvfPEfQ33cw2\nmNm9Pdzuu2Z2ZjdtvmDBLb6fzixKka7pOnwpCtm4fbGZTSe4ffW1Ee1/GnCDu18Qxf5FdIYvRcnM\nEuHrNDP7o5n9xsw+MLMfmNll4QMoFprZQWG7kWb2uJnNCaeT0+hjupn9OnxYxXIzu9bMvmFmr5vZ\nX8xseNjuATP7XPh+uZl9x8zmh/0fFuW/g0h7KvgSB5OAq4HDgb8DJrj78cC9wFfDNncAP3L344DP\nhuvSMZHgwRXHAbcCO9z9GOAV4O+72Gajux9LcKfHG3qejkjvlOU6AJEsmNN2fxUzex+YGS5fCNSG\n788Ejgju0QXAYDOravegiq7Uhw/k2G5mW4Hfttv30V1s03bXynkEHxYiWaGCL3HQ2O59st18kt1/\nAyXACe6+K4J9d7VNa4o2In1OQzoigZnsHt7BzCbnMBaRSKjgiwS+BkwJH5W3mGDMX6So6LJMkTTp\nskwpdDrDF0nfTuDcnv7wKh1m9gXgLmBzX+9bpI3O8EVEYkJn+CIiMaGCLyISEyr4IiIxoYIvIhIT\n/x+WUXDe/Z+mMwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy.integrate import odeint\n",
"from ipywidgets import interact\n",
"\n",
"# simulation time grid\n",
"t = np.linspace(0,30,1000)\n",
"\n",
"# initial condition\n",
"IC = [6,5]\n",
"\n",
"# inlet flowrate\n",
"F0 = 3\n",
"\n",
"# parameters for tank 1 \n",
"A1 = 5\n",
"beta1 = 0.75\n",
"\n",
"# parameters for tank 2\n",
"A2 = 5\n",
"beta2 = 1.0\n",
"\n",
"def hderiv(H,t):\n",
" h1,h2 = H\n",
" h1dot = (F0 - beta1*(h1-h2))/A1\n",
" h2dot = (beta1*(h1-h2) - beta2*h2)/A2\n",
" return [h1dot,h2dot]\n",
"\n",
"sol = odeint(hderiv,IC,t)\n",
"plt.plot(t,sol)\n",
"plt.ylim(0,8)\n",
"plt.grid()\n",
"plt.xlabel('Time [min]')\n",
"plt.ylabel('Level [ft]')"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.3 Further Calculations](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.3-Further-Calculations)",
"section": "3.7.2.3 Further Calculations"
}
},
"source": [
"### 3.7.2.3 Further Calculations\n",
"\n",
"$$\\frac{d}{dt}\\left[\\begin{array}{c} h_1 \\\\ h_2 \\end{array}\\right] = \n",
"\\left[\\begin{array}{cc}-\\frac{\\beta_1}{A_1} & \\frac{\\beta_1}{A_1} \\\\\n",
"\\frac{\\beta_1}{A_2} & -\\frac{\\beta_1}{A_2} - \\frac{\\beta_2}{A_2} \\end{array}\\right]\n",
"\\left[\\begin{array}{c}h_1 \\\\ h_2\\end{array}\\right]\n",
"+\n",
"\\left[\\begin{array}{c}\\frac{1}{A_1} \\\\ 0\\end{array}\\right]F_0$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"nbpages": {
"level": 3,
"link": "[3.7.2.3 Further Calculations](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.3-Further-Calculations)",
"section": "3.7.2.3 Further Calculations"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.3 Further Calculations](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.3-Further-Calculations)",
"section": "3.7.2.3 Further Calculations"
}
},
"source": [
"\n",
"< [3.6 Second Order Models](https://jckantor.github.io/CBE30338/03.06-Second-Order-Models.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.8 Manometer Models and Dynamics](https://jckantor.github.io/CBE30338/03.08-Manometer-Models-and-Dynamics.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[3.7 Interacting Tanks](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7-Interacting-Tanks)",
"section": "3.7 Interacting Tanks"
}
},
"source": [
"# 3.7 Interacting Tanks"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.7.1 Problem Statement](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.1-Problem-Statement)",
"section": "3.7.1 Problem Statement"
}
},
"source": [
"## 3.7.1 Problem Statement\n",
"\n",
"The following diagram shows a pair of interacting tanks.\n",
"\n",
"\n",
"\n",
"Assume the pressure driven flow into and out of the tanks is linearly proportional to tank levels. The steady state flowrate through the tanks is 3 cubic ft per minute, the steady state heights are 7 and 3 feet, respectively, and a constant cross-sectional area 5 sq. ft. The equations are written as\n",
"\n",
"$$\\begin{align*}\n",
"\\frac{dh_1}{dt} & = \\frac{F_0}{A_1} - \\frac{\\beta_1}{A_1}\\left(h_1-h_2\\right) \\\\\n",
"\\frac{dh_2}{dt} & = \\frac{\\beta_1}{A_2}\\left(h_1-h_2\\right) - \\frac{\\beta_2}{A_2}h_2\n",
"\\end{align*}$$\n",
"\n",
"**a.** Use the problem data to determine values for all constants in the model equations.\n",
"\n",
"**b.** Construct a Phython simulation using `odeint`, and show a plot of the tank levels as function of time starting with an initial condition $h_1(0)=6$ and $h_2(0)$ = 5. Is this an overdamped or underdamped system."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[3.7.2 Solution](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2-Solution)",
"section": "3.7.2 Solution"
}
},
"source": [
"## 3.7.2 Solution"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.1 Part a. ](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.1-Part-a.)",
"section": "3.7.2.1 Part a. "
}
},
"source": [
"### 3.7.2.1 Part a. \n",
"\n",
"The parameters that need to be determined are $\\beta_1$ and $\\beta_2$. At steady state all of the flows must be identical and\n",
"\n",
"$$\\begin{align*}\n",
"0 & = F_0 - \\beta_1(h_1 - h_2) \\\\\n",
"0 & = \\beta_1(h_1 - h_2) - \\beta_2h_2 \n",
"\\end{align*}$$\n",
"\n",
"Substituting problem data,\n",
"\n",
"$$\\beta_1 = \\frac{F_0}{h_1-h_2} = \\frac{3\\text{ cu.ft./min}}{4\\text{ ft}} = 0.75\\text{ sq.ft./min}$$ \n",
"\n",
"$$\\beta_2 = \\frac{\\beta_1(h_1 - h_2)}{h_2} = \\frac{3\\text{ cu.ft./min}}{3\\text{ ft}} = 1.0\\text{ sq.ft./min}$$ "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.2 Part b.](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.2-Part-b.)",
"section": "3.7.2.2 Part b."
}
},
"source": [
"### 3.7.2.2 Part b.\n",
"\n",
"The next step is perform a simulation from a specified initial condition. "
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.2 Part b.](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.2-Part-b.)",
"section": "3.7.2.2 Part b."
}
},
"outputs": [
{
"data": {
"text/plain": [
""
]
},
"execution_count": 1,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAXwAAAEKCAYAAAARnO4WAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAHY5JREFUeJzt3XmcFfWZ7/HP0xvQNLvYIjCCC24oaKNxQ2k17jMak1ei\nozOSxEEzmpiJOrlx5kaTjCZ37kyiyWhyXaJO4thxTYzRiJomBmOURRQEFRWQTRZZTwO9nef+UdXS\nNN2nT/fpOlt9369Xvc6pql/V73ko+znl79SpMndHRESKX0muAxARkexQwRcRiQkVfBGRmFDBFxGJ\nCRV8EZGYUMEXEYmJSAu+mf2Tmb1lZovM7GEz6x9lfyIi0rXICr6ZjQa+Bkxx94lAKXBJVP2JiEhq\nUQ/plAEDzKwMqATWRNyfiIh0oSyqHbv7ajP7D+BDYCcw091ndmxnZjOAGQADBgyoGTt2bK/6SyaT\nlJQUx1cSxZJLseQByiUfFUsekFku77777kZ3H5lWY3ePZAKGAX8ARgLlwK+By1NtU1NT471VX1/f\n623zTbHkUix5uCuXfFQsebhnlgsw19Osy1F+PJ4JLHP3De7eDDwBnBRhfyIikkKUBf9D4AQzqzQz\nA84AlkTYn4iIpBBZwXf3V4HHgPnAwrCvu6PqT0REUovsS1sAd78ZuDnKPkREJD3F8RW3iIh0SwVf\nRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0QkJlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0Qk\nJlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0QkJiIr+GZ2qJktaDdtM7OvR9WfiIikFtkz\nbd39HWAygJmVAquBJ6PqT0REUov0IebtnAG87+4rstSfpCGZdBpbkuxqbv3kdVdLK43Nu5c1tiRp\nbk3SknRawtfWdu9bWn2PdS3JsE2rs2JlI/VbF+FA0h13SDqAk0yGy8J1ePt58LC9d2jrnjonsy6W\n92qb3Ss2bNxF3cp53W9jHbbd8wULG9he7TtfT4f97d2+i/UddtB+uzVrGnlhy8K9cuwqlq5y6zKW\nvsqhQ8cd269Y3sQbLUu7jaPH8XdYv3v7NI9dmvG372fZmhamEb1sFfxLgIez1FcsJJPOtl3NbGpo\n+mTavKOJLTuaSTS2sH1XC4nGFhoaWzqdb2xO0tSa7PO4SkuM0hKjvMRIJlupWL+GEgv+GEoMwMJ5\nKDGjJPyvv6Qk+ANoa2sW/IG0tbG25Sn67uqzwLv7lOh0mz3nGxqSJGgI++l8f23b+Cfzvmdc3azf\nvb3vOd+hu7S32yuX4E1jUwtvbvpojyy63Gdf5bDX9l3F2vn+uvTeu900KAyDK4ybstCP9eaPoUcd\nmFUAa4Aj3X1dJ+tnADMAqqura+rq6nrVTyKRoKqqKpNQ88aGLQl2lVayeVeSTbuczbv8k9fNjUm2\nNzmJ5raz5b0Z0L8MBpRZ8Fpqu9+HrxUlRnkpVJRAefi+vAQqSm2P1/KSsIgblBqUGJSVBIW41KC0\nZPfyUtvzrKqYjolyyQ/tPxASiQaqqgaGy/lk+R7tP9mu8+V7fYDt1V/q5Xv10+V+vdPlbXbs2MHo\n4b07JrW1tfPcfUo6bbNR8C8ErnH3s7prO2XKFJ87d26v+pk1axbTpk3r1ba50Nya5P0NCZauS7B8\nYwPLPm5gxcc7WL6xgY8bmvZoawb7DurHfkMGsN/gfoyo6sfwygqGDwymYQMrGF5ZwbCB5QytrKCy\nvJSSklTnwtlRaMckFeWSf4olD8gsFzNLu+BnY0jnUmI+nLOzqZU3V21h4eqtLFm7nSVrt/He+sQe\nQyr7De7PuH0qOevIalq3fMRpU45ivyH9GTWkPyMH9aO8VFfQikhmIi34ZjYQ+DRwVZT95Jv123fx\n2rJNzFuxmfkrNvPWmm20hOMvIwf14/BRg5k6YR+OGDWYCdWDOGBEJZUVuw/FrFmbmHb0qFyFLyJF\nKtKC7+4NwIgo+8gHTS1J5q7YxEvvbuSP725gydptAPQvL2HSmKHMOPVApowbxtFjhrJPVb8cRysi\ncZWtq3SKzq7mVl56dwPPLFzLC0vWk2hsoazEqDlgGDeefSgnH7wPR+4/WEMxIpI3VPB7wN15ddkm\nHpmzkpmL15FobGFoZTnnHbUfZx5ezYkHjWBQ//Jchyki0ikV/DR8nGjk0Xmr+NWclSzb2MCg/mWc\nf9Qozjt6FCcdNEJn8SJSEFTwU1i+sYF7Z3/Ao3NX0diS5Phxw7m29mDOO2oUAypKcx2eiEiPqOB3\n4p2PtvPjF5fy7KK1lJWU8JljRnPl1PEcUj0o16GJiPSaCn47qzbv4EfPL+WJ11dRVVHG1acdxPST\nxrHv4P65Dk1EJGMq+MCOphbueHEp989eDgb/MPVAvnLaQQwbWJHr0ERE+kzsC/7Mtz7ilqfeYs3W\nXXz22DFcf9YE9h86INdhiYj0udgW/E0NTdz0xEJ+/9ZHHFo9iEcvPYbjxg3PdVgiIpGJZcGvf3s9\nNz72Jtt2NvPNcw7jyqnjdWmliBS9WBX85tYkt/5uCQ/8eTmHVg/iF18+nsNHDc51WCIiWRGbgr9+\n+y6ueWg+c5Zv5osnj+Ob5xxG/3JdSy8i8RGLgv/6h5u5+pfz2LqzmTsumcyFk0fnOiQRkawr+oL/\n/OJ1XPs/89l3cD+e+MrJHLG/hnBEJJ6KuuDXvfYhNz25kKNGD+G+6cfp1sQiEmtFW/Dvful9bnvm\nbU6bMJK7LjuWgf2KNlURkbQUZRW8908fcNszb3PB0aP40Rcm65JLERGKsODfN3sZ//a7JZx/1Chu\n/8JkylTsRUQAKKpq+MjclXzv6cWcO3E/br9ExV5EpL1IK6KZDTWzx8zsbTNbYmYnRtXXwg0t3PTE\nQqYesg93XHKMhnFERDqIekjnDuD37v45M6sAKqPoZNHqrdy5oJFDqgdz12XHUlGmYi8i0lFkBd/M\nhgCnAtMB3L0JaOrrfjY3NPGlB+ZQWW7cP/04PVNWRKQL5u7R7NhsMnA3sBiYBMwDrnP3hg7tZgAz\nAKqrq2vq6up61I+7M3NFC+MHNDKhuqpPYs+1RCJBVVXh51IseYByyUfFkgdklkttbe08d5+SVmN3\nj2QCpgAtwKfC+TuA76Xapqamxnurvr6+19vmm2LJpVjycFcu+ahY8nDPLBdgrqdZl6Mc7F4FrHL3\nV8P5x4BjI+xPRERSiKzgu/tHwEozOzRcdAbB8I6IiORA1FfpfBV4KLxC5wPgixH3JyIiXYi04Lv7\nAoKxfBERyTFdsC4iEhMq+CIiMaGCLyISEyr4IiIxoYIvIhITKvgiIjGhgi8iEhMq+CIiMaGCLyIS\nEyr4IiIxoYIvIhITKvgiIjGhgi8iEhMq+CIiMaGCLyISEyr4IiIxoYIvIhITKvgiIjER6SMOzWw5\nsB1oBVrcXY87FBHJkagfYg5Q6+4bI+3BHbw10i5ERApd4Q/p7NoK99QyevUzuY5ERCSvmbtHt3Oz\nZcBWgiGd/+fud3fSZgYwA6C6urqmrq6ux/1Mfv1bVOxcx5wT7sZLsvE/LdFKJBJUVVXlOoyMFUse\noFzyUbHkAZnlUltbOy/t4XJ3j2wCRoev+wJvAKemal9TU+O98vaz7jcPdl9Q17vt80x9fX2uQ+gT\nxZKHu3LJR8WSh3tmuQBzPc2aHOmQjruvDl/XA08Cx0fS0SFn0VA5Fl6+IxjPFxGRvURW8M1soJkN\nansPnAUsiqSzkhJWjv0MrH8L3nshki5ERApdlGf41cBsM3sDeA34nbv/PqrO1lWfCoP2h9m3R9WF\niEhBi+wbTnf/AJgU1f736q+kHE66Fp67CZa/DONOzlbXIiIFIWXBN7Nj09hHs7sv7KN4MlPzxWAc\nv/5WmP47MMt1RCIieaO7M/w/AnOAVJVzPDCurwLKSEUlTL0env1n+GAWHFSb64hERPJGdwV/jruf\nnqqBmf2hD+PJXM10ePnHwVn+gdN0li8iEkr5pW13xT7dNllV1g9OvQFWzYF3n8t1NCIieSOtq3TM\n7MV0luWNYy6H4QfB89+G1uZcRyMikhdSFnwz629mw4F9zGyYmQ0Pp3HA6GwE2Cul5XDWv8HGd2Du\n/bmORkQkL3R3hn8VMA84LHxtm34D/Fe0oWXo0HNh/Kkw6zbYuTnX0YiI5Fx3BX+Nu48HbnT3A919\nfDhNcvf8LvhmcPZtsHMLzPo/uY5GRCTnuiv43wpfp0ccRzT2OwpqroDX7oa1b+Y6GhGRnOqu4H9s\nZjOB8Wb2VMcpGwFm7IyboXI4/PY6SOohKSISX91dh38+cCzwC+A/ow8nApXD4ezvwxNXwpx74VNX\n5ToiEZGcSFnw3b0J+IuZneTuG7IUU9876nPwxsPw4nfhsPNhyJhcRyQiknXdXZZ5C0CqYt/WJq+Z\nwQU/DO6V/+uvQDKZ64hERLKuuyGdK81sW4r1BlwC3NJnEUVl2Dg457ZgLP/Vn8KJ1+Q6IhGRrOru\nS9t7gEEppqqwTWE49go49Dx44TuwbnGuoxERyaruxvC/k61AssIM/vrH8NMT4bEvwT+8CBUDcx2V\niEhWRPpM27xUNRIuvhs2vB0M7+gZuCISE/Er+AAHnQ6n/wssfBReK5wRKRGRTERe8M2s1MxeN7On\no+6rR065HiacC899C1a8kutoREQi190jDn8CdDnm4e5fS6OP64AlwOCehRaxkhL4zM/gntOh7m/h\nyhdgxEG5jkpEJDLdneHPZc+7ZHacUjKzMQS/1r03szAjMmAoXPZo8GXuLz8LDRtzHZGISGTMe/Cl\npZlVuvuOHrR/DPg+wSWcN7j7BZ20mQHMAKiurq6pq6tLO572EokEVVVVvdp28NZ3mPTGv9IwcBwL\nJn+PZGn/Xu2nr2SSSz4pljxAueSjYskDMsultrZ2nrtPSauxu3c7AScCi4EPw/lJwF3dbHNBWxtg\nGvB0d/3U1NR4b9XX1/d6W3d3X/yU+y1D3R+4wL2xIbN9ZSjjXPJEseThrlzyUbHk4Z5ZLsBcT6OO\nu3vaX9reDpwNfBx+SLwBnNrNNicDf2Nmy4E64HQz+2Wa/WXf4X8NF/0Ulv0pGNNv3pXriERE+lTa\nV+m4+8oOi1Lea9jdv+XuY9x9HMHtF/7g7pf3PMQsmnQJXPhf8EE9/OoyaEp79EpEJO+lW/BXmtlJ\ngJtZuZndQHDlTfE55nL4m5/Aey/CLy6CHZtyHZGISJ9It+BfDVxD8ODy1cDkcD4t7j7LO/nCNm8d\n+/fw+Qdhzetw/7mwdXWuIxIRyVi6Bd/c/TJ3r3b3fd39cnf/ONLIcu2IC+HyJ2DbGrinFla+luuI\nREQykm7Bf9nMZprZl81saKQR5ZPxU+FLz0F5Jdx/Hsx7INcRiYj0WloF390nAP8KHAnMN7OnzSy/\nv4DtK9VHwIx6GH9qcLO131wLTQ25jkpEpMd6cpXOa+7+DeB4YBPwYGRR5ZsBw4Jf5E69Hl7/Jfxs\nKqzu9ofGIiJ5Ja2Cb2aDzewKM3sW+DOwlqDwx0dJKZzxbbjit9CyC+47C2b9AFoacx2ZiEha0j3D\nf4PgypzvuvsEd/+mu8fzFHf8VPjKy3DERTDr+/CzU2D57FxHJSLSrXQL/oHu/k8EhV8GDIPP3Qd/\n+2hwtv/A+fDEVbCl42/TRETyR7oF/wQzWwy8DWBmk8zsrujCKhATzoJ/fBVO+Qa89ST8pAZm/m/Y\nuTnXkYmI7CXKe+nEQ0UlnHkzfHUeTLwY/vwTuGMS/OFW3W5ZRPJKZPfSiZ2hY4MHqlw9G8ZNhZf+\nHX40EZ65ETYvz3V0IiKpn3jVzh730mH3U6yko/0mwiUPwYZ34OUfw9yfB8/NPfhMmPJFOORsKE33\nn11EpO9kci+df4wqqKIw8lC46E647k049UZYtyi47fLtE+H5b8PaN6AHD58REclUWqea7r4RuKz9\nMjP7OsHYvqQyZDSc/i9w2jdh6XPB7RleuRNevgNGHAxHXgyHnQ/7HR08Z1dEJCKZjC18AxX89JWW\nBYX9sPODWy4veQoWPQ4v/d9gvL+qOhj2OeTTlDVryEdE+l4mlcX6LIq4qRwONdODKbE+uPf+0pnw\n9tOw4CFOAVh6BPzViXDAScHrkNG5jVlECl4mBV8D0H2hal+YfGkwtbbAqjksq/8F40vXwpu/grn3\nBe0GjYJRk4Khn1FHB++HjAXT566IpCdlwTez7XRe2A0YEElEcVZaBgecyIpxjYyfNi34AFi3CD58\nJXgYy9o3g/8T8GTQvt/g4HuAfQ4JphGHwD4TYNgBUDEwp6mISP5JWfDdfVC2ApFOlJbB/pODqU3T\nDli/GNYugPVvw8Z3g3v5vPmrPbcdMDz4bcCQsTBkTPg6OviuYOC+UDUy+MDQ/yGIxEZk3w6aWX/g\nJaBf2M9j7n5zVP3FRkUljJkSTO01NcDH78HGpbBlBWxdFdzb5+P34YNZ0JTYe1+l/WDgSBi4TzC0\nVDkC+g+B/kPD186mwVA+EErL9WEhUmCivBykETjd3RPhj7Vmm9mz7v6XCPuMr4qBwbj+qEl7r3OH\nXVuCD4HE+uCWDw3roWEDJDaEr+tg/RLYtQ0at3bfn5UGfZZXQvmATt8funELNPw2+GApLYey8LW0\nH5RWQFlF8NrZ+pKycCoJXq00uEV1SRlYuOyT+bZ1peH79uv0oSTSJrKC7+4OtJ1WloeTvujNBbPg\nDp8DhqXXPtkKjdth19Zw2tLu/TZo3hFMTTuguQGad+75fscmaG5geGIzbJ0PrU27p6yz3R8SZsEr\n1m7eOsx3XB/Mn9DYBAv6p9U2mGfv9W0Xtn3yIZTpPJ3Md7+PozdtglUjIoqhj/bXft1efQQOW7cO\nNj2csk13++i8TTfr+6yf3fMHrtsC06Z1sk3fivSCbzMrBeYBBwN3uvurnbSZAcwAqK6uZtasWb3q\nK5FI9HrbfJOfuQwKp1Apwdf2Kb66TyQSVFVV7V7gjnkLJcnmT15Lki2dLGvGPBlOrUDw2jbf9bo9\n3+9e14q5E5xv+CfvO1u25/rwy3GStJQ3U15WCtBu+e425snwdCaJha/t27bfZk8eru98+e71nS9v\nb/c+Om/Ttt6SrWxb136Ir29iSLf/rv4NOm/bFWdQMsnOrUv2WLbnPvbeprP9pJrfex/db9OZrv9t\nA0NLB2Xnb97dI5+AoUA9MDFVu5qaGu+t+vr6Xm+bb4oll2LJw1255KNiycM9s1yAuZ5mLc7Kb/nd\nfUtY8M/JRn8iIrK3yAq+mY00s6Hh+wHApwkfoCIiItkX5Rj+KODBcBy/BHjE3Z+OsD8REUkhyqt0\n3gSOiWr/IiLSM7ofr4hITKjgi4jEhAq+iEhMqOCLiMSECr6ISEyo4IuIxIQKvohITKjgi4jEhAq+\niEhMqOCLiMSECr6ISEyo4IuIxIQKvohITKjgi4jEhAq+iEhMqOCLiMSECr6ISEyo4IuIxESUDzEf\na2b1ZrbYzN4ys+ui6ktERLoX5UPMW4Dr3X2+mQ0C5pnZ8+6+OMI+RUSkC5Gd4bv7WnefH77fDiwB\nRkfVn4iIpGbuHn0nZuOAl4CJ7r6tw7oZwAyA6urqmrq6ul71kUgkqKqqyizQPFEsuRRLHqBc8lGx\n5AGZ5VJbWzvP3aek1djdI52AKmAecHF3bWtqary36uvre71tvimWXIolD3flko+KJQ/3zHIB5nqa\n9TjSq3TMrBx4HHjI3Z+Isi8REUktyqt0DLgPWOLuP4yqHxERSU+UZ/gnA38HnG5mC8LpvAj7ExGR\nFCK7LNPdZwMW1f5FRKRn9EtbEZGYUMEXEYkJFXwRkZhQwRcRiQkVfBGRmFDBFxGJCRV8EZGYUMEX\nEYkJFXwRkZhQwRcRiQkVfBGRmFDBFxGJCRV8EZGYUMEXEYkJFXwRkZhQwRcRiQkVfBGRmFDBFxGJ\niSgfYv5zM1tvZoui6kNERNIX5Rn+A8A5Ee5fRER6ILKC7+4vAZui2r+IiPSMxvBFRGLC3D26nZuN\nA55294kp2swAZgBUV1fX1NXV9aqvRCJBVVVVr7bNN8WSS7HkAcolHxVLHpBZLrW1tfPcfUpajd09\nsgkYByxKt31NTY33Vn19fa+3zTfFkkux5OGuXPJRseThnlkuwFxPs8ZqSEdEJCaivCzzYeAV4FAz\nW2VmX46qLxER6V5ZVDt290uj2reIiPSchnRERGJCBV9EJCZU8EVEYkIFX0QkJlTwRURiQgVfRCQm\nVPBFRGJCBV9EJCZU8EVEYkIFX0QkJlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFX0QkJlTw\nRURiQgVfRCQmVPBFRGIi0oJvZueY2Ttm9p6Z/a8o+xIRkdQiK/hmVgrcCZwLHAFcamZHRNWfiIik\nFuUZ/vHAe+7+gbs3AXXAhRH2JyIiKZRFuO/RwMp286uAT3VsZGYzgBnhbMLM3ullf/sAG3u5bb4p\nllyKJQ9QLvmoWPKAzHI5IN2GURb8tLj73cDdme7HzOa6+5Q+CCnniiWXYskDlEs+KpY8IHu5RDmk\nsxoY225+TLhMRERyIMqCPwc4xMzGm1kFcAnwVIT9iYhICpEN6bh7i5ldCzwHlAI/d/e3ouqPPhgW\nyiPFkkux5AHKJR8VSx6QpVzM3bPRj4iI5Jh+aSsiEhMq+CIiMVHwBb+Ybt9gZsvNbKGZLTCzubmO\npyfM7Odmtt7MFrVbNtzMnjezpeHrsFzGmK4ucrnFzFaHx2aBmZ2XyxjTYWZjzazezBab2Vtmdl24\nvOCOS4pcCvG49Dez18zsjTCX74TLIz8uBT2GH96+4V3g0wQ/7JoDXOrui3MaWC+Z2XJgirsX3I9J\nzOxUIAH8t7tPDJf9O7DJ3X8QfhgPc/dv5jLOdHSRyy1Awt3/I5ex9YSZjQJGuft8MxsEzAMuAqZT\nYMclRS6fp/COiwED3T1hZuXAbOA64GIiPi6Ffoav2zfkCXd/CdjUYfGFwIPh+wcJ/kDzXhe5FBx3\nX+vu88P324ElBL+AL7jjkiKXguOBRDhbHk5OFo5LoRf8zm7fUJD/EYQceMHM5oW3nCh01e6+Nnz/\nEVCdy2D6wFfN7M1wyCfvh0HaM7NxwDHAqxT4cemQCxTgcTGzUjNbAKwHnnf3rByXQi/4xeYUd59M\ncIfRa8KhhaLgwdhh4Y4fwk+BA4HJwFrgP3MbTvrMrAp4HPi6u29rv67QjksnuRTkcXH31vBvfQxw\nvJlN7LA+kuNS6AW/qG7f4O6rw9f1wJMEQ1aFbF049to2Brs+x/H0mruvC/9Ik8A9FMixCceIHwce\ncvcnwsUFeVw6y6VQj0sbd98C1APnkIXjUugFv2hu32BmA8MvozCzgcBZwKLUW+W9p4ArwvdXAL/J\nYSwZaftDDH2GAjg24ZeD9wFL3P2H7VYV3HHpKpcCPS4jzWxo+H4AwUUnb5OF41LQV+kAhJdh3c7u\n2zfcmuOQesXMDiQ4q4fglhf/U0i5mNnDwDSC27yuA24Gfg08AvwVsAL4vLvn/ZehXeQyjWDYwIHl\nwFXtxlvzkpmdAvwJWAgkw8U3EYx9F9RxSZHLpRTecTma4EvZUoKT7kfc/btmNoKIj0vBF3wREUlP\noQ/piIhImlTwRURiQgVfRCQmVPBFRGJCBV9EJCZU8EVEYkIFXwqWmY1od1vcjzrcJvfPEfQ33cw2\nmNm9Pdzuu2Z2ZjdtvmDBLb6fzixKka7pOnwpCtm4fbGZTSe4ffW1Ee1/GnCDu18Qxf5FdIYvRcnM\nEuHrNDP7o5n9xsw+MLMfmNll4QMoFprZQWG7kWb2uJnNCaeT0+hjupn9OnxYxXIzu9bMvmFmr5vZ\nX8xseNjuATP7XPh+uZl9x8zmh/0fFuW/g0h7KvgSB5OAq4HDgb8DJrj78cC9wFfDNncAP3L344DP\nhuvSMZHgwRXHAbcCO9z9GOAV4O+72Gajux9LcKfHG3qejkjvlOU6AJEsmNN2fxUzex+YGS5fCNSG\n788Ejgju0QXAYDOravegiq7Uhw/k2G5mW4Hfttv30V1s03bXynkEHxYiWaGCL3HQ2O59st18kt1/\nAyXACe6+K4J9d7VNa4o2In1OQzoigZnsHt7BzCbnMBaRSKjgiwS+BkwJH5W3mGDMX6So6LJMkTTp\nskwpdDrDF0nfTuDcnv7wKh1m9gXgLmBzX+9bpI3O8EVEYkJn+CIiMaGCLyISEyr4IiIxoYIvIhIT\n/x+WUXDe/Z+mMwAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"%matplotlib inline\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy.integrate import odeint\n",
"from ipywidgets import interact\n",
"\n",
"# simulation time grid\n",
"t = np.linspace(0,30,1000)\n",
"\n",
"# initial condition\n",
"IC = [6,5]\n",
"\n",
"# inlet flowrate\n",
"F0 = 3\n",
"\n",
"# parameters for tank 1 \n",
"A1 = 5\n",
"beta1 = 0.75\n",
"\n",
"# parameters for tank 2\n",
"A2 = 5\n",
"beta2 = 1.0\n",
"\n",
"def hderiv(H,t):\n",
" h1,h2 = H\n",
" h1dot = (F0 - beta1*(h1-h2))/A1\n",
" h2dot = (beta1*(h1-h2) - beta2*h2)/A2\n",
" return [h1dot,h2dot]\n",
"\n",
"sol = odeint(hderiv,IC,t)\n",
"plt.plot(t,sol)\n",
"plt.ylim(0,8)\n",
"plt.grid()\n",
"plt.xlabel('Time [min]')\n",
"plt.ylabel('Level [ft]')"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.3 Further Calculations](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.3-Further-Calculations)",
"section": "3.7.2.3 Further Calculations"
}
},
"source": [
"### 3.7.2.3 Further Calculations\n",
"\n",
"$$\\frac{d}{dt}\\left[\\begin{array}{c} h_1 \\\\ h_2 \\end{array}\\right] = \n",
"\\left[\\begin{array}{cc}-\\frac{\\beta_1}{A_1} & \\frac{\\beta_1}{A_1} \\\\\n",
"\\frac{\\beta_1}{A_2} & -\\frac{\\beta_1}{A_2} - \\frac{\\beta_2}{A_2} \\end{array}\\right]\n",
"\\left[\\begin{array}{c}h_1 \\\\ h_2\\end{array}\\right]\n",
"+\n",
"\\left[\\begin{array}{c}\\frac{1}{A_1} \\\\ 0\\end{array}\\right]F_0$$"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"nbpages": {
"level": 3,
"link": "[3.7.2.3 Further Calculations](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.3-Further-Calculations)",
"section": "3.7.2.3 Further Calculations"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.2.3 Further Calculations](https://jckantor.github.io/CBE30338/03.07-Interacting-Tanks.html#3.7.2.3-Further-Calculations)",
"section": "3.7.2.3 Further Calculations"
}
},
"source": [
"\n",
"< [3.6 Second Order Models](https://jckantor.github.io/CBE30338/03.06-Second-Order-Models.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [3.8 Manometer Models and Dynamics](https://jckantor.github.io/CBE30338/03.08-Manometer-Models-and-Dynamics.html) > 
 "
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"anaconda-cloud": {},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

