{
"cells": [
{
"cell_type": "markdown",
"id": "d95ea367",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE30338](https://jckantor.github.io/CBE30338);\n",
"content is available [on Github](https://github.com/jckantor/CBE30338.git).*\n"
]
},
{
"cell_type": "markdown",
"id": "3e18d162",
"metadata": {},
"source": [
"\n",
"< [7.3 Simulation in Pyomo](https://jckantor.github.io/CBE30338/07.03-Simulation-in-Pyomo.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [7.5 First Order System in Pyomo](https://jckantor.github.io/CBE30338/07.05-First-Order-System-in-Pyomo.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.4 Simulation of an Exothermic CSTR](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4-Simulation-of-an-Exothermic-CSTR)",
"section": "7.4 Simulation of an Exothermic CSTR"
}
},
"source": [
"# 7.4 Simulation of an Exothermic CSTR"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.1 Description](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.1-Description)",
"section": "7.4.1 Description"
}
},
"source": [
"## 7.4.1 Description\n",
"\n",
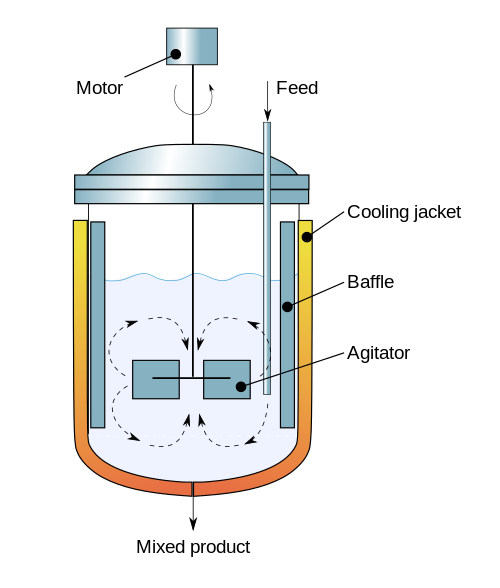
"This example is intended as an introduction to the nonlinear dynamics of an exothermic continuous stirred-tank reactor. The example has been studied by countless researchers and students since the pioneering work of Amundson and Aris in the 1950's. The particular formulation and parameter values described below are taken from example 2.5 from Seborg, Edgar, Mellichamp and Doyle (SEMD).\n",
"\n",
"\n",
"\n",
"(Diagram By [Daniele Pugliesi](https://commons.wikimedia.org/wiki/User:Daniele_Pugliesi) own work, [Creative Commons Attribution-Share Alike 3.0 (CC BY-SA 3.0)](http://creativecommons.org/licenses/by-sa/3.0), [Link](https://commons.wikimedia.org/w/index.php?curid=6915706))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.2 Imports](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.2-Imports)",
"section": "7.4.2 Imports"
}
},
"source": [
"## 7.4.2 Imports\n",
"\n",
"The following code cell imports the libraries and functions needed within this notebook. The code installs Pyomo if necessary. This code is required to run this notebook in Google Colab."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.2 Imports](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.2-Imports)",
"section": "7.4.2 Imports"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"# if missing, install pyomo and ipopt\n",
"import shutil\n",
"\n",
"if not shutil.which(\"pyomo\"):\n",
" !pip install -q pyomo\n",
" assert(shutil.which(\"pyomo\"))\n",
" \n",
"# import pyomo modules\n",
"from pyomo.environ import *\n",
"from pyomo.dae import *\n",
"from pyomo.dae.simulator import Simulator"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.3 Arrehenius Law Kinetics for a First-Order Reaction](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.3-Arrehenius-Law-Kinetics-for-a-First-Order-Reaction)",
"section": "7.4.3 Arrehenius Law Kinetics for a First-Order Reaction"
}
},
"source": [
"## 7.4.3 Arrehenius Law Kinetics for a First-Order Reaction\n",
"\n",
"We assume the kinetics are dominated by a single first order reaction\n",
"\n",
"$$A \\xrightarrow{kc_A}{} \\text{Products}$$\n",
"\n",
"The reaction rate per unit volume is modeled as the product $kc_A$ where $c_A$ is the concentration of $A$. The rate constant $k(T)$ is a increases with temperature following the Arrehenius law\n",
"\n",
"$$k(t) = k_0 e^{-\\frac{E_a}{RT}}$$\n",
"\n",
"$E_a$ is the activation energy, $R$ is the gas constant, $T$ is absolute temperature, and $k_0$ is the pre-exponential factor. \n",
"\n",
"We can see the strong temperature dependence by plotting $k(T)$ versus temperature over typical operating conditions."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.3 Arrehenius Law Kinetics for a First-Order Reaction](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.3-Arrehenius-Law-Kinetics-for-a-First-Order-Reaction)",
"section": "7.4.3 Arrehenius Law Kinetics for a First-Order Reaction"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd5xU1f3/8deHpfcqCCi9SJG2Ara4qAgW7Ik9FhRLjLH8jDHFksQY9WuBaDTEWEARFSyoqChx7SKg9N57h4Wlbvn8/rh3dbMuu7PLzk7Z9/PxmAdzy9z5nLnLfObcc+455u6IiIgcTKVYByAiIvFNiUJERIqkRCEiIkVSohARkSIpUYiISJGUKEREpEhKFJI0zKy1mbmZVT7I9t+b2bPlHZdIolOikDJnZulmtt3MqsU6lvzc/W/ufm1ZHtPM0sws18wyzWyXmS00s6tL8Pp0MzukmMxskJl9Fr7/ZjP71MzOPpRjFvN+RSbkUhwvzczWlMWxJDqUKKRMmVlr4ETAgSK/rMwspcBymXzxxMA6d68N1AVuA/5tZp3K443N7ELgdWAU0BJoCtwDDCmP95eKQYlCytovgW+AF4Ar828wsxfM7Gkzm2hmu4EBZrbCzO4ys1nAbjOrbGb9zewrM9thZjPNLC3fMdLN7C9m9mX4C3qSmTUuEMNlZrbKzLaY2R/yvfY+M3spfP6TX7FhLKeGz/ua2TQz22lmG83sseIK7oGJwDbg6PA4Dczs3fCX/vbwectw2wMESfXJsEbyZLi+s5l9ZGbbwhrKLwp7PzMz4DHgL+7+rLtnuHuuu3/q7teF+1Qysz+a2Uoz22Rmo8ysXrgtr2Zw5UE+r4N9Bp+F/+4I4z7WzNqZ2X/NbGt4nJfNrH6Bz/b/mdksM8sws1fNrLqZ1QLeB5qHx8o0s+bFfdZSztxdDz3K7AEsAW4C+gBZQNN8214AMoDjCX6kVAdWADOAI4AaQAtgK3BGuM/AcLlJeIx0YCnQMdw/Hfh7uK01QU3m3+G2HsB+4Khw+33AS+HzNGBNgdhXAKeGz78Grgif1wb6H6S8PxwnjPdsIBfoFa5rBFwA1ATqEPz6fyvf69OBa/Mt1wJWA1cDlYFewBagSyHv3Tksb5sizsc14TlpG5bjDWB0hJ9XoZ9BvtdVzvc+7cNzVQ1oQpBMnijw2X4LNAcaAvOBGw52LvSIr4dqFFJmzOwEoBXwmrtPJ/hCv7TAbm+7+5ce/PLdF64b4e6r3X0vcDkw0d0nhvt8BEwjSBx5nnf3ReH+rwE9C7zH/e6+191nAjMJvgBLKgtob2aN3T3T3b8pYt/mZrYD2Au8Cdzu7t8DuPtWdx/v7nvcfRfwAHBSEcc6C1jh7s+7e3Z4nPHAzwvZt1H47/oijncZ8Ji7L3P3TOBu4OICl/kO9nlF/Bm4+xJ3/8jd97v7ZoKaTsFyjnD3de6+DXiHn543iVNKFFKWrgQmufuWcHkMBS4/EfxaLij/ulbAz8PLTjvCL+ATgMPz7bMh3/M9BL92KcH2SAwlqLUsMLOpZnZWEfuuc/f6BG0UI4CT8zaYWU0z+1d46WcnwS/t+gXbZ/JpBfQrUP7LgGaF7Ls1/PfwQrblaQ6szLe8kqCm0jTfuoN9XhF/BmbW1MzGmtnasJwvAQUvCZbFeZEYSNTGQ4kzZlYD+AWQYmZ5XwjVCL4Ue4S/ViG4ZFFQ/nWrCS6NXBe9aAHYTXA5CPihYb3JDwG5LwYuMbNKwPnAODNr5O67D3ZAd99vZncBC83sXHd/C7gD6AT0c/cNZtYT+B6wvJcVOMxq4FN3HxhBGRaG+18A/N9B9llHkHzyHAlkAxsJGr8P6mCfQSExA/wtXN/d3beZ2bnAkxGUgYMcT+KIahRSVs4FcoAuBJcUegJHAZ8TNHBH6iVgiAVdPlPCBs+0vAbgMrQIqG5mZ5pZFeCPBIkNADO73MyauHsusCNcnVvcQd39APAoQc8jCNol9hI0/DYE7i3wko0E7Qd53gU6mtkVZlYlfBxjZkcV8l4O3A78ycyuNrO6YeP1CWY2MtztFeA2M2tjZrUJvtBfdffs4spSxGewOfw3f9x1gEwgw8xaAHcWd/wCn0GjvEZ2iT9KFFJWriRoO1jl7hvyHgS/Ki+zCLu+uvtq4Bzg9wRfSKsJvnTK9G/V3TMIGt2fBdYS1DDy94IaDMw1s0xgOHBx2CYSieeAI81sCPAEQUPxFoLeYB8U2Hc4cGHYI2pE2I5xGnAxQW1gA/AQ+ZJYgXKMAy4iaLReR/Cl+1fg7XyxjCa45LUc2Af8OsJyFPoZuPsegraWL8PLY/2B+4HeBJ0V3iNoNI+Iuy8gSGjLwuOp11OcseBHiYiISOFUoxARkSIpUYiISJGUKEREpEhKFCIiUqSkvI+icePG3rp161iHEZHdu3dTq1atWIcRFSpb4krm8qlshZs+ffoWd29S2LakTBStW7dm2rRpsQ4jIunp6aSlpcU6jKhQ2RJXMpdPZSucma082DZdehIRkSIpUYiISJGSKlGY2RAzG5mRkRHrUEREkkZSJQp3f8fdh9WrpyFjRETKSlIlChERKXtKFCIiUiQlChERKZIShYhIEpi+cjvjFx2IyrGT8oY7EZGKwN35bPEW/vnJEqYs30atKrBp5z4Oq1u9TN9HiUJEJMHk5DofzNnA058uYc7anTSrW50/nnkULfevLPMkAUoUIiIJ40B2Lm/NWMsz6UtZtmU3bRrX4qELunNurxZUq5xCevqqqLxvUiWKcOrJIe3bt491KCIiZWZfVg5jv13FyM+WsS5jH10Or8tTl/ZmcLdmpFSyqL9/UiUKd38HeCc1NfW6WMciInKodu3L4qVvVvGfL5axJfMAqa0a8MD53Unr2ASz6CeIPEmVKEREksH23Qd4/svlvPDVCnbuy+ZnHZvwq7R29GvbKCbxKFGIiMSJTbv28Z/PlzP6m5XsOZDDoK5N+dWA9hzdsn5M41KiEBGJsXU79jLys2W88u0qsnJyGdKjOTeltadTszqxDg1QohARiZlVW/fw9KdLGDd9De5wfu8W3JjWnjaN42sGPiUKEZFytmxzJk99spS3ZqwlxYyLjjmCG05qR8sGNWMdWqGUKEREysnijbt48pMlvDNzHVVSKvHLY1tx/c/a0axe2d8kV5aUKEREomzBhp38479LmDh7PTWqpHDdiW259sS2NKlTLdahRUSJQkQkSuat28mIyYv5YO4GalerzE1p7Rh6Qlsa1qoa69BKRIlCRKSMzVmbwYjJi5k0byN1qlXmllM6MPT4NtSrWSXWoZWKEoWISBmZszaDJz5ezMfzN1KnemV+c0oHrkngBJFHiUJE5BDlTxB1q1fm9oEduer41tStntgJIo8ShYhIKc1Zm8HwyYv5aF6QIO4Y2JErkyhB5In7RGFmbYE/APXc/cJYxyMiMnddUIPISxDJVoMoKCaJwsyeA84CNrl7t3zrBwPDgRTgWXf/u7svA4aa2bhYxCoikmfBhp088VHQi6lO9crcdmqQIOrVSM4EkSdWNYoXgCeBUXkrzCwFeAoYCKwBpprZBHefF5MIRURCizfu4onJi3lv1nrqVAsbqU9ok/QJIo+5e2ze2Kw18G5ejcLMjgXuc/dB4fLdAO7+YLg8rqhLT2Y2DBgG0LRp0z5jx46NavxlJTMzk9q1a8c6jKhQ2RJXMpevJGVbn5nL20sPMGV9DtVSYGDrKgxqVYXaVctvLoiSOJTzNmDAgOnunlrYtnhqo2gBrM63vAboZ2aNgAeAXmZ2d17iKMjdRwIjAVJTUz0tLS3K4ZaN9PR0EiXWklLZElcyly+Ssq3cupvhkxfz1vdrqV4lhRvS2nHdifF/o1y0zls8JYpCuftW4IZI9tVUqCJyKNbu2MuT/13M69PWkFLJGHpCG64/qR2NayfGUBvREk+JYi1wRL7lluG6iGkqVBEpjY079/HUJ0sY+21wUePy/q24Ka0dh9WN78H6yks8JYqpQAcza0OQIC4GLo1tSCKSzLbtPsDT6UsY9fVKcnKdn6cewa9Pbk/z+jViHVpciVX32FeANKCxma0B7nX3/5jZzcCHBN1jn3P3uSU8ri49iUixdu7L4tnPlvGfL5azNyuHc3u14NZTOnJko/icDyLWYpIo3P2Sg6yfCEw8hOPq0pOIHNSeA9m8u+wAv/n0EzL2ZnFG92bcPrAj7Q+LjylH41U8XXoSEYmK/dk5vDJlFU9+spQtmVkM6NSEO07rRLcW9WIdWkJIqkShS08ikl92Ti5vfr+WJz5ezNode+nXpiHXdzWuO69vrENLKJViHUBZcvd33H1YvXr6lSBSkbk7E2evZ9ATn3HnuFk0ql2V0UP7MnZYfzo0SIl1eAknqWoUIlKxuTufL97CIx8uZPbaDNofVptnLu/NoK7NMIvPu6kTgRKFiCSF71dt5+EPFvL1sq20qF+D//t5D87r1YKUSkoQhyqpEoXaKEQqniWbdvHIhwv5cO5GGtWqyn1DunBJvyOpVlmXmMpKUiUKdY8VqTjW7djLEx8vYtz0NdSsGgz5PfTENtSullRfa3FBn6iIJJQdew7wz/SlvPDVCnC4+vg23JTWjkYVfDymaFKiEJGEsPdADs9/tZyn05eSuT+b83u15LaBHWjZQHdTR1tSJQq1UYgkn+ycXMZNX8PjHy9i4879nNL5MO4c3InOzerGOrQKI6kShdooRJKHu/PRvI089MEClm7eTa8j6zPi4l70a9so1qFVOEmVKEQkOUxfuZ0HJ85n2srttG1Si2cu78Ogrk11L0SMKFGISNxYtjmThz9YyAdzN9CkTjUeOK8bF6UeQeWUpBpEIuEoUYhIzG3etZ/hkxfxyrerqV65ErcP7Mi1J7ahZlV9RcUDnQURiZm9B3J49vNlPPPpUvZn53JZvyO55ZQOFX7q0XiTVIlCvZ5EEkNOrjN++hoe/WghG3fuZ3DXZvx2cCfaNqkd69CkEEmVKNTrSSS+uTufLtrM399fwIINu+h1ZH2eurQ3qa0bxjo0KUJSJQoRiV/z1+/kbxPn8/niLbRqVJN/Xtab07tpVNdEoEQhIlG1cec+Hpu0iNemr6ZejSrcc1YXLu/fiqqV1ZMpURSZKMzs9giOsdvd/1VG8YhIkthzIJuRny3jX58uIzs3l2tPaMPNAzpQr2aVWIcmJVRcjeJO4GmgqLrhDYAShYgAYUP1d2t4dFLQUH1m98O5a3BnjmykMZkSVXGJYrS7/7moHcysVhnGc0jU60kktr5eupW/vDuPeet30vMINVQniyIThbv/trgDRLJPeVGvJ5HYWL5lNw9OnM+keRtpUb8Gwy/uydk9mquhOklE1JhtZtWAC4DW+V9TXG1DRJJbxp4sRvx3MaO+XkHVlErcOagTQ09oQ/Uqml0umUTa6+ltIAOYDuyPXjgikgiyc3J55dtVPPbRInbszeKi1CO4/bSOHFaneqxDkyiINFG0dPfBUY1ERBLCZ4s285d357F4Uyb92zbkT2d1oWvzerEOS6Io0kTxlZl1d/fZUY1GROLW0s2Z/O29+UxesIlWjWryryv6cFoXDf1dEUSaKE4ArjKz5QSXngxwdz86apGJSFzI2JvFiMmLefGrFVSvksLdp3fmquNbU62y2iEqikgTxelRjUJE4k5OrjN26ioenbSI7XsOcPExR3D7wE40qaORXSua4u7MruvuO4Fd5RSPiMSBBdtyeOgfXzB//U76tmnIvUPUDlGRFVejGAOcRdDbyfnfO7QdaBuluEQkBtZs38ODExfw3ux9tKhvPHVpb87oroH7Krribrg7K/y3TfmEc2h0Z7ZI6ew9kMMzny7lmU+XYgbnta/C3355EjWqqh1CSjB6rJkdzU9vuHsjCjGVmu7MFikZd+f9ORt44L35rN2xl7OOPpzfn3EUi2ZMUZKQH0R6Z/ZzwNHAXCA3XO1AXCUKEYncwg27uG/CXL5etpXOzerw6rD+9GvbCIBFMY5N4kukNYr+7t4lqpGISLnI2JPF4x8vYvQ3K6lTvTJ/ObcblxxzBJVTND+EFC7SRPG1mXVx93lRjUZEoiY313l9+moe+mAhO/Yc4LJ+rbh9YEca1Koa69AkzkWaKEYRJIsN6IY7kYQzc/UO7pkwl5mrd5DaqgH3n9NX3V0lYpEmiv8AVwCz+bGNQkTi3LbdB3jkwwWMnbqaxrWr8fhFPTi3Zwt1d5USiTRRbHb3CVGNRETKTE6uM2bKSv5v0iJ278/m2hPacMspHahTXdOQSslFmii+N7MxwDvkG2Y83rrHighMX7mde96ew9x1OzmuXSPuP7srHZrWiXVYksAiTRQ1CBLEafnWqXusSBzZmrmfhz5YwGvT1tCsbnWevLQXZ3Y/XJeZ5JAVN9bTJcAkd7+6nOIRkRLKyXXGfLuKRz5YwJ4DOVx/UltuObkDtapFfD+tSJGK+0s6EnjdzKoAk4H3gW/d3aMemYgUa8bqHfzprTnMXpvBce0a8edzutL+MF1mkrJV3FhPDwEPmVkd4FTgGuAZM5sPfAB86O4box+miOS3Y88BHv5wIa98u4omtasx4pJeDDlal5kkOiKqm7r7LuDN8IGZdSGYo2IUMChq0QXvVQv4J3AASHf3l6P5fiLxzN0ZN30ND76/gIy9WVxzfBtuPVW9mSS6SnUR093nmVmuuz9amteHY0edBWxy92751g8GhgMpwLPu/nfgfGCcu79jZq8CShRSIS3YsJM/vTWHqSu20/vI+vz13O50aV431mFJBXAorV2TCNowSuMF4EmCGgkAZpYCPAUMBNYAU81sAtCS4EY/gJzSBiuSqHbvz2b45MX854vl1K1emYcvOJoL+7SkUiVdZpLyUVyvpxEH2wTUL+2buvtnZta6wOq+wBJ3Xxa+91jgHIKk0RKYAWjUMqlQJs3dwH0T5rIuYx8XH3MEdw3urLGZpNxZUR2YzGwXcAf5brLL51F3b1zqNw4Sxbt5l57M7EJgsLtfGy5fAfQD7iKofewDvjhYG4WZDQOGATRt2rTP2LFjSxtaucrMzKR27dqxDiMqVLbS27I3l5fnH+D7TTm0rG1c2bUaHRqU3/wQOneJ6VDKNmDAgOnunlrYtuIuPU0F5rj7VwU3mNl9pYqmhNx9N1DsfRzuPhIYCZCamuppaWlRjqxspKenkyixlpTKVnJZObk898VynvhqMQB3n96Za05oQ5VyHgJc5y4xRatsxSWKCwl+yf9EFKZHXQsckW+5ZbguYpoKVRLZ9JXb+cObs1mwYRenHtWU+87uQssGNWMdlkix91FsK69ACGovHcysDUGCuBi4tCQH0FSokogy9mbxyIcLeHnKKprVrc6/rujDoK7NYh2WyA+KrM+a2cjiDhDJPoW85hXga6CTma0xs6Hung3cDHwIzAdec/e5JT22SKJwd96dtY5TH/uUMVNWcfVxbfjo9pOUJCTuFHfp6VwzK/TSU8iAASV9U3e/5CDrJwITS3q8H4LRpSdJEKu37eFPb88hfeFmurWoy3NXHkP3lppISOJTcYnizgiO8XlZBFIWdOlJ4l12Ti7Pfbmcxz5aRIoZ95zVhV8e20rzVUtcK66N4sXyCkQk2c1ek8Hv3pjF3HU7OfWow/jzOd1oXr9GrMMSKVZSjUOsS08Sj3bvz+axjxbx/JfLaVS7Gk9f1pvB3ZppAD9JGEmVKHTpSeLNJws38cc357B2x14u63ckvx3cmXo1NICfJJaIEoWZ/dzdXy9unYgEtmbu5/535jFh5jraH1ab1284lmNaN4x1WCKlEmmN4m6gYFIobJ1IhebuvPn9Wv7y7jwy92dz66kduDGtHdUql9/wGyJlrbhBAU8HzgBaFBggsC6QHc3ASkNtFBJLq7ft4fdvzubzxVvodWR9HrrgaDo21WxzkviKq1GsA6YBZwPT863fBdwWraBKS20UEgs5uc7zXy7n0UmLqGRw/9ldubx/K1I0DLgkieK6x84EZprZGHfPKqeYRBLGoo27+O24WcxYvYMBnZrw1/O600JdXiXJRNpG0TccLbZV+BoD3N3bRiswkXiWnesM/3gxT36ymDrVqzD84p6c3aO5urxKUoo0UfyH4FLTdOJ4ljm1UUh5mLl6B/d9tZc1mYs4u0dz7h3ShUa1q8U6LJGoiTRRZLj7+1GNpAyojUKiaV9WDo99tIhnP19GvarGs79M5dQuTWMdlkjURZooPjGzR4A3yDfbnbt/F5WoROLMt8u3cdf4WSzfsptL+h7JiXW2KElIhRFpougX/pt/mjwHTi7bcETiy54D2Tz8wUJe/HoFLRvUYMy1/TiufWPS09NjHZpIuYkoUbh7iYcSF0l0Xy3Zwl1vzGL1tr1cdVxr7hzUiVrVkmrUG5GIRPxXb2ZnAl2B6nnr3P3P0QiqtNSYLWVh174sHnx/AWOmrKJN41q8dv2x9G2j4Tek4op0rKdngJoEkxQ9SzCX9rdRjKtU1Jgth+qLxVu4a/ws1mfs5boT23D7wE7UqKrhN6Rii7RGcZy7H21ms9z9fjN7FIj7XlAikdq1L4u/TVzAK9+uom2TWrx+w3H0adUg1mGJxIVIE8Xe8N89ZtYc2AocHp2QRMpX/lrEsJ+15faBHaleRbUIkTyRJop3zaw+8AjwHUGPp2ejFpVIOVAtQiQykSaKh919PzDezN4laNDeF72wRKLrqyVbuHOcahEikYg0UXwN9AYIE8Z+M/sub51IothzIJu/v7+AUV+vpE1j1SJEIlHcfBTNgBZADTPrRTAYIATzUdSMcmwlpu6xUpRpK7Zxx+szWbl1D1cf35rfDuqsHk0iESiuRjEIuApoCTzKj4liF/D76IVVOuoeK4XZl5XDo5MW8uwXy2nZoAZjh/Wnf9tGsQ5LJGEUNx/Fi8CLZnaBu48vp5hEysysNTu4/bWZLNmUyaX9juT3ZxxFbd1dLVIikf6PaWlmdQlqEv8maJv4nbtPilpkIocgKyeXJ/+7hCc/WUKT2tV48Zq+nNSxSazDEklIkSaKa9x9uJkNAhoBVwCjASUKiTuLN+7i9tdmMnttBuf1asF9Q7pSr2aVWIclkrAiTRR5bRNnAKPcfa5pKi+JM7m5znNfLufhDxdSq2oKT1/Wm9O7675QkUMVaaKYbmaTgDbA3WZWB8iNXlgiJbNm+x7ueG0mU5Zv49SjDuNv53fnsDrVi3+hiBQr0kQxFOgJLHP3PWbWCLg6emGJRMbdGf/dWu6bMBeAhy84mp+nttTc1SJlKNL5KHLNbCPQxczUZUTiwrbdB/j9G7P5YO4G+rZuyKO/6MERDePu9h6RhBfpMOMPARcB84CccLUDn0UpLpEifbJgE3eOm0XG3gP87vTOXHdiW1IqqRYhEg2R1g7OBTqFw3fELd2Znfz2HMjmgffm8/KUVXRuVodR1/SlS/O6sQ5LJKlFmiiWAVWAuE4UujM7uc1cvYNbX53Biq27NZCfSDmKNFHsAWaY2WTyJQt3vyUqUYnkk52Ty9PpSxk+eTGH1anGmGv7c2w7DcEhUl4iTRQTwodIuVq9bQ+3vTqDaSu3M6RHc/56TjfdPCdSziLt9fSimVUFOoarFrp7VvTCkoouf7dXA4Zf3JNzeraIdVgiFVKkvZ7SgBeBFQR3aR9hZle6u3o9SZnL2JPF79+azXuz1tO3TUMe+0UPWjZQt1eRWIn00tOjwGnuvhDAzDoCrwB9ohWYVExTlm3ltldnsGnXfu4c1IkbTmqnbq8iMRZpoqiSlyQA3H2RmelCsZSZrJxcnvh4Ef9MX0rrRrUYf+Nx9DiifqzDEhEiTxTTzOxZ4KVw+XJgWnRCkopmxZbd/ObVGcxcvYNfpLbk3iFdqaU5I0TiRqT/G28EfgXkdYf9DHg6KhFJhZHXYH3v23NIqWT887LenKHRXkXiTnFzZjcBmrj7POCx8IGZdSWYN3tz1COUpLRzXxZ/fHMOE2auo1+bhjx+UU+a168R67BEpBCVitn+D6BxIesbAsPLPhypCL5btZ0zR3zOe7PXc+egToy5rr+ShEgcK+7SU/vCusC6++dmpktPUiI5uc4zny7lsY8WcXi96rx2/bH0adUg1mGJSDGKSxR1ithWLr2ezKwt8AegnrtfWB7vKWVvQ8Y+bnt1Bl8v28qQHs154Lxu1K2ujnMiiaC4S09LzOyMgivN7HSCgQKLZGbPmdkmM5tTYP1gM1toZkvM7HdFHcPdl7n70OLeS+LX5PkbOX34Z8xcs4NHLjyaERf3VJIQSSDF1ShuBd4zs18A08N1qcCxwFkRHP8F4ElgVN4KM0sBngIGAmuAqWY2AUgBHizw+mvcfVME7yNxKCvX+fM783juy+V0Obwu/7i0F+2a1I51WCJSQkUmCndfbGbdgUuBbuHqT4Hr3X1fcQd398/MrHWB1X2BJe6+DMDMxgLnuPuDRJZ8JAEs37Kbv36zj5U7l3PVca25+4zOVKusIcFFEpG5e3TfIEgU77p7t3D5QmCwu18bLl8B9HP3mw/y+kbAAwQ1kGfDhFLYfsOAYQBNmzbtM3bs2DIuSXRkZmZSu3Zy/cr+al02o+bup5I51x1dnV6HJd/Nc8l43vJL5vKpbIUbMGDAdHdPLWxb3P8PdvetwA0R7DcSGAmQmprqaWlpUY6sbKSnp5MosRZn9/5s7nl7LuNnraFv64Zc1GovF5x+cqzDiopkOm+FSebyqWwlV1xjdjSsBY7It9wyXHfIzGyImY3MyMgoi8NJCSzYsJOzn/yCN75fwy0nt2fMdf1oVCMWf14iUtYi/p9sZjXMrFMZvOdUoIOZtQnnuLiYMpoUyd3fcfdh9erVK4vDSQTcnbHfruKcJ79k575sXh7aj9tP60TlFCUJkWQR0f9mMxsCzAA+CJd7hj2VinvdK8DXQCczW2NmQ909G7gZ+BCYD7zm7nNLWwCJncz92fxm7Ax+98ZsjmndkIm3nMhx7Qu7kV9EElmkbRT3EfRWSgdw9xlm1qa4F7n7JQdZPxGYGOF7RyxMaEPat29f1oeWAuaszeDmMd+xatse/t9pHbkprT2VNG+ESFKK9PpAlrsXvPAf3e5SpaBLT9Hn7oz+ZiXn//Mr9mXlMnbYsdx8cjRtLZcAABKLSURBVAclCZEkFmmNYq6ZXQqkmFkHguHGv4peWBKPMvdn87vxs3h31npO6tiExy/qScNaVWMdlohEWaQ1il8DXYH9wBggA/hNtIIqLfV6ip7563dy9j++YGI44uvzVx2jJCFSQUSaKM509z+4+zHh44/A2dEMrDR06ans5fVqOvepL8ncn82Y6/rzqwFqjxCpSCJNFHdHuE6SyJ4D2dzx2swfejW9d8uJ9G/bKNZhiUg5K26Gu9OBM4AWZjYi36a6QHY0A5PYWrIpkxtfms6SzZncemoHfn1yB1JUixCpkIprzF4HTCO4zDQ93/pdwG3RCqq01D22bEyYuY7fjZ9F9SopjLqmLyd2aBLrkEQkhoobPXYmMNPMxrh7VjnFVGru/g7wTmpq6nWxjiUR7c/O4W/vzefFr1fSp1UDnry0F4fX0xSlIhVdpN1jW5vZg0AXoHreSndvG5WopNyt2b6HX435npmrd3DtCW246/TOVNEwHCJC5InieeBe4HFgAHA1sRlQUKIgfeEmbn11Bjk5zjOX92Zwt8NjHZKIxJFIv+xruPtkgvkrVrr7fcCZ0QurdHQfRcnk5jqPf7SIq1+YSrO61Znw6xOUJETkJyKtUew3s0rAYjO7mWBY8Lib+UNtFJHbvvsAt746g08Xbeb83i144Nzu1KiqGehE5KciTRS/AWoSDN3xF+Bk4JfRCkqia/aaDG54aTqbd+3ngfO6cWnfIzFT11cRKVxEicLdp4ZPM4GrzSyFYB6JKdEKTKJj7LeruGfCXBrXqsprNxxLzyPqxzokEYlzxd1wVxf4FdCCYHKhj8LlO4BZwMvRDlDKxr6sHO59ey6vTlvNCe0bM+KSXhqrSUQiUlyNYjSwnWDyoWuB3wMGnOfuM6IcW4nphrvCrd2xlxtfms6sNRn8akA7bh/YSXdZi0jEiksUbd29O4CZPQusB450931Rj6wU1Jj9U18u2cKvX/meA9m5jLyiD6d1bRbrkEQkwRSXKH64G9vdc8xsTbwmCflf7s7Iz5bx0AcLaNekNs9c0Yd2TeKuo5qIJIDiEkUPM9sZPjegRrhsgLt73ahGJ6WSuT+b346bycTZGzijezMevrAHtatF2sFNROR/FTfWkzrWJ5hlmzO5fvR0lm7O5O7TOzPsZ23V9VVEDol+ZiaR/y7YyG/GzqByJWP00H4c375xrEMSkSSgRJEEcnOdpz5ZwmMfL6LL4XX51xV9aNmgZqzDEpEkkVSJoiJ2j83cn83tr85g0ryNnNuzOQ+ef7SG4hCRMpVUI8BWtDmzl23O5NynvmTygk386awuPH5RTyUJESlzSVWjqEg+WbCJW175niqVKzF6aF+Oa6f2CBGJDiWKBOPuPP3pUh75cKHaI0SkXChRJJC9B3K4c9xM3p21niE9mvPwBWqPEJHoU6JIEGt37GXYqGnMW7+TuwZ35oaTdH+EiJQPJYoEMGXZVm56+TsOZOfy3JXHMKDzYbEOSUQqECWKOPfylJXc+/ZcjmxYk39fmarxmkSk3ClRxKmsnFz+8u48Rn29krROTRh+cS/q1agS67BEpAJSoohD23cf4FdjvuOrpVu5/mdt+e3gzpo/QkRiJqkSRTLcmb144y6uHTWN9Tv28ejPe3BBn5axDklEKjjdmR1H/rtgI+f98yt2789h7PX9lSREJC4kVY0iUeVNMvT3DxbQtXld/v3LVA6vVyPWYYmIAEoUMZeV69w5bhbjpq/hzKMP5/8u7KGb6EQkrihRxNDWzP08MnUfi7av4dZTO/CbUzroJjoRiTtKFDGycMMuhr44lY0Zufzjkl4M6dE81iGJiBQqqRqzE8UnCzZxwdNfcSA7l7v7VVeSEJG4pkRRjtydZz9fxtAXp9KqUU3evvl42tZTe4SIxDddeionWTm53DthLmOmrGJQ16Y8flFPalatzMJYByYiUgwlinKQsTeLm8d8x+eLt3BjWjvuPK0TlXSntYgkCCWKKFu1dQ/XvDiVFVt28/CFR/OL1CNiHZKISIkoUUTRtBXbGDZ6Ojm5zuih/Ti2XaNYhyQiUmJKFFHy9oy13Pn6LFo0qMF/rkylrYYHF5EEFfeJwszOBc4E6gL/cfdJMQ6pSO7OiMlLePzjRfRr05BnLu9Dg1pVYx2WiEipRbV7rJk9Z2abzGxOgfWDzWyhmS0xs98VdQx3f8vdrwNuAC6KZryH6kB2Lv/v9Vk8/vEizu/dgtFD+ylJiEjCi3aN4gXgSWBU3gozSwGeAgYCa4CpZjYBSAEeLPD6a9x9U/j8j+Hr4lLGniyuf2ka3yzbxm2nduSWU9prOA4RSQrm7tF9A7PWwLvu3i1cPha4z90Hhct3A7h7wSSR93oD/g585O4fF/E+w4BhAE2bNu0zduzYMixF0TbtyeXx6fvYvMe5pns1jmseef7NzMykdu3kbL9Q2RJXMpdPZSvcgAEDprt7amHbYtFG0QJYnW95DdCviP1/DZwK1DOz9u7+TGE7uftIYCRAamqqp6WllU20xfhu1XbueHEa2bmVefm6PvRrW7KeTenp6ZRXrOVNZUtcyVw+la3k4r4x291HACNiHUdh3p+9nltfnUHTutV5/upjaKeeTSKShGIx1tNaIP9dZy3DdYfMzIaY2ciMjIyyOFyRnv18GTeN+Y6uzevy5k3HKUmISNKKRaKYCnQwszZmVhW4GJhQFgcuj6lQc3Kd+9+Zy1/fm8+gLs0Yc11/GtWuFrX3ExGJtWh3j30F+BroZGZrzGyou2cDNwMfAvOB19x9bjTjKCt7D+Rw08vTef7LFQw9oQ1PXdab6lU0+quIJLeotlG4+yUHWT8RmFjW72dmQ4Ah7du3L+tDszVzP9eOmsaM1Tu456wuXHNCmzJ/DxGReJRU81FE69LT8i27Of/pr5i3bidPX9ZHSUJEKpS47/UUa9+v2s7QF6cB8Mqw/vQ+skGMIxIRKV9JVaMo615Pk+dv5JJ/f0PtapUZf+NxShIiUiElVaIoy0tPr3y7iutGTaNj0zqMv/E42jSuVQYRiogkHl16KsDdefzjxYyYvJi0Tk146tLe1Kqmj0lEKi59A+aTlZPLH96czWvT1vCL1JY8cF53qqQkVaVLRKTEkipRHEr32APZuVw/ehqfLNzMLSe357aBHTX6q4gIaqP4QZUUo3XjWvztvO7cflonJQkRkVBS1SgOhZlx75CusQ5DRCTuJFWNQkREyl5SJYryHD1WRKSiSKpEUR6jx4qIVDRJlShERKTsKVGIiEiRlChERKRISZUo1JgtIlL2kipRqDFbRKTsmbvHOoYyZ2abgZWxjiNCjYEtsQ4iSlS2xJXM5VPZCtfK3ZsUtiEpE0UiMbNp7p4a6ziiQWVLXMlcPpWt5JLq0pOIiJQ9JQoRESmSEkXsjYx1AFGksiWuZC6fylZCaqMQEZEiqUYhIiJFUqIQEZEiKVFEkZlVN7NvzWymmc01s/vD9W3MbIqZLTGzV82sari+Wri8JNzeOpbxF6WIsr1sZgvNbI6ZPWdmVcL1ZmYjwrLNMrPesS1B0Q5WvnzbR5hZZr7lZDh3ZmYPmNkiM5tvZrfkW58Q566Isp1iZt+Z2Qwz+8LM2ofrE+a85TGzFDP73szeDZej/33i7npE6QEYUDt8XgWYAvQHXgMuDtc/A9wYPr8JeCZ8fjHwaqzLUIqynRFuM+CVfGU7A3g/XN8fmBLrMpSmfOFyKjAayMy3fzKcu6uBUUClcNthiXbuiijbIuCofOfqhUQ7b/nKeDswBng3XI7694lqFFHkgbxfnVXChwMnA+PC9S8C54bPzwmXCbefYnE6effByubuE8NtDnwLtAz3OQcYFW76BqhvZoeXf+SROVj5zCwFeAT4bYGXJPy5A24E/uzuueF+m8J9EubcFVE2B+qG6+sB68LnCXPeAMysJXAm8Gy4bJTD94kSRZSF1cQZwCbgI2ApsMPds8Nd1gAtwuctgNUA4fYMoFH5Rhy5gmVz9yn5tlUBrgA+CFf9ULZQ/nLHpYOU72ZggruvL7B7Mpy7dsBFZjbNzN43sw7h7gl17g5StmuBiWa2huDv8u/h7gl13oAnCH6k5IbLjSiH7xMliihz9xx370nwy7ov0DnGIZWZgmUzs275Nv8T+MzdP49NdIeukPL9DPg58I/YRnboDnLuqgH7PBgC4t/Ac7GMsbQOUrbbgDPcvSXwPPBYLGMsDTM7C9jk7tPL+72VKMqJu+8APgGOJai6Vw43tQTWhs/XAkcAhNvrAVvLOdQSy1e2wQBmdi/QhOBaap4fyhbKX+64lq98A4D2wBIzWwHUNLMl4W7JcO7WAG+Em94Ejg6fJ+S5y1e204Ee+Wq8rwLHhc8T6bwdD5wd/u2NJbjkNJxy+D5RoogiM2tiZvXD5zWAgcB8gj/eC8PdrgTeDp9PCJcJt/83vNYfdw5StgVmdi0wCLgk71p3aALwy7AHTX8go5DLN3HjIOWb7u7N3L21u7cG9rh7+/AlCX/ugLcIkiHASQQNwJBA566I/3P1zKxjuFveOkig8+bud7t7y/Bv72KCWC+jPL5PDqX1XY9ieyccDXwPzALmAPeE69sSNPQuAV4HqoXrq4fLS8LtbWNdhlKULZugHWZG+Mhbb8BT4bbZQGqsy1Ca8hXYJ3+vp2Q4d/WB98Lz8zXBr/CEOndFlO28MPaZQHre+Umk81agnGn82Osp6t8nGsJDRESKpEtPIiJSJCUKEREpkhKFiIgUSYlCRESKpEQhIiJFUqKQmDGzc83MzaxzvnVpeaNiHuKxXzCzC4vZJ83MjitqnwL7DwpHH51hZpkWjJI7w8xGHWq80WBmV5lZ8ygee7OZ5Y059D/nzcz+amYfhCOYvmxm24o7HxK/lCgkli4Bvgj/jYU0frxDt1ju/qG79/RgeIhpwGXh8i+jFWBxwkEKD+YqoESJIt8dvpF41d2vLeQYfyS4i/g8d9/vwU1hE0oSh8QXJQqJCTOrDZwADCW4yzS/umb2XviL/RkzqxQO9PaCBfNczDaz28Lj9DSzbyyYJ+FNM2tQyHutMLPG4fNUM0sPx+a/AbgtrBWcGN7VO97MpoaP4yMsy+UWzIEww8z+lfflHdY6HrFgXoSPzaxv+N7LzOzscJ+rzOztcP3icPiTSI77qJnNBI41s3vCeOeY2cjwDuoLCYZDfzl8fY3CPofw+X1mNtrMvgRGl/ZzCI91B8GQGUPcfW+kr5P4pkQhsXIO8IG7LwK2mlmffNv6Ar8GuhCMaHo+0BNo4e7d3L07wcBuEMyfcJe7H01w5+29RMDdVxCM3f94WCv4nGDcnMfd/RjgAsKhnItiZkcBFwHHhzWNHOCycHMtgmETugK7gL8SDB9xHvDnAuW9gOCu4p+HX+LFHXeKu/dw9y+AJ939GHfvBtQAznL3cfxvrae4L+0uwKnufklpPofQ8QTJ93T/cahvSQIlqWaKlKW8LyQIBji7BMgbFfNbd18GYGavENQ8JgNtzewfBMNMTDKzekB9d/80fN2LBEMWlNapQBf7ccj+umZWu5gvvVOAPsDU8HU1CIa3BjjAj8Oszwb2u3uWmc0GWuc7xkfuvhXAzN4gKG92EcfNAcbne/0AM/stUBNoCMwF3om82EAwdHpeMinN5wDBUBENCJLh+GL2lQSiRCHlzswaEox82d3MHEghmBToznCXguPKuLtvN7MeBAMO3gD8gmDo6Ehk82PtuXoR+1UimMVuX4THhWAcpBfd/e5CtmX5j2Pk5AL7Adw9t0BbwE/KW8xx97l7DgRTfxIM6Z7q7qvN7D4OXsaiPofd+Z6X5nMA2EhQ65lsZtvc/ZMSvl7ilC49SSxcCIx291YejMR6BLAcODHc3teCeYArEVx++SK8tl7J3ccDfwR6u3sGsN3M8l53BfApP7WC4Nc5BJdS8uwC6uRbnkRwyQsI2j8iKMtk4EIzOyx8TUMzaxXB6/IbGL6uBsHsZF+W4Lh5X/hbwnaf/D2LCpZvBYV/DgWV5nMAILyUeD7wUkleJ/FNiUJi4RKC+Q7yG8+PvZ+mAk8SDAW9PNy3BZBuwcxlLwF5v7SvBB4xs1kE7Rj5r/3nuR8YbmbTCC7b5HkHOC+vMRu4BUgNG8bnEdRciuTu8wgS16Qwho+Akk4T+i1B+WcB4919WqTH9WDOhX8TjJT6IcFnl+cF4Jm8xmwO/jkUVOLPoUBMUwnm355gZu1K8lqJTxo9ViSGzOwqgstGN8c6lpIoadxm9gLBsNjjittX4o9qFCJSGnuB0y284a4oZvYywURIJW3zkDihGoWIiBRJNQoRESmSEoWIiBRJiUJERIqkRCEiIkVSohARkSL9fwVLZkXTg5NnAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Ea = 72750 # activation energy J/gmol\n",
"R = 8.314 # gas constant J/gmol/K\n",
"k0 = 7.2e10 # Arrhenius rate constant 1/min\n",
"\n",
"# Arrhenius rate expression\n",
"def k(T):\n",
" return k0*np.exp(-Ea/R/T)\n",
"\n",
"T = np.linspace(290, 400)\n",
"plt.semilogy(T, k(T))\n",
"plt.xlabel('Absolute Temperature [K]')\n",
"plt.ylabel('Rate Constant [1/min]')\n",
"plt.title('Arrenhius Rate Constant')\n",
"plt.grid();"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.3 Arrehenius Law Kinetics for a First-Order Reaction](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.3-Arrehenius-Law-Kinetics-for-a-First-Order-Reaction)",
"section": "7.4.3 Arrehenius Law Kinetics for a First-Order Reaction"
}
},
"source": [
"This graph shows the reaction rate changes by three orders of magnitude over the range of possible operating temperatures. Because an exothermic reaction releases heat faster at higher temperatures, there is a positive feedback that can potentially result in unstable process behavior."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.4 Modeling and Parameter Values](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4-Modeling-and-Parameter-Values)",
"section": "7.4.4 Modeling and Parameter Values"
}
},
"source": [
"## 7.4.4 Modeling and Parameter Values"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.4.1 Mathematical Model](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4.1-Mathematical-Model)",
"section": "7.4.4.1 Mathematical Model"
}
},
"source": [
"### 7.4.4.1 Mathematical Model\n",
"\n",
"The model consists of mole and energy balances on the contents of the well-mixed reactor.\n",
"\n",
"\\begin{align*}\n",
"V\\frac{dc_A}{dt} & = q(c_{Ai}-c_A)-Vkc_A \\\\\n",
"V\\rho C_p\\frac{dT}{dt} & = wC_p(T_i-T) + (-\\Delta H_R)Vkc_A + UA(T_c-T)\n",
"\\end{align*}\n",
"\n",
"which are the equations that will be integrated below.\n",
"\n",
"| Quantity | Symbol | Value | Units | Comments |\n",
"| :------- | :----: | :---: | :---- | |\n",
"| Activation Energy | $E_a$ | 72,750 | J/gmol | |\n",
"| Arrehnius pre-exponential | $k_0$ | 7.2 x 1010 | 1/min | |\n",
"| Gas Constant | $R$ | 8.314 | J/gmol/K | |\n",
"| Reactor Volume | $V$ | 100 | liters | |\n",
"| Density | $\\rho$ | 1000 | g/liter | |\n",
"| Heat Capacity | $C_p$ | 0.239 | J/g/K | |\n",
"| Enthalpy of Reaction | $\\Delta H_r$ | -50,000 | J/gmol | |\n",
"| Heat Transfer Coefficient | $UA$ | 50,000 | J/min/K | |\n",
"| Feed flowrate | $q$ | 100 | liters/min | |\n",
"| Feed concentration | $c_{A,f}$ | 1.0 | gmol/liter | |\n",
"| Feed temperature | $T_f$ | 350 | K | |\n",
"| Initial concentration | $c_{A,0}$ | 0.5 | gmol/liter | |\n",
"| Initial temperature | $T_0$ | 350 | K | |\n",
"| Coolant temperature | $T_c$ | 300 | K | Primary Manipulated Variable |"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.4.2 Pyomo Model](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4.2-Pyomo-Model)",
"section": "7.4.4.2 Pyomo Model"
}
},
"source": [
"### 7.4.4.2 Pyomo Model"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.4.2 Pyomo Model](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4.2-Pyomo-Model)",
"section": "7.4.4.2 Pyomo Model"
}
},
"outputs": [],
"source": [
"# reaction and physical properities parameters\n",
"Ea = 72750 # activation energy J/gmol\n",
"R = 8.314 # gas constant J/gmol/K\n",
"k0 = 7.2e10 # Arrhenius rate constant 1/min\n",
"dHr = -5.0e4 # enthalpy of reaction [J/mol]\n",
"rho = 1000.0 # density [g/L]\n",
"Cp = 0.239 # heat capacity [J/g/K]\n",
"UA = 5.0e4 # heat transfer [J/min/K]\n",
"\n",
"# reactor operating parameters\n",
"V = 100.0 # volume [L]\n",
"q = 100.0 # flowrate [L/min]\n",
"cAi = 1.0 # inlet feed concentration [mol/L]\n",
"Ti = 350.0 # inlet feed temperature [K]\n",
"Tc = 300.0 # coolant temperature [K]\n",
"\n",
"# simulation parameters\n",
"cA0 = 0.5 # initial concentration [mol/L]\n",
"T0 = 350.0 # initial temperature [K]\n",
"t_initial = 0.0 # initial time\n",
"t_final = 10.0 # final time\n",
"\n",
"def cstr(cA0=cA0, T0=T0):\n",
" \"\"\"Return a pyomo model with specified initial conditions.\"\"\"\n",
" \n",
" # create a model instance\n",
" model = ConcreteModel()\n",
" \n",
" # define independent variable\n",
" model.t = ContinuousSet(bounds=(t_initial, t_final))\n",
" \n",
" # define dependent variables\n",
" model.cA = Var(model.t)\n",
" model.T = Var(model.t)\n",
" \n",
" # define derivatives of the dependent variables\n",
" model.dcA = DerivativeVar(model.cA)\n",
" model.dT = DerivativeVar(model.T)\n",
"\n",
" # set initial conditions\n",
" model.cA[0.0] = cA0\n",
" model.T[0.0] = T0\n",
" \n",
" # define constraints using model equations\n",
" def k(T):\n",
" return k0*exp(-Ea/R/T)\n",
" model.ode1 = Constraint(model.t, rule=lambda model, t: \n",
" V*model.dcA[t] == q*(cAi - model.cA[t]) - V*k(model.T[t])*model.cA[t])\n",
" model.ode2 = Constraint(model.t, rule=lambda model, t: \n",
" V*rho*Cp*model.dT[t] == q*rho*Cp*(Ti - model.T[t]) + (-dHr)*V*k(model.T[t])*model.cA[t] + UA*(Tc - model.T[t]))\n",
"\n",
" return model"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.5 Simulation and Visualization](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5-Simulation-and-Visualization)",
"section": "7.4.5 Simulation and Visualization"
}
},
"source": [
"## 7.4.5 Simulation and Visualization"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.1 Simulation](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.1-Simulation)",
"section": "7.4.5.1 Simulation"
}
},
"source": [
"### 7.4.5.1 Simulation"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.1 Simulation](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.1-Simulation)",
"section": "7.4.5.1 Simulation"
}
},
"outputs": [],
"source": [
"tsim, ysim = Simulator(cstr(), package='scipy').simulate(numpoints=100)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.2 Visualization Functions](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.2-Visualization-Functions)",
"section": "7.4.5.2 Visualization Functions"
}
},
"source": [
"### 7.4.5.2 Visualization Functions"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.2 Visualization Functions](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.2-Visualization-Functions)",
"section": "7.4.5.2 Visualization Functions"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtMAAAHwCAYAAABkJOM0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeXxU5fX48c/JHrIBCZCQBBLZFwUkIoJL3Hdp3bW1aqW2v2pra7V28evWxfZbq9YufmvVum91RcW1GBf2HdlFCJAEJIQkkD2ZOb8/5gaHGMJMMlvG83697ouZO/feOY/gM888c+55RFUxxhhjjDHG+C8m3AEYY4wxxhjTW9lg2hhjjDHGmG6ywbQxxhhjjDHdZINpY4wxxhhjuskG08YYY4wxxnSTDaaNMcYYY4zpJhtMGxMmIjJEROpEJDbcsRhjjDGme2wwbcJGRC4XkSXOgHKHiLwlIseGO66ORKRARFRE4np4nVIROaX9uapuU9VUVXX1PEpjjAkNp89u39wi0uj1/Fvhjq87OvbPxvjDBtMmLETkRuB+4PfAIGAI8A9gRjjj6q6eDrSNMaa3cCYBUlU1FdgGnOu17+lwx9dRKPpn+wz4erPBtAk5EckA7gKuU9WXVbVeVVtV9XVVvVlEEkXkfhGpcLb7RSTRObdYRMpE5GcissuZ0b7a69rJIvJnEdkqIrUi8omIJDuvTRWReSJSIyIrRaTY67wSEfmNiMwVkX0i8q6IZDkvf+T8WePMvBwjIlc5x94nIlXAHSIyTETmiEiViOwWkadFpK9z/SfxfGF43bnGzzvOeIvIYBGZJSJ7RGSTiHzPK747ROQFEXnCiW+NiBQF6+/IGGP8JSIxIvILEfnc6QdfEJH+zmvt/d3VIrJdRKpF5AcicpSIrHL65b95Xau9j/2b05evF5GTvV7PEJFHnM+AchH5bXvKXID652IRKevQvv2z106f/KKIPCUie4GruorJRDcbTJtwOAZIAl45yOu/BqYCE4EJwBTgVq/Xs4EMIBe4Bvi7iPRzXrsHmAxMA/oDPwfcIpILvAn81tl/E/CSiAzwuu7lwNXAQCDBOQbgeOfPvs7My3zn+dHAZjwz678DBLgbGAyMAfKBOwBU9QoOnMH5307a/RxQ5px/IfB7ETnJ6/XznGP6ArOAv33lCsYYEz4/Ar4BnICnH6sG/t7hmKOBEcAleH6d/DVwCjAOuFhETuhw7OdAFnA78HL74Bx4DGgDhgOTgNOAmR3ODWT/3JkZwIt4+uSnfYjJRCkbTJtwyAR2q2rbQV7/FnCXqu5S1UrgTuAKr9dbnddbVXU2UAeMEpEY4LvADaparqouVZ2nqs3At4HZqjpbVd2q+h6wBDjL67r/VtWNqtoIvIBnMN+VClX9q6q2qWqjqm5S1fdUtdmJ+148HyqHJCL5wHTgFlVtUtUVwMPAd7wO+8SJ3wU8ieeLhjHGRIofAL9W1TKn370DuLBDCsRvnD7uXaAeeNbp68uBj/EMQtvtAu53+vrngQ3A2SIyCE/f/RPnl81dwH3ApV7nBqx/7sJ8VX1VVd1Aug8xmShlOT4mHKqALBGJO8iAejCw1ev5Vmff/vM7nNcApOKZvUjCM5PR0VDgIhE512tfPPCB1/OdnVyzK9u9nzgd/F+A44A0PF9Wqw9xjXaDgT2qus9r31bAO5WjY3xJXfw3NMaYUBsKvCIibq99Ljyzw+2+8Hrc2Mlz7363XFXV63n7Z8FQPP33DhFpfy2GA/vkQPbPB+P9Hr7EZKKUzUybcJgPNOP5ObAzFXg6pnZDnH2HshtoAoZ18tp24ElV7eu1pajqH3y4rvq4//fOvsNVNR3PbLh0cby3CqC/iKR57RsClPsQnzHGRILtwJkd+tkkZ9a5O3LFa2TKl58F2/F8hmR5vU+6qo7zOran/XM90Kf9iZP7PKDDMd7n+BKTiVI2mDYhp6q1wG14cp2/ISJ9RCReRM4Ukf8FngVuFZEBzk2AtwFP+XBdN/AocK9zM1+sc7NgonP+uSJyurM/ybnBJM+HkCsBN3DYIY5Lw5NyUuvkaN/c4fUvDnYNVd0OzAPudmI7Ak8++CHbbYwxEeL/gN+JyFAApw/vSYWmgcCPnc+Hi/DkOs9W1R3Au8CfRSTdufFxWId864787Z834vn172wRicdz307iwS7ezZhMlLDBtAkLVf0zcCOeDqoSz7f664FX8dwkuARYBXwKLHP2+eIm55zFwB7gj0CMM1idAfzK6/1uxof/B1S1Ac8NLHOdO86nHuTQO4EjgVo8Nzu+3OH1u/F8SagRkZs6ngxcBhTgmXl5BbhdVd8/VHzGGBMh/oLn5uh3RWQfsADPjYDdtRDPzYq78fTBF6pqlfPad/DcKL4WT7rGi0BOF9fyq392Jn1+iOfelXI8M9VldM3fmEyUkAPTkYwxxhhjwktErgJmqmrELeRlTEc2M22MMcYYY0w3hWQwLSKPimeBjdUHeV1E5AHxLFSxSkSODEVcxhhjjDHG9ESoZqYfA87o4vUz8eRFjQCuBR4MQUzGGGOMiUCq+pileJjeIiSDaVX9CM/NYAczA3hCPRYAfUXEkvaNMcYYY0xEi5Sc6VwOLGxe5uwzxhhjjDEmYvW6FRBF5Fo8qSAkJydPzs/P9/sabrebmJhI+R4RWNHcNoju9lnbeq/utG/jxo27VbXjIhBRLSsrSwsKCvw+r76+npSUlMAHFAGiuW0Q3e2L5rZBdLevu21bunRpp/12pAymywHvUXEeB1n5TVUfAh4CKCoq0iVLlvj9ZiUlJRQXF/sfZS8QzW2D6G6fta336k77RGRrcKKJXAUFBViffaBobhtEd/uiuW0Q3e3rbtsO1m9HylTRLOA7TlWPqUCts5qQMcYYY4wxESskM9Mi8ixQDGSJSBlwOxAPoKr/B8wGzgI2AQ3A1aGIyxhjjDHGmJ4IyWBaVS87xOsKXBeKWIwxxhhjjAmUSMmZNsYYWltbKSsro6mpKdyh+CUjI4N169Z1+lpSUhJ5eXnEx8eHOCpjjAmuaOyzwf9+2wbTxpiIUVZWRlpaGgUFBYhIuMPx2b59+0hLS/vKflWlqqqKsrIyCgsLwxCZMcYET7T12dC9fjtSbkA0xhiamprIzMzsVZ1yV0SEzMzMXjdrY4wxvoi2Phu612/bYNoYE1GiqVOG6GuPMcZ4i8Y+zt822WDaGGMcTU1NTJkyhQkTJjBu3Dhuv/12ALZs2cLRRx/N8OHDueSSS2hpaQHgscceY8CAAUyfPp2JEyfy8MMPhzP8gBCRWBFZLiJvdNj/gIjUeT1PFJHnRWSTiCwUkYJQx2qMMd3ptwsLC5k4cWLA+m0bTBtjjCMxMZE5c+awcuVKVqxYwdtvv82CBQu45ZZb+OlPf8qmTZvo168fjzzyyP5zLrnkEubOncuKFSuYOXNmGKMPmBuAA+7MEZEioF+H464BqlV1OHAf8MfQhGeMMV/qTr99/vnns2LFioD12zaYNsYYh4iQmpoKeO5Sb21tRUSYM2cOF154IQBXXnklr776ajjDDBoRyQPOBh722hcL/An4eYfDZwCPO49fBE6WaPy91xgT0SKh37ZqHsaYiHTn62tYW7E3oNccOzid288d1+UxLpeLyZMns2nTJq677jqGDRtG3759iYvzdJd5eXmUl5fvP/6ll16ipKSE0aNHc99995Gfnx/QmEPsfjyDZu/b3K8HZqnqjg5j5VxgO4CqtolILZAJ7A5RrMaYCBKuPhv877dnzZrFggULGDlyZED6bRtMG2OMl9jYWFasWEFNTQ3f/OY3Wb9+/UGPPffcc7nssstoaWnhmWee4corr2TOnDkhjDZwROQcYJeqLhWRYmffYOAiPCvYdve61wLXAgwaNIiSkhK/r1FXV9et83qDaG4bRHf7orlt4Fv7MjIy2LdvHwCtLa24XK6AxtDa0rr/+ofy8ccfU1NTw7e+9S2WLVuG2+3ef25dXd3+58XFxaxcuZI+ffrw6KOP8u1vf5s33njjK9dramry+e/XBtPGmIjky2xEMPXt25cTTzyR+fPnU1NTQ1tbG3FxcZSVlZGbmwtAZmYmAC0tLcycOZOf/7xjJkSvMh04T0TOApKAdGAN0Axscmal+4jIJidPuhzIB8pEJA7IAKo6XlRVHwIeAigqKtLi4mK/AyspKaE757Vbtq2ajOR4hg1I7fY1gqWnbYt00dy+aG4b+Na+devW7a/X/NsLJoYgqq6lpaVxyimnsHLlSvbu3UtycjJxcXHU1NSQn59PWloaaWlp++tMX3/99dx2222d1pxOSkpi0qRJPr2v5UwbY4yjsrKSmpoaABobG3nvvfcYM2YMJ554Ii+++CIAjz/+ODNmzABgx44d+8+dNWsWY8aMCX3QAaKqv1TVPFUtAC4F5qhqP1XNVtUCZ3+DM5AGmAVc6Ty+0DleQx64D255cRV3zz74amfGmN4rEvptm5k2xhjHjh07uPLKK3G5XLjdbi6++GLOOeccxo4dy6WXXsqtt97KpEmTuOaaawB44IEHmDVrFjExMWRlZfHYY4+FtwGh9QjwpIhsAvbgGYBHpLrmNjbvrg93GMaYIOhOv/3qq6+SkJBA//79A9Jv22DaGGMcRxxxBMuXL//K/sMOO4xFixZ9Zf/dd9/N3Xff3eXStL2RqpYAJZ3sT/V63IQnnzriNbW62F3XjMutxMZYwRFjokl3+u1f/epXAe2zLc3DGGNMVGtqddPqUipqGsMdijEmCtlg2hhjTNRSVRpbPRUGSqss1cMYE3g2mDbGGBO1mtvc+x+XVjWEMRJjTLSywbQxJqJEaEGIbou29vQ2Ta1f1r0ttZsQjQm4aOzj/G2TDaaNMREjKSmJqqqqqOmcVZWqqiqSkpLCHcrXVlPrlzPTWy3Nw5iAirY+G7rXb1s1D2NMxMjLy6OsrIzKyspwh+KXpqamg3a8SUlJ5OXlhTgi067Ra2Z6i81MGxNQ0dhng//9tg2mjTERIz4+nsLCwnCH4beSkhKfV8oyodWe5jE0sw/b9zRaeTxjAsj6bA9L8zDGGBO12gfTo7PTaHG52VFr5fGMMYFlg2ljjDFRq3H/YDodgNLdVtHDGBNYNpg2xhgTtZqdGxBHZ3tWO7Na08aYQLPBtDHGmKjVuD9nOoXEuBir6GGMCTgbTBtjjIla7TnTfRJiKchMYYuleRhjAswG08YYY6JW+8x0UnwsQzP72My0MSbgbDBtjDEmarUv2pIcH0tBVgpb9zTgdkfPAhPGmPCzwbQxxpio1Z7mkRgfQ0FmCi1tbnbsbQpzVMaYaGKDaWOMMVGrqdWFCCTGxVCQ2QeArbYSojEmgGwwbYwxJmo1tbpIiotFRBialQLAFsubNsYEkA2mjTHGRK3GVhfJCbEA5KQnkZIQy2df1IU5KmNMNInz5SARWeXDYZWqenIX1zgD+AsQCzysqn/o8PoQ4HGgr3PML1R1ti/xGWOMCQwRiQWWAOWqeo6IPA0UAa3AIuD7qtoqIoKnTz8LaACuUtVl4Yr7YJpa3STFeeaNYmKEUdlprN2xN8xRGWOiiU+DaTyD27O6eF2AWQd90dM5/x04FSgDFovILFVd63XYrcALqvqgiIwFZgMFPsZnjDEmMG4A1gHpzvOngW87j58BZgIPAmcCI5ztaGff0SGN1AeNrS6S4mP3Px+Tk86slRWoKp7vA8YY0zO+pnl8X1W3drGVAj/s4vwpwCZV3ayqLcBzwIwOxyhfdt4ZQIUf7TDGGNNDIpIHnA083L5PVWerA8/MdJ7z0gzgCeelBUBfEckJedCH0NzJYHpfUxvlNY1hjMoYE03E0z/6cKBndvkJVf2W328iciFwhqrOdJ5fARytqtd7HZMDvAv0A1KAU1R1aSfXuha4FmDQoEGTn3vuOX/Doa6ujtTUVL/P6w2iuW0Q3e2ztvVe3WnfiSeeuFRVi4IUUreIyIvA3UAacJOqnuP1WjywELhBVT8WkTeAP6jqJ87r/wVuUdUlHa4Z1j77T4sbaXbBrVOTAdhU7eK3C5u44chEJg309cfZ4LH/N3qvaG4bRHf7utu2g/XbPvckquoSkaEikuDMLgfaZcBjqvpnETkGeFJExququ0McDwEPARQVFWlxcbHfb1RSUkJ3zusNorltEN3ts7b1XtHQPhE5B9ilqktFpLiTQ/4BfKSqH/tz3XD32X9dN4++8TEUF08F4KjmNn636B1iM4dSXDyiW9cMpGj4t9OVaG5fNLcNort9gW6bv1/LNwNzRWQWsL+2kKree4jzyoF8r+d5zj5v1wBnONebLyJJQBawy88YjTHG+G86cJ6InAUkAeki8pSqfltEbgcGAN/3Ot6Xfj3smlpd9E2O3/88JTGOof37sM5uQjTGBIi/pfE+B95wzkvz2g5lMTBCRApFJAG4lK/esLgNOBlARMbg6cwr/YzPGGNMN6jqL1U1T1UL8PTRc5yB9EzgdOCyDr8UzgK+Ix5TgVpV3RH6yLvW2OoiKSH2gH1jctJtMG2MCRi/ZqZV9U4AEemjqg1+nNcmItcD7+CpDPKoqq4RkbuAJao6C/gZ8C8R+SmemxGvUl8Tuo0xxgTL/wFbgflO9YuXVfUuPBWXzgI24SmNd3XYIuxCc6ubpLgDB9Ojs9N5e81O6pvbSEkMf960MaZ386sXcXKZHwFSgSEiMgFPpY+uKnkAnjvC8XS+3vtu83q8Fs/PjMYYY8JIVUuAEudxp58TzmTHdaGLqns8i7Yc+CPsmJw0VGH9zn1MHtovTJEZY6KFv2ke9+P5ua8KQFVXAscHOihjjDEmENqXE/c2JsdThdVSPYwxgeD3cuKqur3DLleAYjHGGGMCRlU9g+n4AwfTef2SSUuKs8G0MSYg/E0W2y4i0wB1ao62r5RljDHGRJQWlxu3QnKHGxBFhDHZ6azfuS9MkRljoom/M9M/wJMjl4unBNJEul750BhjjAmLplZP8ZHEuK9+1I3JSWP9jr243XafuzGmZ/ydmR7VcQVEEZkOzA1cSMYYY0zPNbV6shA7zkyDJ2+6vsXF9uoGhmamhDo0Y0wU8Xdm+q8+7jPGGGPCqn0w3fEGRIDxuRkArCyrDWlMxpjo49PMtFMSbxowQERu9HopHU/daGOMMSaiNHYxMz06O40+CbEsLd3DeRMGhzo0Y0wU8TXNIwFPbek4DlzxcC9wYaCDMsYYY3qqPWc6Kf6rP8LGxcYwaUhfFpdWhzosY0yU8WkwraofAh+KyGOqujXIMRljjDE91lWaB8Dkof3525zP2NfUSlpSfChDM8ZEEV/TPO5X1Z8AfxORr9z6rKrnBTwyY4wxpgfa0zySOknzADiqoB9uheXbajh+5IBQhmaMiSK+pnk86fx5T7ACMcYYYwKp+RAz05OG9CNGYMnWahtMG2O6zdc0j6XOnx8GNxxjjDEmMLq6AREgNTGOMTnpLN26J5RhhZ2qIiLhDsOYqOFrmsenwEEr26vqEQGLyBhjjAmArm5AbFc0tB//WVpGm8tNXKy/1WJ7n58+v4KmVhcPfntyuEMJmdrGVv7y/mf85NQRpH+NcuNbXZ5///Ffg3/X4eZrmsc5QY3CGGOMCbDGFmdmOv7gFVyLCvrz+PytrNuxj8PzMkIVWtjM/7yKnXub2LBzH6Oy0w59QhR4f+0XPDp3C4P7JjHzuMPCHU7IfPexxaQmxn2tvjgBlNc0kts3OaTv6evXlYeA84FkVd3acQtifMYYY0y3NLU5OdNdDqb7AbC4NPpTPeqb29i5twmARz7ZHOZoQmftjr0AvLBkO6pfj+XjaxtbmbtpN++t/YI99S3hDidkXl1ezvQ/zGHF9pqQvq+vM9NXAmcAd4jISGAh8DbwvqrWBys4Y4wxvhGRB3w4bK+q3hr0YCJEkzMznRh38HmjnIxkcvsms3RrNd89tjBUoYXFlt2ej+vcvsm8uryCm08fzYC0xDBHFXxrK/YiAhu/qGNVWS0T8vuGO6Sgm//5btwKblXeXr2Ty48eEu6Qgq7N5eb+9zcC8PrKCiaG8O/Zp5lpVd2pqo+p6qVAEfAEMBl4V0TeF5GfBzNIY4wxhzQDWHqI7YKwRRcGTW1ukuJjDnmzXVFBPxaX7on6Wcv2wfStZ4+h1e3myQXR/8OyqrKmopazD88hKT6GF5ZsD3dIIfHRZ7tJTYyjMCuF11dWhDuckHh1RQWlVQ0MSEvk7dU7Q/r/s99Z6arqVtX5qnqbqk4HLgXKAx+aMcYYP9ynqo93tQH/PNRFRCRWRJaLyBvO80IRWSgim0TkeRFJcPYnOs83Oa8XBLV13dDU6uoyxaPdlML+7NrXzOeV0f1D62anfSeOHsjJowfx1IKt+xe2iVblNY3sbWrj6MMyOXN8DrNWVOzPpY9WqspHGys5Zlgm500YzIItVexy0nuiVZvLzV/nfMa4wencfNooymsaWV2+N2Tv79NgWkT+KiIPdLYBt6nq00GO0xhjTNdeOtgLInIOgKre78N1bgDWeT3/I56B+nCgGrjG2X8NUO3sv885LqI0tri6vPmw3fEjPDWmSzbsCnZIYbVldx25fZNJio9l5nGF7Klv4ZXl0T0XtrbCM6AaNzidi4ry2NfcxjtrdoY5quDaWtVAWXUjx4/I4twJOajC7E93hDusoHpleTlbqxr4ySkjOXXsIGJjhLdWh67Nvs5ML6Hrnw6NMcaE13udzQ6LyHeBv/hyARHJA84GHnaeC3AS8KJzyOPAN5zHM5znOK+fLBFWvNiT5nHowXR+/z6MGJhKyYbKEEQVPpt313PYgBQAji7sz/CBqVGfArDGyZcenZ3G1MJM8vsnR32qx8efef4dHzdiAMMHpjE6O43XV0XvYNrlVv72wSbGDU7nlDED6ZeSwDGHZYY01cPXnOmOPxW+BLzk9dwYY0x43YjnPpYR7TtE5JfAT4ETfLzG/cDPAbfzPBOoUdU253kZkOs8zgW2Aziv1zrHR4zGFt/SPACKRw1g0ZY91De3HfrgXkhV2VJZT2GWZzAtIpw+bhALt+yhOoqrPazdsZfDslLokxBHTIxw4ZH5zPu8ip210Zv28NFnu8nvn8zQzD4AnDthMEu3VlNe0xjmyIJj254GtlY1cMXUofvvjzhjfDabd9ez8Yu6kMTgazUPAERkPJ6lxft7nkol8B1VXROM4IwxxvhGVWeLSDPwloh8A5gJTAGOV9XqQ53vpILsUtWlIlIcqLhE5FrgWoBBgwZRUlLi9zXq6uq6dd6OXY20tOHTuf2aXLS43Dz0WgmTBvr10dgj3W2bv2qblX3NbbhqdlBSshuAzCYXLrfyj1c/ZHpucBYzCVX7DmbZ5gaG943ZH8OAJs/3xL+9+jGnDO1Zm8Pdts60uZWPNzQwdXAcH37oWbR6QKOnzQ+88glnFvre5khsX2fWVnly4Ku3f0ZJg6fkY2qzGwEefGM+3xie8JVzAt02f3uMh4AbVfUDAKfD/RcwLWARGWOM6RZV/a+IXA2UAPOAk1TV1ym46cB5InIWkASk40kP6Ssicc7scx5f3nBeDuQDZSISB2QAVZ3E9BCezw6Kioq0uLjY73aVlJTQnfP+tm4eGXExFBdPPeSx09rc/H3lu1TGD6K4+HC/36u7uts2fy3cXAUfLOC0YyZywkhPjvjxbuWhNXPY5s7g18VFQXnfULWvMzUNLVS9/R7fmzSC4hOG7d//yIYSNrck+fTvoivhbNvBLCndQ9O787nk+CMoPjxn//4nP/+EDQ3CH4un+3ytSGxfZ3Yt2Q6LV3FW8VSGZqbs3//0lnmsr2ujuPj4r5wT6Lb5W80jpX0gDaCqJUDKwQ83xhgTCiKyT0T2ArPxDIRPBnZ57e+Sqv5SVfNUtQBPlaY5qvot4APgQuewK4HXnMeznOc4r8/RCKst19Tme5pHQlwM04dn8eGGyqgskddeFu+wrC8/smNihNPGDeLDjZVRWeGifbGWsTnpB+w/Y3w2C7fsicrFTD7+bDcxAtOGZR2w/4zx2azYXkNFFKZ67KjxzBdkZyQdsP+M8Tms37mPzZXBT/XwdzC9WUT+R0QKnO1W4OuzjJIxxkQoVU1T1XTnzwRVTfF6nn7oKxzULcCNIrIJT070I87+R4BMZ/+NwC961oLAa2r11Jn21YmjB1Je08hnu0KTZxlKm3fXkxAXw+AOyyyfNjabplb3/pvWokl7JY+xgzsMpsfl4HIr76/7IhxhBdWmyjqGZqaQ0efAdI4zx2cD8Pbq6KtkUlHTyIC0RBLjDvzifNbhnjaHopKJv4Pp7wIDgJedbYCzzxhjTJRQ1RJVbS+nt1lVp6jqcFW9SFWbnf1NzvPhzusRN7Hizw2I4LkJEeCD9dFXIm9zZT2FmSnExhxYcOXow/qTlhTHu2ujb2C5tmIvg9ITyUo9cJXH8bnp5PZN5p0oHFiWVTeS1y/5K/sPG5DK6Oy0kJaLC5WK2savfEkEz+qmk4f2481Pg//37NdgWlWrVfXHqnqks93gy40txhhjgktElgXimGjS7EeaB3g+fEdnp/FBFNab3ry7bn8lD2/xsTGcPHog/133BW0udydn9l5rKvYybnDGV/aLCGeMz+bjz3ZTF2XVW8qrG8ntZGAJcOb4HJZsrY66BVzKaxrJ7ZvU6WtnHZ7Duh17g57q4ddgWkSKRORlEVkmIqvat2AFZ4wxxmdjvPvlTrZPgaxDXiWK+Lpoi7dTxw5i0ZY97NoXPQOONpebbVUNFA7o/Ban08dlU93QyqLSPSGOLHia21xsqqxjTE5ap6+fMT6bFpc7qn6FaGp1sbuu+aCD6bMOz0aVqFq0RlWpqGlkcMbB2wzBT/XwN83jaeAx4ALgXK/NGGNMeI3mwH6543YOX6PKS6rqLNri38fcjImDcSu8GUWLXGyvbqTNrQfcfOjthFEDSEmIZdaK6FnAZfueRlxuZcTAzgfTRw7pR1ZqIm9H0cCy/ebC3E7SPABGDEpj+MBUZocg7SFUqhtaaWp1d5rmAV+merwR5P+f/R1MV6rqLFXdoqpb27egRGaMMcZn3n1yF1tZuOMMlVaX4nKr3zPTwwemMTYnndeiaGC5ZbfnJ+7DDjIz3SchjtPHZ/PmpztoamaBeTMAACAASURBVI2Oqh7b9zQAkN+/80FWbIxw5vhs/rvuC/Y1tYYytKApq/YMpvP69TnoMWeOz2bhliqq6ppDFVZQtX+BONhgGuDsw4Nf1cPfwfTtIvKwiFwmIue3b76cKCJniMgGEdkkIp3e9S0iF4vIWhFZIyLP+BmbMcYYA3jK4gF+5Uy3mzFxMCu217C1qj7QYYXF5sr2snipBz3m/El57Gtq47/roiPtYXt1+2D64APL84/MpanVHZJqD6FQfoiZafDkELuVoM/Uhsr+NncxmD4zBKke/g6mrwYmAmdw4E+HXRKRWODvwJnAWOAyERnb4ZgRwC+B6ao6DviJn7EZY4wxAPtnWLszmD53wmCAqEl72LK7nozkePqlfHUluHbHDMtkUHoiryyPjh8vtlU1kBQfw4AOlTy8Tczvy7ABKby0tPygx/Qm5dWNxMYIg9IO3uYxOemMG5zOf5ZuD2FkwfPlzHTnNyCCJ9WjaGg/XltREbQa8v4Opo9S1SJVvVJVr3Y2X0rjTQE2OSWWWoDngBkdjvke8Pf26iCqGh1fj40xJsREZKiInOI8ThaRzhNHo1hTi6cyRXcG04P7JjOlsD+vrQzeh28oba1qoOAg+dLtYmOEb0zMpWRDZVSkAGyvbiC/Xx9E5KDHiAgXTM5jUekeSnf3/l8hymsayU5PIi6266HdxUX5rC7fy5qK2hBFFjwVNY0kxsXQv4svigAXTM7js111LNtWE5Q4/B1Mz+s4o+yjXMD7a1CZs8/bSGCkiMwVkQUickY33scYY77WROR7wIvAP51decCr4YsoPL5M8/D3Y87jvAmD2bSrjnU79gUyrLAoraqnIPPg6Q7tvnlkLm1u5fWVvX9GftueRoZ0keLR7vxJecQIvLys98/Il1U3dFpjuqMZEweTEBvDf5b0/jZX1DaR2ze5yy9N4Pm1qU9CLM8v3haUOOL8PH4qsEJEtgDNgACqqkcEKJYRQDGezv8jETlcVQ/4GiEi1wLXAgwaNIiSkhK/36iurq5b5/UG0dw2iO72Wdt6rwhr33V4fg1cCKCqn4nIwPCGFHrty2P7ewNiu7MOz+GOWWt4dUX5V1bQ602a21xU1DRy/pF5hzx2dHY6Y3LSeWV5OVdNLwxBdMGhqmzf08DRhf0PeWx2RhLHjhjAS8vK+ckpI4mJ6XpQFsnKqxuZOizzkMf17ZPAaeMG8eqKcn551uivrBzYm1TUdL5gS0epiXGcN2Ewr62o4H/O6c6ccNf8HUx3d7a4HMj3ep7n7PNWBixU1VZgi4hsxDO4Xux9kKo+BDwEUFRUpMXFxX4HU1JSQnfO6w2iuW0Q3e2ztvVeEda+ZlVtaZ+pEZE4oPfnKvipJznTAP1TEjh5zEBeXFrGjaeO7PZ1wq2suhG34tPMNMAFR+by2zfXsWHnPkZl987soJqGVuqa27q8+dDbBUfmcsNzK1iwpYppw3pnKfZWl5ude5vI82FgCZ5UjzdW7eD9tbs4+4icIEcXPBU1jZwwcoBPx146ZQjPLd7OrJUVX0mN6Cl/f//a18nmy+9Bi4ERIlIoIgnApcCsDse8imdWGhHJwpP2EXHL0xpjTIT7UER+BSSLyKnAf4DXwxxTyDX2cDANcOUxBeypb+nVNafbK5IMzew6Z7rd+UfmkRgXw+PzS4MXVJBtay+L50PKA3gWrUlLjOP5xb33prydtU24tetKHt6mD89icEYSLyzpvW1uaXOza18zOQdZsKWjCXkZjM5O47lFgW+zv4PpZUAlsBH4zHlc6qyIOPlgJ6lqG3A98A6wDnhBVdeIyF0icp5z2DtAlYisBT4AblbVKj/jM8aYr7tb8PTNnwLfB2YDt4Y1ojBoam2/AbF7OdPgqXAxfGAqT8wvDUxQYVC62zOw9HVmun9KAt+YmMvLy8qoaWgJZmhB014Wb4iPbU6Kj+WionzeXLWDnbW9c+VLX2pMe4uNES6cnMdHn1Xur8nd23yxtwnVrsvieRMRLj0qn0/La9m6N7D11P3tZd4DzlLVLFXNxFPq7g3gh8A/ujpRVWer6khVHaaqv3P23aaqs5zHqqo3qupYVT1cVZ/zvznGGPP15ZQhXaeq/1LVi1T1Qufx1y7No7mtZznT4Pnw/c4xQ1lZVsuK7cGpAhBsW6vqSUuMO2S1A29XTS+gqdXda2dqv5yZ9m1gCXD19ALcqr32i5Mv9ZY7uvzoocSK8OjcLcEKK6jKfViwpaNvTvL88vJhWVtAY/F3MD1VVd9pf6Kq7wLHqOoC4OCFDY0xxgSdqrqADSIyJNyxhFv7DYg9zXU+/8g8UhPjeGJeaQCiCr3SqgaGZnVdIq6jMTnpTD2sP0/M30qbyx3E6IJj+54GMlMSSEn0/baw/P59OG1sNk8v3EZDS2AHWqFQ7sxM53RRb7mj7Iwkzps4mOcXb6e2ofetAulLjemOMvrE85sZ4zk+199bBrvm72B6h4jc4tQwHSoiPwe+cGZDet//ccYYE336AWtE5L8iMqt9C3dQodZ+A2JPZqbBUwXggiNzeWPVDnb3wvrL2/Y0+Jwv7e2qaYWU1zTy/rovghBVcG3f0+jzzYfeZh5XSG1jKy8t632LuJTXNDAoPdHvyhzfO+4wGlpcPLVwa5AiCx5flhLvzMVH5VOQEdgbiv0dTF/OlzVLX8FToeNyIBa4OKCRGWOM6Y7/wbMy7V3An722r5XG1u4v2tLRFccU0OJy8+T83jXgaHO52b6nwed8aW+njh1Ebt9kHv2kNPCBBdm2PQ3dGkxPHtqPCXkZ/PuTLbjdvSszqqy60a8Uj3ZjctI5fuQAHptXuj81qrcor2kiMyUhIirt+DWYVtXdqvojVZ2kqkc6jytVtUVVNwUrSGOMMb5R1Q8728IdV6i1z0wnxnX/BsR2wwemcvq4QTw6dwu1jb3n5/CKmiba3NqtmenYGOG7xxayqHQPCzb3nloAbS43FTWNDOnv/8BSxNPmzbvr+e/63rUIc3lNI7l+5Ih7u/a4w6jc18xry3vXYj2+1pgOBZ96GRG5IxDHGGOMCS4R2Scie52tSURcIrLXh/OSRGSRiKwUkTUicqez/2SnYtMKEflERIY7+xNF5HkR2SQiC0WkILgt809Tq4vEuJiALcLx45NHsK+pjX/3opu1Sp2yeAXdGEwDfOvoIQxMS+Te9zb2mmXVd9R6vkD4c/Oht7MOz2FI/z7c//7GXjM77XYrO2qaujUzDTB9eCZjc9L550ef4+olbYb2wbTv+dLB5OtX9pkicmMX28/w1I42xhgTRqqapqrpqpoOJAMXcIhqS45m4CRVnQBMBM4QkanAg8C3VHUi8Axfltm7BqhW1eHAfcAfA9yUHmlqdQX0599xgzM4fdwgHvmk98xOb90/mO7ewDIpPpbrThzOoi17mLupd8xO7y+L1400D4D42Bh+csoI1lTs5a3VOwMZWtBU1jXT4nL7tJR4Z0SEH500nM8r63vNsurNbS5Kq+opyOreF8VA83Uw/S8grYst1TnGGGNMhHBKjr4KnO7jsXXO03hnU2drX087gy8X6poBPO48fhE4WfwpGRFkTa3uHt982FFvm50urWogOT6WAWndL7Z1yVH55GQkce97G3rF7HR7zeTu5Ey3mzExlxEDU/nzext6RTWTMucLhK8LtnTmjPHZTMjL4L73Nu5PkYpk63bso9WlTMzrG+5QAB+XE1fVO4MdiDHGmJ4TkfO9nsYARYBPK1E4lZmWAsOBv6vqQhGZCcwWkUZgLzDVOTwX2A6ehblEpBbIBHYHpCE9VN3QQnpyYMtfec9OXz2tkIw+8QG9fqBtrapnaKZ/ZfE6SoqP5fqThvPrV1ZTsrGSE0cNDGCEgbdtTwOxMUJORvd//o+NEX522ih+8NRSXl5ezsVF+QGMMPC273EWbOlB/rCIcMsZo7n84YU8tWArM487LFDhBcVKp+77hPxeNJg2xhjTa5zr9bgNKMUzi3xITp3qiSLSF3hFRMYDP8WzWNdCEbkZuBeY6WswInItcC3AoEGDKCkp8fXU/erq6vw+b0NZIxkJ0q3368r0DBfvNrVx8+NzuHxMz5dX6E7bfLV2WwM5qTE9vv4gt5KVLNz24lLuOCaJWD/y0IPZvs4sXd9E/0T45OOPenSdRFUK02P44xuf0m/vJuI7aXOo23Ywb65rJiEWtq5ZQvm6nv04ND4zlvveXcfgpq24m+sjon2deWdVMxmJwoblC9jYjS+Lgf67s8G0McZEl4dVda73DhGZDvhcnkBVa0TkAzyr3E5Q1YXOS88DbzuPy/GURy0TkTg8KSBfSaxV1YeAhwCKioq0uLjYv9YAJSUl+Hte7UfvcuyYHIqLD/f7/Q5lvetTnl+8nZvOn8zIQWk9ulZ32uYLl1vZ/d7bnFs0lOLiMT2+3l0DdvDDp5dRllTIldMKfD4vWO07mPvXzGVkbizFxVMPffAhxOVVcsUji9hAHtcXj/jK66Fu28Hc8+nHFBXEc8pJPW9z1ohazvnrJ6x25TAldWdEtK8zdy0t4ajDUjnxxKJunR/ov7ue1wwyxhgTSf7q474DiMgAZ0YaEUkGTgXWARkiMtI5rH0fwCzgSufxhcCcSFm2vL65jZqG1h7lkHblptNGkZoYx52vr4nYPOKde5tocbm7XcmjozPHZ3Ps8CzueXdDxC5e09LmZuMX+xg2IDUg1ztuxADOHJ/NX+ds2p+LHWnqmttYW7GXooL+Abne+NwMzp+Uy78+3kxFXWTmi9c2trK5sp6J+RnhDmU/vwbTTmf7KxF5SEQebd+CFZwxxhjfiMgxTmWlAR2qLd2BZ2GtQ8kBPhCRVcBi4D1VfQP4HvCSiKwErgBudo5/BMgUkU3AjcAvAtykbmtfGa27pcIOpX9KAj87bSRzN1XxdoRWfNi621PJY2g3K3l0JCLccd44mlpd/PGt9QG5ZqCtLKuhocXFtGGZAbvmbeeOJS5GuH1WZH5xWr6tGrfCUQX9AnbNX509hj4JcTy2pjkiywOuLq8FIidfGvyfmX4Nz0957wNvem3GGGPCKwFPZaU4Dqy2tBfPzHGXVHWVsyDXEao6XlXvcva/oqqHq+oEVS1W1c3O/iZVvUhVh6vqlPb9kaDMGUx3t1SYLy6fMoTR2Wn89s111DW3Be19umtlmWfAMXxgYGZp26/13WML+c/SMpZu3ROw6wbK3E27EYGphwVuMJ2TkcxPTx3JnPW7eGdN5C2tvri0mhiBSUMCN5jOSk3kV2eNZmO1mxeWbA/YdQNlhXPz4RG5vXcw3UdVb1HVF1T1pfYtKJEFSW8o+WKMMf5yVjq8E5iqqnd6bfeq6mfhji+Uyqs9g+lgro4WFxvD7745noraRn735tqgvU93lWzYxZicdAamBXZRix+fNILBGUnc/J9VNLRE1peIeZuqGD84g759EgJ63SunFTA6O407X18TcTXGF2/Zw9jB6aQmBvYWuIuL8hnVL4bfz15H5b7ISutZub2GwqyUiKqm4+9g+g0ROSsokYTIN/8xjx/9t54LHpzHTf9ZybxNEVHFyRhjAqVBRP4kIrNFZE77Fu6gQqmippG4GAn4QLKjyUP78/3jh/Hsou38d13kzFrubWpl6dZqikcNCPi1UxLjuOeiCWzeXc/vZ6879Akh0tDSxvLt1UwbHrhZ6XbxsTH88YIjqNzXzK2vro6YdI9Wl5vl26spGhqYfGlvIsKV4xJpanXzy5dXRUybwZPOMyEvcvKlwf/B9A14BtRNzpK1+3xZpjaSXHpUPkcOiiM+Vvjvui+4/OGFfOfRRaypqA13aMYYEwhPA+uBQuBOPKXxFoczoFArr2kkp69/Jdy666enjmB0dhq3vPQpe+pbgv5+vpj72W7a3Bq0mtDThmcx89hCnlqwjQ/W+1wkJqgWl1bT6lKmDcsKyvUn5Pflp6eO5PWVFby8rDwo7+GvNRV7aWp1M6Uw8INpgMGpMfzizNG8v24Xj88rDcp7+GtnbRNf7G2OqHxp8HMw7SxTG6OqSc7jNGfJ2l7jymkFXD0+keeuPYb5vzyZW88ew6qyGs756yfMWllx6AsYY0xky1TVR4BWJ/Xju8BJ4Q4qlMqrG4N282FHiXGx3HfJRGobW/jFS5Exg1eyoZK0pDiOHBK8AcdNp49idHYaN7+4KiKqe8zbtJv4WAnojXgd/eCEYRxd2J/bXltNqXODZzgtKfXkrRcNDV6br55ewMmjB/L72ev33/gXTivLImuxlnZ+l8YTkfNE5B5nOycYQYVKUnwsM487jA9vPpGiof246T8rWbatOtxhGWNMT7Qnde4QkbNFZBIQnKmrCFVe0xjUfOmOxuSkc8sZo3l37Rf8o+TzkL1vZ1SVDzdWctyILOJig1f9Nine8yViX1MrP3xqGS1t4S2jNvfz3Uwa0o8+CcFbPiM2RrjvkonExcZw/bPLaHaF94vT4tI9DM3sw8D04KUziQh/umgC/VLi+dGzy8N+s+3K7TXExQhjcyJrHtff0nh/wJPqsdbZbhCRu4MRWChlJMfzzyuKyE5P4tonluxf594YY3qh34pIBvAz4CbgYTyrGH4ttLrcfLG3qUdLK3fHNccWMmPiYO55dwNz1ocvf3r9zn3s3NtE8cjgL/s9Jied/73wCBaV7glr6biahhbWVOxlepBSPLwN7pvMvRdPYE3FXh7+NHyl41SVJaXByZfuqH9KAn+5dBLb9jTw42eX0+YKzxcnVWXO+l0cnpdBUrwv1T5Dx9+vrWcBp6rqo6r6KHAGcHbgwwq9/ikJPHpVEc1tbmY+viRs/1iMMaa7RCQWGKGqtaq6WlVPVNXJqjor3LGFys7aJtxK0BZsORgR4Q/nH8HYnHRueHYFn1fWhfT925VsqATghCDcfNiZGRNz+X/Fw3h20TaeWrA1JO/Z0fzPq1CF6UG4+bAzJ48ZxK/OHMPinS7uf39jSN6zo7U79lJV3xLUtBZvUw/L5I7zxjFn/S5++2Z4bjxdsrWa9Tv3cUlRfljevyvd+Q3IO1Elsm6n7KHhA9P4/TcPZ/3OfcyJkJsqjDHGV6rqAi4LdxzhVL5/wZbALFbij+SEWP55xWTi42K46t+L2FnbFPIYPtiwi7E56QwK4k//Hd102ihOGj2QO15fy7trQr+IzUefVZKSEBvSPNqZxxVyXG4cD8zZxMvLykL2vu0e/aSU5PhYTh+XHbL3vGLqUL53XCGPzSvl33O3hOx92z05fytpSXGcN3FwyN/7UPwdTN8NLBeRx0TkcWAp8LvAhxU+Z47PZmBaIs8tjrxC5cYY44O5IvI3ETlORI5s38IdVKh8WWM6dINJb3n9+vDvq46iur6Vbz28gKoQ3pxX09DCsiCVxOtKbIzwwGWTODw3g+ufWc6HGytD9t5f7G3i5WXlnHV4DvFBzBHvyFM6LoFpwzK56T8reT2EBQx21Dby2opyLjkqn34pga2pfSi/PHMMp48bxF1vrOU/IVzQpXJfM2+t3sGFk/OCmhffXf5W83gWmAq8DLwEHKOqzwcjsHCJi43hkqPyKdmwa/8MhzHG9CITgXHAXcCfne2esEYUQu39dihvQOxoQn5fHrmyiLLqRq54ZBG1DaFZ6OPBDz/HpRqWmbvUxDgev3oKwwemcu0TS5j/eVVI3vfBks9pcys/OmlESN7PW1yM8PCVRRQN7c9Pnl/B7E93hOR9H/1kC4onTz/UYmKEv1w6iWOHZ/Hzl1bxQogmHp9fvI1Wl/LtqUND8n7+8mkwLSKjnT+PBHKAMmcbHI0zHhcX5aMQsn8kxhgTKE6edMfta1Mar6KmkazUxLDfoHT0YZn884rJfLZrHxf/c37QUz7Kaxr599xSvjkpl9HZ4al0kNEnnievmcKQ/n24+rFFQU/52FnbxDOLtnHhkXkMyQx9Wg9An4Q4Hr36KCbl9+XHzy7n1eXBrUFd29jKs4u2c/bhOeT3D0+bk+Jj+dd3ijhuxAB+/tIqnl4Y3Fz5Npebpxdu49jhWQwbkBrU9+ouX2emb3T+/HMnW9TNeOT378NxIwbwwpLtuMJ0p64xxnSHiAwSkUdE5C3n+VgRuSbccYVKeU1jyG8+PJjiUQP591VTKK9p5Px/zGXjF/uC9l5/fmcDAD87bVTQ3sMXmamJPHvtVEZlp/P9p5by/tbgzcr/o2QTbrdy/UnDg/YevkhNjOPfVx9FUUE/fvL8Cu5/f2PQKps8s3Abdc1tXHv8YUG5vq+S4mN56IrJnDhqAL9+ZTW/n70uaOOlt9fsZEdtE1ccE5mz0uDjYFpVr3UentlxxgNPhY+oc/mUfHbUNvHhRrsR0RjTqzwGvAO0/9a/EfhJ2KIJMc+CLeHJl+7MsSOyeP77U2l1Kxc+OC8oy46vLq/llRXlXD29IGSL1XQlKzWR5743lVPGDOKpdS3c/tpqmttcAX2PippGnlu0nYuK8sM2Q+stLSmeJ757NBccmcf973/GT59fQWNLYNu8a28Tj3yymWOHZzE+N/z1H5LiY3noO0V855ihPPTRZr73xBL2NQX2y1NFTSO3vbaGkYNSOXl08Ms9dpe/2frzfNzX6508ZhBZqYk8u8hSPYwxvUqWqr4AuAFUtQ0I7Kd6hFJVz8x0BAwovY0bnMHL/28aef36cM3jS7jr9bUBG1y2udz89s21ZCTH88Pi8M7QektOiOX/vj2Z0wvieHz+Vr7x93ls2hWYmfmGljZ+9OxyELjuxGEBuWYgJMTFcM9FR3Dz6aN4bWUFZz/wMSu31wTk2o0tLmY+sYSGFhe/OmtMQK4ZCPGxMdw1Yzy/+cZ4PtxYydkPfMKiLXsCcu2WNjfXPbOM5lYXD357clAXIeopX3Oms0VkMpAsIpO87hAvBsL/lTAI4mNjOGXMQJZutRURjTG9Sr2IZAIKICJTgfCvAxwCVfUtNLe5I24wDZ70wZd/OI2rphXw6NwtnP+PeT1ecbfV5ebHzy1nweY9/OKM0WQkxwco2sCIjREuG53Io1cV8cXeJs756yc89NHnPfoi0dLm5gdPLWP5tmoeuHQief0iawgiIlx34nCennk0Ta0uzn9wHve+t7FHs9Rut3LjCyv4tLyWBy6dxNjBkbX6H3jK5j137VQALnloPr95Yy0NLT1bLfH3s9exfFsNf7poQsTmSrfzdZh/Op7c6DzgXr7Ml74R+FVwQgu/wqwU9tS3UNsYmjuxjTEmAG4EZgHDRGQu8ATwo/CGFBrtZfFyI2yA1S4pPpY7zhvHQ1dMpnJfM+f/Yx7/WtXMrr3+35zY0ubmR88sZ/anO7n17DFcOmVIECIOjJNGD+LtG45j+rAsfj97Pafd9xFvr97pd15xc5uLnz6/go82VvKH84/gjPE5QYq456YNy+KtnxzPuUfk8MB/P+PEe0q6dR9WY4uL/3ltNW+t3smvzxrDKWMHBSninjuqoD9v3XAc3z56KI98soUT/lTCE/NL/V5qvrHFxe2vreaxeaXMPLaQsw6P3L/ndj4V61PVx4HHReQCVX0pyDFFjKGZKQBsrarniLzQFYM3xpjuUtVlInICMAoQYIOqfi1mBL4sixc5OdOdOW1cNtOGZ/G3OZv410efc+wfP+DcCYO5enqBT7mwCzZXcc87G1iytZrbzhnLd8NQIs1fA9OTeOSqoyjZ4FlB7wdPLWXYgBS+PXUo5x+Z1+WsututvL6qgj+9s4Gy6kZ+fdYYLj4q8lbB6ygjOZ77L53EZVOG8Pu31vPzF1fx9w82cXFRPhdOzjvkwjrvr/2C22etobymke8dVxiWUnj+SkmM4zffGM+MiYP537c3cNtra/jnh5u55Kh8vjkp95D57UtK93Dzi6vYsrueq6cXcMuZo0MUec/4VflaVV8SkbPx1DBN8tp/V6ADiwSFWZ7BdGlVgw2mjTG9gogkAT8EjsWT6vGxiPyfqoZ+Ob4QW1uxlxghIm5IO5TUxDh+ceZoCt0VrGkbyItLy3hpWRkjBqYyfXgWxwzLJL9fH/r2iSchLobNlfVs+GIfb6ysYOGWPQxIS+SeiyZw4eS8cDfFL8WjBnLs8CxeW1HBkwu2cufra7l79nom5GdwVEF/xuSkk5IYS3J8HBU1jawqq2H+5io2flHHmJx0nrzmcI4bEdpFaXrq6MMyefWH03h79U7+Pa+UP72zgXvf28gReRlMzO/LEXkZpCXGExsj1DW3sbh0D/M/r+KzXXWMHJTKC98/himF/cPdDL8UFfTn+e9P5aPPdvOPDzZx73sbufe9jUzM78uEvAzG5KSTnZFEm0tpanOxfFsNc9bvYsvuenL7JvPM945m2rCscDfDZ34NpkXk//DkSJ8IPAxcCCzy8dwzgL8AscDDqvqHgxx3AfAicJSqLvEnvkAb4nTIpbvrwxmGMcb44wlgH/BX5/nlwJPARV2d5AzCPwIS8Xw2vKiqt4uIAL91zncBD6rqA87+v+Cp6NQAXKWqy4LQHp+oKrNX72BKYX/SkyIrd7grg1JiuKR4PD87bRQvLyvjgw2VPLd4G4/NK+38+PREbj93LJdNGRL2WtrdFRcbwwWT87hgch6ry2t53fmC8M+PNn8lDaJPQizjczO456IJfHNSLrExEqaoe0ZEOPPwHM48PIctu+t5aWkZi7bs4dlF2/j33APTIPokxHJUQX+uOGYolx41hIS4yL3xrisiwgkjB3DCyAGUVTfw2ooK5qzfxYtLy6jvkEOeEBvDMcMyuXp6Ad+clEtaL/p/GPwcTAPTVPUIEVmlqneKyJ+Btw51kojEAn8HTsWz2MtiEZmlqms7HJcG3AAs9DOuoEhOiCUnI4nSKhtMG2N6jfGqOtbr+QcisvagR3+pGThJVetEJB74xKlVPQbIB0arqltE2utTnQmMcLajgQedP8Ni4xd1bK6s5+ppBeEKoUcykuO5enohV08vpLnNxeryWir3NVPT0Epjq4vCrBRGDkojc9H50AAAIABJREFUJyMJz/eY6DA+N2N/akt9cxtl1Y00tLTR2OIiKy2RYQNSe+0A+mAKs1K46XRPPfBWl5stu+tpanXhcivxsTGMyk4L6dLooZDXrw/XnTic604cjtutbNvTQFV9MwmxscTHCfn9+pCSGHnLhPvK38jbfyZsEJHBQBWeFREPZQqwSVU3A4jIc8AMoGMH/xvgj8DNfsYVNEMz+9jMtDGmN1kmIlNVdQGAiBwNHPJXPvXcDVbnPI13NgX+H3C5qraX2msvvj8DeMI5b4GI9BWRHFUNzZrKHbz56Q5E4PTx2eF4+4BKjItl8tDe9bN+IKQkxjEqOy3cYYRUfGwMIwd9vdocEyMUZKVQ4KTSRgN/v/q8LiJ9gT8By4BS4BkfzssFvAs2lzn79nOWJc9X1Tf9jCmoCrNS2FrVEO4wjDHGV5OBeSJSKiKlwHzgKBH5VERWdXWiiMSKyApgF/Ceqi4EhgGXiMgSEXlLREY4hx+yXw+l2Z/uYEpBfwamRfbNh8aY6OPzzLSIxAD/VdUa4CUReQNIUtUe1y91rn3v/2fvvsOrqrIGDv9WeiWBJIQSIPReRQRs2D4bijoo2HXAjnXGUWcc2zg6xTL2MhYsWBDRQUTFQuyI9NAJPdQQpARIvev7455ARCD3Jrdnvc+Tx+Tcc89ZW2BnZWedtYErPDj3auBqgOzsbPLy8ry+X0lJicfvq9pRTvHuCqZ8Po2k2ND/VZM3YwtHkTw+G1v4CrHxnVbXN6pqFdDHWTT5QER64K6hLlXV/iJyHvAKcKyn1wzEnL1+l4uCLXsZ2DUulP4cPBJif3d8LpLHF8ljg8gen8/HpqoefwBzvDm/xvsGAZ/V+Pou4K4aX6cBW3GvdK/GXU6yAeh/uOseccQRWhfTpk3z+NxP8jdqmzsm6/x12+t0r0DzZmzhKJLHZ2MLX3UZHzBT6zCfevIBNAZ6Af2qP+pwjXuAPwJLgLbOMQF2OJ+/AFxY4/ylQPPDXdNfc/ZjU5dq7p2TdfPOvXW6fjDZv43wFcljU43s8dV1bIeat70t8/hSRH4n3j/98DPQUUTaikgcMBL3pgIAqOoOVc1U1VxVzQWmA2drkLt5wP72eKvsIURjTBgQkb8B84En2b/B1iMevC/LWZFGRBJxPzC+BPgQdwcngOOBZc7nk4DLxG0g7iQ7KPXSU/I3cqSVeBhjgsTbBxCvwb27VqWIlOJepVBVPezelqpaKSJjgM9wt8Z7RVUXisgDuLP8SYd7fzBVt8dbYw8hGmPCwwVAe1Ut9/J9zXFvzhWN+3ma8ao6WUS+A8aJyK24H1Ac7Zw/BXdbvALcrfGu9En0XppfuJ3lW0p4YFj3YNzeGGO83rSlzo+cquoU3JNvzWP3HOLcIXW9j69Vt8ezlWljTJhYAKTjfojQY6o6H+h7kOPbgTMPclyBG+oYo09UuZS/friAzJQ4hvUO2rOPxpgGzttNW75U1ZNqOxZprD2eMSaMPAzMEZEFuHtHA6CqZwcvJP94c/oa5hXu4ImRfUhLCq9NHowxkcOjZNrZGSsJyBSRxrjLOwAaEcRWSIHSNjOZqQs3BzsMY4zxxGu4+/XnA65azg1bm3aU8u/PlnJsx0zO7t0i2OEYYxowT1emrwFuAVoAs9ifTO8EnvZDXCElNyOZ4t3l7CytCKttao0xDdIeVX0y2EH4k6pyz/8WUFHl4sFzekTUjoDGmPDjUTKtqk8AT4jIjar6lJ9jCjltMtwdPdZs3UPPnLQgR2OMMYf1rYg8jLvbRs0yj9nBC8l3XC7lnkkLmLpoM3ed3mXf/GyMMcHi7QOIT4nIYCC35ntV9XUfxxVSarbHs2TaGBPiqh8iHFjjmAInBiEWn6pyKXdNnM/4mYVce3x7rj6uXbBDMsYYrx9AfAP31rJzgSrnsAIRnUxbezxjTLhQ1RNqPyv8FO0q4+4P8/ls4WZuPqkjt5zc0co7jDEhwds+0/2Bbk5LpAYjMS6a7EbxrN22J9ihGGPMYYlINvAQ0EJVTxeRbsAgVX05yKHViculTFtbwU15eeytqOLuM7sy+lhbkTbGhA5vd0BcADTzRyChrlFCLCVllcEOwxhjajMW9wZZ1S0uluF+gDws/XHCPF5bVE73Fml8cvNxlkgbY0KOtyvTmcAiEZlBhPcvPVBSXDR7yqtqP9EYY4JARGJUtRLIVNXxInIX7NuBNmwnr5FHtiajoog/X3SUlXUYY0KSt8n0ff4IIhwkxkWz15JpY0zomgH0A3aLSAbu51kQkYHAjmAGVh8D2jZhz5pYS6SNMSHL224eX4tIG6Cjqn4hIklAtH9CCy1JcTFs2VUa7DCMMeZQqrPN23C3xWsvIt8DWcDwoEVljDERzttuHlcBVwNNcHf1aAk8D0T0duLgXpm2Mg9jTAjLEpHbnM8/AKbgTrDLgJOB+cEKzBhjIpm3ZR43AAOAnwBUdbmINPV5VCEoKdbKPIwxIS0aSGH/CnW1pCDEYowxDYa3yXSZqpZX166JSAxOXV6kswcQjTEhbqOqPhDsIIwxpqHxtjXe1yLyZyBRRE4B3gM+8n1YoSchLpq9FZZMG2NClj2hZ4wxQeBtMn0nUATkA9fgrsm729dBhaKk2BjKK11UuRrEQrwxJvxE/LMrxhgTirwt80gEXlHV/wKISLRzLOK3BkyKczct2VNeSWpCbJCj8R1VZf32vSzfUkLbjGRyM5ODHZIxpg5UdVuwYzDGmIbI22T6S9xPhZc4XycCU4HBvgwqFCU6yfTe8qqISKaXb97Ff75YzjfLi9hVun9nx67NG3Fmz2b8/pi2JMV5+9cjtKkq3y7fyviZ61i7bQ/rf9mLS5Xf9cvhkoFtIvYHiQXrd/D6j6tZumkXu8oq2VNWxTEdM7n5pI60ahKZz6YVbNnFuz+vI29pES5VYqOjaJGeyJ2nd6FTdmqwwwtJIpIAfAPE4/7eMEFV763x+pPA71U1xfk6HngdOAIoBkao6upAx22MMcHmbbaUoKrViTSqWuL0mo54+1emw7tueuOOvfz7s6V8OGc9SXExnNW7Bd1bNKJD0xQWbtjJJ/kbeWTqMuas3c6Ll/UnOioyyjC/WrKZJ75YzrzCHWSmxNG1eSO6t2jEjr0VjP1hNS99t4oL+ufwz9/1ipjNIWas2sYjU5cyY9U2kuKi6Z/bhFZNkhARJs3bwP/mrueiAa258/Su+35YDHeLNuzkvkkLmbF6GzFRwtEdMkmJj6HS5WLGqm2c+eS3XD+kA9ef0J74mMgYsw+VASc683os8J2IfKKq00WkP9D4gPNHAb+oagcRGQn8ExgR4JiNMSbovE2md4tIP1WdDSAiRwB7fR9W6ImEZPqbZUXc/M4c9pRXMfrYdlx7fHuaJMfte31guwxGHdOWN6av4a8fLuBvkxdx39ndgxhx/e0pr+Te/y3kvVmFtGqSyMPn9eS8fi1/lUht2VnKs3krGPvDajo2TeWq49oFMeL6K6908djny3jhmxU0b5TA3Wd25fz+rUhL3P8blY079vLklwW8Pn0NLoW/ndMjiBHXX0WVi+fyVvDkl8tJT4rjL2d05dx+LclMid93TnFJGX+bvIgnvlzOjFXbeOsq2566JlVV9v/WMdb5UKec79/ARcC5Nd4yjP274k4AnhYRca5jjDENhrfJ9C3AeyKyAfeT481oICsRiU7Jw96KylrODD0ul/LUVwX858tldGqaynOX9KNdVsohz790YBvWbN3NS9+tok1GElce3TaA0frO0k27uOGt2awoKuHGEztw00kdiY3+7TO3TRslcO9Z3di8s5R/fLqEvq3T6Z/bJAgR19/a4j1c/9YsFqzfyYUDWvPXoV0PWq7TPM39g0VSXDQvf7eK03s2Y3D7zCBEXH9Fu8oY/fpM5q3bzrA+LbjvrO40rvFDYrWMlHj+M7IvfVqlc99Hi5g0bwPD+rQMQsShy0mcZwEdgGdU9ScRuRmYpKobD/jhoyWwDkBVK0VkB5ABbA1w2MYYE1Tebif+s4h0ATo7h5aqaoXvwwo94boyXVnl4k8T5jNxznrO7duSv5/bw6Na6LvO6MrabXv42+RFnNC5adjVE/+4opjRr/1MYlwMb446iqM7HD5RFBH+ObwXi5/6jjFvzeHjm44ho8aqZjhYuGEHl7/yMxVVLl689Aj+r3uzWt/zx//rzJeLN3PH+/P57Jbjwq5OfkVRCVe8OoOtu8p55qJ+nNmrea3vuXRQLhNmF/LwlCWc0i077MbsT6paBfQRkXTgAxE5DjgfGFLXa4rI1bh3ziU7O5u8vDyvr1FSUlKn94WDSB4bRPb4InlsENnj8/XY6vJd5Egg13lvPxFBVV/3WUQhKjF2/wOI4aK80sUt785hSv4m/vh/nbjhhA4e/1o7Okp4YFgPPl+8mYlz1nPbKZ38HK3vfLl4M9eNm02bJkm8MeoomqUlePS+RgmxPHNxP8599gcembqUh8/r5edIfefHFcVc/fpMUhJieOfqQXRo6tlDdolx0fxreG9GvPgj//p0aViV9cxe+wujxv5MlAhvXz2QPq3SPXpfdJRw31ndGf78jzyXt4I//F/n2t/UwKjqdhGZBpyAe5W6wJk7kkSkQFU7AOuBVkChs4FXGu4HEQ+81ovAiwD9+/fXIUOGeB1PXl4edXlfOIjksUFkjy+SxwaRPT5fj82rPtMi8gbwCHAM7qT6SKC/z6IJYfu6eYTJxi1llVVc9+YspuRv4q9DuzHmxI5e14c2S0vg6PaZfDhnPeFSBjl5/gaueWMWXZqlMv6aQR4n0tW6t0hjaM/mfLJgExVVLj9F6VvfLd/K5a/OIDstgfevG+xxIl1tQNsmXD4ol7E/rKbwl/Docjl33XYue3kGaYmxTLx+sMeJdLX+uU0Y1qcFL3yzknXbwmPM/iYiWc6KNCKSCJwCzFLVZqqaq6q5wB4nkQaYBFzufD4c+MrqpY0xDZG3m7b0B45W1etV9Ubn4yZ/BBZqwqnMw+VS/jB+Hl8u2cKD5/Rg1DF1r3k+t29L1m7bw6w1v/gwQv+YtnQLt7wzl36tGzNu9FEHrZv1xOk9m7N9TwXTV/5mkS3kzF77C1e/MZN2mcm8d80gWqQn1uk6lw1qA8C0pUW+DM8vFm/cyeWvzKBJchzvXD2INhl1K0G68/QuRAm88M0KH0cYtpoD00RkPvAz8LmqTj7M+S8DGSJSANyGe1MvY4xpcLxNphfgfuiwwUmKdVfEhHoyrar87eNFTJ6/kTtP78IlA9vU63qn9WhGYmw0789e76MI/WPWmm1c9+YsujRP5eUr+terF/ixHTNJjotmSv4mH0boe4s37uSKV2aQlRrP66MG1PmHB4C2mcm0yUhi2pItPozQ91YUlXDJSz+RFBfNuNGel/AcTPO0RI5un8n3BaH/Q1MgqOp8Ve2rqr1UtYeqPnCQc1JqfF6qqueragdVHaCqKwMbsTHGhAZvk+lMYJGIfCYik6o//BFYqNm/aUtod/OYsqqCV79fzahj2nKND1q8JcfHcGr3bD6ev4HSEC1xWbZ5F1e++jPN0xIZe+WAem+qkxAbzYlds5m6cBOVIVrqsWH7Xi57ZQZJzgOWTVPrnlSC+wHMEzo35YcVW0P2z7m4pIwrX/0ZERg3+iifbDgzqH0Gq7buZuOOBtHh0xhjjB94m0zfB5wDPAQ8WuMj4sXFRBETJSG9Mv3pgo28t6yCs3u34C9ndPVZD91z++Wws7QyJFcti0vK+P3Yn0mIjeb13w/4VV/h+jijRzOKd5czY3Xo7dC8u6ySUa/NpLS8itdHDfDZLoZDOmdRWuEKyfKW0ooqrnljFpt3lvLfy/oftrWjNwa1zwDcD3AaY4wxdeFVMq2qXwNLgFTnY7FzrEFIjIsO2WR68cad3DZ+Hu3SovjX8F5E+XDnwqPbZ5CVGs/EOaFV6lFe6eK6cbMp2lXGi5f19+nW2EM6NyUxNppPQqzUw+VSbnl3Lks37eSpi/r6dGvsge0ySIiNIi/E6qZVlTven8/MNb/w2AV96Nv6wI346q5rs0akJ8XygyXTxhhj6sjbbh4XADNw9x29APhJRIb7I7BQlBQXHZKt8bbtLueq12eSmhDDTX3jSYj17TbJMdFRnN6jGd8uL8LlCo2H9VWVv364gBmrtvGv4b287uZQm8S4aE7oksWnCzdRFSJjBvj31KV8vmgz957VnSGdm/r02gmx0Qxun8lXS7aEVPeWZ/NW8L+5G7j91M4e9ZH2RlSUMLBtBj+uKA6pMRtjjAkf3pZ5/AU4UlUvV9XLgAHAXz15o4icJiJLRaRARH7z1LeI3CYii0Rkvoh8KSL1e3LODxJjo9kTYvWkVS5lzFuz2bKrjBcv7U96grd/pJ7p1rwRpRUu1m8PjdrSN39ay7sz1zHmhA5+28Xu9B7NKdpVFjKdTD7J38hzeSu4+KjWXD441y/3OKFLU9Zu28PKrbv9cn1vfbu8iEenLmVor+ZcP6S9X+4xqH0G67fvZd220Pi7bYwxJrx4m3lFqWrNwtliT67hbFH7DHA60A24UES6HXDaHKC/qvYCJgD/8jI2v0uMiwm5lenHP1/GDyuK+fs5Pejt49XZmjpmu2tUl2/Z5bd7eGruuu088NFChnTO8utmMsd3zgJg5prg102vKCrh9gnz6dMqnXvOOvCfju8M6eQecyjUxxf+soeb3p5Dh6Yp/PN3vXz2DMCBBlfXTa+0XbCNMcZ4z9tk+lOnk8cVInIF8DHwiQfvGwAUqOpKVS0H3gGG1TxBVaepavXuCdOBHC9j87ukuGj2VoRON49pS7bw9LQCRvRvxfn9W/n1Xh2y3LW5yzaX+PU+tSkpV24YN5umqQn8Z0Qfn9aGH6hRQixNU+NZWRTcVdrdZZVc+8Ys4mKiePbifsTH+LaMp6ZWTZLo2DSFaUuDm0yXVVZx/bjZVFYpL1zan+R4/2353aFpCpkp8VY3bYwxpk68fQDxduAFoJfz8aKq/smDt7YE1tX4utA5diij8CxJD6ikEHoAcf32vdw6fi5dmzfi/mH+3wI6LcmdWC4PYjLtcikvzC+jaFcZz13Sj/SkuvdV9lS7rGRWFgVvzKrKnz/IZ0VRCU9d2LfOm7J4Y1D7DOat2xHUGuKHPl7M/MIdPHpBb9pm1m1TFk+JCIPaW920McaYuvFouUdEOgDZqvq9qk4EJjrHjxGR9qrqsy3EROQS3DstHn+I168GrgbIzs4mLy/P63uUlJTU6X27d5RStMdVp/f6UpVLeXhGKaVlLi7vEMP077/d91pdx+aJzLgKZq/YQF5ecGqIP15ZTv7WKi7rFse2grnkFfj/ngkVZeRvqmTatGl+KzOodrA/u28KK/jfgnLO7RBLReEC8gr9GgIAVb9UUFJWyUef59Eozjdj9ubv5cxNlbw2t4xT28QQV7SEvLwlPonhcDIqK9iyq5y3P55GixTvnzvw5787Y4wxoc3T353+B7jrIMd3OK+dVcv71wM16xBynGO/IiIn437I8XhVLTvYhVT1ReBFgP79++uQIUNqi/038vLyqMv7Ptw0h61rt9fpvb706NSlFGwv4ImRfX7z8F1dx+aJvJ0LGT9zHccff7zfE8sDzV77CxOn/siRzaK5/9KTA3b/guiV5K1bTK8jB5Phox7Wh3Lgn93yzbt468vvGNw+g0d+fxTRfixpqUmXbGHckp9p2bkPR7TxTRs6T/9ertu2hxvzvqV3ThpPXTWYuBj/PFB7oNZFJYxd+DUx2R0ZcqT3JVP+/HdnjDEmtHn6nSpbVfMPPOgcy/Xg/T8DHUWkrYjEASOBX+2cKCJ9cZeQnH3AQ44hIzEuJuhlHj+s2MrT0wo4/4gcv3WxOJSO2SnsKa9iw47SgN53x94Kbnp7Ds0aJXBF9/iAJvLtnc1BAt3dorSiijFvzSE5Lob/jOgTsEQaoE2Gu1/3muLAjrmiysWNb88B4OmL+gUskQZo3SSJmChhzbbQ6GJijDEmfHj63epwbSJqLeJU1UpgDPAZsBgYr6oLReQBETnbOe3fQArwnojMDcVtyt19poP3AOK23eXc+u5c2mYmB6RO+kAdm1Y/hBi4jh6qyp8n5rNxRylPXdSX5NjAroi3y3LX6wa6bvrvHy9m6eZdPHpBb5o2qt9W4d7KaZxElMDq4j21n+xDT3yxnLnrtvOP83r5dAMeT8RER9EiPZG11h7PGGOMlzwt85gpIlep6n9rHhSR0cAsTy6gqlOAKQccu6fG5yd7GEvQVPeZVtWAlzmoKne+P59tu8t5+fIjSYrzX3eDQ+nY1L1KW7C5hBN8vGHIoUyYVcjH+Ru5/dTO9GvdmLyVAbntPjmNk4iLjgpoR48vF2/mjelrGH1MW59vzOKJuJgoWjZODOjK9E8ri3kmr4AL+uf4fGMWT7VuksTabYH9AcIYY0z48zQjuwX4QEQuZn/y3B+IA871R2ChKDEuGlUoq3T5fJfB2oyfuY6pizbz5zO60KNlWkDvXa1xchyZKXEB6zW9png3901ayFFtm3Dt8f7ZsKM20VFCm4wkVgQomd6yq5TbJ8yna/NG3H5a54Dc82ByM5IDtjK9Y08Ft747l9yMZO49K/C/canWqkkSny0Mre3jjTHGhD6PkmlV3QwMFpETgB7O4Y9V9Su/RRaCkuLcCfTe8qqAJtOrtu7m/o8WMbh9BqOPaRew+x5Mx6apLN/i/5KHyioXt7w7l+go4fEA1wwfqF1WckDGrKrc/t58dpdV8uTIPn7tJ12bNhlJTJ6/0e/3UVX+/GE+W3aV8f51g/3aT7o2rZsksW13OSVllaQEMQ5jjDHhxds+09NU9Snno0El0rA/mQ7kluIVVS5ufXcuMVHCoxf09usmJZ7omJ1CweYSv/fjfeqrAuas3c7fz+0ZkN7Kh9MuK4W1xXuoqHL59T5frK3k62VF3H1mVzpmp/r1XrXJzUhm+54Ktu8p9+t9Ppy7no/nb+TWUzr5dQdPT7R26rTXWamHMcYYLwTucfkIkOjUKQfyIcRnphUwd912HjqvJ83TgptUgrtueldZJZt2+q+jx+y1v/D0tALO69uSs3q38Nt9PNUuM5lKl/o1yVq+eRfjl5ZzQucsLhnYxm/38VSbDPeDl2v8WOqxbtse7vlwIUfmNg5aGU9N1cm01U0bY4zxhiXTXkhySjsC1R5v7rrtPPVVAef2bcnQXsFPKgE6OB09/LUT4u6ySm59dy7NGiVwXxA6lhxMu+r2eH6qmy6vdJe0JETDP4f3CvjDrQeT67THW+2nhxCrXMofxs9DgccuCG4ZTzVbmTbGGFMXlkx7YV+ZRwCS6T3l7qQyOzWe+84OjaQS3GUegN9qiP82eRFrt+3h8RF9aJQQ65d7eKt9dXu8rf4Z8+NfLGPhhp1c2SOepqmBbYN3KK2aJCHiv5XpF75ZwYzV23hgWPeAt8E7lLSkWFITYhrsyrSIJIjIDBGZJyILReR+5/g4EVkqIgtE5BURiXWOi4g8KSIFIjJfRPoFdwTGGBMclkx7IbHGA4j+9tCUxawu3s2jF/QhLTE0kkqAjOQ4GifFUuCHjh6fL9rMOz+v45rj2jOgbROfX7+u0pPiaJIc55eV6RmrtvH81ysYeWQr+mWHzkNvCbHRNG+U4JeV6QXrd/D458s4s2dzzu0b2I2HatPA2+OVASeqam+gD3CaiAwExgFdgJ649xUY7Zx/OtDR+bgaeC7gERtjTAiwZNoL1b2d/b0yPW3JFt6cvpbRx7RlUPsMv97LWyJCx6apFPh4ZXrLrlLueH8+3Zo34rZTOvn02r7QLjOZFT7euGVnqbslXOsmSfx1aDefXtsX2mQk+3xlurSiilvenUuT5Dj+fm6PkChpqakhJ9PqVv2XPNb5UFWd4rymwAwgxzlnGPC689J0IF1EgtMk3Bhjgih0lsLCQKJTM73Xj908ikvKuH3CfLo0S+WPpwavz/Dh5GYm8dWSIp9dT1W5Y4K7JdwTI/sEdBtpT7XPSuGLxZt9es37Ji1k085S3rt2UFBbwh1KbmYSny/y7Zj/8ckSCraU8MaoAaQnxfn02r7QukkSXy7ZgsulQe+cEwwiEo17L4EOwDOq+lON12KBS4GbnUMtgXU13l7oHPtVT0URuRr3yjXZ2dnk5eV5HVdJSUmd3hcOInlsENnji+SxQWSPz9djC73v4CFsf5mHf7p5qCp3Tcxn594K3hg1IKh9hg+nbWYKW0sK2Vla4ZO65jd/Wsu0pUXcd1a3oLeEO5R2WckUzyxnx54K0pLqP+Yp+RuZOHs9N53UkX6tG/sgQt9rk5HM1pJydpVWkOqDP+e8pVsY+8Nqrjw6l2M7ZvkgQt9r1SSJ8koXW3aV0SwtNOrXA0lVq4A+IpKOe6OuHqq6wHn5WeAbVf3Wy2u+CLwI0L9/fx0yZIjXceXl5VGX94WDSB4bRPb4InlsENnj8/XYQm8JMIT5+wHE92YWMnXRZv54aie6Nm/kl3v4QttM9wN5q7fWv562YEsJf/94Ecd1yuKyQbn1vp6/VHf0KPBBqceG7Xu5a2I+vVulc+OJHep9PX+p7ujhi1KPneXKH9+bT6fsFO44rUu9r+cv1h7PTVW3A9OA0wBE5F4gC7itxmnrgVY1vs5xjhljTINiybQXEv3YGm/V1t3c99FCBrZrEvRdDmvTzulusaqeyXRZZRU3vzOHxNho/j28V0j/Wr1TdReTzfV78LLKpdw2fi4VVS6eGNGH2OjQ/Sfoq17Tqsor+WXs3FvBEyP7BnT3UG815GRaRLKcFWlEJBE4BVgiIqOBU4ELVbXmzkWTgMucrh4DgR2q6v9tM40xJsRYmYcXoqKEhNgon9dMV1S5uOWdOcRGR/H4iD4hnVSCO+EQqX8y/chnS1m4YSf/vaw/2Y1C+1fqrRonkRAbxbJ69td+4ZsVTF+5jX8N70Wus8Ifqtr4qNcZJM5IAAAgAElEQVT0uJ/WMreoir8O7RbSv3EBaJGeiEjDTKaB5sBrTt10FDBeVSeLSCWwBvjReWB0oqo+AEwBzgAKgD3AlcEJ2xhjgsuSaS8lxcWwx8c1049/vox5hTt47uJ+IbHLYW0SYqNpkZZYrzKPb5cX8d9vV3HJwNac0i3bh9H5R1SUu4vJsnqsTM8v3M5jU90t4c4/Iqf2NwRZUlwMWanx9fpzXrZ5Fw9+vIgeGdFcOTjXd8H5SVxMFC3SEhvkxi2qOh/oe5DjB/0+4XT3uMHfcRljTKgL3d8xh6jE2Giflnn8uKKY575ewYj+rTi9Z/h0lWqXlVznlemtJWXcNn4eHZqm8JczQq8l3KF0zE6pczK9s7SCMW/NoWlqPA+d2zPkWsIdSsemKSyt45j3llcx5q3ZpMTHMLpnXMj/xqVaqyaJDXVl2hhjTB1YMu2lpLhon23aUlxSxs3vzKFtRjL3nBU+SSVAbkYyK7fuxr045TmXS7n13bns3FvBUxf23dchJRx0zk5ly64ytu8p9+p91V1a1m/fy5MX9vVJN5BA6ZWTzuKNOymr9P7v/AOTF7FscwmPXdCH9ITwmWoacq9pY4wx3guf73AhIjHONyvTLpdy6/h5bN9bwdMX9QvJPsOH0zYzmV2llWzb7V1i+dzXK/h2+VbuPat7yNfPHqiT07bP27rpt2es4+P5G/nD/3Wif27o7Ozoid45aVRUKYs3erc6PXn+Bt6esZZrj2/PcZ1Csw3eobRukkTRrrKA7HRqjDEm/Fky7aXE2GifPID4/Dcr+GZZEfcM7Ua3FuGVVAK0rUNHj59WFvPo1KWc3bsFFw5oVfsbQkynZtXJtOeJ5aINO7n/o4Uc2zGTa49r76/Q/KZXq3TAXe/tqYItJdz5fj59W6fzh/8Lvd0sa9Pa6WKycqtvd7w0xhgTmSyZ9pIvyjzcSeUyzuzVnIuPau2jyAKr7b6Ew7NkesvOUm58ew5tMpJ56LzwqRmuqUVaAinxMR63x9u+p5xr3pxJelJsWHRpOZgWaQlkpsQxb90Oj84vKavk2jdnER8TxTMX9Qvp1n+HcmSuexOdHwqKgxyJMcaYcBB+3+mCrL7dPDZs38sNb82mTZMkHg7TpBIgp3EiMVHiUaeHssoqrn1zFiVllTx3ST9SwqykpZqI0MHDB/KqXMpN78xl045SnrvkCDJT4gMQoe+JCL1z0pnnwcp09bbwK4tKeOrCvrRID/3ONAfTPC2Rjk1T+GZ5kUfnT56/gUqXd88OGGOMiRyWTHspsR4r06UVVVz35ixKK1y8eNkRPtmKO1hioqNonZFUa5mHqnLv/xYye+12Hj2/N12ahV9JS02ds1NZ7kHN9GOfL+WbZUU8MKxHyG4X7qleOemsKCqhpOzwP0S++M1KPs7fyJ9O68LgDpkBis4/juuUxYxV2yitpaTrjR9XM+atOXxd6Nt2mcYYY8KHJdNeSoqLZk8daqZVlbs/XMC8wh08ekFvOjRN9UN0gdU2o/b2eG9MX8M7P69jzAkdwqr136F0zE6heHc5W0vKDnnOxNmFPDNtBRcOaMWFA8KzjKemXq3SUIX8wkOXenySv5F/fLqEM3s255rjQnsHT08c2zGTskoXM1ZtO+Q5eUu3cN9HizipS1NOaBWev20xxhhTf5ZMe6mu3Tye+3oFE2YVctOJHTi1ezM/RBZ4bTOTWV28G9chfsX96YKN3DtpISd3bcqtp4Tfg2gH07mWhxC/W76VP02Yz+D2Gdx/do9AhuY3vXPcDyEeqtRj9tpfuOXdufRtlc6jF/QO29Klmo5qm0FcTBTfHqLUY+mmXYx5aw6ds1N58sK+REXAmI0xxtSNJdNeSoqNobzSRZUXNZITZxfyr0/dXSxuOTkykkpwd/QorXCxaWfpb16bvrKYm95xJ1hPXdiP6DB8+O5gqtvjHazUY+GGHVz75iw6NE3h+UuPIC4mMv55NUmOo1WTxIN29Fi1dTdXvTaTZmkJ/Pey/iTEhk/f8MNJjItmQG4Tvlm29Tevrdu2hytfnUFSXDQvX9E/7NpaGmOM8a3I+G4fQIlx7v9lnj6EWL1SOahdBv8+v1dYdnQ4lOqOHgc+hJhfuIOrXp9J6yZJvHz5kWG1MUttmqbGk5YY+5uHEBes38Hlr/xMakIMr155ZFjXwx9Mr5z033T0WLZ5FyNe+BGXKq9ecSQZYfqQ5aEc2zGTpZt3sbnGD4tri/cw4oUf2V1exatXHknztPB8yNIYY4zvWDLtpcQ49yqUJ72mZ6zaxjVvzKR9lnulMj4mcpJK2N9r+ufVv+zbCXHqwk1c8MKPNEqI5bXfD6BxclwwQ/Q5EaFTdsqv2uN9t3wrI1+cTly08MaooyIyweqdk8b67Xv31YrnF+5gxAs/AvDuNYNol5USzPD84tiO7s1mvlnmLvVYtXU3I178kT0VVbx11VF0b5EWzPCMMcaECPv9pJeSnF9j19bR44cVWxk1diYt0hN4fdQA0hIja6USIDs1gS7NUnn8i2VMXbSJAW2bMPaH1fRqmcZ/L+9P09SEYIfoFx2zU5kws5DLX5lB46RYPs7fSLvMFF77/QCapUXmmKvrpv/16RJ2lVbyzbIi0pPiGDf6KHIzk4McnX90bZ5KZko8H8xZz48ri/lo3gZS4mN4a/TAsNxoyRhjjH9YMu2lJKdk4XAPIX69rIhr3phJq8ZJvHXVQLJSI+vX39WiooT/jTmaD+es54VvVvLq96s5vUczHrugT0SVdhxo5JGt2LKzlM07y1iyaSfHdszi8RF9IvIHpmo9WqaRGBvN+JmFtG6SxKndm/HHUzuHbS9pT4gIx3XMZOKc9STFRXPxUW0YfWxbchonBTs0Y4wxIcSSaS8lHiaZVlVe/m4VD01ZTKfsVN4cfVTYbtbhqfiYaEYc2Zrzj2jFkk276NIsNaLqwg+mV046L11+ZLDDCKjk+Bg+v+04EmKjI/7vdE23ntKJI9s24YyezSP6hyVjjDF1Z8m0l5Kqa6YPSKb3llfx5w/y+WDOek7tns2jF/QJ253+6iIqSuxX3xGuIa7ItmqSFBG9wo0xxvhPw8n2fGR/mcf+bh7TlmzhnkkLKPxlL384pRM3nNAh4ldnjTHGGGNMALt5iMhpIrJURApE5M6DvB4vIu86r/8kIrmBis0b1WUeeyuqyC/cwdWvz+TKsT8TFx3FuNFHceNJHS2RNsaEHRFJEJEZIjJPRBaKyP3O8bbOnFzgzNFxzvGwmLONMcbfArIyLSLRwDPAKUAh8LOITFLVRTVOGwX8oqodRGQk8E9gRCDi80ai083j/o8WsW13OUlx0dxxWhdGHdM2YjbpMMY0SGXAiapaIiKxwHci8glwG/C4qr4jIs/jnqufI0zmbGOM8bdAZX8DgAJVXamq5cA7wLADzhkGvOZ8PgE4SUJwX+LGSXGkJcaSmRLH/Wd3Z/qfT+K6Ie0tkTbGhDV1q97aM9b5UOBE3HMyuOfoc5zPw2LONsYYfwtUzXRLYF2NrwuBow51jqpWisgOIAP47X6+QZQYF82su08mOkqw7xvGmEji/BZxFtAB928TVwDbVbX6IZFC3HM1hMmcbYwx/hZ2DyCKyNXA1c6XJSKytA6XySRyJ/xIHhtE9vhsbOGrLuNr449A6kNVq4A+IpIOfAB0qe81bc6uVSSPDSJ7fJE8Nojs8dV1bAedtwOVTK8HWtX4Osc5drBzCkUkBkgDig+8kKq+CLxYn2BEZKaq9q/PNUJVJI8NInt8NrbwFWnjU9XtIjINGASki0iMszpdc+62OdsHInlsENnji+SxQWSPz9djC1Sh789AR+ep8DhgJDDpgHMmAZc7nw8HvlJVDVB8xhjToIlIlrMijYgk4n5gfDEwDfecDO45+n/O5zZnG2MMAVqZdurpxgCfAdHAK6q6UEQeAGaq6iTgZeANESkAtuFOuI0xxgRGc+A1p246ChivqpNFZBHwjog8CMzBPVeDzdnGGAMEsGZaVacAUw44dk+Nz0uB8wMUTr1+5RjiInlsENnjs7GFr7Afn6rOB/oe5PhK3B2ZDjxuc7ZvRPLYILLHF8ljg8gen0/HJvZbOWOMMcYYY+rGmiMbY4wxxhhTRw0qma5tS/NwJiKtRGSaiCxytgK+Odgx+ZqIRIvIHBGZHOxYfElE0kVkgogsEZHFIjIo2DH5kojc6vydXCAib4tIQrBjqisReUVEtojIghrHmojI5yKy3Plv42DGGGkidd62OTu8RfK8HUlzNgRm3m4wyXSNLc1PB7oBF4pIt+BG5VOVwB9UtRswELghwsYHcDPu7gKR5gngU1XtAvQmgsYoIi2Bm4D+qtoD9wPI4fyg2ljgtAOO3Ql8qaodgS+dr40PRPi8bXN2eIvIeTsC52wIwLzdYJJpPNvSPGyp6kZVne18vgv3P+yWh39X+BCRHOBM4KVgx+JLIpIGHIfTIUFVy1V1e3Cj8rkYINHpRZwEbAhyPHWmqt/g7lxRU81ttWtut23qL2LnbZuzw1cDmLcjZs6GwMzbDSmZPtiW5hEzcdUkIrm4n8r/KbiR+NR/gD8BrmAH4mNtgSLgVefXoS+JSHKwg/IVVV0PPAKsBTYCO1R1anCj8rlsVd3ofL4JyA5mMBGmQczbNmeHnYidtxvInA0+nrcbUjLdIIhICvA+cIuq7gx2PL4gIkOBLao6K9ix+EEM0A94TlX7AruJoDIBpw5tGO5vPi2AZBG5JLhR+Y+zaYm1SDIeszk7LEXsvN3Q5mzwzbzdkJJpT7Y0D2siEot7Uh6nqhODHY8PHQ2cLSKrcf+a90QReTO4IflMIVCoqtUrUhNwT9KR4mRglaoWqWoFMBEYHOSYfG2ziDQHcP67JcjxRJKInrdtzg5bkTxvN4Q5G3w8bzekZNqTLc3DlogI7vqtxar6WLDj8SVVvUtVc1Q1F/ef21eqGhE/KavqJmCdiHR2Dp0ELApiSL62FhgoIknO39GTiJAHdWqoua12ze22Tf1F7Lxtc3b4ivB5uyHM2eDjeTtgOyAG26G2NA9yWL50NHApkC8ic51jf3Z2njSh7UZgnJMsrASuDHI8PqOqP4nIBGA27u4FcwjjXbVE5G1gCJApIoXAvcA/gPEiMgpYA1wQvAgjS4TP2zZnh7eInLcjbc6GwMzbtgOiMcYYY4wxddSQyjyMMcYYY4zxKUumjTHGGGOMqSNLpo0xxhhjjKkjS6aNMcYYY4ypI0umjTHGGGOMqSNLpo0xxhhjjKkjS6ZNWBGRDBGZ63xsEpH1zuclIvKsH+43VkRWici1Xr5vioik13LOv50x/LF+URpjTGiyOds0BA1m0xYTGVS1GOgDICL34d704GlVfcmPt71dVSd48wZVPQPA2U53tKp+cZBzbheR3b4J0RhjQs9B5uwSVX3Ez7et85xdyzk2Z5uDspVpE/JEZLWI7HVWMjY7Kw8pB5wzREQmO5/fJyKvici3IrJGRM4TkX+JSL6IfCoisc55R4jI1yIyS0Q+E5HmHsQyVkSeE5HpIrLSua+KiEtEKpxVl8ecmDNx/8D6soj8V0QWishUEUk8yHWHODszGWNMxAvynP2KiCwWkbE1zlstIpkikuu8dtg525iaLJk24eIsVU0B+gH9gbtrOb89cCJwNvAmME1VewJ7gTOdyfkpYLiqHgG8Avzdw1gaA4OAW4FJzrHOwHzgBuAiILXG+TnAM6raHdgO/M7D+xhjTEMRyDn7caA70FNE+hzk/I7YnG28YGUeJqyo6noR+QToAcx0DrcBbga6ishUYC7wiapWiMjdQCLwjojMAxYCubiT3z7AOmeSdgErq+8jIkOBB4FuwCARWaaq852XP1JVFZF8YDPuxFmdawN8C5xaI+yNqjpXROKBFsCzIvIvYDywC4gDPgHiRaTEeU8nVd1Q3/9fxhgTJqrn7HwgGvjUOZ7P/jm7B/C5iOCcs9HDa/9qzlbVfAARqf5+MPeA81epavWxWc45xhySrUybsCIirYAzgDk1Dl8E/BOYijsxHQyUOa99AuwGmgKzgXNx/xApzn9PUdVo5/ULnXv0xb3qcQ3wtnPdSU4yTI1ru2p8Xv11LnAsUF7jeIXz378ArYAXgN7AAOA459zTgQ2qmuJ8WCJtjGlIygBU1QVUqKo6x13sn7MXqmof56Onqv6fN9fm4HP2wRYVa55TdYhzjNnHkmkTLj4Uke3Ad8DXwEM1XnsVKMQ9MY4HmlW/oKqvOP8tA+4DsoEEYCnuyXmoiDQCStg/gV4NvKCqP+Fecf7aeW3gYeKbjTsZvxN4ybnegS4GPgd2q2oRcD/upNoYY8zhLQWyRGQQgIjEikj3IMdkDGDJtAkf56hquqq2UdXrVXVvjdc21fh8D+7VaUQkWkT+ASSJyE5gtXNOsqqWA1cAo4BtuOviLnFebwP8wUneLwJew72i3OIw8fXDvYo9RlUPVc/dAvilxtdr+HVttTHGmINw5uzhwD+dkr25uH8LaUzQyf7fpBgTmg7XXk5E8oA3q1vjicgVzrnHiMilwJ9xl4WsBtJwJ7MdVbWgxjVigTHAbaraSkReANaq6t+dp70nH67Nkojogdc8WOwisgK4UVWnOK/9H+6V9AeBn4Fxqprjzf8bY4wx+3kyZ9fz+vcRmPZ+JozYyrSJZKm4yzOKgSRqlIaISJyIXCwiaapaAezEXSYC8F/gWhE5CtgBPCgiT4tIfVeR3wbuFpEsp23eK849d+N+kDFDRNLqeQ9jjGnIdgB/Ey83bfGEiPwb928wrde0+RUrqjeR7HXcXTXW4y7l+CtwXY3XLwWeFpFo3PV4FwOo6kwRuQp4GneLpL24a63r60GgEe4WegDvAX9S1VIAEXkbWOnE080eQjTGGO+o6s1+vPbtwO3+ur4JX1bmYYwxxhhjTB1ZmYcxxhhjjDF1ZMm0McYYY4wxdWTJtDHGGGOMMXVkybQxxhhjjDF1ZMm0McYYY4wxdRTWrfHS09O1Q4cOwQ4joHbv3k1ycnKwwwgoG3PD0NDGPGvWrK2qmhXsOIwxxtRPWCfT2dnZzJw5M9hhBFReXh5DhgwJdhgBZWNuGBramEVkTbBjMMYYU39W5mGMMcYYY0wdWTJtjDHGGGNMHVkybYwxxhhjTB2Fdc20MSayVFRUUFhYSGlpabBD8ZmEhARycnKIjY0NdijGGGP8wJJpY0zIKCwsJDU1ldzcXEQk2OHUm6pSXFxMYWEhbdu2DXY4xhhj/MDKPIwxIaO0tJSMjIyISKQBRISMjIyIWmk3xhjza5ZMG2NCSqQk0tUibTzGGGN+zZJpY4xxlJaWMmDAAHr37k337t259957AVi1ahVHHXUUHTp0YMSIEZSXlwMwduxYsrKy6NOnD3369OGll14KZvjGGGOCwO/JtIhEi8gcEZl8wPEnRaSkxtfxIvKuiBSIyE8ikuvv2Iwxpqb4+Hi++uor5s2bx9y5c/n000+ZPn06d9xxB7feeisFBQU0btyYl19+ed97RowYwdy5c5k7dy6jR48OYvTGGGOCIRAr0zcDi2seEJH+QOMDzhsF/KKqHYDHgX8GIDZjjNlHREhJSQHcnUUqKioQEb766iuGDx8OwOWXX86HH34YzDCNMcaEEL8m0yKSA5wJvFTjWDTwb+BPB5w+DHjN+XwCcJJYsaExJsCqqqro06cPTZs25ZRTTqF9+/akp6cTE+NufpSTk8P69ev3nf/+++/Tq1cvhg8fzrp164IVtjHGmCDxd2u8/+BOmlNrHBsDTFLVjQfkyi2BdQCqWikiO4AMYGvNk0TkauBqgKysLPLy8vwWfCgqKSmxMTcADXXMaWlp7Nq1C4Cef//GL/fJ/8txtZ7z7bffsn37di6++GJmz56Ny+XaF1dJScm+r4cMGUJ+fj7x8fG88sorXHLJJUyePPk31ystLW1wf57GGNNQ+C2ZFpGhwBZVnSUiQ5xjLYDzgSF1va6qvgi8CNC5c2fVZt1wqXJil6YN4qn5vLw8hgwZEuwwAsrG3DDk5eWRkJBAampq7SfXg6fXT01N5eSTT2bevHns3LmTxMREYmJi2L59O61atSI1NfVX1xozZgz33HPPQa+fkJBA3759fTYGY4wxocOfK9NHA2eLyBlAAtAIWAiUAQVO4pskIgVOnfR6oBVQKCIxQBpQXNtNrhs3i9IKF+f1a8mD5/QgKc72oTEmEqz+x5kBv2dRURGxsbGkp6ezd+9ePv/8c+644w5OOOEEJkyYwMiRI3nttdcYNmwYABs3bqR58+YATJo0ia5duwY8ZmOMMcHlt8xTVe8C7gJwVqb/qKpDa54jIiVOIg0wCbgc+BEYDnylqlrbfWKjoyitcDFx9nrmF+7gmYv60bmZf1e2jDGRaePGjVx++eVUVVXhcrm44IILGDp0KN26dWPkyJHcfffd9O3bl1GjRgHw5JNPMmnSJGJiYmjSpAljx44N7gCMMcYEXCgt474MvCEiBcA2YKQnb8pKiWdXaSVNkuMo2FLCsGe+44Gze3B+/5wGUfZhjPGdXr16MWfOnN8cb9euHTNmzPjN8YcffpiHH344EKEZY4wJUQHZtEVV8w5clXaOp9T4vFRVz1fVDqo6QFVXenLtzJR4AB45vxfDj8ihtMLFn96fzx/Gz2N3WaXPxmCMMcYYY8yBwn4HxMzUOABKyqp45PzePHJ+bxJjo5k4Zz1nP/0dSzbtDHKExhhjjDEmUoV/Mu2sTBeXlAEw/IgcJo05mo5NU1hRtJthT3/Puz+vxYPya2OMMcYYY7wS9sl0RrI7md7qJNMAHbNT+d+Yozn/iBzKKl3c8X4+t1nZhzFhIdJ+8I208RhjjPm1sE+mq8s8tu4q/9XxpLgY/n1+bx51yj4+mLOes6zsw5iQlpCQQHFxccQkoKpKcXExCQkJwQ7FGGOMn4RSN486qS7zqLkyXdPvjsihV04aN7w1m2WbSxj29Pfcf3Z3RhzZyrp9GBNicnJyKCwspKioKNih+ExCQgI5OTnBDsMYY4yfRHwyDU7Zxw3HcO+kBYyfWcidE/P5cWUxfz+3JynxYf+/wJiIERsbS9u2bYMdhjHGGOOxsC/zyNqXTJcf9rzEuGj+Nbw3j13gLvv439wNnP3UdyzeaGUfxhhjjDGmbsI+mc5IcWqmS8o8qrM8r18OH914NJ2zU1m5dTfnPPM9b8+wbh/GGGOMMcZ7YZ9MJ8fHkBgbTVmlixIPu3V0aJrKhzcczcgjW1FW6eKuifnc8u5cj99vjDHGGGMMREAyDTU6etRS6lFTYlw0//hdLx4f0ZukuP1lH4s2WNmHMcYYY4zxTGQk0x48hHgo5/bNYdKYY/aXfTz7PW/9ZGUfxhhjjDGmdpGVTO/yPpkG6NA0ZV/ZR3mliz9/kM9N78xlV2mFL8M0xhhjjDERJrKS6d2el3kcqLrs4z8j+pAUF81H8zZw9tPfs3DDDl+FaYwxxhhjIkyEJNPVuyDWbWW6pnP6tuSjG4+hS7NUVm3dzbnP/sC4n9ZY2YcxxhhjjPmNCEmm614zfTDts9xlHxcOaE15pYu/fLCAG9+eY2UfxhhjjDHmVyyZPoSE2GgePq8nT4zsQ3JcNJPnb+Ssp75jwXor+zDGGGOMMW4RkUw3T08AYN22vT6/9rA+LZnklH2sLt7Dec/9wBvTrezDGGOMMcYEIJkWkWgRmSMik52vx4nIUhFZICKviEisc1xE5EkRKRCR+SLSz9N7dGyaAkBBUQlVLt8nudVlHxcd5S77+OuHCxhjZR/GGGOMMQ1eIFambwYW1/h6HNAF6AkkAqOd46cDHZ2Pq4HnPL1BakIsLdMTKa90saZ4t0+CPlBCbDQPnbu/7ONjK/swxhhjjGnw/JpMi0gOcCbwUvUxVZ2iDmAGkOO8NAx43XlpOpAuIs09vVenbPfq9LLNu3wV/kEN6+Pu9tG1eSN32cezVvZhjDHGGNNQ+Xtl+j/AnwDXgS845R2XAp86h1oC62qcUugc80inZqkALN1UUsdQPdcuK4UPrh/MxUe1przKKft4aw47rezDGGOMMaZBifHXhUVkKLBFVWeJyJCDnPIs8I2qfuvlda/GXQZCVlYWeXl5ALi2uRPZ7xasoHfM+roH7oVTGkNq73jGLijj4/yN/LxiE9f3jic3Ldpv9ywpKdk35obCxtwwNMQxG2OMCX/ir/IEEXkY98pzJZAANAImquolInIv0Bc4T1VdzvkvAHmq+rbz9VJgiKpuPNQ9OnfurEuXLgVgwfodDH3qOzo0TeGL2473y5gOZdXW3Vw/bjaLN+4kLjqKvw7tyiUD2yAiPr9XXl4eQ4YM8fl1Q5mNuWFoaGMWkVmq2j/YcRhjjKkfv5V5qOpdqpqjqrnASOArJ5EeDZwKXFidSDsmAZc5XT0GAjsOl0gfqEPTFKLEndiWVVb5cii1apuZzAfXD+aSgU7Zx/8WcsNbs63swxhjjDEmwgWjz/TzQDbwo4jMFZF7nONTgJVAAfBf4HpvLpoQG02bjGSqXMrKIv909Kjt/g+e05OnL+pLSnwMU/I3MfTJ78gvtG4fxhhjjDGRym810zWpah6Q53x+0Hs63T1uqM99OmWnsGrrbpZt3kXX5o3qc6k6G9qrBT1apHHDW7NZuGEnv3vuB/5yZlcuG+Sfsg9jjDHGGBM8EbEDYrXO2dUdPfzbHq82uZnJvH/dYC4d2IbyKhf3TlrI9eOs7MMYY4wxJtJEVDJd3R7P372mPZEQG83fzumxr+zjkwXuso/5hduDHZoxxhhjjPGRiEqm961Mh0AyXW1orxZMvvEYurdoxNpte/jdcz8w9vtVtsmLMcYYY0wEiKhkOjczmdhoYd22vewuqwx2OPtUl31cNqgNFVXKfR8t4ro3Z7Njr5V9GGOMMcaEs4hKpmOjo2if5d5WfPkW/++E6I2E2GgeGNaDZy/uR2p8DJ8u3MTQpxQBBmsAACAASURBVL61sg9jjDHGmDAWUck0QBenbnru2l+CHMnBndGzOZNvOoYeLRuxbttefvfcD7xqZR/GGGOMMWEp4pLpoztkAvD1sqIgR3JobTLcZR+XO2Uf93+0iGvfnGVlH8YYY4wxYSbikunjO2cB8MOKYkorArsTojfiY6K5v0bZx2cLN3Pmk98yb52VfRhjjDHGhIuIS6abpibQo2UjyipdTF9ZHOxwalVd9tGzZRqFv+xl+PM/8Mp3VvZhjDHGGBMOIi6ZBjihc1MA8paGbqlHTW0ykplw3SCuGJxLRZXywORFXPPGLHbssbIPY4wxxphQFpHJ9BCn1CNv6ZYgR+K5+Jho7ju7O89f0o/UhBimLtrMmU99y1wr+zDGGGOMCVkRmUz3adWYtMRYVhfvYdXW3fuOu1yhXzpxWo/mfHzjsfTKcZd9nP/8D7xsZR/GGGOMMSEpIpPp6CjhuE77V6f3lFfylw/yaffnKfR/8HO+WLQ5yBEeXuuMJN67dhBXHu0u+/jb5EVcbWUfxhhjjDEhJyKTaYAh+5LpIrrd8xnjfloLwNaScka/PpPrx81iy87SYIZ4WPEx0dx71v6yj88XbeaMJ79l5fbQ7VBijDHGGNPQRGwyXb0yfah+01PyNzHgoS95e8bakC7/OK1Hc6bcdCy9c9JYv30vf/+plJe+XWllH8YYY4wxISDmUC+IyJMevH+nqt7tw3h8Jis1nl45acwv3HHY8+6amM/L363i+UuOoEPTlABF551WTZJ479rB/OOTJbzy/Soe/Hgx01du45Hze5GeFBfs8IwxxhhjGqzDrUwPA2bV8vE7fwdYH9WlHrUp2FLCyY99zWNTl1Je6fJzVHUTFxPFPWd148a+8TRKiOGLxZs588nvmB2i26YbY4wxxjQEh0umH1fV1w73AbxQ2w1EJFpE5ojIZOfrtiLyk4gUiMi7IhLnHI93vi5wXs+t7+BO6NL0N8dWPXwGk288hmM7Zv7mtSe/KqDT3Z/w6YKN9b213xyRHcPHNco+Lnj+Ryv7MMYYY4wJksMl0+8f6gURGQqgqv/x4B43A4trfP1P3Il6B+AXYJRzfBTwi3P8cee8eunTKp3O2am/OiYi9GiZxhujjmLFQ2dwz9Buv3nftW/OJvfOj3nth9WUlFXWNwyfqy77+P3Rbal0KQ9+vJirXp/F9j3lwQ7NGGOMMaZBOVwy/fnBVodF5PfAE55cXERygDOBl5yvBTgRmOCc8hpwjvP5MOdrnNdPcs6vMxHhyqNzD/l6dJTw+2PasvofZ/L+dYN/8/q9kxbS497PuPXduWzZFVqdP6rLPl649Agr+zDGGGOM+f/27jy8qure//j7k4FJRhUVQQ2iooiCCopVruBQQazaOlvHH4p2UKudwGod2l7xVq+3aK0T1qGtFW1VyuBQJRVUQFBBQEDUaKHOCooMMnx/f5ydmDAkJyc5Jyfh83qe/bj32tN3AT7PNyvfvVYDqS6Zvhx4StLu5Q2SRgCXAYel+fz/A34GlBcibwMsjYjy4d7FQOdkvzPwb4Dk/LLk+jo5Yb/ONV8EHLBLB8pGDuEv5x+00blHX1nCgb95huc2MzNIQzp67x1SZR87ta8o+7jrOZd9mJmZmeWCqku6JB1Bqi76BOB84EBgSETUOPyZlIIcExHflzQA+AlwLjA1KeVA0k7AxIjoKWkOMCgiFifn3gQOioiPN3juMGAYQMeOHQ8YM2ZMjZ0894mvV0H8Zb8W7Nq+sMZ7Ji9ew+g5G5dN9Nm+kIt6NaeooE6D5hlbvnw5rVtvPOvI2vXBwwu/4smy1M8pvToWcsE+zWndrGHirE+b63NT5j43fQMHDpwZEX0aOg4zM6ubapNpAEn9gUeBF4BTIiKtegdJ1wNnAWuBFkDb5DlHAztExFpJBwPXRMTRkp5M9l+UVAS8D3SMagLs3r17LFiwoMZYlixdySEjn604Lhs5JJ0usH598JNHZvH3l5dsdO5PQw/i0E18xJhtpaWlDBgwYLPnn573AT95eBbLVq5hx3YtuOWM/Tlglw65CzALaupzU+Q+N32SnEybmTUBmy3zkPSFpM+BCaQS4SOADyu1VysiRkREl4goAU4Dno2I7wKTgJOSy84BHk/2xybHJOefrS6Rro3O7VtWOV6X5iItBQXif0/pzWvXfHOjc2eOnkbv657Ku6n0juqxPeMvOZTeO7XnP8tWceodL3Lnc2/m9cI0ZmZmZo3VZpPpiGgTEW2T/zaLiK0qHbetwzt/DlwuaRGpmujRSftoYJuk/XJgeB3esZGR39mnYr/bFRNqdW+bFsWUjRzCYz84pEr70hVr2OPKibzxwRf1EmN96dKhFWMuPJgL+qdm+/jvCfO54P4ZfPalZ/swMzMzq085WU48Ikojonw6vbci4sCI2C0iTo6I1Un7quR4t+T8W/UZw2kH7lznZ/TeqT1lI4fwvQHdqrQfdfNzDLt/Rp2fX5+aFRXwiyE9uOvsPrRrWcwz8z9kyKjJzHzn04YOzczMzKzJqK7M4+Wabk7nmnzyrV47Vuyffc/0jJ/z80F7Mufao6u0PTXvA0qGj+fTPBv9LS/72G/nVNnHKXdM5Y5/uezDzMzMrD5UNzK9l6TZ1WyvAbn/Aq8Objq5V8V+Xae5a928iLKRQ7j77KrfD+3/q6e57h/z6vTs+lZe9jHsv3Zl3frg+onzGXrfS3mX+JuZmZk1NtUl03sC36pmOxbYeKWTPNasqIBdO25VcXxOHUanyx3ZY3ve+u9jqrTd8/zblAwfz5p1+fNxYnFhAVccsxejz+lD+1bFTFrwEUNGTWZGmcs+zMzMzDJV3QeI76SxLc5lsPXhmcu/Xm/mXws/qpfFTQoKRNnIIdx+5v5V2nf/xUSeef2DOj+/Ph2x1/aMv6Q/++/cnveWreLUO6dyu8s+zMzMzDKSkw8Q84kkLjrs6w8Iu46o3cwe1RnUsxPzfzWoStvQ+2bQ7YoJeTWFXuf2LXnowoO5MCn7GDlxPv/PZR9mZmZmtbbFJdMAwwfvWeX4tcXL6u3ZLYoLKRs5hCH7dqpoW7c+2OPKiSz+bEW9vaeuigsLGHHMXtxzbqrso3TBRxzzu8m85LIPMzMzs7SllUxL2kXSkcl+S0ltshtW9k35+cCK/W/dOqXen//7M/Zn/CWHVmk79IZJ/GXau/X+rro4fM/tmXBJfw7YpQPvf76K0+6cym2li1z2YWZmZpaGGpNpSRcAjwB3JE1dgMeyGVQudOnQqspxyfDx9f6OvXdsx6LfDK7SdsWjr9F1xPi0V2HMhR3bt+Svw/px4WGpso//eWIB593rsg8zMzOzmqQzMv0D4BDgc4CIeAPYLptB5UrZyCFVjue/X+Mq6bVWVFhA2cghnPuNkoq2iNQqjB99sbre35ep4sICRgzeiz+e25cOrYr510KXfZiZmZnVJJ1kenVEVAxRSioC8mdYtY7GXfx1Kcag/5tcL7N7bMo1x+3NPyvNJALQ9zf/5O8v59eEKAP33I7xLvswMzMzS0s6yfS/JF0BtJR0FPAw8I/shpU7PTu3q3Jcn7N7bGi37VpvNCf15WNm0f3KiVlL4jNRXvZx0WHdqpR9fLI8f0bSzczMzPJBOsn0z4GPgNeAC4EJwJXZDCrXNiz3OPaWyVl7V/mc1BcetmtF2+q16+k6YgLLVqzJ2ntrq7iwgOGD96xa9jFqMtPfdtmHmZmZWblqk2lJhcDrEXFXRJwcEScl+/kzjFpPKn8oOGfJ5zz+6pKsvm/E4L2Y/LOBVdp6XfcU/5j1n6y+t7YG7rkdEy7tT59dOvDB56s57c4X+f0kl32YmZmZQQ3JdESsAxZI2jlH8TSYosICHv3+16ujX/rXV/n3p9mdF3qnrVvx9vVVyz4ufvAV9rn6ybwq++jULlX28f0B3Vgf8NsnF3Cuyz7MzMzM0irz6ADMlfSMpLHlW7YDawj77dyBK475ekGX/v8zidVr12X1nVKq7OOSw3eraPti9Vq6jpjAl6vXZvXdtVFUWMDPBu3Jveelyj6eS8o+pr31SUOHZmZmZtZg0kmmrwKOBa4Dbqq0NUnD/qsb/XfftuK4+5VP5GSU+PJvdueF4YdXadv76id5Ys57WX93bQzonir76FuSKvs4/a6p3PrsGy77MDMzsy1Sjcl0RPxrU1sugmsoDww9qMpx1xETcpJQ79i+5UYfQ170p5fpde1TWX93bXRq15IHL/i67OPGpxZyzh+n87HLPszMzGwLk84KiF9I+jzZVklaJ6n+VzfJMxsmtV1HTMjZ6GvZyCFcduQeFcfLVq6hZPh4Vq3JbslJbVQu+9h6q2ZMfuNjjvndZKa67MPMzMy2IOmMTLeJiLYR0RZoCZwI3FbTfZJaSJouaZakuZKuTdqPkPSypFclTZG0W9LeXNJDkhZJmiappE49qwcbJtS7XjGBr9auz8m7Lz1yd6ZfcUSVtj2veoI5H+dPQg1J2ccl/TmwZGs+/GI1Z7jsw8zMzLYg6dRMV4iUx4Cj07h8NXB4RPQCegODJPUD/gB8NyJ6A3/h6zmrhwKfRcRuwM3ADbWJLVs2TKj3uHJizuaD3q5ti43ef+OMVVmdBzsTO7RrwV8uOIgfDtyN4OuyD8/2YWZmZk1dOmUe36m0nSRpJLCqpvuSxHt5clicbJFsbZP2dkD5xMrHA/cl+48AR0hS+l3Jng0T2l7XPUXZx1/m9P0XHdat4njOks8pGT6eNetyM0qejqLCAn5ydHfuPe/AirKPY2+Zwsx3Pmvo0MzMzMyyRjV9WCfpj5UO1wJlwF0R8WGND08t+jIT2A34fUT8XFJ/4DFgJfA50C8iPpc0BxgUEYuTe98EDoqIjzd45jBgGEDHjh0PGDNmTFodrQ8/Ll3BJ6u+/vMa2rMZ/bsU5+z9H65Yz8+eW1ml7TeHtqRz61r9giHrPlu1ntteXc0bS9dTKDitezOO3KWITH82Wr58Oa1bt67nKPOb+9z0DRw4cGZE9GnoOMzMrG7SSaYPiYjna2qr4RntgUeBi0lNsXdDREyT9FOge0Scn24yXVn37t1jwYIF6YZRLy56YCZPzH2/4niHti2YukFtczZNmjSJ856supjM+Yd25cpje+QshnSsWbeekRPnM3rK2wAcu28nbjhxX7ZqXlTrZ5WWljJgwIB6jjC/uc9NnyQn02ZmTUA6Q5q3pNm2WRGxFJgEDAZ6RcS05NRDQPmyg0uAnQAkFZEqAcm7qSFuP+sAfnda74rj9z9fRcnw8azL0Qd35Yu8HNR164q2u6e8Tcnw8Xn10V9xYQFXHduD35+xP1s1K2Tc7Pc47tYpvPHBFw0dmpmZmVm92WwyLelgST8GOkq6vNJ2DVBY04MldUxGpJHUEjgKeB1oJ6l83rfyNoCxwDnJ/knAs5FPa2pXcnzvzrx81VFV2rpdMYGZ73yasxgeuvBg7j2vb5W2Xa+YwNIVX+UshnQM2bcTYy8+lD22b82bH33J8b9/nrGz/lPzjWZmZmaNQHUj082A1kAR0KbS9jmpZLcmnYBJkmYDLwFPR8Q44ALgb5JmAWcBP02uHw1sI2kRcDkwvPbdyZ2tt2q20YeJJ/7hRQb/LnczbQzovh2zrv5mlbbe1z3Ny+/m10d/3Tq25rEfHMIJvXdkxVfruOTBV7hm7NycTTNoZmZmli2bTaaTlQ6vJfWB4LWVtv+NiDdqenBEzI6I/SJi34joGRHXJe2PRsQ+EdErIgZExFtJ+6qIODkidouIA8vb813ZyCGcd0hJxfHr76Vm2sjVaoDtWhbz9vXHVGn7zm0v8Ktx83Ly/nS1albEzaf25lcn9KS4UNz7Qhmn3vki7y1bWfPNZmZmZnkqnZrpFZJ+K2mCpGfLt6xH1ohc/a29mfyzgVXa+vz6nwy8sTQn7y+vox609w4VbaOTOup8qpSRxFn9duHhi77Bju1a8Mq7SxkyagpT3tjsN6ZmZmZmeS2dZPrPwHygK3AtqanxXspiTI3STlu3omzkEAoqzf729sdfUjJ8PPP+k5vV128/6wD+uEEdddcRE1i9Nr9WTey9U3vGXdKf/rtvy6dffsVZ90zjlme8aqKZmZk1Pukk09tExGhgTVL68f+Aw7McV6P11vVDmPSTAVXajhk1OWejxAO7b8esX1ato+5+5RM5XWQmHVtv1Yx7zzuQS4/YHYCbnl7I0PteyrsPKM3MzMyqk04yXb529nuShkjaD9i6uhu2dF233YqykUPos0uHqu0jJnDB/TOy/v52rYo3+jhywI2lFXM+54vCAnHZUXvwx3P70r5VMZMWfMSQUVN4bfGyhg7NzMzMLC3pJNO/ltQO+DHwE+Bu4LKsRtVEPPK9b2w028bT8z6gZPh47nuhLOvvLxs5hAMrzUf9q3Hz+ObN/8r6e2trQPftGHfxofTq0o4lS1dy4h9e4C/T3s2rem8zMzOzTak2mU6WA989IpZFxJyIGBgRB0TE2BzF1+i1a5kaJb79zAOqtF89di4lw8czoyy7c1OPufBgbvvu/hXHCz9YnncfJgJ06dCKMRcdzJn9duardeu54tHX+MnDs1n5VX7Ve5uZmZlVVm0yHRHrgNNzFEuTNqjnDpSNHMK53yip0n7S7S9SMnw8L2UxqT5mn05MHVF1yfOuIyawak1+JarNiwr59Qn7cPOpvWhRXMDfXl7Mt297nve/9HzUZmZmlp/SKfN4XtKtkvpL2r98y3pkTdQ1x+1N2cgh7NiuRZX2k5Ok+vFXl2TlvTu0a8HCXw+u0rbnVU/w2Zf598Hft/frwuM/OJRdt92K+e9/wbUvruSJOe83dFhmZmZmG0knme4N7A1cB9yUbDdmM6gtwQsjjthosRWAS//6KiXDx3Pjkwvq/Z3Nigo2eud+v3qaZSvWbOaOhtN9hzY8/sNDGNxzB1auhYv+NJPrJ7zO2nUepTYzM7P8UWMyndRJb7h5arx6UL7YStnIIXTp0LLKuVsnLaJk+HhKho+v1wSy/J2V9bruqbxMqNu0KOa27+7P6Xs2o7BA3PHcW5xx9zQ+/HxVQ4dmZmZmBqSRTEvaXtJoSROT4x6ShmY/tC3LlJ8fTtnIIRy99/YbndvtFxMpGT6eFxbV30qBm0yoV+ZfQi2Jo0uKefCCfmzXpjnT3/6UIbdMYdpbnzR0aGZmZmZplXncCzwJ7JgcLwR+lK2AtnR3nNWHspFD+J+T9t3o3Bl3T+PcJ1KrKtbHqoYbJdTXPsWXq9fW+bnZcGDXrRl3yaH023VrPvpiNWfcPY07n3sz72YlMTMzsy1LOsn0thExBlgPEBFrgfyaBqIJOqXPTpSNHLLRPNXlul/5BCXDx3PW6Gl1Sig3TKj3vvpJ1uRpXfJ2bVrwp6EHcdFh3Vi3PvjvCfO56E8z+XxV/o2om5mZ2ZYhnWT6S0nbAAEgqR/gJepypHye6rKRQ7igf9eNzk9+42O6jphAyfDxnHHXVNatr31ivWFCfd0/5mUcb7YVFRYwfPCe3HV2H9q0KOLJuR9w3C1TeP29zxs6NDMzM9sCpZNMXw6MBbpJeh64H7g4q1HZJv1iSA/uHbQVb/xmMO1bFW90/oU3P6HbFRMqPlx8++Mv0372vOuOrth/YOo79VJGkk1H9diecRcfyl6d2lL2yQq+fdvz/G3m4oYOy8zMzLYwRTVdEBEvSzoM6A4IWBAR/r16AyouLODVX6bKPz76YjV9f/PPTV438MbSKsdjf3gI+3Zpv8lrWzUr4ps9tuepeR8A8PeXl3D6gTvXX9BZsMs2W/Ho97/BVY/N4eGZi/nxw7OY8c5nXP2tHrQoLmzo8MzMzGwLUGMyLakF8H3gUFKlHpMl3R4Rnp8sD3Rs07yiTGP12nV865YpLPxg+SavPe7W59N+7uo8Wx1xc1oUF/Lbk3vRp6QDVz0+lwenv8ucJcv4w5n706VDq4YOz8zMzJq4dMo87ie1aMstwK3J/gM13SSphaTpkmZJmivp2qRdkn4jaaGk1yVdUql9lKRFkmZ7lcXaa15UyFOXHVZRYz36nD4ZP+u0PB+V3tCpfXfm79/7Bjtt3ZLXlizj2Fum8NzCjxo6LDMzM2viahyZBnpGRI9Kx5MkpfOF2mrg8IhYLqkYmJLMVb0XsBOwZ0Ssl7Rdcv1gYPdkOwj4Q/Jfy9ARe21f5ePCdz9ZwU8fmcW0tz/d7D1tmhcx8Uf9G2WZRM/O7fjHDw/lsodeZdKCjzjnj9O57Mg9+OHA3SgoUEOHZ2ZmZk1QOsn0y5L6RcRUAEkHATNquilS87WV1xsUJ1sA3wPOiIjyqfY+TK45Hrg/uW+qpPaSOkXEe7XqkW3Wztu04qELD27oMLKqfatmjD6nL7c8u4j/e2Yh//v0Ql7991JuPqU37Tbx0aaZmZlZXaRT5nEA8IKkMkllwItAX0mvSZpd3Y2SCiW9CnwIPB0R04BuwKmSZkiaKGn35PLOwL8r3b44aTOrlYICcemRu/PHc/vSvlUxz87/kG/dOoW5//GMjmZmZla/0hmZHpTpwyNiHdBbUnvgUUk9gebAqojoI+k7wD1A/3SfKWkYMAygY8eOlJaWZhpeo7R8+XL3uRZ+0aeIW19dxzufruCEW6dwdo9m9O+S/yPU/ns2MzNrHJTO6nmSOpCqc65IviPi5Vq9SPolsAI4HxgcEW9LErA0ItpJugMojYgHk+sXAAOqK/Po3r17LFiwoDZhNHqlpaUMGDCgocPIqbr2edWadVz9+FwempH6xcfpB+7MNcf1oHlR/taF+++56ZM0MyIy/0rYzMzyQo1lHpJ+BcwGRgE3JduNadzXMRmRRlJL4ChgPvAYMDC57DBgYbI/Fjg7mdWjH7DM9dJWH1oUF3LDSftyw4n70KyogAenv8spt7/IkqUrGzo0MzMza+TSKfM4BegWEV/V8tmdgPskFZJK2sdExDhJU4A/S7qM1AeK5yfXTwCOARaRGsE+r5bvM6vWqX13pkendnzvzzOZtXgZx46azF1n96FPydYNHZqZmZk1Uukk03OA9qQ+IkxbRMwG9ttE+1JgyCbaA/hBbd5hVlv7dGnHuIsP5ZK/vspzCz/ijLun8X+n9uaYfTo1dGhmZmbWCKUzm8f1wCuSnpQ0tnzLdmBm2dK+VTPuOacP3z1oZ75au54f/OVl7p78Ful8P2BmZmZWWToj0/cBNwCvAeuzG45ZbhQVFvDrE3rSpUMrbnhiPr8e/zqLP1vJVcf2oNALvJiZmVma0kmmV0TEqKxHYpZjkvjegG7s2L4FP314Nve+UMZ/lq5k1On7NcoVIM3MzCz30inzmCzpekkHS9q/fMt6ZGY5cnzvztw/9EDatijiqXkf8PPho4m2baGgANq2he9/H958s6HDNDMzszyUTjK9H9AP+G9qMTWeWWPSb9dteHDvdWz11UoeL+7Mzb2+BRHwxRdw992w774wcWJDh2lmZmZ5psYyj4gYWNM1Zo3em2+y97knc+sOPRh64lWMOuQM9vj4XY6dPwXWrEltJ50Es2dDt24NHa2ZmZnliXQWbdle0mhJE5PjHpKGZj80sxy66SZYs4aBb83gikn3AHBbv5OrXrNmDdx8cwMEZ2ZmZvkqnTKPe4EngR2T44XAj7IVkFmD+NOfUskycNYr42m7ajnztu/Ggm13+fqaNWvggQcaKEAzMzPLR5tNpiWVl4BsGxFjSKbFi4i1wLocxGaWO8uXV+w2X7eWY1+fTOdlH/Jem202e52ZmZlZdTXT04H9gS8lbQMEgKR+wLIcxGaWO61bpz42TFxReg+/fuo2CoiNrzMzMzNLVFfmUb5yxeXAWKCbpOeB+4GLsx2YWU6deSYUF1cctv5q5caJdHExnHVWjgMzMzOzfFbdyHRHSZcn+48CE0gl2KuBI4HZWY7NLHd+/GO4776KuulNKi6Gyy7LXUxmZmaW96obmS4EWgNtgK1IJd6FQKukzazp6NYNHnkEWrWqMkINpI5btUqd97R4ZmZmVkl1I9PvRcR1OYvErKENHpyaR/rmm1OzdixfnqqRPuus1Ii0E2kzMzPbQHXJtKo5Z9Y0desGt96a2szMzMxqUF2ZxxE5i8LMzMzMrBHabDIdEZ/mMhAzMzMzs8YmnRUQMyKphaTpkmZJmivp2g3Oj5K0vNJxc0kPSVokaZqkkmzFZmZmZmZWH7KWTJOaQu/wiOgF9AYGJQu+IKkP0GGD64cCn0XEbsDNwA1ZjM3MzMzMrM6ylkxHSvnIc3GyhaRC4LfAzza45XjgvmT/EeAISf4I0szMzMzyVjZHppFUKOlV4EPg6YiYBvwQGBsR721weWfg3wARsZbUkuXbZDM+MzMzM7O6qG5qvDqLiHVAb0ntgUcl/RdwMjAg02dKGgYMA+jYsSOlpaX1EGnjsXz5cvd5C+A+m5mZNQ5ZTabLRcRSSZOAgcBuwKKkgqOVpEVJnfQSYCdgsaQioB3wySaedSdwJ0D37t1jwIABuehC3igtLcV9bvrcZzMzs8Yhm7N5dExGpJHUEjgKmBkRO0RESUSUACuSRBpgLHBOsn8S8GxERLbiMzMzMzOrq2yOTHcC7ks+OCwAxkTEuGquHw08IGkR8ClwWhZjMzMzMzOrs6wl0xExG9ivhmtaV9pfRaqe2szMzMysUcjqbB5mZmZmZk2Zk2kzMzMzsww5mTYzMzMzy5CTaTMzMzOzDDmZNjMzMzPLkJNpMzMzM7MMOZk2MzMzM8uQk2kzMzMzsww5mTYzMzMzy5CTaTMzMzOzDDmZNjMzMzPLkJNpMzMzM7MMOZk2MzMzM8uQk2kzMzMzsww5mTYzMzMzy5CTaTMzMzOzDDmZNjMzMzPLkJNpMzMzM7MMZS2ZltRC0nRJsyTNlXRt0v5nSQskzZF0j6TipF2SRklaJGm2pP2zFZuZmZmZWX3I5sj0auDwiOgF9AYGSeoH/BnYE9gHaAmcn1w/dQpXtQAADCdJREFUGNg92YYBf8hibGZmZmZmdZa1ZDpSlieHxckWETEhORfAdKBLcs3xwP3JqalAe0mdshWfmZmZmVldFWXz4ZIKgZnAbsDvI2JapXPFwFnApUlTZ+DflW5fnLS9t8Ezh5EauaZjx46UlpZmK/y8tHz5cvd5C+A+m5mZNQ5ZTaYjYh3QW1J74FFJPSNiTnL6NuC5iJhcy2feCdwJ0L179xgwYEB9hpz3SktLcZ+bPvfZzMysccjJbB4RsRSYBAwCkHQ10BG4vNJlS4CdKh13SdrMzMzMzPJSNmfz6JiMSCOpJXAUMF/S+cDRwOkRsb7SLWOBs5NZPfoByyLivY0ebGZmZmaWJ7JZ5tEJuC+pmy4AxkTEOElrgXeAFyUB/D0irgMmAMcAi4AVwHlZjM3MzMzMrM6ylkxHxGxgv020b/KdyeweP8hWPGZmZmZm9c0rIJqZmZmZZcjJtJmZmZlZhpxMm5mZmZllyMm0mZmZmVmGnEybmZmZmWXIybSZmZmZWYacTJuZmZmZZcjJtJmZmZlZhpxMm5mZmZllyMm0mZmZmVmGnEybmZmZmWXIybSZmZmZWYacTJuZmZmZZcjJtJmZmZlZhpxMm5mZmZllyMm0mZmZmVmGnEybmZmZmWUoa8m0pBaSpkuaJWmupGuT9q6SpklaJOkhSc2S9ubJ8aLkfEm2YjMzMzMzqw/ZHJleDRweEb2A3sAgSf2AG4CbI2I34DNgaHL9UOCzpP3m5DozMzMzs7yVtWQ6UpYnh8XJFsDhwCNJ+33ACcn+8ckxyfkjJClb8ZmZmZmZ1VVWa6YlFUp6FfgQeBp4E1gaEWuTSxYDnZP9zsC/AZLzy4BtshmfmZmZmVldFGXz4RGxDugtqT3wKLBnXZ8paRgwLDlcLWlOXZ/ZyGwLfNzQQeSY+7xl2NL63L2hAzAzs7rLajJdLiKWSpoEHAy0l1SUjD53AZYkly0BdgIWSyoC2gGfbOJZdwJ3AkiaERF9ctGHfOE+bxnc56ZP0oyGjsHMzOoum7N5dExGpJHUEjgKeB2YBJyUXHYO8HiyPzY5Jjn/bEREtuIzMzMzM6urbI5MdwLuk1RIKmkfExHjJM0D/irp18ArwOjk+tHAA5IWAZ8Cp2UxNjMzMzOzOstaMh0Rs4H9NtH+FnDgJtpXASfX8jV3ZhZdo+Y+bxnc56ZvS+uvmVmTJFdSmJmZmZllxsuJm5mZmZllqFEk05IGSVqQLDU+fBPnm9xS5Gn0+XJJ8yTNlvSMpF0aIs76VFOfK113oqSQ1Khnfkinv5JOSf6e50r6S65jrG9p/LveWdIkSa8k/7aPaYg465OkeyR9uLlpPJUyKvkzmS1p/1zHaGZmmcv7ZDr5gPH3wGCgB3C6pB4bXNakliJPs8+vAH0iYl9SK0b+T26jrF9p9hlJbYBLgWm5jbB+pdNfSbsDI4BDImJv4Ec5D7Qepfl3fCWpj5X3I/UR8m25jTIr7gUGVXN+MLB7sg0D/pCDmMzMrJ7kfTJN6mPFRRHxVkR8BfyV1NLjlTW1pchr7HNETIqIFcnhVFJzdjdm6fw9A/yK1A9Lq3IZXBak098LgN9HxGcAEfFhjmOsb+n0OYC2yX474D85jC8rIuI5UjMUbc7xwP2RMpXUXPydchOdmZnVVWNIpiuWGU9UXoJ8o2uayFLk6fS5sqHAxKxGlH019jn59fdOETE+l4FlSTp/x3sAe0h6XtJUSdWNbjYG6fT5GuBMSYuBCcDFuQmtQdX2/3czM8sjOVkB0bJH0plAH+Cwho4lmyQVAP8LnNvAoeRSEalf/Q8g9ZuH5yTtExFLGzSq7DoduDcibpJ0MKm553tGxPqGDszMzGxTGsPIdPky4+UqL0G+0TXVLUXeiKTTZyQdCfwCOC4iVucotmypqc9tgJ5AqaQyoB8wthF/hJjO3/FiYGxErImIt4GFpJLrxiqdPg8FxgBExItAC2DbnETXcNL6/93MzPJTY0imXwJ2l9RVUjNSHyWN3eCaprYUeY19lrQfcAepRLqx19JCDX2OiGURsW1ElERECak68eMiYkbDhFtn6fy7fozUqDSStiVV9vFWLoOsZ+n0+V3gCABJe5FKpj/KaZS5NxY4O5nVox+wLCLea+igzMwsPXlf5hERayX9EHgSKATuiYi5kq4DZkTEWJrYUuRp9vm3QGvg4eRby3cj4rgGC7qO0uxzk5Fmf58EvilpHrAO+GlENNrfuKTZ5x8Dd0m6jNTHiOc28h+MkfQgqR+Ktk1qwa8GigEi4nZSteHHAIuAFcB5DROpmZllwisgmpmZmZllqDGUeZiZmZmZ5SUn02ZmZmZmGXIybWZmZmaWISfTZmZmZmYZcjJtZmZmZpYhJ9O2WZJ2kPRXSW9KmilpgqQ9GjimH0lqlcF950rasdLx3ZJ61EM810hakkzvljVJ/LdWOu4k6SlJJZLmJG19JI1K9gdI+kYG7+kvaV75M83MzKx6TqZtk5SavPpRoDQiukXEAcAIYPuGjYwfAZtMpiUVVnPfuUBFMh0R50fEvHqK6eaI+GU9PStdg0jN11whImZExCXJ4QCgVsm0pKKImExqzmMzMzNLg5Np25yBwJpkUQkAImJWRExOVmr7raQ5kl6TdCpUjIaWSnpE0nxJf06SciT1lfSCpFmSpktqI6kwec5LkmZLurC650i6hFRCPEnSpOTa5ZJukjQLOFjSL5PnzZF0Z3LfSUAf4M+SXpXUMnl+n+QZpyf9mCPphvL+Js/+TRLzVEk1/iAhqaOkpyXNTUa/35G0bTKCPF/SvZIWJn06UtLzkt6QdGBy/9aSHkv+PKZK2nczrxoETNzg3QMkjZNUAlwEXJb0t38S19+SP5uXJB2S3HONpAckPQ88UFP/zMzMrCon07Y5PYGZmzn3HaA30As4EvitpE7Juf1IjR73AHYFDlFq6eiHgEsjovyelcBQUksn9wX6AhdI6rq550TEKOA/wMCIGJhctxUwLSJ6RcQU4NaI6BsRPYGWwLER8QgwA/huRPSOiJXlHUlKP24ADk/61FfSCZWePTWJ+TnggjT+3K4mtZz93sAjwM6Vzu0G3ATsmWxnAIcCPwGuSK65FnglIvZN2u7f8AXJCHz3zY2sR0QZcDupEfPeyWjz75LjvsCJwN2VbukBHBkRp6fRPzMzM6sk75cTt7x0KPBgRKwDPpD0L1LJ8OfA9IhYDCDpVaAEWAa8FxEvAUTE58n5bwL7JiPHAO2A3YGvNvOcKZuIZR3wt0rHAyX9jFQpyNbAXOAf1fSlL6lSlo+Sd/0Z+C/gsSSOccl1M4GjavqDIfVn8+2kn09I+qzSubcj4rXkPXOBZyIiJL2W9K/8/hOT+5+VtI2kthu84yBgWhqxVHYk0CP5RQFAW0mtk/2xlX/AMDMzs/Q5mbbNmQucVONVG1tdaX8d1f8bE3BxRFSp/ZU0oBbPWZUk9UhqAdwG9ImIf0u6BmhRq+irWhMRkUYM6arcp/WVjtfX8tmDgSdq+e4CoF9ErKrcmCTXX9byWWZmZpZwmYdtzrNAc0nDyhsk7SupPzAZODWpee5IaiR3ejXPWgB0ktQ3eU4bSUWkPqD7nqTipH0PSVvVENcXQJvNnCtPnD9ORl0r/zCwufumA4cldc2FwOnAv2qIoTrPA6dAxch7h1rePxn4bnL/AODj8pH8So4A/lnDczbs71PAxeUHknrXMi4zMzPbBCfTtknJiOy3gSOVmhpvLnA98D6pWT5mA7NIJd0/i4j3q3nWV8CpwC3Jh4JPk0p87wbmAS8rNRXbHdQ8Qnsn8ET5B4gbvGcpcBcwh1Si/lKl0/cCt5d/gFjpnveA4cCkpD8zI+LxGmKozrXAN5P+nEzqz+uLWtx/DXCApNnASOCcyieTH15WRURNz/wH8O3yDxCBS4A+yYeN80h9oGhmZmZ1pK9/i21mtZWUkiyPiBuT4+bAuohYK+lg4A8RUW+jwJLOBLpExMj6euYm3lECjEs+4jQzM7NquGbarG6WA8MktU3mmt4ZGCOpgNQHjOnMAJK2iPhTfT5vQ8ko9m3Ax9l8j5mZWVPhkWkzMzMzswy5ZtrMzMzMLENOps3MzMzMMuRk2szMzMwsQ06mzczMzMwy5GTazMzMzCxDTqbNzMzMzDL0/wEsBit5I3pWnAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"def create_cstr_plot_axes():\n",
" fig = plt.figure(figsize=(12,8))\n",
" ax = [plt.subplot(2, 2, k) for k in range(1, 4)]\n",
" \n",
" ax[0].set_xlabel('Time [min]')\n",
" ax[0].set_ylabel('Concentration [gmol/liter]')\n",
" ax[0].set_title('Concentration')\n",
" ax[0].set_ylim(0, 1)\n",
" ax[0].grid(True)\n",
" \n",
" ax[1].set_xlabel('Time [min]')\n",
" ax[1].set_ylabel('Temperature [K]');\n",
" ax[1].set_title('Temperature')\n",
" ax[1].set_ylim(300, 450)\n",
" ax[1].grid(True)\n",
" \n",
" ax[2].set_xlabel(\"Concentration [gmol/liter]\")\n",
" ax[2].set_ylabel(\"Temperature [K]\");\n",
" ax[2].set_title(\"Phase Plot\")\n",
" ax[2].set_xlim(0, 1)\n",
" ax[2].set_ylim(300, 450)\n",
" ax[2].grid(True)\n",
" \n",
" return ax\n",
"\n",
"def cstr_plot(t, y, ax):\n",
" \"\"\"Plot cstr simulation results. Create new axes if needed.\"\"\"\n",
" ax[0].plot(t, y[:, 0], label=str(Tc))\n",
" ax[1].plot(t, y[:, 1], label=str(Tc))\n",
" ax[2].plot(y[0, 0], y[0, 1], 'r.', ms=20)\n",
" ax[2].plot(y[:, 0], y[:, 1], lw=2, label=str(Tc))\n",
" for a in ax:\n",
" a.legend()\n",
"\n",
"ax = create_cstr_plot_axes()\n",
"cstr_plot(tsim, ysim, ax);"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.6 Effect of Cooling Temperature](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.6-Effect-of-Cooling-Temperature)",
"section": "7.4.6 Effect of Cooling Temperature"
}
},
"source": [
"## 7.4.6 Effect of Cooling Temperature\n",
"\n",
"The primary means of controlling the reactoris through temperature of the cooling water jacket. The next calculations explore the effect of plus or minus change of 5 K in cooling water temperature on reactor behavior. These simulations reproduce the behavior shown in Example 2.5 SEMD."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.6 Effect of Cooling Temperature](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.6-Effect-of-Cooling-Temperature)",
"section": "7.4.6 Effect of Cooling Temperature"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtMAAAHwCAYAAABkJOM0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeXiU1fXA8e/JZCUrhD0L+y6yiruyFkUEEbW4okXRqlVLrf5abdXa1tq6tlXrWhVRVKiKiBYVY0VQBFlUAmEnCYEAIWQSMsks5/fHO8EQssyETCYzuZ/neZ+Zd51zRV7O3Ln3vKKqGIZhGIZhGIbhv4hgB2AYhmEYhmEYocok04ZhGIZhGIbRSCaZNgzDMAzDMIxGMsm0YRiGYRiGYTSSSaYNwzAMwzAMo5FMMm0YhmEYhmEYjWSSacMIEhHJFJFSEbEFOxbDMAzDMBrHJNNG0IjIFSKy2ptQFojIhyJyVrDjqklEuouIikjkCV5np4iMr1pX1d2qmqCq7hOP0jAMo3l479lVi0dEyqutXxns+Bqj5v3ZMPxhkmkjKERkDvAE8GegE5AJPA1MDWZcjXWiibZhGEao8HYCJKhqArAbuLDatnnBjq+m5rg/m38DWjeTTBvNTkSSgT8At6jqf1S1TFWdqvq+qv5aRGJE5AkR2eNdnhCRGO+5o0UkT0R+JSKF3h7t66pdO05EHhWRXSJyWESWi0icd99pIrJCRIpFZL2IjK52XpaIPCgiX4qIXUSWikh77+7/eV+LvT0vp4vItd5jHxeRg8D9ItJLRJaJyEEROSAi80QkxXv9uVhfGN73XuOumj3eItJVRBaJSJGIbBWRG6rFd7+IvCUir3rj+0FERgbqz8gwDMNfIhIhIv8nItu898G3RKSdd1/V/e46EckVkUMicpOInCIiG7z35X9Wu1bVPfaf3nv5JhEZV21/soi86P03IF9E/lg1ZK6J7s+jRSSvRvuO9l5778kLROQ1ESkBrq0vJiO8mWTaCIbTgVjgnTr23wOcBgwFhgCjgHur7e8MJANpwCzgKRFp6933CDACOANoB9wFeEQkDfgA+KN3+53AQhHpUO26VwDXAR2BaO8xAOd4X1O8PS8rveunAtuxetb/BAjwENAVGABkAPcDqOrVHNuD89da2j0fyPOefwnwZxEZW23/FO8xKcAi4J/HXcEwDCN4fgFcBJyLdR87BDxV45hTgT7AT7F+nbwHGA8MAi4TkXNrHLsNaA/cB/ynKjkHXgZcQG9gGPAT4Poa5zbl/bk2U4EFWPfkeT7EZIQpk0wbwZAKHFBVVx37rwT+oKqFqrofeAC4utp+p3e/U1WXAKVAPxGJAH4G3K6q+arqVtUVqloBXAUsUdUlqupR1Y+B1cCkatf9t6rmqGo58BZWMl+fPar6D1V1qWq5qm5V1Y9VtcIb92NY/6g0SEQygDOBu1XVoarrgBeAa6odttwbvxuYi/VFwzAMo6W4CbhHVfO89937gUtqDIF40HuPWwqUAW947/X5wBdYSWiVQuAJ773+TWAzcIGIdMK6d9/h/WWzEHgcmFHt3Ca7P9djpaq+q6oeIMmHmIwwZcb4GMFwEGgvIpF1JNRdgV3V1nd5tx09v8Z5R4AErN6LWKyejJq6AZeKyIXVtkUBn1Vb31vLNeuTW33Fe4N/EjgbSMT6snqogWtU6QoUqaq92rZdQPWhHDXji63nv6FhGEZz6wa8IyKeatvcWL3DVfZVe19ey3r1+26+qmq19ap/C7ph3b8LRKRqXwTH3pOb8v5cl+qf4UtMRpgyPdNGMKwEKrB+DqzNHqwbU5VM77aGHAAcQK9a9uUCc1U1pdoSr6p/8eG66uP2P3u3DVbVJKzecKnn+Or2AO1EJLHatkwg34f4DMMwWoJc4Pwa99lYb69zY6RJtcyUH/8tyMX6N6R9tc9JUtVB1Y490ftzGdCmasU79rlDjWOqn+NLTEaYMsm00exU9TDwe6yxzheJSBsRiRKR80Xkr8AbwL0i0sE7CfD3wGs+XNcDvAQ85p3MZ/NOFozxnn+hiEz0bo/1TjBJ9yHk/YAH6NnAcYlYQ04Oe8do/7rG/n11XUNVc4EVwEPe2E7GGg/eYLsNwzBaiH8BfxKRbgDee/iJVGjqCNzm/ffhUqyxzktUtQBYCjwqIkneiY+9aoy3rsnf+3MO1q9/F4hIFNa8nZi6Lt7ImIwwYZJpIyhU9VFgDtYNaj/Wt/pbgXexJgmuBjYA3wHferf54k7vOd8ARcDDQIQ3WZ0K/Lba5/0aH/4OqOoRrAksX3pnnJ9Wx6EPAMOBw1iTHf9TY/9DWF8SikXkzponA5cD3bF6Xt4B7lPVTxqKzzAMo4V4Emty9FIRsQNfYU0EbKyvsSYrHsC6B1+iqge9+67Bmii+EWu4xgKgSz3X8uv+7O30uRlr7ko+Vk91HvXzNyYjTMixw5EMwzAMwzCCS0SuBa5X1Rb3IC/DqMn0TBuGYRiGYRhGIzVLMi0iL4n1gI3v69gvIvJ3sR5UsUFEhjdHXIZhGIZhGIZxIpqrZ/pl4Lx69p+PNS6qDzAbeKYZYjIMwzAMowVS1ZfNEA8jVDRLMq2q/8OaDFaXqcCravkKSBERM2jfMAzDMAzDaNFaypjpNI4tbJ7n3WYYhmEYhmEYLVbIPQFRRGZjDQUhLi5uREZGht/X8Hg8RES0lO8RTSuc2wbh3T7TttDVmPbl5OQcUNWaD4EIa+3bt9fu3bv7fV5ZWRnx8fFNH1ALEM5tg/BuXzi3DcK7fY1t25o1a2q9b7eUZDofqJ4Vp1PHk99U9TngOYCRI0fq6tWr/f6wrKwsRo8e7X+UISCc2wbh3T7TttDVmPaJyK7ARNNyde/eHXPPPlY4tw3Cu33h3DYI7/Y1tm113bdbSlfRIuAab1WP04DD3qcJGYZhGIZhGEaL1Sw90yLyBjAaaC8iecB9QBSAqv4LWAJMArYCR4DrmiMuwzAMwzAMwzgRzZJMq+rlDexX4JbmiMUwDMMwDMMwmkpLGTNtGIZhGIZhhBCn00leXh4OhyPYofglOTmZ7OzsOvfHxsaSnp5OVFSUT9czybRhGIZhGIbht7y8PBITE+nevTsiEuxwfGa320lMTKx1n6py8OBB8vLy6NGjh0/XaykTEA3DMAzDMIwQ4nA4SE1NDalEuiEiQmpqql+97aZn2jACSFXxKLg9ai1qvar31aPg8b4/UO4ht+gIHv1xu6qiytF1j3ddFRTruKrPAO8+vPtVf3yPtaNq3Xv00eOrYtWjgf94DEevV61dNdpYc3v1Y0H5fq8Lx/fHFug59pjjr1v3f9MG9vt0lRP7jJoqyj0n/JmGYRihKJwS6Sr+tskk00ZYqnR5KKtwUVbpoqzCTVmli/JKt7U4rcVxdPFQ4XJT4fRQ4bLeV7o8VLo93lfF6fLgdFctitPtweXxvroVl0dxezzeVz366vb4mZV9/llg/oO0BOu+DXYEATP75Jhgh9BkRMQGrAbyVXVyte1/B36mqgne9RjgVWAEcBD4qarubP6IDcNorXJzc7nmmmvYt28fIsLs2bO5/fbbWb9+PTfddBOlpaV0796defPmkZSUBMBDDz3E888/T1RUFH//+9+ZOHHiCcdhkmmjxVJV7BUuDtgrKCqrpKiskpW5TrKztlFcXsnhI06KjzgpcViL3eHC7nBR6nBR6favp9AWIcRERhAbZSPaFkF0pLVEed/HeF/jYyKJskUQZRMibRFERQiR3vc28b6PECIirFdbxI/bI0SwReB9tdYjIoQIAZsIOTmbGdC//9F9Ita34wgBwToXvOsiCBAR8eP7H1+t461XwLse4f2iLd5re3d534t3X9W7H7+Z/7huXYdq67X58do/HrBmzWpGjhxZ57HHbKPhHoGGOg2aop/En46JnPX+P4ikBbsdyAaSqjaIyEigbY3jZgGHVLW3iMwAHgZ+2mxRGobR6kVGRvLoo48yfPhw7HY7I0aMYMKECVx//fU88sgjnHvuubz00kv87W9/48EHH2Tjxo3Mnz+fVatWYbfbGT9+PDk5OdhsthOLo4naYxh+UVX2l1aQd6ic/EPlFBwuZ0+xg30lVUsF+0srqHTVkhT/sIloWwQpbaJIjosiKS6KDgkx9GyfQFJcJAkxUSTE2IiPibSW6EjaRNtoE20jLtpGXJSN2CjrfWyUjdjICCJtwZ8+kHVkO6NHZjR8YAgqzIlgQJekhg8MUXlR4fEzp4ikAxcAfwLmeLfZgL8BVwDTqh0+Fbjf+34B8E8REVV/B8kYhmE0TpcuXejSpQsAiYmJDBgwgPz8fHJycjjnnHMAmDBhAhMnTuTBBx/kvffeY8aMGcTExNC+fXt69+7NqlWrOP30008oDpNMGwF1qKySLYWlbN9fyrb9pew4cITdRWXsOniEihqJcny0jc7JsXRKimVUj3Z0SIyhfUI07RNiSE2IITU+ms0b1jBp3LnERkWE5TgtwwiyJ4C7gOrT3G8FFqlqQY2/c2lALoCqukTkMJAKHGimWA3DaEEeeP8HNu4padJrDuyaxH0XDvLp2J07d7J27VpOPfVUBg0axHvvvcdFF13E22+/TW5uLgD5+fmcdtppR89JT08nPz//hOM0ybTRJDweZfuBUr7PL+GHPYfJLrCzeZ+d/faKo8fEREbQLbUN3VLjOadPBzJT25CWEkda2zi6psSRGBPZYIJ8YEsEcdEn9nOMYRjHE5HJQKGqrhGR0d5tXYFLsZ5g29jrzgZmA3Tq1ImsrCy/r1FaWtqo80JBOLcNwrt94dw28K19ycnJ2O12AJyVTtxud5PG4Kx0Hr1+fUpLS5k2bRoPPfQQIsI//vEPfv3rX/PAAw9w/vnnExUVhd1up7KykvLyctxuN3a7HafTSXl5ea2f4XA4fP7zNcm00SiHy518u+sQ3+wsYl1uMRvyDlNa4QIgOjKCfp0SObdvB/p1SqR3pwR6d0iga0octgjTm2wYLdSZwBQRmQTEYo2Z/gGoALZ6v+i2EZGtqtobyAcygDwRiQSSsSYiHkNVnwOeAxg5cqSOHj3a78CysrJozHlV1u9fT1J0Ej2SfasZ25xOtG0tXTi3L5zbBr61Lzs7+2i95j9OH9oMUR3P6XRyySWXcPXVV3PllVcCMGLECJYtWwZATk4On3zyCYmJifTo0YMDBw5gs9lITExk37599O7du9aa07GxsQwbNsynGEwybfjE4XTz9Y4iVmw9wPKtB9hYUIIqREYIA7okMW1YGienJzM4PZleHRKIagFjkA3D8J2q/gb4DYC3Z/rO6tU8vNtLvYk0wCJgJrASuARY1lLHS9/35X1kJGbwj3H/CHYohmE0IVVl1qxZDBgwgDlz5hzdXlhYSMeOHfF4PPzxj3/kpptuAmDKlClcccUV3HDDDRw4cIAtW7YwatSoE47DJNNGnfYedvBx9j6WZe9jxbaDVLg8RNmE4ZltuX1cH0Z1b8fQzBTaRJv/jQyjFXoRmCsiW4EiYEaQ46lTqbOUnSU7gx2GYRhN7Msvv2Tu3LkMHjyYoUOtnvE///nPbNmyhaeeegqAiy++mOuuuw6AQYMGcdlll3HKKacQHR3NU089dcKVPMAk00YN+0ocvL9+Dx9+v5c1uw4BkNmuDZePymR0vw6M6tHOJM+GEeZUNQvIqmV7QrX3Dqzx1C1ehbuCg46DuD1ubBFmzoVhhIuzzjqLun4Qu/3222vdfs8993DbbbfV+TjxxjBZkYHD6eaj7/ey8Ns8vtx6AI/CwC5J/GpCX847qTO9OyaYyhmGYYSsCncFLo+LgrIC0hPTgx2OYRhhxiTTrdj2/aXM+3o3C7/No/iIk/S2cdwypjcXDUujV4eEhi9gGIbRwqkq5a5yAHbbd5tk2jCMJmeS6VZGVflqexEvLt/OJ9mFREYIEwd15opTMzm9ZyoRptqGYRhhpNJTefR9bkkudA1iMIZhhCWTTLcSqkrW5v08+ekW1uUW0y4+mtvH9eGq07rRITEm2OEZhmEEhMPlOPp+l31XECMxDCNcmWS6FVi+5QB/++8m1ucdJi0ljj9NO4npw9OJjTITcQzDCG/Vk+ncktwgRmIYRrgyyXQY27S3hD8v2cT/cvaTlhLHXy4ezMXD04mONDWgg04VXA6oLIPKUqgsI7FkM2wXa7uzHFwV1ntXBbgrwF0Jrkrr1eMEjxvcTvC4vIvbelW39V7d1ueox7vuAfTHbXhfa5sJ7W+54NomqFbbNuRQMexq690mNY6RY98fcy05/rhaz6v5uTWPrXG9Y7b7c2zNmCxJtmGcwEMCjQByuE3PtGEYgWWS6TBU4nDy2NIcXl25k4SYSO6ZNIBrzuhGTKTpiQ4IjweOHAR7AZQVQtkBKNtvbTtSBOVFUF4MjmJwHIYKu7V4XMdcZgTAtz58ntjAFg0RkWCLhIgoiLB5XyOs/RE261UivNu8S1WyWnO91sTU1/Hz+mPyfTQJr5aMqxLhcVpfDI5J0vXY41WPO+/446rWq71v6NjjrlfbeT4cW/NzqolK64XRMlX1TGckZpBnzzPl8QwjjDgcDs455xwqKipwuVxccsklPPDAA+zYsYMZM2Zw8OBBRowYwdy5c4mOjqaiooJrrrmGb775hg4dOvDmm2/SvXv3E47DJNNhRFX5ao+LOx/5nKKyCq46rRtzJvQlpU10sEMLbR4PlORB0XY4tNNainfD4XwoybeS6BqJMWAlu3HtoE07iE2BpDToOBBikiAmEWISIDoRouMhOp4Nm7Zx8vBRENUGomIhMhYiY6xXW7T1viphDjFrw/yxuwezsoIdglGHCncFAH3b9iXXnsu+I/vommBmIRpGOIiJiWHZsmUkJCTgdDo566yzOP/883nsscf45S9/yYwZM7jpppt48cUX+fnPf86LL75I27ZtWb9+PR988AF33303b7755gnHYZLpMLHfXsE973zH0o0VDElP5t/XnsLg9ORghxVaVK0kee93ULgRCrNh/2Yo2mb1qlaJiITkdEjOgG5nQlIXSOwCCZ0gsTPEd4A2qRCbXPvwhzoU7c+CHmc3fbsMoxWr6pnu27Yvn+7+lF0lu0wybRhhQkRISLBK+TqdTpxOJyLCsmXLeP311wGYOXMm999/Pz//+c957733uP/++wG45JJLuPXWW1HVE36Whkmmw8CH3xXw23e+o6zSzU/7RfPnmWdiMyXuGlZaCLmrIH815K+BgvXWMIwqKd2gQ3/oNQZSe1tL2+6Q1NUaRmEYRotXNWa6T9s+AOTaczmd04MZkmGEpw//z+qMakqdB8P5f6n3ELfbzYgRI9i6dSu33HILvXr1IiUlhchIK8VNT08nPz8fgPz8fDIyMgCIjIwkOTmZgwcP0r59+xMK0yTTIczhdPOnD7KZ+9UuhqQn8+hlQ8jbuMYk0nUpOwDbs2DH57BrBRzcam2PiIROJ8FJ06HzydZf3o4DrOEXhmGEtKqe6czETGJsMewu2R3kiAzDaEo2m41169ZRXFzMtGnT2LRpU7PHYJLpELXzQBk3z/uWjQUlzD6nJ7+e2I8oWwR5G4MdWQvi8cCetZDzkbXs3WBtj0mGbqfDsKsh83ToMsQao2wYRtipGjMdFxlHRmKGqehhGIHSQA9yoKWkpDBmzBhWrlxJcXExLpeLyMhI8vLySEtLAyAtLY3c3FySk5NxuVwcPnyY1NTUE/5sk0yHoOVbDnDL698iAi9dO5Kx/TsFO6SWw+OB3K/gh3dg4yIo3WtVrcg4Fcb+DnqOga5DzTANw2glqh4lHmOLITMxk10lJpk2jHCxf/9+oqKiSElJoby8nI8//pi7776bMWPGsGDBAmbMmMErr7zC1KlTAZgyZQqvvPIKf/vb31iwYAFjx4494fHSYJLpkKKqvLJiJw9+kE3vDgm8MHMkGe3aBDusluHAFlj3Omx406qwERkLvcfDgCnQZ4JVUcMwjFanqmc6NjKWzKRMlucvx6MeIiT0quIYhnGsgoICZs6cidvtxuPxcNlllzF58mQGDhzIjBkzuPfeexk2bBizZs0CYNasWVx99dUMGTKE9u3bM3/+/CaJwyTTIcLjUR78YCP//nIn4wd04okZQ0mIaeV/fK4KyH4fvnkRdq+weqB7j4cJf4C+E63yc4ZhtGo1k+lKTyX7yvbRJaFLkCMzDONEnXzyyaxdu/a47T179mTVqlXHbY+NjeXtt9/GbreTmNh0OUIrz8ZCQ6XLw51vr2fR+j387Mwe3HvBACJa8yTDsgPwzQvWUrYf2vawEuiTZ0CiGfJiGMaPyl3lCEJ0RDSZiZkA7LbvNsm0YRhNxiTTLVx5pZvZc1fzxZYD3H1ef246t2eTjO8JScW59Mn5Fyz/zKr73GcinDobeo4NyQeZGIYReBWuCmIjYxGRo8n0rpJdnNrl1CBHZhhGuDDJdAtWXunmZy9/w9c7DvLX6Sdz2SkZwQ4pOA7nwRePwrdz6aIKQy+HM34BHfoFOzLDMFo4h9tBrM2q1tMpvhNtItuwrXhbkKMyDCOc+JRMi8gGHw7br6rj6rnGecCTgA14QVX/UmN/JvAKkOI95v9UdYkv8YWj6on0o5cNYdqw9GCH1PzKi60k+utnQT0w/Bq+jjyd08+7NNiRGUbYEhEbsBrIV9XJIjIPGAk4gVXAjarqFOsnsieBScAR4FpV/TZYcdfF4XIQExkDQIRE0KdtHzYf2hzkqAzDCCe+9kzbsG6YdRFgUZ07rZvzU8AEIA/4RkQWqWr1qsj3Am+p6jMiMhBYAnT3Mb6w4nC6mfVKK06k3S5Y/RJk/dlKqIdcDmN+CykZVGRlBTs6wwh3twPZQJJ3fR5wlff968D1wDPA+UAf73Kqd1uLGztRvWcaoF/bfny448MmeYSwYRgGgK8DTW9U1V31LDuBm+s5fxSwVVW3q2olMB+YWuMY5cebdzKwx492hA23R7lj/jpWbDvII5e2wkR699fw/Gj48NfW0whv/B9MewZSWukQF8NoRiKSDlwAvFC1TVWXqBdWz3TVTWkq8Kp311dAioi0uFl9VWOmq/Rr1w+7005BWUEQozIMI5z41DOtqsu9vcuvquqVdR1TzyXSgNxq63kc34NxP7BURH4BxAPja7uQiMwGZgN06tSJrEb0VJaWljbqvEBTVV7ZWElWrovL+0fTrmQrWVlb/bpGS21bQ2yuI/Ta9jJdC/6LIyaVbQPvYn+HM2BzEWzOOnpcqLbPF6ZtoSuM2vcEcBdwXM0oEYkCrsbquYba7+tpQEGN84J6zy44UEClVh49v6yiDICF/1vI4DaDG3XNphRG/+/UKpzbF85tA9/al5ycjN1ub56AauFwODjvvPOorKzE5XIxdepU7rnnHnbu3Ml1111HUVERw4YN47nnniM6Opp58+Zx77330qVLF0SE2bNnM3PmzDqv7fOfr6r6vADLgWh/zvGedwnWOOmq9auBf9Y4Zg7wK+/704GNQER91x0xYoQ2xmeffdao8wLtiY9ztNvdi/UvH2Y3+hottW31yvlY9dGBqvenqH70W1WHvc5DQ7J9PjJtC12NaR+wWv28lwZyASYDT3vfjwYW19j/PPBEtfXFwFnV1j8FRtb3GcG4Z1/1wVU667+zjq6XVZbp4JcH6zPrnmn0NZuS+bsRusK5baq+tW/jxo2BD6QeHo9H7XYrZ6isrNRRo0bpypUr9dJLL9U33nhDVVVvvPFGffrpp1VV9d///rfecsstWlJS0uC1a2tbXfdtf+uJbQe+FJHficicqsWH8/KB6r/Tp3u3VTcLeAtAVVcCsUB7P+MLWe+v38Pjn+QwfXg6d01sJVUqKo/A4jkwbzpEx8Osj2HinyAmIdiRGUZrdCYwRUR2Yg3FGysirwGIyH1AB6xOjyq+3NeDrsJdccyY6TZRbchIzCDnUE4QozIMoymICAkJVs7gdDpxOp2ICMuWLeOSSy4BYObMmbz77rsBjcPf0njbvEsEtfwMWI9vgD4i0gPrZjsDuKLGMbuBccDLIjIAK5ne72d8IWlDXjF3vr2eU7q35c8Xn9Q6JsXs/Q4WzIIDm+H0W2Hs7yAqtuHzDMMICFX9DfAbABEZDdypqleJyPXARGCcqnqqnbIIuFVE5mMN2zusqi1uIHK5q/yYMdNgjZveXGQqehhGU3p41cNsKtrUpNfs364/d4+6u95j3G43I0aMYOvWrdxyyy306tWLlJQUIiOtFDc9PZ38/B+/5y9cuJCsrCz69+/P448/TkbGic/J8iuZVtUHAESkjaoe8eM8l4jcCvwXqzLIS6r6g4j8AavLfBHwK+B5Efkl1mTEa71d6mFtX4mDG15dTfuEGJ65agQxkbZghxRYqvDtK7DkLohrC1e/A73GBjsqwzDq9i9gF7DS+0X/P6r6B6yKS5OArVil8a4LWoT1qHBXEGOLOWZbn7Z9+GTXJxxxHqFNVJsgRWYYRlOw2WysW7eO4uJipk2bxqZNdSf0F154IZdffjmVlZW8/vrrzJw5k2XLlp1wDH4l0yJyOvAikABkisgQrEof9VXyAKwZ4Vg33+rbfl/t/UasnxlbDafbwy3zvsXucLHw52fQPiGm4ZNCmbMcPrgT1r0GPcfA9BcgvtWM5DGMkKGqWUCW932t/054Oztuab6oGsfhchAXGXfMtn5t+6EoOYdyGNpxaJAiM4zw0lAPcqClpKQwZswYVq5cSXFxMS6Xi8jISPLy8khLSwMgNTUVgMrKSq6//nruuuuuJvlsf8dMP4H1c99BAFVdD5zTJJG0Qn/772ZW7zrEQxcPZkCXpIZPCGWH8+GliVYifc5dcNVCk0gbhhFwDrfjuJ7pfu2seSlm3LRhhLb9+/dTXFwMQHl5OR9//DEDBgxgzJgxLFiwAIBXXnmFqVOtaswFBT+ORFu0aBEDBgxokjj8fpy4qubWGNPrbpJIWpmlP+zluf9t56rTMpk6NC3Y4QRW/hp44wqoLIPL50O/84MdkWEYrYCq1jrMo2t8VxKjEs24acMIcQUFBcycORO3243H4+Gyyy5j8uTJDBw4kBkzZnDvvfcybNgwZs2aBcDf//53Fi1aREREBO3bt+fll19ukjj8TaZzReQMQL01R6uelHdDrTUAACAASURBVGX4IbfoCHe+vZ7Bacn8bvLAYIcTWD+8C+/cCAkdrfHRncK8vYZhtBhOjxOPeo4b5iEi9Gnbx/RMG0aIO/nkk1m7du1x23v27MmqVauO2/7QQw/x0EMPYbfbSUz0p45G/fwd5nET1hi5NKyqHEOp/8mHRg1uj/Krt9bjUXjqiuHhPeHw62fh7WuhyxC44TOTSBuG0awcbgfAcT3TYA31yDmUg+eYAiWGYRj+87dnup/WeAKiiJwJfNl0IYW357/YzqqdRTx66RAyU8N0FrkqfPoALH8c+k+2JhpGxTV8nmEYRhNyuKxkumZpPLAmIR5xHSHfnk9G0omXxjIMo/Xyt2f6Hz5uM2qxcU8Jjy7dzPkndebi4WE6TtrjhvdvsxLpEdfBZa+aRNowjKCocFUAtSfTA1KtiUffH/y+WWMyDCP8+NQz7S2JdwbQocYTD5Ow6kYbDahwufnlm+tIaRPNn6YNDs8Hs7id8O7P4bu34Zxfw5h7IBzbaRhGSCh3lwMc8wTEKn3b9iUuMo61hWs5v4eZFG0YjaWqYZfT+PuYE1+HeURj1ZaO5NgnH5YAl/j1ia3UU8u2snmfnX9fewrt4qODHU7Tc1XCgutg02IYdx+c7ctT5g3DMAKnvp7pyIhITu5wMmsLj5+8ZBiGb2JjYzl48CCpqalhk1CrKgcPHiQ21venMvuUTKvq58DnIvKyqu5qbICt1aa9JTydtY1pw9IY079jsMNpem6nNdFw8wdw3sNw2k3BjsgwDKPeCYgAwzoO47kNz1FaWUpCdEJzhmYYYSE9PZ28vDz2798f7FD84nA46k2WY2NjSU9P9/l6vg7zeEJV7wD+KSLH9X2r6hSfP7GVcXuU/1v4HUlxUeFZBs/thAU/sxLp8/8Gp84OdkSGYRhA/RMQwUqmPephw/4NnJF2RnOGZhhhISoqih49egQ7DL9lZWUxbNiwJruer8M85npfH2myT24lXl6xk3W5xTw5Y2j4De/wuOE/syF7EUx8yCTShmG0KBVu7zCPWsZMAwzpMIQIiWDt/rUmmTYMo9F8Heaxxvv6eWDDCS8Fh8t5dOlmxvTrwJQhXYMdTtNShfdvhx/+AxMehNNNuXHDMFqWcpd3AmIdPdPxUfH0a9uv1Y2bDscJY4YRTD6VxhOR70RkQ11LoIMMVX/6IBu3R/nD1JPC68alCkvvhbVz4Zy74Mzbgh2RYRjGcap6pusaMw0wtONQNuzfgMvjaq6wguo3X/yGX33+q2CH0axKKkt4eNXD2CvtwQ6lWTk9TpweZ7DDaBV8HeYxOaBRhKEV2w6weEMBd4zvQ0a7MHs4yxePwsp/wqgbYcxvgx2NYRhGrarGTNd8nHh1wzsO541Nb7D50GYGpQ5qrtCCZtXeVRQeKWTLoS30adsn2OE0i6zcLF7Lfo0u8V24ZtA1wQ6n2dzyyS0kRCfw2OjHgh1KsyooLaBLQpdm/UxfH9ryHHAxEKequ2ouAYwvJDndHu577wcy2sVx07m9gh1O0/r2VVj2IJz8UzjvL6aOtGEYLVZD1TzA6pkGWLsv/Id6HHEeofBIIQBzN85t4OjwsaloEwDvbH3H7/rBoaqksoSv937NZ7s/45DjULDDaTaLty/mJwt/wnf7v2vWz/U1mZ4JHALuF5FvReQZEZkqIvEBjC1kvfzlTrYUlvL7yYOIjQqjZ9ps/gjevwN6jYOpT0GEvw/QNAwjUETk7z4sfwx2nM2pqme6vmS6c3xnusZ3bRXjpneVWH1fXeO7snj7Yg6UHwhyRM1jc9FmBGFr8VZ+OPhDsMNpFqsKVuFRDy518cnuT4IdTrNweVw8s+4ZAD7c+WGzfrZP2ZCq7lXVl1V1BjASeBUYASwVkU9E5K5ABhlKDpZW8PdPt3Bu3w6MHxBGNaVzv7FqSXc52XpEuC0q2BEZhnGsqcCaBpbpQYsuCCrcFcTaYhucszK041DWFq4N+17LqmT6zlPuxOVx8ebmN4McUeCpKtlF2UzsPpFYWyzvbHkn2CE1ixV7VhAfFU+3pG58tOOjYIfTLD7Y/gG77btpH9eeT3d92qx/n/3uWlRVj6quVNXfq+qZwAwgv+lDC01PfrqFI043914wIHwmHRZthzd+Comd4Yq3IcY83MAwWqDHVfWV+hbg2YYuIiI2EVkrIou96z1E5GsR2Soib4pItHd7jHd9q3d/94C2rhEcLgcxkXX3SlcZ0WkE+8v3s6NkRzNEFTxV7Ts77WzOzTiXNze9ebT3PlwVlBVgr7QzstNIxncbz5IdS45WeQlXqsqKPSsY1XkUk3pM4pu937D/SGg9VMVfLo+LZzc8y4B2A7ht2G3sKdvDxqKNzfb5vlbz+EddPxsCv1fVeQGOMyRsLSxl3te7uXxUBn06JTZ8Qig4UgSvXWJV8LhqISR0CHZEhmHUbmFdO0RkMoCqPuHDdW4HsqutP4yVqPfGGu43y7t9FnDIu/1x73EtisPtqLPGdHVnpp0JwPK85YEOKah2leyiS3wXYiNjuWbgNRyqOMTi7YuDHVZAVY2X7p/an2m9p1HqLOXT3Z8GOarAyrXnkl+azxldz+C87uehKEt3LQ12WAG1ePticu25/HzIzxmTMQab2PhkV/MNb/G1Z3o19f90aAAPLcmmTZSNO8b3DXYoTcPpgPlXwOE8uPwNSA2zyZSGEV4+rq13WER+BjzpywVEJB24AHjBuy7AWGCB95BXgIu876d61/HuHyct7Oe4CldFnTWmq0tLSKNXci++yP+iGaIKnp2Hd9I9qTsAIzuNpGdyz7AfArCpaBOC0CelDyM7jyQtIY13t7wb7LACasWeFQCc0fUMeqb0pG/bvmH95+z2uHluw3MMaDeA0RmjSYlN4ZTOp/DJrk+abaiHr2Oma/5UuBBYWG291Vux9QCfbirk5jG9aZ/Q8M+KLZ4qvHcL7F4J056BzNOCHZFhGPWbgzWP5Wi9MxH5DfBL4Fwfr/EEcBfg8a6nAsWqWlWEOQ9I875PA3IBvPsPe49vMcrd5T71TAOclXYWa/at4YjzSICjCg5VZVfJLroldQNARBiXOY7V+1ZT7CgOcnSBs6loE92Tu9Mmqg0REsHU3lP5eu/X7CvbF+zQAmbFnhWkJaSRkZgBwHndz2Pd/nUUlBYEObLAyCvNI9eey0/7/fTo8NoJ3Saws2QnW4u3NksMvtaZBkBETsJ6tHg7a1X2A9eoauuYHlsHVeWhDzeRlhLHdWd2D3Y4TSPrIfh+AYy7D05qVXOWDCMkqeoSEakAPhSRi4DrgVHAOaraYG0s71CQQlVdIyKjmyouEZkNzAbo1KkTWVlZfl+jtLS0Ueft3b+XCk+FT+cmlifi9Dh58eMXGdxmsN+f1ViNbZu/StwllDpLcRW6jn5eckUybnXz7CfPcmrCqQH53OZqX13W7VlHj5geR2No62wLwLPLnuWcxHNO6NrBbltt3OpmZd5KRsSP4PPPrYdWpzhTAHj606cZlzzO52u1xPbVZnP5ZgCKtheRtScLgFh3LILw/OfPMyll0nHnNHXb/EqmsepNz1HVzwC8N9zngTOaLKIQ9OH3e/ku/zCPXDokPErhrX8TPn8Yhl4FZ/0y2NEYhuEjVf1URK4DsoAVwFhV9XWG2ZnAFBGZBMQCSVjDQ1JEJNLb+5zOjxPO84EMIE9EIoFk4GAtMT2H9W8HI0eO1NGjR/vdrqysLBpz3ksfvkRyRLJP557pPpOX5r/EobaHGH26/5/VWI1tm79W710NeTB+xPijY8Q96uHVBa9SEF8QsBiaq321OVxxmEPzD3HtgGsZfdKPMbz+7uvsjt59wnEFs211WVu4FsduB9NHTmd0t9FHty9YvIDtsp0HRz/o87VaYvtqc2jLISiE8844j4ykjKPbF364kK3OrbW2oanb5m81j/iqRBpAVbOAVl1r2uX28Mh/N9OnYwLThqU1fEJLt2slLLoVup8Nkx83D2UxjBAhInYRKQGWYCXC44DCatvrpaq/UdV0Ve2OVaVpmapeCXwGXOI9bCbwnvf9Iu863v3LtIXVlvO1mgdAlC2K07qcxvL85WFZIq+qLF735O5Ht0VIBGMzxvJl/pdhWeFic5HVY9m/bf9jto/PHM/qfavD8mEmK/esJEIiGNV51DHbJ3SbwIYDG9hbtjdIkQXO3iNWmzrFdzpm+/hu49lyaAs7D+8MeAz+JtPbReR3ItLdu9wLbA9EYKFiwZo8th8o49cT+2GLCPHEs2i7NeEwJdOqJR0ZHeyIDMPwkaomqmqS9zVaVeOrrSedwKXvBuaIyFasMdEvere/CKR6t88B/u/EWtD0KtwV9T6wpaaz08+moKyAbcXbAhhVcOws2Ul0RDSd23Q+ZvvYzLE43A5W7lkZpMgCJ7vIKkrTr12/Y7aP6zYOt7rJys0KQlSBtf3wdjISM0iOST5m+/jM8QDNWuGiuewt20v7uPZE247NWSZ0mwDQLJVM/E2mfwZ0AP7jXTp4t7VKDqebJz7ZwvDMFCYM7NTwCS1ZeTG8/lNA4Yq3oE27YEdkGEaQqGqWqlaV09uuqqNUtbeqXqqqFd7tDu96b+/+Ftex4nA5iIuM8/n4s9LOAgjLqh47S3aSmZSJLeLYoYgjO48kMSqRZbuXBSmywNlctJmOcR1JjTt2XuzAdgPpGt81LEvk7SndQ9f4rsdt757cnb5t+/Lxro+DEFVgFZQW0CW+y3HbO8d3ZmiHoSzd2cKSaVU9pKq3qepw73K7LxNbwtVrX+1ib4mDu87rH9oPaHE74e2ZULQDfjrPlMAzjBAkIt82xTHhxOF2+NUz3Tm+M33a9gnPZLpaWbzqoiKiOCfjHD7P+xyXx3X8iSEsuyib/qn9j9suIozrNo4Ve1ZQ5iwLQmSBs6d0D10Tjk+mwRr2sLZwbdg9wKWgrIDO8Z1r3feT7j9h86HNAR/q4VcyLSIjReQ/IvKtiGyoWgIVXEtWVuHi6axtnN2nPaf1bFHVoPyjCh/Mge1ZMOXv0P3MYEdkGEbjDKh+X65l+Q5oH+wgm5PD5fCpznR1YzLGsGbfGg6UHwhQVM3P5XGRZ887WhavpnGZ4yiuKObbfeHzXavSXcmOwzvo17ZfrfvHZ47H6XHyRV74fHGqcFdw0HGw1l5agJ90+wmKhlWPvKqyt2xvnW1urqEe/g7zmAe8DEwHLqy2tDovr9hJUVklv/pJ7X9RQ8aXT8K3r8LZd8LQK4IdjWEYjdefY+/LNZfJtKLKS6pKhbvC5zrTVS7ocQEe9fDfnf8NUGTNL780H5e6jpl8WN2ZXc+kTWQbluxY0ryBBVBeaR5uddMzpWet+4d0GEJqbCqf7A6fMcRVdaTr6pnuldKLnsk9w2qoR3FFMQ63o85kumqoR6D/PvubTO9X1UWqukNVd1UtAYmsBTtc7uTZz7cxfkBHhmakBDucxtv4HnxyHwy6GMbcE+xoDMM4AdXvyfUsecGOs7m4PC7c6va7Z7pnSk/6t+vPku3hk1gereRRyzAPgDZRbRjfbTxLdy6lwl3RjJEFTp7d+l89PSG91v22CBvju43n89zPKa0sbc7QAmZP6R6g7mQarKEeq/etpshR1FxhBVRBmfUFoq5kGmBi94nkHMoJ6FAPf+tM3yciLwCfAkf/xqnqfxo6UUTOw6pZagNeUNW/1HLMZcD9gALrVbVFdpW++MV2ShwufjkhhB8bvvsr+M9sSB8FFz0DEf5+rzKMpuV0OsnLy8Ph8LUscsuRnJxMdnZ2rftiY2NJT08nKiqqmaNq3Rxu6/8jf8ZMV5nUYxKPrXmM3JLcY+rWhqodh3cAdSfTAJN7TmbRtkVk5WYxsfvEZooscPJLrXLo6Ym1J9MAU3pN4c3Nb7J011Iu7nNxc4UWMHvKvMl0LRMQq/yk2094bsNzfLTjI64Y0CJTLL9UJdOdE2ofMw3WF4iHv3mYpbuWMvvk2QGJw99k+jqsnxKj+PFxs4pV2aNOImIDngImYD2O9hsRWaSqG6sd0wf4DXCmqh4SkY5+xtYsisoqeXH5Di4Y3IVBXZMbPqElOrAF3pgBSWlw+XyI8q/nxjACIS8vj8TERLp37x5yE3rtdjuJiYnHbVdVDh48SF5eHj169AhCZK1XVQ+rP9U8qpzf43weW/MYS3Ys4cYhNzZ1aM1ud8lukqKTSImt+5fUUZ1H0TGuI4u3LQ6LZDrPnkesLZbU2LrnNA1uP5geyT14b+t74ZFMl+7BJjY6tOlQ5zH92vVjQLsBvLv13bBIpqvqZtfXM905vjPDOg5jyfYl3DD4hoD8++Jvd+QpqjpSVWeq6nXexZfSeKOArd4SS5XAfGBqjWNuAJ6qqg6iqoV+xtYsnv18G+VON3eM7xPsUBrHvg9euxjEBlctgPgQnjxphBWHw0FqamrIJdL1ERFSU1ObvbddRLqJyHjv+zgROT7TD3NVDyFpTM905/jOjOg0giU7loTFA1x223fXOfmwii3CxgU9L2B5/vKwGAKQX5pPWkJavfcTEWFKryl8W/gtu0t2N2N0gVFQVkCnNp2IjKi/n/Si3heRXZTNpqJNzRRZ4BSUFhBji6FtTNt6j5vSawrbDm9j/f71AYnD32R6hYgMbMTnpAG51dbzvNuq6wv0FZEvReQr77CQFqWwxMErK3dy0dA0+nQKwX+byoth3nQoOwBXvgXtap+YYRjBEk6JdJXmbpOI3AAsAJ71bkoH3m3WIFqACpfVM+3rExBrmtRjEtsPbyfnUE5ThhUUufZcMhIbHq4yuddkXOriwx0fNkNUgZVnz6t3iEeVC3teSIREsGjbomaIKrDqK4tX3QU9LyAqIop3t4b+bWHvEauSR0P32fN7nE9cZBz/2dLgqORG8XeYx2nAOhHZgTVmWgBV1ZObKJY+wGism///RGSwqhZXP0hEZgOzATp16kRWVpbfH1RaWtqo817bWEGly8NpiUWNOr851NW2CHcFJ2+4n6SSHL4bfA+Htthhy/HHtXSN/bMLBa29bcnJydjt9uYJqA55eXnceOONFBYWIiJce+213HzzzXz33XfccccdlJWVkZmZyQsvvEBSkvVQwUcffZRXX30Vm83GX//6V8aPH3/cdR0OR3P+2d6C9Wvg1wCquqWlDpsLpKox03E2/4d5gFVS66GvH2Lx9sXHPUEvlFS6KykoK+DCXg0X3urbti/92vZj8bbFXDngymaILjBUlbzSPEZ0GtHgsZ3iO3F6l9N5f9v73Dz0ZiIkdOcP7Snbc9xjxGuTHJPMuMxxLN6+mDkj5hz35MBQUl+N6erio+KZ1GMSS3Ys4a5T7mryOPxNphvbW5wPVP9anO7dVl0e8LWqOoEdIpKDlVx/U/0gVX0OeA5g5MiROnr0aL+DycrKwt/z8ovL+d/HWVw2MoPLJjXFd4fAqLVtbqf1mPDD2XDJSww5KXTHhjXmzy5UtPa2ZWdn1zruuDmlpKTwxBNPMHz4cOx2OyNGjODCCy/k9ttv55FHHuHcc8/lpZde4l//+hcPPvggGzdu5J133mHVqlXY7XbGjx9PTk4ONtuxT5mLjY1l2LBhzdWMClWtrOqpEZFIrLktrYrD5Z2A2Mie6baxbTk341ze2/oetw67tVHDRVqC/NJ8POohMzHTp+Mv7HUhj6x+hC2HttCnbWgOZzxccZgyZ5lPPdNgDQG4+4u7Wb13NaO6NJyMtkROj5PCI4X1jh2ublrvaXy08yM+y/0spMfI7y3dy5lpvj0fY3qf6SzcspAlO5bQkabtX/D3K5i9lmWPD+d9A/QRkR4iEg3MAGr+pvIuVq80ItIea9hHi3k87T+XbQHgF+NC7ObidsKC62DLUpj8OIRwIm0YgdalSxeGDx8OQGJiIgMGDCA/P5+cnBzOOeccACZMmMDChQsBeO+995gxYwYxMTH06NGD3r17s2rVqqDF7/W5iPwWiBORCcDbwPtBjqnZVfVM+1tnurrL+1/OoYpDIV1zOtdujbD0ZZgHWIlljC2GNza9EciwAiqv1CqLl5ZQczRp7cZmjiUhKoGFWxYGMqyAKjxSiEc9Pg3zADi1y6l0ju/MO1vfCXBkgeN0O9lfvt+nnmmAk9qfRJ+2fQLy5+xvz/S3WD3Mh7CGeKQAe0VkH3CDqq6p7SRVdYnIrcB/sUrjvaSqP4jIH4DVqrrIu+8nIrIRcAO/VtWDjWpVE9u+v5S3Vudx1amZpKU07ifDoKhKpLPfh4kPwcjrgh2RYfjkgfd/YOOekia95sCuSdx34SCfj9+5cydr167l1FNPZdCgQbz33ntcdNFFvP322+TmWglKfn4+p5122tFz0tPTyc+v+aNbs7sbuB74DrgRWAK8ENSIgqBqzLS/daarG9V5FD2Te/JG9htM6TWlqUJrVlUT6zKTfOuZbhvblgt6XsD7297n9uG3kxwTelWrqpJpX3umYyNjuaj3RczfNJ85I+bQKb5TIMMLCF9qTFdni7AxtddUntvwnM/jy1uafUf2oajPvfEiwvQ+0/nLqr+QG53b8Al+8Ldn+mNgkqq2V9VU4HxgMXAz8HR9J6rqElXtq6q9VPVP3m2/9ybSqGWOqg5U1cGqOt//5gTGI0s3ExMZwa1jQ6hX2lUJC372YyJ9+s3BjsgwQkZpaSnTp0/niSeeICkpiZdeeomnn36aESNGYLfbiY5umWMMvWVIs1X1eVW9VFUv8b5vfcM8mqBnWkSY0X8G3x/8nu/2f9dUoTWr3fbdJEQlNFjtoLor+l+Bw+0I2GStQGvogS21uXLAlXjwMH9zi0k9/HI0ma6nxnRNl/a9FJvYmJc9L1BhBdTRGtM+9kyDVU89xhbDSvvKJo3F7wmIqnpD1YqqLhWRR1T1RhEJzQFlDViXW8yS7/Zy+7g+dEgMkSZW2OHNq2H7ZyaRNkKSPz3ITc3pdDJ9+nSuvPJKLr7YGhbVv39/li5dCkBOTg4ffPABAGlpaUd7qcGawJiW5ttPy4Ggqm4R2Swimaoa+rW+TkDVmOkT6ZkGa9jDk98+yRub3mBwh8FNEVqz2m3fTUZihl9VZfq168cpnU/hjU1vcPXAqxsstdbS5NnzaBfbjjZRbXw+Jz0xnbEZY3lr81vcMPgGv85tCaoe2OJPYtkpvhOTek5i4ZaF3DTkppD7FcKXGtM1Jcckc8+p92Df3rST3f3tmS4Qkbu9NUy7ichdwD5vb4inoZNDjarylw+zSY2P5oZzQqOMXFTlYXjlQtjxP5j6lEmkDcMPqsqsWbMYMGAAc+bMObq9sNAqe+/xePjjH//ITTfdBMCUKVOYP38+FRUV7Nixgy1btjBqVNAnMLUFfhCRT0VkUdUS7KCaW1P0TINVBWBKryl8tPMjDpa3iJGHfsmz5/k8xKO6K/tfSUFZAVm5WU0fVIDll+b71Std5ZpB11BSWcL720JvikFBaQEd4zr6XZnjmoHXUO4q5+2ctwMUWeA0pmcaYFqfaWTG+P93oj7+JtNX8GPN0newxk9fgTUO+rImjawF+DxnP19tL+IXY3uTEBMC38wLNzFs7d1QuAlmvA7Drgp2RIYRUr788kvmzp3LsmXLGDp0KEOHDmXJkiW88cYb9O3bl/79+9O1a1euu86afzBo0CAuu+wyTjnlFM477zyeeuqp4yp5BMHvgMnAH4BHqy2tyolW86huRv8ZOD1O3tz85glfqzm5PC7y7fk+V/KobnTGaLrGd2XuxrkBiCyw8ux5Pk8+rG5oh6GclHoSr2W/hkdDq39wT+keuiT43kNbpV+7fpzZ9UzmZc+j0l0ZgMgCp6CsgHax7U7416em4FeGqKoHgF/UsXvriYfTcjjdHv70QTaZ7dpwxan1PzmqRch+H965iUiNhJmLICPovWOGEXLOOuusOp94d/vtt9e6/Z577uG2224Lelm/Kqr6ebBjaAmqHifeFCXteib3ZFzmOF7b+BpXDbyKpOikE75mcygoK8ClLp8reVRni7Bx1cCr+Os3f+Wbvd9wSudTAhBh03N5XOwt28v5Pc73+1wR4eqBV3P3F3fzee7njMkcE4AIA2NP2R5OSj2pUefOHDST2R/P5oPtHzCtz7QmjixwfK0x3Rx86pkWkfub4phQ8tLyHWwpLOX3kwcSHdmCi7i7KuGTB+DNq6BDP1aPfMwk0obRiomIXURKvItDRNwi0mBpFBGJFZFVIrJeRH4QkQe828eJyLcisk5ElotIb+/2GBF5U0S2isjXItI9sC3zj8PlIMYW02QP4bhpyE3YnXbmbQydyVq5JdZ4/sYM8wBrglqHuA48te6pkHms+r4j+3Cpq1E90wATuk8gPSGdZ9Y/EzK90x71sLdsb6N6pgFO63Ia/dv1598//Bu3x93E0QXO3tK9fo2XDiRf7zLXi8icepZfYdWODgsFh8t58tMtjOvfkfEDW3CJnMJN8OJ4WP4YDL8Grl1CZUxqsKMyDCOIVDVRVZNUNQmIA6bTQLUlrwpgrKoOAYYC54nIacAzwJWqOhR4HbjXe/ws4JCq9gYeBx5u4qacEIfb0aQPWunfrj/jMscxd+NcSiqbtmxjoOy2e8viNWKYB1iTN68ffD1r9q3hq4KvmjK0gMm3W6UpG1vqLSoiipuH3kx2UTYf7/q4KUMLmAPlB3B6nI3+AiEizD55NjsO7+D97aExXrzSXcku+65Gf1Fsar4m088DifUsCd5jwsIfF2fj9ij3TwleRYF6uSrgi0fh2XPgcB78dB5M+QdEBX/ckGEYLYe35Oi7QIOPOPMeW+pdjfIu6l2qxjUk8+ODuqYCr3jfLwDGiT8lIwKswl3R5GMpQ613erd9N3GRcbSPa9/oa0zvO51ObTqFTO+0vw9sqc2kHpPoldyLf679Jy6Pq6lCC5iqsngn0ks7PnM8J6WexFPrnjo6RKol21y0GZfHxeD2LaPCjk9jplX1gUAH0lJ8trmQD74rYM6EvmS0a2Gl+Ei0uAAAIABJREFUcVQh5yP46DdwaAcMuBAueAwSmvaxmIZhhC4Rqf6Y0whgJODw8VwbsAboDTylql+LyPXAEhEpB0qAqqfUpAG5cPTBXIeBVOBAkzTkBBU7ipt8bHP13ukrBlzR4kuJ5Zbk+l0Wr6YYWwyzT57Ng189yPL85ZydfnYTRtj08ux52MR2QmNpbRE2fjHsF9yRdQfvb3u/xY8jrvoC4esDW2ojItwx4g6uX3o98zfNZ+agmU0VXkB8d8Cq+x5SyXRrUXC4nF+9tZ4+HROY3ZJK4alajwP/398g7xto3w+ufgd6jQ12ZIZhtDwXVnvvAnZi9SI36P/ZO+/wqIouDr+z2U3vIYSQEEIPvQWCFClSRClWUGmfitiwgCiCiKhIE1RQUBQUe6MIIqBgCAEEQg9IDT0QQgqkl83ufH/cDQSkZJNtCfd9nvtkd3Zmzm9SNmfnnjlHSmkAWgghfIFlQogmwCiUYl3bhBCvAh+gVFgsFUKIEcAIgKCgIGJiYko79DLZ2dlmjzuSfARvjXeZ7N2MSH0k0fpoJvwxgQf9Hyz3fGVZW2k5lHyIIF3Zvucl8Zf++Dv5817se7wa/CpOovQZa6y5vuuxK2UXfk5+bIrdVK55NFJDmHMYH277EM9ET3RC958+tl7bjViTvgZn4czJ3Sc5I8pX2S/CNYJ5u+ZRNbkqhlyDQ6zveqxLXYe3kzcH4w5ySBwye7ylf3aqM21CbzAy8ofdFOgNfDq4Na46u6e3gvxM2Pcr7PgKkveBTxjcOwtaDQOn//5hq6ioqAALpJSbSzYIIToAF0o7gZTykhBiPUqV2+ZSym2ml34G1pgen0VJj5oohNCihID8JxGzlPJz4HOAyMhI2aVLF/NWA8TExGDuuAk/TaB9WHu63GG+vVtxfMtxlh5dyktdX6KuX91yzVWWtZUGg9FA2vdp9G7Qmy6tyz+/8aSRVza8QnK1ZB5r+Fipx1lrfTfiiz++oI5PHYvYdDnnwtNrn+ZEwAlGNBvxn9dtvbYbMe/3ebQMasldXe8q91xBaUEMWDmAI75HaK5p7hDrux6zls2iVfVWdO1atowrlv7ZOXCaCtsybfUhdp66yLQHm1G3qqf9hBTmKGnulo6AWQ3gj9EgjdB/Hry4C9oMVx1pFRUrkZ+fT9u2bWnevDmNGzfmrbfeAuDEiRNERUVRt25dBg4cSGGhko+1oKCAgQMH0rx5c6Kiojh58qQd1V/m41K2XYUQItC0I40Qwg3oARwEfIQQ9U3ditsAVgDF94IfAqIdpWx5rj6XjIKMMmc3uBUvtHwBD50H07ZPc9g44gu5F9Ab9WU+fHgtPWr2oF1wOz7Z/YnDFq/RG/QcvXSUWt61LDJf++rt6VGzB5/Hf365RLmjkaPP4fDFw7QMammR+RoGNKRv7b4s+ncR5/XnLTKnpckszORk5kmHCfEAM51p05vteCHE50KIL4sva4mzBVJK5vx9lIWbTvC/9uH0bV72mKMyUVQAZ+Jg4wfw3YMwo7aS5u7In9D0IRgeDc9uhpaDVCdaRcXKuLi4EB0dzd69e9mzZw9r1qxh69atjB07llGjRpGQkICfnx8LFy4EYOHChfj5+bF3715GjRrF2LFj7aZdCHGHKbNS4DXZliahFNa6FcHAeiFEPLAdWCulXAk8BSwRQuwFhgCvmvovBAKEEAnAaOB1Cy+pzBRXRqvuYZ33cz9XP0a2HMm2pG2sO73OKjbKS3kzeVyLEIJxUePIM+Tx0a6PLDKnpdmXuo+8ojyigqMsNudrbV7DSTgxNW6qQ35w2puyF6M00rKqZZxpgFciX8Fd685PaT85ZHrAA2kHAGhSpWx5ta2BuWEey4GNwDqg4iQjvAF5hQZeXbyXlfFJ3N8yhPH3NLSOISkh/5KSeSP9OKQlQOpRSIqH1MNQfFo4MEIJ4Yi4F2q2V51nFRUbI4TA01O5M6XX69Hr9QghiI6O5ocffgBg2LBhTJo0iWeffZbly5czadIkAB566CFGjhyJlLJcB77KgTNKZiUtSpalYjJRdo5vipQyHvjPf2Qp5TKUirfXtucDD5dVrDUpzm5QngNZt+Lh+g/z65FfeX/7+7Sv3h4PnYfVbJWF/an7Aajta7nzP7V9ajOk0RC+2v8VD9Z7kBZVW1hsbkuwLWkbAmHRAjPVPKrxXIvnmLljJtGno7mrZvlDKSzJ7gu70QgNzQObW2zOALcAXol8hbf+eYtlR5fxYP3ynw2wJMW/240DHCfjmrnOtLuU0n5bLxYgT5/PqUwD89YfZfnuRBJSshnfqx5PdQxHyAIoMIA0gLH4KgKjHgzFV4FSKKUoD/T5oM9VQjMKc6AwC/IuQX4G5KVDTipkX4Cs86DPuVqIVzAENYEGd0NwC8V59ih7+iIVlUrF6tfh/D7LzlmtKfSedstuBoOB1q1bk5CQwPPPP0+dOnXw9fVFq1XeLkNDQzl7Vslle/bsWWrUUKrLabVafHx8SEtLo0oV2/8tmyofbhBCLJJSnrK5AAeieGfamtXRtBotE9tNZOjqoby//X0mtZ9kNVtlYdPZTTTwa1CutHjX45lmz7D6xGre3PwmP/f5GXed42S92pq0lYYBDS2eZeWxho+x/NhypsZNpU1wG4eqgLkreRcN/BpY/MPc/XXv59ud3zJr5yw61+hs8d+j8rAvZR81vWs6VDYdc53plUKIe6SUq6yixspIKRm4KJJLTkZqJhXRxlnPOz45RG0oAEsV4NW6gqsPuPmBRyAEN4P6vcA7BHxCwL+2crk4RulhFRWVq3FycmLPnj1cunSJ+++/n0OHzD8pbmdyhRDvA42By4mWpZS3TfqfpJwktEJLoFugVe20qNqCx5s8zpf7v6Rrja50rtHZqvZKS1ZhFnsu7LFKejN3nTuTO0xm+F/D+WDnB0xoN+HWg2xArj6X+NR4hjQaYvG5dRod77R/hyGrhjB5y2Sm3zndXnefrkJv1BOfEm+VnWMhBAMDBjLj/Aze/udt5nSb4xBrBmVnuk2wY5W3N9eZfgkYL4QoBPSmNmmqtOXwCCFo5xbJ6bzT5HnDhqJMlnt50sGtOi/7tSbCLRCEBoQTaLSgcTJdOiXkwkkHTi6gdVGcZp2b8tXFE5xNl1o4RUWl/JRiB9na+Pr60rVrV7Zs2cKlS5coKipCq9WSmJhISIhSECIkJIQzZ87g4+NDUVERGRkZBATYvQrp9yhZN/oAz6AcEkyxqyIbcy77HEEeQThprJ+V6fkWz7Pp7Cbllnj/Zfi5+lnd5q3YmrSVIllktZzQUcFRDG00lG8OfMOdoXdyZ+idVrFjDrsv7KbIWERUNcvFS5ekSZUmPNfiOebsnkPH0I70q9PPKnbM4VDaIfIN+bSq2soq81fTVWN069FM3z6dHw79wKCGg6xixxySc5K5kHfBoQ4fgpkHEE1lajVSSlfTY6+K4kgXM37wIh6pN5GvH41m3WObGRM5hv3GHAacW8nqkAjo8BK0HwntnoG2T0HkE9BqCDR/BJo8CA37QL0eUKsThEZCtSbgF66EaKiOtIpKhSYlJYVLly4BkJeXx9q1a2nYsCFdu3Zl8eLFAHz99df076+kbe7Xrx9ff60UAVy8eDHdunVzhN2bACnlQkAvpdwgpXwCuG12pUHZmbZmvHRJnJ2cmdJxChmFGUz6Z5JDHFLbdHYTXjovi8bRXsuLrV6knl89Jm6e6BDZPbYlbUOr0Vr0IN61PNHkCSKDInlv63uczjxtNTulZdeFXQBWXfOghoPoHNqZWTtmcTDt4K0HWJn9aUq8tCMdPoQypMYTQvQTQsw0XX2sIcpWuDi5MKzxMFY9sIqWVVsyYdME9qbstbcsFRUVO5GUlETXrl1p1qwZbdq0oUePHvTp04fp06fzwQcfULduXdLS0njyyScBePLJJ0lLS6N58+Z88MEHTJtm/x11rtw1TBJC3CuEaAn421OQrTmXfa5cpZXNpYF/A0a1GkX0mWgW7FtgM7vXQ0rJprObaFe9HVqN9UpJuDi5MLXjVLL12YyOGY3eoL/1ICuyNWkrzQObWzWG20njxNROU9FqtIzZMIZCY6HVbJWG3Rd2U8OrBoHu1gtnEkLwbod38XPx49XYV8m59vyXjdmfuh+t0BLhH2FXHddibmq8aSihHgdM10tCiKnWEGZLvJ29+ajrR1R1r8qL0S9ePgmuoqJye9GsWTN2795NfHw8+/fvZ+LEiQDUrl2buLg4EhIS+PXXX3FxcQHA1dWVX3/9lb179xIXF0ft2g5ROXWyEMIHeAUYAyxAqWJ4W6A36knJS7GpMw0wpNEQ7ql1Dx/v/pjYxFib2i7JkYtHuJB7gU4h1i/73cC/AW+3f5tdF3YxJW6K3XblMwoyOJR+yKIp8W5ENY9qTOk4hUPph/gu7Tu7pY6TUrL7wm6r7koX4+fqx7Q7p5GYlchrsa9RVJyBzMZIKYlNjKVRlUa4OLnYRcONMHdn+h6gh5TySynll8DdwL2Wl2V7/Fz9mHvXXPQGPS9Ev2C3XxYVFRWVsiKEcALqSSkzpJT7pZRdpZStpZQr7K3NVlzIvYBRGm0W5lGMEIJJ7ScR4R/B2NixnMg4YVP7xWw6q5TR7hDSwSb27q19L082eZLFRxbz8+GfbWLzWuLOxyGRtAtuZxN7nWt05pXIV9idu5t5e+bZxOa1HL54mPT8dKvFS19Lm2ptGNd2HLGJsby//X2b2LyW3Rd2c+TiER6o+4Bd7N+MslRA9C3x2HHykliA2r61mXjHRI5cPGLXnQUVFRWVsiClNACP2luHPSm+s2jrnWkAN60bH3X9CJ1Gx7PrniU5J9nmGjae3UiEfwRV3avazOYLLV/gztA7mRY3jejT0TazW8zms5tx17rbNI52aKOhtPNox/z4+fx+7Heb2S3m2wPf4qZ1464w2+W9HhgxkGGNhvHDoR/4/uD3NrNbzE+Hf8JL50XvWr1tbvtWmOtMTwV2CyEWCSG+BnYC71lelv3oXrM7gW6BLDm6xN5SVFRUVMrCZiHEJ0KITkKIVsWXvUXZiuIc0/ZwpkEpFDOv+zwuFVziqbVPkZ6fbjPbGQUZ7L2wl44hHW1mE5RY4hl3zqBxQGPGbBjD5rObbWb7Qu4FVh5fSc/wnug0tit0Vpw6LqpaFBM2T2DNiTU2s30+5zyrjq/igXoP4Ovqe+sBFmR05GjuCruL6XHT+S3hN5vZTc1LZe2ptfSv29+hcpsXY242jx+BdsBSYAlwh5TSPvd1rIRWo+X+evez6ewmkrKT7C1HRUVFxVxaoOSYfgeYZbpm2lWRDbm8M+1pH2calEwDn3T7hHPZ53h67dNkFGTYxO7C/QsxSINddu48dB7M6z6POr51eGn9S2w/v90mdhfuW0iRsYgRzUbYxF5JtELLnG5zaBHYgtc3vs5fJ/+yid3vDnyHRFolp/at0AgN0zpNo11wOyZunsiyo/8pjmoVlh5dSpGxiAENBtjEnrmUypkWQkSYvrYCgoFE01W9Mu54PFDvAaSULEuwzS+JioqKiqUwxUlfe902qfHO55wnwDXA7geUIqtF8lHXj0i4lMD/1vzP6iEfSdlJfH/ge/rW6Ut9v/pWtXUjfFx8mN9jPqGeoTy37jmrh3wk5ySz+Mhi+tftTw2vGla1dSPcde7M6z6PZoHNGBs7lpXHV1rVXmZhJouPLqZneE9CPEOsautGuGpdmdNtDu2rt2fiPxP55fAvVrVXZCzil8O/0C64HbV8alnVVlkp7c70aNPXWde5Kt2OR4hnCO2rt2fp0aUYjAZ7y1FRUVEpNUKIICHEQiHEatPzRkKIJ+2ty1acyz5n88OHN6JjSEfm3TWPpJwkBq8eTMLFBKvZ+nj3xwCMbDHSajZKg7+rPwt7LaSeXz1eXv8yGzItVV74vyzYtwCjNNplV7okHjoP5t01j5ZBLRm3cRyf7vnUaplNfj38Kzn6HB5v/LhV5i8trlpXZnebTaeQTry79V1m7ZhlNX9p3el1JOcm80jEI1aZ3xKUypmWUhb/pva+dscDJcNHpeOh+g+RnJvM5nO2i/1SUVGxL/n5+bRt25bmzZvTuHFj3nrrLQBOnDhBVFQUdevWZeDAgRQWKvllFy1aRGBgIB06dKBFixYsWGDfHMMmFgF/AsUe5RHgZbupsTFJOUlU86hmbxmXuaP6HSy6exFFxiKGrhnKhjOWdy4Pph1k5fGVDGo0yK7hLcUEuAWwsNdCutTowuKLi5mybQqFBsvmZD6fc54lR5dwX7377LZDWxJPZ0/md59Pvzr9mLd3HuM2jSOvKM+iNlJyU/jmwDe0C25Hw4CGFp27LLg4uTC722weafAIi/5dxIvrXyS7MNuiNs7nnGfK1inU9a1L59DOFp3bkph7APGfUrZVeDrX6EyAawCLjyy2txQVFRUb4eLiQnR0NHv37mXPnj2sWbOGrVu3MnbsWEaNGkVCQgJ+fn4sXLjw8piBAweyefNm9uzZw/Dhw+2o/jJVpJS/AEYAKWURcFvcYpNSKtUPPRxjZ7qYCP8IvrvnO0I8QxgZPZLpcdMt5lwWGYt4f8f7eLt4M7ypQ/z+AUpmkw+7fEhXr678eOhHHvvjMY5fOm6RuXP1uby64VUEgqeaPmWROS2BzknH5A6TebHli6w6vooBvw9gf+p+i8ydV5THC9EvkFeUx5jIMRaZ0xLoNDreaPcGE6ImsPnsZh7+/WF2Ju+0yNx6g55XNrxCgaGAD7p8YNUiROWltDHT1YQQrQE3IUTLEifEuwCOd6zSAug0OrrU6MKeC3vsLUVFRcVGCCHw9PQEQK/Xo9frEUIQHR3NQw89BMCwYcP47TfbnWIvAzlCiABAAggh2gG2OQFnZ9Lz0ykwFDjE7uy1hHiG8N093/FYxGN8d/A7Bq8aXO6Ku3qjntdiX2P7+e2MajUKb2dvC6m1DE4aJx7wf4C5d83lQu4FBq4cyKL9i8r1QUJv0DM6ZjTxqfFMv3O6w4T0FCOE4KlmT7Gg5wLyDfkMXjWYuXvmlmuX2iiNvLHpDQ6kHWDGnTNo4N/Agootw8CIgXzZ60sAHl/zODO2zyBXn1uuOWfumEl8SjzvdnjXYWOliymtm98L+B8QCnxQoj0LGG9hTQ5DTe+aXCy4SGZhpsO9SamoVGamx03nUPohi84Z4R/B2LZjb9nPYDDQunVrEhISeP7556lTpw6+vr5otcrbZWhoKGfPnr3cf8mSJcTExBAREcGHH35IjRr2OQhVgtHACqCOEGIzEAg8ZF9JtqE4LZ6j7UwX4+LkwriocUQFRzF562QGrxpMW4+2NM5tbHZJaL1BcaTXnV7Hq5Gv8mD9B62kuvzcGXonS/ot4e0tbzNr5yx+OfILr7R+hW5h3RBClHqeQkMh4zaOY/O5zbzT/h261+xuRdXlo21wW5b0W8KUbVP4bO9nLD26lJEtRtKvTj+cNE6lnievKI+Z22ey9tRaxkSOoUuNLtYTXU5aBbViSb8lfLDzA7498C2rT6xmRLMRPFTvIXROpU9bmFeUx4c7P+THQz8ytNFQeob3tKJqy1DamOmvTfHR/7smZrqflHKplTXajTCvMADOZJ6xsxIVFRVb4eTkxJ49e0hMTCQuLo5Dh27s1Pft25eTJ0+yZcsWevTowbBhw2yo9PpIKXcBnYH2wNNAYyllvH1V2QZHSItXGrqFdeP3+3/niSZPsDNnJ72W9OKNTW9wMO1gqcZvP7+dJ/96knWn1zG2zViGNh5qZcXlJ9A9kE/u+oRPu3+KTqPj5ZiX6b+8P98f/J7MwsybjjVKI6uOr6Lfb/3469RfjIkcw/317reR8rLj7ezNtE7T+KrXVwS5BzHxn4n0/a0vC/Yt4ELuhVuOjzkTw32/3ccvR35hWKNhDG3k+D9nd507E9pN4Jve3xDmFcaUbVPos6wPn+39jMSsxFuO331hNw///jA/HvqRwQ0H83LrinHcw6wAFCnlEiHEvSg5TF1LtL9jaWGOQJi34kyfzjpN4yqN7axGReX2oTQ7yNbG19eXrl27smXLFi5dukRRURFarZbExERCQpQDTwEBAQAUFhYyfPhwXnvtNXtKBkAI4Qo8B3RECfXYKIT4TEqZb19l1udQ+iE0QuMQB9JuhYfOg1GtRxGaHsoRryMsP7acFcdWUMenDlHBUbQNbkuoZyg+Lj7oNDpOZp4k4WICa06uYUfyDqq4VWFyh8n0r9vf3ksxi44hHWkX3I5VJ1bx86GfmRY3jVk7ZtG0SlNaBbWigV8D3HXuuGndSMpJYn/qfraf307CpQQa+DVgfo/5tK/e3t7LMIvIapF8f8/3rDu9ju8Pfs/sXbP5ZPcnNK7SmGZVmtEooBFezl5ohIZcfS47k3ey/fx2jmUco65vXRbdvYjWQa3tvQyzaFm1JYvuXsQ/5/5hwb4FzN0zl7l75tKsSjMaV2lMA78GBHkEUWQsIt+QT3xKPLGJsZzKPEWwRzALey6kbXBbey+j1JjlTAshPkOJke4KLEC5dRhXyrF3A7MBJ2CBlHLaDfo9CCwG2kgpd5ijz9KEeoUCcCrzlD1lqKio2IiUlBR0Oh2+vr7k5eWxdu1axo4dS9euXVm8eDGPPPIIX3/9Nf37Kw5MUlISwcHKLuiKFSto2ND+J+yBb1BC8D42PX8M+BZ4+GaDTE54LOCC8r9hsZTyLaHch59sGm8APpVSzjG1z0bJ6JSLcudylxXWUyqklKw9tZbWQa3xcvaylwyzCdQF8nC7h3mh1Qv8fux3NiZuZOnRpfxw6Ifr9q/qVpXX277Og/UexFXret0+jo5Wo6VfnX70q9OPA2kHWHNiDTuTd/LV/q8wyKvPyrpp3WgU0IjJHSbTp3Yfs0IkHAkhBD1q9qBHzR6cyjzF8oTl7EzeyeIji8k3XP05103rRqugVgyMGGh2iIQjIYSgQ0gHOoR04Fz2Of44/gexibEsT1hObtHV8dQ6jY62wW0Z1HAQfWv3xdPZ006qy4a5RyPbSymbCSHipZRvCyFmAatvNUgI4QTMBXqgFHvZLoRYIaU8cE0/L+AlYJuZuqyCm9aNIPcgzmSpYR4qKrcDSUlJDBs2DIPBgNFoZMCAAfTp04dGjRrxyCOPMGHCBFq2bMmTTyppm+fMmcOKFSvQaDRUqVKFRYsW2XcBCk2klI1KPF8vhDhww95XKAC6SSmzhRA6YJMpV3VDoAYQIaU0CiGqmvr3BuqZrijgU9NXu5BwKYGTmScZ1HCQvSSUC29nbwY1HMSghoMoNBRyIO0AqXmpZBRkkG/Ip6Z3Ter61iXIPcisOGNHp1FAIxoFKL+uufpczmafJa8oj7yiPAJcA6jlU6vCOtA3oqZ3TV5s9SKgHCI9lXGKAkMBBmlAp9FR16+uTUuj24LqntV5qtlTPNXsKYzSSGJWIun56eicdOg0OkI9Qx2yTHhpMdeZLv74lCuEqA6koVREvBVtgQQp5XEAIcRPQH/g2jf4d4HpwKtm6rIaYd5h6s60isptQrNmzdi9e/d/2mvXrk1c3H9vwk2dOpWpU6eSlZWFl5fD7IbuEkK0k1JuBRBCRAG3vMsnlSoTxUlidaZLAs8Cj0kpi1PtFQd79ge+MY3bKoTwFUIESymTLLuc0vHXqb8QCIc+lFZanJ2caVG1hb1l2Bx3nTv1/OrZW4ZNKXaebyc0QkOYd9jlUNrKgLl5pn8XQvgC7wO7gJPA9e9FXU0IUHJ7N9HUdhlTWfIaUso/zNRkVcK8wtSdaRUVlYpEa+AfIcRJIcRJYAvQRgixTwhx04OIQggnIcQe4AKwVkq5DagDDBRC7BBCrBZCFHs7t3xftyV/nfyL1kGtqeJWxV4SVFRUblNKvTMthNAAf0spLwFLhBArAVcpZbnzl5rm/gAl/d6t+o4ARgAEBQURExNjtr3s7OxSjyvKKCI9P53V0atx07iZbcvWmLO2ikhlXt/tvjYfHx+ysrJsI8jCGAyGm2rPz8+35c/27rIOlFIagBamTZNlQogmKDHU+VLKSCHEA8CXQKfSzmmL9+ykwiSOZxyntVPrCvc3VJn/7qFyr68yrw0q9/osvjYpZakvYLc5/UuMuwP4s8TzccC4Es99gFSUne6TKOEk54DIm83bunVrWRbWr19f6r7rTq6TTRY1kftT95fJlq0xZ20Vkcq8vtt9bQcOHLC+ECuRmZl509evtzZghyzD+2lpLsAPaAa0Kr7KMMdEYAxwCKhlahNAhunxfODREv0PA8E3m9Na79lzd8+VTRc1lSm5KWWa355U5r97KSv3+irz2qSs3Osr69pu9L5tbpjH30KIB4X5px+2A/WEELWEEM7AIyhFBQCQUmZIKatIKcOllOHAVqCftHM2DyiRHi/ztJ2VqKhUfpT3qsqFrdckhHgXiAfmALNM18xSjAs07UgjhHBDOTB+CPgNJYMTKPmrj5gerwCGCoV2KE62feKlT/5Fq6BWaoiHioqKXTD3AOLTKNW1ioQQ+Si7FFJKedPygFLKIiHESOBPlNR4X0op/xVCvIPi5a+42Xh7UpweT3WmVVSsi6urK2lpaQQEBFSabAVSStLS0nB1tWkKswFAHSmluTWbg4GvTdmXNMAvUsqVQohNwPdCiFEoBxSHm/qvQkmLl4CSGu9xi6g3k39T/+VYxjHGR1TaYrwqKioOjrlFW8p8XF1KuQrlzbdk28Qb9O1SVjuWpjg93uks1ZlWUbEmoaGhJCYmkpKSYm8pZpOfn39Dh9nV1ZXQ0FBbytkP+KIcIiw1UqmS2PI67ZeAe6/TLoHny6jRIhiMBiZvnYy/qz/31LrHnlJUVFRuY8wt2vK3lPKuW7VVNtT0eCoq1ken01GrVi17yygTMTExtGz5Hz/UXkwFdgsh9qPkjgZAStnPfpKsw8+Hf2Z/2n6md5qOj4uPveWoqKjcppTKmTZVxnIHqggh/FDCOwC8sWPLjXlpAAAgAElEQVQqJFsR5hXG+jPr7S1DRUVFpTR8jZKvfx9gtLMWq5Gck8yc3XNoX709vWv1trccFRWV25jS7kw/DbwMVAd2csWZzgQ+sYIuh6Kmd03S89PJKsyqUGVqVVRUbktypZRz7C3CmkgpmbJtCkXGIiZETag0MfYqKioVk1I501LK2cBsIcQLUsqPrazJ4QjzMmX0yDpN44DGdlajoqKiclM2CiGmomTbKBnmsct+kiyHURqZsm0K0WeiGd16NDW8a9hbkoqKym2OuQcQPxZCtAfCS46VUn5jYV0ORcn0eKozraKi4uAUB2+3K9EmgW520GJRDEYDb295m2UJy3iiyRP8r/H/7C1JRUVFxewDiN+ilJbdAxhMzRKo1M60mh5PRUWloiCl7HrrXhWP1LxUJm+dzN+n/+bZ5s/ybPNn1fAOFRUVh8DcPNORQCNZGSsr3AQ3rRtV3aqSmJ1obykqKioqN0UIEQRMAapLKXsLIRoBd0gpF9pZWpkozM9mbWo045eNJ8+Qx5iWLzOs0RAwGkBoQGNu7TEVFRUVy2KuM70fqAbYpcqVPfFy9iJHn2NvGSoqKiq3YhHwFfCG6fkR4GegQjrTI7/pzRaXS7TNy+eNtHRqHxsNS0df3UloQKP97+XkDE465avWBXRupq8e4OwOzh7g4g2uPsrlHgBufuARCF7BynPVWVdRUbkF5jrTVYADQog4Knn+0mtx07qRW5RrbxkqKioq10UIoZVSFgFVpJS/CCHGweUKtIZbDHdY+tZ5CHbEcqc2jJqdQovr7oI0XrmMBpAGMBYpjw16MOqVr4ZCKCpQvurzoCgf8i5CYY5y5WdCUd71jWu04B0CfuHKVaU+VG0IVRuBd7ANvwsqKiqOjLnO9CRriKgIuOncyNPf4A1XRUVFxf7EAa2AHCFEAMp5FoQQ7YAMeworD33veol9yY2ZEF/AofQwJt/X1PJGDHrIz4DcdMhNg+xk5co8BxmJcPEkHFqpvFaMVzCEtIYaUVC7CwQ1UXexVVRuU8zN5rFBCFETqCelXCeEcAecrCPNsXDTupGSW/HKHKuoqNw2FJ/GG42SFq+OEGIzEAg8ZDdVFqB9dS0av1A+23CMRsE+PBYVZlkDTjrwqKJcNyMnFS4chOR/4exOSNyuONkA7lWgXg9ofD/U7gpaZ8tqVFFRcVjMzebxFDAC8EfJ6hECfAZU6nLioDjTeTe6FaiioqJifwKFEMXBxMuAVSgOdgHQHYi3lzBL8GqvBvx7LoPJfxygS4NAqvu62V6ERxWo1Um5islMguMxcOxvOLwK9v6oxF83eRAin4BqVthJV1FRcSjMvSf1PNABpfIhUsqjQFVLi3JEVGdaRUXFwXECPAEvwANls8QJcDe1VWicNIIp9zfFKCVv//6vveVcwTsYWjwKDy6AMQnw2C9Q/27Y8wN81hEW9IADK8BYaSu7q6jc9pgbM10gpSwszu0phNBiisur7KjOtIqKioOTJKV8x94irEkNf3deuqs+09ccYt2BZLo3CrK3pKvROkP9Xsp19zTFod6+AH4ZAoEN4c4x0PgBNbZaRaWSYe5f9AYhxHjATQjRA/gV+N3yshwPV60r+UX59pahoqKiciNuiwomwzvVon6QJ2+t+JfcwiJ7y7kx7v7QfiSM3AEPLAAkLHkSvugCJzfZW52KiooFMdeZfh1IAfYBT6PE5E2wtChHxE3rRqGxEIOxwmaYUlFRqdxU+rMrADonDe/d35Szl/KYt/6YveXcGictNHsYnt0CD3wBOWmw6F74ebCSKURFRaXCY64z7QZ8KaV8WEr5EPClqa3S4651B6h0oR5SSs5ln2Nj4ka1XLqKSgVGSplubw22ok24P32bV2fhphNcyKogdww1Gmg2AF7YAd0mwNF1MDeKkMQ/lNzYKioqFRZzY6b/RjkVnm167gb8BbS3pChHxE2rfGbIK8rD09nTzmrKz7FLx5i3Zx5bzm0hS591ub2BXwN6hvdkcMPBuOvc7ajQ8kgp2XJuC8sSlnEm6wxJOUkYpZF+dfoxsMFAwrwtnG7LQTiQdoCfDv3E0YtHydZnk1uUyx3Bd/Bsi2cJ8QyxtzyrcPzScZYeXcqms5swYkSr0RLsEcyoVqOo61fX3vIcEiGEKxALuKD8b1gspXyrxOtzgCeklJ6m5y7AN0BrIA0YKKU8aSu9r/Soz+p9SXwSncA7/ZvYymz50bnBna9C04dh5SjqJXwOX+2F+z6FgDr2VqeiolIGzHWmXaWUxY40UspsU67pSk9JZ7oicz7nPB/v/piVx1fipnWjd63eNPRvSC2fWhxKP8TaU2v5ePfHxKfEM7vrbJw0lSONeGxiLJ/u+ZT9afvxd/Unwj+CCP8IMgsz+eHgD3xz4Bvur3s/b7d/m+IDthWdnck7+Xj3x+xM3omb1o1WVVsR6hWKQLD6xGr+OPEHD9d/mFGtR13+/a7oHE4/zJRtU9h1YRdaoSWqehQeWg8M0sDO5J08vPJhnmr6FMObDsfZSc0DfA0FQDfT+7oO2CSEWC2l3CqEiAT8run/JHBRSllXCPEIMB0YaCux4VU8GNCmBj9sO83wjrUJC6hg/4r8wmHwUg7+PImGJ7+CzzpBr8nQ+nGoJO9BKiq3C+Y60zlCiFZSyl0AQojWQMX2LktJZXCm/zn7D2M3jiWvKI+hjYbyRJMn8HO98v+xTbU2DGk0hJ8P/czkbZOZsX0G46LG2VFx+cnV5zI1biq/JfxGiGcIb93xFv3q9LvKkUrJTWHh/oV8f/B76vjWYVjjYXZUXH70Bj2f7PmEr/Z/RZBHEGMix3B/vfvxdva+3Od8znnmx8/np0M/YZRGJrSr2Ecf9EY9C/ctZP7e+fi4+DAmcgx9avchwC3gcp/0/HRmbJ/Bp3s/ZWfyThb0XFBpPjhZAiml5MpdR53pkkIIJ+B94DHg/hJD+nOlKu5i4BMhhDDNYxNeuqseS3Ym8uG6I3w4sIWtzFoOIUiu1pWGvUfA8udg5Sg48hfcN085wKiiolIhMNeZfhn4VQhxDuXkeDVsuBNhTyqyM22URubHz+fTPZ9Sx7cOH3b5kHCf8Bv2HxgxkNNZp/nmwDeEeYcxqOEg24m1IEcvHmXMhjGcyDjBiGYjeKb5M+g0uv/0C3QPZGybsVzIvcCHOz+kWWAzWlZtaQfF5edM1hleiXmFg+kHeaj+Q7wa+ep1w3WqeVTjrTvewk3rxrcHvqVnzZ60DW5rB8XlJzUvlRejX2Rf6j7uqXUP49qOw9fV9z/9/F39mdZpGk2rNGVa3DRWnVjFvbXvtYNix8XkOO8E6gJzpZTbhBAvASuklEnXfPgIAc4ASCmLhBAZQACQaiu9Qd6uPN6hFvNjj/F059pEVPO+9SBHxCcEBi+DuPmwdiJ82kHJWx3ewd7KVFRUSoG55cS3CyEigAampsNSSr3lZTkexc50blGunZWYR5GxiImbJ/L78d/pU7sPb7Z7s1Sx0KNbjyYxK5EZ22fQKaRThYsn3n5+OyP/Homb1o3Pe35Ou+B2N+0vhODt9m9zOP0wYzaM4de+v+LvWrF2hg6lH+KZtc+gN+qZ3XU23cK63XLMCy1fYMOZDUz8ZyJL+y2tcHHyJzJO8Oy6Z0nPT2dm55n0Cu91yzGPNHiE5QnL+WDnB3St0bXCrdmaSCkNQAshhC+wTAhxJ/Aw0KWscwohRqBUziUoKIiYmBiz58jOzr7huKZaiasTvPHjP7zQ0rWsMu3G1WtriGeLaTQ6MBO3RX04Gf4Ip2o+DKLi5qW+2c+uolOZ1waVe32WXpu5O9MAbYBw09hWQgiklN9YTJGD4qpV3qQrUq5pvUHP2I1jWXtqLS+0fIGnmj5V6tvaThonxkeNZ/2Z9fx+/Heeb/G8ldVajg1nNjA6ZjQ1vGowv8d8gjxKV9jBy9mLWV1mMeiPQczZNYdJ7SdZV6gF2X5+Oy9Gv4iHzoMve31Jbd/apRrnpnXjnQ7v8Piax5m9a3aFCuvZm7KXkX+PRCM0LOy5kKaBpSvb7KRxYlzUOIauHsrC/Qt5oeULVlZa8ZBSXhJCrAe6ouxSJ5jeO9yFEAlSyrrAWaAGkGgq4OWDchDx2rk+Bz4HiIyMlF26dDFbT0xMDDcbd1Qc4aN1R6lSryVNQnzMnt+e/HdtXaDnAFg5mlr7fqCW03klpZ5HFTspLB+3+tlVZCrz2qByr8/SazPr464Q4ltgJtARxaluA0RaTI0DU9HCPAoNhYyKGcXaU2t5rc1rjGg2wuz40CCPIKKCo1h5bCU2DIMsF2tOruHl9S9Tz68ei+5eVGpHupgI/wh6hfdi3el16I0V46bLlnNbeGbtM1R1r8p393xXake6mNZBrXk04lF+OPQD57LPWUmlZdmXso+n1z6Nt7M33/X+rtSOdDEtq7bknlr3sGj/IhKz1Fy/AEKIQNOONEIIN6AHsFNKWU1KGS6lDAdyTY40wAqg+IDBQ0C0LeOlS/JEx1p4u2r5aN1Re5i3PC5e8MDn0Hc2nNyslCU/9Y+9VamoqNwAc+8dRQIdpJTPSSlfMF0vWkOYo1GRnGmjNPLGpjfYkLiBN9u9yZBGQ8o8V986fUnMTmRPyh4LKrQOGxM3Mi52HM0Cm7Gg54Lrxs2Whh41e5BRkMH289strNDy7E3Zy0vrX6KmT02+vvtrqnlUK9M8j0Y8CijfQ0fncPphnln3DH4ufnzZ60tqeNco0zyjWo9CIzQs+neRZQVWXIKB9UKIeGA7sFZKufIm/RcCAUKIBGA0SlEvu+DtqmPEnbVZdzCZ+MRL9pJhWYSA1v+D4etA5w6L+sDGWWA02luZiorKNZjrTO9HOXR421FRnGkpJe9vf581J9cwqvUoBjQYUK75uod1x03rxopjKyyk0DrsubCH0TGjqedXj7l3zS1XLvD2Ie1x17qz9tRaCyq0PIfTD/Psumep4laFz3t8XuYPDwA1vWtSw6sGsWdjLajQ8pzIOMGItSNw07qxoNcCs+88lKSaRzWigqPYmrTVggorLlLKeCllSyllMyllEynlO9fp41nicb6pgFddKWVbKeVx2yq+mv91qIWvu44P1x6xpwzLE9wMRsRAo/7w9zvww8OQnWJvVSoqKiUw15muAhwQQvwphFhRfFlDmKNRUSogrstcx3cHv2NIoyE83vjxcs/nrnOnW1g3/jz5JwWGAgsotDwJFxN47u/nCPII4tPun5a7qI6LkwudQzsTfTqaImORhVRalvM553lm3TO4ad34oucXVHErXzylEIJOIZ2IS4pz2HMB6fnpPLfuOQAW9FxgkYIzbaq14VTmKc7nnC/3XCr2xdNFy9N31mH94RR2nqpkxSBdveGhL+HeWXBiI3zWAY7H2FuVioqKCXOd6UnAfcAUYFaJq9Kjc9KhFVqHdqbXnVrHiksr6F2rN2Mix1gsh27f2n3JKswiNtHxdi3T89MZGT0SVydX5veYf1Ve4fLQI7wH6fnp7EreZZH5LEmuPpeRf48kvyif+d3nW6yKYafQTuQb8tmRvMMi81mSAkMBL69/mZS8FD7u9vFNUzuaQ1RwFECFCOlRuTXD2tekiqcLM9YcrjDnPEqNENBmODwVDa6+8M19sPYtKCq0tzIVldses5xpKeUG4BDgZboOmtpuC9y0bg7rTB9OP8z4TeMJdw7n3Q7vorFgKqWo4CiquFXh92O/W2xOS6A36BkdM5rUvFRmd51t0dLYHUM64qZ1469Tf1lsTktglEZe3/g6Ry8d5f3O71u0NHZkUCSuTq4OFzctpWTi5onsvrCb9zq+R7PAZhabu75ffXxcfNiWtM1ic6rYD3dnLS90q8u2E+nEHrVZumvbUq0JjFgPrYbA5o9gQTdIPmBvVSoqtzXmZvMYAMSh5B0dAGwTQjxkDWGOiKM60xfzL/LS+pfw0nkxPHA4Lk4uFp1fq9HSPaw7W85twSgd4/CLlJLJ2yazM3kn77R/x+xsDrfCTetGx5CO/H36bwxGg0XnLg9zds1h/Zn1jG0zlo4hHS06t6vWlbbBbYlNjHWoXb2F+xey6sQqXmz5YqnySJuDRmhoE9SGuPNxDrVmlbLzaNswQv3ceP/PQ5X3Z+rsAf0+hkd+hMwk+LwzbPoQDI4ZlqaiUtkxd/vyDaCNlHKYlHIo0BZ4szQDhRB3CyEOCyEShBD/OfUthBgthDgghIgXQvwthKhppjar46p1JU/vWM60wWjg1Q2vkpKbwuxus/HRWifHaoR/BPmGfIdJnfbL4V9YenQpTzV9intq32MVGz1r9iQ1L9VhMpmsPbWWhfsXMqD+AB5r+JhVbNwZcieJ2YmczDxplfnN5Z9z//Dx7o+5O/xuhjcdbhUbbaq1ISknicRsNUVeZcBZq2FU9/rsP5vJ6v2VPBY+4h54bivU7wXrJsEXXeGcY7xfqajcTpjrTGuklBdKPE8rzRymErVzgd5AI+BRIUSja7rtBiKllM2AxcAMM7VZHTetG3kGx3Km5+6Zy7bz23jzjjdpUqWJ1ezU8a0DwPEMux7YB5Qcw9O2T6NjSEdGthxpNTsdQpRSvrsv7LaajdJyIuMEb25+k2ZVmjG27Vir2ekYqux2O0Kox7nsc4yNHUttn9q83f5ti50BuBY1brrycV/LEOpV9WTmn4cpLHKMu2lWwzMQBn4HA76F7GT4ohuseg1yK9khTBUVB8ZcZ3qNKZPH/4QQ/wP+AFaXYlxbIEFKeVxKWQj8BPQv2UFKuV5KWVyreysQaqY2q+NoYR6xibF8se8LHqj3APfVvc+qtmr51AIg4VKCVe3cihxDDq9seIWqblWZ1mmaRWPDr8XL2YtAt0BOZpy0mo3SkKvPZdT6UThrnJnVZRbOTs5WsxXiGUIdnzp2T5FXaChkdMxoioxFfNT1I6uW/K7tU5sA1wA1broS4aQRjLsnguOpOXyz5aS95diGRv3g+TglN/X2L+Dj1rB9ARgqRvEpFZWKjLkHEF8F5gPNTNfnUsrXSjE0BDhT4nmiqe1GPEnpnHSb4kjOdFJ2EuM3jaeBXwPGtbV+CWgfFx8C3QI5dumY1W3dCKM08nXq16TmpfJBlw/wcbF+2eBwn3C7hjxIKXl7y9ucyDzBjM4zylyUxRzaVGvD/tT9do03nbljJv+m/ct7Hd+jprd1I76EELSt1pbt57dX3hjb25BuEUF0aRDI7HVHSclyzLSeFsfNF/p8AE/HQtVG8McrMLctxP+qFntRUbEi2tJ0EkLUBYKklJullEuBpab2jkKIOlJKi3lYQojBKJUWO9/g9RHACICgoCBiYmLMtpGdnV2mcTmXckgtSi3TWEtikAZmJ8+moLCAAQED2LrpStGJsq6tNPhJP/ac2WO39a/NWMvB/IMM8B9Ayv4UYrC+DudsZ/7N/Zf169dbLcygmOv97LZkb2FV2iru9bmX/MP5xByOue5YS6LP1JOjz2Fl9Eq8nLwsMqc5v5d7cvfwY8qPdPXqiua4hhgb5NP1yfIhJS+Fn9f9TDWd+R9YrPl3p1J23uzTiF4fxjLzz8NMf8hyWWAcnmpN4X8r4cgaiJ4MS4fDxpnQ/kVo+jBorXd3S0XldqRUzjTwEXC97c8M02t9bzH+LFCy5m+oqe0qhBDdUQ45dpZSXncrQUr5OfA5QGRkpOzSpcuttP+HmJgYyjJuzcY1pF9IL9NYS/Lx7o85cfoE0ztN/8/hu7KurTRsjdvK0qNL6dy5s9Udy2vZm7KXP1b/QUv3lkzoM8Fm9k//e5rNOzbT/I7m+Lv6W9XWtT+7Y5eO8erKV4mqFsV7Pd7DSeNkVfvFaBI1LPl7CTWa1qBF1RYWmbO0v5eJWYmM/308TQKaMKv3LHROOovYvxXhGeH89NtPuIS70KVeF7PHW/PvTqXs1An05PEO4SzYdILB7WrSNNT6d7McBiGgQW+o1wsOLIPYWbD8OYh+V8lX3XIIeJW9gqiKisoVShvmESSl3Hdto6ktvBTjtwP1hBC1hBDOwCPAVZUThRAtUUJI+l1zyNFhcIQwj7ikOL6I/4L76t5ntSwWN6K2T23yivJsXi0uszCTsbFjCXIP4pGAR2zqyBcXB7F13HR+UT5jNozBXefO1E5TbeZIA4R5hQFwJuvMLXpaFr1Rz9hY5XDl+53ft5kjDRDqFYpWaG2+ZhXr88Jd9QjwcOaN3/ZRZLgNQx00GmjyIDy7GQYvgcAGikP9YSP4aRAcXAl6x6x6qqJSUSitM+17k9fcbjVYSlkEjAT+BA4Cv0gp/xVCvCOE6Gfq9j7gCfwqhNjjiGXK7e1MX8y/yLiN46jpXdMmcdLXUpzRw5aHEKWUvP3P25zPOc+MzjNw11jvINr1qOWtHLy0ddz0zB0zSbiUwHsd3yPQPdCmtkM8Q9AIDaezTtvU7qd7PiU+NZ632r9FqJdtzx9rNVqqeVQjMUtNj1fZ8HbV8Xa/JsQnZjA/1v7ZiOyGEFC3OwxdDiN3Qrvn4PRW+HkQzKwHS5+GA8shP8PeSlVUKhylDfPYIYR4Skr5RclGIcRwYGdpJpBSrgJWXdM2scTj7qXUYjdcnVzJK8pDSmnzMAcpJZP+mUR6QTqf3PWJVbMb3Ig6PlfS43UK7WQTm8uPLeevU3/xUquXaB7Y3CZx0iWp7lkdnUZn053pDWc28PPhnxnaaKjFC7OUBp2TjmCPYE5n2s6Z3nF+Bwv2LeD+uvdbvDBLaQn1ClVzTVdS7m0WzOr9wXy07gh3NaxKRDVve0uyL1XqQs934a6JcGID7F8Gh36H+J9Ao4UaURDeEWq2h9A2SpEYFRWVG1JaZ/plYJkQYhBXnOdIwBm43xrCHBF3nTsSSaGx0OJVBm/FsoRlRJ+J5pXWr9AwoKFNbRfj6+qLv6u/zTJ6nMk8w9RtU4kMiuTxxo/bxOa1OGmcCPMK40TmCZvYS81L5c3Nb9LArwEvtXrJJjavR5hXmM1CHjIKMhi3aRxh3mG83vY/9ZxsRqhXKH+f+ttu9lWsyzv9m7D1eBqv/LKX357vgM7Jemk1KwxOOmW3um53MMyGxDg4+hck/A2x74M0gtBAYEOo3kI52BgYoVxe1ZTdbhUVldI501LKZKC9EKIrUFwZ5A8pZbTVlDkgbloloiVPn2dTZ/pU5immxU0jqloUQxsPtZnd61HXty7HMqzvTBcZi3h90+s4aZxsHjN8LeE+4Tb5ACGlZMLmCeQW5TL9zulWzSd9K8K8w1hzco3V7UgpeXfru6TmpvLtPd/a5Y5LMaGeoVwsuEiOPgcPnboTV9nw93Bm8n1Neea7ncz86zDjettnU8JhcdIqO9E120P3SUq4x5k4OLNNqap45E/Y8/2V/joP8AsH/1rgHQLe1cErWCki41EV3AOUVH23E1IqH0CMBpCGK1+lUUlNKI0lnhtKPJfXtF17mV5H3qRNlniM6XHJPvI6X7npa1WTD8C+1CtrQ1691itPrnnOzfte7/t2629uKfqUfj7vjFygS+nnvAWl3ZkGlMIqwHqLWa9gXHami/LwvWkYueXQG/WM3zgerUbL5I6TrVqkpDTU9qnNyuMrrR7q8nn858SnxPP+ne/bJLfyzQj3DmfDmQ3ojXp0GusdiovNimXzxc28EfXG5fh0e1HDqwYZBRlkFGRYNZ/3yuMr+fPkn7zU6iWrVvAsDcVx2olZiTTwb2BXLSrW4e4m1XgsKoz5G47TNMSHPs2q21uS4+LqA/V6KBcoDkpOClw4CCmHIf04XDwJaQlwIhYKMq87TSeNM2z3BRdPcPZUQkZ0bqBzBydn5dI6K+ElGh1onJTd8OKviKt3wP/j+JkcyZLO6VVOrOFq59ZYVOJ50ZXXjUVXrst9S7Ybrn5NGuioL4BNXG2vEtEIlFNulZCg6ncDz1psPrOc6dudks60rVgQv4D41Hje72x/pxKUQ4jZ+mySc5Otpmdvyl4+j/+cvrX7cnetu61iwxzCfcIpkkWczTp7ObuHpTl26RjLLy2nU0gnBjYYaBUb5lAyo4e1nOmz2WeZsm0Kraq2slsYT0kuO9PZqjNdmZnUtzFHzmfx6q/x1An0pGHwbR4/XVqEAM+qylX7OmUg8jMh6zzkpkL2BchNg/xLnD2yj7CqPlCQDYXZoM+FgiylT1EBGAqgqPBqp/Wyw1piV/WqzZtiB1tccbpLXhonEMVOuVbJaCKcTI9NrzlplefF7Vpn0Hjc+PWr5lH6JJ1LokZYzRL9TGOv6XfVh4OrHl/bJq5pF6bH4spzxJUxxe3F34+rPnwUt4n/tpX8Wvyzvc5rcXFxtG3btsT3/poPNtf+fiCu01biZ3bd9uu8fiPM2sC7ed8TcbtvWjnQXFRn2gxs7UzvS9nH/Pj59Kndh7vD7e9UwpWMHscvHbeKM52rz2XcxnEEuQcxLsr2GUuuR7h3OKBk9LCGM6036Bm3cRwuwoV3Orxj88Ot1yPMW3GmT2eetsqOscFoYPzG8UgkUzpNsWsYTzGhnld2plUqL85aDfMGt6Lvx5sY8e0OfnuuAwGetj0DUylx9VYu6l/VfNwQQ1glzcF+LCaGGpV0bQC5HucgsP6tO1ZAinRHLTqfegLDDIqd6dyiXKvbytXnMm7TOALdAx3GqQQlzAOwWtz0jO0zSMxKZEqnKXg5W6b6Xnmp5WNKj2eljB5z98zlYPpBHg14lCpuVaxiw1xCvUIRCKulx/vq36/YdWEXb0S9QYinJfcHyo6Piw9eOq/b1pkWQrgKIeKEEHuFEP8KId42tX8vhDgshNgvhPhSCKEztQshxBwhRIIQIl4I0cq+Kyg9Vb1c+Wxway5kFjBowTYu5hTaW5KKikoFRnWmzcCWO9Mf7PyA05mnmdJxCt7OjnMb0t/VH18XX6scyFt/ej1Lji7h8SaP0zqotcXnLys+Lj74ufhZJdf0zuSdfLn/Sx6s9yDN3B2n3LGLkwtBHkFWyehxIO0Ac7MB/DQAACAASURBVPfMpWfNnvSp3cfi85eH2zw9XgHQTUrZHGgB3C2EaAd8D0QATVHqCgw39e8N1DNdI4BPba64HLQM82PBsEiOp+YweOE2MnL19pakoqJSQVGdaTOwlTMdmxh7Oc9wm2ptrGrLXIQQ1PapzYkMy6aKS81L5a1/3iLCP4KRLUZadG5LEO4TbvE1ZxVmMX7jeEK9QnmtzWsWndsShHmFWTzXdH5RPuM2jsPfxZ+Jd0x0iJCWkoR6hd62O9NSIdv0VGe6pJRylek1CcQBxRV1+gPfmF7aCvgKIYJtr7zsdKoXyPwhrTmanM2QL7eRklVgb0kqKioVEDVm2gxcta6A4hBYi/T8dCZunkg9v3q82OpFq9kpDzW9axKbGGux+aSUTNw8kdyiXKZ1mmbTMtKlpZZPLWLOxFh0zmlx00jOTebr3l/bNSXcjajhVYP1ZyybvOfDnR9yPOM483vMt2qWkLIS6hnKhjMbMEqj3TPn2AMhhBNKLYG6wFwp5bYSr+mAIUBxAvQQoOSti0RTW9I1c45A2bkmKCiImJgYs3VlZ2eXaVxpEMBzzXXM25NBr1l/81IrF2p62y6G35prcwQq8/oq89qgcq/P0mtTnWkzsPbOdHHp7MzCTOb3mG/XPMM3o6Z3TdLy08gqzLJIXPMvh39h49mNvN72dbunhLsR4d7hpOenWyxV3F8n/2LFsRU80/wZmgc2t4BCyxPmHUZ6fjrZhdl4OnuWe75NZzfxw6EfGNxwMO2rt7eAQssT6hVKobGQlNwUgjyC7C3H5kgpDUALIYQvSqGuJlLK/aaX5wGxUsqNZs75OfA5QGRkpOxShgNbMTExlGVcaekCdO+QwVPf7GDq9kKmP9iM/i1sE8tv7bXZm8q8vsq8Nqjc67P02m6/rZdy4K5Vdg+t5Uz/lvAb0WeiebHliw6dmqs4u4UlQgCOZxxn5o6ZdKjegUcjHi33fP9n787DqqrWB45/XwYZREARR8wJNQcQtTTNSjPNUjNvTpVFpre61c3UyqZfpWk2mbd5uFnilFO3UjPLHBrMnDUcUskZNRVHFGRavz/OBkERDnAGOLyf5zmPZ6+9z97vNlu8rPPutZwl+54dUepx+OxhRq8cTVTVKB6IfqDE53OW3NPjldSZzDM8/+vzRIZGunVlx8LkzOhRfuumATDGnMS2pkB3ABF5EQgHRuQ6LBGok2s7wmork1rUDmHeox1pXiuEYTM38q9p67TsQyllF02miyC7zMMZyfTe03sZv3o8V9e42u2rHBambnBdwBZzSaRlpvH0z0/j7+PPmGvHlOqv1SNDIwFK/OBlZlYmz/76LOlZ6baSFicuAlNSdSrZ8qSSzuhhjGFG0gxOp53m1etezfn/qDTKvXBLeSMi4daINCISAHQF/hSRocDNwJ3G5FmVYh5wrzWrxzXAKWPMoUtOXIaEV/Jj5gPX8OTNTVjy5xG6TvyJ6av2kp7pWYtxKKUcq/RmL6WQl3jh7+3v8GQ6PSudp39+Gl8vX17p+EqpTioB6gTXQZASJ9PvrH+Hbce3MabDGKoFVnNQdM5Ru1Jt/L39STiZUKLzfL7lc9YcXsMzbZ/Jmcu5tMpOpks6Mj1nxxw2p2xmeJvhpfobF4CaFWsiSHkdma4JLBORP4A1wGJjzALgI6A6sFJENorIC9bxC4FdQALwX+BhN8TscL7eXjzSOZKFj11Ho2pBPPfVZrpM+In/rT9AhibVSql8aM10EQX4BDg8mf5g4wdsTtrMW53eKhWrHBbGz9uPmhVrsvdM8ZPp3w7+RtzWOAY0GUDnKzo7MDrn8BIvGoQ2KFEyveXYFt7fYJsS7vbI2x0YnXME+gZSNaBqiX5pSjiRwBtr3uBK/yu5u+ndDozOOXy9falRsUa5HJk2xvwBtMqnPd+fE9bsHo84Oy53iawWxOwH27Ns+xHe/H4HI2Zv4vVF2+l/dR0GXl2HWqEB7g5RKVVKaDJdRI5OptccXsOk+En8o9E/6Fq3q8PO62x1g+uy91TxkqyklCSe+/U5GoQ0YORVIx0cmfNEhkay8uDKYn32TNoZnvjpCaoGVi2VU8JdTsOQhuw8UbyVolIyUnjy5ycJ9A1kUNigUv+NS7byPD2eyktEuPHK6nRqXI0lfx5h2u97eXfpTt5dupM2V1SmW/PqdGlanQZVK5aZ/6eVUo6nyXQROTKZPp56nFE/j6JucF1GXT3KIed0lSuCr2DhroUYY4r0QyTLZPHsr89yJu0MH930Uc4MKWVBZGgk8/6aV+QZPYwxjF45mkNnD/F5989L5ZRwl9O8anOmbJ1CWmZakWeXeX3N6yScTODjmz4mbWfZWWEuIiiCXxKLNGGF8nBeXkLXZtXp2qw6+4+f48v1B/hhy9+8svBPXln4J+GV/Ghbvwqtr6hM05qVaFYzmNDA0jkbk1LK8TSZLiJ/H3+HLCeeZbJ49pdnOXX+FB/e9GGpnGe4IPWC63Em/Qwnzp+gin8Vuz83KX4Svx38jRfav1Dq62cvlj1tX8LJhCKt0Dh351y+3/M9w1oPo1W1S75FL9VaVG1BRlYG249vJyo8yu7PLdqziLk75nJ/i/vpULsDy3cud16QDhZRKYJjKcdIyUgpU7/sKdeoUyWQx29qzOM3NWb/8XP8tOMoa/YcZ/Xu43z7x4XnL6sG+VEvLJC6YRWpFepP9WB/agT7UyWoAlUCK1A5sAJB/vojWClPoP8nF1GAT4BDFm35bPNnrDi4gv+75v/KXFIJeWf0sDeZXnt4Le9tfI9b6t9C30Z9nRmeUzQKbQTYZvSwN5nefnw7r61+jQ61OnB/i/udGZ5TtAhrAcDmpM12J9O7Tu3ipd9eIjo8mkdblb7VLAuT/eDl3tN7ubLKlW6ORpVmdaoEMuiaugy6xtYfHjmTyrZDZ9h26DS7jiazN+kcKxKOceRMKlkm/3P4e0PIbz8S4OtNQAUf/H298PPxws/HG19vwcfLCx9vwcdL8PbywtsLvEQQEURsi87Y/rz0G0LDhYsaAyb7T2OsbZO3PXvb2D6Zles9BrLy/dxF7/Ncy3D8eAqfJqzK+QwXXcs6NZgLMWd//kLsJuc4k2tHnr/SXNfOz8V/F/m9z/e8+cSR7ezZFCpuLNoCZpeLz+7PXzY6xzt79hwVN/zksuvZq6R/hwAtgtNw5BTamkwXUYBPAEmpSSU6x9rDa3lvw3vcXO9m+jXu56DIXCs7md5zao9do61Hzx3lqZ+fok6lOrzY/sUyWV9Yo2INKvpWtPshxFPnTzFs2TBCKoSUiVla8lOjYg2q+Fdh87HNhR8MnE0/y/Blw/Hz9mPCDRNK9dR/l5P973nVoVWaTKsiqVbJn2qV/LmhcXie9ozMLI4mn+fv0+c5cTaN42fTOHEujTOpGWxL2E3l8GqcS88kJS2D8xlZnM/I4mRKOukZWWRkZZGRacjIMmRaL4O5kOjmk3jm7l9z97S2ZsFLLiTgFxJy673VbjvGStGtY7xyEvjsY+VCMn/R+bD2pWbAubSMPMfaTik55xVAvLJ/IcgbR97Ys99f/v7kov25Xfp3kd+e/Pbnf+SxrHNUrZL3W2V7frTl94tPUbjqx+dRUggPL/mCXc5Q0r+DkCzHlh5qMl1EJa2ZPnz2MCN/Glmmk0qAWkG18BEfu+YgTstMY/jy4SSnJ/NR14+o6FvRBRE6nojQMKShXcl0ZlYmo34exd/n/mZy98mEBYS5IELHExGiqkbZlUxnLwu/5/QePun6SZmYmSY/NSrWoGFIQ347+BuxzWMLPX7RnkX4mrL3S4NyHR9vL2qGBFAz5NKyoeW+B+nUKdoNUbmGbaW5a90dhlPY7u0qd4fhNLb7s7+ksSxx9DLpZW+ozM1KkkyfzzzP8GXDOZ95nrc7v+2QpbjdxcfLh4hKEYVOm2aM4ZVVr7Dp6CbGdRxH48qNXRShc0RWjrRr4Zb3N77PioMreK7dc6V2uXB7Na/anN2ndnM2/WyBx03eMpkf9v7AsNbDaFeznYuic44OtTuw7u91hZZ0zfxzJk/+9CQrkle4KDKllFKljSbTRVTcZNoYw8srX2Zz0mbGdRxHg9AGTojOteoG1y00mZ65fSZf7vySf0b9s0xN/Xc5DUMacjz1OEkply/1mf/XfP4b/1/uaHQHfRuXvdrwi7UIa4HBsDVp62WPWbx3MRPXTaRb3W4Mbj7YhdE5R4daHTifeZ71f6+/7DG/Jv7Kq6tf5YaIG+gY1NGF0SmllCpNNJkuogDfAFLSi55MT9o8iW/++oYHox+kyxVdnBCZ69UNrsu+0/vIMvmvCvbj3h8Zv2o8nSI68UiMZ6ztEFm54GXFVx5cyQsrXqBdjXY81+45V4bmNC2q2h5CjD8Wn+/+TUc38cwvzxAdHs24juPKbOlSbm2qt6GCVwV+O/hbvvt3ntjJEz89QaPKjXj9+tfLZD28Ukopx9CfAEUU4BNAWlYamVmZdn9m/l/zeXv929xS/xYejvGIFXcBWzKdmpnKkXNHLtm35vAaRv08iujwaF6/4XW8vbzdEKHjRYbakun86qb/PP4nw5cPp35ofSZ2noivt2fU0Vb2r0ztoNr51k3vPb2Xx5Y+RrXAarxz4zv4+/i7IULHC/AJoHX11qw4eGn5xoEzB3h4ycME+gTy7o3vlrlpLZVSSjmWJtNFFOBte4DE3lKP7JHKtjXaMvbasR41gpV7erzctiRtYdjSYURUiuC9G9/zqLl6wwPCCa4QfEkyvS1pGw8tfogg3yA+6PJBma6Hz0+Lqi3YcmxLnraEEwkMXjSYLJPFB10+KNJ842VBh1odSDiZkOeXxf1n9jP4+8GcSz/HBzd9UGYfslRKKeU4npPZuUh2YpiaWfhc0+v+Xsfjyx6nXkg9JnaeWOQV5Eq77GR6/ZH1OfNvLt23lMGLBhNUIYiPbvqIUP9Qd4bocCJCZGjehxBXHlzJ4O8H4+vtyyfdyu4sFgVpEdaCg2cP5tSKb0nawuDvbbXRn9/8OfVC6rkxOufoUKsDQE6px97Texm8aDApGSlMunmSTpunlFIK0KnxiizA1xqZTk+BAgZcVx9azaNLH6VGxRp83PVjgisEuyhC16kWWI3GlRvzwcYPWLZvGW2qt2H6tuk0D2vOu13epWpAVXeH6BQNQxvydcLXPPTjQ4T6hfL9nu+pF1yPj276iOoVq7s7PKfIrpt+e/3bJKcnsyJxBaF+ofy323+5IvgKN0fnHI0rNybMP4wFfy1gzeE1LNy9kCDfICZ1m1QmF1pSSinlHJpMF1H2yHRBS4qvSFzB48sep3ZQbT69+VOPTSq9xIsvenzBgl0L+Hzz50zbNo2udbsyruM4jyrtuNgdje7g6LmjHEk5ws7jO+lQqwPjrxvvkb8wZWsW1owAnwC+SviKiKAIulzRhcdaP+aRo/DZRIQOtTowf9d8AnwC6N+4P7HNY6kVVMvdoSmllCpFNJkuouwkMb+aaWMMU7dOZcK6CUSGRvJJ10/K7GId9qrgXYF/NPoHt0fezs4TO2lUuZFH1YXnp3lV28h7eRLoG8jXvb/Gz9vP4/9N5/ZIq0doXb013ep18+hflpRSShWfJtNFdLlkOiUjhTErx7Bg1wK6XNGFcR3HldmV/orDS7z0q28PVx5HZGsH1faIucKVUko5jybTRZRfMv3zgZ95ZdUrHEw+yKMxj/LP6H96/OisUkoppZRy4WweItJdRLaLSIKIPJ3Pfj8RmWXtXyUi9VwVW1HkTqazp4B7ZMkjVPCuwKfdPuXBlg9qIq2UKnNExF9EVovIJhHZIiKjrfb6Vp+cYPXRFaz2MtFnK6WUs7lkZFpEvIH3ga7AAWCNiMwzxuRen3gIcMIYEykiA4HXgAGuiK8ospPp11a/xonzJwjwCeDx1o9zb7N7PWaRDqVUuXQeuNEYkywivsCvIvIdMAKYaIyZKSIfYeurP6SM9NlKKeVsrhpCbQskGGN2GWPSgJlA74uO6Q3EWe/nAl2kFK5LHOIXQnCFYMICwnim7TMs6beEIVFDNJFWSpVpxibZ2vS1Xga4EVufDLY++nbrfZnos5VSytlcVTNdG9ifa/sA0O5yxxhjMkTkFBAGHHNJhHYK8AngpwE/4S3e6M8NpZQnsb5FXAdEYvs28S/gpDEmwzrkALa+GspIn62UUs5W5h5AFJEHgAeszWQR2V6M01TFczt8T7438Oz703sru4pzf3WdEUhJGGMygRgRCQW+Akq8zKP22YXy5HsDz74/T7438Oz7K+695dtvuyqZTgTq5NqOsNryO+aAiPgAIUDSxScyxnwCfFKSYERkrTHmqpKco7Ty5HsDz74/vbeyy9PuzxhzUkSWAe2BUBHxsUanc/fd2mc7gCffG3j2/XnyvYFn35+j781VNdNrgEbWU+EVgIHAvIuOmQfEWu/7AkuNMcZF8SmlVLkmIuHWiDQiEoDtgfFtwDJsfTLY+uhvrPfaZyulFC4ambbq6R4Fvge8gc+MMVtEZAyw1hgzD5gETBWRBOA4toRbKaWUa9QE4qy6aS9gtjFmgYhsBWaKyFhgA7a+GrTPVkopwIU108aYhcDCi9peyPU+FejnonBK9JVjKefJ9waefX96b2VXmb8/Y8wfQKt82ndhm5Hp4nbtsx3Dk+8NPPv+PPnewLPvz6H3JvqtnFJKKaWUUsWjS/UppZRSSilVTOUqmS5sSfOyTETqiMgyEdlqLQU8zN0xOZqIeIvIBhFZ4O5YHElEQkVkroj8KSLbRKS9u2NyJBEZbv2b3CwiX4iIv7tjKi4R+UxEjojI5lxtVURksYjstP6s7M4YPY2n9tvaZ5dtntxve1KfDa7pt8tNMp1rSfNbgGbAnSLSzL1ROVQGMNIY0wy4BnjEw+4PYBi22QU8zdvAImPMlUBLPOgeRaQ28BhwlTGmBbYHkMvyg2qTge4XtT0NLDHGNAKWWNvKATy839Y+u2zzyH7bA/tscEG/XW6Saexb0rzMMsYcMsast96fwfY/du2CP1V2iEgE0AP41N2xOJKIhADXY82QYIxJM8acdG9UDucDBFhzEQcCB90cT7EZY37GNnNFbrmX1c693LYqOY/tt7XPLrvKQb/tMX02uKbfLk/JdH5LmntMx5WbiNTD9lT+KvdG4lD/AZ4CstwdiIPVB44Cn1tfh34qIhXdHZSjGGMSgTeBfcAh4JQx5gf3RuVw1Y0xh6z3h4Hq7gzGw5SLflv77DLHY/vtctJng4P77fKUTJcLIhIEfAk8bow57e54HEFEegJHjDHr3B2LE/gArYEPjTGtgLN4UJmAVYfWG9sPn1pARREZ5N6onMdatESnSFJ20z67TPLYfru89dngmH67PCXT9ixpXqaJiC+2Tnm6MeZ/7o7Hga4FbhORPdi+5r1RRKa5NySHOQAcMMZkj0jNxdZJe4qbgN3GmKPGmHTgf0AHN8fkaH+LSE0A688jbo7Hk3h0v619dpnlyf12eeizwcH9dnlKpu1Z0rzMEhHBVr+1zRjzlrvjcSRjzDPGmAhjTD1s/92WGmM84jdlY8xhYL+INLGaugBb3RiSo+0DrhGRQOvfaBc85EGdXHIvq517uW1Vch7bb2ufXXZ5eL9dHvpscHC/7bIVEN3tckuauzksR7oWuAeIF5GNVtuz1sqTqnT7NzDdShZ2AYPdHI/DGGNWichcYD222Qs2UIZX1RKRL4BOQFUROQC8CLwKzBaRIcBeoL/7IvQsHt5va59dtnlkv+1pfTa4pt/WFRCVUkoppZQqpvJU5qGUUkoppZRDaTKtlFJKKaVUMWkyrZRSSimlVDFpMq2UUkoppVQxaTKtlFJKKaVUMWkyrZRSSimlVDFpMq3KFBEJE5GN1uuwiCRa75NF5AMnXG+yiOwWkYeK+LmFIhJayDFvWPfwRMmiVEqp0kn7bFUelJtFW5RnMMYkATEAIvIStkUP3jPGfOrEyz5pjJlblA8YY24FsJbTHWqM+TGfY54UkbOOCVEppUqffPrsZGPMm06+bLH77EKO0T5b5UtHplWpJyJ7RCTFGsn42xp5CLromE4issB6/5KIxInILyKyV0T+ISKvi0i8iCwSEV/ruDYi8pOIrBOR70Wkph2xTBaRD0XkdxHZZV3XiEiWiKRboy5vWTFXxfYL6yQR+a+IbBGRH0QkIJ/zdrJWZlJKKY/n5j77MxHZJiKTcx23R0Sqikg9a1+BfbZSuWkyrcqKXsaYIKA1cBXwfCHHNwRuBG4DpgHLjDFRQArQw+qc3wX6GmPaAJ8B4+yMpTLQHhgOzLPamgB/AI8AdwGVch0fAbxvjGkOnATusPM6SilVXriyz54INAeiRCQmn+MboX22KgIt81BlijEmUUS+A1oAa63musAwoKmI/ABsBL4zxqSLyPNAADBTRDYBW4B62JLfGGC/1UlnAbuyryMiPYGxQDOgvYjsMMb8Ye2eb4wxIhIP/I0tcTbWuQF+AW7OFfYhY8xGEfEDagEfiMjrwGzgDFAB+A7wE5Fk6zONjTEHS/r3pZRSZUR2nx0PeAOLrPZ4LvTZLYDFIoJ1zCE7z52nzzbGxAOISPbPg40XHb/bGJPdts46RqnL0pFpVaaISB3gVmBDrua7gNeAH7Alph2A89a+74CzQDVgPdAH2y+RYv3Z1Rjjbe2/07pGK2yjHg8CX1jnnWclw+Q6d1au99nb9YDrgLRc7enWn88BdYCPgZZAW+B669hbgIPGmCDrpYm0Uqo8OQ9gjMkC0o0xxmrP4kKfvcUYE2O9oowx3YpybvLvs/MbVMx9TOZljlEqhybTqqz4WkROAr8CPwGv5Nr3OXAAW8c4G6iRvcMY85n153ngJaA64A9sx9Y59xSRYCCZCx3oA8DHxphV2Eacf7L2XVNAfOuxJeNPA59a57vY3cBi4Kwx5igwGltSrZRSqmDbgXARaQ8gIr4i0tzNMSkFaDKtyo7bjTGhxpi6xpiHjTEpufYdzvX+HLbRaUTEW0ReBQJF5DSwxzqmojEmDbgPGAIcx1YXN8jaXxcYaSXvdwFx2EaUaxUQX2tso9iPGmMuV89dCziRa3sveWurlVJK5cPqs/sCr1klexuxfQuplNvJhW9SlCqdCppeTkSWA9Oyp8YTkfusYzuKyD3As9jKQvYAIdiS2UbGmIRc5/AFHgVGGGPqiMjHwD5jzDjrae8FBU2zJCLm4nPmF7uI/AX82xiz0NrXDdtI+lhgDTDdGBNRlL8bpZRSF9jTZ5fw/C/hmun9VBmiI9PKk1XCVp6RBASSqzRERCqIyN0iEmKMSQdOYysTAfgv8JCItANOAWNF5D0RKeko8hfA8yISbk2b95l1zbPYHmQME5GQEl5DKaXKs1PAy1LERVvsISJvYPsGU+eaVnloUb3yZFOwzaqRiK2U4/+Af+Xafw/wnoh4Y6vHuxvAGLNWRP4JvIdtiqQUbLXWJTUWCMY2hR7AHOApY0wqgIh8Aeyy4mmmDyEqpVTRGGOGOfHcTwJPOuv8quzSMg+llFJKKaWKScs8lFJKKaWUKiZNppVSSimllComTaaVUkoppZQqJk2mlVJKKaWUKiZNppVSSimllCqmMj01XmhoqImMjHR3GC519uxZKlas6O4wXErvuXwob/e8bt26Y8aYcHfHoZRSqmTKdDJdvXp11q5d6+4wXGr58uV06tTJ3WG4lN5z+VDe7llE9ro7BqWUUiWnZR5KKaWUUkoVkybTSimllFJKFZMm00oppZRSShVTma6ZVkp5DhFh9+7dpKamujsUh/L39yciIgJfX193h6KUUsoJNJlWSpUKFStWpFKlStSrVw8RcXc4DmGMISkpiQMHDlC/fn13h6OUUsoJtMxDKVUqeHt7ExYW5jGJNNhG28PCwjxutF0ppdQFmkwrpUoNT0qks3niPSmllLpAk2mllLLs37+fzp0706xZM5o3b87bb78NwKZNm2jfvj1RUVH06tWL06dP53xm/PjxREZG0qRJE77//nt3ha6UUspNnJ5Mi4i3iGwQkQUXtb8jIsm5tv1EZJaIJIjIKhGp5+zYlFIqNx8fHyZMmMDWrVv5/fffef/999m6dStDhw7l1VdfJT4+nj59+vDGG28AsHXrVmbOnMmWLVtYtGgRDz/8MJmZmW6+C6WUUq7kipHpYcC23A0ichVQ+aLjhgAnjDGRwETgNRfEppRSOWrWrEnr1q0BqFSpEk2bNiUxMZEdO3Zw/fXXA9C1a1e+/PJLAL755hsGDhyIn58f9evXJzIyktWrV7stfqWUUq7n1GRaRCKAHsCnudq8gTeApy46vDcQZ72fC3QRLTZUSrnJnj172LBhA+3ataN58+Z88803AMyZM4f9+/cDkJiYSJ06dXI+ExERQWJiolviVUop5R7OnhrvP9iS5kq52h4F5hljDl2UK9cG9gMYYzJE5BQQBhzLfZCIPAA8ABAeHs7y5cudFnxplJycrPdcDpTHew4ODubMmTMARI372SnXiH/ueruOS05Opk+fPowfPx4R4d133+XJJ59k9OjR3HLLLfj6+nLmzBnS0tJISUnJiTs9PT3PdrbU1NRy999TKaXKC6cl0yLSEzhijFknIp2stlpAP6BTcc9rjPkE+ASgSZMmxivSC2MM10dcXy6eml++fDmdOnVydxgupfdcPmzYsIFKlSoVfmAJ2HP+9PR0+vbtyz333MPdd98NQJs2bVi6dCkAO3bs4Mcff6RSpUrUr1+fY8eO5Zz377//JjIy8pLr+Pv706pVKwffjVJKqdLAmSPT1wK3icitgD8QDGwBzgMJVuIbKCIJVp10IlAHOCAiPkAIkFTYRUYuH0lqZiq3NbyN59o9R6BvoJNuRynlKnte7eGW6xpjGDJkCE2bNmXEiBE57UeOHKFatWpkZWUxduxYHnroIQBuu+027rrrLkaMGMHBgwfZuXMnbdu2dUvsSiml3MNpNdPGVht6BAAAIABJREFUmGeMMRHGmHrAQGCpMaayMaaGMaae1X7OSqQB5gGx1vu+1vGmsOv4etmW6J331zzu/PZOdp7Y6ehbUUqVEytWrGDq1KksXbqUmJgYYmJiWLhwIV988QWNGzfmyiuvpFatWgwePBiA5s2b079/f5o1a0b37t15//338fb2dvNdKKWUcqXStJz4JGCqiCQAx7El4IUKCwjjTPoZKvtVZtepXdz17V082+5Zbo+8vVyUfSilHKdjx45c7nf4YcOG5dv+3HPP8dxzzzkzLKWUUqWYSxZtMcYsN8b0zKc9KNf7VGNMP2NMpDGmrTFmlz3nruJfBYCxHcfSu2FvUjNTeeG3F3ju1+c4l37OYfeglFJKKaXUxcr8CohhAWEAnE0/y9iOYxl77VgCfAKYv2s+A78dyI4TO9wcoVJKKaWU8lRlP5n2tyXTx1OPA9A7sjdf9PiChiEN2X1qN3d9exf/2/m/y351q5RSSimlVHGV+WS6SoCtzCMp5cLEHw1DGzKjxwxuj7yd85nnefG3F3n212e17EMppZRSSjlUmU+ms0emk1LzzqIX6BvIy9e+zLiO4wjwCWDBrgUMWDBAyz6UUkoppZTDlP1k2qqZzj0yndttDW/jix5fEBkayZ7Te7jr27v4cseXWvahlFJKKaVKrOwn0/4FJ9NwoeyjT2Qfzmee56WVL/H0L09zNv2sq8JUSpUBqamptG3blpYtW9K8eXNefPFFAHbv3k27du2IjIxkwIABpKWlAXD+/HkGDBhAZGQk7dq1Y8+ePW6MXimllDuU/WQ6IO8DiJcT4BPAmGvH8ErHVwjwCWDh7oUMXDCQ7ce3uyJMpVQZ4Ofnx9KlS9m0aRMbN25k0aJF/P7774waNYrhw4eTkJBA5cqVmTRpEgCTJk2icuXKJCQkMHz4cEaNGuXmO1BKKeVqZT+ZzlUzbU/pRq+GvZjZY2ZO2cfdC+9m7o65WvahlEJECAqyTX+fnp5Oeno6IsLSpUvp27cvALGxsXz99dcAfPPNN8TG2hZu7du3L0uWLNG+RCmlypkyn0wH+gYS4BPA+czzdpdtNAhtwIweM7ij0R2czzzP6JWjtexDKQVAZmYmMTExVKtWja5du9KwYUNCQ0Px8bEtGBsREUFiYiIAiYmJ1KlTBwAfHx9CQkJISrp8yZlSSinPU5qWEy+2Kv5VSExOJCk1iaAKQYV/AFvZx0sdXqJN9Ta8/PvLLNy9kK1JW3nzhjdpUqWJkyNWShXopRAnnfdUoYd4e3uzceNGTp48SZ8+ffjzzz+dE4tSSimPUOZHpqHwGT0K0qthL2b2nJlnto85O+boV7VKlXOhoaF07tyZlStXcvLkSTIyMgA4cOAAtWvXBqB27drs378fgIyMDE6dOkVYWJjbYlZKKeV6HjEyfbm5pu3VIMRW9vHa6tf4cueXjFk5hjWH1vBC+xfsHulWSjmQHSPIznD06FF8fX0JDQ0lJSWFxYsXM2rUKDp37szcuXMZOHAgcXFx9O7dG4DbbruNuLg42rdvz9y5c7nxxhsREbfErpRSyj08amT6eErBM3oUJLvsY/x14wnwCeC7Pd8x8NuB/Hlcv+JVqrw4dOgQnTt3Jjo6mquvvpquXbvSs2dPXnvtNd566y0iIyNJSkpiyJAhAAwZMoSkpCQiIyN56623ePXVV918B0oppVzNI0amq/hbS4oXc2Q6t54NetI8rDkjfxrJzhM7ufvbuxnVdhT9GvfTESelPFx0dDQbNmy4pL1BgwasXr36knZ/f3/mzJnjitCUUkqVUp4xMm3Hwi1FUT+kPjNunUHfxn1Jy0rj5d9f5qmfnyI5Ldkh51dKKaWUUp7BM5LpgJLVTOfH38efF9u/yKvXvUqgTyCL9ixiwIIBbEva5rBrKKWUUkqpss0jkukaFWsAkJic6PBz92jQg5k9Z9K4cmP2ndnHoIWDmPXnLJ3tQymllFJKOT+ZFhFvEdkgIgus7ekisl1ENovIZyLia7WLiLwjIgki8oeItLb3Gg1DGgKw6+QuMrMyHX4P9UPqM/3W6fRr3I+0rDTGrhrLkz8/qWUfSimllFLlnCtGpocBuWsjpgNXAlFAADDUar8FaGS9HgA+tPcCQRWCqFmxJmlZaew/s98hQV/M38efF9q/wGvXvUagTyDf7/leyz6UUkoppco5pybTIhIB9AA+zW4zxiw0FmA1EGHt6g1MsXb9DoSKSE17rxUZGglAwskER4Wfr1sb3MqsnrNoUrkJ+87s4+6Fd2vZh1JKKaVUOeXsken/AE8BWRfvsMo77gEWWU21gdzDygesNrtEVrYl0ztP7ixmqParF1KP6T2m079xf9Kz0hm7aixP/PQEZ9LOOP3aSinnSU1NpW3btrRs2ZLmzZvz4osvArB7927atWtHZGQkAwYMIC0tDYDJkycTHh5OTEwMMTExfPrppwWdXimllAdy2jzTItITOGKMWScinfI55APgZ2PML0U87wPYykAIDw9n+fLlAGQk25b6XbljJU1PNC1+4EVwHdcRWDWQL5K+4Ie9P7A+cT33V72fOn51nHbN5OTknHsuL/Sey4fg4GDOnHHvL6TGGL755huCgoJIT0+nW7duXH/99bz//vs89NBD9O3bl8cff5z333+foUOHkpqaSp8+fZgwYULOOfK7h9TU1HL331MppcoLZy7aci1wm4jcCvgDwSIyzRgzSEReBMKBB3MdnwjkzkIjrLY8jDGfAJ8ANGnSxHTq1AmA6knVmbpgKqd8T5Hd5gqd6ETf030ZuXwk209sZ+KRiTx19VMMaDLAKYu8LF++3KX3VxroPZcPGzZsoFKlSu4Og+DgYADOnTtHVlYWQUFB/Pzzz8yePRsfHx+GDh3KSy+9xPDhw/H396dChQqFxu3v70+rVq1cEb5SSikXc1qZhzHmGWNMhDGmHjAQWGol0kOBm4E7jTG5yz/mAfdas3pcA5wyxhyy93r1Q+rjJV7sPb2XtMw0R95KoeoG12V6j+kMaDKA9Kx0xq0ax8ifRmrZh1JlUGZmJjExMVSrVo2uXbvSsGFDQkND8fGxjT1ERESQmHjh9/wvv/yS6Oho+vbty/79znkAWimlVOnljuXEPwL2Aiutkdv/GWPGAAuBW4EE4BwwuCgn9ffxp06lOuw9vZfdp3bTpEoTB4ddMD9vP56/5nmuqnEVL/32Eov3LmZb0jbe7PQmzcOauzQWpcq6qLgop5w3Pja+0GO8vb3ZuHEjJ0+epE+fPvz555+XPbZXr17ceeed+Pn58fHHHxMbG8vSpUsdGbJSSqlSziWLthhjlhtjelrvfYwxDY0xMdZrjNVujDGPWPuijDFri3odV83oUZDu9bozu+dsmlZpyoHkA9yz8B5mbJuhs30oVcaEhobSuXNnVq5cycmTJ8nIsD2XceDAAWrXtj0bHRYWhp+fHwBDhw5l3bp1botXKaWUe7hjZNppIkMjWbJviVuTaYArgq9g6q1TeWPNG8zaPovxq8ez9u+1jO4wmkoV3F8TqlRpZ88IsjMcPXoUX19fQkNDSUlJYfHixYwaNYrOnTszd+5cBg4cSFxcHL179wbg0KFD1Kxpm8Fz3rx5NG3qmoeflVJKlR6elUxb0+MlnHBvMg0FlH3c8CbNq2rZh1Kl0aFDh4iNjSUzM5OsrCz69+9Pz549adasGQMHDuT555+nVatWDBkyBIB33nmHefPm4ePjQ5UqVZg8ebJ7b0AppZTLeVQy3Si0EeCauabt1b1ed5pVacYTPz3BtuPbGPTdIJ646gnuuvIup8z2oZQqvujoaDZs2HBJe4MGDVi9evUl7ePHj2f8+PGuCE0ppVQp5ZKaaVe5IvgKfLx8SExO5Fz6OXeHkyO77GNgk4FkZGXw6upXGbF8BKfTTrs7NKWUUkopVQIelUz7evlSP6Q+AH+d/MvN0eTl5+3Hc9c8x4QbJhDkG8SP+36k//z+bDm2xd2hKaWUUkqpYvKoZBqgceXGAPxx7A83R5K/bvW65cz2kZicyKDvBjF923Sd7UMppZRSqgzyuGT6mprXALAicYWbI7m8OsF1mHbrNO688s6cso/hy4dr2Ycq9zzxl0pPvCellFIXeFwy3bF2RwBWH15Nakaqm6O5vAreFXi23bM5ZR9L9i2h//z+bD622d2hKeUWmZmZJCUleVTyaYwhKSkJf39/d4eilFLKSTxqNg+AqgFVaVqlKduOb2Pt32tzkuvSqlu9bjSt0pQnfn6CrUlbuee7exjZZiR3N71bZ/tQ5crZs2c5c+YMR48edXcoDuXv709ERIS7w1BKKeUkHpdMA1wXcR3bjm/jlwO/lPpkGmxlH1NvmcqEtROY8ecMXlvzGmsOr2HMtWMI8Qtxd3hKuYQxhvr167s7DKWUUqpIPK7MA+C62tcB8Gvir26OxH4VvCvwTLtnmNhpIpV8K7F0/1IGLBhA/FH3rASnlFJKKaUK55HJdFTVKIIrBLPvzD72nt6b055lstwYlX1uqnsTs3rNonlYcxKTE7l30b1M3TrVo+pIlVJKKaU8hUcm095e3lxb61rANjp9Lv0cL698mZZTWnLDrBtYvn+5ewMsRJ1KdZhyyxQGNR1ERlYGr695nWHLhnHq/Cl3h6aUUkoppXLxyGQaoGOErVb6l8RfaDejHbN3zAbgeOpx/r3034xYPoKj50rvg04VvCswqu2onLKPZfuX0X9+f/ac3+Pu0JRSSimllMVjk+kOtToAl59vevHexdw450bm7phbqss/bqp7E7N7zaZFWAsOnj3IxMMTmbJlipZ9KKWUUkqVApedzUNE3rHj86eNMc87MB6HqRpQleZhzdmSVPBy3aNXjmbq1qlM7DyRBiENXBRd0URUimDKLVN4a91bTNs2jTfWvsGav9cw9tqxOtuHUkoppZQbFTQy3RtYV8jrDmcHWBL2Tou369Quen/dm/c2vEd6ZrqToyoeX29fRrUdxdDwoVSqUInl+5fTb34/Nh3d5O7QlFJKKaXKrYKS6YnGmLiCXsDHhV1ARLxFZIOILLC264vIKhFJEJFZIlLBavezthOs/fVKenPXR1x/Sdsf9/7BrJ6zaF+z/SX7Pv7jY1pPa82Pe38s6aWdpmVgS2b3tJV9HDp7iPu+u4+4LXFa9qGUUkop5QYFJdNfXm6HiPQEMMb8x45rDAO25dp+DVuiHgmcAIZY7UOAE1b7ROu4EomqGkVkaGSeNhGhWVgzPun2CRvv2cioq0dd8rnhy4cTFRfFjG0zOJt+tqRhOFx22cegpoPIMBm8ufZNHlv2mM72oZRSSinlYgUl04vzGx0WkfuBt+05uYhEAD2AT61tAW4E5lqHxAG3W+97W9tY+7tICdfTFhEGNR102f3eXt4MajaI+Nh4pt4y9ZL941eP55oZ1/DML89wLOVYSUJxuOyyj/90/o+WfSillFJKuUlByfQI4AcRaZTdICLPAMOBG+w8/3+Ap4Ds6TLCgJPGmAxr+wBQ23pfG9gPYO0/ZR1fIj0a9LDruJhqMcTHxvNpt08v2bdg1wI6z+7Mb4m/lTQch+tyRRfm9JpDVNUoLftQSimllHIxKSjpEpEu2OqibweGAm2BHsaYE4We2FYKcqsx5mER6QQ8AdwH/G6VciAidYDvjDEtRGQz0N0Yc8Da9xfQzhhz7KLzPgA8ABAeHt5m9uzZhd7kv/f+O+f9yBojqedXr9DP/J78O9OTpl/SHhMYw31V78NbvAs9hzMkJycTFBR0SXuGyWDeiXksO7MMgBYBLRgUNoiK3hVdHaLDXe6ePZnes+fr3LnzOmPMVe6OQymlVMkUmEwDiMh1wFfAb0B/Y0yqXScWGQ/cA2QA/kCwdZ6bgRrGmAwRaQ+8ZIy5WUS+t96vFBEf4DAQbgoIsEmTJmb79u2FxnIo+RDdvuyWsx0fG2/PLZBlsvi/Ff/HvL/mXbLvk66f0L7WpQ8xOtvy5cvp1KnTZfcv27eM51c8z+m009SoWIM3rn+DmGoxrgvQCQq7Z0+k9+z5RESTaaWU8gCXLfMQkTMichpYiC0R7gIcydVeIGPMM8aYCGNMPWAgsNQYczewDOhrHRYLfGO9n2dtY+1fWlAiXRQ1g2rm2c7MyrTrc17ixbiO41h558pL9j2w+AE6zuxY6qbS63xFZ+b0mkN01WgOnz3M4EWDmbx5cqlemEYppZRSqqy6bDJtjKlkjAm2/qxgjKmYazu4BNccBYwQkQRsNdGTrPZJQJjVPgJ4ugTXuMRL7V/KeR8ztWgjtUEVgoiPjWfGrTPytJ86f4rW01rz18m/HBGiw9QKqsXk7pOJbRZLhslgwroJPLb0MU6mnnR3aEoppZRSHsUly4kbY5YbY7Kn09tljGlrjIk0xvQzxpy32lOt7Uhr/y5HxnBH45KvLxMVHkV8bDxDWgzJ0377N7czbOmwEp/fkXy9fXni6id4p/M7BFcI5qcDP9FvQT82Htno7tCUUkoppTxGQWUe6wv7sD3HlCa31Lsl5/1Dix8q9nkeb/M4v9/1e562pfuXEhUXxYnUQp/NdKmcso9wW9nHfYvu4/PNn2vZh1JKKaWUAxQ0Mt1URP4o4BUPVHVVoI4wruO4nPcrDq4o0bkq+lYkPjaed298N0/79bOu57XVJV5vxqGyyz7ua34fmSaTt9a9xaNLHi11ib9SSimlVFlTUDJ9JdCrgFdPoIOzA3QkX29f6gXXy9l+6Mfij05n61SnE5vuzbtQyrRt04iKiyI9q/Q8nOjr5cvIq0by3o3vEeIXwi+Jv9Bvfj82HNng7tCUUkoppcqsgh5A3GvH64Arg3WEebdfmOZuReIKhyxu4iVexMfGM7HTxDztrae25qf9P5X4/I50Q50bmNNzDi3DW/L3ub8ZvGgwn23+TMs+lFJKKaWKwSUPIJYmIsL9Le7P2Y6eEu2wc99U9ybWDlqbp+3RpY8SMyWmVE2hVzOoJp93/5zBzQeTaTKZuG4ijyx5RMs+lFJKKaWKqNwl0wDD2wzPs70laYvDzu3n7Ud8bDw317s5py3TZNJ6WmsOJh902HVKytfLlxFXjeD9Lu8T4hfCr4m/0nd+X9b/XaaeKVVKKaWUciu7kmkRqSsiN1nvA0SkknPDcr7v7/g+5/3ABQMdfv43b3iTOb3m5Gm7+cubmbNjzmU+4R7XR1zP3F5ziQmP4ci5I9z//f18Gv+pln0opZRSStmh0GRaRP4JzAU+tpoigK+dGZQr1AqqlWc7Ki7K4de4ssqVbLgn7wN+Y1aOITou2u5VGF2hRsUafNb9Mwa3sJV9vL3+bR5e8rCWfSillFJKFcKekelHgGuB0wDGmJ1ANWcG5SrxsfF5tnec2OHwa/h4+RAfG8/dTe/OaTMYYqbGcCzlmMOvV1y+Xr6MaGMr+wj1C2VF4got+1BKKaWUKoQ9yfR5Y0xa9oaI+AAlnwKjlJjVc1bO+zvm3eGQ2T3y83Tbp/nm9m/ytHWe3Zn5f813yvWK6/qI65nTa46WfSillFJK2cGeZPonEXkWCBCRrsAcoHRlgCXQLKxZnm1Hzu5xsQYhDS6Zk/rZX5/lqmlXOS2JL47sso/7W9yfp+zjeOpxd4emlFJKKVWq2JNMjwKOAvHAg8BC4HlnBuVqF5d79J/f32nXyp6TenCLwTlt5zPPEz0lmlPnTzntukXl6+XL8DbD85R99JvXj3V/r3N3aEoppZRSpUaBybSIeAPbjDH/Ncb0M8b0td6XnmFUB8n9oOC249v4dte3Tr3eiDYj+O4f3+Vp6zizI4t2L3LqdYsqu+yjVbVWHEnRsg+llFJKqdwKTKaNMZnAdhG5wkXxuI2Plw/Tb52es/30L0+TmJzo1GtGVIrgj3v/yNP25M9P0n5G+9JX9nHzZwyNGkqWybKVffyoZR9KKaWUUvaUeVQGtojIEhGZl/1ydmDuEB0ezcg2I3O2u3/ZnbTMtAI+UXIiQnxsPA9GP5jTlpyeTPSUaM6ln3PqtYvCx8uHYa2H8eFNH9rKPg7ayj7WHl5b+IeVUkoppTyUPcn0/wE9gTHAhFwvj3Rfi/toX7N9znabaW1cMkr8aKtHWdx3cZ62djPa8ePeH51+7aLoWLsjc3rNoXW11hxJOcKQH4bwyR+faNmHUkoppcqlQpNpY8xP+b1cEZy7fNLtkzzb0VOiXZJQ16hY45KHIYcvH861X1zr9GsXRY2KNZh086Scso93N7zLv378F0kpSe4OTSmllFLKpexZAfGMiJy2Xqkikikip10RnDtdnNRGT4l22ehrfGw8D8c8nLN9Ou00UXFRpGakuuT69shd9lHZrzK/HfyNfvP7sebwGneHppRSSinlMvaMTFcyxgQbY4KBAOAO4IPCPici/iKyWkQ2icgWERlttXcRkfUislFEfhWRSKvdT0RmiUiCiKwSkXolujMHuDihbjmlJemZ6S659r9a/oul/Zbmabt6+tX8mfKnS65vr9xlH0dTjjL0h6Fa9qGUUkqpcsOemukcxuZr4GY7Dj8P3GiMaQnEAN1F5BrgQ+BuY0wMMIMLc1YPAU4YYyKBicBrRYnNWS5OqFtPa+2y+aDDA8Mvuf77R9536jzYxVG9YnUm3TyJf0b9E2MM7254l4cWP6SzfSillFLK49lT5vGPXK++IvIqUGi9gZV4J1ubvtbLWK9gqz0EOGi97w3EWe/nAl1EROy/Fee5OKHtOLMj+07vc+n1729xf872tuPbiIqLIj3LNaPk9vDx8uGx1o/llH2sPLSS/vP7s/HIRneHppRSSinlNFLYg3Ui8nmuzQxgD/BfY8yRQk9uW/RlHRAJvG+MGSUi1wFfAynAaeAaY8xpEdkMdDfGHLA++xfQzhhz7KJzPgA8ABAeHt5m9uzZdt2oI7x44EWOZ14Ybb077G6uCbrGZdc/ln6M0QdH52l7tuaz1KxQ02Ux2ONkxkk+P/Y5u87vwgsv+lTuww2VbqC4vxslJycTFBTk4ChLN71nz9e5c+d1xpir3B2HUkqpkrEnmb7WGLOisLZCzhEKfAX8G9sUe68ZY1aJyJNAE2PMUHuT6dyaNGlitm/fbm8YDjF82XB+3HdhurpqgdVY0m+Jy66/bNkyHtv3WJ62e5vdy5NXP+myGOyRnpXOxHUTmbp1KgDd63VndIfRBPoGFvlcy5cvp1OnTg6OsHTTe/Z8IqLJtFJKeQB7aqbftbPtsowxJ4FlwC1AS2PMKmvXLKCD9T4RqAMgIj7YSkBK3VxrEztP5NXrXs3ZPnLuCFFxUWRmZbrk+tmLvFxV/cLP4ClbpxAVF1WqHvrz9fLlqauf4s0b3iTQJ5BFexYx8NuB/HXyL3eHppRSSinlMJdNpkWkvYiMBMJFZESu10uAd2EnFpFwa0QaEQkAugLbgBARaWwdlt0GMA+Itd73BZaa0rSmdi49GvTg5wE/52mLmRrj0vrgz7t/zoc3fZinreWUli57ONJeN9e7mZk9ZxIZGsnuU7u589s7+W73d+4OSymllFLKIQoama4ABAE+QKVcr9PYkt3C1ASWicgfwBpgsTFmAfBP4EsR2QTcA2TXJ0wCwkQkARgBPF3023Gdyv6VL3kw8Z7v7qHvPHv+ahyjY+2OrLgzb7VNx5kd2XR0k8tisEf9kPpMv3U6PRr0ICUjhad+forxq8a7bJpBpZRSSilnuWwyba10OBrbA4Kjc73eMsbsLOzExpg/jDGtjDHRxpgWxpgxVvtXxpgoY0xLY0wnY8wuqz3VGNPPGBNpjGmb3V7axcfGM6jpoJzt7Se2ExUX5bLVAIMrBPPHvX/kaRu0cBCvr3ndJde3V6BvIOM7juf5ds/j4+XDjD9ncN/393H47GF3h6aUUkopVWz21EyfE5E3RGShiCzNfjk9sjJkVNtRfPePvKULnWZ3oudXPV1y/ew66puuuCmnberWqUTFRblkGXR7iQgDrhzAlO5TqFGxBn8c/YP+8/uz8uBKd4emlFJKKVUs9iTT04E/gfrAaGxT4+ma0ReJqBRBfGw8XnLhr3Tv6b1ExUWx/bhrZhyZ2HkiH3TJuzhl9JRo0jLTXHJ9e0WFRzG752w61OrAifMneHDxg3y86eNS9QClUkoppZQ97Emmw4wxk4B0q/TjfuBGJ8dVZm26dxML+izI09Z3fl+XjRJfF3Edvw78NU9bm2ltXLrIjD0q+1fmgy4f8K+W/wLgvY3v8eiSR0vdA5RKKaWUUgWxJ5nOfkrskIj0EJFWQBUnxlTm1Q2uS3xsPK2qtcrTHj0lmseWPnaZTzlOiF/IJQ9H9viqR86cz6WFt5c3D8c8zAc3fUCIXwi/JP5C//n92ZK0xd2hKaWUUkrZxZ5keqyIhAAjgSeAT4HhTo3KQ0y5Zcols20s27+MqLgoZmyb4fTrx8fG06Z6m5zt19e8Tp9v+jj9ukXVsXZHZvecTYuwFhw8e5B7Ft7DnB1zSlW9t1JKKaVUfgpMpq3lwBsZY04ZYzYbYzobY9oYY+a5KL4yL7hCMPGx8fyn03/ytI9fPZ6ouCg2HNng1OtP7j6ZCTdMyNlOOJlQ6h5MBKgVVIu4W+IY0GQA6VnpjFk5hudXPE9KRoq7Q1NKKaWUuqwCk2ljTCZwp4ti8Whd6nYhPjaeu668K0/7vd/dS1RcFOv/Xu+0a3er140f+/6Ypy16SjSpGalOu2ZxVPCuwPPXPM8rHV/B39ufeX/NY9DCQRxJP+Lu0JRSSiml8mVPmccKEXlPRK4TkdbZL6dH5qGeafcM8bHx1KhYI0977KJYouKiWLhroVOuW71iddYPypuwXz39ak6mnnTK9UqiV8NezOgxg3rB9dhxYgdvHHqDJXuXuDsspZRSSqlL2JNMxwDNgTHABOv1pjODKg8W9118yWIrAKN+GUVUXBTvrH/H4df09fa95JrXzbquVM6g0ahyI77o8QVd63Yl1aTy+PLHeWvtW2RkZbjoHoIIAAAgAElEQVQ7NKWUUkqpHIUm01ad9MUvnRrPAbIXW4mPjad2UO08+/4b/1+i4qKIiotyaAKZfc3cOs7sWCoT6qAKQUy4YQJ9KvfBW7z5fMvnDP1hKEfPHXV3aEoppZRSgB3JtIhUF5FJIvKdtd1MRIY4P7TyZdEdi4iPjafLFV0u2ddqaiui4qJYdWiVw66XX0J9Ou20w87vKCLCjcE3MunmSYQHhLPu73X0X9CftYfXujs0pZRSSim7yjwmA98DtaztHcDjzgqovPtP5/8QHxvPmA5jLtk39Ieh/Hvvv4mKi3LIqoYXJ9TXfnEt59LPlfi8ztCmehtm95rN1TWu5ljKMYb+MJTJmyeXullJlFJKKVW+2JNMVzXGzAayAIwxGUCmU6NS9GnUh/jY+Evmqc7WZlobouKieHDxgyVKKC9OqNvNaEd6VvpljnavqgFV+aTrJ9zf4n4yTSYT1k1g+PLhnEk74+7QlFJKKVVO2ZNMnxWRMMAAiMg1QOkrsPVQ2fNUx8fGE9ss9pL9vx38jegp0UTFRTH0+6FkZhX995yLE+rXVr9W7HidzcfLh+FthvNO53eo5FuJJfuWMHDBQLYf3+7u0JRSSilVDtmTTI8A5gENRWQFMAX4t1OjUvl64uoneLfuu6y/Zz0hfiGX7F91eBUxU2NyHlzce3qv3ededdeFeuxZ22c5pIzEmTpf0ZlZPWfRpHIT9p3Zx6CFg5j3l64lpJRSSinXsmc2j/XADUAH4EGguTHm0jndlMv4evny68BfiY+NZ1n/ZZc9rudXPXMS66i4KLYc23LZYwN9A7mxzoVJWspCYlonuA7Tbp3G7ZG3k5qZynO/PsfolaM5n3ne3aEppZRSqpzwKewAEfEHHgY6Yiv1+EVEPjLGlK7l88qpqgFVc8o00jLTGLBgAAknE/I9duC3A+0+b1lJSP19/Hn52pdpVa0V434fx9wdc9matJWJnSZSK6hW4SdQSimllCoBe8o8pmBbtOVd4D3r/dTCPiQi/iKyWkQ2icgWERlttYuIjBORHSKyTUQey9X+jogkiMgfuspi0VXwrsBXvb/KqbF+78b3in2uvo37OjAy5/tHo38w9dap1A6qzdakrfRf0J/fEn9zd1hKKaWU8nCFjkwDLYwxzXJtLxORrXZ87jxwozEmWUR8gV+tuaqbAnWAK40xWSJSzTr+FqCR9WoHfGj9qYrphjo35Hm4cP+Z/byw4gXW/n35OZqDfIP48rYv8fP2c0WIDtUsrBmzes7imV+e4ZfEX3jox4d4OOZhHoh+AC+x5/dGpZRSSqmisSeZXi8i1xhjfgcQkXZAoStmGNt8bcnWpq/1MsC/gLuMMdlT7R2xjukNTLE+9//t3Xd8lfXd//HXJyebhAAh7BFFDCIyZAhOEFSg1j2w2mp/WmxrFa1tb+3t7Wjv2trWWm3dE0dVbltbpG4FQWUrsmTJHrJXgOzP74/rio0Iyck4Jwm8n4/H9fBc63t9vudE8sn3fMc0M2tmZm3dfUO1aiQH1TGzI08Pf7q+w4iprJQs/jr0rzw691EenvMwD855kHlb5nH3yXcfcNCmiIiISG1E01zXF/jYzFaa2UpgKtDfzOaZWaUDEc0sYmZzgE3AO+4+HegCXGpms8zsDTPrGl7eHlhT4fa14TGRakmwBH7U60c8NOwhslKymLx2MqMmjGLRtkX1HZqIiIgcYqJpmR5e08LdvRTobWbNgFfNrAeQAhS4ez8zuwB4Cjgl2jLNbDQwGiAnJ4dJkybVNLxGKT8/X3Wuhpta3sSTm59kTf4avjPhO1zS4hIGZgys2wBjQJ+ziIhI42DRrJ5nZs0J+jl/lXyHU+ZF/yCz24G9wDXACHdfYWYG7HD3LDN7FJjk7i+G1y8GBlfWzSMvL88XLz68FuuYNGkSgwcPru8w4qq2dS4sLeTu6Xfzj6X/AILBlbcOuJXkSHIdRVj39Dkf+sxstrv3q+84RESkdqrs5mFmvwbmAg8A94bbH6O4LydskcbM0oAzgEXAP4Eh4WWnAUvC1+OB74WzegwEdqq/tNSFlEgKd514F3edeBfJCcm8suQVrnzjSjbk68dLREREaieabh6XAF3cvbpL4rUFxppZhCBpH+fuE8zsQ+AFM7uJYIDiNeH1rwMjgWUELdjfr+bzRCp1QdcLyGuRx82Tbmb+1vlcMuESHjj9Afq06lPfoYmIiEgjFc0AxPlAs+oW7O5z3b2Pu/d09x7u/qvw+A53/5a7H+fug9z9s/C4u/t17t4lPFfljCEi1XVs9rG8fPbLnNTuJHYU7uCat67h7ZVv13dYIiIi0khFk0z/FvjUzN4ys/HlW6wDE4mV8unzLjn6EorKivjZBz9j7IKxRDN+QERERKSiaLp5jAXuAeYBZbENRyQ+EhMSuW3gbbTLaMefP/kzf5z1Rzbs2cDP+/2cSEKkvsMTERGRRiKaZHqvuz8Q80hE4szMuPq4q2nbpC23fXQbL3z+AhvyN/D7037fKFeAFBERkfiLppvHFDP7rZkNMrPjy7eYRyYSJyOPHMmjZzxKZnIm7695n9tv6o6bQfnWogU8/3x9hykiIiINUDTJdB9gIHA31ZgaT6Qx6d+mP09Nbkv6vlJe75vOQ+e1+s/J7dvhu98NNhEREZEKqkym3X3IAbbT4xGcSNw8/zzdHvkHf3h4DQllziPnteLN/k2/cY1aqEVERKSiaBZtaW1mT5rZG+F+dzO7OvahicTRDTcAcOrcfG5+6UsAnjw755vXjRkTz6hERESkgYumm8czwFtAu3B/CXBjrAISqRfbt3/1ctT728jcU8qizmksbb/fQMRt2+IcmIiIiDRkB02mzax8po+W7j6OcFo8dy8BSuMQm0i9SC5xhs/YSdstRWxskVTf4YiIiEgDVtnUeDOA44E9ZpYNOICZDQR2xiE2kXpz88tfctuzZSTsv46L1Us4IiIi0kBV1s2jPG34KTAe6GJmHwHPAtfHOjCRuGre/Gu7TQoOkEgnAH2T4J/Xwa4NcQtNREREGq7KkukcM/spMBh4Ffg98AbwODAs9qGJxNEDUa5LdGI6zHke/nI8TPodFObHNi4RERFp0CpLpiNABpAJNCHoEhIB0sNjIoeOK64ItgPw8u07V8Dts+GYb0PxXpj02yCpnvU0lJbENVwRERFpGCrrM73B3X8Vt0hE6ttzz8FZZwXT34WzdjiwpGUn7hh2LcNGj+Ka7CPh0udh1cfw9m2wbjZMuBGmPghDbw8SbVPHahERkcNFNH2mRQ4fV1wBW7eCO7hj7qyYOJ1pnXvx2zcWMfWLrcF1nU+Ea96Di56GFkfC1qUw7rvwxFBYPqleqyAiIiLxU1kyPTRuUYg0YMN7tOHHg7tQWub86IXZzFsbTmZjBj0ugOtmwMg/QpNWQUv1s+fC2HNgzcz6DVxERERi7qDJtLtrdQqR0M1n5jHsmNbs2FvMZY9PY/ryrf85GUmCAT+AMXPg9P+BlCxY8QE8OQxeuATWz6m/wEVERCSmolkBsUbMLNXMZpjZZ2a2wMzu2u/8A2aWX2E/xcxeNrNlZjbdzHJjFZtIdUUSjIcuP56ze7Ylv7CE7z01g4mLNn39ouQmcOrPgqT6lJshqQksfQseOw1euhw2fFY/wYuIiEjMxCyZBgqB0929F9AbGB4u+IKZ9QOa73f91cB2dz8KuA+4J4axiVRbcmIC94/qw2UDOlFYUsYPnp3Fa5+t/+aF6S2CwYhjPoNBP4HEVFg0AR49FV78jlqqRUREDiExS6Y9UN7ynBRubmYR4A/AL/a75VxgbPj6FWComaZFkIYlkmDcfX4Prj31SErKnBte+pS/TV994IszcuCs3wRJ9cDrIDENFv87aKl+4RJYPT2+wYuIiEidi2XLNGYWMbM5wCbgHXefDvwEGO/u+y8h1x5YA+DuJQRLlmfHMj6RmjAzbhnRjZ+flYc7/PLVedz3zhLKyvZfMjGU2QaG3w03zg1aqpPSg+4fT50JT38Llr0bzB4iIiIijY55HH6Jm1kzglUU7wDuBga7e4mZ5bt7RnjNfGC4u68N978ATnD3LfuVNRoYDZCTk9N33LhxMY+/IcnPzycjI6O+w4irhlzn91YX8/zCIhzo2TLC6J4pZCRX/oVKUtFO2q+bQIe1/yaxdA8AuzOOZE3H89mccxKeEGnQdY6Vw63OQ4YMme3u/eo7DhERqZ24JNMAZnY7wdzVPwIKwsOdgOXufpSZvQXc6e5TzSwR+BLI8UoCzMvL88WLF8c69AZl0qRJDB48uL7DiKuGXucPlmxmzEufsmNvMe2bpfHIFX05rkNW1TcW7IJZTwYLvuzZHBzL6ggDf8yUPbmcMmxkbANvYBr651zXzEzJtIjIISCWs3nkhC3SmFkacAYw293buHuuu+cCe8MBhwDjgSvD1xcB71eWSIs0FKcdncOE60+mV4cs1u3Yx4UPf8yLM1ZT5Y9valM4+Sa4cT58+37IPgp2roG3bmXgtGuCFRZ3HKQ/toiIiDQIsewz3RaYaGZzgZkEfaYnVHL9k0C2mS0DfgrcEsPYROpUh+bpjPvhIC4/oRNFpWXc+o95/OKVuRQUl1Z9c1Iq9L0KrpsJo16EToNIKtkDH/8F7u8FL18BKz9Uv2oREZEGKDFWBbv7XKBPFddkVHhdAFwcq3hEYi0lMcJvzj+O4zs157//OY//m72WBet38dDlx5PbsknVBSQkQLeR0G0ks8c/Tt+SmTD/H/D5a8HW+jjofzUcdzGkHD59i0VERBqymM7mIXI4urBvB1798UnkZqezcMMuRtw/hbEfrzz4bB8HsLtpV7jgMbhpPpx2CzTJgY3zYMKNcG83mPBT+HJeDGshIiIi0VAyLRIDx7Rtyr9+cjLf7tWOfcWl3DF+AaMen8aqrXuqV1BmGxhyK9y0AC54AjqdCEW7g4GLj5wMTwyD2WODwYwiIiISd0qmRWIkKy2Jv1zWh0eu6EvLjBRmrNjGWX+ezNMfrahWKzUAiSnQ82L4f2/Aj6fBgGshpSmsnQmv3QD35sGrP1TfahERkThTMi0SY8N7tOGdm07l3N7tKCgu467XFjLqsWms2FLNVupyrY6Bkb+HmxfBuQ9B55OgeC989iI88y14oDdMvBu2LKvbioiIiMg3KJkWiYPmTZK5f1QfHvtuX3IyU5ixchsj7p/Mkx+uoLS6rdTlkptAn8vh+6/D9Z/AKT+DzHawfSV8cA/8tS88NhimPgS7v6zL6oiIiEhIybRIHJ15bNBKfX6f9hQUl/HrCQs5/6GPmL1qW+0Kzu4CQ/8nGLD43Veh9+WQnAnrP4W3boU/HQPPnA0zHldiLSIiUoeUTIvEWbP0ZO67tDdPfK8frZumMHftTi58eCo3vPgp63fsq13hCRHocjqc9xD8fClcPBa6nQ0JibByCrz+s2A2kKeGw7SHYfuquqmUiIjIYSpm80yLSOWGdW/NoC7ZPPLBFzw2eTnjP1vP2wu/5NpTu9A9oQ4GESalwbHnBVvBTlj8Jiz8Fyx7F1ZPDbY3b4FWx0LecMgbCe2OD+a7FhERkagomRapR01SErn5zDwu6deR372xiH/P28D97y2lRapRkL2Oc3q1w8xq/6DULOh1abAV7oYlbwULwSx7DzYtCLYp9wbzWXc5HboMDf6bkVP7Z4uIiBzClEyLNAAdW6Tz4OXH873lW/nVhIUsWL+LMS/NYezHK7n928fSu2OzuntYSiYcd1GwlRTBqg9h8RtBy/XO1TD35WADaNMTugyB3FOh00CtvCgiIrIfJdMiDcgJR2Yz/icn879/e5fXVsInq3dw3oMfMbRbK8YM60rPDnWYVAMkJoct0afDiN/D5sXwxXtBi/Wqj+DLucH20f1gEWh/POSeDJ0GQccBkNa8buMRERFpZJRMizQwkQTjtA5J/PSik3hw4hc88/EK3lu0ifcWbeL0bq0YM7QrveqypbqcGbTqFmyDroPifbDqY1gxORi8uP7TYJGYtTOB+4J7co6BTidA+75Bf+ucbhDRPysiInL40G89kQYqMzWJW0Z04+qTj+DxKct5buoq3l+0ifcXbWJIXg5jhh1dt90/9peUBkcNDTYIlixfPS3oFrJ6Oqz/BDZ/HmyznwnvSQ+6hrTtCW2OC17ndIOk1NjFKSIiUo+UTIs0cDmZKfxy5DGMPvVIHp+8nGenrmLi4s1MXLyZwXk5jBnalT6d4tDdIrUpHH1msAGUFML6ObB2Bqz7BNbNhh2rYM20YCtnCdD8iGDlxpw8yO4KLbsGc2Orm4iIiDRySqZFGomWGSncGibVj4Ut1ZMWb2bS4s0MOKIF3z8xlzO6tyYxEqep7RJTgi4enU74z7E9W2HDHPhyXtjfeh5s/QK2hduiCV8vIzUrSLSbd6bLLiD1c8hsG2wZrYItuUnt4pzzt6C/93EXBfNwi4iI1CEl0yKNTHZGCreOOIbRpxzJ41NW8Py0VcxYsY0ZK7bRvlka3x3UmVH9O9IsPTn+wTXJ/nrXEAhasLcshU2fw5bFsHVZuC0P5r/eMAc2zKEjwNp/fbPMxDRIbwFpLYLW8ZTMoDtJUnowgDIhKWj9xqGsJHhe4W7Ytx12b4AtS4JyUjKh28g4vAkiInI4UTIt0khlZ6Rwy4huXDekC3+fvZaxU1exYssefvfGIv787hLO79OBq07MJa9NZv0GmpgCbXoEW0XusGcLbF8BO1bzxacf0CU7OVjufNd62LMZ8jdByT7YtS7YaqrzSdChX+3qISIicgBKpkUauczUJK466Qi+NyiXD5Zs5umPVzJ5yWZenLGaF2es5sQu2Ywa0Ikzu7cmNakBdXMwCxaFyciBjgNYs7UlXQYP/vo17lCUD3u3QcGOYBBk4W4o2hMk2aVFUFoMXgZYsGx6YkrQNSStGWS0gRZH1L6riIiIyEHELJk2s1RgMpASPucVd7/DzF4A+gHFwAzgWncvtmCZt/uBkcBe4Cp3/yRW8YkcahISjCHdWjGkWyuWbcrn2akreWX2Wj7+Yisff7GVzNREzu7ZlguP70Dfzs3rZmXFWDMLumekZAKd6zsaERGRb4jlSKVC4HR37wX0Boab2UDgBaAbcByQBlwTXj8C6Bpuo4GHYxibyCHtqFYZ/OrcHky9dSh3nXMsPTtksbughBdnrOGiR6Yy5I+TeOC9pazZtre+QxUREWnUYtYy7e4O5Ie7SeHm7v56+TVmNgPoEO6eCzwb3jfNzJqZWVt33xCrGEUOdVlpSVx5Yi5XnpjLko27+fsna3n1k3Ws3LqXP72zhD+9s4QTjmjBiB5tOKtHG9pmpdV3yCIiIo2KBblrjAo3iwCzgaOAB939vyqcSwKmA2PcfYqZTQB+5+4fhuffA/7L3WftV+ZogpZrcnJy+o4bNy5m8TdE+fn5ZGRk1HcYcaU6163SMmfB1lI+WlfCJ5tKKS77z7kjsxLo2zpC39aJtGkSpyn2Qofb5zxkyJDZ7q5RkSIijVxMk+mvHmLWDHgVuN7d54fHHgf2uPuN4X5UyXRFeXl5vnjx4pjH35BMmjSJwfsP0jrEqc6xs6ugmPc+38ib87/kgyWbKaiQWR/dOoOzjm3D4LwcenVoFvP5qw+3z9nMlEyLiBwC4jKbh7vvMLOJwHBgvpndAeQA11a4bB0EU82GOoTHRCRGmqYmcX6fDpzfpwP7ikr5YMlm3l7wJe9+vpElG/NZsnEZf3l/GZkpiZx4VDYnd83h1K4t6Zyt2TFEREQgtrN55ADFYSKdBpwB3GNm1wBnAUPdvcIXzIwHfmJmLwEnADvVX1okftKSIwzv0YbhPdpQXFrGtOVbeXfhRqYs3cLyLXt4a8FG3lqwEYBOLdI56aiW9M9tTv/cFnRontY4ZgcRERGpY7FsmW4LjA37TScA49x9gpmVAKuAqeEv33+4+6+A1wmmxVtGMDXe92MYm4hUIimSwCldczilaw4Aa7fv5cOlW5iydAsfLtvC6m17WR3OYw3QKjOF/rkt6Nu5Of1ym5PXJpOUxAY0p7WIiEiMxHI2j7lAnwMcP+Azw1k8rotVPCJScx2apzNqQCdGDehEaZkzb91Opi/fysyV25m9ahubdhfy73kb+Pe84MukpIiR1yaT49pn0aN9Fj3aZZHXJrNhLRojIiJSB7QCoohUSyTB6N2xGb07NuPa08Dd+WLzHmat3MbMldv5dM12VmzZw/x1u5i/bhewBoAEg87ZTejaKoOjW2fStXUGXVtlktsynfRk/VMkIiKNk36DiUitmBlHtcrgqFYZjBrQCYDdBcUsXL+Leet2Mn/dTuat28mKLXu+2t5euPFrZbTKTKF5YjFvbJlLxxZptG+eRvtm6bRvnkbrzJSYzyQiIiJSU0qmRaTOZaYmccKR2ZxwZPZXxwqKS1m+eQ9LN+1mycbdLNmYz/LN+azetpdNuwvZBCyeteYbZSUYZGek0LppCq0zU8nJTKFFk2RaNEkmOyOZZunJNEtLoll6Mk1TE8lITVR/bRERiRsl0yISF6lJEbq3a0r3dk2/dry0zFm/Yx//en8qWe27sHb7Ptbu2Mf6HftYt30fm3YXsjnc5rMrqmclRxJIT4nQJDmRtOQIqUkJpCVFSE5MIDmSQGIkgaSIkZiQQCTBMAMj+K87OE5ZmVPqUFbmFJeWhZtTVFJGYUkpBcVl7CsupXN2Os9dfUIs3jIREWkElEyLSL2KJBgdW6TTo2WEwYNyv3G+uLSMLfmFbNxVyMZdBWzeXci2PUVs21PE1j1F7NhbxM59xezYW8zugmJ2F5RQVFpG0d4yduwtjnn8iRFNCSgicjhTMi0iDVpSJIG2WWm0zUqL6np3p7CkjD2FJewtKmVfcSkFxUFLclFJGUWlpRSVBK3NZe6UlDoOlFVYDdYIkvxIgpFgRlLESIokkBRJIDkxgZTEBFKTIqQlRWiSon9GRUQOZ/otICKHFDMjNSlCalKE7KovFxERqRUNkRcRERERqSEl0yIiIiIiNaRkWkRERESkhpRMi4iIiIjUkJJpEREREZEaUjItIiIiIlJDSqZFRERERGpIybSIiIiISA0pmRYRERERqSEl0yIiIiIiNRSzZNrMUs1shpl9ZmYLzOyu8PgRZjbdzJaZ2ctmlhweTwn3l4Xnc2MVm4iIiIhIXYhly3QhcLq79wJ6A8PNbCBwD3Cfux8FbAeuDq+/GtgeHr8vvE5EREREpMGKWTLtgfxwNyncHDgdeCU8PhY4L3x9brhPeH6omVms4hMRERERqa2Y9pk2s4iZzQE2Ae8AXwA73L0kvGQt0D583R5YAxCe3wlkxzI+EREREZHaSIxl4e5eCvQ2s2bAq0C32pZpZqOB0eFuoZnNr22ZjUxLYEt9BxFnqvPh4XCrc159ByAiIrUX02S6nLvvMLOJwCCgmZklhq3PHYB14WXrgI7AWjNLBLKArQco6zHgMQAzm+Xu/eJRh4ZCdT48qM6HPjObVd8xiIhI7cVyNo+csEUaM0sDzgA+ByYCF4WXXQn8K3w9PtwnPP++u3us4hMRERERqa1Ytky3BcaaWYQgaR/n7hPMbCHwkpn9L/Ap8GR4/ZPAc2a2DNgGjIphbCIiIiIitRazZNrd5wJ9DnB8OTDgAMcLgIur+ZjHahZdo6Y6Hx5U50Pf4VZfEZFDkqknhYiIiIhIzWg5cRERERGRGmoUybSZDTezxeFS47cc4PwhtxR5FHX+qZktNLO5ZvaemXWujzjrUlV1rnDdhWbmZtaoZ36Ipr5mdkn4OS8ws7/FO8a6FsXPdSczm2hmn4Y/2yPrI866ZGZPmdmmg03jaYEHwvdkrpkdH+8YRUSk5hp8Mh0OYHwQGAF0By4zs+77XXZILUUeZZ0/Bfq5e0+CFSN/H98o61aUdcbMMoExwPT4Rli3oqmvmXUFbgVOcvdjgRvjHmgdivIzvo1gsHIfgkHID8U3yph4BhheyfkRQNdwGw08HIeYRESkjjT4ZJpgsOIyd1/u7kXASwRLj1d0qC1FXmWd3X2iu+8Nd6cRzNndmEXzOQP8muCPpYJ4BhcD0dT3B8CD7r4dwN03xTnGuhZNnR1oGr7OAtbHMb6YcPfJBDMUHcy5wLMemEYwF3/b+EQnIiK11RiS6a+WGQ9VXIL8G9ccIkuRR1Pniq4G3ohpRLFXZZ3Dr787uvu/4xlYjETzGR8NHG1mH5nZNDOrrHWzMYimzncCV5jZWuB14Pr4hFavqvv/u4iINCBxWQFRYsfMrgD6AafVdyyxZGYJwJ+Aq+o5lHhKJPjqfzDBNw+Tzew4d99Rr1HF1mXAM+5+r5kNIph7voe7l9V3YCIiIgfSGFqmy5cZL1dxCfJvXFPZUuSNSDR1xsyGAf8NnOPuhXGKLVaqqnMm0AOYZGYrgYHA+EY8CDGaz3gtMN7di919BbCEILlurKKp89XAOAB3nwqkAi3jEl39ier/dxERaZgaQzI9E+hqZkeYWTLBoKTx+11zqC1FXmWdzawP8ChBIt3Y+9JCFXV2953u3tLdc909l6Cf+DnuPqt+wq21aH6u/0nQKo2ZtSTo9rE8nkHWsWjqvBoYCmBmxxAk05vjGmX8jQe+F87qMRDY6e4b6jsoERGJToPv5uHuJWb2E+AtIAI85e4LzOxXwCx3H88hthR5lHX+A5AB/F841nK1u59Tb0HXUpR1PmREWd+3gDPNbCFQCvzc3RvtNy5R1vlm4HEzu4lgMOJVjfwPY8zsRYI/ilqGfcHvAJIA3P0Rgr7hI4FlwF7g+/UTqYiI1IRWQBQRERERqaHG0M1DRERERKRBUjItIiIiIlJDSqZFRERERGpIybSIiIiISA0pmRYRERERqSEl03JQZtbGzF4ysy/MbLaZvW5mR9dzTDeaWXoN7rvKzNpV2H/CzLrXQTx3mtm6cHq3mAnj/2uF/bZm9raZ5ZrZ/PBYPzN7IHw92MxOrPdP3nwAAAT/SURBVMFzTjGzheVlioiISOWUTMsBWTB59avAJHfv4u59gVuB1vUbGTcCB0ymzSxSyX1XAV8l0+5+jbsvrKOY7nP32+uorGgNJ5iv+SvuPsvdbwh3BwPVSqbNLNHdpxDMeSwiIiJRUDItBzMEKA4XlQDA3T9z9ynhSm1/MLP5ZjbPzC6Fr1pDJ5nZK2a2yMxeCJNyzKy/mX1sZp+Z2QwzyzSzSFjOTDOba2bXVlaOmd1AkBBPNLOJ4bX5ZnavmX0GDDKz28Py5pvZY+F9FwH9gBfMbI6ZpYXl9wvLuCysx3wzu6e8vmHZvwljnmZmVf4hYWY5ZvaOmS0IW79XmVnLsAV5kZk9Y2ZLwjoNM7OPzGypmQ0I729hZv8M349pZtbzII8aDryx37MHm9kEM8sFfgjcFNb3lDCuv4fvzUwzOym8504ze87MPgKeq6p+IiIi8nVKpuVgegCzD3LuAqA30AsYBvzBzNqG5/oQtB53B44ETrJg6eiXgTHuXn7PPuBqgqWT+wP9gR+Y2REHK8fdHwDWA0PcfUh4XRNgurv3cvcPgb+6e3937wGkAWe7+yvALOByd+/t7vvKKxJ2/bgHOD2sU38zO69C2dPCmCcDP4jifbuDYDn7Y4FXgE4Vzh0F3At0C7fvACcDPwN+GV5zF/Cpu/cMjz27/wPCFvi8g7Wsu/tK4BGCFvPeYWvz/eF+f+BC4IkKt3QHhrn7ZVHUT0RERCpo8MuJS4N0MvCiu5cCG83sA4JkeBcww93XApjZHCAX2AlscPeZAO6+Kzx/JtAzbDkGyAK6AkUHKefDA8RSCvy9wv4QM/sFQVeQFsAC4LVK6tKfoCvL5vBZLwCnAv8M45gQXjcbOKOqN4bgvTk/rOebZra9wrkV7j4vfM4C4D13dzObF9av/P4Lw/vfN7NsM2u63zNOAKZHEUtFw4Du4RcFAE3NLCN8Pb7iHxgiIiISPSXTcjALgIuqvOqbCiu8LqXynzEDrnf3r/X9NbPB1SinIEzqMbNU4CGgn7uvMbM7gdRqRf91xe7uUcQQrYp1KquwX1bNskcAb1bz2QnAQHcvqHgwTK73VLMsERERCambhxzM+0CKmY0uP2BmPc3sFGAKcGnY5zmHoCV3RiVlLQbamln/sJxMM0skGED3IzNLCo8fbWZNqohrN5B5kHPlifOWsNW14h8DB7tvBnBa2K85AlwGfFBFDJX5CLgEvmp5b17N+6cAl4f3Dwa2lLfkVzAUeLeKcvav79vA9eU7Zta7mnGJiIjIASiZlgMKW2TPB4ZZMDXeAuC3wJcEs3zMBT4jSLp/4e5fVlJWEXAp8JdwoOA7BInvE8BC4BMLpmJ7lKpbaB8D3iwfgLjfc3YAjwPzCRL1mRVOPwM8Uj4AscI9G4BbgIlhfWa7+7+qiKEydwFnhvW5mOD92l2N++8E+prZXOB3wJUVT4Z/vBS4e1VlvgacXz4AEbgB6BcObFxIMEBRREREasn+8y22iFRX2JUk393/GO6nAKXuXmJmg4CH3b3OWoHN7Aqgg7v/rq7KPMAzcoEJ4SBOERERqYT6TIvUTj4w2syahnNNdwLGmVkCwQDGaGYAiZq7P1+X5e0vbMV+CNgSy+eIiIgcKtQyLSIiIiJSQ+ozLSIiIiJSQ0qmRURERERqSMm0iIiIiEgNKZkWEREREakhJdMiIiIiIjWkZFpEREREpIb+PxYAkQwN3h2oAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"ax = create_cstr_plot_axes()\n",
"for Tc in [290, 300, 305]:\n",
" tsim, ysim = Simulator(cstr(), package='scipy').simulate(numpoints=100)\n",
" cstr_plot(tsim, ysim, ax)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.6 Effect of Cooling Temperature](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.6-Effect-of-Cooling-Temperature)",
"section": "7.4.6 Effect of Cooling Temperature"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "817485d9",
"metadata": {},
"source": [
"\n",
"< [7.3 Simulation in Pyomo](https://jckantor.github.io/CBE30338/07.03-Simulation-in-Pyomo.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [7.5 First Order System in Pyomo](https://jckantor.github.io/CBE30338/07.05-First-Order-System-in-Pyomo.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[7.4 Simulation of an Exothermic CSTR](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4-Simulation-of-an-Exothermic-CSTR)",
"section": "7.4 Simulation of an Exothermic CSTR"
}
},
"source": [
"# 7.4 Simulation of an Exothermic CSTR"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.1 Description](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.1-Description)",
"section": "7.4.1 Description"
}
},
"source": [
"## 7.4.1 Description\n",
"\n",
"This example is intended as an introduction to the nonlinear dynamics of an exothermic continuous stirred-tank reactor. The example has been studied by countless researchers and students since the pioneering work of Amundson and Aris in the 1950's. The particular formulation and parameter values described below are taken from example 2.5 from Seborg, Edgar, Mellichamp and Doyle (SEMD).\n",
"\n",
"\n",
"\n",
"(Diagram By [Daniele Pugliesi](https://commons.wikimedia.org/wiki/User:Daniele_Pugliesi) own work, [Creative Commons Attribution-Share Alike 3.0 (CC BY-SA 3.0)](http://creativecommons.org/licenses/by-sa/3.0), [Link](https://commons.wikimedia.org/w/index.php?curid=6915706))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.2 Imports](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.2-Imports)",
"section": "7.4.2 Imports"
}
},
"source": [
"## 7.4.2 Imports\n",
"\n",
"The following code cell imports the libraries and functions needed within this notebook. The code installs Pyomo if necessary. This code is required to run this notebook in Google Colab."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.2 Imports](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.2-Imports)",
"section": "7.4.2 Imports"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import matplotlib.pyplot as plt\n",
"import numpy as np\n",
"\n",
"# if missing, install pyomo and ipopt\n",
"import shutil\n",
"\n",
"if not shutil.which(\"pyomo\"):\n",
" !pip install -q pyomo\n",
" assert(shutil.which(\"pyomo\"))\n",
" \n",
"# import pyomo modules\n",
"from pyomo.environ import *\n",
"from pyomo.dae import *\n",
"from pyomo.dae.simulator import Simulator"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.3 Arrehenius Law Kinetics for a First-Order Reaction](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.3-Arrehenius-Law-Kinetics-for-a-First-Order-Reaction)",
"section": "7.4.3 Arrehenius Law Kinetics for a First-Order Reaction"
}
},
"source": [
"## 7.4.3 Arrehenius Law Kinetics for a First-Order Reaction\n",
"\n",
"We assume the kinetics are dominated by a single first order reaction\n",
"\n",
"$$A \\xrightarrow{kc_A}{} \\text{Products}$$\n",
"\n",
"The reaction rate per unit volume is modeled as the product $kc_A$ where $c_A$ is the concentration of $A$. The rate constant $k(T)$ is a increases with temperature following the Arrehenius law\n",
"\n",
"$$k(t) = k_0 e^{-\\frac{E_a}{RT}}$$\n",
"\n",
"$E_a$ is the activation energy, $R$ is the gas constant, $T$ is absolute temperature, and $k_0$ is the pre-exponential factor. \n",
"\n",
"We can see the strong temperature dependence by plotting $k(T)$ versus temperature over typical operating conditions."
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.3 Arrehenius Law Kinetics for a First-Order Reaction](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.3-Arrehenius-Law-Kinetics-for-a-First-Order-Reaction)",
"section": "7.4.3 Arrehenius Law Kinetics for a First-Order Reaction"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEWCAYAAAB42tAoAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd5xU1f3/8deHpfcqCCi9SJG2Ara4qAgW7Ik9FhRLjLH8jDHFksQY9WuBaDTEWEARFSyoqChx7SKg9N57h4Wlbvn8/rh3dbMuu7PLzk7Z9/PxmAdzy9z5nLnLfObcc+455u6IiIgcTKVYByAiIvFNiUJERIqkRCEiIkVSohARkSIpUYiISJGUKEREpEhKFJI0zKy1mbmZVT7I9t+b2bPlHZdIolOikDJnZulmtt3MqsU6lvzc/W/ufm1ZHtPM0sws18wyzWyXmS00s6tL8Pp0MzukmMxskJl9Fr7/ZjP71MzOPpRjFvN+RSbkUhwvzczWlMWxJDqUKKRMmVlr4ETAgSK/rMwspcBymXzxxMA6d68N1AVuA/5tZp3K443N7ELgdWAU0BJoCtwDDCmP95eKQYlCytovgW+AF4Ar828wsxfM7Gkzm2hmu4EBZrbCzO4ys1nAbjOrbGb9zewrM9thZjPNLC3fMdLN7C9m9mX4C3qSmTUuEMNlZrbKzLaY2R/yvfY+M3spfP6TX7FhLKeGz/ua2TQz22lmG83sseIK7oGJwDbg6PA4Dczs3fCX/vbwectw2wMESfXJsEbyZLi+s5l9ZGbbwhrKLwp7PzMz4DHgL+7+rLtnuHuuu3/q7teF+1Qysz+a2Uoz22Rmo8ysXrgtr2Zw5UE+r4N9Bp+F/+4I4z7WzNqZ2X/NbGt4nJfNrH6Bz/b/mdksM8sws1fNrLqZ1QLeB5qHx8o0s+bFfdZSztxdDz3K7AEsAW4C+gBZQNN8214AMoDjCX6kVAdWADOAI4AaQAtgK3BGuM/AcLlJeIx0YCnQMdw/Hfh7uK01QU3m3+G2HsB+4Khw+33AS+HzNGBNgdhXAKeGz78Grgif1wb6H6S8PxwnjPdsIBfoFa5rBFwA1ATqEPz6fyvf69OBa/Mt1wJWA1cDlYFewBagSyHv3Tksb5sizsc14TlpG5bjDWB0hJ9XoZ9BvtdVzvc+7cNzVQ1oQpBMnijw2X4LNAcaAvOBGw52LvSIr4dqFFJmzOwEoBXwmrtPJ/hCv7TAbm+7+5ce/PLdF64b4e6r3X0vcDkw0d0nhvt8BEwjSBx5nnf3ReH+rwE9C7zH/e6+191nAjMJvgBLKgtob2aN3T3T3b8pYt/mZrYD2Au8Cdzu7t8DuPtWdx/v7nvcfRfwAHBSEcc6C1jh7s+7e3Z4nPHAzwvZt1H47/oijncZ8Ji7L3P3TOBu4OICl/kO9nlF/Bm4+xJ3/8jd97v7ZoKaTsFyjnD3de6+DXiHn543iVNKFFKWrgQmufuWcHkMBS4/EfxaLij/ulbAz8PLTjvCL+ATgMPz7bMh3/M9BL92KcH2SAwlqLUsMLOpZnZWEfuuc/f6BG0UI4CT8zaYWU0z+1d46WcnwS/t+gXbZ/JpBfQrUP7LgGaF7Ls1/PfwQrblaQ6szLe8kqCm0jTfuoN9XhF/BmbW1MzGmtnasJwvAQUvCZbFeZEYSNTGQ4kzZlYD+AWQYmZ5XwjVCL4Ue4S/ViG4ZFFQ/nWrCS6NXBe9aAHYTXA5CPihYb3JDwG5LwYuMbNKwPnAODNr5O67D3ZAd99vZncBC83sXHd/C7gD6AT0c/cNZtYT+B6wvJcVOMxq4FN3HxhBGRaG+18A/N9B9llHkHzyHAlkAxsJGr8P6mCfQSExA/wtXN/d3beZ2bnAkxGUgYMcT+KIahRSVs4FcoAuBJcUegJHAZ8TNHBH6iVgiAVdPlPCBs+0vAbgMrQIqG5mZ5pZFeCPBIkNADO73MyauHsusCNcnVvcQd39APAoQc8jCNol9hI0/DYE7i3wko0E7Qd53gU6mtkVZlYlfBxjZkcV8l4O3A78ycyuNrO6YeP1CWY2MtztFeA2M2tjZrUJvtBfdffs4spSxGewOfw3f9x1gEwgw8xaAHcWd/wCn0GjvEZ2iT9KFFJWriRoO1jl7hvyHgS/Ki+zCLu+uvtq4Bzg9wRfSKsJvnTK9G/V3TMIGt2fBdYS1DDy94IaDMw1s0xgOHBx2CYSieeAI81sCPAEQUPxFoLeYB8U2Hc4cGHYI2pE2I5xGnAxQW1gA/AQ+ZJYgXKMAy4iaLReR/Cl+1fg7XyxjCa45LUc2Af8OsJyFPoZuPsegraWL8PLY/2B+4HeBJ0V3iNoNI+Iuy8gSGjLwuOp11OcseBHiYiISOFUoxARkSIpUYiISJGUKEREpEhKFCIiUqSkvI+icePG3rp161iHEZHdu3dTq1atWIcRFSpb4krm8qlshZs+ffoWd29S2LakTBStW7dm2rRpsQ4jIunp6aSlpcU6jKhQ2RJXMpdPZSucma082DZdehIRkSIpUYiISJGSKlGY2RAzG5mRkRHrUEREkkZSJQp3f8fdh9WrpyFjRETKSlIlChERKXtKFCIiUiQlChERKZIShYhIEpi+cjvjFx2IyrGT8oY7EZGKwN35bPEW/vnJEqYs30atKrBp5z4Oq1u9TN9HiUJEJMHk5DofzNnA058uYc7anTSrW50/nnkULfevLPMkAUoUIiIJ40B2Lm/NWMsz6UtZtmU3bRrX4qELunNurxZUq5xCevqqqLxvUiWKcOrJIe3bt491KCIiZWZfVg5jv13FyM+WsS5jH10Or8tTl/ZmcLdmpFSyqL9/UiUKd38HeCc1NfW6WMciInKodu3L4qVvVvGfL5axJfMAqa0a8MD53Unr2ASz6CeIPEmVKEREksH23Qd4/svlvPDVCnbuy+ZnHZvwq7R29GvbKCbxKFGIiMSJTbv28Z/PlzP6m5XsOZDDoK5N+dWA9hzdsn5M41KiEBGJsXU79jLys2W88u0qsnJyGdKjOTeltadTszqxDg1QohARiZlVW/fw9KdLGDd9De5wfu8W3JjWnjaN42sGPiUKEZFytmxzJk99spS3ZqwlxYyLjjmCG05qR8sGNWMdWqGUKEREysnijbt48pMlvDNzHVVSKvHLY1tx/c/a0axe2d8kV5aUKEREomzBhp38479LmDh7PTWqpHDdiW259sS2NKlTLdahRUSJQkQkSuat28mIyYv5YO4GalerzE1p7Rh6Qlsa1qoa69BKRIlCRKSMzVmbwYjJi5k0byN1qlXmllM6MPT4NtSrWSXWoZWKEoWISBmZszaDJz5ezMfzN1KnemV+c0oHrkngBJFHiUJE5BDlTxB1q1fm9oEduer41tStntgJIo8ShYhIKc1Zm8HwyYv5aF6QIO4Y2JErkyhB5In7RGFmbYE/APXc/cJYxyMiMnddUIPISxDJVoMoKCaJwsyeA84CNrl7t3zrBwPDgRTgWXf/u7svA4aa2bhYxCoikmfBhp088VHQi6lO9crcdmqQIOrVSM4EkSdWNYoXgCeBUXkrzCwFeAoYCKwBpprZBHefF5MIRURCizfu4onJi3lv1nrqVAsbqU9ok/QJIo+5e2ze2Kw18G5ejcLMjgXuc/dB4fLdAO7+YLg8rqhLT2Y2DBgG0LRp0z5jx46NavxlJTMzk9q1a8c6jKhQ2RJXMpevJGVbn5nL20sPMGV9DtVSYGDrKgxqVYXaVctvLoiSOJTzNmDAgOnunlrYtnhqo2gBrM63vAboZ2aNgAeAXmZ2d17iKMjdRwIjAVJTUz0tLS3K4ZaN9PR0EiXWklLZElcyly+Ssq3cupvhkxfz1vdrqV4lhRvS2nHdifF/o1y0zls8JYpCuftW4IZI9tVUqCJyKNbu2MuT/13M69PWkFLJGHpCG64/qR2NayfGUBvREk+JYi1wRL7lluG6iGkqVBEpjY079/HUJ0sY+21wUePy/q24Ka0dh9WN78H6yks8JYqpQAcza0OQIC4GLo1tSCKSzLbtPsDT6UsY9fVKcnKdn6cewa9Pbk/z+jViHVpciVX32FeANKCxma0B7nX3/5jZzcCHBN1jn3P3uSU8ri49iUixdu7L4tnPlvGfL5azNyuHc3u14NZTOnJko/icDyLWYpIo3P2Sg6yfCEw8hOPq0pOIHNSeA9m8u+wAv/n0EzL2ZnFG92bcPrAj7Q+LjylH41U8XXoSEYmK/dk5vDJlFU9+spQtmVkM6NSEO07rRLcW9WIdWkJIqkShS08ikl92Ti5vfr+WJz5ezNode+nXpiHXdzWuO69vrENLKJViHUBZcvd33H1YvXr6lSBSkbk7E2evZ9ATn3HnuFk0ql2V0UP7MnZYfzo0SIl1eAknqWoUIlKxuTufL97CIx8uZPbaDNofVptnLu/NoK7NMIvPu6kTgRKFiCSF71dt5+EPFvL1sq20qF+D//t5D87r1YKUSkoQhyqpEoXaKEQqniWbdvHIhwv5cO5GGtWqyn1DunBJvyOpVlmXmMpKUiUKdY8VqTjW7djLEx8vYtz0NdSsGgz5PfTENtSullRfa3FBn6iIJJQdew7wz/SlvPDVCnC4+vg23JTWjkYVfDymaFKiEJGEsPdADs9/tZyn05eSuT+b83u15LaBHWjZQHdTR1tSJQq1UYgkn+ycXMZNX8PjHy9i4879nNL5MO4c3InOzerGOrQKI6kShdooRJKHu/PRvI089MEClm7eTa8j6zPi4l70a9so1qFVOEmVKEQkOUxfuZ0HJ85n2srttG1Si2cu78Ogrk11L0SMKFGISNxYtjmThz9YyAdzN9CkTjUeOK8bF6UeQeWUpBpEIuEoUYhIzG3etZ/hkxfxyrerqV65ErcP7Mi1J7ahZlV9RcUDnQURiZm9B3J49vNlPPPpUvZn53JZvyO55ZQOFX7q0XiTVIlCvZ5EEkNOrjN++hoe/WghG3fuZ3DXZvx2cCfaNqkd69CkEEmVKNTrSSS+uTufLtrM399fwIINu+h1ZH2eurQ3qa0bxjo0KUJSJQoRiV/z1+/kbxPn8/niLbRqVJN/Xtab07tpVNdEoEQhIlG1cec+Hpu0iNemr6ZejSrcc1YXLu/fiqqV1ZMpURSZKMzs9giOsdvd/1VG8YhIkthzIJuRny3jX58uIzs3l2tPaMPNAzpQr2aVWIcmJVRcjeJO4GmgqLrhDYAShYgAYUP1d2t4dFLQUH1m98O5a3BnjmykMZkSVXGJYrS7/7moHcysVhnGc0jU60kktr5eupW/vDuPeet30vMINVQniyIThbv/trgDRLJPeVGvJ5HYWL5lNw9OnM+keRtpUb8Gwy/uydk9mquhOklE1JhtZtWAC4DW+V9TXG1DRJJbxp4sRvx3MaO+XkHVlErcOagTQ09oQ/Uqml0umUTa6+ltIAOYDuyPXjgikgiyc3J55dtVPPbRInbszeKi1CO4/bSOHFaneqxDkyiINFG0dPfBUY1ERBLCZ4s285d357F4Uyb92zbkT2d1oWvzerEOS6Io0kTxlZl1d/fZUY1GROLW0s2Z/O29+UxesIlWjWryryv6cFoXDf1dEUSaKE4ArjKz5QSXngxwdz86apGJSFzI2JvFiMmLefGrFVSvksLdp3fmquNbU62y2iEqikgTxelRjUJE4k5OrjN26ioenbSI7XsOcPExR3D7wE40qaORXSua4u7MruvuO4Fd5RSPiMSBBdtyeOgfXzB//U76tmnIvUPUDlGRFVejGAOcRdDbyfnfO7QdaBuluEQkBtZs38ODExfw3ux9tKhvPHVpb87oroH7Krribrg7K/y3TfmEc2h0Z7ZI6ew9kMMzny7lmU+XYgbnta/C3355EjWqqh1CSjB6rJkdzU9vuHsjCjGVmu7MFikZd+f9ORt44L35rN2xl7OOPpzfn3EUi2ZMUZKQH0R6Z/ZzwNHAXCA3XO1AXCUKEYncwg27uG/CXL5etpXOzerw6rD+9GvbCIBFMY5N4kukNYr+7t4lqpGISLnI2JPF4x8vYvQ3K6lTvTJ/ObcblxxzBJVTND+EFC7SRPG1mXVx93lRjUZEoiY313l9+moe+mAhO/Yc4LJ+rbh9YEca1Koa69AkzkWaKEYRJIsN6IY7kYQzc/UO7pkwl5mrd5DaqgH3n9NX3V0lYpEmiv8AVwCz+bGNQkTi3LbdB3jkwwWMnbqaxrWr8fhFPTi3Zwt1d5USiTRRbHb3CVGNRETKTE6uM2bKSv5v0iJ278/m2hPacMspHahTXdOQSslFmii+N7MxwDvkG2Y83rrHighMX7mde96ew9x1OzmuXSPuP7srHZrWiXVYksAiTRQ1CBLEafnWqXusSBzZmrmfhz5YwGvT1tCsbnWevLQXZ3Y/XJeZ5JAVN9bTJcAkd7+6nOIRkRLKyXXGfLuKRz5YwJ4DOVx/UltuObkDtapFfD+tSJGK+0s6EnjdzKoAk4H3gW/d3aMemYgUa8bqHfzprTnMXpvBce0a8edzutL+MF1mkrJV3FhPDwEPmVkd4FTgGuAZM5sPfAB86O4box+miOS3Y88BHv5wIa98u4omtasx4pJeDDlal5kkOiKqm7r7LuDN8IGZdSGYo2IUMChq0QXvVQv4J3AASHf3l6P5fiLxzN0ZN30ND76/gIy9WVxzfBtuPVW9mSS6SnUR093nmVmuuz9amteHY0edBWxy92751g8GhgMpwLPu/nfgfGCcu79jZq8CShRSIS3YsJM/vTWHqSu20/vI+vz13O50aV431mFJBXAorV2TCNowSuMF4EmCGgkAZpYCPAUMBNYAU81sAtCS4EY/gJzSBiuSqHbvz2b45MX854vl1K1emYcvOJoL+7SkUiVdZpLyUVyvpxEH2wTUL+2buvtnZta6wOq+wBJ3Xxa+91jgHIKk0RKYAWjUMqlQJs3dwH0T5rIuYx8XH3MEdw3urLGZpNxZUR2YzGwXcAf5brLL51F3b1zqNw4Sxbt5l57M7EJgsLtfGy5fAfQD7iKofewDvjhYG4WZDQOGATRt2rTP2LFjSxtaucrMzKR27dqxDiMqVLbS27I3l5fnH+D7TTm0rG1c2bUaHRqU3/wQOneJ6VDKNmDAgOnunlrYtuIuPU0F5rj7VwU3mNl9pYqmhNx9N1DsfRzuPhIYCZCamuppaWlRjqxspKenkyixlpTKVnJZObk898VynvhqMQB3n96Za05oQ5VyHgJc5y4xRatsxSWKCwl+yf9EFKZHXQsckW+5ZbguYpoKVRLZ9JXb+cObs1mwYRenHtWU+87uQssGNWMdlkix91FsK69ACGovHcysDUGCuBi4tCQH0FSokogy9mbxyIcLeHnKKprVrc6/rujDoK7NYh2WyA+KrM+a2cjiDhDJPoW85hXga6CTma0xs6Hung3cDHwIzAdec/e5JT22SKJwd96dtY5TH/uUMVNWcfVxbfjo9pOUJCTuFHfp6VwzK/TSU8iAASV9U3e/5CDrJwITS3q8H4LRpSdJEKu37eFPb88hfeFmurWoy3NXHkP3lppISOJTcYnizgiO8XlZBFIWdOlJ4l12Ti7Pfbmcxz5aRIoZ95zVhV8e20rzVUtcK66N4sXyCkQk2c1ek8Hv3pjF3HU7OfWow/jzOd1oXr9GrMMSKVZSjUOsS08Sj3bvz+axjxbx/JfLaVS7Gk9f1pvB3ZppAD9JGEmVKHTpSeLNJws38cc357B2x14u63ckvx3cmXo1NICfJJaIEoWZ/dzdXy9unYgEtmbu5/535jFh5jraH1ab1284lmNaN4x1WCKlEmmN4m6gYFIobJ1IhebuvPn9Wv7y7jwy92dz66kduDGtHdUql9/wGyJlrbhBAU8HzgBaFBggsC6QHc3ASkNtFBJLq7ft4fdvzubzxVvodWR9HrrgaDo21WxzkviKq1GsA6YBZwPT863fBdwWraBKS20UEgs5uc7zXy7n0UmLqGRw/9ldubx/K1I0DLgkieK6x84EZprZGHfPKqeYRBLGoo27+O24WcxYvYMBnZrw1/O600JdXiXJRNpG0TccLbZV+BoD3N3bRiswkXiWnesM/3gxT36ymDrVqzD84p6c3aO5urxKUoo0UfyH4FLTdOJ4ljm1UUh5mLl6B/d9tZc1mYs4u0dz7h3ShUa1q8U6LJGoiTRRZLj7+1GNpAyojUKiaV9WDo99tIhnP19GvarGs79M5dQuTWMdlkjURZooPjGzR4A3yDfbnbt/F5WoROLMt8u3cdf4WSzfsptL+h7JiXW2KElIhRFpougX/pt/mjwHTi7bcETiy54D2Tz8wUJe/HoFLRvUYMy1/TiufWPS09NjHZpIuYkoUbh7iYcSF0l0Xy3Zwl1vzGL1tr1cdVxr7hzUiVrVkmrUG5GIRPxXb2ZnAl2B6nnr3P3P0QiqtNSYLWVh174sHnx/AWOmrKJN41q8dv2x9G2j4Tek4op0rKdngJoEkxQ9SzCX9rdRjKtU1Jgth+qLxVu4a/ws1mfs5boT23D7wE7UqKrhN6Rii7RGcZy7H21ms9z9fjN7FIj7XlAikdq1L4u/TVzAK9+uom2TWrx+w3H0adUg1mGJxIVIE8Xe8N89ZtYc2AocHp2QRMpX/lrEsJ+15faBHaleRbUIkTyRJop3zaw+8AjwHUGPp2ejFpVIOVAtQiQykSaKh919PzDezN4laNDeF72wRKLrqyVbuHOcahEikYg0UXwN9AYIE8Z+M/sub51IothzIJu/v7+AUV+vpE1j1SJEIlHcfBTNgBZADTPrRTAYIATzUdSMcmwlpu6xUpRpK7Zxx+szWbl1D1cf35rfDuqsHk0iESiuRjEIuApoCTzKj4liF/D76IVVOuoeK4XZl5XDo5MW8uwXy2nZoAZjh/Wnf9tGsQ5LJGEUNx/Fi8CLZnaBu48vp5hEysysNTu4/bWZLNmUyaX9juT3ZxxFbd1dLVIikf6PaWlmdQlqEv8maJv4nbtPilpkIocgKyeXJ/+7hCc/WUKT2tV48Zq+nNSxSazDEklIkSaKa9x9uJkNAhoBVwCjASUKiTuLN+7i9tdmMnttBuf1asF9Q7pSr2aVWIclkrAiTRR5bRNnAKPcfa5pKi+JM7m5znNfLufhDxdSq2oKT1/Wm9O7675QkUMVaaKYbmaTgDbA3WZWB8iNXlgiJbNm+x7ueG0mU5Zv49SjDuNv53fnsDrVi3+hiBQr0kQxFOgJLHP3PWbWCLg6emGJRMbdGf/dWu6bMBeAhy84mp+nttTc1SJlKNL5KHLNbCPQxczUZUTiwrbdB/j9G7P5YO4G+rZuyKO/6MERDePu9h6RhBfpMOMPARcB84CccLUDn0UpLpEifbJgE3eOm0XG3gP87vTOXHdiW1IqqRYhEg2R1g7OBTqFw3fELd2Znfz2HMjmgffm8/KUVXRuVodR1/SlS/O6sQ5LJKlFmiiWAVWAuE4UujM7uc1cvYNbX53Biq27NZCfSDmKNFHsAWaY2WTyJQt3vyUqUYnkk52Ty9PpSxk+eTGH1anGmGv7c2w7DcEhUl4iTRQTwodIuVq9bQ+3vTqDaSu3M6RHc/56TjfdPCdSziLt9fSimVUFOoarFrp7VvTCkoouf7dXA4Zf3JNzeraIdVgiFVKkvZ7SgBeBFQR3aR9hZle6u3o9SZnL2JPF79+azXuz1tO3TUMe+0UPWjZQt1eRWIn00tOjwGnuvhDAzDoCrwB9ohWYVExTlm3ltldnsGnXfu4c1IkbTmqnbq8iMRZpoqiSlyQA3H2RmelCsZSZrJxcnvh4Ef9MX0rrRrUYf+Nx9DiifqzDEhEiTxTTzOxZ4KVw+XJgWnRCkopmxZbd/ObVGcxcvYNfpLbk3iFdqaU5I0TiRqT/G28EfgXkdYf9DHg6KhFJhZHXYH3v23NIqWT887LenKHRXkXiTnFzZjcBmrj7POCx8IGZdSWYN3tz1COUpLRzXxZ/fHMOE2auo1+bhjx+UU+a168R67BEpBCVitn+D6BxIesbAsPLPhypCL5btZ0zR3zOe7PXc+egToy5rr+ShEgcK+7SU/vCusC6++dmpktPUiI5uc4zny7lsY8WcXi96rx2/bH0adUg1mGJSDGKSxR1ithWLr2ezKwt8AegnrtfWB7vKWVvQ8Y+bnt1Bl8v28qQHs154Lxu1K2ujnMiiaC4S09LzOyMgivN7HSCgQKLZGbPmdkmM5tTYP1gM1toZkvM7HdFHcPdl7n70OLeS+LX5PkbOX34Z8xcs4NHLjyaERf3VJIQSSDF1ShuBd4zs18A08N1qcCxwFkRHP8F4ElgVN4KM0sBngIGAmuAqWY2AUgBHizw+mvcfVME7yNxKCvX+fM783juy+V0Obwu/7i0F+2a1I51WCJSQkUmCndfbGbdgUuBbuHqT4Hr3X1fcQd398/MrHWB1X2BJe6+DMDMxgLnuPuDRJZ8JAEs37Kbv36zj5U7l3PVca25+4zOVKusIcFFEpG5e3TfIEgU77p7t3D5QmCwu18bLl8B9HP3mw/y+kbAAwQ1kGfDhFLYfsOAYQBNmzbtM3bs2DIuSXRkZmZSu3Zy/cr+al02o+bup5I51x1dnV6HJd/Nc8l43vJL5vKpbIUbMGDAdHdPLWxb3P8PdvetwA0R7DcSGAmQmprqaWlpUY6sbKSnp5MosRZn9/5s7nl7LuNnraFv64Zc1GovF5x+cqzDiopkOm+FSebyqWwlV1xjdjSsBY7It9wyXHfIzGyImY3MyMgoi8NJCSzYsJOzn/yCN75fwy0nt2fMdf1oVCMWf14iUtYi/p9sZjXMrFMZvOdUoIOZtQnnuLiYMpoUyd3fcfdh9erVK4vDSQTcnbHfruKcJ79k575sXh7aj9tP60TlFCUJkWQR0f9mMxsCzAA+CJd7hj2VinvdK8DXQCczW2NmQ909G7gZ+BCYD7zm7nNLWwCJncz92fxm7Ax+98ZsjmndkIm3nMhx7Qu7kV9EElmkbRT3EfRWSgdw9xlm1qa4F7n7JQdZPxGYGOF7RyxMaEPat29f1oeWAuaszeDmMd+xatse/t9pHbkprT2VNG+ESFKK9PpAlrsXvPAf3e5SpaBLT9Hn7oz+ZiXn//Mr9mXlMnbYsdx8cjRtLZcAABKLSURBVAclCZEkFmmNYq6ZXQqkmFkHguHGv4peWBKPMvdn87vxs3h31npO6tiExy/qScNaVWMdlohEWaQ1il8DXYH9wBggA/hNtIIqLfV6ip7563dy9j++YGI44uvzVx2jJCFSQUSaKM509z+4+zHh44/A2dEMrDR06ans5fVqOvepL8ncn82Y6/rzqwFqjxCpSCJNFHdHuE6SyJ4D2dzx2swfejW9d8uJ9G/bKNZhiUg5K26Gu9OBM4AWZjYi36a6QHY0A5PYWrIpkxtfms6SzZncemoHfn1yB1JUixCpkIprzF4HTCO4zDQ93/pdwG3RCqq01D22bEyYuY7fjZ9F9SopjLqmLyd2aBLrkEQkhoobPXYmMNPMxrh7VjnFVGru/g7wTmpq6nWxjiUR7c/O4W/vzefFr1fSp1UDnry0F4fX0xSlIhVdpN1jW5vZg0AXoHreSndvG5WopNyt2b6HX435npmrd3DtCW246/TOVNEwHCJC5InieeBe4HFgAHA1sRlQUKIgfeEmbn11Bjk5zjOX92Zwt8NjHZKIxJFIv+xruPtkgvkrVrr7fcCZ0QurdHQfRcnk5jqPf7SIq1+YSrO61Znw6xOUJETkJyKtUew3s0rAYjO7mWBY8Lib+UNtFJHbvvsAt746g08Xbeb83i144Nzu1KiqGehE5KciTRS/AWoSDN3xF+Bk4JfRCkqia/aaDG54aTqbd+3ngfO6cWnfIzFT11cRKVxEicLdp4ZPM4GrzSyFYB6JKdEKTKJj7LeruGfCXBrXqsprNxxLzyPqxzokEYlzxd1wVxf4FdCCYHKhj8LlO4BZwMvRDlDKxr6sHO59ey6vTlvNCe0bM+KSXhqrSUQiUlyNYjSwnWDyoWuB3wMGnOfuM6IcW4nphrvCrd2xlxtfms6sNRn8akA7bh/YSXdZi0jEiksUbd29O4CZPQusB450931Rj6wU1Jj9U18u2cKvX/meA9m5jLyiD6d1bRbrkEQkwRSXKH64G9vdc8xsTbwmCflf7s7Iz5bx0AcLaNekNs9c0Yd2TeKuo5qIJIDiEkUPM9sZPjegRrhsgLt73ahGJ6WSuT+b346bycTZGzijezMevrAHtatF2sFNROR/FTfWkzrWJ5hlmzO5fvR0lm7O5O7TOzPsZ23V9VVEDol+ZiaR/y7YyG/GzqByJWP00H4c375xrEMSkSSgRJEEcnOdpz5ZwmMfL6LL4XX51xV9aNmgZqzDEpEkkVSJoiJ2j83cn83tr85g0ryNnNuzOQ+ef7SG4hCRMpVUI8BWtDmzl23O5NynvmTygk386awuPH5RTyUJESlzSVWjqEg+WbCJW175niqVKzF6aF+Oa6f2CBGJDiWKBOPuPP3pUh75cKHaI0SkXChRJJC9B3K4c9xM3p21niE9mvPwBWqPEJHoU6JIEGt37GXYqGnMW7+TuwZ35oaTdH+EiJQPJYoEMGXZVm56+TsOZOfy3JXHMKDzYbEOSUQqECWKOPfylJXc+/ZcjmxYk39fmarxmkSk3ClRxKmsnFz+8u48Rn29krROTRh+cS/q1agS67BEpAJSoohD23cf4FdjvuOrpVu5/mdt+e3gzpo/QkRiJqkSRTLcmb144y6uHTWN9Tv28ejPe3BBn5axDklEKjjdmR1H/rtgI+f98yt2789h7PX9lSREJC4kVY0iUeVNMvT3DxbQtXld/v3LVA6vVyPWYYmIAEoUMZeV69w5bhbjpq/hzKMP5/8u7KGb6EQkrihRxNDWzP08MnUfi7av4dZTO/CbUzroJjoRiTtKFDGycMMuhr44lY0Zufzjkl4M6dE81iGJiBQqqRqzE8UnCzZxwdNfcSA7l7v7VVeSEJG4pkRRjtydZz9fxtAXp9KqUU3evvl42tZTe4SIxDddeionWTm53DthLmOmrGJQ16Y8flFPalatzMJYByYiUgwlinKQsTeLm8d8x+eLt3BjWjvuPK0TlXSntYgkCCWKKFu1dQ/XvDiVFVt28/CFR/OL1CNiHZKISIkoUUTRtBXbGDZ6Ojm5zuih/Ti2XaNYhyQiUmJKFFHy9oy13Pn6LFo0qMF/rkylrYYHF5EEFfeJwszOBc4E6gL/cfdJMQ6pSO7OiMlLePzjRfRr05BnLu9Dg1pVYx2WiEipRbV7rJk9Z2abzGxOgfWDzWyhmS0xs98VdQx3f8vdrwNuAC6KZryH6kB2Lv/v9Vk8/vEizu/dgtFD+ylJiEjCi3aN4gXgSWBU3gozSwGeAgYCa4CpZjYBSAEeLPD6a9x9U/j8j+Hr4lLGniyuf2ka3yzbxm2nduSWU9prOA4RSQrm7tF9A7PWwLvu3i1cPha4z90Hhct3A7h7wSSR93oD/g585O4fF/E+w4BhAE2bNu0zduzYMixF0TbtyeXx6fvYvMe5pns1jmseef7NzMykdu3kbL9Q2RJXMpdPZSvcgAEDprt7amHbYtFG0QJYnW95DdCviP1/DZwK1DOz9u7+TGE7uftIYCRAamqqp6WllU20xfhu1XbueHEa2bmVefm6PvRrW7KeTenp6ZRXrOVNZUtcyVw+la3k4r4x291HACNiHUdh3p+9nltfnUHTutV5/upjaKeeTSKShGIx1tNaIP9dZy3DdYfMzIaY2ciMjIyyOFyRnv18GTeN+Y6uzevy5k3HKUmISNKKRaKYCnQwszZmVhW4GJhQFgcuj6lQc3Kd+9+Zy1/fm8+gLs0Yc11/GtWuFrX3ExGJtWh3j30F+BroZGZrzGyou2cDNwMfAvOB19x9bjTjKCt7D+Rw08vTef7LFQw9oQ1PXdab6lU0+quIJLeotlG4+yUHWT8RmFjW72dmQ4Ah7du3L+tDszVzP9eOmsaM1Tu456wuXHNCmzJ/DxGReJRU81FE69LT8i27Of/pr5i3bidPX9ZHSUJEKpS47/UUa9+v2s7QF6cB8Mqw/vQ+skGMIxIRKV9JVaMo615Pk+dv5JJ/f0PtapUZf+NxShIiUiElVaIoy0tPr3y7iutGTaNj0zqMv/E42jSuVQYRiogkHl16KsDdefzjxYyYvJi0Tk146tLe1Kqmj0lEKi59A+aTlZPLH96czWvT1vCL1JY8cF53qqQkVaVLRKTEkipRHEr32APZuVw/ehqfLNzMLSe357aBHTX6q4gIaqP4QZUUo3XjWvztvO7cflonJQkRkVBS1SgOhZlx75CusQ5DRCTuJFWNQkREyl5SJYryHD1WRKSiSKpEUR6jx4qIVDRJlShERKTsKVGIiEiRlChERKRISZUo1JgtIlL2kipRqDFbRKTsmbvHOoYyZ2abgZWxjiNCjYEtsQ4iSlS2xJXM5VPZCtfK3ZsUtiEpE0UiMbNp7p4a6ziiQWVLXMlcPpWt5JLq0pOIiJQ9JQoRESmSEkXsjYx1AFGksiWuZC6fylZCaqMQEZEiqUYhIiJFUqIQEZEiKVFEkZlVN7NvzWymmc01s/vD9W3MbIqZLTGzV82sari+Wri8JNzeOpbxF6WIsr1sZgvNbI6ZPWdmVcL1ZmYjwrLNMrPesS1B0Q5WvnzbR5hZZr7lZDh3ZmYPmNkiM5tvZrfkW58Q566Isp1iZt+Z2Qwz+8LM2ofrE+a85TGzFDP73szeDZej/33i7npE6QEYUDt8XgWYAvQHXgMuDtc/A9wYPr8JeCZ8fjHwaqzLUIqynRFuM+CVfGU7A3g/XN8fmBLrMpSmfOFyKjAayMy3fzKcu6uBUUClcNthiXbuiijbIuCofOfqhUQ7b/nKeDswBng3XI7694lqFFHkgbxfnVXChwMnA+PC9S8C54bPzwmXCbefYnE6effByubuE8NtDnwLtAz3OQcYFW76BqhvZoeXf+SROVj5zCwFeAT4bYGXJPy5A24E/uzuueF+m8J9EubcFVE2B+qG6+sB68LnCXPeAMysJXAm8Gy4bJTD94kSRZSF1cQZwCbgI2ApsMPds8Nd1gAtwuctgNUA4fYMoFH5Rhy5gmVz9yn5tlUBrgA+CFf9ULZQ/nLHpYOU72ZggruvL7B7Mpy7dsBFZjbNzN43sw7h7gl17g5StmuBiWa2huDv8u/h7gl13oAnCH6k5IbLjSiH7xMliihz9xx370nwy7ov0DnGIZWZgmUzs275Nv8T+MzdP49NdIeukPL9DPg58I/YRnboDnLuqgH7PBgC4t/Ac7GMsbQOUrbbgDPcvSXwPPBYLGMsDTM7C9jk7tPL+72VKMqJu+8APgGOJai6Vw43tQTWhs/XAkcAhNvrAVvLOdQSy1e2wQBmdi/QhOBaap4fyhbKX+64lq98A4D2wBIzWwHUNLMl4W7JcO7WAG+Em94Ejg6fJ+S5y1e204Ee+Wq8rwLHhc8T6bwdD5wd/u2NJbjkNJxy+D5RoogiM2tiZvXD5zWAgcB8gj/eC8PdrgTeDp9PCJcJt/83vNYfdw5StgVmdi0wCLgk71p3aALwy7AHTX8go5DLN3HjIOWb7u7N3L21u7cG9rh7+/AlCX/ugLcIkiHASQQNwJBA566I/3P1zKxjuFveOkig8+bud7t7y/Bv72KCWC+jPL5PDqX1XY9ieyccDXwPzALmAPeE69sSNPQuAV4HqoXrq4fLS8LtbWNdhlKULZugHWZG+Mhbb8BT4bbZQGqsy1Ca8hXYJ3+vp2Q4d/WB98Lz8zXBr/CEOndFlO28MPaZQHre+Umk81agnGn82Osp6t8nGsJDRESKpEtPIiJSJCUKEREpkhKFiIgUSYlCRESKpEQhIiJFUqKQmDGzc83MzaxzvnVpeaNiHuKxXzCzC4vZJ83MjitqnwL7DwpHH51hZpkWjJI7w8xGHWq80WBmV5lZ8ygee7OZ5Y059D/nzcz+amYfhCOYvmxm24o7HxK/lCgkli4Bvgj/jYU0frxDt1ju/qG79/RgeIhpwGXh8i+jFWBxwkEKD+YqoESJIt8dvpF41d2vLeQYfyS4i/g8d9/vwU1hE0oSh8QXJQqJCTOrDZwADCW4yzS/umb2XviL/RkzqxQO9PaCBfNczDaz28Lj9DSzbyyYJ+FNM2tQyHutMLPG4fNUM0sPx+a/AbgtrBWcGN7VO97MpoaP4yMsy+UWzIEww8z+lfflHdY6HrFgXoSPzaxv+N7LzOzscJ+rzOztcP3icPiTSI77qJnNBI41s3vCeOeY2cjwDuoLCYZDfzl8fY3CPofw+X1mNtrMvgRGl/ZzCI91B8GQGUPcfW+kr5P4pkQhsXIO8IG7LwK2mlmffNv6Ar8GuhCMaHo+0BNo4e7d3L07wcBuEMyfcJe7H01w5+29RMDdVxCM3f94WCv4nGDcnMfd/RjgAsKhnItiZkcBFwHHhzWNHOCycHMtgmETugK7gL8SDB9xHvDnAuW9gOCu4p+HX+LFHXeKu/dw9y+AJ939GHfvBtQAznL3cfxvrae4L+0uwKnufklpPofQ8QTJ93T/cahvSQIlqWaKlKW8LyQIBji7BMgbFfNbd18GYGavENQ8JgNtzewfBMNMTDKzekB9d/80fN2LBEMWlNapQBf7ccj+umZWu5gvvVOAPsDU8HU1CIa3BjjAj8Oszwb2u3uWmc0GWuc7xkfuvhXAzN4gKG92EcfNAcbne/0AM/stUBNoCMwF3om82EAwdHpeMinN5wDBUBENCJLh+GL2lQSiRCHlzswaEox82d3MHEghmBToznCXguPKuLtvN7MeBAMO3gD8gmDo6Ehk82PtuXoR+1UimMVuX4THhWAcpBfd/e5CtmX5j2Pk5AL7Adw9t0BbwE/KW8xx97l7DgRTfxIM6Z7q7qvN7D4OXsaiPofd+Z6X5nMA2EhQ65lsZtvc/ZMSvl7ilC49SSxcCIx291YejMR6BLAcODHc3teCeYArEVx++SK8tl7J3ccDfwR6u3sGsN3M8l53BfApP7WC4Nc5BJdS8uwC6uRbnkRwyQsI2j8iKMtk4EIzOyx8TUMzaxXB6/IbGL6uBsHsZF+W4Lh5X/hbwnaf/D2LCpZvBYV/DgWV5nMAILyUeD7wUkleJ/FNiUJi4RKC+Q7yG8+PvZ+mAk8SDAW9PNy3BZBuwcxlLwF5v7SvBB4xs1kE7Rj5r/3nuR8YbmbTCC7b5HkHOC+vMRu4BUgNG8bnEdRciuTu8wgS16Qwho+Akk4T+i1B+WcB4919WqTH9WDOhX8TjJT6IcFnl+cF4Jm8xmwO/jkUVOLPoUBMUwnm355gZu1K8lqJTxo9ViSGzOwqgstGN8c6lpIoadxm9gLBsNjjittX4o9qFCJSGnuB0y284a4oZvYywURIJW3zkDihGoWIiBRJNQoRESmSEoWIiBRJiUJERIqkRCEiIkVSohARkSL9fwVLZkXTg5NnAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"Ea = 72750 # activation energy J/gmol\n",
"R = 8.314 # gas constant J/gmol/K\n",
"k0 = 7.2e10 # Arrhenius rate constant 1/min\n",
"\n",
"# Arrhenius rate expression\n",
"def k(T):\n",
" return k0*np.exp(-Ea/R/T)\n",
"\n",
"T = np.linspace(290, 400)\n",
"plt.semilogy(T, k(T))\n",
"plt.xlabel('Absolute Temperature [K]')\n",
"plt.ylabel('Rate Constant [1/min]')\n",
"plt.title('Arrenhius Rate Constant')\n",
"plt.grid();"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.3 Arrehenius Law Kinetics for a First-Order Reaction](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.3-Arrehenius-Law-Kinetics-for-a-First-Order-Reaction)",
"section": "7.4.3 Arrehenius Law Kinetics for a First-Order Reaction"
}
},
"source": [
"This graph shows the reaction rate changes by three orders of magnitude over the range of possible operating temperatures. Because an exothermic reaction releases heat faster at higher temperatures, there is a positive feedback that can potentially result in unstable process behavior."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.4 Modeling and Parameter Values](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4-Modeling-and-Parameter-Values)",
"section": "7.4.4 Modeling and Parameter Values"
}
},
"source": [
"## 7.4.4 Modeling and Parameter Values"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.4.1 Mathematical Model](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4.1-Mathematical-Model)",
"section": "7.4.4.1 Mathematical Model"
}
},
"source": [
"### 7.4.4.1 Mathematical Model\n",
"\n",
"The model consists of mole and energy balances on the contents of the well-mixed reactor.\n",
"\n",
"\\begin{align*}\n",
"V\\frac{dc_A}{dt} & = q(c_{Ai}-c_A)-Vkc_A \\\\\n",
"V\\rho C_p\\frac{dT}{dt} & = wC_p(T_i-T) + (-\\Delta H_R)Vkc_A + UA(T_c-T)\n",
"\\end{align*}\n",
"\n",
"which are the equations that will be integrated below.\n",
"\n",
"| Quantity | Symbol | Value | Units | Comments |\n",
"| :------- | :----: | :---: | :---- | |\n",
"| Activation Energy | $E_a$ | 72,750 | J/gmol | |\n",
"| Arrehnius pre-exponential | $k_0$ | 7.2 x 1010 | 1/min | |\n",
"| Gas Constant | $R$ | 8.314 | J/gmol/K | |\n",
"| Reactor Volume | $V$ | 100 | liters | |\n",
"| Density | $\\rho$ | 1000 | g/liter | |\n",
"| Heat Capacity | $C_p$ | 0.239 | J/g/K | |\n",
"| Enthalpy of Reaction | $\\Delta H_r$ | -50,000 | J/gmol | |\n",
"| Heat Transfer Coefficient | $UA$ | 50,000 | J/min/K | |\n",
"| Feed flowrate | $q$ | 100 | liters/min | |\n",
"| Feed concentration | $c_{A,f}$ | 1.0 | gmol/liter | |\n",
"| Feed temperature | $T_f$ | 350 | K | |\n",
"| Initial concentration | $c_{A,0}$ | 0.5 | gmol/liter | |\n",
"| Initial temperature | $T_0$ | 350 | K | |\n",
"| Coolant temperature | $T_c$ | 300 | K | Primary Manipulated Variable |"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.4.2 Pyomo Model](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4.2-Pyomo-Model)",
"section": "7.4.4.2 Pyomo Model"
}
},
"source": [
"### 7.4.4.2 Pyomo Model"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.4.2 Pyomo Model](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.4.2-Pyomo-Model)",
"section": "7.4.4.2 Pyomo Model"
}
},
"outputs": [],
"source": [
"# reaction and physical properities parameters\n",
"Ea = 72750 # activation energy J/gmol\n",
"R = 8.314 # gas constant J/gmol/K\n",
"k0 = 7.2e10 # Arrhenius rate constant 1/min\n",
"dHr = -5.0e4 # enthalpy of reaction [J/mol]\n",
"rho = 1000.0 # density [g/L]\n",
"Cp = 0.239 # heat capacity [J/g/K]\n",
"UA = 5.0e4 # heat transfer [J/min/K]\n",
"\n",
"# reactor operating parameters\n",
"V = 100.0 # volume [L]\n",
"q = 100.0 # flowrate [L/min]\n",
"cAi = 1.0 # inlet feed concentration [mol/L]\n",
"Ti = 350.0 # inlet feed temperature [K]\n",
"Tc = 300.0 # coolant temperature [K]\n",
"\n",
"# simulation parameters\n",
"cA0 = 0.5 # initial concentration [mol/L]\n",
"T0 = 350.0 # initial temperature [K]\n",
"t_initial = 0.0 # initial time\n",
"t_final = 10.0 # final time\n",
"\n",
"def cstr(cA0=cA0, T0=T0):\n",
" \"\"\"Return a pyomo model with specified initial conditions.\"\"\"\n",
" \n",
" # create a model instance\n",
" model = ConcreteModel()\n",
" \n",
" # define independent variable\n",
" model.t = ContinuousSet(bounds=(t_initial, t_final))\n",
" \n",
" # define dependent variables\n",
" model.cA = Var(model.t)\n",
" model.T = Var(model.t)\n",
" \n",
" # define derivatives of the dependent variables\n",
" model.dcA = DerivativeVar(model.cA)\n",
" model.dT = DerivativeVar(model.T)\n",
"\n",
" # set initial conditions\n",
" model.cA[0.0] = cA0\n",
" model.T[0.0] = T0\n",
" \n",
" # define constraints using model equations\n",
" def k(T):\n",
" return k0*exp(-Ea/R/T)\n",
" model.ode1 = Constraint(model.t, rule=lambda model, t: \n",
" V*model.dcA[t] == q*(cAi - model.cA[t]) - V*k(model.T[t])*model.cA[t])\n",
" model.ode2 = Constraint(model.t, rule=lambda model, t: \n",
" V*rho*Cp*model.dT[t] == q*rho*Cp*(Ti - model.T[t]) + (-dHr)*V*k(model.T[t])*model.cA[t] + UA*(Tc - model.T[t]))\n",
"\n",
" return model"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.5 Simulation and Visualization](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5-Simulation-and-Visualization)",
"section": "7.4.5 Simulation and Visualization"
}
},
"source": [
"## 7.4.5 Simulation and Visualization"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.1 Simulation](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.1-Simulation)",
"section": "7.4.5.1 Simulation"
}
},
"source": [
"### 7.4.5.1 Simulation"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.1 Simulation](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.1-Simulation)",
"section": "7.4.5.1 Simulation"
}
},
"outputs": [],
"source": [
"tsim, ysim = Simulator(cstr(), package='scipy').simulate(numpoints=100)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.2 Visualization Functions](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.2-Visualization-Functions)",
"section": "7.4.5.2 Visualization Functions"
}
},
"source": [
"### 7.4.5.2 Visualization Functions"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 3,
"link": "[7.4.5.2 Visualization Functions](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.5.2-Visualization-Functions)",
"section": "7.4.5.2 Visualization Functions"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtMAAAHwCAYAAABkJOM0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeXxU5fX48c/JHrIBCZCQBBLZFwUkIoJL3Hdp3bW1aqW2v2pra7V28evWxfZbq9YufmvVum91RcW1GBf2HdlFCJAEJIQkkD2ZOb8/5gaHGMJMMlvG83697ouZO/feOY/gM888c+55RFUxxhhjjDHG+C8m3AEYY4wxxhjTW9lg2hhjjDHGmG6ywbQxxhhjjDHdZINpY4wxxhhjuskG08YYY4wxxnSTDaaNMcYYY4zpJhtMGxMmIjJEROpEJDbcsRhjjDGme2wwbcJGRC4XkSXOgHKHiLwlIseGO66ORKRARFRE4np4nVIROaX9uapuU9VUVXX1PEpjjAkNp89u39wi0uj1/Fvhjq87OvbPxvjDBtMmLETkRuB+4PfAIGAI8A9gRjjj6q6eDrSNMaa3cCYBUlU1FdgGnOu17+lwx9dRKPpn+wz4erPBtAk5EckA7gKuU9WXVbVeVVtV9XVVvVlEEkXkfhGpcLb7RSTRObdYRMpE5GcissuZ0b7a69rJIvJnEdkqIrUi8omIJDuvTRWReSJSIyIrRaTY67wSEfmNiMwVkX0i8q6IZDkvf+T8WePMvBwjIlc5x94nIlXAHSIyTETmiEiViOwWkadFpK9z/SfxfGF43bnGzzvOeIvIYBGZJSJ7RGSTiHzPK747ROQFEXnCiW+NiBQF6+/IGGP8JSIxIvILEfnc6QdfEJH+zmvt/d3VIrJdRKpF5AcicpSIrHL65b95Xau9j/2b05evF5GTvV7PEJFHnM+AchH5bXvKXID652IRKevQvv2z106f/KKIPCUie4GruorJRDcbTJtwOAZIAl45yOu/BqYCE4EJwBTgVq/Xs4EMIBe4Bvi7iPRzXrsHmAxMA/oDPwfcIpILvAn81tl/E/CSiAzwuu7lwNXAQCDBOQbgeOfPvs7My3zn+dHAZjwz678DBLgbGAyMAfKBOwBU9QoOnMH5307a/RxQ5px/IfB7ETnJ6/XznGP6ArOAv33lCsYYEz4/Ar4BnICnH6sG/t7hmKOBEcAleH6d/DVwCjAOuFhETuhw7OdAFnA78HL74Bx4DGgDhgOTgNOAmR3ODWT/3JkZwIt4+uSnfYjJRCkbTJtwyAR2q2rbQV7/FnCXqu5S1UrgTuAKr9dbnddbVXU2UAeMEpEY4LvADaparqouVZ2nqs3At4HZqjpbVd2q+h6wBDjL67r/VtWNqtoIvIBnMN+VClX9q6q2qWqjqm5S1fdUtdmJ+148HyqHJCL5wHTgFlVtUtUVwMPAd7wO+8SJ3wU8ieeLhjHGRIofAL9W1TKn370DuLBDCsRvnD7uXaAeeNbp68uBj/EMQtvtAu53+vrngQ3A2SIyCE/f/RPnl81dwH3ApV7nBqx/7sJ8VX1VVd1Aug8xmShlOT4mHKqALBGJO8iAejCw1ev5Vmff/vM7nNcApOKZvUjCM5PR0VDgIhE512tfPPCB1/OdnVyzK9u9nzgd/F+A44A0PF9Wqw9xjXaDgT2qus9r31bAO5WjY3xJXfw3NMaYUBsKvCIibq99Ljyzw+2+8Hrc2Mlz7363XFXV63n7Z8FQPP33DhFpfy2GA/vkQPbPB+P9Hr7EZKKUzUybcJgPNOP5ObAzFXg6pnZDnH2HshtoAoZ18tp24ElV7eu1pajqH3y4rvq4//fOvsNVNR3PbLh0cby3CqC/iKR57RsClPsQnzHGRILtwJkd+tkkZ9a5O3LFa2TKl58F2/F8hmR5vU+6qo7zOran/XM90Kf9iZP7PKDDMd7n+BKTiVI2mDYhp6q1wG14cp2/ISJ9RCReRM4Ukf8FngVuFZEBzk2AtwFP+XBdN/AocK9zM1+sc7NgonP+uSJyurM/ybnBJM+HkCsBN3DYIY5Lw5NyUuvkaN/c4fUvDnYNVd0OzAPudmI7Ak8++CHbbYwxEeL/gN+JyFAApw/vSYWmgcCPnc+Hi/DkOs9W1R3Au8CfRSTdufFxWId864787Z834vn172wRicdz307iwS7ezZhMlLDBtAkLVf0zcCOeDqoSz7f664FX8dwkuARYBXwKLHP2+eIm55zFwB7gj0CMM1idAfzK6/1uxof/B1S1Ac8NLHOdO86nHuTQO4EjgVo8Nzu+3OH1u/F8SagRkZs6ngxcBhTgmXl5BbhdVd8/VHzGGBMh/oLn5uh3RWQfsADPjYDdtRDPzYq78fTBF6pqlfPad/DcKL4WT7rGi0BOF9fyq392Jn1+iOfelXI8M9VldM3fmEyUkAPTkYwxxhhjwktErgJmqmrELeRlTEc2M22MMcYYY0w3hWQwLSKPimeBjdUHeV1E5AHxLFSxSkSODEVcxhhjjDHG9ESoZqYfA87o4vUz8eRFjQCuBR4MQUzGGGOMiUCq+pileJjeIiSDaVX9CM/NYAczA3hCPRYAfUXEkvaNMcYYY0xEi5Sc6VwOLGxe5uwzxhhjjDEmYvW6FRBF5Fo8qSAkJydPzs/P9/sabrebmJhI+R4RWNHcNoju9lnbeq/utG/jxo27VbXjIhBRLSsrSwsKCvw+r76+npSUlMAHFAGiuW0Q3e2L5rZBdLevu21bunRpp/12pAymywHvUXEeB1n5TVUfAh4CKCoq0iVLlvj9ZiUlJRQXF/sfZS8QzW2D6G6fta336k77RGRrcKKJXAUFBViffaBobhtEd/uiuW0Q3e3rbtsO1m9HylTRLOA7TlWPqUCts5qQMcYYY4wxESskM9Mi8ixQDGSJSBlwOxAPoKr/B8wGzgI2AQ3A1aGIyxhjjDHGmJ4IyWBaVS87xOsKXBeKWIwxxhhjjAmUSMmZNsYYWltbKSsro6mpKdyh+CUjI4N169Z1+lpSUhJ5eXnEx8eHOCpjjAmuaOyzwf9+2wbTxpiIUVZWRlpaGgUFBYhIuMPx2b59+0hLS/vKflWlqqqKsrIyCgsLwxCZMcYET7T12dC9fjtSbkA0xhiamprIzMzsVZ1yV0SEzMzMXjdrY4wxvoi2Phu612/bYNoYE1GiqVOG6GuPMcZ4i8Y+zt822WDaGGMcTU1NTJkyhQkTJjBu3Dhuv/12ALZs2cLRRx/N8OHDueSSS2hpaQHgscceY8CAAUyfPp2JEyfy8MMPhzP8gBCRWBFZLiJvdNj/gIjUeT1PFJHnRWSTiCwUkYJQx2qMMd3ptwsLC5k4cWLA+m0bTBtjjCMxMZE5c+awcuVKVqxYwdtvv82CBQu45ZZb+OlPf8qmTZvo168fjzzyyP5zLrnkEubOncuKFSuYOXNmGKMPmBuAA+7MEZEioF+H464BqlV1OHAf8MfQhGeMMV/qTr99/vnns2LFioD12zaYNsYYh4iQmpoKeO5Sb21tRUSYM2cOF154IQBXXnklr776ajjDDBoRyQPOBh722hcL/An4eYfDZwCPO49fBE6WaPy91xgT0SKh37ZqHsaYiHTn62tYW7E3oNccOzid288d1+UxLpeLyZMns2nTJq677jqGDRtG3759iYvzdJd5eXmUl5fvP/6ll16ipKSE0aNHc99995Gfnx/QmEPsfjyDZu/b3K8HZqnqjg5j5VxgO4CqtolILZAJ7A5RrMaYCBKuPhv877dnzZrFggULGDlyZED6bRtMG2OMl9jYWFasWEFNTQ3f/OY3Wb9+/UGPPffcc7nssstoaWnhmWee4corr2TOnDkhjDZwROQcYJeqLhWRYmffYOAiPCvYdve61wLXAgwaNIiSkhK/r1FXV9et83qDaG4bRHf7orlt4Fv7MjIy2LdvHwCtLa24XK6AxtDa0rr/+ofy8ccfU1NTw7e+9S2WLVuG2+3ef25dXd3+58XFxaxcuZI+ffrw6KOP8u1vf5s33njjK9dramry+e/XBtPGmIjky2xEMPXt25cTTzyR+fPnU1NTQ1tbG3FxcZSVlZGbmwtAZmYmAC0tLcycOZOf/7xjJkSvMh04T0TOApKAdGAN0Axscmal+4jIJidPuhzIB8pEJA7IAKo6XlRVHwIeAigqKtLi4mK/AyspKaE757Vbtq2ajOR4hg1I7fY1gqWnbYt00dy+aG4b+Na+devW7a/X/NsLJoYgqq6lpaVxyimnsHLlSvbu3UtycjJxcXHU1NSQn59PWloaaWlp++tMX3/99dx2222d1pxOSkpi0qRJPr2v5UwbY4yjsrKSmpoaABobG3nvvfcYM2YMJ554Ii+++CIAjz/+ODNmzABgx44d+8+dNWsWY8aMCX3QAaKqv1TVPFUtAC4F5qhqP1XNVtUCZ3+DM5AGmAVc6Ty+0DleQx64D255cRV3zz74amfGmN4rEvptm5k2xhjHjh07uPLKK3G5XLjdbi6++GLOOeccxo4dy6WXXsqtt97KpEmTuOaaawB44IEHmDVrFjExMWRlZfHYY4+FtwGh9QjwpIhsAvbgGYBHpLrmNjbvrg93GMaYIOhOv/3qq6+SkJBA//79A9Jv22DaGGMcRxxxBMuXL//K/sMOO4xFixZ9Zf/dd9/N3Xff3eXStL2RqpYAJZ3sT/V63IQnnzriNbW62F3XjMutxMZYwRFjokl3+u1f/epXAe2zLc3DGGNMVGtqddPqUipqGsMdijEmCtlg2hhjTNRSVRpbPRUGSqss1cMYE3g2mDbGGBO1mtvc+x+XVjWEMRJjTLSywbQxJqJEaEGIbou29vQ2Ta1f1r0ttZsQjQm4aOzj/G2TDaaNMREjKSmJqqqqqOmcVZWqqiqSkpLCHcrXVlPrlzPTWy3Nw5iAirY+G7rXb1s1D2NMxMjLy6OsrIzKyspwh+KXpqamg3a8SUlJ5OXlhTgi067Ra2Z6i81MGxNQ0dhng//9tg2mjTERIz4+nsLCwnCH4beSkhKfV8oyodWe5jE0sw/b9zRaeTxjAsj6bA9L8zDGGBO12gfTo7PTaHG52VFr5fGMMYFlg2ljjDFRq3H/YDodgNLdVtHDGBNYNpg2xhgTtZqdGxBHZ3tWO7Na08aYQLPBtDHGmKjVuD9nOoXEuBir6GGMCTgbTBtjjIla7TnTfRJiKchMYYuleRhjAswG08YYY6JW+8x0UnwsQzP72My0MSbgbDBtjDEmarUv2pIcH0tBVgpb9zTgdkfPAhPGmPCzwbQxxpio1Z7mkRgfQ0FmCi1tbnbsbQpzVMaYaGKDaWOMMVGrqdWFCCTGxVCQ2QeArbYSojEmgGwwbYwxJmo1tbpIiotFRBialQLAFsubNsYEkA2mjTHGRK3GVhfJCbEA5KQnkZIQy2df1IU5KmNMNInz5SARWeXDYZWqenIX1zgD+AsQCzysqn/o8PoQ4HGgr3PML1R1ti/xGWOMCQwRiQWWAOWqeo6IPA0UAa3AIuD7qtoqIoKnTz8LaACuUtVl4Yr7YJpa3STFeeaNYmKEUdlprN2xN8xRGWOiiU+DaTyD27O6eF2AWQd90dM5/x04FSgDFovILFVd63XYrcALqvqgiIwFZgMFPsZnjDEmMG4A1gHpzvOngW87j58BZgIPAmcCI5ztaGff0SGN1AeNrS6S4mP3Px+Tk86slRWoKp7vA8YY0zO+pnl8X1W3drGVAj/s4vwpwCZV3ayqLcBzwIwOxyhfdt4ZQIUf7TDGGNNDIpIHnA083L5PVWerA8/MdJ7z0gzgCeelBUBfEckJedCH0NzJYHpfUxvlNY1hjMoYE03E0z/6cKBndvkJVf2W328iciFwhqrOdJ5fARytqtd7HZMDvAv0A1KAU1R1aSfXuha4FmDQoEGTn3vuOX/Doa6ujtTUVL/P6w2iuW0Q3e2ztvVe3WnfiSeeuFRVi4IUUreIyIvA3UAacJOqnuP1WjywELhBVT8WkTeAP6jqJ87r/wVuUdUlHa4Z1j77T4sbaXbBrVOTAdhU7eK3C5u44chEJg309cfZ4LH/N3qvaG4bRHf7utu2g/XbPvckquoSkaEikuDMLgfaZcBjqvpnETkGeFJExququ0McDwEPARQVFWlxcbHfb1RSUkJ3zusNorltEN3ts7b1XtHQPhE5B9ilqktFpLiTQ/4BfKSqH/tz3XD32X9dN4++8TEUF08F4KjmNn636B1iM4dSXDyiW9cMpGj4t9OVaG5fNLcNort9gW6bv1/LNwNzRWQWsL+2kKree4jzyoF8r+d5zj5v1wBnONebLyJJQBawy88YjTHG+G86cJ6InAUkAeki8pSqfltEbgcGAN/3Ot6Xfj3smlpd9E2O3/88JTGOof37sM5uQjTGBIi/pfE+B95wzkvz2g5lMTBCRApFJAG4lK/esLgNOBlARMbg6cwr/YzPGGNMN6jqL1U1T1UL8PTRc5yB9EzgdOCyDr8UzgK+Ix5TgVpV3RH6yLvW2OoiKSH2gH1jctJtMG2MCRi/ZqZV9U4AEemjqg1+nNcmItcD7+CpDPKoqq4RkbuAJao6C/gZ8C8R+SmemxGvUl8Tuo0xxgTL/wFbgflO9YuXVfUuPBWXzgI24SmNd3XYIuxCc6ubpLgDB9Ojs9N5e81O6pvbSEkMf960MaZ386sXcXKZHwFSgSEiMgFPpY+uKnkAnjvC8XS+3vtu83q8Fs/PjMYYY8JIVUuAEudxp58TzmTHdaGLqns8i7Yc+CPsmJw0VGH9zn1MHtovTJEZY6KFv2ke9+P5ua8KQFVXAscHOihjjDEmENqXE/c2JsdThdVSPYwxgeD3cuKqur3DLleAYjHGGGMCRlU9g+n4AwfTef2SSUuKs8G0MSYg/E0W2y4i0wB1ao62r5RljDHGRJQWlxu3QnKHGxBFhDHZ6azfuS9MkRljoom/M9M/wJMjl4unBNJEul750BhjjAmLplZP8ZHEuK9+1I3JSWP9jr243XafuzGmZ/ydmR7VcQVEEZkOzA1cSMYYY0zPNbV6shA7zkyDJ2+6vsXF9uoGhmamhDo0Y0wU8Xdm+q8+7jPGGGPCqn0w3fEGRIDxuRkArCyrDWlMxpjo49PMtFMSbxowQERu9HopHU/daGOMMSaiNHYxMz06O40+CbEsLd3DeRMGhzo0Y0wU8TXNIwFPbek4DlzxcC9wYaCDMsYYY3qqPWc6Kf6rP8LGxcYwaUhfFpdWhzosY0yU8WkwraofAh+KyGOqujXIMRljjDE91lWaB8Dkof3525zP2NfUSlpSfChDM8ZEEV/TPO5X1Z8AfxORr9z6rKrnBTwyY4wxpgfa0zySOknzADiqoB9uheXbajh+5IBQhmaMiSK+pnk86fx5T7ACMcYYYwKp+RAz05OG9CNGYMnWahtMG2O6zdc0j6XOnx8GNxxjjDEmMLq6AREgNTGOMTnpLN26J5RhhZ2qIiLhDsOYqOFrmsenwEEr26vqEQGLyBhjjAmArm5AbFc0tB//WVpGm8tNXKy/1WJ7n58+v4KmVhcPfntyuEMJmdrGVv7y/mf85NQRpH+NcuNbXZ5///Ffg3/X4eZrmsc5QY3CGGOMCbDGFmdmOv7gFVyLCvrz+PytrNuxj8PzMkIVWtjM/7yKnXub2LBzH6Oy0w59QhR4f+0XPDp3C4P7JjHzuMPCHU7IfPexxaQmxn2tvjgBlNc0kts3OaTv6evXlYeA84FkVd3acQtifMYYY0y3NLU5OdNdDqb7AbC4NPpTPeqb29i5twmARz7ZHOZoQmftjr0AvLBkO6pfj+XjaxtbmbtpN++t/YI99S3hDidkXl1ezvQ/zGHF9pqQvq+vM9NXAmcAd4jISGAh8DbwvqrWBys4Y4wxvhGRB3w4bK+q3hr0YCJEkzMznRh38HmjnIxkcvsms3RrNd89tjBUoYXFlt2ej+vcvsm8uryCm08fzYC0xDBHFXxrK/YiAhu/qGNVWS0T8vuGO6Sgm//5btwKblXeXr2Ty48eEu6Qgq7N5eb+9zcC8PrKCiaG8O/Zp5lpVd2pqo+p6qVAEfAEMBl4V0TeF5GfBzNIY4wxhzQDWHqI7YKwRRcGTW1ukuJjDnmzXVFBPxaX7on6Wcv2wfStZ4+h1e3myQXR/8OyqrKmopazD88hKT6GF5ZsD3dIIfHRZ7tJTYyjMCuF11dWhDuckHh1RQWlVQ0MSEvk7dU7Q/r/s99Z6arqVtX5qnqbqk4HLgXKAx+aMcYYP9ynqo93tQH/PNRFRCRWRJaLyBvO80IRWSgim0TkeRFJcPYnOs83Oa8XBLV13dDU6uoyxaPdlML+7NrXzOeV0f1D62anfSeOHsjJowfx1IKt+xe2iVblNY3sbWrj6MMyOXN8DrNWVOzPpY9WqspHGys5Zlgm500YzIItVexy0nuiVZvLzV/nfMa4wencfNooymsaWV2+N2Tv79NgWkT+KiIPdLYBt6nq00GO0xhjTNdeOtgLInIOgKre78N1bgDWeT3/I56B+nCgGrjG2X8NUO3sv885LqI0tri6vPmw3fEjPDWmSzbsCnZIYbVldx25fZNJio9l5nGF7Klv4ZXl0T0XtrbCM6AaNzidi4ry2NfcxjtrdoY5quDaWtVAWXUjx4/I4twJOajC7E93hDusoHpleTlbqxr4ySkjOXXsIGJjhLdWh67Nvs5ML6Hrnw6NMcaE13udzQ6LyHeBv/hyARHJA84GHnaeC3AS8KJzyOPAN5zHM5znOK+fLBFWvNiT5nHowXR+/z6MGJhKyYbKEEQVPpt313PYgBQAji7sz/CBqVGfArDGyZcenZ3G1MJM8vsnR32qx8efef4dHzdiAMMHpjE6O43XV0XvYNrlVv72wSbGDU7nlDED6ZeSwDGHZYY01cPXnOmOPxW+BLzk9dwYY0x43YjnPpYR7TtE5JfAT4ETfLzG/cDPAbfzPBOoUdU253kZkOs8zgW2Aziv1zrHR4zGFt/SPACKRw1g0ZY91De3HfrgXkhV2VJZT2GWZzAtIpw+bhALt+yhOoqrPazdsZfDslLokxBHTIxw4ZH5zPu8ip210Zv28NFnu8nvn8zQzD4AnDthMEu3VlNe0xjmyIJj254GtlY1cMXUofvvjzhjfDabd9ez8Yu6kMTgazUPAERkPJ6lxft7nkol8B1VXROM4IwxxvhGVWeLSDPwloh8A5gJTAGOV9XqQ53vpILsUtWlIlIcqLhE5FrgWoBBgwZRUlLi9zXq6uq6dd6OXY20tOHTuf2aXLS43Dz0WgmTBvr10dgj3W2bv2qblX3NbbhqdlBSshuAzCYXLrfyj1c/ZHpucBYzCVX7DmbZ5gaG943ZH8OAJs/3xL+9+jGnDO1Zm8Pdts60uZWPNzQwdXAcH37oWbR6QKOnzQ+88glnFvre5khsX2fWVnly4Ku3f0ZJg6fkY2qzGwEefGM+3xie8JVzAt02f3uMh4AbVfUDAKfD/RcwLWARGWOM6RZV/a+IXA2UAPOAk1TV1ym46cB5InIWkASk40kP6Ssicc7scx5f3nBeDuQDZSISB2QAVZ3E9BCezw6Kioq0uLjY73aVlJTQnfP+tm4eGXExFBdPPeSx09rc/H3lu1TGD6K4+HC/36u7uts2fy3cXAUfLOC0YyZywkhPjvjxbuWhNXPY5s7g18VFQXnfULWvMzUNLVS9/R7fmzSC4hOG7d//yIYSNrck+fTvoivhbNvBLCndQ9O787nk+CMoPjxn//4nP/+EDQ3CH4un+3ytSGxfZ3Yt2Q6LV3FW8VSGZqbs3//0lnmsr2ujuPj4r5wT6Lb5W80jpX0gDaCqJUDKwQ83xhgTCiKyT0T2ArPxDIRPBnZ57e+Sqv5SVfNUtQBPlaY5qvot4APgQuewK4HXnMeznOc4r8/RCKst19Tme5pHQlwM04dn8eGGyqgskddeFu+wrC8/smNihNPGDeLDjZVRWeGifbGWsTnpB+w/Y3w2C7fsicrFTD7+bDcxAtOGZR2w/4zx2azYXkNFFKZ67KjxzBdkZyQdsP+M8Tms37mPzZXBT/XwdzC9WUT+R0QKnO1W4OuzjJIxxkQoVU1T1XTnzwRVTfF6nn7oKxzULcCNIrIJT070I87+R4BMZ/+NwC961oLAa2r11Jn21YmjB1Je08hnu0KTZxlKm3fXkxAXw+AOyyyfNjabplb3/pvWokl7JY+xgzsMpsfl4HIr76/7IhxhBdWmyjqGZqaQ0efAdI4zx2cD8Pbq6KtkUlHTyIC0RBLjDvzifNbhnjaHopKJv4Pp7wIDgJedbYCzzxhjTJRQ1RJVbS+nt1lVp6jqcFW9SFWbnf1NzvPhzusRN7Hizw2I4LkJEeCD9dFXIm9zZT2FmSnExhxYcOXow/qTlhTHu2ujb2C5tmIvg9ITyUo9cJXH8bnp5PZN5p0oHFiWVTeS1y/5K/sPG5DK6Oy0kJaLC5WK2savfEkEz+qmk4f2481Pg//37NdgWlWrVfXHqnqks93gy40txhhjgktElgXimGjS7EeaB3g+fEdnp/FBFNab3ry7bn8lD2/xsTGcPHog/133BW0udydn9l5rKvYybnDGV/aLCGeMz+bjz3ZTF2XVW8qrG8ntZGAJcOb4HJZsrY66BVzKaxrJ7ZvU6WtnHZ7Duh17g57q4ddgWkSKRORlEVkmIqvat2AFZ4wxxmdjvPvlTrZPgaxDXiWK+Lpoi7dTxw5i0ZY97NoXPQOONpebbVUNFA7o/Ban08dlU93QyqLSPSGOLHia21xsqqxjTE5ap6+fMT6bFpc7qn6FaGp1sbuu+aCD6bMOz0aVqFq0RlWpqGlkcMbB2wzBT/XwN83jaeAx4ALgXK/NGGNMeI3mwH6543YOX6PKS6rqLNri38fcjImDcSu8GUWLXGyvbqTNrQfcfOjthFEDSEmIZdaK6FnAZfueRlxuZcTAzgfTRw7pR1ZqIm9H0cCy/ebC3E7SPABGDEpj+MBUZocg7SFUqhtaaWp1d5rmAV+merwR5P+f/R1MV6rqLFXdoqpb27egRGaMMcZn3n1yF1tZuOMMlVaX4nKr3zPTwwemMTYnndeiaGC5ZbfnJ+7DDjIz3SchjtPHZ/PmpztoamaBeTMAACAASURBVI2Oqh7b9zQAkN+/80FWbIxw5vhs/rvuC/Y1tYYytKApq/YMpvP69TnoMWeOz2bhliqq6ppDFVZQtX+BONhgGuDsw4Nf1cPfwfTtIvKwiFwmIue3b76cKCJniMgGEdkkIp3e9S0iF4vIWhFZIyLP+BmbMcYYA3jK4gF+5Uy3mzFxMCu217C1qj7QYYXF5sr2snipBz3m/El57Gtq47/roiPtYXt1+2D64APL84/MpanVHZJqD6FQfoiZafDkELuVoM/Uhsr+NncxmD4zBKke/g6mrwYmAmdw4E+HXRKRWODvwJnAWOAyERnb4ZgRwC+B6ao6DviJn7EZY4wxAPtnWLszmD53wmCAqEl72LK7nozkePqlfHUluHbHDMtkUHoiryyPjh8vtlU1kBQfw4AOlTy8Tczvy7ABKby0tPygx/Qm5dWNxMYIg9IO3uYxOemMG5zOf5ZuD2FkwfPlzHTnNyCCJ9WjaGg/XltREbQa8v4Opo9S1SJVvVJVr3Y2X0rjTQE2OSWWWoDngBkdjvke8Pf26iCqGh1fj40xJsREZKiInOI8ThaRzhNHo1hTi6cyRXcG04P7JjOlsD+vrQzeh28oba1qoOAg+dLtYmOEb0zMpWRDZVSkAGyvbiC/Xx9E5KDHiAgXTM5jUekeSnf3/l8hymsayU5PIi6266HdxUX5rC7fy5qK2hBFFjwVNY0kxsXQv4svigAXTM7js111LNtWE5Q4/B1Mz+s4o+yjXMD7a1CZs8/bSGCkiMwVkQUickY33scYY77WROR7wIvAP51decCr4YsoPL5M8/D3Y87jvAmD2bSrjnU79gUyrLAoraqnIPPg6Q7tvnlkLm1u5fWVvX9GftueRoZ0keLR7vxJecQIvLys98/Il1U3dFpjuqMZEweTEBvDf5b0/jZX1DaR2ze5yy9N4Pm1qU9CLM8v3haUOOL8PH4qsEJEtgDNgACqqkcEKJYRQDGezv8jETlcVQ/4GiEi1wLXAgwaNIiSkhK/36iurq5b5/UG0dw2iO72Wdt6rwhr33V4fg1cCKCqn4nIwPCGFHrty2P7ewNiu7MOz+GOWWt4dUX5V1bQ602a21xU1DRy/pF5hzx2dHY6Y3LSeWV5OVdNLwxBdMGhqmzf08DRhf0PeWx2RhLHjhjAS8vK+ckpI4mJ6XpQFsnKqxuZOizzkMf17ZPAaeMG8eqKcn551uivrBzYm1TUdL5gS0epiXGcN2Ewr62o4H/O6c6ccNf8HUx3d7a4HMj3ep7n7PNWBixU1VZgi4hsxDO4Xux9kKo+BDwEUFRUpMXFxX4HU1JSQnfO6w2iuW0Q3e2ztvVeEda+ZlVtaZ+pEZE4oPfnKvipJznTAP1TEjh5zEBeXFrGjaeO7PZ1wq2suhG34tPMNMAFR+by2zfXsWHnPkZl987soJqGVuqa27q8+dDbBUfmcsNzK1iwpYppw3pnKfZWl5ude5vI82FgCZ5UjzdW7eD9tbs4+4icIEcXPBU1jZwwcoBPx146ZQjPLd7OrJUVX0mN6Cl/f//a18nmy+9Bi4ERIlIoIgnApcCsDse8imdWGhHJwpP2EXHL0xpjTIT7UER+BSSLyKnAf4DXwxxTyDX2cDANcOUxBeypb+nVNafbK5IMzew6Z7rd+UfmkRgXw+PzS4MXVJBtay+L50PKA3gWrUlLjOP5xb33prydtU24tetKHt6mD89icEYSLyzpvW1uaXOza18zOQdZsKWjCXkZjM5O47lFgW+zv4PpZUAlsBH4zHlc6qyIOPlgJ6lqG3A98A6wDnhBVdeIyF0icp5z2DtAlYisBT4AblbVKj/jM8aYr7tb8PTNnwLfB2YDt4Y1ojBoam2/AbF7OdPgqXAxfGAqT8wvDUxQYVC62zOw9HVmun9KAt+YmMvLy8qoaWgJZmhB014Wb4iPbU6Kj+WionzeXLWDnbW9c+VLX2pMe4uNES6cnMdHn1Xur8nd23yxtwnVrsvieRMRLj0qn0/La9m6N7D11P3tZd4DzlLVLFXNxFPq7g3gh8A/ujpRVWer6khVHaaqv3P23aaqs5zHqqo3qupYVT1cVZ/zvznGGPP15ZQhXaeq/1LVi1T1Qufx1y7No7mtZznT4Pnw/c4xQ1lZVsuK7cGpAhBsW6vqSUuMO2S1A29XTS+gqdXda2dqv5yZ9m1gCXD19ALcqr32i5Mv9ZY7uvzoocSK8OjcLcEKK6jKfViwpaNvTvL88vJhWVtAY/F3MD1VVd9pf6Kq7wLHqOoC4OCFDY0xxgSdqrqADSIyJNyxhFv7DYg9zXU+/8g8UhPjeGJeaQCiCr3SqgaGZnVdIq6jMTnpTD2sP0/M30qbyx3E6IJj+54GMlMSSEn0/baw/P59OG1sNk8v3EZDS2AHWqFQ7sxM53RRb7mj7Iwkzps4mOcXb6e2ofetAulLjemOMvrE85sZ4zk+199bBrvm72B6h4jc4tQwHSoiPwe+cGZDet//ccYYE336AWtE5L8iMqt9C3dQodZ+A2JPZqbBUwXggiNzeWPVDnb3wvrL2/Y0+Jwv7e2qaYWU1zTy/rovghBVcG3f0+jzzYfeZh5XSG1jKy8t632LuJTXNDAoPdHvyhzfO+4wGlpcPLVwa5AiCx5flhLvzMVH5VOQEdgbiv0dTF/OlzVLX8FToeNyIBa4OKCRGWOM6Y7/wbMy7V3An722r5XG1u4v2tLRFccU0OJy8+T83jXgaHO52b6nwed8aW+njh1Ebt9kHv2kNPCBBdm2PQ3dGkxPHtqPCXkZ/PuTLbjdvSszqqy60a8Uj3ZjctI5fuQAHptXuj81qrcor2kiMyUhIirt+DWYVtXdqvojVZ2kqkc6jytVtUVVNwUrSGOMMb5R1Q8728IdV6i1z0wnxnX/BsR2wwemcvq4QTw6dwu1jb3n5/CKmiba3NqtmenYGOG7xxayqHQPCzb3nloAbS43FTWNDOnv/8BSxNPmzbvr+e/63rUIc3lNI7l+5Ih7u/a4w6jc18xry3vXYj2+1pgOBZ96GRG5IxDHGGOMCS4R2Scie52tSURcIrLXh/OSRGSRiKwUkTUicqez/2SnYtMKEflERIY7+xNF5HkR2SQiC0WkILgt809Tq4vEuJiALcLx45NHsK+pjX/3opu1Sp2yeAXdGEwDfOvoIQxMS+Te9zb2mmXVd9R6vkD4c/Oht7MOz2FI/z7c//7GXjM77XYrO2qaujUzDTB9eCZjc9L550ef4+olbYb2wbTv+dLB5OtX9pkicmMX28/w1I42xhgTRqqapqrpqpoOJAMXcIhqS45m4CRVnQBMBM4QkanAg8C3VHUi8Axfltm7BqhW1eHAfcAfA9yUHmlqdQX0599xgzM4fdwgHvmk98xOb90/mO7ewDIpPpbrThzOoi17mLupd8xO7y+L1400D4D42Bh+csoI1lTs5a3VOwMZWtBU1jXT4nL7tJR4Z0SEH500nM8r63vNsurNbS5Kq+opyOreF8VA83Uw/S8grYst1TnGGGNMhHBKjr4KnO7jsXXO03hnU2drX087gy8X6poBPO48fhE4WfwpGRFkTa3uHt982FFvm50urWogOT6WAWndL7Z1yVH55GQkce97G3rF7HR7zeTu5Ey3mzExlxEDU/nzext6RTWTMucLhK8LtnTmjPHZTMjL4L73Nu5PkYpk63bso9WlTMzrG+5QAB+XE1fVO4MdiDHGmJ4TkfO9nsYARYBPK1E4lZmWAsOBv6vqQhGZCcwWkUZgLzDVOTwX2A6ehblEpBbIBHYHpCE9VN3QQnpyYMtfec9OXz2tkIw+8QG9fqBtrapnaKZ/ZfE6SoqP5fqThvPrV1ZTsrGSE0cNDGCEgbdtTwOxMUJORvd//o+NEX522ih+8NRSXl5ezsVF+QGMMPC273EWbOlB/rCIcMsZo7n84YU8tWArM487LFDhBcVKp+77hPxeNJg2xhjTa5zr9bgNKMUzi3xITp3qiSLSF3hFRMYDP8WzWNdCEbkZuBeY6WswInItcC3AoEGDKCkp8fXU/erq6vw+b0NZIxkJ0q3368r0DBfvNrVx8+NzuHxMz5dX6E7bfLV2WwM5qTE9vv4gt5KVLNz24lLuOCaJWD/y0IPZvs4sXd9E/0T45OOPenSdRFUK02P44xuf0m/vJuI7aXOo23Ywb65rJiEWtq5ZQvm6nv04ND4zlvveXcfgpq24m+sjon2deWdVMxmJwoblC9jYjS+Lgf67s8G0McZEl4dVda73DhGZDvhcnkBVa0TkAzyr3E5Q1YXOS88DbzuPy/GURy0TkTg8KSBfSaxV1YeAhwCKioq0uLjYv9YAJSUl+Hte7UfvcuyYHIqLD/f7/Q5lvetTnl+8nZvOn8zIQWk9ulZ32uYLl1vZ/d7bnFs0lOLiMT2+3l0DdvDDp5dRllTIldMKfD4vWO07mPvXzGVkbizFxVMPffAhxOVVcsUji9hAHtcXj/jK66Fu28Hc8+nHFBXEc8pJPW9z1ohazvnrJ6x25TAldWdEtK8zdy0t4ajDUjnxxKJunR/ov7ue1wwyxhgTSf7q474DiMgAZ0YaEUkGTgXWARkiMtI5rH0fwCzgSufxhcCcSFm2vL65jZqG1h7lkHblptNGkZoYx52vr4nYPOKde5tocbm7XcmjozPHZ3Ps8CzueXdDxC5e09LmZuMX+xg2IDUg1ztuxADOHJ/NX+ds2p+LHWnqmttYW7GXooL+Abne+NwMzp+Uy78+3kxFXWTmi9c2trK5sp6J+RnhDmU/vwbTTmf7KxF5SEQebd+CFZwxxhjfiMgxTmWlAR2qLd2BZ2GtQ8kBPhCRVcBi4D1VfQP4HvCSiKwErgBudo5/BMgUkU3AjcAvAtykbmtfGa27pcIOpX9KAj87bSRzN1XxdoRWfNi621PJY2g3K3l0JCLccd44mlpd/PGt9QG5ZqCtLKuhocXFtGGZAbvmbeeOJS5GuH1WZH5xWr6tGrfCUQX9AnbNX509hj4JcTy2pjkiywOuLq8FIidfGvyfmX4Nz0957wNvem3GGGPCKwFPZaU4Dqy2tBfPzHGXVHWVsyDXEao6XlXvcva/oqqHq+oEVS1W1c3O/iZVvUhVh6vqlPb9kaDMGUx3t1SYLy6fMoTR2Wn89s111DW3Be19umtlmWfAMXxgYGZp26/13WML+c/SMpZu3ROw6wbK3E27EYGphwVuMJ2TkcxPTx3JnPW7eGdN5C2tvri0mhiBSUMCN5jOSk3kV2eNZmO1mxeWbA/YdQNlhXPz4RG5vXcw3UdVb1HVF1T1pfYtKJEFSW8o+WKMMf5yVjq8E5iqqnd6bfeq6mfhji+Uyqs9g+lgro4WFxvD7745noraRn735tqgvU93lWzYxZicdAamBXZRix+fNILBGUnc/J9VNLRE1peIeZuqGD84g759EgJ63SunFTA6O407X18TcTXGF2/Zw9jB6aQmBvYWuIuL8hnVL4bfz15H5b7ISutZub2GwqyUiKqm4+9g+g0ROSsokYTIN/8xjx/9t54LHpzHTf9ZybxNEVHFyRhjAqVBRP4kIrNFZE77Fu6gQqmippG4GAn4QLKjyUP78/3jh/Hsou38d13kzFrubWpl6dZqikcNCPi1UxLjuOeiCWzeXc/vZ6879Akh0tDSxvLt1UwbHrhZ6XbxsTH88YIjqNzXzK2vro6YdI9Wl5vl26spGhqYfGlvIsKV4xJpanXzy5dXRUybwZPOMyEvcvKlwf/B9A14BtRNzpK1+3xZpjaSXHpUPkcOiiM+Vvjvui+4/OGFfOfRRaypqA13aMYYEwhPA+uBQuBOPKXxFoczoFArr2kkp69/Jdy666enjmB0dhq3vPQpe+pbgv5+vpj72W7a3Bq0mtDThmcx89hCnlqwjQ/W+1wkJqgWl1bT6lKmDcsKyvUn5Pflp6eO5PWVFby8rDwo7+GvNRV7aWp1M6Uw8INpgMGpMfzizNG8v24Xj88rDcp7+GtnbRNf7G2OqHxp8HMw7SxTG6OqSc7jNGfJ2l7jymkFXD0+keeuPYb5vzyZW88ew6qyGs756yfMWllx6AsYY0xky1TVR4BWJ/Xju8BJ4Q4qlMqrG4N282FHiXGx3HfJRGobW/jFS5Exg1eyoZK0pDiOHBK8AcdNp49idHYaN7+4KiKqe8zbtJv4WAnojXgd/eCEYRxd2J/bXltNqXODZzgtKfXkrRcNDV6br55ewMmjB/L72ev33/gXTivLImuxlnZ+l8YTkfNE5B5nOycYQYVKUnwsM487jA9vPpGiof246T8rWbatOtxhGWNMT7Qnde4QkbNFZBIQnKmrCFVe0xjUfOmOxuSkc8sZo3l37Rf8o+TzkL1vZ1SVDzdWctyILOJig1f9Nine8yViX1MrP3xqGS1t4S2jNvfz3Uwa0o8+CcFbPiM2RrjvkonExcZw/bPLaHaF94vT4tI9DM3sw8D04KUziQh/umgC/VLi+dGzy8N+s+3K7TXExQhjcyJrHtff0nh/wJPqsdbZbhCRu4MRWChlJMfzzyuKyE5P4tonluxf594YY3qh34pIBvAz4CbgYTyrGH4ttLrcfLG3qUdLK3fHNccWMmPiYO55dwNz1ocvf3r9zn3s3NtE8cjgL/s9Jied/73wCBaV7glr6biahhbWVOxlepBSPLwN7pvMvRdPYE3FXh7+NHyl41SVJaXByZfuqH9KAn+5dBLb9jTw42eX0+YKzxcnVWXO+l0cnpdBUrwv1T5Dx9+vrWcBp6rqo6r6KHAGcHbgwwq9/ikJPHpVEc1tbmY+viRs/1iMMaa7RCQWGKGqtaq6WlVPVNXJqjor3LGFys7aJtxK0BZsORgR4Q/nH8HYnHRueHYFn1fWhfT925VsqATghCDcfNiZGRNz+X/Fw3h20TaeWrA1JO/Z0fzPq1CF6UG4+bAzJ48ZxK/OHMPinS7uf39jSN6zo7U79lJV3xLUtBZvUw/L5I7zxjFn/S5++2Z4bjxdsrWa9Tv3cUlRfljevyvd+Q3IO1Elsm6n7KHhA9P4/TcPZ/3OfcyJkJsqjDHGV6rqAi4LdxzhVL5/wZbALFbij+SEWP55xWTi42K46t+L2FnbFPIYPtiwi7E56QwK4k//Hd102ihOGj2QO15fy7trQr+IzUefVZKSEBvSPNqZxxVyXG4cD8zZxMvLykL2vu0e/aSU5PhYTh+XHbL3vGLqUL53XCGPzSvl33O3hOx92z05fytpSXGcN3FwyN/7UPwdTN8NLBeRx0TkcWAp8LvAhxU+Z47PZmBaIs8tjrxC5cYY44O5IvI3ETlORI5s38IdVKh8WWM6dINJb3n9+vDvq46iur6Vbz28gKoQ3pxX09DCsiCVxOtKbIzwwGWTODw3g+ufWc6HGytD9t5f7G3i5WXlnHV4DvFBzBHvyFM6LoFpwzK56T8reT2EBQx21Dby2opyLjkqn34pga2pfSi/PHMMp48bxF1vrOU/IVzQpXJfM2+t3sGFk/OCmhffXf5W83gWmAq8DLwEHKOqzwcjsHCJi43hkqPyKdmwa/8MhzHG9CITgXHAXcCfne2esEYUQu39dihvQOxoQn5fHrmyiLLqRq54ZBG1DaFZ6OPBDz/HpRqWmbvUxDgev3oKwwemcu0TS5j/eVVI3vfBks9pcys/OmlESN7PW1yM8PCVRRQN7c9Pnl/B7E93hOR9H/1kC4onTz/UYmKEv1w6iWOHZ/Hzl1bxQogmHp9fvI1Wl/LtqUND8n7+8mkwLSKjnT+PBHKAMmcbHI0zHhcX5aMQsn8kxhgTKE6edMfta1Mar6KmkazUxLDfoHT0YZn884rJfLZrHxf/c37QUz7Kaxr599xSvjkpl9HZ4al0kNEnnievmcKQ/n24+rFFQU/52FnbxDOLtnHhkXkMyQx9Wg9An4Q4Hr36KCbl9+XHzy7n1eXBrUFd29jKs4u2c/bhOeT3D0+bk+Jj+dd3ijhuxAB+/tIqnl4Y3Fz5Npebpxdu49jhWQwbkBrU9+ouX2emb3T+/HMnW9TNeOT378NxIwbwwpLtuMJ0p64xxnSHiAwSkUdE5C3n+VgRuSbccYVKeU1jyG8+PJjiUQP591VTKK9p5Px/zGXjF/uC9l5/fmcDAD87bVTQ3sMXmamJPHvtVEZlp/P9p5by/tbgzcr/o2QTbrdy/UnDg/YevkhNjOPfVx9FUUE/fvL8Cu5/f2PQKps8s3Abdc1tXHv8YUG5vq+S4mN56IrJnDhqAL9+ZTW/n70uaOOlt9fsZEdtE1ccE5mz0uDjYFpVr3UentlxxgNPhY+oc/mUfHbUNvHhRrsR0RjTqzwGvAO0/9a/EfhJ2KIJMc+CLeHJl+7MsSOyeP77U2l1Kxc+OC8oy46vLq/llRXlXD29IGSL1XQlKzWR5743lVPGDOKpdS3c/tpqmttcAX2PippGnlu0nYuK8sM2Q+stLSmeJ757NBccmcf973/GT59fQWNLYNu8a28Tj3yymWOHZzE+N/z1H5LiY3noO0V855ihPPTRZr73xBL2NQX2y1NFTSO3vbaGkYNSOXl08Ms9dpe/2frzfNzX6508ZhBZqYk8u8hSPYwxvUqWqr4AuAFUtQ0I7Kd6hFJVz8x0BAwovY0bnMHL/28aef36cM3jS7jr9bUBG1y2udz89s21ZCTH88Pi8M7QektOiOX/vj2Z0wvieHz+Vr7x93ls2hWYmfmGljZ+9OxyELjuxGEBuWYgJMTFcM9FR3Dz6aN4bWUFZz/wMSu31wTk2o0tLmY+sYSGFhe/OmtMQK4ZCPGxMdw1Yzy/+cZ4PtxYydkPfMKiLXsCcu2WNjfXPbOM5lYXD357clAXIeopX3Oms0VkMpAsIpO87hAvBsL/lTAI4mNjOGXMQJZutRURjTG9Sr2IZAIKICJTgfCvAxwCVfUtNLe5I24wDZ70wZd/OI2rphXw6NwtnP+PeT1ecbfV5ebHzy1nweY9/OKM0WQkxwco2sCIjREuG53Io1cV8cXeJs756yc89NHnPfoi0dLm5gdPLWP5tmoeuHQief0iawgiIlx34nCennk0Ta0uzn9wHve+t7FHs9Rut3LjCyv4tLyWBy6dxNjBkbX6H3jK5j137VQALnloPr95Yy0NLT1bLfH3s9exfFsNf7poQsTmSrfzdZh/Op7c6DzgXr7Ml74R+FVwQgu/wqwU9tS3UNsYmjuxjTEmAG4EZgHDRGQu8ATwo/CGFBrtZfFyI2yA1S4pPpY7zhvHQ1dMpnJfM+f/Yx7/WtXMrr3+35zY0ubmR88sZ/anO7n17DFcOmVIECIOjJNGD+LtG45j+rAsfj97Pafd9xFvr97pd15xc5uLnz6/go82VvKH84/gjPE5QYq456YNy+KtnxzPuUfk8MB/P+PEe0q6dR9WY4uL/3ltNW+t3smvzxrDKWMHBSninjuqoD9v3XAc3z56KI98soUT/lTCE/NL/V5qvrHFxe2vreaxeaXMPLaQsw6P3L/ndj4V61PVx4HHReQCVX0pyDFFjKGZKQBsrarniLzQFYM3xpjuUtVlInICMAoQYIOqfi1mBL4sixc5OdOdOW1cNtOGZ/G3OZv410efc+wfP+DcCYO5enqBT7mwCzZXcc87G1iytZrbzhnLd8NQIs1fA9OTeOSqoyjZ4FlB7wdPLWXYgBS+PXUo5x+Z1+WsututvL6qgj+9s4Gy6kZ+fdYYLj4q8lbB6ygjOZ77L53EZVOG8Pu31vPzF1fx9w82cXFRPhdOzjvkwjrvr/2C22etobymke8dVxiWUnj+SkmM4zffGM+MiYP537c3cNtra/jnh5u55Kh8vjkp95D57UtK93Dzi6vYsrueq6cXcMuZo0MUec/4VflaVV8SkbPx1DBN8tp/V6ADiwSFWZ7BdGlVgw2mjTG9gogkAT8EjsWT6vGxiPyfqoZ+Ob4QW1uxlxghIm5IO5TUxDh+ceZoCt0VrGkbyItLy3hpWRkjBqYyfXgWxwzLJL9fH/r2iSchLobNlfVs+GIfb6ysYOGWPQxIS+SeiyZw4eS8cDfFL8WjBnLs8CxeW1HBkwu2cufra7l79nom5GdwVEF/xuSkk5IYS3J8HBU1jawqq2H+5io2flHHmJx0nrzmcI4bEdpFaXrq6MMyefWH03h79U7+Pa+UP72zgXvf28gReRlMzO/LEXkZpCXGExsj1DW3sbh0D/M/r+KzXXWMHJTKC98/himF/cPdDL8UFfTn+e9P5aPPdvOPDzZx73sbufe9jUzM78uEvAzG5KSTnZFEm0tpanOxfFsNc9bvYsvuenL7JvPM945m2rCscDfDZ34NpkXk//DkSJ8IPAxcCCzy8dwzgL8AscDDqvqHgxx3AfAicJSqLvEnvkAb4nTIpbvrwxmGMcb44wlgH/BX5/nlwJPARV2d5AzCPwIS8Xw2vKiqt4uIAL91zncBD6rqA87+v+Cp6NQAXKWqy4LQHp+oKrNX72BKYX/SkyIrd7grg1JiuKR4PD87bRQvLyvjgw2VPLd4G4/NK+38+PREbj93LJdNGRL2WtrdFRcbwwWT87hgch6ry2t53fmC8M+PNn8lDaJPQizjczO456IJfHNSLrExEqaoe0ZEOPPwHM48PIctu+t5aWkZi7bs4dlF2/j33APTIPokxHJUQX+uOGYolx41hIS4yL3xrisiwgkjB3DCyAGUVTfw2ooK5qzfxYtLy6jvkEOeEBvDMcMyuXp6Ad+clEtaL/p/GPwcTAPTVPUIEVmlqneKyJ+Btw51kojEAn8HTsWz2MtiEZmlqms7HJcG3AAs9DOuoEhOiCUnI4nSKhtMG2N6jfGqOtbr+QcisvagR3+pGThJVetEJB74xKlVPQbIB0arqltE2utTnQmMcLajgQedP8Ni4xd1bK6s5+ppBeEKoUcykuO5enohV08vpLnNxeryWir3NVPT0Epjq4vCrBRGDkojc9H50AAAIABJREFUJyMJz/eY6DA+N2N/akt9cxtl1Y00tLTR2OIiKy2RYQNSe+0A+mAKs1K46XRPPfBWl5stu+tpanXhcivxsTGMyk4L6dLooZDXrw/XnTic604cjtutbNvTQFV9MwmxscTHCfn9+pCSGHnLhPvK38jbfyZsEJHBQBWeFREPZQqwSVU3A4jIc8AMoGMH/xvgj8DNfsYVNEMz+9jMtDGmN1kmIlNVdQGAiBwNHPJXPvXcDVbnPI13NgX+H3C5qraX2msvvj8DeMI5b4GI9BWRHFUNzZrKHbz56Q5E4PTx2eF4+4BKjItl8tDe9bN+IKQkxjEqOy3cYYRUfGwMIwd9vdocEyMUZKVQ4KTSRgN/v/q8LiJ9gT8By4BS4BkfzssFvAs2lzn79nOWJc9X1Tf9jCmoCrNS2FrVEO4wjDHGV5OBeSJSKiKlwHzgKBH5VERWdXWiiMSKyApgF/Ceqi4EhgGXiMgSEXlLREY4hx+yXw+l2Z/uYEpBfwamRfbNh8aY6OPzzLSIxAD/VdUa4CUReQNIUtUe1y91rn3v/2fvvsOrqrIGDv9WeiWBJIQSIPReRQRs2D4bijoo2HXAjnXGUWcc2zg6xTL2MhYsWBDRQUTFQuyI9NAJPdQQpARIvev7455ARCD3Jrdnvc+Tx+Tcc89ZW2BnZWedtYErPDj3auBqgOzsbPLy8ry+X0lJicfvq9pRTvHuCqZ8Po2k2ND/VZM3YwtHkTw+G1v4CrHxnVbXN6pqFdDHWTT5QER64K6hLlXV/iJyHvAKcKyn1wzEnL1+l4uCLXsZ2DUulP4cPBJif3d8LpLHF8ljg8gen8/HpqoefwBzvDm/xvsGAZ/V+Pou4K4aX6cBW3GvdK/GXU6yAeh/uOseccQRWhfTpk3z+NxP8jdqmzsm6/x12+t0r0DzZmzhKJLHZ2MLX3UZHzBT6zCfevIBNAZ6Af2qP+pwjXuAPwJLgLbOMQF2OJ+/AFxY4/ylQPPDXdNfc/ZjU5dq7p2TdfPOvXW6fjDZv43wFcljU43s8dV1bIeat70t8/hSRH4n3j/98DPQUUTaikgcMBL3pgIAqOoOVc1U1VxVzQWmA2drkLt5wP72eKvsIURjTBgQkb8B84En2b/B1iMevC/LWZFGRBJxPzC+BPgQdwcngOOBZc7nk4DLxG0g7iQ7KPXSU/I3cqSVeBhjgsTbBxCvwb27VqWIlOJepVBVPezelqpaKSJjgM9wt8Z7RVUXisgDuLP8SYd7fzBVt8dbYw8hGmPCwwVAe1Ut9/J9zXFvzhWN+3ma8ao6WUS+A8aJyK24H1Ac7Zw/BXdbvALcrfGu9En0XppfuJ3lW0p4YFj3YNzeGGO83rSlzo+cquoU3JNvzWP3HOLcIXW9j69Vt8ezlWljTJhYAKTjfojQY6o6H+h7kOPbgTMPclyBG+oYo09UuZS/friAzJQ4hvUO2rOPxpgGzttNW75U1ZNqOxZprD2eMSaMPAzMEZEFuHtHA6CqZwcvJP94c/oa5hXu4ImRfUhLCq9NHowxkcOjZNrZGSsJyBSRxrjLOwAaEcRWSIHSNjOZqQs3BzsMY4zxxGu4+/XnA65azg1bm3aU8u/PlnJsx0zO7t0i2OEYYxowT1emrwFuAVoAs9ifTO8EnvZDXCElNyOZ4t3l7CytCKttao0xDdIeVX0y2EH4k6pyz/8WUFHl4sFzekTUjoDGmPDjUTKtqk8AT4jIjar6lJ9jCjltMtwdPdZs3UPPnLQgR2OMMYf1rYg8jLvbRs0yj9nBC8l3XC7lnkkLmLpoM3ed3mXf/GyMMcHi7QOIT4nIYCC35ntV9XUfxxVSarbHs2TaGBPiqh8iHFjjmAInBiEWn6pyKXdNnM/4mYVce3x7rj6uXbBDMsYYrx9AfAP31rJzgSrnsAIRnUxbezxjTLhQ1RNqPyv8FO0q4+4P8/ls4WZuPqkjt5zc0co7jDEhwds+0/2Bbk5LpAYjMS6a7EbxrN22J9ihGGPMYYlINvAQ0EJVTxeRbsAgVX05yKHViculTFtbwU15eeytqOLuM7sy+lhbkTbGhA5vd0BcADTzRyChrlFCLCVllcEOwxhjajMW9wZZ1S0uluF+gDws/XHCPF5bVE73Fml8cvNxlkgbY0KOtyvTmcAiEZlBhPcvPVBSXDR7yqtqP9EYY4JARGJUtRLIVNXxInIX7NuBNmwnr5FHtiajoog/X3SUlXUYY0KSt8n0ff4IIhwkxkWz15JpY0zomgH0A3aLSAbu51kQkYHAjmAGVh8D2jZhz5pYS6SNMSHL224eX4tIG6Cjqn4hIklAtH9CCy1JcTFs2VUa7DCMMeZQqrPN23C3xWsvIt8DWcDwoEVljDERzttuHlcBVwNNcHf1aAk8D0T0duLgXpm2Mg9jTAjLEpHbnM8/AKbgTrDLgJOB+cEKzBhjIpm3ZR43AAOAnwBUdbmINPV5VCEoKdbKPIwxIS0aSGH/CnW1pCDEYowxDYa3yXSZqpZX166JSAxOXV6kswcQjTEhbqOqPhDsIIwxpqHxtjXe1yLyZyBRRE4B3gM+8n1YoSchLpq9FZZMG2NClj2hZ4wxQeBtMn0nUATkA9fgrsm729dBhaKk2BjKK11UuRrEQrwxJvxE/LMrxhgTirwt80gEXlHV/wKISLRzLOK3BkyKczct2VNeSWpCbJCj8R1VZf32vSzfUkLbjGRyM5ODHZIxpg5UdVuwYzDGmIbI22T6S9xPhZc4XycCU4HBvgwqFCU6yfTe8qqISKaXb97Ff75YzjfLi9hVun9nx67NG3Fmz2b8/pi2JMV5+9cjtKkq3y7fyviZ61i7bQ/rf9mLS5Xf9cvhkoFtIvYHiQXrd/D6j6tZumkXu8oq2VNWxTEdM7n5pI60ahKZz6YVbNnFuz+vI29pES5VYqOjaJGeyJ2nd6FTdmqwwwtJIpIAfAPE4/7eMEFV763x+pPA71U1xfk6HngdOAIoBkao6upAx22MMcHmbbaUoKrViTSqWuL0mo54+1emw7tueuOOvfz7s6V8OGc9SXExnNW7Bd1bNKJD0xQWbtjJJ/kbeWTqMuas3c6Ll/UnOioyyjC/WrKZJ75YzrzCHWSmxNG1eSO6t2jEjr0VjP1hNS99t4oL+ufwz9/1ipjNIWas2sYjU5cyY9U2kuKi6Z/bhFZNkhARJs3bwP/mrueiAa258/Su+35YDHeLNuzkvkkLmbF6GzFRwtEdMkmJj6HS5WLGqm2c+eS3XD+kA9ef0J74mMgYsw+VASc683os8J2IfKKq00WkP9D4gPNHAb+oagcRGQn8ExgR4JiNMSbovE2md4tIP1WdDSAiRwB7fR9W6ImEZPqbZUXc/M4c9pRXMfrYdlx7fHuaJMfte31guwxGHdOWN6av4a8fLuBvkxdx39ndgxhx/e0pr+Te/y3kvVmFtGqSyMPn9eS8fi1/lUht2VnKs3krGPvDajo2TeWq49oFMeL6K6908djny3jhmxU0b5TA3Wd25fz+rUhL3P8blY079vLklwW8Pn0NLoW/ndMjiBHXX0WVi+fyVvDkl8tJT4rjL2d05dx+LclMid93TnFJGX+bvIgnvlzOjFXbeOsq2566JlVV9v/WMdb5UKec79/ARcC5Nd4yjP274k4AnhYRca5jjDENhrfJ9C3AeyKyAfeT481oICsRiU7Jw96KylrODD0ul/LUVwX858tldGqaynOX9KNdVsohz790YBvWbN3NS9+tok1GElce3TaA0frO0k27uOGt2awoKuHGEztw00kdiY3+7TO3TRslcO9Z3di8s5R/fLqEvq3T6Z/bJAgR19/a4j1c/9YsFqzfyYUDWvPXoV0PWq7TPM39g0VSXDQvf7eK03s2Y3D7zCBEXH9Fu8oY/fpM5q3bzrA+LbjvrO40rvFDYrWMlHj+M7IvfVqlc99Hi5g0bwPD+rQMQsShy0mcZwEdgGdU9ScRuRmYpKobD/jhoyWwDkBVK0VkB5ABbA1w2MYYE1Tebif+s4h0ATo7h5aqaoXvwwo94boyXVnl4k8T5jNxznrO7duSv5/bw6Na6LvO6MrabXv42+RFnNC5adjVE/+4opjRr/1MYlwMb446iqM7HD5RFBH+ObwXi5/6jjFvzeHjm44ho8aqZjhYuGEHl7/yMxVVLl689Aj+r3uzWt/zx//rzJeLN3PH+/P57Jbjwq5OfkVRCVe8OoOtu8p55qJ+nNmrea3vuXRQLhNmF/LwlCWc0i077MbsT6paBfQRkXTgAxE5DjgfGFLXa4rI1bh3ziU7O5u8vDyvr1FSUlKn94WDSB4bRPb4InlsENnj8/XY6vJd5Egg13lvPxFBVV/3WUQhKjF2/wOI4aK80sUt785hSv4m/vh/nbjhhA4e/1o7Okp4YFgPPl+8mYlz1nPbKZ38HK3vfLl4M9eNm02bJkm8MeoomqUlePS+RgmxPHNxP8599gcembqUh8/r5edIfefHFcVc/fpMUhJieOfqQXRo6tlDdolx0fxreG9GvPgj//p0aViV9cxe+wujxv5MlAhvXz2QPq3SPXpfdJRw31ndGf78jzyXt4I//F/n2t/UwKjqdhGZBpyAe5W6wJk7kkSkQFU7AOuBVkChs4FXGu4HEQ+81ovAiwD9+/fXIUOGeB1PXl4edXlfOIjksUFkjy+SxwaRPT5fj82rPtMi8gbwCHAM7qT6SKC/z6IJYfu6eYTJxi1llVVc9+YspuRv4q9DuzHmxI5e14c2S0vg6PaZfDhnPeFSBjl5/gaueWMWXZqlMv6aQR4n0tW6t0hjaM/mfLJgExVVLj9F6VvfLd/K5a/OIDstgfevG+xxIl1tQNsmXD4ol7E/rKbwl/Docjl33XYue3kGaYmxTLx+sMeJdLX+uU0Y1qcFL3yzknXbwmPM/iYiWc6KNCKSCJwCzFLVZqqaq6q5wB4nkQaYBFzufD4c+MrqpY0xDZG3m7b0B45W1etV9Ubn4yZ/BBZqwqnMw+VS/jB+Hl8u2cKD5/Rg1DF1r3k+t29L1m7bw6w1v/gwQv+YtnQLt7wzl36tGzNu9FEHrZv1xOk9m7N9TwXTV/5mkS3kzF77C1e/MZN2mcm8d80gWqQn1uk6lw1qA8C0pUW+DM8vFm/cyeWvzKBJchzvXD2INhl1K0G68/QuRAm88M0KH0cYtpoD00RkPvAz8LmqTj7M+S8DGSJSANyGe1MvY4xpcLxNphfgfuiwwUmKdVfEhHoyrar87eNFTJ6/kTtP78IlA9vU63qn9WhGYmw0789e76MI/WPWmm1c9+YsujRP5eUr+terF/ixHTNJjotmSv4mH0boe4s37uSKV2aQlRrP66MG1PmHB4C2mcm0yUhi2pItPozQ91YUlXDJSz+RFBfNuNGel/AcTPO0RI5un8n3BaH/Q1MgqOp8Ve2rqr1UtYeqPnCQc1JqfF6qqueragdVHaCqKwMbsTHGhAZvk+lMYJGIfCYik6o//BFYqNm/aUtod/OYsqqCV79fzahj2nKND1q8JcfHcGr3bD6ev4HSEC1xWbZ5F1e++jPN0xIZe+WAem+qkxAbzYlds5m6cBOVIVrqsWH7Xi57ZQZJzgOWTVPrnlSC+wHMEzo35YcVW0P2z7m4pIwrX/0ZERg3+iifbDgzqH0Gq7buZuOOBtHh0xhjjB94m0zfB5wDPAQ8WuMj4sXFRBETJSG9Mv3pgo28t6yCs3u34C9ndPVZD91z++Wws7QyJFcti0vK+P3Yn0mIjeb13w/4VV/h+jijRzOKd5czY3Xo7dC8u6ySUa/NpLS8itdHDfDZLoZDOmdRWuEKyfKW0ooqrnljFpt3lvLfy/oftrWjNwa1zwDcD3AaY4wxdeFVMq2qXwNLgFTnY7FzrEFIjIsO2WR68cad3DZ+Hu3SovjX8F5E+XDnwqPbZ5CVGs/EOaFV6lFe6eK6cbMp2lXGi5f19+nW2EM6NyUxNppPQqzUw+VSbnl3Lks37eSpi/r6dGvsge0ySIiNIi/E6qZVlTven8/MNb/w2AV96Nv6wI346q5rs0akJ8XygyXTxhhj6sjbbh4XADNw9x29APhJRIb7I7BQlBQXHZKt8bbtLueq12eSmhDDTX3jSYj17TbJMdFRnN6jGd8uL8LlCo2H9VWVv364gBmrtvGv4b287uZQm8S4aE7oksWnCzdRFSJjBvj31KV8vmgz957VnSGdm/r02gmx0Qxun8lXS7aEVPeWZ/NW8L+5G7j91M4e9ZH2RlSUMLBtBj+uKA6pMRtjjAkf3pZ5/AU4UlUvV9XLgAHAXz15o4icJiJLRaRARH7z1LeI3CYii0Rkvoh8KSL1e3LODxJjo9kTYvWkVS5lzFuz2bKrjBcv7U96grd/pJ7p1rwRpRUu1m8PjdrSN39ay7sz1zHmhA5+28Xu9B7NKdpVFjKdTD7J38hzeSu4+KjWXD441y/3OKFLU9Zu28PKrbv9cn1vfbu8iEenLmVor+ZcP6S9X+4xqH0G67fvZd220Pi7bYwxJrx4m3lFqWrNwtliT67hbFH7DHA60A24UES6HXDaHKC/qvYCJgD/8jI2v0uMiwm5lenHP1/GDyuK+fs5Pejt49XZmjpmu2tUl2/Z5bd7eGruuu088NFChnTO8utmMsd3zgJg5prg102vKCrh9gnz6dMqnXvOOvCfju8M6eQecyjUxxf+soeb3p5Dh6Yp/PN3vXz2DMCBBlfXTa+0XbCNMcZ4z9tk+lOnk8cVInIF8DHwiQfvGwAUqOpKVS0H3gGG1TxBVaepavXuCdOBHC9j87ukuGj2VoRON49pS7bw9LQCRvRvxfn9W/n1Xh2y3LW5yzaX+PU+tSkpV24YN5umqQn8Z0Qfn9aGH6hRQixNU+NZWRTcVdrdZZVc+8Ys4mKiePbifsTH+LaMp6ZWTZLo2DSFaUuDm0yXVVZx/bjZVFYpL1zan+R4/2353aFpCpkp8VY3bYwxpk68fQDxduAFoJfz8aKq/smDt7YE1tX4utA5diij8CxJD6ikEHoAcf32vdw6fi5dmzfi/mH+3wI6LcmdWC4PYjLtcikvzC+jaFcZz13Sj/SkuvdV9lS7rGRWFgVvzKrKnz/IZ0VRCU9d2LfOm7J4Y1D7DOat2xHUGuKHPl7M/MIdPHpBb9pm1m1TFk+JCIPaW920McaYuvFouUdEOgDZqvq9qk4EJjrHjxGR9qrqsy3EROQS3DstHn+I168GrgbIzs4mLy/P63uUlJTU6X27d5RStMdVp/f6UpVLeXhGKaVlLi7vEMP077/d91pdx+aJzLgKZq/YQF5ecGqIP15ZTv7WKi7rFse2grnkFfj/ngkVZeRvqmTatGl+KzOodrA/u28KK/jfgnLO7RBLReEC8gr9GgIAVb9UUFJWyUef59Eozjdj9ubv5cxNlbw2t4xT28QQV7SEvLwlPonhcDIqK9iyq5y3P55GixTvnzvw5787Y4wxoc3T353+B7jrIMd3OK+dVcv71wM16xBynGO/IiIn437I8XhVLTvYhVT1ReBFgP79++uQIUNqi/038vLyqMv7Ptw0h61rt9fpvb706NSlFGwv4ImRfX7z8F1dx+aJvJ0LGT9zHccff7zfE8sDzV77CxOn/siRzaK5/9KTA3b/guiV5K1bTK8jB5Phox7Wh3Lgn93yzbt468vvGNw+g0d+fxTRfixpqUmXbGHckp9p2bkPR7TxTRs6T/9ertu2hxvzvqV3ThpPXTWYuBj/PFB7oNZFJYxd+DUx2R0ZcqT3JVP+/HdnjDEmtHn6nSpbVfMPPOgcy/Xg/T8DHUWkrYjEASOBX+2cKCJ9cZeQnH3AQ44hIzEuJuhlHj+s2MrT0wo4/4gcv3WxOJSO2SnsKa9iw47SgN53x94Kbnp7Ds0aJXBF9/iAJvLtnc1BAt3dorSiijFvzSE5Lob/jOgTsEQaoE2Gu1/3muLAjrmiysWNb88B4OmL+gUskQZo3SSJmChhzbbQ6GJijDEmfHj63epwbSJqLeJU1UpgDPAZsBgYr6oLReQBETnbOe3fQArwnojMDcVtyt19poP3AOK23eXc+u5c2mYmB6RO+kAdm1Y/hBi4jh6qyp8n5rNxRylPXdSX5NjAroi3y3LX6wa6bvrvHy9m6eZdPHpBb5o2qt9W4d7KaZxElMDq4j21n+xDT3yxnLnrtvOP83r5dAMeT8RER9EiPZG11h7PGGOMlzwt85gpIlep6n9rHhSR0cAsTy6gqlOAKQccu6fG5yd7GEvQVPeZVtWAlzmoKne+P59tu8t5+fIjSYrzX3eDQ+nY1L1KW7C5hBN8vGHIoUyYVcjH+Ru5/dTO9GvdmLyVAbntPjmNk4iLjgpoR48vF2/mjelrGH1MW59vzOKJuJgoWjZODOjK9E8ri3kmr4AL+uf4fGMWT7VuksTabYH9AcIYY0z48zQjuwX4QEQuZn/y3B+IA871R2ChKDEuGlUoq3T5fJfB2oyfuY6pizbz5zO60KNlWkDvXa1xchyZKXEB6zW9png3901ayFFtm3Dt8f7ZsKM20VFCm4wkVgQomd6yq5TbJ8yna/NG3H5a54Dc82ByM5IDtjK9Y08Ft747l9yMZO49K/C/canWqkkSny0Mre3jjTHGhD6PkmlV3QwMFpETgB7O4Y9V9Su/RRaCkuLcCfTe8qqAJtOrtu7m/o8WMbh9BqOPaRew+x5Mx6apLN/i/5KHyioXt7w7l+go4fEA1wwfqF1WckDGrKrc/t58dpdV8uTIPn7tJ12bNhlJTJ6/0e/3UVX+/GE+W3aV8f51g/3aT7o2rZsksW13OSVllaQEMQ5jjDHhxds+09NU9Snno0El0rA/mQ7kluIVVS5ufXcuMVHCoxf09usmJZ7omJ1CweYSv/fjfeqrAuas3c7fz+0ZkN7Kh9MuK4W1xXuoqHL59T5frK3k62VF3H1mVzpmp/r1XrXJzUhm+54Ktu8p9+t9Ppy7no/nb+TWUzr5dQdPT7R26rTXWamHMcYYLwTucfkIkOjUKQfyIcRnphUwd912HjqvJ83TgptUgrtueldZJZt2+q+jx+y1v/D0tALO69uSs3q38Nt9PNUuM5lKl/o1yVq+eRfjl5ZzQucsLhnYxm/38VSbDPeDl2v8WOqxbtse7vlwIUfmNg5aGU9N1cm01U0bY4zxhiXTXkhySjsC1R5v7rrtPPVVAef2bcnQXsFPKgE6OB09/LUT4u6ySm59dy7NGiVwXxA6lhxMu+r2eH6qmy6vdJe0JETDP4f3CvjDrQeT67THW+2nhxCrXMofxs9DgccuCG4ZTzVbmTbGGFMXlkx7YV+ZRwCS6T3l7qQyOzWe+84OjaQS3GUegN9qiP82eRFrt+3h8RF9aJQQ65d7eKt9dXu8rf4Z8+NfLGPhhp1c2SOepqmBbYN3KK2aJCHiv5XpF75ZwYzV23hgWPeAt8E7lLSkWFITYhrsyrSIJIjIDBGZJyILReR+5/g4EVkqIgtE5BURiXWOi4g8KSIFIjJfRPoFdwTGGBMclkx7IbHGA4j+9tCUxawu3s2jF/QhLTE0kkqAjOQ4GifFUuCHjh6fL9rMOz+v45rj2jOgbROfX7+u0pPiaJIc55eV6RmrtvH81ysYeWQr+mWHzkNvCbHRNG+U4JeV6QXrd/D458s4s2dzzu0b2I2HatPA2+OVASeqam+gD3CaiAwExgFdgJ649xUY7Zx/OtDR+bgaeC7gERtjTAiwZNoL1b2d/b0yPW3JFt6cvpbRx7RlUPsMv97LWyJCx6apFPh4ZXrLrlLueH8+3Zo34rZTOvn02r7QLjOZFT7euGVnqbslXOsmSfx1aDefXtsX2mQk+3xlurSiilvenUuT5Dj+fm6PkChpqakhJ9PqVv2XPNb5UFWd4rymwAwgxzlnGPC689J0IF1EgtMk3Bhjgih0lsLCQKJTM73Xj908ikvKuH3CfLo0S+WPpwavz/Dh5GYm8dWSIp9dT1W5Y4K7JdwTI/sEdBtpT7XPSuGLxZt9es37Ji1k085S3rt2UFBbwh1KbmYSny/y7Zj/8ckSCraU8MaoAaQnxfn02r7QukkSXy7ZgsulQe+cEwwiEo17L4EOwDOq+lON12KBS4GbnUMtgXU13l7oHPtVT0URuRr3yjXZ2dnk5eV5HVdJSUmd3hcOInlsENnji+SxQWSPz9djC73v4CFsf5mHf7p5qCp3Tcxn594K3hg1IKh9hg+nbWYKW0sK2Vla4ZO65jd/Wsu0pUXcd1a3oLeEO5R2WckUzyxnx54K0pLqP+Yp+RuZOHs9N53UkX6tG/sgQt9rk5HM1pJydpVWkOqDP+e8pVsY+8Nqrjw6l2M7ZvkgQt9r1SSJ8koXW3aV0SwtNOrXA0lVq4A+IpKOe6OuHqq6wHn5WeAbVf3Wy2u+CLwI0L9/fx0yZIjXceXl5VGX94WDSB4bRPb4InlsENnj8/XYQm8JMIT5+wHE92YWMnXRZv54aie6Nm/kl3v4QttM9wN5q7fWv562YEsJf/94Ecd1yuKyQbn1vp6/VHf0KPBBqceG7Xu5a2I+vVulc+OJHep9PX+p7ujhi1KPneXKH9+bT6fsFO44rUu9r+cv1h7PTVW3A9OA0wBE5F4gC7itxmnrgVY1vs5xjhljTINiybQXEv3YGm/V1t3c99FCBrZrEvRdDmvTzulusaqeyXRZZRU3vzOHxNho/j28V0j/Wr1TdReTzfV78LLKpdw2fi4VVS6eGNGH2OjQ/Sfoq17Tqsor+WXs3FvBEyP7BnT3UG815GRaRLKcFWlEJBE4BVgiIqOBU4ELVbXmzkWTgMucrh4DgR2q6v9tM40xJsRYmYcXoqKEhNgon9dMV1S5uOWdOcRGR/H4iD4hnVSCO+EQqX8y/chnS1m4YSf/vaw/2Y1C+1fqrRonkRAbxbJ69td+4ZsVTF+5jX8N70Wus8Ifqtr4qNcZJM5IAAAgAElEQVT0uJ/WMreoir8O7RbSv3EBaJGeiEjDTKaB5sBrTt10FDBeVSeLSCWwBvjReWB0oqo+AEwBzgAKgD3AlcEJ2xhjgsuSaS8lxcWwx8c1049/vox5hTt47uJ+IbHLYW0SYqNpkZZYrzKPb5cX8d9vV3HJwNac0i3bh9H5R1SUu4vJsnqsTM8v3M5jU90t4c4/Iqf2NwRZUlwMWanx9fpzXrZ5Fw9+vIgeGdFcOTjXd8H5SVxMFC3SEhvkxi2qOh/oe5DjB/0+4XT3uMHfcRljTKgL3d8xh6jE2Giflnn8uKKY575ewYj+rTi9Z/h0lWqXlVznlemtJWXcNn4eHZqm8JczQq8l3KF0zE6pczK9s7SCMW/NoWlqPA+d2zPkWsIdSsemKSyt45j3llcx5q3ZpMTHMLpnXMj/xqVaqyaJDXVl2hhjTB1YMu2lpLhon23aUlxSxs3vzKFtRjL3nBU+SSVAbkYyK7fuxr045TmXS7n13bns3FvBUxf23dchJRx0zk5ly64ytu8p9+p91V1a1m/fy5MX9vVJN5BA6ZWTzuKNOymr9P7v/AOTF7FscwmPXdCH9ITwmWoacq9pY4wx3guf73AhIjHONyvTLpdy6/h5bN9bwdMX9QvJPsOH0zYzmV2llWzb7V1i+dzXK/h2+VbuPat7yNfPHqiT07bP27rpt2es4+P5G/nD/3Wif27o7Ozoid45aVRUKYs3erc6PXn+Bt6esZZrj2/PcZ1Csw3eobRukkTRrrKA7HRqjDEm/Fky7aXE2GifPID4/Dcr+GZZEfcM7Ua3FuGVVAK0rUNHj59WFvPo1KWc3bsFFw5oVfsbQkynZtXJtOeJ5aINO7n/o4Uc2zGTa49r76/Q/KZXq3TAXe/tqYItJdz5fj59W6fzh/8Lvd0sa9Pa6WKycqtvd7w0xhgTmSyZ9pIvyjzcSeUyzuzVnIuPau2jyAKr7b6Ew7NkesvOUm58ew5tMpJ56LzwqRmuqUVaAinxMR63x9u+p5xr3pxJelJsWHRpOZgWaQlkpsQxb90Oj84vKavk2jdnER8TxTMX9Qvp1n+HcmSuexOdHwqKgxyJMcaYcBB+3+mCrL7dPDZs38sNb82mTZMkHg7TpBIgp3EiMVHiUaeHssoqrn1zFiVllTx3ST9SwqykpZqI0MHDB/KqXMpN78xl045SnrvkCDJT4gMQoe+JCL1z0pnnwcp09bbwK4tKeOrCvrRID/3ONAfTPC2Rjk1T+GZ5kUfnT56/gUqXd88OGGOMiRyWTHspsR4r06UVVVz35ixKK1y8eNkRPtmKO1hioqNonZFUa5mHqnLv/xYye+12Hj2/N12ahV9JS02ds1NZ7kHN9GOfL+WbZUU8MKxHyG4X7qleOemsKCqhpOzwP0S++M1KPs7fyJ9O68LgDpkBis4/juuUxYxV2yitpaTrjR9XM+atOXxd6Nt2mcYYY8KHJdNeSoqLZk8daqZVlbs/XMC8wh08ekFvOjRN9UN0gdU2o/b2eG9MX8M7P69jzAkdwqr136F0zE6heHc5W0vKDnnOxNmFPDNtBRcOaMWFA8KzjKemXq3SUIX8wkOXenySv5F/fLqEM3s255rjQnsHT08c2zGTskoXM1ZtO+Q5eUu3cN9HizipS1NOaBWev20xxhhTf5ZMe6mu3Tye+3oFE2YVctOJHTi1ezM/RBZ4bTOTWV28G9chfsX96YKN3DtpISd3bcqtp4Tfg2gH07mWhxC/W76VP02Yz+D2Gdx/do9AhuY3vXPcDyEeqtRj9tpfuOXdufRtlc6jF/QO29Klmo5qm0FcTBTfHqLUY+mmXYx5aw6ds1N58sK+REXAmI0xxtSNJdNeSoqNobzSRZUXNZITZxfyr0/dXSxuOTkykkpwd/QorXCxaWfpb16bvrKYm95xJ1hPXdiP6DB8+O5gqtvjHazUY+GGHVz75iw6NE3h+UuPIC4mMv55NUmOo1WTxIN29Fi1dTdXvTaTZmkJ/Pey/iTEhk/f8MNJjItmQG4Tvlm29Tevrdu2hytfnUFSXDQvX9E/7NpaGmOM8a3I+G4fQIlx7v9lnj6EWL1SOahdBv8+v1dYdnQ4lOqOHgc+hJhfuIOrXp9J6yZJvHz5kWG1MUttmqbGk5YY+5uHEBes38Hlr/xMakIMr155ZFjXwx9Mr5z033T0WLZ5FyNe+BGXKq9ecSQZYfqQ5aEc2zGTpZt3sbnGD4tri/cw4oUf2V1exatXHknztPB8yNIYY4zvWDLtpcQ49yqUJ72mZ6zaxjVvzKR9lnulMj4mcpJK2N9r+ufVv+zbCXHqwk1c8MKPNEqI5bXfD6BxclwwQ/Q5EaFTdsqv2uN9t3wrI1+cTly08MaooyIyweqdk8b67Xv31YrnF+5gxAs/AvDuNYNol5USzPD84tiO7s1mvlnmLvVYtXU3I178kT0VVbx11VF0b5EWzPCMMcaECPv9pJeSnF9j19bR44cVWxk1diYt0hN4fdQA0hIja6USIDs1gS7NUnn8i2VMXbSJAW2bMPaH1fRqmcZ/L+9P09SEYIfoFx2zU5kws5DLX5lB46RYPs7fSLvMFF77/QCapUXmmKvrpv/16RJ2lVbyzbIi0pPiGDf6KHIzk4McnX90bZ5KZko8H8xZz48ri/lo3gZS4mN4a/TAsNxoyRhjjH9YMu2lJKdk4XAPIX69rIhr3phJq8ZJvHXVQLJSI+vX39WiooT/jTmaD+es54VvVvLq96s5vUczHrugT0SVdhxo5JGt2LKzlM07y1iyaSfHdszi8RF9IvIHpmo9WqaRGBvN+JmFtG6SxKndm/HHUzuHbS9pT4gIx3XMZOKc9STFRXPxUW0YfWxbchonBTs0Y4wxIcSSaS8lHiaZVlVe/m4VD01ZTKfsVN4cfVTYbtbhqfiYaEYc2Zrzj2jFkk276NIsNaLqwg+mV046L11+ZLDDCKjk+Bg+v+04EmKjI/7vdE23ntKJI9s24YyezSP6hyVjjDF1Z8m0l5Kqa6YPSKb3llfx5w/y+WDOek7tns2jF/QJ253+6iIqSuxX3xGuIa7ItmqSFBG9wo0xxvhPw8n2fGR/mcf+bh7TlmzhnkkLKPxlL384pRM3nNAh4ldnjTHGGGNMALt5iMhpIrJURApE5M6DvB4vIu86r/8kIrmBis0b1WUeeyuqyC/cwdWvz+TKsT8TFx3FuNFHceNJHS2RNsaEHRFJEJEZIjJPRBaKyP3O8bbOnFzgzNFxzvGwmLONMcbfArIyLSLRwDPAKUAh8LOITFLVRTVOGwX8oqodRGQk8E9gRCDi80ai083j/o8WsW13OUlx0dxxWhdGHdM2YjbpMMY0SGXAiapaIiKxwHci8glwG/C4qr4jIs/jnqufI0zmbGOM8bdAZX8DgAJVXamq5cA7wLADzhkGvOZ8PgE4SUJwX+LGSXGkJcaSmRLH/Wd3Z/qfT+K6Ie0tkTbGhDV1q97aM9b5UOBE3HMyuOfoc5zPw2LONsYYfwtUzXRLYF2NrwuBow51jqpWisgOIAP47X6+QZQYF82su08mOkqw7xvGmEji/BZxFtAB928TVwDbVbX6IZFC3HM1hMmcbYwx/hZ2DyCKyNXA1c6XJSKytA6XySRyJ/xIHhtE9vhsbOGrLuNr449A6kNVq4A+IpIOfAB0qe81bc6uVSSPDSJ7fJE8Nojs8dV1bAedtwOVTK8HWtX4Osc5drBzCkUkBkgDig+8kKq+CLxYn2BEZKaq9q/PNUJVJI8NInt8NrbwFWnjU9XtIjINGASki0iMszpdc+62OdsHInlsENnji+SxQWSPz9djC1Sh789AR+ep8DhgJDDpgHMmAZc7nw8HvlJVDVB8xhjToIlIlrMijYgk4n5gfDEwDfecDO45+n/O5zZnG2MMAVqZdurpxgCfAdHAK6q6UEQeAGaq6iTgZeANESkAtuFOuI0xxgRGc+A1p246ChivqpNFZBHwjog8CMzBPVeDzdnGGAMEsGZaVacAUw44dk+Nz0uB8wMUTr1+5RjiInlsENnjs7GFr7Afn6rOB/oe5PhK3B2ZDjxuc7ZvRPLYILLHF8ljg8gen0/HJvZbOWOMMcYYY+rGmiMbY4wxxhhTRw0qma5tS/NwJiKtRGSaiCxytgK+Odgx+ZqIRIvIHBGZHOxYfElE0kVkgogsEZHFIjIo2DH5kojc6vydXCAib4tIQrBjqisReUVEtojIghrHmojI5yKy3Plv42DGGGkidd62OTu8RfK8HUlzNgRm3m4wyXSNLc1PB7oBF4pIt+BG5VOVwB9UtRswELghwsYHcDPu7gKR5gngU1XtAvQmgsYoIi2Bm4D+qtoD9wPI4fyg2ljgtAOO3Ql8qaodgS+dr40PRPi8bXN2eIvIeTsC52wIwLzdYJJpPNvSPGyp6kZVne18vgv3P+yWh39X+BCRHOBM4KVgx+JLIpIGHIfTIUFVy1V1e3Cj8rkYINHpRZwEbAhyPHWmqt/g7lxRU81ttWtut23qL2LnbZuzw1cDmLcjZs6GwMzbDSmZPtiW5hEzcdUkIrm4n8r/KbiR+NR/gD8BrmAH4mNtgSLgVefXoS+JSHKwg/IVVV0PPAKsBTYCO1R1anCj8rlsVd3ofL4JyA5mMBGmQczbNmeHnYidtxvInA0+nrcbUjLdIIhICvA+cIuq7gx2PL4gIkOBLao6K9ix+EEM0A94TlX7AruJoDIBpw5tGO5vPi2AZBG5JLhR+Y+zaYm1SDIeszk7LEXsvN3Q5mzwzbzdkJJpT7Y0D2siEot7Uh6nqhODHY8PHQ2cLSKrcf+a90QReTO4IflMIVCoqtUrUhNwT9KR4mRglaoWqWoFMBEYHOSYfG2ziDQHcP67JcjxRJKInrdtzg5bkTxvN4Q5G3w8bzekZNqTLc3DlogI7vqtxar6WLDj8SVVvUtVc1Q1F/ef21eqGhE/KavqJmCdiHR2Dp0ELApiSL62FhgoIknO39GTiJAHdWqoua12ze22Tf1F7Lxtc3b4ivB5uyHM2eDjeTtgOyAG26G2NA9yWL50NHApkC8ic51jf3Z2njSh7UZgnJMsrASuDHI8PqOqP4nIBGA27u4FcwjjXbVE5G1gCJApIoXAvcA/gPEiMgpYA1wQvAgjS4TP2zZnh7eInLcjbc6GwMzbtgOiMcYYY4wxddSQyjyMMcYYY4zxKUumjTHGGGOMqSNLpo0xxhhjjKkjS6aNMcYYY4ypI0umjTHGGGOMqSNLpo0xxhhjjKkjS6ZNWBGRDBGZ63xsEpH1zuclIvKsH+43VkRWici1Xr5vioik13LOv50x/LF+URpjTGiyOds0BA1m0xYTGVS1GOgDICL34d704GlVfcmPt71dVSd48wZVPQPA2U53tKp+cZBzbheR3b4J0RhjQs9B5uwSVX3Ez7et85xdyzk2Z5uDspVpE/JEZLWI7HVWMjY7Kw8pB5wzREQmO5/fJyKvici3IrJGRM4TkX+JSL6IfCoisc55R4jI1yIyS0Q+E5HmHsQyVkSeE5HpIrLSua+KiEtEKpxVl8ecmDNx/8D6soj8V0QWishUEUk8yHWHODszGWNMxAvynP2KiCwWkbE1zlstIpkikuu8dtg525iaLJk24eIsVU0B+gH9gbtrOb89cCJwNvAmME1VewJ7gTOdyfkpYLiqHgG8Avzdw1gaA4OAW4FJzrHOwHzgBuAiILXG+TnAM6raHdgO/M7D+xhjTEMRyDn7caA70FNE+hzk/I7YnG28YGUeJqyo6noR+QToAcx0DrcBbga6ishUYC7wiapWiMjdQCLwjojMAxYCubiT3z7AOmeSdgErq+8jIkOBB4FuwCARWaaq852XP1JVFZF8YDPuxFmdawN8C5xaI+yNqjpXROKBFsCzIvIvYDywC4gDPgHiRaTEeU8nVd1Q3/9fxhgTJqrn7HwgGvjUOZ7P/jm7B/C5iOCcs9HDa/9qzlbVfAARqf5+MPeA81epavWxWc45xhySrUybsCIirYAzgDk1Dl8E/BOYijsxHQyUOa99AuwGmgKzgXNx/xApzn9PUdVo5/ULnXv0xb3qcQ3wtnPdSU4yTI1ru2p8Xv11LnAsUF7jeIXz378ArYAXgN7AAOA459zTgQ2qmuJ8WCJtjGlIygBU1QVUqKo6x13sn7MXqmof56Onqv6fN9fm4HP2wRYVa55TdYhzjNnHkmkTLj4Uke3Ad8DXwEM1XnsVKMQ9MY4HmlW/oKqvOP8tA+4DsoEEYCnuyXmoiDQCStg/gV4NvKCqP+Fecf7aeW3gYeKbjTsZvxN4ybnegS4GPgd2q2oRcD/upNoYY8zhLQWyRGQQgIjEikj3IMdkDGDJtAkf56hquqq2UdXrVXVvjdc21fh8D+7VaUQkWkT+ASSJyE5gtXNOsqqWA1cAo4BtuOviLnFebwP8wUneLwJew72i3OIw8fXDvYo9RlUPVc/dAvilxtdr+HVttTHGmINw5uzhwD+dkr25uH8LaUzQyf7fpBgTmg7XXk5E8oA3q1vjicgVzrnHiMilwJ9xl4WsBtJwJ7MdVbWgxjVigTHAbaraSkReANaq6t+dp70nH67Nkojogdc8WOwisgK4UVWnOK/9H+6V9AeBn4Fxqprjzf8bY4wx+3kyZ9fz+vcRmPZ+JozYyrSJZKm4yzOKgSRqlIaISJyIXCwiaapaAezEXSYC8F/gWhE5CtgBPCgiT4tIfVeR3wbuFpEsp23eK849d+N+kDFDRNLqeQ9jjGnIdgB/Ey83bfGEiPwb928wrde0+RUrqjeR7HXcXTXW4y7l+CtwXY3XLwWeFpFo3PV4FwOo6kwRuQp4GneLpL24a63r60GgEe4WegDvAX9S1VIAEXkbWOnE080eQjTGGO+o6s1+vPbtwO3+ur4JX1bmYYwxxhhjTB1ZmYcxxhhjjDF1ZMm0McYYY4wxdWTJtDHGGGOMMXVkybQxxhhjjDF1ZMm0McYYY4wxdRTWrfHS09O1Q4cOwQ4joHbv3k1ycnKwwwgoG3PD0NDGPGvWrK2qmhXsOIwxxtRPWCfT2dnZzJw5M9hhBFReXh5DhgwJdhgBZWNuGBramEVkTbBjMMYYU39W5mGMMcYYY0wdWTJtjDHGGGNMHVkybYwxxhhjTB2Fdc20MSayVFRUUFhYSGlpabBD8ZmEhARycnKIjY0NdijGGGP8wJJpY0zIKCwsJDU1ldzcXEQk2OHUm6pSXFxMYWEhbdu2DXY4xhhj/MDKPIwxIaO0tJSMjIyISKQBRISMjIyIWmk3xhjza5ZMG2NCSqQk0tUibTzGGGN+zZJpY4xxlJaWMmDAAHr37k337t259957AVi1ahVHHXUUHTp0YMSIEZSXlwMwduxYsrKy6NOnD3369OGll14KZvjGGGOCwO/JtIhEi8gcEZl8wPEnRaSkxtfxIvKuiBSIyE8ikuvv2Iwxpqb4+Hi++uor5s2bx9y5c/n000+ZPn06d9xxB7feeisFBQU0btyYl19+ed97RowYwdy5c5k7dy6jR48OYvTGGGOCIRAr0zcDi2seEJH+QOMDzhsF/KKqHYDHgX8GIDZjjNlHREhJSQHcnUUqKioQEb766iuGDx8OwOWXX86HH34YzDCNMcaEEL8m0yKSA5wJvFTjWDTwb+BPB5w+DHjN+XwCcJJYsaExJsCqqqro06cPTZs25ZRTTqF9+/akp6cTE+NufpSTk8P69ev3nf/+++/Tq1cvhg8fzrp164IVtjHGmCDxd2u8/+BOmlNrHBsDTFLVjQfkyi2BdQCqWikiO4AMYGvNk0TkauBqgKysLPLy8vwWfCgqKSmxMTcADXXMaWlp7Nq1C4Cef//GL/fJ/8txtZ7z7bffsn37di6++GJmz56Ny+XaF1dJScm+r4cMGUJ+fj7x8fG88sorXHLJJUyePPk31ystLW1wf57GGNNQ+C2ZFpGhwBZVnSUiQ5xjLYDzgSF1va6qvgi8CNC5c2fVZt1wqXJil6YN4qn5vLw8hgwZEuwwAsrG3DDk5eWRkJBAampq7SfXg6fXT01N5eSTT2bevHns3LmTxMREYmJi2L59O61atSI1NfVX1xozZgz33HPPQa+fkJBA3759fTYGY4wxocOfK9NHA2eLyBlAAtAIWAiUAQVO4pskIgVOnfR6oBVQKCIxQBpQXNtNrhs3i9IKF+f1a8mD5/QgKc72oTEmEqz+x5kBv2dRURGxsbGkp6ezd+9ePv/8c+644w5OOOEEJkyYwMiRI3nttdcYNmwYABs3bqR58+YATJo0ia5duwY8ZmOMMcHlt8xTVe8C7gJwVqb/qKpDa54jIiVOIg0wCbgc+BEYDnylqlrbfWKjoyitcDFx9nrmF+7gmYv60bmZf1e2jDGRaePGjVx++eVUVVXhcrm44IILGDp0KN26dWPkyJHcfffd9O3bl1GjRgHw5JNPMmnSJGJiYmjSpAljx44N7gCMMcYEXCgt474MvCEiBcA2YKQnb8pKiWdXaSVNkuMo2FLCsGe+44Gze3B+/5wGUfZhjPGdXr16MWfOnN8cb9euHTNmzPjN8YcffpiHH344EKEZY4wJUQHZtEVV8w5clXaOp9T4vFRVz1fVDqo6QFVXenLtzJR4AB45vxfDj8ihtMLFn96fzx/Gz2N3WaXPxmCMMcYYY8yBwn4HxMzUOABKyqp45PzePHJ+bxJjo5k4Zz1nP/0dSzbtDHKExhhjjDEmUoV/Mu2sTBeXlAEw/IgcJo05mo5NU1hRtJthT3/Puz+vxYPya2OMMcYYY7wS9sl0RrI7md7qJNMAHbNT+d+Yozn/iBzKKl3c8X4+t1nZhzFhIdJ+8I208RhjjPm1sE+mq8s8tu4q/9XxpLgY/n1+bx51yj4+mLOes6zsw5iQlpCQQHFxccQkoKpKcXExCQkJwQ7FGGOMn4RSN486qS7zqLkyXdPvjsihV04aN7w1m2WbSxj29Pfcf3Z3RhzZyrp9GBNicnJyKCwspKioKNih+ExCQgI5OTnBDsMYY4yfRHwyDU7Zxw3HcO+kBYyfWcidE/P5cWUxfz+3JynxYf+/wJiIERsbS9u2bYMdhjHGGOOxsC/zyNqXTJcf9rzEuGj+Nbw3j13gLvv439wNnP3UdyzeaGUfxhhjjDGmbsI+mc5IcWqmS8o8qrM8r18OH914NJ2zU1m5dTfnPPM9b8+wbh/GGGOMMcZ7YZ9MJ8fHkBgbTVmlixIPu3V0aJrKhzcczcgjW1FW6eKuifnc8u5cj99vjDHGGGMMREAyDTU6etRS6lFTYlw0//hdLx4f0ZukuP1lH4s2WNmHMcYYY4zxTGQk0x48hHgo5/bNYdKYY/aXfTz7PW/9ZGUfxhhjjDGmdpGVTO/yPpkG6NA0ZV/ZR3mliz9/kM9N78xlV2mFL8M0xhhjjDERJrKS6d2el3kcqLrs4z8j+pAUF81H8zZw9tPfs3DDDl+FaYwxxhhjIkyEJNPVuyDWbWW6pnP6tuSjG4+hS7NUVm3dzbnP/sC4n9ZY2YcxxhhjjPmNCEmm614zfTDts9xlHxcOaE15pYu/fLCAG9+eY2UfxhhjjDHmVyyZPoSE2GgePq8nT4zsQ3JcNJPnb+Ssp75jwXor+zDGGGOMMW4RkUw3T08AYN22vT6/9rA+LZnklH2sLt7Dec/9wBvTrezDGGOMMcYEIJkWkWgRmSMik52vx4nIUhFZICKviEisc1xE5EkRKRCR+SLSz9N7dGyaAkBBUQlVLt8nudVlHxcd5S77+OuHCxhjZR/GGGOMMQ1eIFambwYW1/h6HNAF6AkkAqOd46cDHZ2Pq4HnPL1BakIsLdMTKa90saZ4t0+CPlBCbDQPnbu/7ONjK/swxhhjjGnw/JpMi0gOcCbwUvUxVZ2iDmAGkOO8NAx43XlpOpAuIs09vVenbPfq9LLNu3wV/kEN6+Pu9tG1eSN32cezVvZhjDHGGNNQ+Xtl+j/AnwDXgS845R2XAp86h1oC62qcUugc80inZqkALN1UUsdQPdcuK4UPrh/MxUe1przKKft4aw47rezDGGOMMaZBifHXhUVkKLBFVWeJyJCDnPIs8I2qfuvlda/GXQZCVlYWeXl5ALi2uRPZ7xasoHfM+roH7oVTGkNq73jGLijj4/yN/LxiE9f3jic3Ldpv9ywpKdk35obCxtwwNMQxG2OMCX/ir/IEEXkY98pzJZAANAImquolInIv0Bc4T1VdzvkvAHmq+rbz9VJgiKpuPNQ9OnfurEuXLgVgwfodDH3qOzo0TeGL2473y5gOZdXW3Vw/bjaLN+4kLjqKvw7tyiUD2yAiPr9XXl4eQ4YM8fl1Q5mNuWFoaGMWkVmq2j/YcRhjjKkfv5V5qOpdqpqjqrnASOArJ5EeDZwKXFidSDsmAZc5XT0GAjsOl0gfqEPTFKLEndiWVVb5cii1apuZzAfXD+aSgU7Zx/8WcsNbs63swxhjjDEmwgWjz/TzQDbwo4jMFZF7nONTgJVAAfBf4HpvLpoQG02bjGSqXMrKIv909Kjt/g+e05OnL+pLSnwMU/I3MfTJ78gvtG4fxhhjjDGRym810zWpah6Q53x+0Hs63T1uqM99OmWnsGrrbpZt3kXX5o3qc6k6G9qrBT1apHHDW7NZuGEnv3vuB/5yZlcuG+Sfsg9jjDHGGBM8EbEDYrXO2dUdPfzbHq82uZnJvH/dYC4d2IbyKhf3TlrI9eOs7MMYY4wxJtJEVDJd3R7P372mPZEQG83fzumxr+zjkwXuso/5hduDHZoxxhhjjPGRiEqm961Mh0AyXW1orxZMvvEYurdoxNpte/jdcz8w9vtVtsmLMcYYY0wEiKhkOjczmdhoYd22vewuqwx2OPtUl31cNqgNFVXKfR8t4ro3Z7Njr5V9GGOMMcaEs4hKpmOjo2if5d5WfPkW/++E6I2E2GgeGNaDZy/uR2p8DJ8u3MTQpxQBBmsAACAASURBVL61sg9jjDHGmDAWUck0QBenbnru2l+CHMnBndGzOZNvOoYeLRuxbttefvfcD7xqZR/GGGOMMWEp4pLpoztkAvD1sqIgR3JobTLcZR+XO2Uf93+0iGvfnGVlH8YYY4wxYSbikunjO2cB8MOKYkorArsTojfiY6K5v0bZx2cLN3Pmk98yb52VfRhjjDHGhIuIS6abpibQo2UjyipdTF9ZHOxwalVd9tGzZRqFv+xl+PM/8Mp3VvZhjDHGGBMOIi6ZBjihc1MA8paGbqlHTW0ykplw3SCuGJxLRZXywORFXPPGLHbssbIPY4wxxphQFpHJ9BCn1CNv6ZYgR+K5+Jho7ju7O89f0o/UhBimLtrMmU99y1wr+zDGGGOMCVkRmUz3adWYtMRYVhfvYdXW3fuOu1yhXzpxWo/mfHzjsfTKcZd9nP/8D7xsZR/GGGOMMSEpIpPp6CjhuE77V6f3lFfylw/yaffnKfR/8HO+WLQ5yBEeXuuMJN67dhBXHu0u+/jb5EVcbWUfxhhjjDEhJyKTaYAh+5LpIrrd8xnjfloLwNaScka/PpPrx81iy87SYIZ4WPEx0dx71v6yj88XbeaMJ79l5fbQ7VBijDHGGNPQRGwyXb0yfah+01PyNzHgoS95e8bakC7/OK1Hc6bcdCy9c9JYv30vf/+plJe+XWllH8YYY4wxISDmUC+IyJMevH+nqt7tw3h8Jis1nl45acwv3HHY8+6amM/L363i+UuOoEPTlABF551WTZJ479rB/OOTJbzy/Soe/Hgx01du45Hze5GeFBfs8IwxxhhjGqzDrUwPA2bV8vE7fwdYH9WlHrUp2FLCyY99zWNTl1Je6fJzVHUTFxPFPWd148a+8TRKiOGLxZs588nvmB2i26YbY4wxxjQEh0umH1fV1w73AbxQ2w1EJFpE5ojIZOfrtiLyk4gUiMi7IhLnHI93vi5wXs+t7+BO6NL0N8dWPXwGk288hmM7Zv7mtSe/KqDT3Z/w6YKN9b213xyRHcPHNco+Lnj+Ryv7MMYYY4wJksMl0+8f6gURGQqgqv/x4B43A4trfP1P3Il6B+AXYJRzfBTwi3P8cee8eunTKp3O2am/OiYi9GiZxhujjmLFQ2dwz9Buv3nftW/OJvfOj3nth9WUlFXWNwyfqy77+P3Rbal0KQ9+vJirXp/F9j3lwQ7NGGOMMaZBOVwy/fnBVodF5PfAE55cXERygDOBl5yvBTgRmOCc8hpwjvP5MOdrnNdPcs6vMxHhyqNzD/l6dJTw+2PasvofZ/L+dYN/8/q9kxbS497PuPXduWzZFVqdP6rLPl649Agr+zDGGGOM+f/27jy8qure//j7k4FJRhUVQQ2iooiCCopVruBQQazaOlvHH4p2UKudwGod2l7xVq+3aK0T1qGtFW1VyuBQJRVUQFBBQEDUaKHOCooMMnx/f5ydmDAkJyc5Jyfh83qe/bj32tN3AT7PNyvfvVYDqS6Zvhx4StLu5Q2SRgCXAYel+fz/A34GlBcibwMsjYjy4d7FQOdkvzPwb4Dk/LLk+jo5Yb/ONV8EHLBLB8pGDuEv5x+00blHX1nCgb95huc2MzNIQzp67x1SZR87ta8o+7jrOZd9mJmZmeWCqku6JB1Bqi76BOB84EBgSETUOPyZlIIcExHflzQA+AlwLjA1KeVA0k7AxIjoKWkOMCgiFifn3gQOioiPN3juMGAYQMeOHQ8YM2ZMjZ0894mvV0H8Zb8W7Nq+sMZ7Ji9ew+g5G5dN9Nm+kIt6NaeooE6D5hlbvnw5rVtvPOvI2vXBwwu/4smy1M8pvToWcsE+zWndrGHirE+b63NT5j43fQMHDpwZEX0aOg4zM6ubapNpAEn9gUeBF4BTIiKtegdJ1wNnAWuBFkDb5DlHAztExFpJBwPXRMTRkp5M9l+UVAS8D3SMagLs3r17LFiwoMZYlixdySEjn604Lhs5JJ0usH598JNHZvH3l5dsdO5PQw/i0E18xJhtpaWlDBgwYLPnn573AT95eBbLVq5hx3YtuOWM/Tlglw65CzALaupzU+Q+N32SnEybmTUBmy3zkPSFpM+BCaQS4SOADyu1VysiRkREl4goAU4Dno2I7wKTgJOSy84BHk/2xybHJOefrS6Rro3O7VtWOV6X5iItBQXif0/pzWvXfHOjc2eOnkbv657Ku6n0juqxPeMvOZTeO7XnP8tWceodL3Lnc2/m9cI0ZmZmZo3VZpPpiGgTEW2T/zaLiK0qHbetwzt/DlwuaRGpmujRSftoYJuk/XJgeB3esZGR39mnYr/bFRNqdW+bFsWUjRzCYz84pEr70hVr2OPKibzxwRf1EmN96dKhFWMuPJgL+qdm+/jvCfO54P4ZfPalZ/swMzMzq085WU48Ikojonw6vbci4sCI2C0iTo6I1Un7quR4t+T8W/UZw2kH7lznZ/TeqT1lI4fwvQHdqrQfdfNzDLt/Rp2fX5+aFRXwiyE9uOvsPrRrWcwz8z9kyKjJzHzn04YOzczMzKzJqK7M4+Wabk7nmnzyrV47Vuyffc/0jJ/z80F7Mufao6u0PTXvA0qGj+fTPBv9LS/72G/nVNnHKXdM5Y5/uezDzMzMrD5UNzK9l6TZ1WyvAbn/Aq8Objq5V8V+Xae5a928iLKRQ7j77KrfD+3/q6e57h/z6vTs+lZe9jHsv3Zl3frg+onzGXrfS3mX+JuZmZk1NtUl03sC36pmOxbYeKWTPNasqIBdO25VcXxOHUanyx3ZY3ve+u9jqrTd8/zblAwfz5p1+fNxYnFhAVccsxejz+lD+1bFTFrwEUNGTWZGmcs+zMzMzDJV3QeI76SxLc5lsPXhmcu/Xm/mXws/qpfFTQoKRNnIIdx+5v5V2nf/xUSeef2DOj+/Ph2x1/aMv6Q/++/cnveWreLUO6dyu8s+zMzMzDKSkw8Q84kkLjrs6w8Iu46o3cwe1RnUsxPzfzWoStvQ+2bQ7YoJeTWFXuf2LXnowoO5MCn7GDlxPv/PZR9mZmZmtbbFJdMAwwfvWeX4tcXL6u3ZLYoLKRs5hCH7dqpoW7c+2OPKiSz+bEW9vaeuigsLGHHMXtxzbqrso3TBRxzzu8m85LIPMzMzs7SllUxL2kXSkcl+S0ltshtW9k35+cCK/W/dOqXen//7M/Zn/CWHVmk79IZJ/GXau/X+rro4fM/tmXBJfw7YpQPvf76K0+6cym2li1z2YWZmZpaGGpNpSRcAjwB3JE1dgMeyGVQudOnQqspxyfDx9f6OvXdsx6LfDK7SdsWjr9F1xPi0V2HMhR3bt+Svw/px4WGpso//eWIB593rsg8zMzOzmqQzMv0D4BDgc4CIeAPYLptB5UrZyCFVjue/X+Mq6bVWVFhA2cghnPuNkoq2iNQqjB99sbre35ep4sICRgzeiz+e25cOrYr510KXfZiZmZnVJJ1kenVEVAxRSioC8mdYtY7GXfx1Kcag/5tcL7N7bMo1x+3NPyvNJALQ9zf/5O8v59eEKAP33I7xLvswMzMzS0s6yfS/JF0BtJR0FPAw8I/shpU7PTu3q3Jcn7N7bGi37VpvNCf15WNm0f3KiVlL4jNRXvZx0WHdqpR9fLI8f0bSzczMzPJBOsn0z4GPgNeAC4EJwJXZDCrXNiz3OPaWyVl7V/mc1BcetmtF2+q16+k6YgLLVqzJ2ntrq7iwgOGD96xa9jFqMtPfdtmHmZmZWblqk2lJhcDrEXFXRJwcEScl+/kzjFpPKn8oOGfJ5zz+6pKsvm/E4L2Y/LOBVdp6XfcU/5j1n6y+t7YG7rkdEy7tT59dOvDB56s57c4X+f0kl32YmZmZQQ3JdESsAxZI2jlH8TSYosICHv3+16ujX/rXV/n3p9mdF3qnrVvx9vVVyz4ufvAV9rn6ybwq++jULlX28f0B3Vgf8NsnF3Cuyz7MzMzM0irz6ADMlfSMpLHlW7YDawj77dyBK475ekGX/v8zidVr12X1nVKq7OOSw3eraPti9Vq6jpjAl6vXZvXdtVFUWMDPBu3Jveelyj6eS8o+pr31SUOHZmZmZtZg0kmmrwKOBa4Dbqq0NUnD/qsb/XfftuK4+5VP5GSU+PJvdueF4YdXadv76id5Ys57WX93bQzonir76FuSKvs4/a6p3PrsGy77MDMzsy1Sjcl0RPxrU1sugmsoDww9qMpx1xETcpJQ79i+5UYfQ170p5fpde1TWX93bXRq15IHL/i67OPGpxZyzh+n87HLPszMzGwLk84KiF9I+jzZVklaJ6n+VzfJMxsmtV1HTMjZ6GvZyCFcduQeFcfLVq6hZPh4Vq3JbslJbVQu+9h6q2ZMfuNjjvndZKa67MPMzMy2IOmMTLeJiLYR0RZoCZwI3FbTfZJaSJouaZakuZKuTdqPkPSypFclTZG0W9LeXNJDkhZJmiappE49qwcbJtS7XjGBr9auz8m7Lz1yd6ZfcUSVtj2veoI5H+dPQg1J2ccl/TmwZGs+/GI1Z7jsw8zMzLYg6dRMV4iUx4Cj07h8NXB4RPQCegODJPUD/gB8NyJ6A3/h6zmrhwKfRcRuwM3ADbWJLVs2TKj3uHJizuaD3q5ti43ef+OMVVmdBzsTO7RrwV8uOIgfDtyN4OuyD8/2YWZmZk1dOmUe36m0nSRpJLCqpvuSxHt5clicbJFsbZP2dkD5xMrHA/cl+48AR0hS+l3Jng0T2l7XPUXZx1/m9P0XHdat4njOks8pGT6eNetyM0qejqLCAn5ydHfuPe/AirKPY2+Zwsx3Pmvo0MzMzMyyRjV9WCfpj5UO1wJlwF0R8WGND08t+jIT2A34fUT8XFJ/4DFgJfA50C8iPpc0BxgUEYuTe98EDoqIjzd45jBgGEDHjh0PGDNmTFodrQ8/Ll3BJ6u+/vMa2rMZ/bsU5+z9H65Yz8+eW1ml7TeHtqRz61r9giHrPlu1ntteXc0bS9dTKDitezOO3KWITH82Wr58Oa1bt67nKPOb+9z0DRw4cGZE9GnoOMzMrG7SSaYPiYjna2qr4RntgUeBi0lNsXdDREyT9FOge0Scn24yXVn37t1jwYIF6YZRLy56YCZPzH2/4niHti2YukFtczZNmjSJ856supjM+Yd25cpje+QshnSsWbeekRPnM3rK2wAcu28nbjhxX7ZqXlTrZ5WWljJgwIB6jjC/uc9NnyQn02ZmTUA6Q5q3pNm2WRGxFJgEDAZ6RcS05NRDQPmyg0uAnQAkFZEqAcm7qSFuP+sAfnda74rj9z9fRcnw8azL0Qd35Yu8HNR164q2u6e8Tcnw8Xn10V9xYQFXHduD35+xP1s1K2Tc7Pc47tYpvPHBFw0dmpmZmVm92WwyLelgST8GOkq6vNJ2DVBY04MldUxGpJHUEjgKeB1oJ6l83rfyNoCxwDnJ/knAs5FPa2pXcnzvzrx81VFV2rpdMYGZ73yasxgeuvBg7j2vb5W2Xa+YwNIVX+UshnQM2bcTYy8+lD22b82bH33J8b9/nrGz/lPzjWZmZmaNQHUj082A1kAR0KbS9jmpZLcmnYBJkmYDLwFPR8Q44ALgb5JmAWcBP02uHw1sI2kRcDkwvPbdyZ2tt2q20YeJJ/7hRQb/LnczbQzovh2zrv5mlbbe1z3Ny+/m10d/3Tq25rEfHMIJvXdkxVfruOTBV7hm7NycTTNoZmZmli2bTaaTlQ6vJfWB4LWVtv+NiDdqenBEzI6I/SJi34joGRHXJe2PRsQ+EdErIgZExFtJ+6qIODkidouIA8vb813ZyCGcd0hJxfHr76Vm2sjVaoDtWhbz9vXHVGn7zm0v8Ktx83Ly/nS1albEzaf25lcn9KS4UNz7Qhmn3vki7y1bWfPNZmZmZnkqnZrpFZJ+K2mCpGfLt6xH1ohc/a29mfyzgVXa+vz6nwy8sTQn7y+vox609w4VbaOTOup8qpSRxFn9duHhi77Bju1a8Mq7SxkyagpT3tjsN6ZmZmZmeS2dZPrPwHygK3AtqanxXspiTI3STlu3omzkEAoqzf729sdfUjJ8PPP+k5vV128/6wD+uEEdddcRE1i9Nr9WTey9U3vGXdKf/rtvy6dffsVZ90zjlme8aqKZmZk1Pukk09tExGhgTVL68f+Aw7McV6P11vVDmPSTAVXajhk1OWejxAO7b8esX1ato+5+5RM5XWQmHVtv1Yx7zzuQS4/YHYCbnl7I0PteyrsPKM3MzMyqk04yXb529nuShkjaD9i6uhu2dF233YqykUPos0uHqu0jJnDB/TOy/v52rYo3+jhywI2lFXM+54vCAnHZUXvwx3P70r5VMZMWfMSQUVN4bfGyhg7NzMzMLC3pJNO/ltQO+DHwE+Bu4LKsRtVEPPK9b2w028bT8z6gZPh47nuhLOvvLxs5hAMrzUf9q3Hz+ObN/8r6e2trQPftGHfxofTq0o4lS1dy4h9e4C/T3s2rem8zMzOzTak2mU6WA989IpZFxJyIGBgRB0TE2BzF1+i1a5kaJb79zAOqtF89di4lw8czoyy7c1OPufBgbvvu/hXHCz9YnncfJgJ06dCKMRcdzJn9duardeu54tHX+MnDs1n5VX7Ve5uZmZlVVm0yHRHrgNNzFEuTNqjnDpSNHMK53yip0n7S7S9SMnw8L2UxqT5mn05MHVF1yfOuIyawak1+JarNiwr59Qn7cPOpvWhRXMDfXl7Mt297nve/9HzUZmZmlp/SKfN4XtKtkvpL2r98y3pkTdQ1x+1N2cgh7NiuRZX2k5Ok+vFXl2TlvTu0a8HCXw+u0rbnVU/w2Zf598Hft/frwuM/OJRdt92K+e9/wbUvruSJOe83dFhmZmZmG0knme4N7A1cB9yUbDdmM6gtwQsjjthosRWAS//6KiXDx3Pjkwvq/Z3Nigo2eud+v3qaZSvWbOaOhtN9hzY8/sNDGNxzB1auhYv+NJPrJ7zO2nUepTYzM7P8UWMyndRJb7h5arx6UL7YStnIIXTp0LLKuVsnLaJk+HhKho+v1wSy/J2V9bruqbxMqNu0KOa27+7P6Xs2o7BA3PHcW5xx9zQ+/HxVQ4dmZmZmBqSRTEvaXtJoSROT4x6ShmY/tC3LlJ8fTtnIIRy99/YbndvtFxMpGT6eFxbV30qBm0yoV+ZfQi2Jo0uKefCCfmzXpjnT3/6UIbdMYdpbnzR0aGZmZmZplXncCzwJ7JgcLwR+lK2AtnR3nNWHspFD+J+T9t3o3Bl3T+PcJ1KrKtbHqoYbJdTXPsWXq9fW+bnZcGDXrRl3yaH023VrPvpiNWfcPY07n3sz72YlMTMzsy1LOsn0thExBlgPEBFrgfyaBqIJOqXPTpSNHLLRPNXlul/5BCXDx3PW6Gl1Sig3TKj3vvpJ1uRpXfJ2bVrwp6EHcdFh3Vi3PvjvCfO56E8z+XxV/o2om5mZ2ZYhnWT6S0nbAAEgqR/gJepypHye6rKRQ7igf9eNzk9+42O6jphAyfDxnHHXVNatr31ivWFCfd0/5mUcb7YVFRYwfPCe3HV2H9q0KOLJuR9w3C1TeP29zxs6NDMzM9sCpZNMXw6MBbpJeh64H7g4q1HZJv1iSA/uHbQVb/xmMO1bFW90/oU3P6HbFRMqPlx8++Mv0372vOuOrth/YOo79VJGkk1H9diecRcfyl6d2lL2yQq+fdvz/G3m4oYOy8zMzLYwRTVdEBEvSzoM6A4IWBAR/r16AyouLODVX6bKPz76YjV9f/PPTV438MbSKsdjf3gI+3Zpv8lrWzUr4ps9tuepeR8A8PeXl3D6gTvXX9BZsMs2W/Ho97/BVY/N4eGZi/nxw7OY8c5nXP2tHrQoLmzo8MzMzGwLUGMyLakF8H3gUFKlHpMl3R4Rnp8sD3Rs07yiTGP12nV865YpLPxg+SavPe7W59N+7uo8Wx1xc1oUF/Lbk3vRp6QDVz0+lwenv8ucJcv4w5n706VDq4YOz8zMzJq4dMo87ie1aMstwK3J/gM13SSphaTpkmZJmivp2qRdkn4jaaGk1yVdUql9lKRFkmZ7lcXaa15UyFOXHVZRYz36nD4ZP+u0PB+V3tCpfXfm79/7Bjtt3ZLXlizj2Fum8NzCjxo6LDMzM2viahyZBnpGRI9Kx5MkpfOF2mrg8IhYLqkYmJLMVb0XsBOwZ0Ssl7Rdcv1gYPdkOwj4Q/Jfy9ARe21f5ePCdz9ZwU8fmcW0tz/d7D1tmhcx8Uf9G2WZRM/O7fjHDw/lsodeZdKCjzjnj9O57Mg9+OHA3SgoUEOHZ2ZmZk1QOsn0y5L6RcRUAEkHATNquilS87WV1xsUJ1sA3wPOiIjyqfY+TK45Hrg/uW+qpPaSOkXEe7XqkW3Wztu04qELD27oMLKqfatmjD6nL7c8u4j/e2Yh//v0Ql7991JuPqU37Tbx0aaZmZlZXaRT5nEA8IKkMkllwItAX0mvSZpd3Y2SCiW9CnwIPB0R04BuwKmSZkiaKGn35PLOwL8r3b44aTOrlYICcemRu/PHc/vSvlUxz87/kG/dOoW5//GMjmZmZla/0hmZHpTpwyNiHdBbUnvgUUk9gebAqojoI+k7wD1A/3SfKWkYMAygY8eOlJaWZhpeo7R8+XL3uRZ+0aeIW19dxzufruCEW6dwdo9m9O+S/yPU/ns2MzNrHJTO6nmSOpCqc65IviPi5Vq9SPolsAI4HxgcEW9LErA0ItpJugMojYgHk+sXAAOqK/Po3r17LFiwoDZhNHqlpaUMGDCgocPIqbr2edWadVz9+FwempH6xcfpB+7MNcf1oHlR/taF+++56ZM0MyIy/0rYzMzyQo1lHpJ+BcwGRgE3JduNadzXMRmRRlJL4ChgPvAYMDC57DBgYbI/Fjg7mdWjH7DM9dJWH1oUF3LDSftyw4n70KyogAenv8spt7/IkqUrGzo0MzMza+TSKfM4BegWEV/V8tmdgPskFZJK2sdExDhJU4A/S7qM1AeK5yfXTwCOARaRGsE+r5bvM6vWqX13pkendnzvzzOZtXgZx46azF1n96FPydYNHZqZmZk1Uukk03OA9qQ+IkxbRMwG9ttE+1JgyCbaA/hBbd5hVlv7dGnHuIsP5ZK/vspzCz/ijLun8X+n9uaYfTo1dGhmZmbWCKUzm8f1wCuSnpQ0tnzLdmBm2dK+VTPuOacP3z1oZ75au54f/OVl7p78Ful8P2BmZmZWWToj0/cBNwCvAeuzG45ZbhQVFvDrE3rSpUMrbnhiPr8e/zqLP1vJVcf2oNALvJiZmVma0kmmV0TEqKxHYpZjkvjegG7s2L4FP314Nve+UMZ/lq5k1On7NcoVIM3MzCz30inzmCzpekkHS9q/fMt6ZGY5cnzvztw/9EDatijiqXkf8PPho4m2baGgANq2he9/H958s6HDNDMzszyUTjK9H9AP+G9qMTWeWWPSb9dteHDvdWz11UoeL+7Mzb2+BRHwxRdw992w774wcWJDh2lmZmZ5psYyj4gYWNM1Zo3em2+y97knc+sOPRh64lWMOuQM9vj4XY6dPwXWrEltJ50Es2dDt24NHa2ZmZnliXQWbdle0mhJE5PjHpKGZj80sxy66SZYs4aBb83gikn3AHBbv5OrXrNmDdx8cwMEZ2ZmZvkqnTKPe4EngR2T44XAj7IVkFmD+NOfUskycNYr42m7ajnztu/Ggm13+fqaNWvggQcaKEAzMzPLR5tNpiWVl4BsGxFjSKbFi4i1wLocxGaWO8uXV+w2X7eWY1+fTOdlH/Jem202e52ZmZlZdTXT04H9gS8lbQMEgKR+wLIcxGaWO61bpz42TFxReg+/fuo2CoiNrzMzMzNLVFfmUb5yxeXAWKCbpOeB+4GLsx2YWU6deSYUF1cctv5q5caJdHExnHVWjgMzMzOzfFbdyHRHSZcn+48CE0gl2KuBI4HZWY7NLHd+/GO4776KuulNKi6Gyy7LXUxmZmaW96obmS4EWgNtgK1IJd6FQKukzazp6NYNHnkEWrWqMkINpI5btUqd97R4ZmZmVkl1I9PvRcR1OYvErKENHpyaR/rmm1OzdixfnqqRPuus1Ii0E2kzMzPbQHXJtKo5Z9Y0desGt96a2szMzMxqUF2ZxxE5i8LMzMzMrBHabDIdEZ/mMhAzMzMzs8YmnRUQMyKphaTpkmZJmivp2g3Oj5K0vNJxc0kPSVokaZqkkmzFZmZmZmZWH7KWTJOaQu/wiOgF9AYGJQu+IKkP0GGD64cCn0XEbsDNwA1ZjM3MzMzMrM6ylkxHSvnIc3GyhaRC4LfAzza45XjgvmT/EeAISf4I0szMzMzyVjZHppFUKOlV4EPg6YiYBvwQGBsR721weWfg3wARsZbUkuXbZDM+MzMzM7O6qG5qvDqLiHVAb0ntgUcl/RdwMjAg02dKGgYMA+jYsSOlpaX1EGnjsXz5cvd5C+A+m5mZNQ5ZTabLRcRSSZOAgcBuwKKkgqOVpEVJnfQSYCdgsaQioB3wySaedSdwJ0D37t1jwIABuehC3igtLcV9bvrcZzMzs8Yhm7N5dExGpJHUEjgKmBkRO0RESUSUACuSRBpgLHBOsn8S8GxERLbiMzMzMzOrq2yOTHcC7ks+OCwAxkTEuGquHw08IGkR8ClwWhZjMzMzMzOrs6wl0xExG9ivhmtaV9pfRaqe2szMzMysUcjqbB5mZmZmZk2Zk2kzMzMzsww5mTYzMzMzy5CTaTMzMzOzDDmZNjMzMzPLkJNpMzMzM7MMOZk2MzMzM8uQk2kzMzMzsww5mTYzMzMzy5CTaTMzMzOzDDmZNjMzMzPLkJNpMzMzM7MMOZk2MzMzM8uQk2kzMzMzsww5mTYzMzMzy5CTaTMzMzOzDDmZNjMzMzPLkJNpMzMzM7MMZS2ZltRC0nRJsyTNlXRt0v5nSQskzZF0j6TipF2SRklaJGm2pP2zFZuZmZmZWX3I5sj0auDwiOgF9AYGSeoH/BnYE9gHaAmcn1w/dQpXtQAADCdJREFUGNg92YYBf8hibGZmZmZmdZa1ZDpSlieHxckWETEhORfAdKBLcs3xwP3JqalAe0mdshWfmZmZmVldFWXz4ZIKgZnAbsDvI2JapXPFwFnApUlTZ+DflW5fnLS9t8Ezh5EauaZjx46UlpZmK/y8tHz5cvd5C+A+m5mZNQ5ZTaYjYh3QW1J74FFJPSNiTnL6NuC5iJhcy2feCdwJ0L179xgwYEB9hpz3SktLcZ+bPvfZzMysccjJbB4RsRSYBAwCkHQ10BG4vNJlS4CdKh13SdrMzMzMzPJSNmfz6JiMSCOpJXAUMF/S+cDRwOkRsb7SLWOBs5NZPfoByyLivY0ebGZmZmaWJ7JZ5tEJuC+pmy4AxkTEOElrgXeAFyUB/D0irgMmAMcAi4AVwHlZjM3MzMzMrM6ylkxHxGxgv020b/KdyeweP8hWPGZmZmZm9c0rIJqZmZmZZcjJtJmZmZlZhpxMm5mZmZllyMm0mZmZmVmGnEybmZmZmWXIybSZmZmZWYacTJuZmZmZZcjJtJmZmZlZhpxMm5mZmZllyMm0mZmZmVmGnEybmZmZmWXIybSZmZmZWYacTJuZmZmZZcjJtJmZmZlZhpxMm5mZmZllyMm0mZmZmVmGnEybmZmZmWUoa8m0pBaSpkuaJWmupGuT9q6SpklaJOkhSc2S9ubJ8aLkfEm2YjMzMzMzqw/ZHJleDRweEb2A3sAgSf2AG4CbI2I34DNgaHL9UOCzpP3m5DozMzMzs7yVtWQ6UpYnh8XJFsDhwCNJ+33ACcn+8ckxyfkjJClb8ZmZmZmZ1VVWa6YlFUp6FfgQeBp4E1gaEWuTSxYDnZP9zsC/AZLzy4BtshmfmZmZmVldFGXz4RGxDugtqT3wKLBnXZ8paRgwLDlcLWlOXZ/ZyGwLfNzQQeSY+7xl2NL63L2hAzAzs7rLajJdLiKWSpoEHAy0l1SUjD53AZYkly0BdgIWSyoC2gGfbOJZdwJ3AkiaERF9ctGHfOE+bxnc56ZP0oyGjsHMzOoum7N5dExGpJHUEjgKeB2YBJyUXHYO8HiyPzY5Jjn/bEREtuIzMzMzM6urbI5MdwLuk1RIKmkfExHjJM0D/irp18ArwOjk+tHAA5IWAZ8Cp2UxNjMzMzOzOstaMh0Rs4H9NtH+FnDgJtpXASfX8jV3ZhZdo+Y+bxnc56ZvS+uvmVmTJFdSmJmZmZllxsuJm5mZmZllqFEk05IGSVqQLDU+fBPnm9xS5Gn0+XJJ8yTNlvSMpF0aIs76VFOfK113oqSQ1Khnfkinv5JOSf6e50r6S65jrG9p/LveWdIkSa8k/7aPaYg465OkeyR9uLlpPJUyKvkzmS1p/1zHaGZmmcv7ZDr5gPH3wGCgB3C6pB4bXNakliJPs8+vAH0iYl9SK0b+T26jrF9p9hlJbYBLgWm5jbB+pdNfSbsDI4BDImJv4Ec5D7Qepfl3fCWpj5X3I/UR8m25jTIr7gUGVXN+MLB7sg0D/pCDmMzMrJ7kfTJN6mPFRRHxVkR8BfyV1NLjlTW1pchr7HNETIqIFcnhVFJzdjdm6fw9A/yK1A9Lq3IZXBak098LgN9HxGcAEfFhjmOsb+n0OYC2yX474D85jC8rIuI5UjMUbc7xwP2RMpXUXPydchOdmZnVVWNIpiuWGU9UXoJ8o2uayFLk6fS5sqHAxKxGlH019jn59fdOETE+l4FlSTp/x3sAe0h6XtJUSdWNbjYG6fT5GuBMSYuBCcDFuQmtQdX2/3czM8sjOVkB0bJH0plAH+Cwho4lmyQVAP8LnNvAoeRSEalf/Q8g9ZuH5yTtExFLGzSq7DoduDcibpJ0MKm553tGxPqGDszMzGxTGsPIdPky4+UqL0G+0TXVLUXeiKTTZyQdCfwCOC4iVucotmypqc9tgJ5AqaQyoB8wthF/hJjO3/FiYGxErImIt4GFpJLrxiqdPg8FxgBExItAC2DbnETXcNL6/93MzPJTY0imXwJ2l9RVUjNSHyWN3eCaprYUeY19lrQfcAepRLqx19JCDX2OiGURsW1ElERECak68eMiYkbDhFtn6fy7fozUqDSStiVV9vFWLoOsZ+n0+V3gCABJe5FKpj/KaZS5NxY4O5nVox+wLCLea+igzMwsPXlf5hERayX9EHgSKATuiYi5kq4DZkTEWJrYUuRp9vm3QGvg4eRby3cj4rgGC7qO0uxzk5Fmf58EvilpHrAO+GlENNrfuKTZ5x8Dd0m6jNTHiOc28h+MkfQgqR+Ktk1qwa8GigEi4nZSteHHAIuAFcB5DROpmZllwisgmpmZmZllqDGUeZiZmZmZ5SUn02ZmZmZmGXIybWZmZmaWISfTZmZmZmYZcjJtZmZmZpYhJ9O2WZJ2kPRXSW9KmilpgqQ9GjimH0lqlcF950rasdLx3ZJ61EM810hakkzvljVJ/LdWOu4k6SlJJZLmJG19JI1K9gdI+kYG7+kvaV75M83MzKx6TqZtk5SavPpRoDQiukXEAcAIYPuGjYwfAZtMpiUVVnPfuUBFMh0R50fEvHqK6eaI+GU9PStdg0jN11whImZExCXJ4QCgVsm0pKKImExqzmMzMzNLg5Np25yBwJpkUQkAImJWRExOVmr7raQ5kl6TdCpUjIaWSnpE0nxJf06SciT1lfSCpFmSpktqI6kwec5LkmZLurC650i6hFRCPEnSpOTa5ZJukjQLOFjSL5PnzZF0Z3LfSUAf4M+SXpXUMnl+n+QZpyf9mCPphvL+Js/+TRLzVEk1/iAhqaOkpyXNTUa/35G0bTKCPF/SvZIWJn06UtLzkt6QdGBy/9aSHkv+PKZK2nczrxoETNzg3QMkjZNUAlwEXJb0t38S19+SP5uXJB2S3HONpAckPQ88UFP/zMzMrCon07Y5PYGZmzn3HaA30As4EvitpE7Juf1IjR73AHYFDlFq6eiHgEsjovyelcBQUksn9wX6AhdI6rq550TEKOA/wMCIGJhctxUwLSJ6RcQU4NaI6BsRPYGWwLER8QgwA/huRPSOiJXlHUlKP24ADk/61FfSCZWePTWJ+TnggjT+3K4mtZz93sAjwM6Vzu0G3ATsmWxnAIcCPwGuSK65FnglIvZN2u7f8AXJCHz3zY2sR0QZcDupEfPeyWjz75LjvsCJwN2VbukBHBkRp6fRPzMzM6sk75cTt7x0KPBgRKwDPpD0L1LJ8OfA9IhYDCDpVaAEWAa8FxEvAUTE58n5bwL7JiPHAO2A3YGvNvOcKZuIZR3wt0rHAyX9jFQpyNbAXOAf1fSlL6lSlo+Sd/0Z+C/gsSSOccl1M4GjavqDIfVn8+2kn09I+qzSubcj4rXkPXOBZyIiJL2W9K/8/hOT+5+VtI2kthu84yBgWhqxVHYk0CP5RQFAW0mtk/2xlX/AMDMzs/Q5mbbNmQucVONVG1tdaX8d1f8bE3BxRFSp/ZU0oBbPWZUk9UhqAdwG9ImIf0u6BmhRq+irWhMRkUYM6arcp/WVjtfX8tmDgSdq+e4CoF9ErKrcmCTXX9byWWZmZpZwmYdtzrNAc0nDyhsk7SupPzAZODWpee5IaiR3ejXPWgB0ktQ3eU4bSUWkPqD7nqTipH0PSVvVENcXQJvNnCtPnD9ORl0r/zCwufumA4cldc2FwOnAv2qIoTrPA6dAxch7h1rePxn4bnL/AODj8pH8So4A/lnDczbs71PAxeUHknrXMi4zMzPbBCfTtknJiOy3gSOVmhpvLnA98D6pWT5mA7NIJd0/i4j3q3nWV8CpwC3Jh4JPk0p87wbmAS8rNRXbHdQ8Qnsn8ET5B4gbvGcpcBcwh1Si/lKl0/cCt5d/gFjpnveA4cCkpD8zI+LxGmKozrXAN5P+nEzqz+uLWtx/DXCApNnASOCcyieTH15WRURNz/wH8O3yDxCBS4A+yYeN80h9oGhmZmZ1pK9/i21mtZWUkiyPiBuT4+bAuohYK+lg4A8RUW+jwJLOBLpExMj6euYm3lECjEs+4jQzM7NquGbarG6WA8MktU3mmt4ZGCOpgNQHjOnMAJK2iPhTfT5vQ8ko9m3Ax9l8j5mZWVPhkWkzMzMzswy5ZtrMzMzMLENOps3MzMzMMuRk2szMzMwsQ06mzczMzMwy5GTazMzMzCxDTqbNzMzMzDL0/wEsBit5I3pWnAAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"def create_cstr_plot_axes():\n",
" fig = plt.figure(figsize=(12,8))\n",
" ax = [plt.subplot(2, 2, k) for k in range(1, 4)]\n",
" \n",
" ax[0].set_xlabel('Time [min]')\n",
" ax[0].set_ylabel('Concentration [gmol/liter]')\n",
" ax[0].set_title('Concentration')\n",
" ax[0].set_ylim(0, 1)\n",
" ax[0].grid(True)\n",
" \n",
" ax[1].set_xlabel('Time [min]')\n",
" ax[1].set_ylabel('Temperature [K]');\n",
" ax[1].set_title('Temperature')\n",
" ax[1].set_ylim(300, 450)\n",
" ax[1].grid(True)\n",
" \n",
" ax[2].set_xlabel(\"Concentration [gmol/liter]\")\n",
" ax[2].set_ylabel(\"Temperature [K]\");\n",
" ax[2].set_title(\"Phase Plot\")\n",
" ax[2].set_xlim(0, 1)\n",
" ax[2].set_ylim(300, 450)\n",
" ax[2].grid(True)\n",
" \n",
" return ax\n",
"\n",
"def cstr_plot(t, y, ax):\n",
" \"\"\"Plot cstr simulation results. Create new axes if needed.\"\"\"\n",
" ax[0].plot(t, y[:, 0], label=str(Tc))\n",
" ax[1].plot(t, y[:, 1], label=str(Tc))\n",
" ax[2].plot(y[0, 0], y[0, 1], 'r.', ms=20)\n",
" ax[2].plot(y[:, 0], y[:, 1], lw=2, label=str(Tc))\n",
" for a in ax:\n",
" a.legend()\n",
"\n",
"ax = create_cstr_plot_axes()\n",
"cstr_plot(tsim, ysim, ax);"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.6 Effect of Cooling Temperature](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.6-Effect-of-Cooling-Temperature)",
"section": "7.4.6 Effect of Cooling Temperature"
}
},
"source": [
"## 7.4.6 Effect of Cooling Temperature\n",
"\n",
"The primary means of controlling the reactoris through temperature of the cooling water jacket. The next calculations explore the effect of plus or minus change of 5 K in cooling water temperature on reactor behavior. These simulations reproduce the behavior shown in Example 2.5 SEMD."
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.6 Effect of Cooling Temperature](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.6-Effect-of-Cooling-Temperature)",
"section": "7.4.6 Effect of Cooling Temperature"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAtMAAAHwCAYAAABkJOM0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeXiU1fXA8e/JZCUrhD0L+y6yiruyFkUEEbW4okXRqlVLrf5abdXa1tq6tlXrWhVRVKiKiBYVY0VQBFlUAmEnCYEAIWQSMsks5/fHO8EQssyETCYzuZ/neZ+Zd51zRV7O3Ln3vKKqGIZhGIZhGIbhv4hgB2AYhmEYhmEYocok04ZhGIZhGIbRSCaZNgzDMAzDMIxGMsm0YRiGYRiGYTSSSaYNwzAMwzAMo5FMMm0YhmEYhmEYjWSSacMIEhHJFJFSEbEFOxbDMAzDMBrHJNNG0IjIFSKy2ptQFojIhyJyVrDjqklEuouIikjkCV5np4iMr1pX1d2qmqCq7hOP0jAMo3l479lVi0dEyqutXxns+Bqj5v3ZMPxhkmkjKERkDvAE8GegE5AJPA1MDWZcjXWiibZhGEao8HYCJKhqArAbuLDatnnBjq+m5rg/m38DWjeTTBvNTkSSgT8At6jqf1S1TFWdqvq+qv5aRGJE5AkR2eNdnhCRGO+5o0UkT0R+JSKF3h7t66pdO05EHhWRXSJyWESWi0icd99pIrJCRIpFZL2IjK52XpaIPCgiX4qIXUSWikh77+7/eV+LvT0vp4vItd5jHxeRg8D9ItJLRJaJyEEROSAi80QkxXv9uVhfGN73XuOumj3eItJVRBaJSJGIbBWRG6rFd7+IvCUir3rj+0FERgbqz8gwDMNfIhIhIv8nItu898G3RKSdd1/V/e46EckVkUMicpOInCIiG7z35X9Wu1bVPfaf3nv5JhEZV21/soi86P03IF9E/lg1ZK6J7s+jRSSvRvuO9l5778kLROQ1ESkBrq0vJiO8mWTaCIbTgVjgnTr23wOcBgwFhgCjgHur7e8MJANpwCzgKRFp6933CDACOANoB9wFeEQkDfgA+KN3+53AQhHpUO26VwDXAR2BaO8xAOd4X1O8PS8rveunAtuxetb/BAjwENAVGABkAPcDqOrVHNuD89da2j0fyPOefwnwZxEZW23/FO8xKcAi4J/HXcEwDCN4fgFcBJyLdR87BDxV45hTgT7AT7F+nbwHGA8MAi4TkXNrHLsNaA/cB/ynKjkHXgZcQG9gGPAT4Poa5zbl/bk2U4EFWPfkeT7EZIQpk0wbwZAKHFBVVx37rwT+oKqFqrofeAC4utp+p3e/U1WXAKVAPxGJAH4G3K6q+arqVtUVqloBXAUsUdUlqupR1Y+B1cCkatf9t6rmqGo58BZWMl+fPar6D1V1qWq5qm5V1Y9VtcIb92NY/6g0SEQygDOBu1XVoarrgBeAa6odttwbvxuYi/VFwzAMo6W4CbhHVfO89937gUtqDIF40HuPWwqUAW947/X5wBdYSWiVQuAJ773+TWAzcIGIdMK6d9/h/WWzEHgcmFHt3Ca7P9djpaq+q6oeIMmHmIwwZcb4GMFwEGgvIpF1JNRdgV3V1nd5tx09v8Z5R4AErN6LWKyejJq6AZeKyIXVtkUBn1Vb31vLNeuTW33Fe4N/EjgbSMT6snqogWtU6QoUqaq92rZdQPWhHDXji63nv6FhGEZz6wa8IyKeatvcWL3DVfZVe19ey3r1+26+qmq19ap/C7ph3b8LRKRqXwTH3pOb8v5cl+qf4UtMRpgyPdNGMKwEKrB+DqzNHqwbU5VM77aGHAAcQK9a9uUCc1U1pdoSr6p/8eG66uP2P3u3DVbVJKzecKnn+Or2AO1EJLHatkwg34f4DMMwWoJc4Pwa99lYb69zY6RJtcyUH/8tyMX6N6R9tc9JUtVB1Y490ftzGdCmasU79rlDjWOqn+NLTEaYMsm00exU9TDwe6yxzheJSBsRiRKR80Xkr8AbwL0i0sE7CfD3wGs+XNcDvAQ85p3MZ/NOFozxnn+hiEz0bo/1TjBJ9yHk/YAH6NnAcYlYQ04Oe8do/7rG/n11XUNVc4EVwEPe2E7GGg/eYLsNwzBaiH8BfxKRbgDee/iJVGjqCNzm/ffhUqyxzktUtQBYCjwqIkneiY+9aoy3rsnf+3MO1q9/F4hIFNa8nZi6Lt7ImIwwYZJpIyhU9VFgDtYNaj/Wt/pbgXexJgmuBjYA3wHferf54k7vOd8ARcDDQIQ3WZ0K/Lba5/0aH/4OqOoRrAksX3pnnJ9Wx6EPAMOBw1iTHf9TY/9DWF8SikXkzponA5cD3bF6Xt4B7lPVTxqKzzAMo4V4Emty9FIRsQNfYU0EbKyvsSYrHsC6B1+iqge9+67Bmii+EWu4xgKgSz3X8uv+7O30uRlr7ko+Vk91HvXzNyYjTMixw5EMwzAMwzCCS0SuBa5X1Rb3IC/DqMn0TBuGYRiGYRhGIzVLMi0iL4n1gI3v69gvIvJ3sR5UsUFEhjdHXIZhGIZhGIZxIpqrZ/pl4Lx69p+PNS6qDzAbeKYZYjIMwzAMowVS1ZfNEA8jVDRLMq2q/8OaDFaXqcCravkKSBERM2jfMAzDMAzDaNFaypjpNI4tbJ7n3WYYhmEYhmEYLVbIPQFRRGZjDQUhLi5uREZGht/X8Hg8RES0lO8RTSuc2wbh3T7TttDVmPbl5OQcUNWaD4EIa+3bt9fu3bv7fV5ZWRnx8fFNH1ALEM5tg/BuXzi3DcK7fY1t25o1a2q9b7eUZDofqJ4Vp1PHk99U9TngOYCRI0fq6tWr/f6wrKwsRo8e7X+UISCc2wbh3T7TttDVmPaJyK7ARNNyde/eHXPPPlY4tw3Cu33h3DYI7/Y1tm113bdbSlfRIuAab1WP04DD3qcJGYZhGIZhGEaL1Sw90yLyBjAaaC8iecB9QBSAqv4LWAJMArYCR4DrmiMuwzAMwzAMwzgRzZJMq+rlDexX4JbmiMUwDMMwDMMwmkpLGTNtGIZhGIZhhBCn00leXh4OhyPYofglOTmZ7OzsOvfHxsaSnp5OVFSUT9czybRhGIZhGIbht7y8PBITE+nevTsiEuxwfGa320lMTKx1n6py8OBB8vLy6NGjh0/XaykTEA3DMAzDMIwQ4nA4SE1NDalEuiEiQmpqql+97aZn2jACSFXxKLg9ai1qvar31aPg8b4/UO4ht+gIHv1xu6qiytF1j3ddFRTruKrPAO8+vPtVf3yPtaNq3Xv00eOrYtWjgf94DEevV61dNdpYc3v1Y0H5fq8Lx/fHFug59pjjr1v3f9MG9vt0lRP7jJoqyj0n/JmGYRihKJwS6Sr+tskk00ZYqnR5KKtwUVbpoqzCTVmli/JKt7U4rcVxdPFQ4XJT4fRQ4bLeV7o8VLo93lfF6fLgdFctitPtweXxvroVl0dxezzeVz366vb4mZV9/llg/oO0BOu+DXYEATP75Jhgh9BkRMQGrAbyVXVyte1/B36mqgne9RjgVWAEcBD4qarubP6IDcNorXJzc7nmmmvYt28fIsLs2bO5/fbbWb9+PTfddBOlpaV0796defPmkZSUBMBDDz3E888/T1RUFH//+9+ZOHHiCcdhkmmjxVJV7BUuDtgrKCqrpKiskpW5TrKztlFcXsnhI06KjzgpcViL3eHC7nBR6nBR6favp9AWIcRERhAbZSPaFkF0pLVEed/HeF/jYyKJskUQZRMibRFERQiR3vc28b6PECIirFdbxI/bI0SwReB9tdYjIoQIAZsIOTmbGdC//9F9Ita34wgBwToXvOsiCBAR8eP7H1+t461XwLse4f2iLd5re3d534t3X9W7H7+Z/7huXYdq67X58do/HrBmzWpGjhxZ57HHbKPhHoGGOg2aop/En46JnPX+P4ikBbsdyAaSqjaIyEigbY3jZgGHVLW3iMwAHgZ+2mxRGobR6kVGRvLoo48yfPhw7HY7I0aMYMKECVx//fU88sgjnHvuubz00kv87W9/48EHH2Tjxo3Mnz+fVatWYbfbGT9+PDk5OdhsthOLo4naYxh+UVX2l1aQd6ic/EPlFBwuZ0+xg30lVUsF+0srqHTVkhT/sIloWwQpbaJIjosiKS6KDgkx9GyfQFJcJAkxUSTE2IiPibSW6EjaRNtoE20jLtpGXJSN2CjrfWyUjdjICCJtwZ8+kHVkO6NHZjR8YAgqzIlgQJekhg8MUXlR4fEzp4ikAxcAfwLmeLfZgL8BVwDTqh0+Fbjf+34B8E8REVV/B8kYhmE0TpcuXejSpQsAiYmJDBgwgPz8fHJycjjnnHMAmDBhAhMnTuTBBx/kvffeY8aMGcTExNC+fXt69+7NqlWrOP30008oDpNMGwF1qKySLYWlbN9fyrb9pew4cITdRWXsOniEihqJcny0jc7JsXRKimVUj3Z0SIyhfUI07RNiSE2IITU+ms0b1jBp3LnERkWE5TgtwwiyJ4C7gOrT3G8FFqlqQY2/c2lALoCqukTkMJAKHGimWA3DaEEeeP8HNu4padJrDuyaxH0XDvLp2J07d7J27VpOPfVUBg0axHvvvcdFF13E22+/TW5uLgD5+fmcdtppR89JT08nPz//hOM0ybTRJDweZfuBUr7PL+GHPYfJLrCzeZ+d/faKo8fEREbQLbUN3VLjOadPBzJT25CWEkda2zi6psSRGBPZYIJ8YEsEcdEn9nOMYRjHE5HJQKGqrhGR0d5tXYFLsZ5g29jrzgZmA3Tq1ImsrCy/r1FaWtqo80JBOLcNwrt94dw28K19ycnJ2O12AJyVTtxud5PG4Kx0Hr1+fUpLS5k2bRoPPfQQIsI//vEPfv3rX/PAAw9w/vnnExUVhd1up7KykvLyctxuN3a7HafTSXl5ea2f4XA4fP7zNcm00SiHy518u+sQ3+wsYl1uMRvyDlNa4QIgOjKCfp0SObdvB/p1SqR3pwR6d0iga0octgjTm2wYLdSZwBQRmQTEYo2Z/gGoALZ6v+i2EZGtqtobyAcygDwRiQSSsSYiHkNVnwOeAxg5cqSOHj3a78CysrJozHlV1u9fT1J0Ej2SfasZ25xOtG0tXTi3L5zbBr61Lzs7+2i95j9OH9oMUR3P6XRyySWXcPXVV3PllVcCMGLECJYtWwZATk4On3zyCYmJifTo0YMDBw5gs9lITExk37599O7du9aa07GxsQwbNsynGEwybfjE4XTz9Y4iVmw9wPKtB9hYUIIqREYIA7okMW1YGienJzM4PZleHRKIagFjkA3D8J2q/gb4DYC3Z/rO6tU8vNtLvYk0wCJgJrASuARY1lLHS9/35X1kJGbwj3H/CHYohmE0IVVl1qxZDBgwgDlz5hzdXlhYSMeOHfF4PPzxj3/kpptuAmDKlClcccUV3HDDDRw4cIAtW7YwatSoE47DJNNGnfYedvBx9j6WZe9jxbaDVLg8RNmE4ZltuX1cH0Z1b8fQzBTaRJv/jQyjFXoRmCsiW4EiYEaQ46lTqbOUnSU7gx2GYRhN7Msvv2Tu3LkMHjyYoUOtnvE///nPbNmyhaeeegqAiy++mOuuuw6AQYMGcdlll3HKKacQHR3NU089dcKVPMAk00YN+0ocvL9+Dx9+v5c1uw4BkNmuDZePymR0vw6M6tHOJM+GEeZUNQvIqmV7QrX3Dqzx1C1ehbuCg46DuD1ubBFmzoVhhIuzzjqLun4Qu/3222vdfs8993DbbbfV+TjxxjBZkYHD6eaj7/ey8Ns8vtx6AI/CwC5J/GpCX847qTO9OyaYyhmGYYSsCncFLo+LgrIC0hPTgx2OYRhhxiTTrdj2/aXM+3o3C7/No/iIk/S2cdwypjcXDUujV4eEhi9gGIbRwqkq5a5yAHbbd5tk2jCMJmeS6VZGVflqexEvLt/OJ9mFREYIEwd15opTMzm9ZyoRptqGYRhhpNJTefR9bkkudA1iMIZhhCWTTLcSqkrW5v08+ekW1uUW0y4+mtvH9eGq07rRITEm2OEZhmEEhMPlOPp+l31XECMxDCNcmWS6FVi+5QB/++8m1ucdJi0ljj9NO4npw9OJjTITcQzDCG/Vk+ncktwgRmIYRrgyyXQY27S3hD8v2cT/cvaTlhLHXy4ezMXD04mONDWgg04VXA6oLIPKUqgsI7FkM2wXa7uzHFwV1ntXBbgrwF0Jrkrr1eMEjxvcTvC4vIvbelW39V7d1ueox7vuAfTHbXhfa5sJ7W+54NomqFbbNuRQMexq690mNY6RY98fcy05/rhaz6v5uTWPrXG9Y7b7c2zNmCxJtmGcwEMCjQByuE3PtGEYgWWS6TBU4nDy2NIcXl25k4SYSO6ZNIBrzuhGTKTpiQ4IjweOHAR7AZQVQtkBKNtvbTtSBOVFUF4MjmJwHIYKu7V4XMdcZgTAtz58ntjAFg0RkWCLhIgoiLB5XyOs/RE261UivNu8S1WyWnO91sTU1/Hz+mPyfTQJr5aMqxLhcVpfDI5J0vXY41WPO+/446rWq71v6NjjrlfbeT4cW/NzqolK64XRMlX1TGckZpBnzzPl8QwjjDgcDs455xwqKipwuVxccsklPPDAA+zYsYMZM2Zw8OBBRowYwdy5c4mOjqaiooJrrrmGb775hg4dOvDmm2/SvXv3E47DJNNhRFX5ao+LOx/5nKKyCq46rRtzJvQlpU10sEMLbR4PlORB0XY4tNNainfD4XwoybeS6BqJMWAlu3HtoE07iE2BpDToOBBikiAmEWISIDoRouMhOp4Nm7Zx8vBRENUGomIhMhYiY6xXW7T1viphDjFrw/yxuwezsoIdglGHCncFAH3b9iXXnsu+I/vommBmIRpGOIiJiWHZsmUkJCTgdDo566yzOP/883nsscf45S9/yYwZM7jpppt48cUX+fnPf86LL75I27ZtWb9+PR988AF33303b7755gnHYZLpMLHfXsE973zH0o0VDElP5t/XnsLg9ORghxVaVK0kee93ULgRCrNh/2Yo2mb1qlaJiITkdEjOgG5nQlIXSOwCCZ0gsTPEd4A2qRCbXPvwhzoU7c+CHmc3fbsMoxWr6pnu27Yvn+7+lF0lu0wybRhhQkRISLBK+TqdTpxOJyLCsmXLeP311wGYOXMm999/Pz//+c957733uP/++wG45JJLuPXWW1HVE36Whkmmw8CH3xXw23e+o6zSzU/7RfPnmWdiMyXuGlZaCLmrIH815K+BgvXWMIwqKd2gQ3/oNQZSe1tL2+6Q1NUaRmEYRotXNWa6T9s+AOTaczmd04MZkmGEpw//z+qMakqdB8P5f6n3ELfbzYgRI9i6dSu33HILvXr1IiUlhchIK8VNT08nPz8fgPz8fDIyMgCIjIwkOTmZgwcP0r59+xMK0yTTIczhdPOnD7KZ+9UuhqQn8+hlQ8jbuMYk0nUpOwDbs2DH57BrBRzcam2PiIROJ8FJ06HzydZf3o4DrOEXhmGEtKqe6czETGJsMewu2R3kiAzDaEo2m41169ZRXFzMtGnT2LRpU7PHYJLpELXzQBk3z/uWjQUlzD6nJ7+e2I8oWwR5G4MdWQvi8cCetZDzkbXs3WBtj0mGbqfDsKsh83ToMsQao2wYRtipGjMdFxlHRmKGqehhGIHSQA9yoKWkpDBmzBhWrlxJcXExLpeLyMhI8vLySEtLAyAtLY3c3FySk5NxuVwcPnyY1NTUE/5sk0yHoOVbDnDL698iAi9dO5Kx/TsFO6SWw+OB3K/gh3dg4yIo3WtVrcg4Fcb+DnqOga5DzTANw2glqh4lHmOLITMxk10lJpk2jHCxf/9+oqKiSElJoby8nI8//pi7776bMWPGsGDBAmbMmMErr7zC1KlTAZgyZQqvvPIKf/vb31iwYAFjx4494fHSYJLpkKKqvLJiJw9+kE3vDgm8MHMkGe3aBDusluHAFlj3Omx406qwERkLvcfDgCnQZ4JVUcMwjFanqmc6NjKWzKRMlucvx6MeIiT0quIYhnGsgoICZs6cidvtxuPxcNlllzF58mQGDhzIjBkzuPfeexk2bBizZs0CYNasWVx99dUMGTKE9u3bM3/+/CaJwyTTIcLjUR78YCP//nIn4wd04okZQ0mIaeV/fK4KyH4fvnkRdq+weqB7j4cJf4C+E63yc4ZhtGo1k+lKTyX7yvbRJaFLkCMzDONEnXzyyaxdu/a47T179mTVqlXHbY+NjeXtt9/GbreTmNh0OUIrz8ZCQ6XLw51vr2fR+j387Mwe3HvBACJa8yTDsgPwzQvWUrYf2vawEuiTZ0CiGfJiGMaPyl3lCEJ0RDSZiZkA7LbvNsm0YRhNxiTTLVx5pZvZc1fzxZYD3H1ef246t2eTjO8JScW59Mn5Fyz/zKr73GcinDobeo4NyQeZGIYReBWuCmIjYxGRo8n0rpJdnNrl1CBHZhhGuDDJdAtWXunmZy9/w9c7DvLX6Sdz2SkZwQ4pOA7nwRePwrdz6aIKQy+HM34BHfoFOzLDMFo4h9tBrM2q1tMpvhNtItuwrXhbkKMyDCOc+JRMi8gGHw7br6rj6rnGecCTgA14QVX/UmN/JvAKkOI95v9UdYkv8YWj6on0o5cNYdqw9GCH1PzKi60k+utnQT0w/Bq+jjyd08+7NNiRGUbYEhEbsBrIV9XJIjIPGAk4gVXAjarqFOsnsieBScAR4FpV/TZYcdfF4XIQExkDQIRE0KdtHzYf2hzkqAzDCCe+9kzbsG6YdRFgUZ07rZvzU8AEIA/4RkQWqWr1qsj3Am+p6jMiMhBYAnT3Mb6w4nC6mfVKK06k3S5Y/RJk/dlKqIdcDmN+CykZVGRlBTs6wwh3twPZQJJ3fR5wlff968D1wDPA+UAf73Kqd1uLGztRvWcaoF/bfny448MmeYSwYRgGgK8DTW9U1V31LDuBm+s5fxSwVVW3q2olMB+YWuMY5cebdzKwx492hA23R7lj/jpWbDvII5e2wkR699fw/Gj48NfW0whv/B9MewZSWukQF8NoRiKSDlwAvFC1TVWXqBdWz3TVTWkq8Kp311dAioi0uFl9VWOmq/Rr1w+7005BWUEQozIMI5z41DOtqsu9vcuvquqVdR1TzyXSgNxq63kc34NxP7BURH4BxAPja7uQiMwGZgN06tSJrEb0VJaWljbqvEBTVV7ZWElWrovL+0fTrmQrWVlb/bpGS21bQ2yuI/Ta9jJdC/6LIyaVbQPvYn+HM2BzEWzOOnpcqLbPF6ZtoSuM2vcEcBdwXM0oEYkCrsbquYba7+tpQEGN84J6zy44UEClVh49v6yiDICF/1vI4DaDG3XNphRG/+/UKpzbF85tA9/al5ycjN1ub56AauFwODjvvPOorKzE5XIxdepU7rnnHnbu3Ml1111HUVERw4YN47nnniM6Opp58+Zx77330qVLF0SE2bNnM3PmzDqv7fOfr6r6vADLgWh/zvGedwnWOOmq9auBf9Y4Zg7wK+/704GNQER91x0xYoQ2xmeffdao8wLtiY9ztNvdi/UvH2Y3+hottW31yvlY9dGBqvenqH70W1WHvc5DQ7J9PjJtC12NaR+wWv28lwZyASYDT3vfjwYW19j/PPBEtfXFwFnV1j8FRtb3GcG4Z1/1wVU667+zjq6XVZbp4JcH6zPrnmn0NZuS+bsRusK5baq+tW/jxo2BD6QeHo9H7XYrZ6isrNRRo0bpypUr9dJLL9U33nhDVVVvvPFGffrpp1VV9d///rfecsstWlJS0uC1a2tbXfdtf+uJbQe+FJHficicqsWH8/KB6r/Tp3u3VTcLeAtAVVcCsUB7P+MLWe+v38Pjn+QwfXg6d01sJVUqKo/A4jkwbzpEx8Osj2HinyAmIdiRGUZrdCYwRUR2Yg3FGysirwGIyH1AB6xOjyq+3NeDrsJdccyY6TZRbchIzCDnUE4QozIMoymICAkJVs7gdDpxOp2ICMuWLeOSSy4BYObMmbz77rsBjcPf0njbvEsEtfwMWI9vgD4i0gPrZjsDuKLGMbuBccDLIjIAK5ne72d8IWlDXjF3vr2eU7q35c8Xn9Q6JsXs/Q4WzIIDm+H0W2Hs7yAqtuHzDMMICFX9DfAbABEZDdypqleJyPXARGCcqnqqnbIIuFVE5mMN2zusqi1uIHK5q/yYMdNgjZveXGQqehhGU3p41cNsKtrUpNfs364/d4+6u95j3G43I0aMYOvWrdxyyy306tWLlJQUIiOtFDc9PZ38/B+/5y9cuJCsrCz69+/P448/TkbGic/J8iuZVtUHAESkjaoe8eM8l4jcCvwXqzLIS6r6g4j8AavLfBHwK+B5Efkl1mTEa71d6mFtX4mDG15dTfuEGJ65agQxkbZghxRYqvDtK7DkLohrC1e/A73GBjsqwzDq9i9gF7DS+0X/P6r6B6yKS5OArVil8a4LWoT1qHBXEGOLOWZbn7Z9+GTXJxxxHqFNVJsgRWYYRlOw2WysW7eO4uJipk2bxqZNdSf0F154IZdffjmVlZW8/vrrzJw5k2XLlp1wDH4l0yJyOvAikABkisgQrEof9VXyAKwZ4Vg33+rbfl/t/UasnxlbDafbwy3zvsXucLHw52fQPiGm4ZNCmbMcPrgT1r0GPcfA9BcgvtWM5DGMkKGqWUCW932t/054Oztuab6oGsfhchAXGXfMtn5t+6EoOYdyGNpxaJAiM4zw0lAPcqClpKQwZswYVq5cSXFxMS6Xi8jISPLy8khLSwMgNTUVgMrKSq6//nruuuuuJvlsf8dMP4H1c99BAFVdD5zTJJG0Qn/772ZW7zrEQxcPZkCXpIZPCGWH8+GliVYifc5dcNVCk0gbhhFwDrfjuJ7pfu2seSlm3LRhhLb9+/dTXFwMQHl5OR9//DEDBgxgzJgxLFiwAIBXXnmFqVOtaswFBT+ORFu0aBEDBgxokjj8fpy4qubWGNPrbpJIWpmlP+zluf9t56rTMpk6NC3Y4QRW/hp44wqoLIPL50O/84MdkWEYrYCq1jrMo2t8VxKjEs24acMIcQUFBcycORO3243H4+Gyyy5j8uTJDBw4kBkzZnDvvfcybNgwZs2aBcDf//53Fi1aREREBO3bt+fll19ukjj8TaZzReQMQL01R6uelHdDrTUAACAASURBVGX4IbfoCHe+vZ7Bacn8bvLAYIcTWD+8C+/cCAkdrfHRncK8vYZhtBhOjxOPeo4b5iEi9Gnbx/RMG0aIO/nkk1m7du1x23v27MmqVauO2/7QQw/x0EMPYbfbSUz0p45G/fwd5nET1hi5NKyqHEOp/8mHRg1uj/Krt9bjUXjqiuHhPeHw62fh7WuhyxC44TOTSBuG0awcbgfAcT3TYA31yDmUg+eYAiWGYRj+87dnup/WeAKiiJwJfNl0IYW357/YzqqdRTx66RAyU8N0FrkqfPoALH8c+k+2JhpGxTV8nmEYRhNyuKxkumZpPLAmIR5xHSHfnk9G0omXxjIMo/Xyt2f6Hz5uM2qxcU8Jjy7dzPkndebi4WE6TtrjhvdvsxLpEdfBZa+aRNowjKCocFUAtSfTA1KtiUffH/y+WWMyDCP8+NQz7S2JdwbQocYTD5Ow6kYbDahwufnlm+tIaRPNn6YNDs8Hs7id8O7P4bu34Zxfw5h7IBzbaRhGSCh3lwMc8wTEKn3b9iUuMo61hWs5v4eZFG0YjaWqYZfT+PuYE1+HeURj1ZaO5NgnH5YAl/j1ia3UU8u2snmfnX9fewrt4qODHU7Tc1XCgutg02IYdx+c7ctT5g3DMAKnvp7pyIhITu5wMmsLj5+8ZBiGb2JjYzl48CCpqalhk1CrKgcPHiQ21venMvuUTKvq58DnIvKyqu5qbICt1aa9JTydtY1pw9IY079jsMNpem6nNdFw8wdw3sNw2k3BjsgwDKPeCYgAwzoO47kNz1FaWUpCdEJzhmYYYSE9PZ28vDz2798f7FD84nA46k2WY2NjSU9P9/l6vg7zeEJV7wD+KSLH9X2r6hSfP7GVcXuU/1v4HUlxUeFZBs/thAU/sxLp8/8Gp84OdkSGYRhA/RMQwUqmPephw/4NnJF2RnOGZhhhISoqih49egQ7DL9lZWUxbNiwJruer8M85npfH2myT24lXl6xk3W5xTw5Y2j4De/wuOE/syF7EUx8yCTShmG0KBVu7zCPWsZMAwzpMIQIiWDt/rUmmTYMo9F8Heaxxvv6eWDDCS8Fh8t5dOlmxvTrwJQhXYMdTtNShfdvhx/+AxMehNNNuXHDMFqWcpd3AmIdPdPxUfH0a9uv1Y2bDscJY4YRTD6VxhOR70RkQ11LoIMMVX/6IBu3R/nD1JPC68alCkvvhbVz4Zy74Mzbgh2RYRjGcap6pusaMw0wtONQNuzfgMvjaq6wguo3X/yGX33+q2CH0axKKkt4eNXD2CvtwQ6lWTk9TpweZ7DDaBV8HeYxOaBRhKEV2w6weEMBd4zvQ0a7MHs4yxePwsp/wqgbYcxvgx2NYRhGrarGTNd8nHh1wzsO541Nb7D50GYGpQ5qrtCCZtXeVRQeKWTLoS30adsn2OE0i6zcLF7Lfo0u8V24ZtA1wQ6n2dzyyS0kRCfw2OjHgh1KsyooLaBLQpdm/UxfH9ryHHAxEKequ2ouAYwvJDndHu577wcy2sVx07m9gh1O0/r2VVj2IJz8UzjvL6aOtGEYLVZD1TzA6pkGWLsv/Id6HHEeofBIIQBzN85t4OjwsaloEwDvbH3H7/rBoaqksoSv937NZ7s/45DjULDDaTaLty/mJwt/wnf7v2vWz/U1mZ4JHALuF5FvReQZEZkqIvEBjC1kvfzlTrYUlvL7yYOIjQqjZ9ps/gjevwN6jYOpT0GEvw/QNAwjUETk7z4sfwx2nM2pqme6vmS6c3xnusZ3bRXjpneVWH1fXeO7snj7Yg6UHwhyRM1jc9FmBGFr8VZ+OPhDsMNpFqsKVuFRDy518cnuT4IdTrNweVw8s+4ZAD7c+WGzfrZP2ZCq7lXVl1V1BjASeBUYASwVkU9E5K5ABhlKDpZW8PdPt3Bu3w6MHxBGNaVzv7FqSXc52XpEuC0q2BEZhnGsqcCaBpbpQYsuCCrcFcTaYhucszK041DWFq4N+17LqmT6zlPuxOVx8ebmN4McUeCpKtlF2UzsPpFYWyzvbHkn2CE1ixV7VhAfFU+3pG58tOOjYIfTLD7Y/gG77btpH9eeT3d92qx/n/3uWlRVj6quVNXfq+qZwAwgv+lDC01PfrqFI043914wIHwmHRZthzd+Comd4Yq3IcY83MAwWqDHVfWV+hbg2YYuIiI2EVkrIou96z1E5GsR2Soib4pItHd7jHd9q3d/94C2rhEcLgcxkXX3SlcZ0WkE+8v3s6NkRzNEFTxV7Ts77WzOzTiXNze9ebT3PlwVlBVgr7QzstNIxncbz5IdS45WeQlXqsqKPSsY1XkUk3pM4pu937D/SGg9VMVfLo+LZzc8y4B2A7ht2G3sKdvDxqKNzfb5vlbz+EddPxsCv1fVeQGOMyRsLSxl3te7uXxUBn06JTZ8Qig4UgSvXWJV8LhqISR0CHZEhmHUbmFdO0RkMoCqPuHDdW4HsqutP4yVqPfGGu43y7t9FnDIu/1x73EtisPtqLPGdHVnpp0JwPK85YEOKah2leyiS3wXYiNjuWbgNRyqOMTi7YuDHVZAVY2X7p/an2m9p1HqLOXT3Z8GOarAyrXnkl+azxldz+C87uehKEt3LQ12WAG1ePticu25/HzIzxmTMQab2PhkV/MNb/G1Z3o19f90aAAPLcmmTZSNO8b3DXYoTcPpgPlXwOE8uPwNSA2zyZSGEV4+rq13WER+BjzpywVEJB24AHjBuy7AWGCB95BXgIu876d61/HuHyct7Oe4CldFnTWmq0tLSKNXci++yP+iGaIKnp2Hd9I9qTsAIzuNpGdyz7AfArCpaBOC0CelDyM7jyQtIY13t7wb7LACasWeFQCc0fUMeqb0pG/bvmH95+z2uHluw3MMaDeA0RmjSYlN4ZTOp/DJrk+abaiHr2Oma/5UuBBYWG291Vux9QCfbirk5jG9aZ/Q8M+KLZ4qvHcL7F4J056BzNOCHZFhGPWbgzWP5Wi9MxH5DfBL4Fwfr/EEcBfg8a6nAsWqWlWEOQ9I875PA3IBvPsPe49vMcrd5T71TAOclXYWa/at4YjzSICjCg5VZVfJLroldQNARBiXOY7V+1ZT7CgOcnSBs6loE92Tu9Mmqg0REsHU3lP5eu/X7CvbF+zQAmbFnhWkJaSRkZgBwHndz2Pd/nUUlBYEObLAyCvNI9eey0/7/fTo8NoJ3Saws2QnW4u3NksMvtaZBkBETsJ6tHg7a1X2A9eoauuYHlsHVeWhDzeRlhLHdWd2D3Y4TSPrIfh+AYy7D05qVXOWDCMkqeoSEakAPhSRi4DrgVHAOaraYG0s71CQQlVdIyKjmyouEZkNzAbo1KkTWVlZfl+jtLS0Ueft3b+XCk+FT+cmlifi9Dh58eMXGdxmsN+f1ViNbZu/StwllDpLcRW6jn5eckUybnXz7CfPcmrCqQH53OZqX13W7VlHj5geR2No62wLwLPLnuWcxHNO6NrBbltt3OpmZd5KRsSP4PPPrYdWpzhTAHj606cZlzzO52u1xPbVZnP5ZgCKtheRtScLgFh3LILw/OfPMyll0nHnNHXb/EqmsepNz1HVzwC8N9zngTOaLKIQ9OH3e/ku/zCPXDokPErhrX8TPn8Yhl4FZ/0y2NEYhuEjVf1URK4DsoAVwFhV9XWG2ZnAFBGZBMQCSVjDQ1JEJNLb+5zOjxPO84EMIE9EIoFk4GAtMT2H9W8HI0eO1NGjR/vdrqysLBpz3ksfvkRyRLJP557pPpOX5r/EobaHGH26/5/VWI1tm79W710NeTB+xPijY8Q96uHVBa9SEF8QsBiaq321OVxxmEPzD3HtgGsZfdKPMbz+7uvsjt59wnEFs211WVu4FsduB9NHTmd0t9FHty9YvIDtsp0HRz/o87VaYvtqc2jLISiE8844j4ykjKPbF364kK3OrbW2oanb5m81j/iqRBpAVbOAVl1r2uX28Mh/N9OnYwLThqU1fEJLt2slLLoVup8Nkx83D2UxjBAhInYRKQGWYCXC44DCatvrpaq/UdV0Ve2OVaVpmapeCXwGXOI9bCbwnvf9Iu863v3LtIXVlvO1mgdAlC2K07qcxvL85WFZIq+qLF735O5Ht0VIBGMzxvJl/pdhWeFic5HVY9m/bf9jto/PHM/qfavD8mEmK/esJEIiGNV51DHbJ3SbwIYDG9hbtjdIkQXO3iNWmzrFdzpm+/hu49lyaAs7D+8MeAz+JtPbReR3ItLdu9wLbA9EYKFiwZo8th8o49cT+2GLCPHEs2i7NeEwJdOqJR0ZHeyIDMPwkaomqmqS9zVaVeOrrSedwKXvBuaIyFasMdEvere/CKR6t88B/u/EWtD0KtwV9T6wpaaz08+moKyAbcXbAhhVcOws2Ul0RDSd23Q+ZvvYzLE43A5W7lkZpMgCJ7vIKkrTr12/Y7aP6zYOt7rJys0KQlSBtf3wdjISM0iOST5m+/jM8QDNWuGiuewt20v7uPZE247NWSZ0mwDQLJVM/E2mfwZ0AP7jXTp4t7VKDqebJz7ZwvDMFCYM7NTwCS1ZeTG8/lNA4Yq3oE27YEdkGEaQqGqWqlaV09uuqqNUtbeqXqqqFd7tDu96b+/+Ftex4nA5iIuM8/n4s9LOAgjLqh47S3aSmZSJLeLYoYgjO48kMSqRZbuXBSmywNlctJmOcR1JjTt2XuzAdgPpGt81LEvk7SndQ9f4rsdt757cnb5t+/Lxro+DEFVgFZQW0CW+y3HbO8d3ZmiHoSzd2cKSaVU9pKq3qepw73K7LxNbwtVrX+1ib4mDu87rH9oPaHE74e2ZULQDfjrPlMAzjBAkIt82xTHhxOF2+NUz3Tm+M33a9gnPZLpaWbzqoiKiOCfjHD7P+xyXx3X8iSEsuyib/qn9j9suIozrNo4Ve1ZQ5iwLQmSBs6d0D10Tjk+mwRr2sLZwbdg9wKWgrIDO8Z1r3feT7j9h86HNAR/q4VcyLSIjReQ/IvKtiGyoWgIVXEtWVuHi6axtnN2nPaf1bFHVoPyjCh/Mge1ZMOXv0P3MYEdkGEbjDKh+X65l+Q5oH+wgm5PD5fCpznR1YzLGsGbfGg6UHwhQVM3P5XGRZ887WhavpnGZ4yiuKObbfeHzXavSXcmOwzvo17ZfrfvHZ47H6XHyRV74fHGqcFdw0HGw1l5agJ90+wmKhlWPvKqyt2xvnW1urqEe/g7zmAe8DEwHLqy2tDovr9hJUVklv/pJ7X9RQ8aXT8K3r8LZd8LQK4IdjWEYjdefY+/LNZfJtKLKS6pKhbvC5zrTVS7ocQEe9fDfnf8NUGTNL780H5e6jpl8WN2ZXc+kTWQbluxY0ryBBVBeaR5uddMzpWet+4d0GEJqbCqf7A6fMcRVdaTr6pnuldKLnsk9w2qoR3FFMQ63o85kumqoR6D/PvubTO9X1UWqukNVd1UtAYmsBTtc7uTZz7cxfkBHhmakBDucxtv4HnxyHwy6GMbcE+xoDMM4AdXvyfUsecGOs7m4PC7c6va7Z7pnSk/6t+vPku3hk1gereRRyzAPgDZRbRjfbTxLdy6lwl3RjJEFTp7d+l89PSG91v22CBvju43n89zPKa0sbc7QAmZP6R6g7mQarKEeq/etpshR1FxhBVRBmfUFoq5kGmBi94nkHMoJ6FAPf+tM3yciLwCfAkf/xqnqfxo6UUTOw6pZagNeUNW/1HLMZcD9gALrVbVFdpW++MV2ShwufjkhhB8bvvsr+M9sSB8FFz0DEf5+rzKMpuV0OsnLy8Ph8LUscsuRnJxMdnZ2rftiY2NJT08nKiqqmaNq3Rxu6/8jf8ZMV5nUYxKPrXmM3JLcY+rWhqodh3cAdSfTAJN7TmbRtkVk5WYxsfvEZooscPJLrXLo6Ym1J9MAU3pN4c3Nb7J011Iu7nNxc4UWMHvKvMl0LRMQq/yk2094bsNzfLTjI64Y0CJTLL9UJdOdE2ofMw3WF4iHv3mYpbuWMvvk2QGJw99k+jqsnxKj+PFxs4pV2aNOImIDngImYD2O9hsRWaSqG6sd0wf4DXCmqh4SkY5+xtYsisoqeXH5Di4Y3IVBXZMbPqElOrAF3pgBSWlw+XyI8q/nxjACIS8vj8TERLp37x5yE3rtdjuJiYnHbVdVDh48SF5eHj169AhCZK1XVQ+rP9U8qpzf43weW/MYS3Ys4cYhNzZ1aM1ud8lukqKTSImt+5fUUZ1H0TGuI4u3LQ6LZDrPnkesLZbU2LrnNA1uP5geyT14b+t74ZFMl+7BJjY6tOlQ5zH92vVjQLsBvLv13bBIpqvqZtfXM905vjPDOg5jyfYl3DD4hoD8++Jvd+QpqjpSVWeq6nXexZfSeKOArd4SS5XAfGBqjWNuAJ6qqg6iqoV+xtYsnv18G+VON3eM7xPsUBrHvg9euxjEBlctgPgQnjxphBWHw0FqamrIJdL1ERFSU1ObvbddRLqJyHjv+zgROT7TD3NVDyFpTM905/jOjOg0giU7loTFA1x223fXOfmwii3CxgU9L2B5/vKwGAKQX5pPWkJavfcTEWFKryl8W/gtu0t2N2N0gVFQVkCnNp2IjKi/n/Si3heRXZTNpqJNzRRZ4BSUFhBji6FtTNt6j5vSawrbDm9j/f71AYnD32R6hYgMbMTnpAG51dbzvNuq6wv0FZEvReQr77CQFqWwxMErK3dy0dA0+nQKwX+byoth3nQoOwBXvgXtap+YYRjBEk6JdJXmbpOI3AAsAJ71bkoH3m3WIFqACpfVM+3rExBrmtRjEtsPbyfnUE5ThhUUufZcMhIbHq4yuddkXOriwx0fNkNUgZVnz6t3iEeVC3teSIREsGjbomaIKrDqK4tX3QU9LyAqIop3t4b+bWHvEauSR0P32fN7nE9cZBz/2dLgqORG8XeYx2nAOhHZgTVmWgBV1ZObKJY+wGism///RGSwqhZXP0hEZgOzATp16kRWVpbfH1RaWtqo817bWEGly8NpiUWNOr851NW2CHcFJ2+4n6SSHL4bfA+Htthhy/HHtXSN/bMLBa29bcnJydjt9uYJqA55eXnceOONFBYWIiJce+213HzzzXz33XfccccdlJWVkZmZyQsvvEBSkvVQwUcffZRXX30Vm83GX//6V8aPH3/cdR0OR3P+2d6C9Wvg1wCquqWlDpsLpKox03E2/4d5gFVS66GvH2Lx9sXHPUEvlFS6KykoK+DCXg0X3urbti/92vZj8bbFXDngymaILjBUlbzSPEZ0GtHgsZ3iO3F6l9N5f9v73Dz0ZiIkdOcP7Snbc9xjxGuTHJPMuMxxLN6+mDkj5hz35MBQUl+N6erio+KZ1GMSS3Ys4a5T7mryOPxNphvbW5wPVP9anO7dVl0e8LWqOoEdIpKDlVx/U/0gVX0OeA5g5MiROnr0aL+DycrKwt/z8ovL+d/HWVw2MoPLJjXFd4fAqLVtbqf1mPDD2XDJSww5KXTHhjXmzy5UtPa2ZWdn1zruuDmlpKTwxBNPMHz4cOx2OyNGjODCCy/k9ttv55FHHuHcc8/lpZde4l//+hcPPvggGzdu5J133mHVqlXY7XbGjx9PTk4ONtuxT5mLjY1l2LBhzdWMClWtrOqpEZFIrLktrYrD5Z2A2Mie6baxbTk341ze2/oetw67tVHDRVqC/NJ8POohMzHTp+Mv7HUhj6x+hC2HttCnbWgOZzxccZgyZ5lPPdNgDQG4+4u7Wb13NaO6NJyMtkROj5PCI4X1jh2ublrvaXy08yM+y/0spMfI7y3dy5lpvj0fY3qf6SzcspAlO5bQkabtX/D3K5i9lmWPD+d9A/QRkR4iEg3MAGr+pvIuVq80ItIea9hHi3k87T+XbQHgF+NC7ObidsKC62DLUpj8OIRwIm0YgdalSxeGDx8OQGJiIgMGDCA/P5+cnBzOOeccACZMmMDChQsBeO+995gxYwYxMTH06NGD3r17s2rVqqDF7/W5iPwWiBORCcDbwPtBjqnZVfVM+1tnurrL+1/OoYpDIV1zOtdujbD0ZZgHWIlljC2GNza9EciwAiqv1CqLl5ZQczRp7cZmjiUhKoGFWxYGMqyAKjxSiEc9Pg3zADi1y6l0ju/MO1vfCXBkgeN0O9lfvt+nnmmAk9qfRJ+2fQLy5+xvz/S3WD3Mh7CGeKQAe0VkH3CDqq6p7SRVdYnIrcB/sUrjvaSqP4jIH4DVqrrIu+8nIrIRcAO/VtWDjWpVE9u+v5S3Vudx1amZpKU07ifDoKhKpLPfh4kPwcjrgh2RYfjkgfd/YOOekia95sCuSdx34SCfj9+5cydr167l1FNPZdCgQbz33ntcdNFFvP322+TmWglKfn4+p5122tFz0tPTyc+v+aNbs7sbuB74DrgRWAK8ENSIgqBqzLS/daarG9V5FD2Te/JG9htM6TWlqUJrVlUT6zKTfOuZbhvblgt6XsD7297n9uG3kxwTelWrqpJpX3umYyNjuaj3RczfNJ85I+bQKb5TIMMLCF9qTFdni7AxtddUntvwnM/jy1uafUf2oajPvfEiwvQ+0/nLqr+QG53b8Al+8Ldn+mNgkqq2V9VU4HxgMXAz8HR9J6rqElXtq6q9VPVP3m2/9ybSqGWOqg5U1cGqOt//5gTGI0s3ExMZwa1jQ6hX2lUJC372YyJ9+s3BjsgwQkZpaSnTp0/niSeeICkpiZdeeomnn36aESNGYLfbiY5umWMMvWVIs1X1eVW9VFUv8b5vfcM8mqBnWkSY0X8G3x/8nu/2f9dUoTWr3fbdJEQlNFjtoLor+l+Bw+0I2GStQGvogS21uXLAlXjwMH9zi0k9/HI0ma6nxnRNl/a9FJvYmJc9L1BhBdTRGtM+9kyDVU89xhbDSvvKJo3F7wmIqnpD1YqqLhWRR1T1RhEJzQFlDViXW8yS7/Zy+7g+dEgMkSZW2OHNq2H7ZyaRNkKSPz3ITc3pdDJ9+nSuvPJKLr7YGhbVv39/li5dCkBOTg4ffPABAGlpaUd7qcGawJiW5ttPy4Ggqm4R2Swimaoa+rW+TkDVmOkT6ZkGa9jDk98+yRub3mBwh8FNEVqz2m3fTUZihl9VZfq168cpnU/hjU1vcPXAqxsstdbS5NnzaBfbjjZRbXw+Jz0xnbEZY3lr81vcMPgGv85tCaoe2OJPYtkpvhOTek5i4ZaF3DTkppD7FcKXGtM1Jcckc8+p92Df3rST3f3tmS4Qkbu9NUy7ichdwD5vb4inoZNDjarylw+zSY2P5oZzQqOMXFTlYXjlQtjxP5j6lEmkDcMPqsqsWbMYMGAAc+bMObq9sNAqe+/xePjjH//ITTfdBMCUKVOYP38+FRUV7Nixgy1btjBqVNAnMLUFfhCRT0VkUdUS7KCaW1P0TINVBWBKryl8tPMjDpa3iJGHfsmz5/k8xKO6K/tfSUFZAVm5WU0fVIDll+b71Std5ZpB11BSWcL720JvikFBaQEd4zr6XZnjmoHXUO4q5+2ctwMUWeA0pmcaYFqfaWTG+P93oj7+JtNX8GPN0newxk9fgTUO+rImjawF+DxnP19tL+IXY3uTEBMC38wLNzFs7d1QuAlmvA7Drgp2RIYRUr788kvmzp3LsmXLGDp0KEOHDmXJkiW88cYb9O3bl/79+9O1a1euu86afzBo0CAuu+wyTjnlFM477zyeeuqp4yp5BMHvgMnAH4BHqy2tyolW86huRv8ZOD1O3tz85glfqzm5PC7y7fk+V/KobnTGaLrGd2XuxrkBiCyw8ux5Pk8+rG5oh6GclHoSr2W/hkdDq39wT+keuiT43kNbpV+7fpzZ9UzmZc+j0l0ZgMgCp6CsgHax7U7416em4FeGqKoHgF/UsXvriYfTcjjdHv70QTaZ7dpwxan1PzmqRch+H965iUiNhJmLICPovWOGEXLOOuusOp94d/vtt9e6/Z577uG2224Lelm/Kqr6ebBjaAmqHifeFCXteib3ZFzmOF7b+BpXDbyKpOikE75mcygoK8ClLp8reVRni7Bx1cCr+Os3f+Wbvd9wSudTAhBh03N5XOwt28v5Pc73+1wR4eqBV3P3F3fzee7njMkcE4AIA2NP2R5OSj2pUefOHDST2R/P5oPtHzCtz7QmjixwfK0x3Rx86pkWkfub4phQ8tLyHWwpLOX3kwcSHdmCi7i7KuGTB+DNq6BDP1aPfMwk0obRiomIXURKvItDRNwi0mBpFBGJFZFVIrJeRH4QkQe828eJyLcisk5ElotIb+/2GBF5U0S2isjXItI9sC3zj8PlIMYW02QP4bhpyE3YnXbmbQydyVq5JdZ4/sYM8wBrglqHuA48te6pkHms+r4j+3Cpq1E90wATuk8gPSGdZ9Y/EzK90x71sLdsb6N6pgFO63Ia/dv1598//Bu3x93E0QXO3tK9fo2XDiRf7zLXi8icepZfYdWODgsFh8t58tMtjOvfkfEDW3CJnMJN8OJ4WP4YDL8Grl1CZUxqsKMyDCOIVDVRVZNUNQmIA6bTQLUlrwpgrKoOAYYC54nIacAzwJWqOhR4HbjXe/ws4JCq9gYeBx5u4qacEIfb0aQPWunfrj/jMscxd+NcSiqbtmxjoOy2e8viNWKYB1iTN68ffD1r9q3hq4KvmjK0gMm3W6UpG1vqLSoiipuH3kx2UTYf7/q4KUMLmAPlB3B6nI3+AiEizD55NjsO7+D97aExXrzSXcku+65Gf1Fsar4m088DifUsCd5jwsIfF2fj9ij3TwleRYF6uSrgi0fh2XPgcB78dB5M+QdEBX/ckGEYLYe35Oi7QIOPOPMeW+pdjfIu6l2qxjUk8+ODuqYCr3jfLwDGiT8lIwKswl3R5GMpQ613erd9N3GRcbSPa9/oa0zvO51ObTqFTO+0vw9sqc2kHpPoldyLf679Jy6Pq6lCC5iqsngn0ks7PnM8J6WexFPrnjo6RKol21y0GZfHxeD2LaPCjk9jplX1gUAH0lJ8trmQD74rYM6EvmS0a2Gl+Ei0uAAAIABJREFUcVQh5yP46DdwaAcMuBAueAwSmvaxmIZhhC4Rqf6Y0whgJODw8VwbsAboDTylql+LyPXAEhEpB0qAqqfUpAG5cPTBXIeBVOBAkzTkBBU7ipt8bHP13ukrBlzR4kuJ5Zbk+l0Wr6YYWwyzT57Ng189yPL85ZydfnYTRtj08ux52MR2QmNpbRE2fjHsF9yRdQfvb3u/xY8jrvoC4esDW2ojItwx4g6uX3o98zfNZ+agmU0VXkB8d8Cq+x5SyXRrUXC4nF+9tZ4+HROY3ZJK4alajwP/398g7xto3w+ufgd6jQ12ZIZhtDwXVnvvAnZi9SI36P/ZO+/wqIouDr+z2U3vIYSQEEIPvQWCFClSRClWUGmfitiwgCiCiKhIE1RQUBQUe6MIIqBgCAEEQg9IDT0QQgqkl83ufH/cDQSkZJNtCfd9nvtkd3Zmzm9SNmfnnjlHSmkAWgghfIFlQogmwCiUYl3bhBCvAh+gVFgsFUKIEcAIgKCgIGJiYko79DLZ2dlmjzuSfARvjXeZ7N2MSH0k0fpoJvwxgQf9Hyz3fGVZW2k5lHyIIF3Zvucl8Zf++Dv5817se7wa/CpOovQZa6y5vuuxK2UXfk5+bIrdVK55NFJDmHMYH277EM9ET3RC958+tl7bjViTvgZn4czJ3Sc5I8pX2S/CNYJ5u+ZRNbkqhlyDQ6zveqxLXYe3kzcH4w5ySBwye7ylf3aqM21CbzAy8ofdFOgNfDq4Na46u6e3gvxM2Pcr7PgKkveBTxjcOwtaDQOn//5hq6ioqAALpJSbSzYIIToAF0o7gZTykhBiPUqV2+ZSym2ml34G1pgen0VJj5oohNCihID8JxGzlPJz4HOAyMhI2aVLF/NWA8TExGDuuAk/TaB9WHu63GG+vVtxfMtxlh5dyktdX6KuX91yzVWWtZUGg9FA2vdp9G7Qmy6tyz+/8aSRVza8QnK1ZB5r+Fipx1lrfTfiiz++oI5PHYvYdDnnwtNrn+ZEwAlGNBvxn9dtvbYbMe/3ebQMasldXe8q91xBaUEMWDmAI75HaK5p7hDrux6zls2iVfVWdO1atowrlv7ZOXCaCtsybfUhdp66yLQHm1G3qqf9hBTmKGnulo6AWQ3gj9EgjdB/Hry4C9oMVx1pFRUrkZ+fT9u2bWnevDmNGzfmrbfeAuDEiRNERUVRt25dBg4cSGGhko+1oKCAgQMH0rx5c6Kiojh58qQd1V/m41K2XYUQItC0I40Qwg3oARwEfIQQ9U3ditsAVgDF94IfAqIdpWx5rj6XjIKMMmc3uBUvtHwBD50H07ZPc9g44gu5F9Ab9WU+fHgtPWr2oF1wOz7Z/YnDFq/RG/QcvXSUWt61LDJf++rt6VGzB5/Hf365RLmjkaPP4fDFw7QMammR+RoGNKRv7b4s+ncR5/XnLTKnpckszORk5kmHCfEAM51p05vteCHE50KIL4sva4mzBVJK5vx9lIWbTvC/9uH0bV72mKMyUVQAZ+Jg4wfw3YMwo7aS5u7In9D0IRgeDc9uhpaDVCdaRcXKuLi4EB0dzd69e9mzZw9r1qxh69atjB07llGjRpGQkICfnx8LFy4EYOHChfj5+bF3715GjRrF2LFj7aZdCHGHKbNS4DXZliahFNa6FcHAeiFEPLAdWCulXAk8BSwRQuwFhgCvmvovBAKEEAnAaOB1Cy+pzBRXRqvuYZ33cz9XP0a2HMm2pG2sO73OKjbKS3kzeVyLEIJxUePIM+Tx0a6PLDKnpdmXuo+8ojyigqMsNudrbV7DSTgxNW6qQ35w2puyF6M00rKqZZxpgFciX8Fd685PaT85ZHrAA2kHAGhSpWx5ta2BuWEey4GNwDqg4iQjvAF5hQZeXbyXlfFJ3N8yhPH3NLSOISkh/5KSeSP9OKQlQOpRSIqH1MNQfFo4MEIJ4Yi4F2q2V51nFRUbI4TA01O5M6XX69Hr9QghiI6O5ocffgBg2LBhTJo0iWeffZbly5czadIkAB566CFGjhyJlLJcB77KgTNKZiUtSpalYjJRdo5vipQyHvjPf2Qp5TKUirfXtucDD5dVrDUpzm5QngNZt+Lh+g/z65FfeX/7+7Sv3h4PnYfVbJWF/an7Aajta7nzP7V9ajOk0RC+2v8VD9Z7kBZVW1hsbkuwLWkbAmHRAjPVPKrxXIvnmLljJtGno7mrZvlDKSzJ7gu70QgNzQObW2zOALcAXol8hbf+eYtlR5fxYP3ynw2wJMW/240DHCfjmrnOtLuU0n5bLxYgT5/PqUwD89YfZfnuRBJSshnfqx5PdQxHyAIoMIA0gLH4KgKjHgzFV4FSKKUoD/T5oM9VQjMKc6AwC/IuQX4G5KVDTipkX4Cs86DPuVqIVzAENYEGd0NwC8V59ih7+iIVlUrF6tfh/D7LzlmtKfSedstuBoOB1q1bk5CQwPPPP0+dOnXw9fVFq1XeLkNDQzl7Vslle/bsWWrUUKrLabVafHx8SEtLo0oV2/8tmyofbhBCLJJSnrK5AAeieGfamtXRtBotE9tNZOjqoby//X0mtZ9kNVtlYdPZTTTwa1CutHjX45lmz7D6xGre3PwmP/f5GXed42S92pq0lYYBDS2eZeWxho+x/NhypsZNpU1wG4eqgLkreRcN/BpY/MPc/XXv59ud3zJr5yw61+hs8d+j8rAvZR81vWs6VDYdc53plUKIe6SUq6yixspIKRm4KJJLTkZqJhXRxlnPOz45RG0oAEsV4NW6gqsPuPmBRyAEN4P6vcA7BHxCwL+2crk4RulhFRWVq3FycmLPnj1cunSJ+++/n0OHzD8pbmdyhRDvA42By4mWpZS3TfqfpJwktEJLoFugVe20qNqCx5s8zpf7v6Rrja50rtHZqvZKS1ZhFnsu7LFKejN3nTuTO0xm+F/D+WDnB0xoN+HWg2xArj6X+NR4hjQaYvG5dRod77R/hyGrhjB5y2Sm3zndXnefrkJv1BOfEm+VnWMhBAMDBjLj/Aze/udt5nSb4xBrBmVnuk2wY5W3N9eZfgkYL4QoBPSmNmmqtOXwCCFo5xbJ6bzT5HnDhqJMlnt50sGtOi/7tSbCLRCEBoQTaLSgcTJdOiXkwkkHTi6gdVGcZp2b8tXFE5xNl1o4RUWl/JRiB9na+Pr60rVrV7Zs2cKlS5coKipCq9WSmJhISIhSECIkJIQzZ87g4+NDUVERGRkZBATYvQrp9yhZN/oAz6AcEkyxqyIbcy77HEEeQThprJ+V6fkWz7Pp7Cbllnj/Zfi5+lnd5q3YmrSVIllktZzQUcFRDG00lG8OfMOdoXdyZ+idVrFjDrsv7KbIWERUNcvFS5ekSZUmPNfiOebsnkPH0I70q9PPKnbM4VDaIfIN+bSq2soq81fTVWN069FM3z6dHw79wKCGg6xixxySc5K5kHfBoQ4fgpkHEE1lajVSSlfTY6+K4kgXM37wIh6pN5GvH41m3WObGRM5hv3GHAacW8nqkAjo8BK0HwntnoG2T0HkE9BqCDR/BJo8CA37QL0eUKsThEZCtSbgF66EaKiOtIpKhSYlJYVLly4BkJeXx9q1a2nYsCFdu3Zl8eLFAHz99df076+kbe7Xrx9ff60UAVy8eDHdunVzhN2bACnlQkAvpdwgpXwCuG12pUHZmbZmvHRJnJ2cmdJxChmFGUz6Z5JDHFLbdHYTXjovi8bRXsuLrV6knl89Jm6e6BDZPbYlbUOr0Vr0IN61PNHkCSKDInlv63uczjxtNTulZdeFXQBWXfOghoPoHNqZWTtmcTDt4K0HWJn9aUq8tCMdPoQypMYTQvQTQsw0XX2sIcpWuDi5MKzxMFY9sIqWVVsyYdME9qbstbcsFRUVO5GUlETXrl1p1qwZbdq0oUePHvTp04fp06fzwQcfULduXdLS0njyyScBePLJJ0lLS6N58+Z88MEHTJtm/x11rtw1TBJC3CuEaAn421OQrTmXfa5cpZXNpYF/A0a1GkX0mWgW7FtgM7vXQ0rJprObaFe9HVqN9UpJuDi5MLXjVLL12YyOGY3eoL/1ICuyNWkrzQObWzWG20njxNROU9FqtIzZMIZCY6HVbJWG3Rd2U8OrBoHu1gtnEkLwbod38XPx49XYV8m59vyXjdmfuh+t0BLhH2FXHddibmq8aSihHgdM10tCiKnWEGZLvJ29+ajrR1R1r8qL0S9ePgmuoqJye9GsWTN2795NfHw8+/fvZ+LEiQDUrl2buLg4EhIS+PXXX3FxcQHA1dWVX3/9lb179xIXF0ft2g5ROXWyEMIHeAUYAyxAqWJ4W6A36knJS7GpMw0wpNEQ7ql1Dx/v/pjYxFib2i7JkYtHuJB7gU4h1i/73cC/AW+3f5tdF3YxJW6K3XblMwoyOJR+yKIp8W5ENY9qTOk4hUPph/gu7Tu7pY6TUrL7wm6r7koX4+fqx7Q7p5GYlchrsa9RVJyBzMZIKYlNjKVRlUa4OLnYRcONMHdn+h6gh5TySynll8DdwL2Wl2V7/Fz9mHvXXPQGPS9Ev2C3XxYVFRWVsiKEcALqSSkzpJT7pZRdpZStpZQr7K3NVlzIvYBRGm0W5lGMEIJJ7ScR4R/B2NixnMg4YVP7xWw6q5TR7hDSwSb27q19L082eZLFRxbz8+GfbWLzWuLOxyGRtAtuZxN7nWt05pXIV9idu5t5e+bZxOa1HL54mPT8dKvFS19Lm2ptGNd2HLGJsby//X2b2LyW3Rd2c+TiER6o+4Bd7N+MslRA9C3x2HHykliA2r61mXjHRI5cPGLXnQUVFRWVsiClNACP2luHPSm+s2jrnWkAN60bH3X9CJ1Gx7PrniU5J9nmGjae3UiEfwRV3avazOYLLV/gztA7mRY3jejT0TazW8zms5tx17rbNI52aKOhtPNox/z4+fx+7Heb2S3m2wPf4qZ1464w2+W9HhgxkGGNhvHDoR/4/uD3NrNbzE+Hf8JL50XvWr1tbvtWmOtMTwV2CyEWCSG+BnYC71lelv3oXrM7gW6BLDm6xN5SVFRUVMrCZiHEJ0KITkKIVsWXvUXZiuIc0/ZwpkEpFDOv+zwuFVziqbVPkZ6fbjPbGQUZ7L2wl44hHW1mE5RY4hl3zqBxQGPGbBjD5rObbWb7Qu4FVh5fSc/wnug0tit0Vpw6LqpaFBM2T2DNiTU2s30+5zyrjq/igXoP4Ovqe+sBFmR05GjuCruL6XHT+S3hN5vZTc1LZe2ptfSv29+hcpsXY242jx+BdsBSYAlwh5TSPvd1rIRWo+X+evez6ewmkrKT7C1HRUVFxVxaoOSYfgeYZbpm2lWRDbm8M+1pH2calEwDn3T7hHPZ53h67dNkFGTYxO7C/QsxSINddu48dB7M6z6POr51eGn9S2w/v90mdhfuW0iRsYgRzUbYxF5JtELLnG5zaBHYgtc3vs5fJ/+yid3vDnyHRFolp/at0AgN0zpNo11wOyZunsiyo/8pjmoVlh5dSpGxiAENBtjEnrmUypkWQkSYvrYCgoFE01W9Mu54PFDvAaSULEuwzS+JioqKiqUwxUlfe902qfHO55wnwDXA7geUIqtF8lHXj0i4lMD/1vzP6iEfSdlJfH/ge/rW6Ut9v/pWtXUjfFx8mN9jPqGeoTy37jmrh3wk5ySz+Mhi+tftTw2vGla1dSPcde7M6z6PZoHNGBs7lpXHV1rVXmZhJouPLqZneE9CPEOsautGuGpdmdNtDu2rt2fiPxP55fAvVrVXZCzil8O/0C64HbV8alnVVlkp7c70aNPXWde5Kt2OR4hnCO2rt2fp0aUYjAZ7y1FRUVEpNUKIICHEQiHEatPzRkKIJ+2ty1acyz5n88OHN6JjSEfm3TWPpJwkBq8eTMLFBKvZ+nj3xwCMbDHSajZKg7+rPwt7LaSeXz1eXv8yGzItVV74vyzYtwCjNNplV7okHjoP5t01j5ZBLRm3cRyf7vnUaplNfj38Kzn6HB5v/LhV5i8trlpXZnebTaeQTry79V1m7ZhlNX9p3el1JOcm80jEI1aZ3xKUypmWUhb/pva+dscDJcNHpeOh+g+RnJvM5nO2i/1SUVGxL/n5+bRt25bmzZvTuHFj3nrrLQBOnDhBVFQUdevWZeDAgRQWKvllFy1aRGBgIB06dKBFixYsWGDfHMMmFgF/AsUe5RHgZbupsTFJOUlU86hmbxmXuaP6HSy6exFFxiKGrhnKhjOWdy4Pph1k5fGVDGo0yK7hLcUEuAWwsNdCutTowuKLi5mybQqFBsvmZD6fc54lR5dwX7377LZDWxJPZ0/md59Pvzr9mLd3HuM2jSOvKM+iNlJyU/jmwDe0C25Hw4CGFp27LLg4uTC722weafAIi/5dxIvrXyS7MNuiNs7nnGfK1inU9a1L59DOFp3bkph7APGfUrZVeDrX6EyAawCLjyy2txQVFRUb4eLiQnR0NHv37mXPnj2sWbOGrVu3MnbsWEaNGkVCQgJ+fn4sXLjw8piBAweyefNm9uzZw/Dhw+2o/jJVpJS/AEYAKWURcFvcYpNSKtUPPRxjZ7qYCP8IvrvnO0I8QxgZPZLpcdMt5lwWGYt4f8f7eLt4M7ypQ/z+AUpmkw+7fEhXr678eOhHHvvjMY5fOm6RuXP1uby64VUEgqeaPmWROS2BzknH5A6TebHli6w6vooBvw9gf+p+i8ydV5THC9EvkFeUx5jIMRaZ0xLoNDreaPcGE6ImsPnsZh7+/WF2Ju+0yNx6g55XNrxCgaGAD7p8YNUiROWltDHT1YQQrQE3IUTLEifEuwCOd6zSAug0OrrU6MKeC3vsLUVFRcVGCCHw9PQEQK/Xo9frEUIQHR3NQw89BMCwYcP47TfbnWIvAzlCiABAAggh2gG2OQFnZ9Lz0ykwFDjE7uy1hHiG8N093/FYxGN8d/A7Bq8aXO6Ku3qjntdiX2P7+e2MajUKb2dvC6m1DE4aJx7wf4C5d83lQu4FBq4cyKL9i8r1QUJv0DM6ZjTxqfFMv3O6w4T0FCOE4KlmT7Gg5wLyDfkMXjWYuXvmlmuX2iiNvLHpDQ6kHWDGnTNo4N/Agootw8CIgXzZ60sAHl/zODO2zyBXn1uuOWfumEl8SjzvdnjXYWOliymtm98L+B8QCnxQoj0LGG9hTQ5DTe+aXCy4SGZhpsO9SamoVGamx03nUPohi84Z4R/B2LZjb9nPYDDQunVrEhISeP7556lTpw6+vr5otcrbZWhoKGfPnr3cf8mSJcTExBAREcGHH35IjRr2OQhVgtHACqCOEGIzEAg8ZF9JtqE4LZ6j7UwX4+LkwriocUQFRzF562QGrxpMW4+2NM5tbHZJaL1BcaTXnV7Hq5Gv8mD9B62kuvzcGXonS/ot4e0tbzNr5yx+OfILr7R+hW5h3RBClHqeQkMh4zaOY/O5zbzT/h261+xuRdXlo21wW5b0W8KUbVP4bO9nLD26lJEtRtKvTj+cNE6lnievKI+Z22ey9tRaxkSOoUuNLtYTXU5aBbViSb8lfLDzA7498C2rT6xmRLMRPFTvIXROpU9bmFeUx4c7P+THQz8ytNFQeob3tKJqy1DamOmvTfHR/7smZrqflHKplTXajTCvMADOZJ6xsxIVFRVb4eTkxJ49e0hMTCQuLo5Dh27s1Pft25eTJ0+yZcsWevTowbBhw2yo9PpIKXcBnYH2wNNAYyllvH1V2QZHSItXGrqFdeP3+3/niSZPsDNnJ72W9OKNTW9wMO1gqcZvP7+dJ/96knWn1zG2zViGNh5qZcXlJ9A9kE/u+oRPu3+KTqPj5ZiX6b+8P98f/J7MwsybjjVKI6uOr6Lfb/3469RfjIkcw/317reR8rLj7ezNtE7T+KrXVwS5BzHxn4n0/a0vC/Yt4ELuhVuOjzkTw32/3ccvR35hWKNhDG3k+D9nd507E9pN4Jve3xDmFcaUbVPos6wPn+39jMSsxFuO331hNw///jA/HvqRwQ0H83LrinHcw6wAFCnlEiHEvSg5TF1LtL9jaWGOQJi34kyfzjpN4yqN7axGReX2oTQ7yNbG19eXrl27smXLFi5dukRRURFarZbExERCQpQDTwEBAQAUFhYyfPhwXnvtNXtKBkAI4Qo8B3RECfXYKIT4TEqZb19l1udQ+iE0QuMQB9JuhYfOg1GtRxGaHsoRryMsP7acFcdWUMenDlHBUbQNbkuoZyg+Lj7oNDpOZp4k4WICa06uYUfyDqq4VWFyh8n0r9vf3ksxi44hHWkX3I5VJ1bx86GfmRY3jVk7ZtG0SlNaBbWigV8D3HXuuGndSMpJYn/qfraf307CpQQa+DVgfo/5tK/e3t7LMIvIapF8f8/3rDu9ju8Pfs/sXbP5ZPcnNK7SmGZVmtEooBFezl5ohIZcfS47k3ey/fx2jmUco65vXRbdvYjWQa3tvQyzaFm1JYvuXsQ/5/5hwb4FzN0zl7l75tKsSjMaV2lMA78GBHkEUWQsIt+QT3xKPLGJsZzKPEWwRzALey6kbXBbey+j1JjlTAshPkOJke4KLEC5dRhXyrF3A7MBJ2CBlHLaDfo9CCwG2kgpd5ijz9KEeoUCcCrzlD1lqKio2IiUlBR0Oh2+vr7k5eWxdu1axo4dS9euXVm8eDGPPPIIX3/9Nf37Kw5MUlISwcHKLuiKFSto2ND+J+yBb1BC8D42PX8M+BZ4+GaDTE54LOCC8r9hsZTyLaHch59sGm8APpVSzjG1z0bJ6JSLcudylxXWUyqklKw9tZbWQa3xcvaylwyzCdQF8nC7h3mh1Qv8fux3NiZuZOnRpfxw6Ifr9q/qVpXX277Og/UexFXret0+jo5Wo6VfnX70q9OPA2kHWHNiDTuTd/LV/q8wyKvPyrpp3WgU0IjJHSbTp3Yfs0IkHAkhBD1q9qBHzR6cyjzF8oTl7EzeyeIji8k3XP05103rRqugVgyMGGh2iIQjIYSgQ0gHOoR04Fz2Of44/gexibEsT1hObtHV8dQ6jY62wW0Z1HAQfWv3xdPZ006qy4a5RyPbSymbCSHipZRvCyFmAatvNUgI4QTMBXqgFHvZLoRYIaU8cE0/L+AlYJuZuqyCm9aNIPcgzmSpYR4qKrcDSUlJDBs2DIPBgNFoZMCAAfTp04dGjRrxyCOPMGHCBFq2bMmTTyppm+fMmcOKFSvQaDRUqVKFRYsW2XcBCk2klI1KPF8vhDhww95XKAC6SSmzhRA6YJMpV3VDoAYQIaU0CiGqmvr3BuqZrijgU9NXu5BwKYGTmScZ1HCQvSSUC29nbwY1HMSghoMoNBRyIO0AqXmpZBRkkG/Ip6Z3Ter61iXIPcisOGNHp1FAIxoFKL+uufpczmafJa8oj7yiPAJcA6jlU6vCOtA3oqZ3TV5s9SKgHCI9lXGKAkMBBmlAp9FR16+uTUuj24LqntV5qtlTPNXsKYzSSGJWIun56eicdOg0OkI9Qx2yTHhpMdeZLv74lCuEqA6koVREvBVtgQQp5XEAIcRPQH/g2jf4d4HpwKtm6rIaYd5h6s60isptQrNmzdi9e/d/2mvXrk1c3H9vwk2dOpWpU6eSlZWFl5fD7IbuEkK0k1JuBRBCRAG3vMsnlSoTxUlidaZLAs8Cj0kpi1PtFQd79ge+MY3bKoTwFUIESymTLLuc0vHXqb8QCIc+lFZanJ2caVG1hb1l2Bx3nTv1/OrZW4ZNKXaebyc0QkOYd9jlUNrKgLl5pn8XQvgC7wO7gJPA9e9FXU0IUHJ7N9HUdhlTWfIaUso/zNRkVcK8wtSdaRUVlYpEa+AfIcRJIcRJYAvQRgixTwhx04OIQggnIcQe4AKwVkq5DagDDBRC7BBCrBZCFHs7t3xftyV/nfyL1kGtqeJWxV4SVFRUblNKvTMthNAAf0spLwFLhBArAVcpZbnzl5rm/gAl/d6t+o4ARgAEBQURExNjtr3s7OxSjyvKKCI9P53V0atx07iZbcvWmLO2ikhlXt/tvjYfHx+ysrJsI8jCGAyGm2rPz8+35c/27rIOlFIagBamTZNlQogmKDHU+VLKSCHEA8CXQKfSzmmL9+ykwiSOZxyntVPrCvc3VJn/7qFyr68yrw0q9/osvjYpZakvYLc5/UuMuwP4s8TzccC4Es99gFSUne6TKOEk54DIm83bunVrWRbWr19f6r7rTq6TTRY1kftT95fJlq0xZ20Vkcq8vtt9bQcOHLC+ECuRmZl509evtzZghyzD+2lpLsAPaAa0Kr7KMMdEYAxwCKhlahNAhunxfODREv0PA8E3m9Na79lzd8+VTRc1lSm5KWWa355U5r97KSv3+irz2qSs3Osr69pu9L5tbpjH30KIB4X5px+2A/WEELWEEM7AIyhFBQCQUmZIKatIKcOllOHAVqCftHM2DyiRHi/ztJ2VqKhUfpT3qsqFrdckhHgXiAfmALNM18xSjAs07UgjhHBDOTB+CPgNJYMTKPmrj5gerwCGCoV2KE62feKlT/5Fq6BWaoiHioqKXTD3AOLTKNW1ioQQ+Si7FFJKedPygFLKIiHESOBPlNR4X0op/xVCvIPi5a+42Xh7UpweT3WmVVSsi6urK2lpaQQEBFSabAVSStLS0nB1tWkKswFAHSmluTWbg4GvTdmXNMAvUsqVQohNwPdCiFEoBxSHm/qvQkmLl4CSGu9xi6g3k39T/+VYxjHGR1TaYrwqKioOjrlFW8p8XF1KuQrlzbdk28Qb9O1SVjuWpjg93uks1ZlWUbEmoaGhJCYmkpKSYm8pZpOfn39Dh9nV1ZXQ0FBbytkP+KIcIiw1UqmS2PI67ZeAe6/TLoHny6jRIhiMBiZvnYy/qz/31LrHnlJUVFRuY8wt2vK3lPKuW7VVNtT0eCoq1ken01GrVi17yygTMTExtGz5Hz/UXkwFdgsh9qPkjgZAStnPfpKsw8+Hf2Z/2n6md5qOj4uPveWoqKjcppTKmTZVxnIHqggh/FDCOwC8sWPLjXlpAAAgAElEQVQqJFsR5hXG+jPr7S1DRUVFpTR8jZKvfx9gtLMWq5Gck8yc3XNoX709vWv1trccFRWV25jS7kw/DbwMVAd2csWZzgQ+sYIuh6Kmd03S89PJKsyqUGVqVVRUbktypZRz7C3CmkgpmbJtCkXGIiZETag0MfYqKioVk1I501LK2cBsIcQLUsqPrazJ4QjzMmX0yDpN44DGdlajoqKiclM2CiGmomTbKBnmsct+kiyHURqZsm0K0WeiGd16NDW8a9hbkoqKym2OuQcQPxZCtAfCS46VUn5jYV0ORcn0eKozraKi4uAUB2+3K9EmgW520GJRDEYDb295m2UJy3iiyRP8r/H/7C1JRUVFxewDiN+ilJbdAxhMzRKo1M60mh5PRUWloiCl7HrrXhWP1LxUJm+dzN+n/+bZ5s/ybPNn1fAOFRUVh8DcPNORQCNZGSsr3AQ3rRtV3aqSmJ1obykqKioqN0UIEQRMAapLKXsLIRoBd0gpF9pZWpkozM9mbWo045eNJ8+Qx5iWLzOs0RAwGkBoQGNu7TEVFRUVy2KuM70fqAbYpcqVPfFy9iJHn2NvGSoqKiq3YhHwFfCG6fkR4GegQjrTI7/pzRaXS7TNy+eNtHRqHxsNS0df3UloQKP97+XkDE465avWBXRupq8e4OwOzh7g4g2uPsrlHgBufuARCF7BynPVWVdRUbkF5jrTVYADQog4Knn+0mtx07qRW5RrbxkqKioq10UIoZVSFgFVpJS/CCHGweUKtIZbDHdY+tZ5CHbEcqc2jJqdQovr7oI0XrmMBpAGMBYpjw16MOqVr4ZCKCpQvurzoCgf8i5CYY5y5WdCUd71jWu04B0CfuHKVaU+VG0IVRuBd7ANvwsqKiqOjLnO9CRriKgIuOncyNPf4A1XRUVFxf7EAa2AHCFEAMp5FoQQ7YAMeworD33veol9yY2ZEF/AofQwJt/X1PJGDHrIz4DcdMhNg+xk5co8BxmJcPEkHFqpvFaMVzCEtIYaUVC7CwQ1UXexVVRuU8zN5rFBCFETqCelXCeEcAecrCPNsXDTupGSW/HKHKuoqNw2FJ/GG42SFq+OEGIzEAg8ZDdVFqB9dS0av1A+23CMRsE+PBYVZlkDTjrwqKJcNyMnFS4chOR/4exOSNyuONkA7lWgXg9ofD/U7gpaZ8tqVFFRcVjMzebxFDAC8EfJ6hECfAZU6nLioDjTeTe6FaiioqJifwKFEMXBxMuAVSgOdgHQHYi3lzBL8GqvBvx7LoPJfxygS4NAqvu62V6ERxWo1Um5islMguMxcOxvOLwK9v6oxF83eRAin4BqVthJV1FRcSjMvSf1PNABpfIhUsqjQFVLi3JEVGdaRUXFwXECPAEvwANls8QJcDe1VWicNIIp9zfFKCVv//6vveVcwTsYWjwKDy6AMQnw2C9Q/27Y8wN81hEW9IADK8BYaSu7q6jc9pgbM10gpSwszu0phNBiisur7KjOtIqKioOTJKV8x94irEkNf3deuqs+09ccYt2BZLo3CrK3pKvROkP9Xsp19zTFod6+AH4ZAoEN4c4x0PgBNbZaRaWSYe5f9AYhxHjATQjRA/gV+N3yshwPV60r+UX59pahoqKiciNuiwomwzvVon6QJ2+t+JfcwiJ7y7kx7v7QfiSM3AEPLAAkLHkSvugCJzfZW52KiooFMdeZfh1IAfYBT6PE5E2wtChHxE3rRqGxEIOxwmaYUlFRqdxU+rMrADonDe/d35Szl/KYt/6YveXcGictNHsYnt0CD3wBOWmw6F74ebCSKURFRaXCY64z7QZ8KaV8WEr5EPClqa3S4651B6h0oR5SSs5ln2Nj4ka1XLqKSgVGSplubw22ok24P32bV2fhphNcyKogdww1Gmg2AF7YAd0mwNF1MDeKkMQ/lNzYKioqFRZzY6b/RjkVnm167gb8BbS3pChHxE2rfGbIK8rD09nTzmrKz7FLx5i3Zx5bzm0hS591ub2BXwN6hvdkcMPBuOvc7ajQ8kgp2XJuC8sSlnEm6wxJOUkYpZF+dfoxsMFAwrwtnG7LQTiQdoCfDv3E0YtHydZnk1uUyx3Bd/Bsi2cJ8QyxtzyrcPzScZYeXcqms5swYkSr0RLsEcyoVqOo61fX3vIcEiGEKxALuKD8b1gspXyrxOtzgCeklJ6m5y7AN0BrIA0YKKU8aSu9r/Soz+p9SXwSncA7/ZvYymz50bnBna9C04dh5SjqJXwOX+2F+z6FgDr2VqeiolIGzHWmXaWUxY40UspsU67pSk9JZ7oicz7nPB/v/piVx1fipnWjd63eNPRvSC2fWhxKP8TaU2v5ePfHxKfEM7vrbJw0lSONeGxiLJ/u+ZT9afvxd/Unwj+CCP8IMgsz+eHgD3xz4Bvur3s/b7d/m+IDthWdnck7+Xj3x+xM3omb1o1WVVsR6hWKQLD6xGr+OPEHD9d/mFGtR13+/a7oHE4/zJRtU9h1YRdaoSWqehQeWg8M0sDO5J08vPJhnmr6FMObDsfZSc0DfA0FQDfT+7oO2CSEWC2l3CqEiAT8run/JHBRSllXCPEIMB0YaCux4VU8GNCmBj9sO83wjrUJC6hg/4r8wmHwUg7+PImGJ7+CzzpBr8nQ+nGoJO9BKiq3C+Y60zlCiFZSyl0AQojWQMX2LktJZXCm/zn7D2M3jiWvKI+hjYbyRJMn8HO98v+xTbU2DGk0hJ8P/czkbZOZsX0G46LG2VFx+cnV5zI1biq/JfxGiGcIb93xFv3q9LvKkUrJTWHh/oV8f/B76vjWYVjjYXZUXH70Bj2f7PmEr/Z/RZBHEGMix3B/vfvxdva+3Od8znnmx8/np0M/YZRGJrSr2Ecf9EY9C/ctZP7e+fi4+DAmcgx9avchwC3gcp/0/HRmbJ/Bp3s/ZWfyThb0XFBpPjhZAiml5MpdR53pkkIIJ+B94DHg/hJD+nOlKu5i4BMhhDDNYxNeuqseS3Ym8uG6I3w4sIWtzFoOIUiu1pWGvUfA8udg5Sg48hfcN085wKiiolIhMNeZfhn4VQhxDuXkeDVsuBNhTyqyM22URubHz+fTPZ9Sx7cOH3b5kHCf8Bv2HxgxkNNZp/nmwDeEeYcxqOEg24m1IEcvHmXMhjGcyDjBiGYjeKb5M+g0uv/0C3QPZGybsVzIvcCHOz+kWWAzWlZtaQfF5edM1hleiXmFg+kHeaj+Q7wa+ep1w3WqeVTjrTvewk3rxrcHvqVnzZ60DW5rB8XlJzUvlRejX2Rf6j7uqXUP49qOw9fV9z/9/F39mdZpGk2rNGVa3DRWnVjFvbXvtYNix8XkOO8E6gJzpZTbhBAvASuklEnXfPgIAc4ASCmLhBAZQACQaiu9Qd6uPN6hFvNjj/F059pEVPO+9SBHxCcEBi+DuPmwdiJ82kHJWx3ewd7KVFRUSoG55cS3CyEigAampsNSSr3lZTkexc50blGunZWYR5GxiImbJ/L78d/pU7sPb7Z7s1Sx0KNbjyYxK5EZ22fQKaRThYsn3n5+OyP/Homb1o3Pe35Ou+B2N+0vhODt9m9zOP0wYzaM4de+v+LvWrF2hg6lH+KZtc+gN+qZ3XU23cK63XLMCy1fYMOZDUz8ZyJL+y2tcHHyJzJO8Oy6Z0nPT2dm55n0Cu91yzGPNHiE5QnL+WDnB3St0bXCrdmaSCkNQAshhC+wTAhxJ/Aw0KWscwohRqBUziUoKIiYmBiz58jOzr7huKZaiasTvPHjP7zQ0rWsMu3G1WtriGeLaTQ6MBO3RX04Gf4Ip2o+DKLi5qW+2c+uolOZ1waVe32WXpu5O9MAbYBw09hWQgiklN9YTJGD4qpV3qQrUq5pvUHP2I1jWXtqLS+0fIGnmj5V6tvaThonxkeNZ/2Z9fx+/Heeb/G8ldVajg1nNjA6ZjQ1vGowv8d8gjxKV9jBy9mLWV1mMeiPQczZNYdJ7SdZV6gF2X5+Oy9Gv4iHzoMve31Jbd/apRrnpnXjnQ7v8Piax5m9a3aFCuvZm7KXkX+PRCM0LOy5kKaBpSvb7KRxYlzUOIauHsrC/Qt5oeULVlZa8ZBSXhJCrAe6ouxSJ5jeO9yFEAlSyrrAWaAGkGgq4OWDchDx2rk+Bz4HiIyMlF26dDFbT0xMDDcbd1Qc4aN1R6lSryVNQnzMnt+e/HdtXaDnAFg5mlr7fqCW03klpZ5HFTspLB+3+tlVZCrz2qByr8/SazPr464Q4ltgJtARxaluA0RaTI0DU9HCPAoNhYyKGcXaU2t5rc1rjGg2wuz40CCPIKKCo1h5bCU2DIMsF2tOruHl9S9Tz68ei+5eVGpHupgI/wh6hfdi3el16I0V46bLlnNbeGbtM1R1r8p393xXake6mNZBrXk04lF+OPQD57LPWUmlZdmXso+n1z6Nt7M33/X+rtSOdDEtq7bknlr3sGj/IhKz1Fy/AEKIQNOONEIIN6AHsFNKWU1KGS6lDAdyTY40wAqg+IDBQ0C0LeOlS/JEx1p4u2r5aN1Re5i3PC5e8MDn0Hc2nNyslCU/9Y+9VamoqNwAc+8dRQIdpJTPSSlfMF0vWkOYo1GRnGmjNPLGpjfYkLiBN9u9yZBGQ8o8V986fUnMTmRPyh4LKrQOGxM3Mi52HM0Cm7Gg54Lrxs2Whh41e5BRkMH289strNDy7E3Zy0vrX6KmT02+vvtrqnlUK9M8j0Y8CijfQ0fncPphnln3DH4ufnzZ60tqeNco0zyjWo9CIzQs+neRZQVWXIKB9UKIeGA7sFZKufIm/RcCAUKIBGA0SlEvu+DtqmPEnbVZdzCZ+MRL9pJhWYSA1v+D4etA5w6L+sDGWWA02luZiorKNZjrTO9HOXR421FRnGkpJe9vf581J9cwqvUoBjQYUK75uod1x03rxopjKyyk0DrsubCH0TGjqedXj7l3zS1XLvD2Ie1x17qz9tRaCyq0PIfTD/Psumep4laFz3t8XuYPDwA1vWtSw6sGsWdjLajQ8pzIOMGItSNw07qxoNcCs+88lKSaRzWigqPYmrTVggorLlLKeCllSyllMyllEynlO9fp41nicb6pgFddKWVbKeVx2yq+mv91qIWvu44P1x6xpwzLE9wMRsRAo/7w9zvww8OQnWJvVSoqKiUw15muAhwQQvwphFhRfFlDmKNRUSogrstcx3cHv2NIoyE83vjxcs/nrnOnW1g3/jz5JwWGAgsotDwJFxN47u/nCPII4tPun5a7qI6LkwudQzsTfTqaImORhVRalvM553lm3TO4ad34oucXVHErXzylEIJOIZ2IS4pz2HMB6fnpPLfuOQAW9FxgkYIzbaq14VTmKc7nnC/3XCr2xdNFy9N31mH94RR2nqpkxSBdveGhL+HeWXBiI3zWAY7H2FuVioqKCXOd6UnAfcAUYFaJq9Kjc9KhFVqHdqbXnVrHiksr6F2rN2Mix1gsh27f2n3JKswiNtHxdi3T89MZGT0SVydX5veYf1Ve4fLQI7wH6fnp7EreZZH5LEmuPpeRf48kvyif+d3nW6yKYafQTuQb8tmRvMMi81mSAkMBL69/mZS8FD7u9vFNUzuaQ1RwFECFCOlRuTXD2tekiqcLM9YcrjDnPEqNENBmODwVDa6+8M19sPYtKCq0tzIVldses5xpKeUG4BDgZboOmtpuC9y0bg7rTB9OP8z4TeMJdw7n3Q7vorFgKqWo4CiquFXh92O/W2xOS6A36BkdM5rUvFRmd51t0dLYHUM64qZ1469Tf1lsTktglEZe3/g6Ry8d5f3O71u0NHZkUCSuTq4OFzctpWTi5onsvrCb9zq+R7PAZhabu75ffXxcfNiWtM1ic6rYD3dnLS90q8u2E+nEHrVZumvbUq0JjFgPrYbA5o9gQTdIPmBvVSoqtzXmZvMYAMSh5B0dAGwTQjxkDWGOiKM60xfzL/LS+pfw0nkxPHA4Lk4uFp1fq9HSPaw7W85twSgd4/CLlJLJ2yazM3kn77R/x+xsDrfCTetGx5CO/H36bwxGg0XnLg9zds1h/Zn1jG0zlo4hHS06t6vWlbbBbYlNjHWoXb2F+xey6sQqXmz5YqnySJuDRmhoE9SGuPNxDrVmlbLzaNswQv3ceP/PQ5X3Z+rsAf0+hkd+hMwk+LwzbPoQDI4ZlqaiUtkxd/vyDaCNlHKYlHIo0BZ4szQDhRB3CyEOCyEShBD/OfUthBgthDgghIgXQvwthKhppjar46p1JU/vWM60wWjg1Q2vkpKbwuxus/HRWifHaoR/BPmGfIdJnfbL4V9YenQpTzV9intq32MVGz1r9iQ1L9VhMpmsPbWWhfsXMqD+AB5r+JhVbNwZcieJ2YmczDxplfnN5Z9z//Dx7o+5O/xuhjcdbhUbbaq1ISknicRsNUVeZcBZq2FU9/rsP5vJ6v2VPBY+4h54bivU7wXrJsEXXeGcY7xfqajcTpjrTGuklBdKPE8rzRymErVzgd5AI+BRIUSja7rtBiKllM2AxcAMM7VZHTetG3kGx3Km5+6Zy7bz23jzjjdpUqWJ1ezU8a0DwPEMux7YB5Qcw9O2T6NjSEdGthxpNTsdQpRSvrsv7LaajdJyIuMEb25+k2ZVmjG27Vir2ekYqux2O0Kox7nsc4yNHUttn9q83f5ti50BuBY1brrycV/LEOpV9WTmn4cpLHKMu2lWwzMQBn4HA76F7GT4ohuseg1yK9khTBUVB8ZcZ3qNKZPH/4QQ/wP+AFaXYlxbIEFKeVxKWQj8BPQv2UFKuV5KWVyreysQaqY2q+NoYR6xibF8se8LHqj3APfVvc+qtmr51AIg4VKCVe3cihxDDq9seIWqblWZ1mmaRWPDr8XL2YtAt0BOZpy0mo3SkKvPZdT6UThrnJnVZRbOTs5WsxXiGUIdnzp2T5FXaChkdMxoioxFfNT1I6uW/K7tU5sA1wA1broS4aQRjLsnguOpOXyz5aS95diGRv3g+TglN/X2L+Dj1rB9ARgqRvEpFZWKjLkHEF8F5gPNTNfnUsrXSjE0BDhT4nmiqe1GPEnpnHSb4kjOdFJ2EuM3jaeBXwPGtbV+CWgfFx8C3QI5dumY1W3dCKM08nXq16TmpfJBlw/wcbF+2eBwn3C7hjxIKXl7y9ucyDzBjM4zylyUxRzaVGvD/tT9do03nbljJv+m/ct7Hd+jprd1I76EELSt1pbt57dX3hjb25BuEUF0aRDI7HVHSclyzLSeFsfNF/p8AE/HQtVG8McrMLctxP+qFntRUbEi2tJ0EkLUBYKklJullEuBpab2jkKIOlJKi3lYQojBKJUWO9/g9RHACICgoCBiYmLMtpGdnV2mcTmXckgtSi3TWEtikAZmJ8+moLCAAQED2LrpStGJsq6tNPhJP/ac2WO39a/NWMvB/IMM8B9Ayv4UYrC+DudsZ/7N/Zf169dbLcygmOv97LZkb2FV2iru9bmX/MP5xByOue5YS6LP1JOjz2Fl9Eq8nLwsMqc5v5d7cvfwY8qPdPXqiua4hhgb5NP1yfIhJS+Fn9f9TDWd+R9YrPl3p1J23uzTiF4fxjLzz8NMf8hyWWAcnmpN4X8r4cgaiJ4MS4fDxpnQ/kVo+jBorXd3S0XldqRUzjTwEXC97c8M02t9bzH+LFCy5m+oqe0qhBDdUQ45dpZSXncrQUr5OfA5QGRkpOzSpcuttP+HmJgYyjJuzcY1pF9IL9NYS/Lx7o85cfoE0ztN/8/hu7KurTRsjdvK0qNL6dy5s9Udy2vZm7KXP1b/QUv3lkzoM8Fm9k//e5rNOzbT/I7m+Lv6W9XWtT+7Y5eO8erKV4mqFsV7Pd7DSeNkVfvFaBI1LPl7CTWa1qBF1RYWmbO0v5eJWYmM/308TQKaMKv3LHROOovYvxXhGeH89NtPuIS70KVeF7PHW/PvTqXs1An05PEO4SzYdILB7WrSNNT6d7McBiGgQW+o1wsOLIPYWbD8OYh+V8lX3XIIeJW9gqiKisoVShvmESSl3Hdto6ktvBTjtwP1hBC1hBDOwCPAVZUThRAtUUJI+l1zyNFhcIQwj7ikOL6I/4L76t5ntSwWN6K2T23yivJsXi0uszCTsbFjCXIP4pGAR2zqyBcXB7F13HR+UT5jNozBXefO1E5TbeZIA4R5hQFwJuvMLXpaFr1Rz9hY5XDl+53ft5kjDRDqFYpWaG2+ZhXr88Jd9QjwcOaN3/ZRZLgNQx00GmjyIDy7GQYvgcAGikP9YSP4aRAcXAl6x6x6qqJSUSitM+17k9fcbjVYSlkEjAT+BA4Cv0gp/xVCvCOE6Gfq9j7gCfwqhNjjiGXK7e1MX8y/yLiN46jpXdMmcdLXUpzRw5aHEKWUvP3P25zPOc+MzjNw11jvINr1qOWtHLy0ddz0zB0zSbiUwHsd3yPQPdCmtkM8Q9AIDaezTtvU7qd7PiU+NZ632r9FqJdtzx9rNVqqeVQjMUtNj1fZ8HbV8Xa/JsQnZjA/1v7ZiOyGEFC3OwxdDiN3Qrvn4PRW+HkQzKwHS5+GA8shP8PeSlVUKhylDfPYIYR4Skr5RclGIcRwYGdpJpBSrgJWXdM2scTj7qXUYjdcnVzJK8pDSmnzMAcpJZP+mUR6QTqf3PWJVbMb3Ig6PlfS43UK7WQTm8uPLeevU3/xUquXaB7Y3CZx0iWp7lkdnUZn053pDWc28PPhnxnaaKjFC7OUBp2TjmCPYE5n2s6Z3nF+Bwv2LeD+uvdbvDBLaQn1ClVzTVdS7m0WzOr9wXy07gh3NaxKRDVve0uyL1XqQs934a6JcGID7F8Gh36H+J9Ao4UaURDeEWq2h9A2SpEYFRWVG1JaZ/plYJkQYhBXnOdIwBm43xrCHBF3nTsSSaGx0OJVBm/FsoRlRJ+J5pXWr9AwoKFNbRfj6+qLv6u/zTJ6nMk8w9RtU4kMiuTxxo/bxOa1OGmcCPMK40TmCZvYS81L5c3Nb9LArwEvtXrJJjavR5hXmM1CHjIKMhi3aRxh3mG83vY/9ZxsRqhXKH+f+ttu9lWsyzv9m7D1eBqv/LKX357vgM7Jemk1KwxOOmW3um53MMyGxDg4+hck/A2x74M0gtBAYEOo3kI52BgYoVxe1ZTdbhUVldI501LKZKC9EKIrUFwZ5A8pZbTVlDkgbloloiVPn2dTZ/pU5immxU0jqloUQxsPtZnd61HXty7HMqzvTBcZi3h90+s4aZxsHjN8LeE+4Tb5ACGlZMLmCeQW5TL9zulWzSd9K8K8w1hzco3V7UgpeXfru6TmpvLtPd/a5Y5LMaGeoVwsuEiOPgcPnboTV9nw93Bm8n1Neea7ncz86zDjettnU8JhcdIqO9E120P3SUq4x5k4OLNNqap45E/Y8/2V/joP8AsH/1rgHQLe1cErWCki41EV3AOUVH23E1IqH0CMBpCGK1+lUUlNKI0lnhtKPJfXtF17mV5H3qRNlniM6XHJPvI6X7npa1WTD8C+1CtrQ1691itPrnnOzfte7/t2629uKfqUfj7vjFygS+nnvAWl3ZkGlMIqwHqLWa9gXHami/LwvWkYueXQG/WM3zgerUbL5I6TrVqkpDTU9qnNyuMrrR7q8nn858SnxPP+ne/bJLfyzQj3DmfDmQ3ojXp0GusdiovNimXzxc28EfXG5fh0e1HDqwYZBRlkFGRYNZ/3yuMr+fPkn7zU6iWrVvAsDcVx2olZiTTwb2BXLSrW4e4m1XgsKoz5G47TNMSHPs2q21uS4+LqA/V6KBcoDkpOClw4CCmHIf04XDwJaQlwIhYKMq87TSeNM2z3BRdPcPZUQkZ0bqBzBydn5dI6K+ElGh1onJTd8OKviKt3wP/j+JkcyZLO6VVOrOFq59ZYVOJ50ZXXjUVXrst9S7Ybrn5NGuioL4BNXG2vEtEIlFNulZCg6ncDz1psPrOc6dudks60rVgQv4D41Hje72x/pxKUQ4jZ+mySc5Otpmdvyl4+j/+cvrX7cnetu61iwxzCfcIpkkWczTp7ObuHpTl26RjLLy2nU0gnBjYYaBUb5lAyo4e1nOmz2WeZsm0Kraq2slsYT0kuO9PZqjNdmZnUtzFHzmfx6q/x1An0pGHwbR4/XVqEAM+qylX7OmUg8jMh6zzkpkL2BchNg/xLnD2yj7CqPlCQDYXZoM+FgiylT1EBGAqgqPBqp/Wyw1piV/WqzZtiB1tccbpLXhonEMVOuVbJaCKcTI9NrzlplefF7Vpn0Hjc+PWr5lH6JJ1LokZYzRL9TGOv6XfVh4OrHl/bJq5pF6bH4spzxJUxxe3F34+rPnwUt4n/tpX8Wvyzvc5rcXFxtG3btsT3/poPNtf+fiCu01biZ3bd9uu8fiPM2sC7ed8TcbtvWjnQXFRn2gxs7UzvS9nH/Pj59Kndh7vD7e9UwpWMHscvHbeKM52rz2XcxnEEuQcxLsr2GUuuR7h3OKBk9LCGM6036Bm3cRwuwoV3Orxj88Ot1yPMW3GmT2eetsqOscFoYPzG8UgkUzpNsWsYTzGhnld2plUqL85aDfMGt6Lvx5sY8e0OfnuuAwGetj0DUylx9VYu6l/VfNwQQ1glzcF+LCaGGpV0bQC5HucgsP6tO1ZAinRHLTqfegLDDIqd6dyiXKvbytXnMm7TOALdAx3GqQQlzAOwWtz0jO0zSMxKZEqnKXg5W6b6Xnmp5WNKj2eljB5z98zlYPpBHg14lCpuVaxiw1xCvUIRCKulx/vq36/YdWEXb0S9QYinJfcHyo6Piw9eOq/b1pkWQrgKIeKEEHuFEP8KId42tX8vhDgshNgvhPhSCKEztQshxBwhRIIQIl4I0cq+Kyg9Vb1c+Wxway5kFjBowTYu5hTaW5KKikoFRnWmzcCWO9Mf7PyA05mnmdJxCt7OjnMb0t/VH18XX6scyFt/ej1Lji7h8SaP0zqotcXnLys+Lj74ufhZJdf0zuSdfLn/Sx6s9yDN3B2n3LGLkwtBHkFWyehxIO0Ac7MB/DQAACAASURBVPfMpWfNnvSp3cfi85eH2zw9XgHQTUrZHGgB3C2EaAd8D0QATVHqCgw39e8N1DNdI4BPba64HLQM82PBsEiOp+YweOE2MnL19pakoqJSQVGdaTOwlTMdmxh7Oc9wm2ptrGrLXIQQ1PapzYkMy6aKS81L5a1/3iLCP4KRLUZadG5LEO4TbvE1ZxVmMX7jeEK9QnmtzWsWndsShHmFWTzXdH5RPuM2jsPfxZ+Jd0x0iJCWkoR6hd62O9NSIdv0VGe6pJRylek1CcQBxRV1+gPfmF7aCvgKIYJtr7zsdKoXyPwhrTmanM2QL7eRklVgb0kqKioVEDVm2gxcta6A4hBYi/T8dCZunkg9v3q82OpFq9kpDzW9axKbGGux+aSUTNw8kdyiXKZ1mmbTMtKlpZZPLWLOxFh0zmlx00jOTebr3l/bNSXcjajhVYP1ZyybvOfDnR9yPOM483vMt2qWkLIS6hnKhjMbMEqj3TPn2AMhhBNKLYG6wFwp5bYSr+mAIUBxAvQQoOSti0RTW9I1c45A2bkmKCiImJgYs3VlZ2eXaVxpEMBzzXXM25NBr1l/81IrF2p62y6G35prcwQq8/oq89qgcq/P0mtTnWkzsPbOdHHp7MzCTOb3mG/XPMM3o6Z3TdLy08gqzLJIXPMvh39h49mNvN72dbunhLsR4d7hpOenWyxV3F8n/2LFsRU80/wZmgc2t4BCyxPmHUZ6fjrZhdl4OnuWe75NZzfxw6EfGNxwMO2rt7eAQssT6hVKobGQlNwUgjyC7C3H5kgpDUALIYQvSqGuJlLK/aaX5wGxUsqNZs75OfA5QGRkpOxShgNbMTExlGVcaekCdO+QwVPf7GDq9kKmP9iM/i1sE8tv7bXZm8q8vsq8Nqjc67P02m6/rZdy4K5Vdg+t5Uz/lvAb0WeiebHliw6dmqs4u4UlQgCOZxxn5o6ZdKjegUcjHi33fP9n787DqqrWB45/XwYZREARR8wJNQcQtTTNSjPNUjNvTpVFpre61c3UyqZfpWk2mbd5uFnilFO3UjPLHBrMnDUcUskZNRVHFGRavz/OBkERDnAGOLyf5zmPZ6+9z97vNlu8rPPutZwl+54dUepx+OxhRq8cTVTVKB6IfqDE53OW3NPjldSZzDM8/+vzRIZGunVlx8LkzOhRfuumATDGnMS2pkB3ABF5EQgHRuQ6LBGok2s7wmork1rUDmHeox1pXiuEYTM38q9p67TsQyllF02miyC7zMMZyfTe03sZv3o8V9e42u2rHBambnBdwBZzSaRlpvH0z0/j7+PPmGvHlOqv1SNDIwFK/OBlZlYmz/76LOlZ6baSFicuAlNSdSrZ8qSSzuhhjGFG0gxOp53m1etezfn/qDTKvXBLeSMi4daINCISAHQF/hSRocDNwJ3G5FmVYh5wrzWrxzXAKWPMoUtOXIaEV/Jj5gPX8OTNTVjy5xG6TvyJ6av2kp7pWYtxKKUcq/RmL6WQl3jh7+3v8GQ6PSudp39+Gl8vX17p+EqpTioB6gTXQZASJ9PvrH+Hbce3MabDGKoFVnNQdM5Ru1Jt/L39STiZUKLzfL7lc9YcXsMzbZ/Jmcu5tMpOpks6Mj1nxxw2p2xmeJvhpfobF4CaFWsiSHkdma4JLBORP4A1wGJjzALgI6A6sFJENorIC9bxC4FdQALwX+BhN8TscL7eXjzSOZKFj11Ho2pBPPfVZrpM+In/rT9AhibVSql8aM10EQX4BDg8mf5g4wdsTtrMW53eKhWrHBbGz9uPmhVrsvdM8ZPp3w7+RtzWOAY0GUDnKzo7MDrn8BIvGoQ2KFEyveXYFt7fYJsS7vbI2x0YnXME+gZSNaBqiX5pSjiRwBtr3uBK/yu5u+ndDozOOXy9falRsUa5HJk2xvwBtMqnPd+fE9bsHo84Oy53iawWxOwH27Ns+xHe/H4HI2Zv4vVF2+l/dR0GXl2HWqEB7g5RKVVKaDJdRI5OptccXsOk+En8o9E/6Fq3q8PO62x1g+uy91TxkqyklCSe+/U5GoQ0YORVIx0cmfNEhkay8uDKYn32TNoZnvjpCaoGVi2VU8JdTsOQhuw8UbyVolIyUnjy5ycJ9A1kUNigUv+NS7byPD2eyktEuPHK6nRqXI0lfx5h2u97eXfpTt5dupM2V1SmW/PqdGlanQZVK5aZ/6eVUo6nyXQROTKZPp56nFE/j6JucF1GXT3KIed0lSuCr2DhroUYY4r0QyTLZPHsr89yJu0MH930Uc4MKWVBZGgk8/6aV+QZPYwxjF45mkNnD/F5989L5ZRwl9O8anOmbJ1CWmZakWeXeX3N6yScTODjmz4mbWfZWWEuIiiCXxKLNGGF8nBeXkLXZtXp2qw6+4+f48v1B/hhy9+8svBPXln4J+GV/Ghbvwqtr6hM05qVaFYzmNDA0jkbk1LK8TSZLiJ/H3+HLCeeZbJ49pdnOXX+FB/e9GGpnGe4IPWC63Em/Qwnzp+gin8Vuz83KX4Svx38jRfav1Dq62cvlj1tX8LJhCKt0Dh351y+3/M9w1oPo1W1S75FL9VaVG1BRlYG249vJyo8yu7PLdqziLk75nJ/i/vpULsDy3cud16QDhZRKYJjKcdIyUgpU7/sKdeoUyWQx29qzOM3NWb/8XP8tOMoa/YcZ/Xu43z7x4XnL6sG+VEvLJC6YRWpFepP9WB/agT7UyWoAlUCK1A5sAJB/vojWClPoP8nF1GAT4BDFm35bPNnrDi4gv+75v/KXFIJeWf0sDeZXnt4Le9tfI9b6t9C30Z9nRmeUzQKbQTYZvSwN5nefnw7r61+jQ61OnB/i/udGZ5TtAhrAcDmpM12J9O7Tu3ipd9eIjo8mkdblb7VLAuT/eDl3tN7ubLKlW6ORpVmdaoEMuiaugy6xtYfHjmTyrZDZ9h26DS7jiazN+kcKxKOceRMKlkm/3P4e0PIbz8S4OtNQAUf/H298PPxws/HG19vwcfLCx9vwcdL8PbywtsLvEQQEURsi87Y/rz0G0LDhYsaAyb7T2OsbZO3PXvb2D6Zles9BrLy/dxF7/Ncy3D8eAqfJqzK+QwXXcs6NZgLMWd//kLsJuc4k2tHnr/SXNfOz8V/F/m9z/e8+cSR7ezZFCpuLNoCZpeLz+7PXzY6xzt79hwVN/zksuvZq6R/hwAtgtNw5BTamkwXUYBPAEmpSSU6x9rDa3lvw3vcXO9m+jXu56DIXCs7md5zao9do61Hzx3lqZ+fok6lOrzY/sUyWV9Yo2INKvpWtPshxFPnTzFs2TBCKoSUiVla8lOjYg2q+Fdh87HNhR8MnE0/y/Blw/Hz9mPCDRNK9dR/l5P973nVoVWaTKsiqVbJn2qV/LmhcXie9ozMLI4mn+fv0+c5cTaN42fTOHEujTOpGWxL2E3l8GqcS88kJS2D8xlZnM/I4mRKOukZWWRkZZGRacjIMmRaL4O5kOjmk3jm7l9z97S2ZsFLLiTgFxJy673VbjvGStGtY7xyEvjsY+VCMn/R+bD2pWbAubSMPMfaTik55xVAvLJ/IcgbR97Ys99f/v7kov25Xfp3kd+e/Pbnf+SxrHNUrZL3W2V7frTl94tPUbjqx+dRUggPL/mCXc5Q0r+DkCzHlh5qMl1EJa2ZPnz2MCN/Glmmk0qAWkG18BEfu+YgTstMY/jy4SSnJ/NR14+o6FvRBRE6nojQMKShXcl0ZlYmo34exd/n/mZy98mEBYS5IELHExGiqkbZlUxnLwu/5/QePun6SZmYmSY/NSrWoGFIQ347+BuxzWMLPX7RnkX4mrL3S4NyHR9vL2qGBFAz5NKyoeW+B+nUKdoNUbmGbaW5a90dhlPY7u0qd4fhNLb7s7+ksSxx9DLpZW+ozM1KkkyfzzzP8GXDOZ95nrc7v+2QpbjdxcfLh4hKEYVOm2aM4ZVVr7Dp6CbGdRxH48qNXRShc0RWjrRr4Zb3N77PioMreK7dc6V2uXB7Na/anN2ndnM2/WyBx03eMpkf9v7AsNbDaFeznYuic44OtTuw7u91hZZ0zfxzJk/+9CQrkle4KDKllFKljSbTRVTcZNoYw8srX2Zz0mbGdRxHg9AGTojOteoG1y00mZ65fSZf7vySf0b9s0xN/Xc5DUMacjz1OEkply/1mf/XfP4b/1/uaHQHfRuXvdrwi7UIa4HBsDVp62WPWbx3MRPXTaRb3W4Mbj7YhdE5R4daHTifeZ71f6+/7DG/Jv7Kq6tf5YaIG+gY1NGF0SmllCpNNJkuogDfAFLSi55MT9o8iW/++oYHox+kyxVdnBCZ69UNrsu+0/vIMvmvCvbj3h8Zv2o8nSI68UiMZ6ztEFm54GXFVx5cyQsrXqBdjXY81+45V4bmNC2q2h5CjD8Wn+/+TUc38cwvzxAdHs24juPKbOlSbm2qt6GCVwV+O/hbvvt3ntjJEz89QaPKjXj9+tfLZD28Ukopx9CfAEUU4BNAWlYamVmZdn9m/l/zeXv929xS/xYejvGIFXcBWzKdmpnKkXNHLtm35vAaRv08iujwaF6/4XW8vbzdEKHjRYbakun86qb/PP4nw5cPp35ofSZ2noivt2fU0Vb2r0ztoNr51k3vPb2Xx5Y+RrXAarxz4zv4+/i7IULHC/AJoHX11qw4eGn5xoEzB3h4ycME+gTy7o3vlrlpLZVSSjmWJtNFFOBte4DE3lKP7JHKtjXaMvbasR41gpV7erzctiRtYdjSYURUiuC9G9/zqLl6wwPCCa4QfEkyvS1pGw8tfogg3yA+6PJBma6Hz0+Lqi3YcmxLnraEEwkMXjSYLJPFB10+KNJ842VBh1odSDiZkOeXxf1n9jP4+8GcSz/HBzd9UGYfslRKKeU4npPZuUh2YpiaWfhc0+v+Xsfjyx6nXkg9JnaeWOQV5Eq77GR6/ZH1OfNvLt23lMGLBhNUIYiPbvqIUP9Qd4bocCJCZGjehxBXHlzJ4O8H4+vtyyfdyu4sFgVpEdaCg2cP5tSKb0nawuDvbbXRn9/8OfVC6rkxOufoUKsDQE6px97Texm8aDApGSlMunmSTpunlFIK0KnxiizA1xqZTk+BAgZcVx9azaNLH6VGxRp83PVjgisEuyhC16kWWI3GlRvzwcYPWLZvGW2qt2H6tuk0D2vOu13epWpAVXeH6BQNQxvydcLXPPTjQ4T6hfL9nu+pF1yPj276iOoVq7s7PKfIrpt+e/3bJKcnsyJxBaF+ofy323+5IvgKN0fnHI0rNybMP4wFfy1gzeE1LNy9kCDfICZ1m1QmF1pSSinlHJpMF1H2yHRBS4qvSFzB48sep3ZQbT69+VOPTSq9xIsvenzBgl0L+Hzz50zbNo2udbsyruM4jyrtuNgdje7g6LmjHEk5ws7jO+lQqwPjrxvvkb8wZWsW1owAnwC+SviKiKAIulzRhcdaP+aRo/DZRIQOtTowf9d8AnwC6N+4P7HNY6kVVMvdoSmllCpFNJkuouwkMb+aaWMMU7dOZcK6CUSGRvJJ10/K7GId9qrgXYF/NPoHt0fezs4TO2lUuZFH1YXnp3lV28h7eRLoG8jXvb/Gz9vP4/9N5/ZIq0doXb013ep18+hflpRSShWfJtNFdLlkOiUjhTErx7Bg1wK6XNGFcR3HldmV/orDS7z0q28PVx5HZGsH1faIucKVUko5jybTRZRfMv3zgZ95ZdUrHEw+yKMxj/LP6H96/OisUkoppZRy4WweItJdRLaLSIKIPJ3Pfj8RmWXtXyUi9VwVW1HkTqazp4B7ZMkjVPCuwKfdPuXBlg9qIq2UKnNExF9EVovIJhHZIiKjrfb6Vp+cYPXRFaz2MtFnK6WUs7lkZFpEvIH3ga7AAWCNiMwzxuRen3gIcMIYEykiA4HXgAGuiK8ospPp11a/xonzJwjwCeDx1o9zb7N7PWaRDqVUuXQeuNEYkywivsCvIvIdMAKYaIyZKSIfYeurP6SM9NlKKeVsrhpCbQskGGN2GWPSgJlA74uO6Q3EWe/nAl2kFK5LHOIXQnCFYMICwnim7TMs6beEIVFDNJFWSpVpxibZ2vS1Xga4EVufDLY++nbrfZnos5VSytlcVTNdG9ifa/sA0O5yxxhjMkTkFBAGHHNJhHYK8AngpwE/4S3e6M8NpZQnsb5FXAdEYvs28S/gpDEmwzrkALa+GspIn62UUs5W5h5AFJEHgAeszWQR2V6M01TFczt8T7438Oz703sru4pzf3WdEUhJGGMygRgRCQW+Akq8zKP22YXy5HsDz74/T7438Oz7K+695dtvuyqZTgTq5NqOsNryO+aAiPgAIUDSxScyxnwCfFKSYERkrTHmqpKco7Ty5HsDz74/vbeyy9PuzxhzUkSWAe2BUBHxsUanc/fd2mc7gCffG3j2/XnyvYFn35+j781VNdNrgEbWU+EVgIHAvIuOmQfEWu/7AkuNMcZF8SmlVLkmIuHWiDQiEoDtgfFtwDJsfTLY+uhvrPfaZyulFC4ambbq6R4Fvge8gc+MMVtEZAyw1hgzD5gETBWRBOA4toRbKaWUa9QE4qy6aS9gtjFmgYhsBWaKyFhgA7a+GrTPVkopwIU108aYhcDCi9peyPU+FejnonBK9JVjKefJ9waefX96b2VXmb8/Y8wfQKt82ndhm5Hp4nbtsx3Dk+8NPPv+PPnewLPvz6H3JvqtnFJKKaWUUsWjS/UppZRSSilVTOUqmS5sSfOyTETqiMgyEdlqLQU8zN0xOZqIeIvIBhFZ4O5YHElEQkVkroj8KSLbRKS9u2NyJBEZbv2b3CwiX4iIv7tjKi4R+UxEjojI5lxtVURksYjstP6s7M4YPY2n9tvaZ5dtntxve1KfDa7pt8tNMp1rSfNbgGbAnSLSzL1ROVQGMNIY0wy4BnjEw+4PYBi22QU8zdvAImPMlUBLPOgeRaQ28BhwlTGmBbYHkMvyg2qTge4XtT0NLDHGNAKWWNvKATy839Y+u2zzyH7bA/tscEG/XW6Saexb0rzMMsYcMsast96fwfY/du2CP1V2iEgE0AP41N2xOJKIhADXY82QYIxJM8acdG9UDucDBFhzEQcCB90cT7EZY37GNnNFbrmX1c693LYqOY/tt7XPLrvKQb/tMX02uKbfLk/JdH5LmntMx5WbiNTD9lT+KvdG4lD/AZ4CstwdiIPVB44Cn1tfh34qIhXdHZSjGGMSgTeBfcAh4JQx5gf3RuVw1Y0xh6z3h4Hq7gzGw5SLflv77DLHY/vtctJng4P77fKUTJcLIhIEfAk8bow57e54HEFEegJHjDHr3B2LE/gArYEPjTGtgLN4UJmAVYfWG9sPn1pARREZ5N6onMdatESnSFJ20z67TPLYfru89dngmH67PCXT9ixpXqaJiC+2Tnm6MeZ/7o7Hga4FbhORPdi+5r1RRKa5NySHOQAcMMZkj0jNxdZJe4qbgN3GmKPGmHTgf0AHN8fkaH+LSE0A688jbo7Hk3h0v619dpnlyf12eeizwcH9dnlKpu1Z0rzMEhHBVr+1zRjzlrvjcSRjzDPGmAhjTD1s/92WGmM84jdlY8xhYL+INLGaugBb3RiSo+0DrhGRQOvfaBc85EGdXHIvq517uW1Vch7bb2ufXXZ5eL9dHvpscHC/7bIVEN3tckuauzksR7oWuAeIF5GNVtuz1sqTqnT7NzDdShZ2AYPdHI/DGGNWichcYD222Qs2UIZX1RKRL4BOQFUROQC8CLwKzBaRIcBeoL/7IvQsHt5va59dtnlkv+1pfTa4pt/WFRCVUkoppZQqpvJU5qGUUkoppZRDaTKtlFJKKaVUMWkyrZRSSimlVDFpMq2UUkoppVQxaTKtlFJKKaVUMWkyrZRSSimlVDFpMq3KFBEJE5GN1uuwiCRa75NF5AMnXG+yiOwWkYeK+LmFIhJayDFvWPfwRMmiVEqp0kn7bFUelJtFW5RnMMYkATEAIvIStkUP3jPGfOrEyz5pjJlblA8YY24FsJbTHWqM+TGfY54UkbOOCVEppUqffPrsZGPMm06+bLH77EKO0T5b5UtHplWpJyJ7RCTFGsn42xp5CLromE4issB6/5KIxInILyKyV0T+ISKvi0i8iCwSEV/ruDYi8pOIrBOR70Wkph2xTBaRD0XkdxHZZV3XiEiWiKRboy5vWTFXxfYL6yQR+a+IbBGRH0QkIJ/zdrJWZlJKKY/n5j77MxHZJiKTcx23R0Sqikg9a1+BfbZSuWkyrcqKXsaYIKA1cBXwfCHHNwRuBG4DpgHLjDFRQArQw+qc3wX6GmPaAJ8B4+yMpTLQHhgOzLPamgB/AI8AdwGVch0fAbxvjGkOnATusPM6SilVXriyz54INAeiRCQmn+MboX22KgIt81BlijEmUUS+A1oAa63musAwoKmI/ABsBL4zxqSLyPNAADBTRDYBW4B62JLfGGC/1UlnAbuyryMiPYGxQDOgvYjsMMb8Ye2eb4wxIhIP/I0tcTbWuQF+AW7OFfYhY8xGEfEDagEfiMjrwGzgDFAB+A7wE5Fk6zONjTEHS/r3pZRSZUR2nx0PeAOLrPZ4LvTZLYDFIoJ1zCE7z52nzzbGxAOISPbPg40XHb/bGJPdts46RqnL0pFpVaaISB3gVmBDrua7gNeAH7Alph2A89a+74CzQDVgPdAH2y+RYv3Z1Rjjbe2/07pGK2yjHg8CX1jnnWclw+Q6d1au99nb9YDrgLRc7enWn88BdYCPgZZAW+B669hbgIPGmCDrpYm0Uqo8OQ9gjMkC0o0xxmrP4kKfvcUYE2O9oowx3YpybvLvs/MbVMx9TOZljlEqhybTqqz4WkROAr8CPwGv5Nr3OXAAW8c4G6iRvcMY85n153ngJaA64A9sx9Y59xSRYCCZCx3oA8DHxphV2Eacf7L2XVNAfOuxJeNPA59a57vY3cBi4Kwx5igwGltSrZRSqmDbgXARaQ8gIr4i0tzNMSkFaDKtyo7bjTGhxpi6xpiHjTEpufYdzvX+HLbRaUTEW0ReBQJF5DSwxzqmojEmDbgPGAIcx1YXN8jaXxcYaSXvdwFx2EaUaxUQX2tso9iPGmMuV89dCziRa3sveWurlVJK5cPqs/sCr1klexuxfQuplNvJhW9SlCqdCppeTkSWA9Oyp8YTkfusYzuKyD3As9jKQvYAIdiS2UbGmIRc5/AFHgVGGGPqiMjHwD5jzDjrae8FBU2zJCLm4nPmF7uI/AX82xiz0NrXDdtI+lhgDTDdGBNRlL8bpZRSF9jTZ5fw/C/hmun9VBmiI9PKk1XCVp6RBASSqzRERCqIyN0iEmKMSQdOYysTAfgv8JCItANOAWNF5D0RKeko8hfA8yISbk2b95l1zbPYHmQME5GQEl5DKaXKs1PAy1LERVvsISJvYPsGU+eaVnloUb3yZFOwzaqRiK2U4/+Af+Xafw/wnoh4Y6vHuxvAGLNWRP4JvIdtiqQUbLXWJTUWCMY2hR7AHOApY0wqgIh8Aeyy4mmmDyEqpVTRGGOGOfHcTwJPOuv8quzSMg+llFJKKaWKScs8lFJKKaWUKiZNppVSSimllComTaaVUkoppZQqJk2mlVJKKaWUKiZNppVSSimllCqmMj01XmhoqImMjHR3GC519uxZKlas6O4wXErvuXwob/e8bt26Y8aYcHfHoZRSqmTKdDJdvXp11q5d6+4wXGr58uV06tTJ3WG4lN5z+VDe7llE9ro7BqWUUiWnZR5KKaWUUkoVkybTSimllFJKFZMm00oppZRSShVTma6ZVkp5DhFh9+7dpKamujsUh/L39yciIgJfX193h6KUUsoJNJlWSpUKFStWpFKlStSrVw8RcXc4DmGMISkpiQMHDlC/fn13h6OUUsoJtMxDKVUqeHt7ExYW5jGJNNhG28PCwjxutF0ppdQFmkwrpUoNT0qks3niPSmllLpAk2mllLLs37+fzp0706xZM5o3b87bb78NwKZNm2jfvj1RUVH06tWL06dP53xm/PjxREZG0qRJE77//nt3ha6UUspNnJ5Mi4i3iGwQkQUXtb8jIsm5tv1EZJaIJIjIKhGp5+zYlFIqNx8fHyZMmMDWrVv5/fffef/999m6dStDhw7l1VdfJT4+nj59+vDGG28AsHXrVmbOnMmWLVtYtGgRDz/8MJmZmW6+C6WUUq7kipHpYcC23A0ichVQ+aLjhgAnjDGRwETgNRfEppRSOWrWrEnr1q0BqFSpEk2bNiUxMZEdO3Zw/fXXA9C1a1e+/PJLAL755hsGDhyIn58f9evXJzIyktWrV7stfqWUUq7n1GRaRCKAHsCnudq8gTeApy46vDcQZ72fC3QRLTZUSrnJnj172LBhA+3ataN58+Z88803AMyZM4f9+/cDkJiYSJ06dXI+ExERQWJiolviVUop5R7OnhrvP9iS5kq52h4F5hljDl2UK9cG9gMYYzJE5BQQBhzLfZCIPAA8ABAeHs7y5cudFnxplJycrPdcDpTHew4ODubMmTMARI372SnXiH/ueruOS05Opk+fPowfPx4R4d133+XJJ59k9OjR3HLLLfj6+nLmzBnS0tJISUnJiTs9PT3PdrbU1NRy999TKaXKC6cl0yLSEzhijFknIp2stlpAP6BTcc9rjPkE+ASgSZMmxivSC2MM10dcXy6eml++fDmdOnVydxgupfdcPmzYsIFKlSoVfmAJ2HP+9PR0+vbtyz333MPdd98NQJs2bVi6dCkAO3bs4Mcff6RSpUrUr1+fY8eO5Zz377//JjIy8pLr+Pv706pVKwffjVJKqdLAmSPT1wK3icitgD8QDGwBzgMJVuIbKCIJVp10IlAHOCAiPkAIkFTYRUYuH0lqZiq3NbyN59o9R6BvoJNuRynlKnte7eGW6xpjGDJkCE2bNmXEiBE57UeOHKFatWpkZWUxduxYHnroIQBuu+027rrrLkaMGMHBgwfZuXMnbdu2dUvsSiml3MNpNdPGVht6BAAAIABJREFUmGeMMRHGmHrAQGCpMaayMaaGMaae1X7OSqQB5gGx1vu+1vGmsOv4etmW6J331zzu/PZOdp7Y6ehbUUqVEytWrGDq1KksXbqUmJgYYmJiWLhwIV988QWNGzfmyiuvpFatWgwePBiA5s2b079/f5o1a0b37t15//338fb2dvNdKKWUcqXStJz4JGCqiCQAx7El4IUKCwjjTPoZKvtVZtepXdz17V082+5Zbo+8vVyUfSilHKdjx45c7nf4YcOG5dv+3HPP8dxzzzkzLKWUUqWYSxZtMcYsN8b0zKc9KNf7VGNMP2NMpDGmrTFmlz3nruJfBYCxHcfSu2FvUjNTeeG3F3ju1+c4l37OYfeglFJKKaXUxcr8CohhAWEAnE0/y9iOYxl77VgCfAKYv2s+A78dyI4TO9wcoVJKKaWU8lRlP5n2tyXTx1OPA9A7sjdf9PiChiEN2X1qN3d9exf/2/m/y351q5RSSimlVHGV+WS6SoCtzCMp5cLEHw1DGzKjxwxuj7yd85nnefG3F3n212e17EMppZRSSjlUmU+ms0emk1LzzqIX6BvIy9e+zLiO4wjwCWDBrgUMWDBAyz6UUkoppZTDlP1k2qqZzj0yndttDW/jix5fEBkayZ7Te7jr27v4cseXWvahlFJKKaVKrOwn0/4FJ9NwoeyjT2Qfzmee56WVL/H0L09zNv2sq8JUSpUBqamptG3blpYtW9K8eXNefPFFAHbv3k27du2IjIxkwIABpKWlAXD+/HkGDBhAZGQk7dq1Y8+ePW6MXimllDuU/WQ6IO8DiJcT4BPAmGvH8ErHVwjwCWDh7oUMXDCQ7ce3uyJMpVQZ4Ofnx9KlS9m0aRMbN25k0aJF/P7774waNYrhw4eTkJBA5cqVmTRpEgCTJk2icuXKJCQkMHz4cEaNGuXmO1BKKeVqZT+ZzlUzbU/pRq+GvZjZY2ZO2cfdC+9m7o65WvahlEJECAqyTX+fnp5Oeno6IsLSpUvp27cvALGxsXz99dcAfPPNN8TG2hZu7du3L0uWLNG+RCmlypkyn0wH+gYS4BPA+czzdpdtNAhtwIweM7ij0R2czzzP6JWjtexDKQVAZmYmMTExVKtWja5du9KwYUNCQ0Px8bEtGBsREUFiYiIAiYmJ1KlTBwAfHx9CQkJISrp8yZlSSinPU5qWEy+2Kv5VSExOJCk1iaAKQYV/AFvZx0sdXqJN9Ta8/PvLLNy9kK1JW3nzhjdpUqWJkyNWShXopRAnnfdUoYd4e3uzceNGTp48SZ8+ffjzzz+dE4tSSimPUOZHpqHwGT0K0qthL2b2nJlnto85O+boV7VKlXOhoaF07tyZlStXcvLkSTIyMgA4cOAAtWvXBqB27drs378fgIyMDE6dOkVYWJjbYlZKKeV6HjEyfbm5pu3VIMRW9vHa6tf4cueXjFk5hjWH1vBC+xfsHulWSjmQHSPIznD06FF8fX0JDQ0lJSWFxYsXM2rUKDp37szcuXMZOHAgcXFx9O7dG4DbbruNuLg42rdvz9y5c7nxxhsREbfErpRSyj08amT6eErBM3oUJLvsY/x14wnwCeC7Pd8x8NuB/Hlcv+JVqrw4dOgQnTt3Jjo6mquvvpquXbvSs2dPXnvtNd566y0iIyNJSkpiyJAhAAwZMoSkpCQiIyN56623ePXVV918B0oppVzNI0amq/hbS4oXc2Q6t54NetI8rDkjfxrJzhM7ufvbuxnVdhT9GvfTESelPFx0dDQbNmy4pL1BgwasXr36knZ/f3/mzJnjitCUUkqVUp4xMm3Hwi1FUT+kPjNunUHfxn1Jy0rj5d9f5qmfnyI5Ldkh51dKKaWUUp7BM5LpgJLVTOfH38efF9u/yKvXvUqgTyCL9ixiwIIBbEva5rBrKKWUUkqpss0jkukaFWsAkJic6PBz92jQg5k9Z9K4cmP2ndnHoIWDmPXnLJ3tQymllFJKOT+ZFhFvEdkgIgus7ekisl1ENovIZyLia7WLiLwjIgki8oeItLb3Gg1DGgKw6+QuMrMyHX4P9UPqM/3W6fRr3I+0rDTGrhrLkz8/qWUfSimllFLlnCtGpocBuWsjpgNXAlFAADDUar8FaGS9HgA+tPcCQRWCqFmxJmlZaew/s98hQV/M38efF9q/wGvXvUagTyDf7/leyz6UUkoppco5pybTIhIB9AA+zW4zxiw0FmA1EGHt6g1MsXb9DoSKSE17rxUZGglAwskER4Wfr1sb3MqsnrNoUrkJ+87s4+6Fd2vZh1JKKaVUOeXsken/AE8BWRfvsMo77gEWWU21gdzDygesNrtEVrYl0ztP7ixmqParF1KP6T2m079xf9Kz0hm7aixP/PQEZ9LOOP3aSinnSU1NpW3btrRs2ZLmzZvz4osvArB7927atWtHZGQkAwYMIC0tDYDJkycTHh5OTEwMMTExfPrppwWdXimllAdy2jzTItITOGKMWScinfI55APgZ2PML0U87wPYykAIDw9n+fLlAGQk25b6XbljJU1PNC1+4EVwHdcRWDWQL5K+4Ie9P7A+cT33V72fOn51nHbN5OTknHsuL/Sey4fg4GDOnHHvL6TGGL755huCgoJIT0+nW7duXH/99bz//vs89NBD9O3bl8cff5z333+foUOHkpqaSp8+fZgwYULOOfK7h9TU1HL331MppcoLZy7aci1wm4jcCvgDwSIyzRgzSEReBMKBB3MdnwjkzkIjrLY8jDGfAJ8ANGnSxHTq1AmA6knVmbpgKqd8T5Hd5gqd6ETf030ZuXwk209sZ+KRiTx19VMMaDLAKYu8LF++3KX3VxroPZcPGzZsoFKlSu4Og+DgYADOnTtHVlYWQUFB/Pzzz8yePRsfHx+GDh3KSy+9xPDhw/H396dChQqFxu3v70+rVq1cEb5SSikXc1qZhzHmGWNMhDGmHjAQWGol0kOBm4E7jTG5yz/mAfdas3pcA5wyxhyy93r1Q+rjJV7sPb2XtMw0R95KoeoG12V6j+kMaDKA9Kx0xq0ax8ifRmrZh1JlUGZmJjExMVSrVo2uXbvSsGFDQkND8fGxjT1ERESQmHjh9/wvv/yS6Oho+vbty/79znkAWimlVOnljuXEPwL2Aiutkdv/GWPGAAuBW4EE4BwwuCgn9ffxp06lOuw9vZfdp3bTpEoTB4ddMD9vP56/5nmuqnEVL/32Eov3LmZb0jbe7PQmzcOauzQWpcq6qLgop5w3Pja+0GO8vb3ZuHEjJ0+epE+fPvz555+XPbZXr17ceeed+Pn58fHHHxMbG8vSpUsdGbJSSqlSziWLthhjlhtjelrvfYwxDY0xMdZrjNVujDGPWPuijDFri3odV83oUZDu9bozu+dsmlZpyoHkA9yz8B5mbJuhs30oVcaEhobSuXNnVq5cycmTJ8nIsD2XceDAAWrXtj0bHRYWhp+fHwBDhw5l3bp1botXKaWUe7hjZNppIkMjWbJviVuTaYArgq9g6q1TeWPNG8zaPovxq8ez9u+1jO4wmkoV3F8TqlRpZ88IsjMcPXoUX19fQkNDSUlJYfHixYwaNYrOnTszd+5cBg4cSFxcHL179wbg0KFD1Kxpm8Fz3rx5NG3qmoeflVJKlR6elUxb0+MlnHBvMg0FlH3c8CbNq2rZh1Kl0aFDh4iNjSUzM5OsrCz69+9Pz549adasGQMHDuT555+nVatWDBkyBIB33nmHefPm4ePjQ5UqVZg8ebJ7b0AppZTLeVQy3Si0EeCauabt1b1ed5pVacYTPz3BtuPbGPTdIJ646gnuuvIup8z2oZQqvujoaDZs2HBJe4MGDVi9evUl7ePHj2f8+PGuCE0ppVQp5ZKaaVe5IvgKfLx8SExO5Fz6OXeHkyO77GNgk4FkZGXw6upXGbF8BKfTTrs7NKWUUkopVQIelUz7evlSP6Q+AH+d/MvN0eTl5+3Hc9c8x4QbJhDkG8SP+36k//z+bDm2xd2hKaWUUkqpYvKoZBqgceXGAPxx7A83R5K/bvW65cz2kZicyKDvBjF923Sd7UMppZRSqgzyuGT6mprXALAicYWbI7m8OsF1mHbrNO688s6cso/hy4dr2Ycq9zzxl0pPvCellFIXeFwy3bF2RwBWH15Nakaqm6O5vAreFXi23bM5ZR9L9i2h//z+bD622d2hKeUWmZmZJCUleVTyaYwhKSkJf39/d4eilFLKSTxqNg+AqgFVaVqlKduOb2Pt32tzkuvSqlu9bjSt0pQnfn6CrUlbuee7exjZZiR3N71bZ/tQ5crZs2c5c+YMR48edXcoDuXv709ERIS7w1BKKeUkHpdMA1wXcR3bjm/jlwO/lPpkGmxlH1NvmcqEtROY8ecMXlvzGmsOr2HMtWMI8Qtxd3hKuYQxhvr167s7DKWUUqpIPK7MA+C62tcB8Gvir26OxH4VvCvwTLtnmNhpIpV8K7F0/1IGLBhA/FH3rASnlFJKKaUK55HJdFTVKIIrBLPvzD72nt6b055lstwYlX1uqnsTs3rNonlYcxKTE7l30b1M3TrVo+pIlVJKKaU8hUcm095e3lxb61rANjp9Lv0cL698mZZTWnLDrBtYvn+5ewMsRJ1KdZhyyxQGNR1ERlYGr695nWHLhnHq/Cl3h6aUUkoppXLxyGQaoGOErVb6l8RfaDejHbN3zAbgeOpx/r3034xYPoKj50rvg04VvCswqu2onLKPZfuX0X9+f/ac3+Pu0JRSSimllMVjk+kOtToAl59vevHexdw450bm7phbqss/bqp7E7N7zaZFWAsOnj3IxMMTmbJlipZ9KKWUUkqVApedzUNE3rHj86eNMc87MB6HqRpQleZhzdmSVPBy3aNXjmbq1qlM7DyRBiENXBRd0URUimDKLVN4a91bTNs2jTfWvsGav9cw9tqxOtuHUkoppZQbFTQy3RtYV8jrDmcHWBL2Tou369Quen/dm/c2vEd6ZrqToyoeX29fRrUdxdDwoVSqUInl+5fTb34/Nh3d5O7QlFJKKaXKrYKS6YnGmLiCXsDHhV1ARLxFZIOILLC264vIKhFJEJFZIlLBavezthOs/fVKenPXR1x/Sdsf9/7BrJ6zaF+z/SX7Pv7jY1pPa82Pe38s6aWdpmVgS2b3tJV9HDp7iPu+u4+4LXFa9qGUUkop5QYFJdNfXm6HiPQEMMb8x45rDAO25dp+DVuiHgmcAIZY7UOAE1b7ROu4EomqGkVkaGSeNhGhWVgzPun2CRvv2cioq0dd8rnhy4cTFRfFjG0zOJt+tqRhOFx22cegpoPIMBm8ufZNHlv2mM72oZRSSinlYgUl04vzGx0WkfuBt+05uYhEAD2AT61tAW4E5lqHxAG3W+97W9tY+7tICdfTFhEGNR102f3eXt4MajaI+Nh4pt4y9ZL941eP55oZ1/DML89wLOVYSUJxuOyyj/90/o+WfSillFJKuUlByfQI4AcRaZTdICLPAMOBG+w8/3+Ap4Ds6TLCgJPGmAxr+wBQ23pfG9gPYO0/ZR1fIj0a9LDruJhqMcTHxvNpt08v2bdg1wI6z+7Mb4m/lTQch+tyRRfm9JpDVNUoLftQSimllHIxKSjpEpEu2OqibweGAm2BHsaYE4We2FYKcqsx5mER6QQ8AdwH/G6VciAidYDvjDEtRGQz0N0Yc8Da9xfQzhhz7KLzPgA8ABAeHt5m9uzZhd7kv/f+O+f9yBojqedXr9DP/J78O9OTpl/SHhMYw31V78NbvAs9hzMkJycTFBR0SXuGyWDeiXksO7MMgBYBLRgUNoiK3hVdHaLDXe6ePZnes+fr3LnzOmPMVe6OQymlVMkUmEwDiMh1wFfAb0B/Y0yqXScWGQ/cA2QA/kCwdZ6bgRrGmAwRaQ+8ZIy5WUS+t96vFBEf4DAQbgoIsEmTJmb79u2FxnIo+RDdvuyWsx0fG2/PLZBlsvi/Ff/HvL/mXbLvk66f0L7WpQ8xOtvy5cvp1KnTZfcv27eM51c8z+m009SoWIM3rn+DmGoxrgvQCQq7Z0+k9+z5RESTaaWU8gCXLfMQkTMichpYiC0R7gIcydVeIGPMM8aYCGNMPWAgsNQYczewDOhrHRYLfGO9n2dtY+1fWlAiXRQ1g2rm2c7MyrTrc17ixbiO41h558pL9j2w+AE6zuxY6qbS63xFZ+b0mkN01WgOnz3M4EWDmbx5cqlemEYppZRSqqy6bDJtjKlkjAm2/qxgjKmYazu4BNccBYwQkQRsNdGTrPZJQJjVPgJ4ugTXuMRL7V/KeR8ztWgjtUEVgoiPjWfGrTPytJ86f4rW01rz18m/HBGiw9QKqsXk7pOJbRZLhslgwroJPLb0MU6mnnR3aEoppZRSHsUly4kbY5YbY7Kn09tljGlrjIk0xvQzxpy32lOt7Uhr/y5HxnBH45KvLxMVHkV8bDxDWgzJ0377N7czbOmwEp/fkXy9fXni6id4p/M7BFcI5qcDP9FvQT82Htno7tCUUkoppTxGQWUe6wv7sD3HlCa31Lsl5/1Dix8q9nkeb/M4v9/1e562pfuXEhUXxYnUQp/NdKmcso9wW9nHfYvu4/PNn2vZh1JKKaWUAxQ0Mt1URP4o4BUPVHVVoI4wruO4nPcrDq4o0bkq+lYkPjaed298N0/79bOu57XVJV5vxqGyyz7ua34fmSaTt9a9xaNLHi11ib9SSimlVFlTUDJ9JdCrgFdPoIOzA3QkX29f6gXXy9l+6Mfij05n61SnE5vuzbtQyrRt04iKiyI9q/Q8nOjr5cvIq0by3o3vEeIXwi+Jv9Bvfj82HNng7tCUUkoppcqsgh5A3GvH64Arg3WEebdfmOZuReIKhyxu4iVexMfGM7HTxDztrae25qf9P5X4/I50Q50bmNNzDi3DW/L3ub8ZvGgwn23+TMs+lFJKKaWKwSUPIJYmIsL9Le7P2Y6eEu2wc99U9ybWDlqbp+3RpY8SMyWmVE2hVzOoJp93/5zBzQeTaTKZuG4ijyx5RMs+lFJKKaWKqNwl0wDD2wzPs70laYvDzu3n7Ud8bDw317s5py3TZNJ6WmsOJh902HVKytfLlxFXjeD9Lu8T4hfCr4m/0nd+X9b/XaaeKVVKKaWUciu7kmkRqSsiN1nvA0SkknPDcr7v7/g+5/3ABQMdfv43b3iTOb3m5Gm7+cubmbNjzmU+4R7XR1zP3F5ziQmP4ci5I9z//f18Gv+pln0opZRSStmh0GRaRP4JzAU+tpoigK+dGZQr1AqqlWc7Ki7K4de4ssqVbLgn7wN+Y1aOITou2u5VGF2hRsUafNb9Mwa3sJV9vL3+bR5e8rCWfSillFJKFcKekelHgGuB0wDGmJ1ANWcG5SrxsfF5tnec2OHwa/h4+RAfG8/dTe/OaTMYYqbGcCzlmMOvV1y+Xr6MaGMr+wj1C2VF4got+1BKKaWUKoQ9yfR5Y0xa9oaI+AAlnwKjlJjVc1bO+zvm3eGQ2T3y83Tbp/nm9m/ytHWe3Zn5f813yvWK6/qI65nTa46WfSillFJK2cGeZPonEXkWCBCRrsAcoHRlgCXQLKxZnm1Hzu5xsQYhDS6Zk/rZX5/lqmlXOS2JL47sso/7W9yfp+zjeOpxd4emlFJKKVWq2JNMjwKOAvHAg8BC4HlnBuVqF5d79J/f32nXyp6TenCLwTlt5zPPEz0lmlPnTzntukXl6+XL8DbD85R99JvXj3V/r3N3aEoppZRSpUaBybSIeAPbjDH/Ncb0M8b0td6XnmFUB8n9oOC249v4dte3Tr3eiDYj+O4f3+Vp6zizI4t2L3LqdYsqu+yjVbVWHEnRsg+llFJKqdwKTKaNMZnAdhG5wkXxuI2Plw/Tb52es/30L0+TmJzo1GtGVIrgj3v/yNP25M9P0n5G+9JX9nHzZwyNGkqWybKVffyoZR9KKaWUUvaUeVQGtojIEhGZl/1ydmDuEB0ezcg2I3O2u3/ZnbTMtAI+UXIiQnxsPA9GP5jTlpyeTPSUaM6ln3PqtYvCx8uHYa2H8eFNH9rKPg7ayj7WHl5b+IeVUkoppTyUPcn0/wE9gTHAhFwvj3Rfi/toX7N9znabaW1cMkr8aKtHWdx3cZ62djPa8ePeH51+7aLoWLsjc3rNoXW11hxJOcKQH4bwyR+faNmHUkoppcqlQpNpY8xP+b1cEZy7fNLtkzzb0VOiXZJQ16hY45KHIYcvH861X1zr9GsXRY2KNZh086Scso93N7zLv378F0kpSe4OTSmllFLKpexZAfGMiJy2Xqkikikip10RnDtdnNRGT4l22ehrfGw8D8c8nLN9Ou00UXFRpGakuuT69shd9lHZrzK/HfyNfvP7sebwGneHppRSSinlMvaMTFcyxgQbY4KBAOAO4IPCPici/iKyWkQ2icgWERlttXcRkfUislFEfhWRSKvdT0RmiUiCiKwSkXolujMHuDihbjmlJemZ6S659r9a/oul/Zbmabt6+tX8mfKnS65vr9xlH0dTjjL0h6Fa9qGUUkqpcsOemukcxuZr4GY7Dj8P3GiMaQnEAN1F5BrgQ+BuY0wMMIMLc1YPAU4YYyKBicBrRYnNWS5OqFtPa+2y+aDDA8Mvuf77R9536jzYxVG9YnUm3TyJf0b9E2MM7254l4cWP6SzfSillFLK49lT5vGPXK++IvIqUGi9gZV4J1ubvtbLWK9gqz0EOGi97w3EWe/nAl1EROy/Fee5OKHtOLMj+07vc+n1729xf872tuPbiIqLIj3LNaPk9vDx8uGx1o/llH2sPLSS/vP7s/HIRneHppRSSinlNFLYg3Ui8nmuzQxgD/BfY8yRQk9uW/RlHRAJvG+MGSUi1wFfAynAaeAaY8xpEdkMdDfGHLA++xfQzhhz7KJzPgA8ABAeHt5m9uzZdt2oI7x44EWOZ14Ybb077G6uCbrGZdc/ln6M0QdH52l7tuaz1KxQ02Ux2ONkxkk+P/Y5u87vwgsv+lTuww2VbqC4vxslJycTFBTk4ChLN71nz9e5c+d1xpir3B2HUkqpkrEnmb7WGLOisLZCzhEKfAX8G9sUe68ZY1aJyJNAE2PMUHuT6dyaNGlitm/fbm8YDjF82XB+3HdhurpqgdVY0m+Jy66/bNkyHtv3WJ62e5vdy5NXP+myGOyRnpXOxHUTmbp1KgDd63VndIfRBPoGFvlcy5cvp1OnTg6OsHTTe/Z8IqLJtFJKeQB7aqbftbPtsowxJ4FlwC1AS2PMKmvXLKCD9T4RqAMgIj7YSkBK3VxrEztP5NXrXs3ZPnLuCFFxUWRmZbrk+tmLvFxV/cLP4ClbpxAVF1WqHvrz9fLlqauf4s0b3iTQJ5BFexYx8NuB/HXyL3eHppRSSinlMJdNpkWkvYiMBMJFZESu10uAd2EnFpFwa0QaEQkAugLbgBARaWwdlt0GMA+Itd73BZaa0rSmdi49GvTg5wE/52mLmRrj0vrgz7t/zoc3fZinreWUli57ONJeN9e7mZk9ZxIZGsnuU7u589s7+W73d+4OSymllFLKIQoama4ABAE+QKVcr9PYkt3C1ASWicgfwBpgsTFmAfBP4EsR2QTcA2TXJ0wCwkQkARgBPF3023Gdyv6VL3kw8Z7v7qHvPHv+ahyjY+2OrLgzb7VNx5kd2XR0k8tisEf9kPpMv3U6PRr0ICUjhad+forxq8a7bJpBpZRSSilnuWwyba10OBrbA4Kjc73eMsbsLOzExpg/jDGtjDHRxpgWxpgxVvtXxpgoY0xLY0wnY8wuqz3VGNPPGBNpjGmb3V7axcfGM6jpoJzt7Se2ExUX5bLVAIMrBPPHvX/kaRu0cBCvr3ndJde3V6BvIOM7juf5ds/j4+XDjD9ncN/393H47GF3h6aUUkopVWz21EyfE5E3RGShiCzNfjk9sjJkVNtRfPePvKULnWZ3oudXPV1y/ew66puuuCmnberWqUTFRblkGXR7iQgDrhzAlO5TqFGxBn8c/YP+8/uz8uBKd4emlFJKKVUs9iTT04E/gfrAaGxT4+ma0ReJqBRBfGw8XnLhr3Tv6b1ExUWx/bhrZhyZ2HkiH3TJuzhl9JRo0jLTXHJ9e0WFRzG752w61OrAifMneHDxg3y86eNS9QClUkoppZQ97Emmw4wxk4B0q/TjfuBGJ8dVZm26dxML+izI09Z3fl+XjRJfF3Edvw78NU9bm2ltXLrIjD0q+1fmgy4f8K+W/wLgvY3v8eiSR0vdA5RKKaWUUgWxJ5nOfkrskIj0EJFWQBUnxlTm1Q2uS3xsPK2qtcrTHj0lmseWPnaZTzlOiF/IJQ9H9viqR86cz6WFt5c3D8c8zAc3fUCIXwi/JP5C//n92ZK0xd2hKaWUUkrZxZ5keqyIhAAjgSeAT4HhTo3KQ0y5Zcols20s27+MqLgoZmyb4fTrx8fG06Z6m5zt19e8Tp9v+jj9ukXVsXZHZvecTYuwFhw8e5B7Ft7DnB1zSlW9t1JKKaVUfgpMpq3lwBsZY04ZYzYbYzobY9oYY+a5KL4yL7hCMPGx8fyn03/ytI9fPZ6ouCg2HNng1OtP7j6ZCTdMyNlOOJlQ6h5MBKgVVIu4W+IY0GQA6VnpjFk5hudXPE9KRoq7Q1NKKaWUuqwCk2ljTCZwp4ti8Whd6nYhPjaeu668K0/7vd/dS1RcFOv/Xu+0a3er140f+/6Ypy16SjSpGalOu2ZxVPCuwPPXPM8rHV/B39ufeX/NY9DCQRxJP+Lu0JRSSiml8mVPmccKEXlPRK4TkdbZL6dH5qGeafcM8bHx1KhYI0977KJYouKiWLhroVOuW71iddYPypuwXz39ak6mnnTK9UqiV8NezOgxg3rB9dhxYgdvHHqDJXuXuDsspZRSSqlL2JNMxwDNgTHABOv1pjODKg8W9118yWIrAKN+GUVUXBTvrH/H4df09fa95JrXzbquVM6g0ahyI77o8QVd63Yl1aTy+PLHeWvtW2RkZbjoHoIIAAAgAElEQVQ7NKWUUkqpHIUm01ad9MUvnRrPAbIXW4mPjad2UO08+/4b/1+i4qKIiotyaAKZfc3cOs7sWCoT6qAKQUy4YQJ9KvfBW7z5fMvnDP1hKEfPHXV3aEoppZRSgB3JtIhUF5FJIvKdtd1MRIY4P7TyZdEdi4iPjafLFV0u2ddqaiui4qJYdWiVw66XX0J9Ou20w87vKCLCjcE3MunmSYQHhLPu73X0X9CftYfXujs0pZRSSim7yjwmA98DtaztHcDjzgqovPtP5/8QHxvPmA5jLtk39Ieh/Hvvv4mKi3LIqoYXJ9TXfnEt59LPlfi8ztCmehtm95rN1TWu5ljKMYb+MJTJmyeXullJlFJKKVW+2JNMVzXGzAayAIwxGUCmU6NS9GnUh/jY+Evmqc7WZlobouKieHDxgyVKKC9OqNvNaEd6VvpljnavqgFV+aTrJ9zf4n4yTSYT1k1g+PLhnEk74+7QlFJKKVVO2ZNMnxWRMMAAiMg1QOkrsPVQ2fNUx8fGE9ss9pL9vx38jegp0UTFRTH0+6FkZhX995yLE+rXVr9W7HidzcfLh+FthvNO53eo5FuJJfuWMHDBQLYf3+7u0JRSSilVDtmTTI8A5gENRWQFMAX4t1OjUvl64uoneLfuu6y/Zz0hfiGX7F91eBUxU2NyHlzce3qv3ededdeFeuxZ22c5pIzEmTpf0ZlZPWfRpHIT9p3Zx6CFg5j3l64lpJRSSinXsmc2j/XADUAH4EGguTHm0jndlMv4evny68BfiY+NZ1n/ZZc9rudXPXMS66i4KLYc23LZYwN9A7mxzoVJWspCYlonuA7Tbp3G7ZG3k5qZynO/PsfolaM5n3ne3aEppZRSqpzwKewAEfEHHgY6Yiv1+EVEPjLGlK7l88qpqgFVc8o00jLTGLBgAAknE/I9duC3A+0+b1lJSP19/Hn52pdpVa0V434fx9wdc9matJWJnSZSK6hW4SdQSimllCoBe8o8pmBbtOVd4D3r/dTCPiQi/iKyWkQ2icgWERlttYuIjBORHSKyTUQey9X+jogkiMgfuspi0VXwrsBXvb/KqbF+78b3in2uvo37OjAy5/tHo38w9dap1A6qzdakrfRf0J/fEn9zd1hKKaWU8nCFjkwDLYwxzXJtLxORrXZ87jxwozEmWUR8gV+tuaqbAnWAK40xWSJSzTr+FqCR9WoHfGj9qYrphjo35Hm4cP+Z/byw4gXW/n35OZqDfIP48rYv8fP2c0WIDtUsrBmzes7imV+e4ZfEX3jox4d4OOZhHoh+AC+x5/dGpZRSSqmisSeZXi8i1xhjfgcQkXZAoStmGNt8bcnWpq/1MsC/gLuMMdlT7R2xjukNTLE+9//t3Xd8lfXd//HXJyebhAAh7BFFDCIyZAhOEFSg1j2w2mp/WmxrFa1tb+3t7Wjv2trWWm3dE0dVbltbpG4FQWUrsmTJHrJXgOzP74/rio0Iyck4Jwm8n4/H9fBc63t9vudE8sn3fMc0M2tmZm3dfUO1aiQH1TGzI08Pf7q+w4iprJQs/jr0rzw691EenvMwD855kHlb5nH3yXcfcNCmiIiISG1E01zXF/jYzFaa2UpgKtDfzOaZWaUDEc0sYmZzgE3AO+4+HegCXGpms8zsDTPrGl7eHlhT4fa14TGRakmwBH7U60c8NOwhslKymLx2MqMmjGLRtkX1HZqIiIgcYqJpmR5e08LdvRTobWbNgFfNrAeQAhS4ez8zuwB4Cjgl2jLNbDQwGiAnJ4dJkybVNLxGKT8/X3Wuhpta3sSTm59kTf4avjPhO1zS4hIGZgys2wBjQJ+ziIhI42DRrJ5nZs0J+jl/lXyHU+ZF/yCz24G9wDXACHdfYWYG7HD3LDN7FJjk7i+G1y8GBlfWzSMvL88XLz68FuuYNGkSgwcPru8w4qq2dS4sLeTu6Xfzj6X/AILBlbcOuJXkSHIdRVj39Dkf+sxstrv3q+84RESkdqrs5mFmvwbmAg8A94bbH6O4LydskcbM0oAzgEXAP4Eh4WWnAUvC1+OB74WzegwEdqq/tNSFlEgKd514F3edeBfJCcm8suQVrnzjSjbk68dLREREaieabh6XAF3cvbpL4rUFxppZhCBpH+fuE8zsQ+AFM7uJYIDiNeH1rwMjgWUELdjfr+bzRCp1QdcLyGuRx82Tbmb+1vlcMuESHjj9Afq06lPfoYmIiEgjFc0AxPlAs+oW7O5z3b2Pu/d09x7u/qvw+A53/5a7H+fug9z9s/C4u/t17t4lPFfljCEi1XVs9rG8fPbLnNTuJHYU7uCat67h7ZVv13dYIiIi0khFk0z/FvjUzN4ys/HlW6wDE4mV8unzLjn6EorKivjZBz9j7IKxRDN+QERERKSiaLp5jAXuAeYBZbENRyQ+EhMSuW3gbbTLaMefP/kzf5z1Rzbs2cDP+/2cSEKkvsMTERGRRiKaZHqvuz8Q80hE4szMuPq4q2nbpC23fXQbL3z+AhvyN/D7037fKFeAFBERkfiLppvHFDP7rZkNMrPjy7eYRyYSJyOPHMmjZzxKZnIm7695n9tv6o6bQfnWogU8/3x9hykiIiINUDTJdB9gIHA31ZgaT6Qx6d+mP09Nbkv6vlJe75vOQ+e1+s/J7dvhu98NNhEREZEKqkym3X3IAbbT4xGcSNw8/zzdHvkHf3h4DQllziPnteLN/k2/cY1aqEVERKSiaBZtaW1mT5rZG+F+dzO7OvahicTRDTcAcOrcfG5+6UsAnjw755vXjRkTz6hERESkgYumm8czwFtAu3B/CXBjrAISqRfbt3/1ctT728jcU8qizmksbb/fQMRt2+IcmIiIiDRkB02mzax8po+W7j6OcFo8dy8BSuMQm0i9SC5xhs/YSdstRWxskVTf4YiIiEgDVtnUeDOA44E9ZpYNOICZDQR2xiE2kXpz88tfctuzZSTsv46L1Us4IiIi0kBV1s2jPG34KTAe6GJmHwHPAtfHOjCRuGre/Gu7TQoOkEgnAH2T4J/Xwa4NcQtNREREGq7KkukcM/spMBh4Ffg98AbwODAs9qGJxNEDUa5LdGI6zHke/nI8TPodFObHNi4RERFp0CpLpiNABpAJNCHoEhIB0sNjIoeOK64ItgPw8u07V8Dts+GYb0PxXpj02yCpnvU0lJbENVwRERFpGCrrM73B3X8Vt0hE6ttzz8FZZwXT34WzdjiwpGUn7hh2LcNGj+Ka7CPh0udh1cfw9m2wbjZMuBGmPghDbw8SbVPHahERkcNFNH2mRQ4fV1wBW7eCO7hj7qyYOJ1pnXvx2zcWMfWLrcF1nU+Ea96Di56GFkfC1qUw7rvwxFBYPqleqyAiIiLxU1kyPTRuUYg0YMN7tOHHg7tQWub86IXZzFsbTmZjBj0ugOtmwMg/QpNWQUv1s+fC2HNgzcz6DVxERERi7qDJtLtrdQqR0M1n5jHsmNbs2FvMZY9PY/ryrf85GUmCAT+AMXPg9P+BlCxY8QE8OQxeuATWz6m/wEVERCSmolkBsUbMLNXMZpjZZ2a2wMzu2u/8A2aWX2E/xcxeNrNlZjbdzHJjFZtIdUUSjIcuP56ze7Ylv7CE7z01g4mLNn39ouQmcOrPgqT6lJshqQksfQseOw1euhw2fFY/wYuIiEjMxCyZBgqB0929F9AbGB4u+IKZ9QOa73f91cB2dz8KuA+4J4axiVRbcmIC94/qw2UDOlFYUsYPnp3Fa5+t/+aF6S2CwYhjPoNBP4HEVFg0AR49FV78jlqqRUREDiExS6Y9UN7ynBRubmYR4A/AL/a75VxgbPj6FWComaZFkIYlkmDcfX4Prj31SErKnBte+pS/TV994IszcuCs3wRJ9cDrIDENFv87aKl+4RJYPT2+wYuIiEidi2XLNGYWMbM5wCbgHXefDvwEGO/u+y8h1x5YA+DuJQRLlmfHMj6RmjAzbhnRjZ+flYc7/PLVedz3zhLKyvZfMjGU2QaG3w03zg1aqpPSg+4fT50JT38Llr0bzB4iIiIijY55HH6Jm1kzglUU7wDuBga7e4mZ5bt7RnjNfGC4u68N978ATnD3LfuVNRoYDZCTk9N33LhxMY+/IcnPzycjI6O+w4irhlzn91YX8/zCIhzo2TLC6J4pZCRX/oVKUtFO2q+bQIe1/yaxdA8AuzOOZE3H89mccxKeEGnQdY6Vw63OQ4YMme3u/eo7DhERqZ24JNMAZnY7wdzVPwIKwsOdgOXufpSZvQXc6e5TzSwR+BLI8UoCzMvL88WLF8c69AZl0qRJDB48uL7DiKuGXucPlmxmzEufsmNvMe2bpfHIFX05rkNW1TcW7IJZTwYLvuzZHBzL6ggDf8yUPbmcMmxkbANvYBr651zXzEzJtIjIISCWs3nkhC3SmFkacAYw293buHuuu+cCe8MBhwDjgSvD1xcB71eWSIs0FKcdncOE60+mV4cs1u3Yx4UPf8yLM1ZT5Y9valM4+Sa4cT58+37IPgp2roG3bmXgtGuCFRZ3HKQ/toiIiDQIsewz3RaYaGZzgZkEfaYnVHL9k0C2mS0DfgrcEsPYROpUh+bpjPvhIC4/oRNFpWXc+o95/OKVuRQUl1Z9c1Iq9L0KrpsJo16EToNIKtkDH/8F7u8FL18BKz9Uv2oREZEGKDFWBbv7XKBPFddkVHhdAFwcq3hEYi0lMcJvzj+O4zs157//OY//m72WBet38dDlx5PbsknVBSQkQLeR0G0ks8c/Tt+SmTD/H/D5a8HW+jjofzUcdzGkHD59i0VERBqymM7mIXI4urBvB1798UnkZqezcMMuRtw/hbEfrzz4bB8HsLtpV7jgMbhpPpx2CzTJgY3zYMKNcG83mPBT+HJeDGshIiIi0VAyLRIDx7Rtyr9+cjLf7tWOfcWl3DF+AaMen8aqrXuqV1BmGxhyK9y0AC54AjqdCEW7g4GLj5wMTwyD2WODwYwiIiISd0qmRWIkKy2Jv1zWh0eu6EvLjBRmrNjGWX+ezNMfrahWKzUAiSnQ82L4f2/Aj6fBgGshpSmsnQmv3QD35sGrP1TfahERkThTMi0SY8N7tOGdm07l3N7tKCgu467XFjLqsWms2FLNVupyrY6Bkb+HmxfBuQ9B55OgeC989iI88y14oDdMvBu2LKvbioiIiMg3KJkWiYPmTZK5f1QfHvtuX3IyU5ixchsj7p/Mkx+uoLS6rdTlkptAn8vh+6/D9Z/AKT+DzHawfSV8cA/8tS88NhimPgS7v6zL6oiIiEhIybRIHJ15bNBKfX6f9hQUl/HrCQs5/6GPmL1qW+0Kzu4CQ/8nGLD43Veh9+WQnAnrP4W3boU/HQPPnA0zHldiLSIiUoeUTIvEWbP0ZO67tDdPfK8frZumMHftTi58eCo3vPgp63fsq13hCRHocjqc9xD8fClcPBa6nQ0JibByCrz+s2A2kKeGw7SHYfuquqmUiIjIYSpm80yLSOWGdW/NoC7ZPPLBFzw2eTnjP1vP2wu/5NpTu9A9oQ4GESalwbHnBVvBTlj8Jiz8Fyx7F1ZPDbY3b4FWx0LecMgbCe2OD+a7FhERkagomRapR01SErn5zDwu6deR372xiH/P28D97y2lRapRkL2Oc3q1w8xq/6DULOh1abAV7oYlbwULwSx7DzYtCLYp9wbzWXc5HboMDf6bkVP7Z4uIiBzClEyLNAAdW6Tz4OXH873lW/nVhIUsWL+LMS/NYezHK7n928fSu2OzuntYSiYcd1GwlRTBqg9h8RtBy/XO1TD35WADaNMTugyB3FOh00CtvCgiIrIfJdMiDcgJR2Yz/icn879/e5fXVsInq3dw3oMfMbRbK8YM60rPDnWYVAMkJoct0afDiN/D5sXwxXtBi/Wqj+DLucH20f1gEWh/POSeDJ0GQccBkNa8buMRERFpZJRMizQwkQTjtA5J/PSik3hw4hc88/EK3lu0ifcWbeL0bq0YM7QrveqypbqcGbTqFmyDroPifbDqY1gxORi8uP7TYJGYtTOB+4J7co6BTidA+75Bf+ucbhDRPysiInL40G89kQYqMzWJW0Z04+qTj+DxKct5buoq3l+0ifcXbWJIXg5jhh1dt90/9peUBkcNDTYIlixfPS3oFrJ6Oqz/BDZ/HmyznwnvSQ+6hrTtCW2OC17ndIOk1NjFKSIiUo+UTIs0cDmZKfxy5DGMPvVIHp+8nGenrmLi4s1MXLyZwXk5jBnalT6d4tDdIrUpHH1msAGUFML6ObB2Bqz7BNbNhh2rYM20YCtnCdD8iGDlxpw8yO4KLbsGc2Orm4iIiDRySqZFGomWGSncGibVj4Ut1ZMWb2bS4s0MOKIF3z8xlzO6tyYxEqep7RJTgi4enU74z7E9W2HDHPhyXtjfeh5s/QK2hduiCV8vIzUrSLSbd6bLLiD1c8hsG2wZrYItuUnt4pzzt6C/93EXBfNwi4iI1CEl0yKNTHZGCreOOIbRpxzJ41NW8Py0VcxYsY0ZK7bRvlka3x3UmVH9O9IsPTn+wTXJ/nrXEAhasLcshU2fw5bFsHVZuC0P5r/eMAc2zKEjwNp/fbPMxDRIbwFpLYLW8ZTMoDtJUnowgDIhKWj9xqGsJHhe4W7Ytx12b4AtS4JyUjKh28g4vAkiInI4UTIt0khlZ6Rwy4huXDekC3+fvZaxU1exYssefvfGIv787hLO79OBq07MJa9NZv0GmpgCbXoEW0XusGcLbF8BO1bzxacf0CU7OVjufNd62LMZ8jdByT7YtS7YaqrzSdChX+3qISIicgBKpkUauczUJK466Qi+NyiXD5Zs5umPVzJ5yWZenLGaF2es5sQu2Ywa0Ikzu7cmNakBdXMwCxaFyciBjgNYs7UlXQYP/vo17lCUD3u3QcGOYBBk4W4o2hMk2aVFUFoMXgZYsGx6YkrQNSStGWS0gRZH1L6riIiIyEHELJk2s1RgMpASPucVd7/DzF4A+gHFwAzgWncvtmCZt/uBkcBe4Cp3/yRW8YkcahISjCHdWjGkWyuWbcrn2akreWX2Wj7+Yisff7GVzNREzu7ZlguP70Dfzs3rZmXFWDMLumekZAKd6zsaERGRb4jlSKVC4HR37wX0Boab2UDgBaAbcByQBlwTXj8C6Bpuo4GHYxibyCHtqFYZ/OrcHky9dSh3nXMsPTtksbughBdnrOGiR6Yy5I+TeOC9pazZtre+QxUREWnUYtYy7e4O5Ie7SeHm7v56+TVmNgPoEO6eCzwb3jfNzJqZWVt33xCrGEUOdVlpSVx5Yi5XnpjLko27+fsna3n1k3Ws3LqXP72zhD+9s4QTjmjBiB5tOKtHG9pmpdV3yCIiIo2KBblrjAo3iwCzgaOAB939vyqcSwKmA2PcfYqZTQB+5+4fhuffA/7L3WftV+ZogpZrcnJy+o4bNy5m8TdE+fn5ZGRk1HcYcaU6163SMmfB1lI+WlfCJ5tKKS77z7kjsxLo2zpC39aJtGkSpyn2Qofb5zxkyJDZ7q5RkSIijVxMk+mvHmLWDHgVuN7d54fHHgf2uPuN4X5UyXRFeXl5vnjx4pjH35BMmjSJwfsP0jrEqc6xs6ugmPc+38ib87/kgyWbKaiQWR/dOoOzjm3D4LwcenVoFvP5qw+3z9nMlEyLiBwC4jKbh7vvMLOJwHBgvpndAeQA11a4bB0EU82GOoTHRCRGmqYmcX6fDpzfpwP7ikr5YMlm3l7wJe9+vpElG/NZsnEZf3l/GZkpiZx4VDYnd83h1K4t6Zyt2TFEREQgtrN55ADFYSKdBpwB3GNm1wBnAUPdvcIXzIwHfmJmLwEnADvVX1okftKSIwzv0YbhPdpQXFrGtOVbeXfhRqYs3cLyLXt4a8FG3lqwEYBOLdI56aiW9M9tTv/cFnRontY4ZgcRERGpY7FsmW4LjA37TScA49x9gpmVAKuAqeEv33+4+6+A1wmmxVtGMDXe92MYm4hUIimSwCldczilaw4Aa7fv5cOlW5iydAsfLtvC6m17WR3OYw3QKjOF/rkt6Nu5Of1ym5PXJpOUxAY0p7WIiEiMxHI2j7lAnwMcP+Azw1k8rotVPCJScx2apzNqQCdGDehEaZkzb91Opi/fysyV25m9ahubdhfy73kb+Pe84MukpIiR1yaT49pn0aN9Fj3aZZHXJrNhLRojIiJSB7QCoohUSyTB6N2xGb07NuPa08Dd+WLzHmat3MbMldv5dM12VmzZw/x1u5i/bhewBoAEg87ZTejaKoOjW2fStXUGXVtlktsynfRk/VMkIiKNk36DiUitmBlHtcrgqFYZjBrQCYDdBcUsXL+Leet2Mn/dTuat28mKLXu+2t5euPFrZbTKTKF5YjFvbJlLxxZptG+eRvtm6bRvnkbrzJSYzyQiIiJSU0qmRaTOZaYmccKR2ZxwZPZXxwqKS1m+eQ9LN+1mycbdLNmYz/LN+azetpdNuwvZBCyeteYbZSUYZGek0LppCq0zU8nJTKFFk2RaNEkmOyOZZunJNEtLoll6Mk1TE8lITVR/bRERiRsl0yISF6lJEbq3a0r3dk2/dry0zFm/Yx//en8qWe27sHb7Ptbu2Mf6HftYt30fm3YXsjnc5rMrqmclRxJIT4nQJDmRtOQIqUkJpCVFSE5MIDmSQGIkgaSIkZiQQCTBMAMj+K87OE5ZmVPqUFbmFJeWhZtTVFJGYUkpBcVl7CsupXN2Os9dfUIs3jIREWkElEyLSL2KJBgdW6TTo2WEwYNyv3G+uLSMLfmFbNxVyMZdBWzeXci2PUVs21PE1j1F7NhbxM59xezYW8zugmJ2F5RQVFpG0d4yduwtjnn8iRFNCSgicjhTMi0iDVpSJIG2WWm0zUqL6np3p7CkjD2FJewtKmVfcSkFxUFLclFJGUWlpRSVBK3NZe6UlDoOlFVYDdYIkvxIgpFgRlLESIokkBRJIDkxgZTEBFKTIqQlRWiSon9GRUQOZ/otICKHFDMjNSlCalKE7KovFxERqRUNkRcRERERqSEl0yIiIiIiNaRkWkRERESkhpRMi4iIiIjUkJJpEREREZEaUjItIiIiIlJDSqZFRERERGpIybSIiIiISA0pmRYRERERqSEl0yIiIiIiNRSzZNrMUs1shpl9ZmYLzOyu8PgRZjbdzJaZ2ctmlhweTwn3l4Xnc2MVm4iIiIhIXYhly3QhcLq79wJ6A8PNbCBwD3Cfux8FbAeuDq+/GtgeHr8vvE5EREREpMGKWTLtgfxwNyncHDgdeCU8PhY4L3x9brhPeH6omVms4hMRERERqa2Y9pk2s4iZzQE2Ae8AXwA73L0kvGQt0D583R5YAxCe3wlkxzI+EREREZHaSIxl4e5eCvQ2s2bAq0C32pZpZqOB0eFuoZnNr22ZjUxLYEt9BxFnqvPh4XCrc159ByAiIrUX02S6nLvvMLOJwCCgmZklhq3PHYB14WXrgI7AWjNLBLKArQco6zHgMQAzm+Xu/eJRh4ZCdT48qM6HPjObVd8xiIhI7cVyNo+csEUaM0sDzgA+ByYCF4WXXQn8K3w9PtwnPP++u3us4hMRERERqa1Ytky3BcaaWYQgaR/n7hPMbCHwkpn9L/Ap8GR4/ZPAc2a2DNgGjIphbCIiIiIitRazZNrd5wJ9DnB8OTDgAMcLgIur+ZjHahZdo6Y6Hx5U50Pf4VZfEZFDkqknhYiIiIhIzWg5cRERERGRGmoUybSZDTezxeFS47cc4PwhtxR5FHX+qZktNLO5ZvaemXWujzjrUlV1rnDdhWbmZtaoZ36Ipr5mdkn4OS8ws7/FO8a6FsXPdSczm2hmn4Y/2yPrI866ZGZPmdmmg03jaYEHwvdkrpkdH+8YRUSk5hp8Mh0OYHwQGAF0By4zs+77XXZILUUeZZ0/Bfq5e0+CFSN/H98o61aUdcbMMoExwPT4Rli3oqmvmXUFbgVOcvdjgRvjHmgdivIzvo1gsHIfgkHID8U3yph4BhheyfkRQNdwGw08HIeYRESkjjT4ZJpgsOIyd1/u7kXASwRLj1d0qC1FXmWd3X2iu+8Nd6cRzNndmEXzOQP8muCPpYJ4BhcD0dT3B8CD7r4dwN03xTnGuhZNnR1oGr7OAtbHMb6YcPfJBDMUHcy5wLMemEYwF3/b+EQnIiK11RiS6a+WGQ9VXIL8G9ccIkuRR1Pniq4G3ohpRLFXZZ3Dr787uvu/4xlYjETzGR8NHG1mH5nZNDOrrHWzMYimzncCV5jZWuB14Pr4hFavqvv/u4iINCBxWQFRYsfMrgD6AafVdyyxZGYJwJ+Aq+o5lHhKJPjqfzDBNw+Tzew4d99Rr1HF1mXAM+5+r5kNIph7voe7l9V3YCIiIgfSGFqmy5cZL1dxCfJvXFPZUuSNSDR1xsyGAf8NnOPuhXGKLVaqqnMm0AOYZGYrgYHA+EY8CDGaz3gtMN7di919BbCEILlurKKp89XAOAB3nwqkAi3jEl39ier/dxERaZgaQzI9E+hqZkeYWTLBoKTx+11zqC1FXmWdzawP8ChBIt3Y+9JCFXV2953u3tLdc909l6Cf+DnuPqt+wq21aH6u/0nQKo2ZtSTo9rE8nkHWsWjqvBoYCmBmxxAk05vjGmX8jQe+F87qMRDY6e4b6jsoERGJToPv5uHuJWb2E+AtIAI85e4LzOxXwCx3H88hthR5lHX+A5AB/F841nK1u59Tb0HXUpR1PmREWd+3gDPNbCFQCvzc3RvtNy5R1vlm4HEzu4lgMOJVjfwPY8zsRYI/ilqGfcHvAJIA3P0Rgr7hI4FlwF7g+/UTqYiI1IRWQBQRERERqaHG0M1DRERERKRBUjItIiIiIlJDSqZFRERERGpIybSIiIiISA0pmRYRERERqSEl03JQZtbGzF4ysy/MbLaZvW5mR9dzTDeaWXoN7rvKzNpV2H/CzLrXQTx3mtm6cHq3mAnj/2uF/bZm9raZ5ZrZ/PBYPzN7IHw92MxOrPdP3nwAAAT/SURBVMFzTjGzheVlioiISOWUTMsBWTB59avAJHfv4u59gVuB1vUbGTcCB0ymzSxSyX1XAV8l0+5+jbsvrKOY7nP32+uorGgNJ5iv+SvuPsvdbwh3BwPVSqbNLNHdpxDMeSwiIiJRUDItBzMEKA4XlQDA3T9z9ynhSm1/MLP5ZjbPzC6Fr1pDJ5nZK2a2yMxeCJNyzKy/mX1sZp+Z2QwzyzSzSFjOTDOba2bXVlaOmd1AkBBPNLOJ4bX5ZnavmX0GDDKz28Py5pvZY+F9FwH9gBfMbI6ZpYXl9wvLuCysx3wzu6e8vmHZvwljnmZmVf4hYWY5ZvaOmS0IW79XmVnLsAV5kZk9Y2ZLwjoNM7OPzGypmQ0I729hZv8M349pZtbzII8aDryx37MHm9kEM8sFfgjcFNb3lDCuv4fvzUwzOym8504ze87MPgKeq6p+IiIi8nVKpuVgegCzD3LuAqA30AsYBvzBzNqG5/oQtB53B44ETrJg6eiXgTHuXn7PPuBqgqWT+wP9gR+Y2REHK8fdHwDWA0PcfUh4XRNgurv3cvcPgb+6e3937wGkAWe7+yvALOByd+/t7vvKKxJ2/bgHOD2sU38zO69C2dPCmCcDP4jifbuDYDn7Y4FXgE4Vzh0F3At0C7fvACcDPwN+GV5zF/Cpu/cMjz27/wPCFvi8g7Wsu/tK4BGCFvPeYWvz/eF+f+BC4IkKt3QHhrn7ZVHUT0RERCpo8MuJS4N0MvCiu5cCG83sA4JkeBcww93XApjZHCAX2AlscPeZAO6+Kzx/JtAzbDkGyAK6AkUHKefDA8RSCvy9wv4QM/sFQVeQFsAC4LVK6tKfoCvL5vBZLwCnAv8M45gQXjcbOKOqN4bgvTk/rOebZra9wrkV7j4vfM4C4D13dzObF9av/P4Lw/vfN7NsM2u63zNOAKZHEUtFw4Du4RcFAE3NLCN8Pb7iHxgiIiISPSXTcjALgIuqvOqbCiu8LqXynzEDrnf3r/X9NbPB1SinIEzqMbNU4CGgn7uvMbM7gdRqRf91xe7uUcQQrYp1KquwX1bNskcAb1bz2QnAQHcvqHgwTK73VLMsERERCambhxzM+0CKmY0uP2BmPc3sFGAKcGnY5zmHoCV3RiVlLQbamln/sJxMM0skGED3IzNLCo8fbWZNqohrN5B5kHPlifOWsNW14h8DB7tvBnBa2K85AlwGfFBFDJX5CLgEvmp5b17N+6cAl4f3Dwa2lLfkVzAUeLeKcvav79vA9eU7Zta7mnGJiIjIASiZlgMKW2TPB4ZZMDXeAuC3wJcEs3zMBT4jSLp/4e5fVlJWEXAp8JdwoOA7BInvE8BC4BMLpmJ7lKpbaB8D3iwfgLjfc3YAjwPzCRL1mRVOPwM8Uj4AscI9G4BbgIlhfWa7+7+qiKEydwFnhvW5mOD92l2N++8E+prZXOB3wJUVT4Z/vBS4e1VlvgacXz4AEbgB6BcObFxIMEBRREREasn+8y22iFRX2JUk393/GO6nAKXuXmJmg4CH3b3OWoHN7Aqgg7v/rq7KPMAzcoEJ4SBOERERqYT6TIvUTj4w2syahnNNdwLGmVkCwQDGaGYAiZq7P1+X5e0vbMV+CNgSy+eIiIgcKtQyLSIiIiJSQ+ozLSIiIiJSQ0qmRURERERqSMm0iIiIiEgNKZkWEREREakhJdMiIiIiIjWkZFpEREREpIb+PxYAkQwN3h2oAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"ax = create_cstr_plot_axes()\n",
"for Tc in [290, 300, 305]:\n",
" tsim, ysim = Simulator(cstr(), package='scipy').simulate(numpoints=100)\n",
" cstr_plot(tsim, ysim, ax)"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 2,
"link": "[7.4.6 Effect of Cooling Temperature](https://jckantor.github.io/CBE30338/07.04-Simulation-of-an-Exothermic-CSTR.html#7.4.6-Effect-of-Cooling-Temperature)",
"section": "7.4.6 Effect of Cooling Temperature"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"id": "817485d9",
"metadata": {},
"source": [
"\n",
"< [7.3 Simulation in Pyomo](https://jckantor.github.io/CBE30338/07.03-Simulation-in-Pyomo.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [7.5 First Order System in Pyomo](https://jckantor.github.io/CBE30338/07.05-First-Order-System-in-Pyomo.html) > 
 "
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 2
}

