None Notebook

This notebook contains material from CBE30338; content is available on Github.

< 9.0 Discrete Events | Contents | Tag Index | 9.2 State-Task Networks >

Open in Colab

Download

9.1 Scheduling State-Task Networks

9.1.1 Example (Kondili, et al., 1993)

A state-task network is a graphical representation of the activities in a multiproduct batch process. The representation includes the minimum details needed for short term scheduling of batch operations.

Shown below is a well-studied example due to Kondili (1993). Other examples are available in the references cited above.

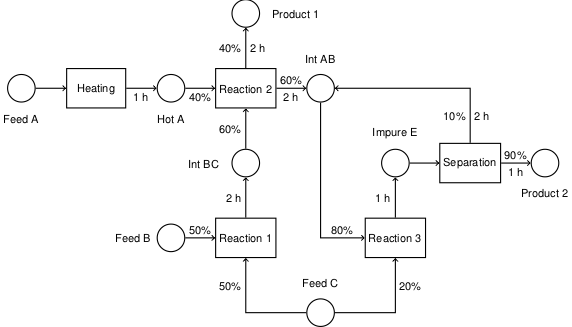
Kondili_1993

Each circular node in the diagram designates material in a particular state. The materials are generally held in suitable vessels with a known capacity. The relevant information for each state is the initial inventory, storage capacity, and the unit price of the material in that state. The price of materials in intermediate states may be assigned penalities in order to minimize the amount of work in progress.

The rectangular nodes denote process tasks. When scheduled for execution, each task is assigned an appropriate piece of equipment, and assigned a batch of material according to the incoming arcs. Each incoming arc begins at a state where the associated label indicates the mass fraction of the batch coming from that particular state. Outgoing arcs indicate the disposition of the batch to product states. The outgoing are labels indicate the fraction of the batch assigned to each product state, and the time necessary to produce that product.

Not shown in the diagram is the process equipment used to execute the tasks. A separate list of process units is available, each characterized by a capacity and list of tasks which can be performed in that unit.

9.1.2 Encoding the STN data

The basic data structure specifies the states, tasks, and units comprising a state-task network. The intention is for all relevant problem data to be contained in a single JSON-like structure.

9.1.2.1 Setting a Time Grid

The following computations can be done on any time grid, including real-valued time points. TIME is a list of time points commencing at 0.

9.1.3 Creating a Pyomo Model

The following Pyomo model closely follows the development in Kondili, et al. (1993). In particular, the first step in the model is to process the STN data to create sets as given in Kondili. Two differences from Kondili are:

\begin{align*} Q_{jt} & = Q_{j(t-1)} + \sum_{i\in I_j}B_{ijt} - \sum_{i\in I_j}\sum_{\substack{s \in \bar{S}_i\\s\ni t-P_{is} \geq 0}}\bar{\rho}_{is}B_{ij(t-P_{is})} \qquad \forall j,t \end{align*}

Following Kondili's notation, $I_j$ is the set of tasks that can be performed in unit $j$, and $\bar{S}_i$ is the set of states fed by task $j$. We assume the units are empty at the beginning and end of production period, i.e.,

\begin{align*} Q_{j(-1)} & = 0 \qquad \forall j \\ Q_{j,H} & = 0 \qquad \forall j \end{align*}

The unit allocation constraints are written the full backward aggregation method described by Shah (1993). The allocation constraint reads

\begin{align*} \sum_{i \in I_j} \sum_{t'=t}^{t-p_i+1} W_{ijt'} & \leq 1 \qquad \forall j,t \end{align*}

Each processing unit $j$ is tagged with a minimum and maximum capacity, $B_{ij}^{min}$ and $B_{ij}^{max}$, respectively, denoting the minimum and maximum batch sizes for each task $i$. A minimum capacity may be needed to cover heat exchange coils in a reactor or mixing blades in a blender, for example. The capacity may depend on the nature of the task being performed. These constraints are written

\begin{align*} B_{ij}^{min}W_{ijt} & \leq B_{ijt} \leq B_{ij}^{max}W_{ijt} \qquad \forall j, \forall i\in I_j, \forall t \end{align*}

9.1.3.1 Characterization of Tasks

9.1.3.2 Characterization of States

9.1.3.3 Characterization of Units

9.1.3.4 Pyomo Model

9.1.4 Analysis

9.1.4.1 Profitability

9.1.4.2 State Inventories

9.1.4.3 Unit Assignment

9.1.4.4 Unit Batch Inventories

9.1.4.5 Gannt Chart

9.1.5 Trace of Events and States

< 9.0 Discrete Events | Contents | Tag Index | 9.2 State-Task Networks >

Open in Colab

Download