{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"*This notebook contains material from [CBE40455-2020](https://jckantor.github.io/CBE40455-2020);\n",
"content is available [on Github](https://github.com/jckantor/CBE40455-2020.git).*\n"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [2.2 Campus SEIR Modeling](https://jckantor.github.io/CBE40455-2020/02.02-Campus-SEIR-modeling.html) | [Contents](toc.html) | [2.4 Linear Analysis of Campus Reopening](https://jckantor.github.io/CBE40455-2020/02.04-Linear-Analysis-of-Campus-Reopening.html) > 
 "
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "eAbATGsb5fwf",
"nbpages": {
"level": 1,
"link": "[2.3 Campus Re-opening Model](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3-Campus-Re-opening-Model)",
"section": "2.3 Campus Re-opening Model"
}
},
"source": [
"# 2.3 Campus Re-opening Model\n",
"\n",
"Following [Paltiel, et al. (2020)](https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2768923). \n",
"\n",
"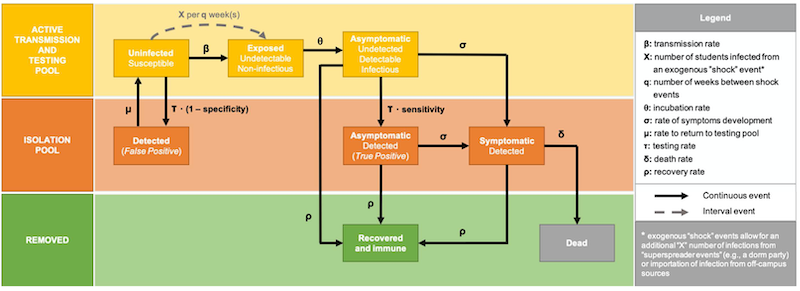\n",
"\n",
"(Figure e1 from Paltiel, et al., 2020)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "fmDN0ArmBQ5C",
"nbpages": {
"level": 3,
"link": "[2.3.1 Active transmission and testing pool. ](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.1-Active-transmission-and-testing-pool.)",
"section": "2.3.1 Active transmission and testing pool. "
}
},
"source": [
"\n",
"### 2.3.1 Active transmission and testing pool. \n",
"\n",
"This pool consists of individuals in the campus population subject to testing and the transmission of virus.\n",
"\n",
"* $U$ uninfected, susceptible individuals\n",
"* $E$ exposed, asymptomatic, non-infectious\n",
"* $A$ infected, asymptomatic\n",
"\n",
"\\begin{align*}\n",
"\\frac{dU}{dt} & = -\\beta U \\frac{A}{U + E + A} - \\tau (1-S_p) U + \\mu F_p - x(t) \\\\\n",
"\\frac{dE}{dt} & = \\beta U \\frac{A}{U + E + A} - \\theta E + x(t) \\\\\n",
"\\frac{dA}{dt} & = \\theta E - (\\sigma + \\rho + \\tau S_e)A\n",
"\\end{align*} \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "H3sOz0YPBYOW",
"nbpages": {
"level": 3,
"link": "[2.3.2 Isolation pool](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.2-Isolation-pool)",
"section": "2.3.2 Isolation pool"
}
},
"source": [
"### 2.3.2 Isolation pool\n",
"\n",
"* $S$ infected, symptomatic with a true positive test result.\n",
"* $T_p$ infected, asymptomatic with a true positive test result\n",
"* $F_p$ uninfected with a false positive result.\n",
"\n",
"\\begin{align*}\n",
"\\frac{dF_p}{dt} & = -\\mu F_p + \\tau(1-S_p) U \\\\\n",
"\\frac{dT_p}{dt} & = -(\\sigma + \\rho) T_p + \\tau S_e A\\\\\n",
"\\frac{dS}{dt} & = -(\\rho + \\delta)S + \\sigma (T_p + A)\n",
"\\end{align*} "
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "D64CeE2hCIdC",
"nbpages": {
"level": 3,
"link": "[2.3.3 Removed pool](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.3-Removed-pool)",
"section": "2.3.3 Removed pool"
}
},
"source": [
"### 2.3.3 Removed pool\n",
"\n",
"* $R$ recovered. These individuals assumed to be immune for the remainder of the simulation, and not returned to the campus population.\n",
"* $D$ dead.\n",
"\n",
"\\begin{align*}\n",
"\\frac{dR}{dt} & = \\rho (T_p + A + S)\\\\\\\n",
"\\frac{dD}{dt} & = \\delta S\n",
"\\end{align*} "
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "Yso2VSWXrssr",
"nbpages": {
"level": 3,
"link": "[2.3.4 Parameter estimates](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4-Parameter-estimates)",
"section": "2.3.4 Parameter estimates"
}
},
"source": [
"### 2.3.4 Parameter estimates\n",
"\n",
"Given:\n",
"\n",
"* $\\rho$ recovery rate \n",
"* $R_t$ basic reproductive number for asymptomatic transmission \n",
"* $p_{si}$ probability that an infected individual will become symptomatic.\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "6SpT6hhJ5lmU",
"nbpages": {
"level": 4,
"link": "[2.3.4.1 Odds of becoming symptomatic if infected](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.1-Odds-of-becoming-symptomatic-if-infected)",
"section": "2.3.4.1 Odds of becoming symptomatic if infected"
}
},
"source": [
"#### 2.3.4.1 Odds of becoming symptomatic if infected\n",
"\n",
"Based on the compartmental relationships and rates, the probability of symptom development for infected individuals is given by\n",
"\n",
"$$p_{si} = \\frac{\\sigma}{\\sigma + \\rho}$$\n",
"\n",
"Inverting this relationship\n",
"\n",
"$$\\sigma = \\frac{p_{si}}{1 - p_{si}}\\rho$$\n",
"\n",
"where $\\frac{p_{si}}{1 - p_{si}}$ is the 'odds' that an infected individual becomes symptomatic.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "-N4_RCNk5xPJ",
"nbpages": {
"level": 4,
"link": "[2.3.4.2 Effective reproductive number with isolation of symptomatic individuals](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.2-Effective-reproductive-number-with-isolation-of-symptomatic-individuals)",
"section": "2.3.4.2 Effective reproductive number with isolation of symptomatic individuals"
}
},
"source": [
"#### 2.3.4.2 Effective reproductive number with isolation of symptomatic individuals\n",
"\n",
"For an initially uninfected population with no testing regime, where transmission is solely due to non-isolated, asymptomatic individuals, the effective reproductive number is\n",
"\n",
"$$R_t = \\frac{\\beta}{\\sigma + \\rho}$$\n",
"\n",
"Expressed in terms of recovery rate and probability of becoming symptomatic\n",
"\n",
"$$R_t = \\frac{\\beta}{\\rho}(1 - p_{si})$$"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "8e0Q1QYCAtcK",
"nbpages": {
"level": 4,
"link": "[2.3.4.3 Testing threshold](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.3-Testing-threshold)",
"section": "2.3.4.3 Testing threshold"
}
},
"source": [
"#### 2.3.4.3 Testing threshold\n",
"\n",
"With a testing regime, for effective herd immunity requires\n",
"\n",
"$$\\beta \\leq \\sigma + \\rho + \\tau S_e $$\n",
"\n",
"where $\\tau$ is the testing rate and $S_e$ is the test sensitivity. With some manipulation using the above relationships, the testing treshhold becomes\n",
"\n",
"$$\\tau S_e \\geq \\frac{(R_t - 1) \\rho}{1 - p_{si}}$$\n",
"\n",
"or \n",
"\n",
"$$\\frac{1}{\\tau} \\leq S_e \\left(\\frac{1 - p_{si}}{R_t - 1}\\right)\\frac{1}{\\rho} $$"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "DM1O_lhAEPEN",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
}
},
"source": [
"#### 2.3.4.4 Parameter values\n",
"\n",
"| parameter | value |\n",
"| :--: | :--: |\n",
"| $p_{si}$ | 0.3 |\n",
"| $R_t$ | [1.5, 2.5, 3.5] |\n",
"| $\\frac{1}{\\rho}$ | 14 d |\n",
"| $S_e$ | 0.7 |\n",
"\n",
"\n",
"t"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 283
},
"colab_type": "code",
"executionInfo": {
"elapsed": 594,
"status": "ok",
"timestamp": 1596387599982,
"user": {
"displayName": "Jeffrey Kantor",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gg_n8V7bVINy02QRuRgOoMo11Ri7NKU3OUKdC1bkQ=s64",
"userId": "09038942003589296665"
},
"user_tz": 300
},
"id": "Nlvxm2wvE-hm",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
},
"outputId": "cab1ce50-2134-4b13-f688-59a4ebaed9a1"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAEKCAYAAADAVygjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd3gc1dX48e9Rr1a3LFm2ZRts425L2BgMSJTQjCGB0GsITiAhkIQU/943QMqbQEghCQm9JRTTAzG9WDbNNi64997lKltylXV+f+yYyGJXGq12drXa83meebQzO+Xcmd09mpk794qqYowxxnghLtIBGGOM6bgsyRhjjPGMJRljjDGesSRjjDHGM5ZkjDHGeCYh0gG4kZ+fr6WlpUEtW1dXR3p6emgDaueszLHByhwb2lLmmTNnblPVghCH1CpRkWRKS0uZMWNGUMtWVVVRUVER2oDaOStzbLAyx4a2lFlE1oQ2mtbz7HKZiHQTkUkislBEFojIrc70XBF5T0SWOX9zvIrBGGNMZHl5T6Ye+LGq9gdOAL4nIv2BnwMfqOqxwAfOuDHGmA7IsySjqptUdZbzeg+wCOgKXAA85cz2FHChVzEYY4yJLAlHszIiUgpMAQYCa1U125kuwM4j402WGQeMAygsLCybMGFCUNuura0lIyMjuMCjlJU5NliZY0NbylxZWTlTVctDHFLrqKqnA5ABzAS+4YzvavL+zpbWUVZWpsGaNGlS0MtGKytzbLAyx4a2lBmYoR7/xrc0ePqcjIgkAi8Dz6jqK87kLSJS5LxfBFR7GYMxxpjI8bJ2mQCPAYtU9U+N3noduNZ5fS3wmlcxGGOMiSwvz2ROAq4GThORL5zhXOBu4EwRWQac4Yx7ompJNRNXHPRq9cYYY1rg2cOYqvoxIAHePt2r7Tb26YrtvLr8EL88UE96clQ8d2qMMR1Kh267rKJPAYfVl2yMMcaEX4dOMmWlOSTHw+SlVrfAGGMioUMnmeSEePrnxVO1ZOuR6tLGGGPCqEMnGYBB+fGs37mPldvqIh2KMcbEnJhIMgCTl2yNcCTGGBN7OnySKUiLo1dBOlVLLckYY0y4dfgkA3BqnwKmrdzO/kOHIx2KMcbElJhIMhV9O3OgvoHPVlpVZmOMCaeYSDIje+aSnBBn92WMMSbMYiLJpCTGc0KvPKbYfRljjAmrmEgyABV9C1i5rY612/dGOhRjjIkZMZNkTu1TANjT/8YYE04xk2R65qfTPTeNyXbJzBhjwiZmkoyIcGqfAj5dsZ0D9VaV2RhjwiFmkgz4LpntPXiYGat3RjoUY4yJCV72jPm4iFSLyPxG04aKyFSnA7MZIjLCq+37M6p3HknxcVQtsfsyxhgTDl6eyTwJnN1k2u+BX6rqUOAOZzxs0pMTOL5njt2XMcaYMPEsyajqFGBH08lAJ+d1FrDRq+0HUtGnM0u31LJx175wb9oYY2JOuO/J3AbcKyLrgD8A48O8fU7te6Qqs53NGGOM18TLzrxEpBSYqKoDnfG/ApNV9WURuQQYp6pnBFh2HDAOoLCwsGzChAlBxVBbW0tGRsaX46rKjyfvo2dWHLcMSwlqne1d0zLHAitzbLAyt05lZeVMVS0PcUito6qeDUApML/ReA3/TWwC7HaznrKyMg3WpEmTvjLt5y/P0YF3vK0H6w8Hvd72zF+ZOzorc2ywMrcOMEM9/I13M4T7ctlG4FTn9WnAsjBvH4DKvp3Zc6Cez1ZYq8zGGOOlBK9WLCLPARVAvoisB+4EbgT+IiIJwH6cy2HhdkqfAjKSE5g4dyOnOM3NGGOMCT3PkoyqXh7grTKvtulWSmI8Z/Yv5O35m/nNhYNISoipZ1KNMSZsYvbX9fwhRezeX8/Hy62WmTHGeCVmk8zoYwrISk1k4pxNkQ7FGGM6rJhNMkkJcZw1oJB3F25h/yFrMNMYY7wQs0kGYMzgYmoP1FNl3TIbY4wnYjrJnNg7j9z0JCbODXvrNsYYExNiOskkxMdx9sAufLComr0H6yMdjjHGdDgxnWQAxgwuYt+hw3y42Jr/N8aYUIv5JDOyZx4FmclWy8wYYzwQ80kmPk44b1ARk5ZUU3vALpkZY0woxXySAd8lswP1Dby/cEukQzHGmA7FkgwwvHsORVkp/GeO1TIzxphQsiQDxDmXzKYs20rN3kORDscYYzoMSzKOMUOKOXRYeWfh5kiHYowxHYYlGceQkiy65aYyca7VMjPGmFCxJOMQEcYMLuaT5dvYUXcw0uEYY0yHYEmmkfMHF3O4Qa0CgDHGhEiLSUZEbhWRTuLzmIjMEpGvuVjucRGpFpH5TabfIiKLRWSBiPy+LcGHWv/iTgzqmsVz09fi6x7bGGNMW7g5k/mWqu4GvgbkAFcDd7tY7kng7MYTRKQSuAAYoqoDgD+0KtowuGJkdxZv3sOstTsjHYoxxkQ9N0lGnL/nAv9S1QWNpgWkqlOAHU0m3wTcraoHnHnaXYNhY4cUk5GcwDPT1kY6FGOMiXrS0mUhEXkC6Ar0BIYA8UCVqpa1uHKRUmCiqg50xr8AXsN3hrMfuF1VPw+w7DhgHEBhYWHZhAkT3JWoidraWjIyMlq1zD8XHOCjDfX8uSKNjKQW82m7E0yZo52VOTZYmVunsrJypqqWhzik1lHVZgd8ZzvDgWxnPA8Y3NJyzrylwPxG4/OBv+E7ExoBrMJJdM0NZWVlGqxJkya1epkFG2q0x88m6qMfrQx6u5EUTJmjnZU5NliZWweYoS5+q70c3FwuexEoAnY7SWm7qs4NMqetB15xyj8daADyg1yXZ/oXd2JY92yenbbGKgAYY0wbuEkyDwBXAMtE5G4R6duG7f0bqAQQkT5AErCtDevzzBUjurNiax3TVzW9rWSMMcatFpOMqr6vqlfiu2S2GnhfRD4VketFJDHQciLyHPAZ0FdE1ovIDcDjQC+nWvME4Fptp6cKYwYXk5liFQCMMaYtEtzMJCJ5wFX4qi/PBp4BRgPXAhX+llHVywOs7qpWRxkBqUnxXDS8hGenrWVH3UFy05MiHZIxxkQdNw9jvgp8BKQB56vqWFV9XlVvATp0NY8rR3bn4OEGXpq5LtKhGGNMVHJzT+avqtpfVX+nqke1HqmRrhrnsWMLMzm+NIdnp62loaFdXtUzxph2zc09mUkiMlBELhGRa44M4QiuPbhyZA9Wb9/LZyu3RzoUY4yJOm4ul92J79mWv+GrGfZ7YKzHcbUbZw/sQk5aIs9aBQBjjGk1N5fLLgZOBzar6vX4nvrP8jSqdiQlMZ6Ly0p4Z8Fmtu45EOlwjDEmqrhJMvtUtQGoF5FOQDXQzduw2pfLR3SnvkF5/nM7mzHGmNZwk2RmiEg28AgwE5iF7/mXmNGrIINT+xTw5Ker2X/ocKTDMcaYqOHmxv/NqrpLVR8EzsT3AOX13ofWvtxU0ZtttQd5cYZVZzbGGLcCPowpIsObe09VZ3kTUvs0smcuw7tn89CUlVw+ojsJ8dapqDHGtKS5J/7/6PxNAcqBOfhaTx4MzABGeRta+yIi3FxxDN/+5wz+M3cjXx9WEumQjDGm3Qv477iqVqpqJbAJGK6q5errQ2YYsCFcAbYnp/XrTN/CTB6oWmEPZxpjjAturvn0VdV5R0ZUdT5wnHchtV9xccJ3K3qxdEstHy5ud516GmNMu+MmycwVkUdFpMIZHgGC7U8m6p0/uJiSnFT+UbXc+poxxpgWuEky1wMLgFudYaEzLSYlxMfxnVN6MWvtLqZZXzPGGNMsN1WY96vqn1X1687wZ1XdH47g2qtvlncjPyOJf1StiHQoxhjTrnlWD1dEHheRaqeDsqbv/VhEVETaXdfLbqQkxnP9ST2ZsnQr8zfURDocY4xpt7x82ONJ4OymE0WkG/A1IKrbaLl6VA8ykxN4wM5mjDEmoIBJRkTGi8iwYFesqlMAfzct/gz8FIjqu+adUhK5alQP3py/iZVbayMdjjHGtEsSqIaUiFwKnIOv1eU5wFvAu6q60/XKRUqBiao60Bm/ADhNVW8VkdVAuapuC7DsOGAcQGFhYdmECRPcbvYotbW1ZGR404FnzQHlx5P3MqoogRsGJXuyjWB4Web2ysocG6zMrVNZWTkz4p1LqmqLA74HMMcDk4ApwB3ACBfLlQLznddpwDQgyxlfDeS72X5ZWZkGa9KkSUEv68adr83XXuPf0GVbdnu6ndbwusztkZU5NliZWweYoS5+Y70cXN2TUdXZ6ut+uRIYg69K87dbmc96Az2BOc5ZTAkwS0S6tHI97cotpx1DamI897y9JNKhGGNMu9PqG/+qultVX1bVca1cbp6qdlbVUlUtBdbja65mc2tjaE/yMpL57qm9eG/hFj5fbc/NGGNMY15WYX4OX78zfUVkvYjc4NW2Iu2G0b0o7JTMb99cZK0AGGNMI54lGVW9XFWLVDVRVUtU9bEm75dqgJv+0SY1KZ4fndmH2Wt38fb8qD4xM8aYkGoxyYjIKyJynohYByrNuGh4Ccd2zuD37yzh0OGGSIdjjDHtgpvE8Q/gCmCZiNwtIn09jikqJcTH8fNz+rFqWx0Tpkf1c6bGGBMybtoue19VrwSG46t2/L6IfCoi14tIotcBRpPT+nVmZM9c7nt/GbUH6iMdjjHGRJyrS2Aikgdch6/a8mzgL/iSznueRRaFRITx5x7H9rqDPDzZmpsxxhg392ReBT7C9zDl+ao6VlWfV9VbgNh69NaFod2yOW9wEY98tIrq3THdWLUxxrg6k/mrqvZ3Hsbc1PgNjXRzBe3UT8/qS31DA39+f1mkQzHGmIhyk2T6i0j2kRERyRGRmz2MKer1yEvnypE9eP7ztcxbb10BGGNil5skc6Oq7joyor4GMm/0LqSO4Ydn9iEvI5nxr86l3qo0G2NilJskEy8icmREROKBJO9C6hiyUhO58/z+zN+wm39+tibS4RhjTES4STJvA8+LyOkicjrwnDPNtOC8QUVU9C3gj+8uYeOufZEOxxhjws5NkvkZvib+b3KGD/B1OmZaICL8+oKBHFblrtcXRDocY4wJOzcPYzao6gOqerEzPKSqh8MRXEfQLTeNW0/vw7sLt/DOAmvXzBgTW9w8J3OSiLwnIktFZKWIrBKRleEIrqP49sk96VuYyV2vL7CWAIwxMcXN5bLHgD8Bo4HjgXLnr3EpMT6O335jEJtq9vOnd5dGOhxjjAkbN0mmRlXfUtVqVd1+ZPA8sg6mrEcOV47szpOfrrJnZ4wxMcNNkpkkIveKyCgRGX5kaGkhEXlcRKpFZH6jafeKyGIRmSsirzZ+yDMW/PTsfuSm27MzxpjY4SbJjMR3iey3wB+d4Q8ulnsSOLvJtPeAgao6GFgKjHcdaQeQlZrIXWN9z848UGUNaBpjOr6ElmZQ1cpgVqyqU0SktMm0dxuNTgUuDmbd0ey8QUW8O2QL932wjJP7FDC0W0ydzBljYoy01Ce9iBTiO4spVtVzRKQ/MKppd8oBli0FJqrqQD/v/Qd4XlWfDrDsOGAcQGFhYdmECRNa2pxftbW1ZGS0r8ai6w4pd3yyj4Q4+OWJqaQkSMsLtUJ7LLPXrMyxwcrcOpWVlTMj3pCxqjY7AG8BlwBznPEEYF5LyznzlgLz/Uz/H+BVnCTX0lBWVqbBmjRpUtDLemnqim1a+vOJ+tMX54R83e21zF6yMscGK3PrADPUxW+sl4ObezL5qvoC0OAkpXog6IcxReQ6YAxwpbMTYtLIXnncXNGb52es4+35m1pewBhjopCbJFPn9IypACJyAhBUHVwRORtfkzRjVXVvMOvoSG47ow+DS7L4+Svz2FxjHZwZYzoeN0nmR8DrQG8R+QT4J3BLSwuJyHPAZ0BfEVkvIjcA9wOZwHsi8oWIPBh86NEvMT6O+y4dyoFDDdz+4hwaGmL2xM4Y00G5qV02S0ROBfoCAixR1UMulrvcz+QWKwvEml4FGdxxfn/GvzKPxz9ZxbdP7hXpkIwxJmRaTDIick2TScNFBFX9p0cxxZzLju/GpMXV/P7tJZzQK4+BXbMiHZIxxoSEm8tlxzcaTgbuAsZ6GFPMERHuvmgwuelJfPfpmeysOxjpkIwxJiTcNPV/S6PhRmA4EFsV1cMgNz2JB68uo3rPAW55brY1O2OM6RDcnMk0VQf0DHUgBoZ2y+Y3Fw7k4+XbuPedJZEOxxhj2szNPZn/4FRfxpeU+gMveBlULLukvBvz1tfw0JSVDOiaxdghxZEOyRhjgtZikuHoxjDrgTWqut6jeAzwizH9Wbx5Nz99aQ7HFGTQv7hTpEMyxpiguLknM7nR8IklGO8lJcTx9yuHk52axHeenmEVAYwxUctN98t7RGS3n2GPiOwOR5CxqHNmCg9cNZwtNQf4wQSrCGCMiU5ubvzfB/wc6AqUAD8D7lPVTFW16zgeGtY9h19fOICPlm3jd28tjnQ4xhjTam7uyYxV1SGNxh8QkTnAHR7FZBq59PjuLNq0h8c+XkVRVoq1CGCMiSpuG8i8UkTiRSRORK7EV43ZhMkvxvTn3EFd+M0bi3h9zsZIh2OMMa65STJX4OtPZoszfNOZZsIkPk740yVDGdEzlx+/8AWfLt8W6ZCMMcYVN7XLVqvqBaqar6oFqnqhqq4OQ2ymkZTEeB65upye+emM+9dMFm60OhfGmPbPTe2yPiLygYjMd8YHi8j/eh+aaSorLZGnvjWCzJQErntiOut2xHyXPMaYds7N5bJHgPHAIQBVnQtc5mVQJrCirFSe+tYI9h86zLVPTLdnaIwx7ZqbJJOmqtObTKtvaSEReVxEqo+cATnTckXkPRFZ5vzNaW3ABvoUZvLotcezfuc+rn/yc/bsb7F7H2OMiQg3SWabiPTmv90vXwy46ZT+SeDsJtN+DnygqscCHzjjJggjeuZy/+XDmL+hhmsfn26JxhjTLrlJMt8DHgL6icgG4Dbguy0tpKpTgB1NJl8APOW8fgq40H2opqmvDejC/VcMZ+76Gq574nNqD7R4gmmMMWElqoH7lReReOAeVb1dRNKBOFXd43rlIqXARFUd6IzvUtVs57UAO4+M+1l2HDAOoLCwsGzChAluN3uU2tpaMjI6dvc3n2+u54E5B+idFcePylM4vL+uw5e5qVg4zk1ZmWNDW8pcWVk5U1XLQxxSqzT7xL+qHhaR0c7rkD6AqaoqIgEznKo+DDwMUF5erhUVFUFtp6qqimCXjRYVwMABm/j+c7N5fHky3zqGDl/mpmLhODdlZY4N0V5mN83KzBaR14EXafSkv6q+EsT2tohIkapuEpEioDqIdRg/zhlUxN+AW56bTU2NcMrJ9aQnuzm8xhjjHTf3ZFKA7cBpwPnOMCbI7b0OXOu8vhZ4Lcj1GD/OHVTEXy8bxvJdDVz/hNU6M8ZEXsB/dUXkHlX9GfCmqr7Y2hWLyHP4ruTki8h64E7gbuAFEbkBWIOvuRoTQucNLmLBgmQenreTSx+aypPfOp7OmSmRDssYE6OaO5M517k5Pz6YFavq5apapKqJqlqiqo+p6nZVPV1Vj1XVM1S1ae0zEwIjihJ47LrjWb29josf+Iw12609U2NMZDSXZN4GdgKDrbOy6HNqnwKevfEE9uw/xEUPfMr8DTWRDskYE4MCJhlV/YlTvfgNVe3UaLDOyqLE0G7ZvPjdE0lOiOeyh6da683GmLBz0wrzBeEIxHjjmM4ZvHzTiRRnp3DdE5/z5jw3jTUYY0xouKldZqJcl6wUXvzOiQwuyeJ7z87i4SkraO4hXGOMCRVLMjEiKy2Rf90wknMHFvHbNxfz4xfnsP/Q4UiHZYzp4CzJxJDUpHjuv2IYPzyjD6/M2sDlj0yles/+SIdljOnA3HRaNk9E5jYZPhKRP4tIXjiCNKEjItx6xrE8cOVwFm/awwX3f2I1z4wxnnFzJvMW8AZwpTP8B5gBbMbXnL+JQucMKuKlm0YhwMUPfsobc61CgDEm9Nw0bnWGqg5vND5PRGap6nARucqrwIz3BhRn8dr3R/Odf83ge8/OYv7G3vz4zD4kxNtVVGNMaLj5NYkXkRFHRkTkeCDeGbUOTKJcQWYyz407gctHdOOBqhVc8cg0NtfYfRpjTGi4STLfBh4TkVUishp4DLjR6V/md14GZ8IjOSGe331jMPddOpT5G2s4968fMXnp1kiHZYzpANw8jPm5qg4ChgJDVHWwqk5X1TpVfcH7EE24XDisK69/fzQFGclc98R0/vjuEg432PM0xpjgtXhPRkSSgYuAUiDB12YmqOqvPI3MRMQxnTP49/dO4q7XF/C3D5fz+eod/PWyYXTuZC05G2Naz83lsteAC/Ddf6lrNJgOKjUpnnsuHswfvzmEOetqOOu+KdYcjTEmKG5ql5Wo6tmeR2LanYvKShjaPZsfPf8FNz8zi68P68pdYweQlZoY6dCMMVHCzZnMpyIyKJQbFZEfisgCEZkvIs+JiF2Laad6F2Tw0k0nctsZx/L6nI2cfd8UPl5mrTkbY9xxk2RGAzNFZInztP88EZkb7AZFpCvwA6BcVQfiqw59WbDrM95LjI/jtjP68OrNJ5KWFM9Vj03jrtcXsO+gtX1mjGmem8tl53i03VQROQSkARs92IYJscEl2bzxg5O5+63FPPnpaqYs3cpvvzGIE3pZ60LGGP8CnsmIyJGOyfYEGIKiqhuAPwBrgU1Ajaq+G+z6THilJMZz19gBPPPtkdQ3KJc9PJWfvTSXXXsPRjo0Y0w7JIH6FRGRiao6RkRWAQpIo7dVVXsFtUGRHOBl4FJgF/Ai8JKqPt1kvnHAOIDCwsKyCRMmBLM5amtrycjICGrZaBWuMh84rLy2/BBvrz5ERiJceVwyI7rEc6SaezjZcY4NVubWqaysnKmq5SEOqVUCJhnPNijyTeBsVb3BGb8GOEFVbw60THl5uc6YMSOo7VVVVVFRURHUstEq3GVesLGG8a/MY+76Gir7FvDrCwdSkpMWtu2DHedYYWVuHRGJeJJx09T/B26mtcJa4AQRSRPfv7ynA4vasD4TYQOKs3j15pP4xZj+TFu1gzP/NIW/T1punaIZY5q9J5MiIrlAvojkiEiuM5QCXYPdoKpOA14CZgHznBgeDnZ9pn2IjxNuGN2Td394Cqf2KeDed5bwtT9P4b2FW6yrZ2NiWHNnMt8BZgL9nL9HhteA+9uyUVW9U1X7qepAVb1aVQ+0ZX2m/SjJSePBq8t4+oaRJCfEceM/Z3DN49NZXh10XRFjTBQLmGRU9S+q2hO4XVV7qWpPZxiiqm1KMqbjG31sPm/eejJ3jOnPF+t2cfZ9H/HriQup2Xso0qEZY8LIzcOYm0UkE0BE/ldEXhGR4S0tZExifBzfGt2TSbdXcHFZCY9/sopT7p3Ew1NW2P0aY2KEmyTzC1XdIyKjgTPw9SfzgLdhmY4kPyOZuy8azBu3nMzQbtn89s3FnP7Hybw8c711JWBMB+cmyRz5l/M84GFVfQNI8i4k01H1L+7EU98awbPfHkluehI/fnEO5/31IyYtqbbKAcZ0UG6SzAYReQjfw5NvOv3LWCfwJmgnHpPPa987ifuvGMa+Q4e5/onPueShz/h0+TZLNsZ0MG6SxSXAO8BZqroLyAV+4mlUpsOLixPGDC7mvR+eyq8vGMC6Hfu44tFpXPrwVD5bsT3S4RljQsRN98t7gWp8rTGDr/OyZV4GZWJHUkIcV48qpeonFfxy7ADWbK/j8kemculDnzF1pSUbY6Kdmyf+7wR+Box3JiUCTwdewpjWS0mM59oTS5n8k0ruPL8/q7bVcdnDU7nkoc/sno0xUczN5bKvA2NxulxW1Y1AppdBmdiVkhjP9Sf1ZMpPK7ljTH/W7djL9U98zjl/+YjXvthA/eGGSIdojGkFN0nmoPr+jVQAEUn3NiRjfMnmW6N7Mvknlfzhm0Oob1BunfAFFX+o4p+frbYO04yJEm6SzAtO7bJsEbkReB941NuwjPFJSojj4rIS3r3tFB6+uoyCzGTueG0BJ93zIX98dwlbdu+PdIjGmGa02DOmqv5BRM4EdgN9gTtU9T3PIzOmkbg44WsDunBm/0Kmr9rBox+v4v5Jy3lw8grOG1TEkNTDVEQ6SGPMV7SYZETkHlX9GfCen2nGhJWIMLJXHiN75bFmex1PfrqaF2es598H6pm48VOuP6mUswZ0ITHeHuUypj1w800808+0c0IdiDGt1SMvnTvPH8Bn40/jin5JbKs9wPefnc2Jd/supW3YtS/SIRoT8wKeyYjITcDNQC8RmdvorUzgE68DM8atzJREvlaayK+vOZXJS6t5Zupa7p+0nL9PWs5p/Tpz5cgenNKngPi48HcLbUysa+5y2bPAW8DvgJ83mr5HVXd4GpUxQYiPE07rV8hp/QpZv3MvE6avY8Ln63h/0ed0zU7lkvJuXFxeQtfs1EiHakzMCJhkVLUGqAEuD/VGRSQbXw21gfiqRn9LVT8L9XZM7CrJSeP2s/ryg9OP5b2FW3h2+hr+/P5S7vtgKaOPyeeb5d34Wv9CUhLjIx2qMR1aizf+PfIX4G1VvVhEkoC0CMVhOrikhDjOG1zEeYOLWLdjLy/NXM9LM9fzg+dm0yklgQuGduXishIGl2QhYpfTjAm1sCcZEckCTgGuA1DVg8DBcMdhYk+33DR+eGYfbj39WD5buZ0XZqzj+Rnr+NfUNfTKT+fCYV25cGhXuufZ/zzGhIqEu00oERkKPAwsBIYAM4FbVbWuyXzjgHEAhYWFZRMmTAhqe7W1tWRkZLQp5mhjZXav7pAyY0s9n22sZ/EOX5M1x2THcWJxAsd3SSAzqf2e3dhxjg1tKXNlZeVMVS0PcUitEokkUw5MBU5S1Wki8hdgt6r+ItAy5eXlOmPGjKC2V1VVRUVFRVDLRisrc3A27NrH619s5NXZ61m6pZb4OOGkY/IZM6iIswZ0ISstMTTBhogd59jQljKLSMSTTCTuyawH1qvqNGf8JY6uvWZMRHTNTuWmit5899ReLNq0h//M3cgbczfx05fn8j//nsfoY/I5b3AxZ/YvJCu1fSUcY9qrsCcZVd0sIutEpK+qLgFOx3fpzJh2QUToX9yJ/sWd+OlZfZm/YTcT5xjRRIwAABQuSURBVG5k4txNTHpxDonxwom98znLaeamIDM50iEb025FqnbZLcAzTs2ylcD1EYrDmGaJCINKshhUksXPz+nHnPU1vDlvE+8s2Mz/e3Ue//PveZT3yOGsAV04a0AXuuVapQFjGotIklHVL4CIXic0prVEhKHdshnaLZvx5/Rj8eY9vLNgM2/P38xv3ljEb95YRL8umZx+XGdO61fI0G7Z1sqAiXmROpMxJqqJCMcVdeK4ok7cdkYf1myv490FW3h/0RYenLySv09aQV56EpX9OnPGcZ0ZfWwBGcn2dTOxxz71xoRAj7x0bjylFzee0ouavYeoWlrNB4uqeXfBZl6auZ6EOKG8NIeKvp2p6FtA38JMe/jTxARLMsaEWFZaIhcM7coFQ7ty6HADM1bvpGppNZOXbOXutxZz91uL6dIphVP7FHBKnwJOOiaP7LSkSIdtjCcsyRjjocT4OEb1zmNU7zzGn3Mcm2v2M3lpNZOXbuXN+Zt4fsY6RGBQ1yxGH5PP6GPzKeuRQ3KCtalmOgZLMsaEUZesFC49vjuXHt+d+sMNzFm/i4+WbePjZdt4aMpK/lG1gpTEOI4vzeXE3vmM6p3HwOJOJFgnbCZKWZIxJkIS4uMo65FLWY9cbjujD3v2H2Lqyh18vGwrn67Yzj1vLwYgMzmBET1zGdU7jxN65XFcUSertWaihiUZY9qJzJREzuxfyJn9CwGo3rOfqSt38NmK7UxduZ0PFlc78yVwfGku+Q0H6dRrJ4O6Zll306bdsiRjTDvVOTOFsUOKGTukGIBNNfuYunI701ftZPqq7Xy49RAvLP2U1MR4hvfIpqxHLuU9chjWPZvMFGv2xrQPlmSMiRJFWal8fVgJXx9WAsBr70wiqbgf01btYNqqHdz/4TIaFOIE+nbpRHmPHMpLcxjePYeSnFSrMm0iwpKMMVEqK1moGFTEOYOKANiz/xCz1+5ixpqdzFyzg5dnredfU9cAkJ+RzLDu2Qzrns3w7jkMLskiLcm+/sZ79ikzpoPITEnkFOfZG4D6ww0s3ryH2et2MXvNTmav28V7C7cAEB8n9CnMZGi3LAaXZDOkJJs+hRlWi82EnCUZYzqohPg4BnbNYmDXLK4+oQcAO+sO8sW6Xcxau9Np7HMzz01fB0BKYhwDi32NgQ4uyWJQ1yx65mdYTTbTJpZkjIkhOU57apX9OgOgqqzZvpc563cxZ10Nc9bv4rnpa3niE18voWlJ8Qwo7sTArr6kM6A4i94F6XbGY1yzJGNMDBMRSvPTKc1P54KhXQHfZbYVW+uYt6GG+RtqmLehxpd4DvkST1JCHP26ZDKguBP9i7MYUNyJfl0y7R6P8cs+FcaYoyTEx9G3SyZ9u2RycZmvJlv94QZWbqtjwcYaFmzYzYKNu3lj7qYvL7WJQGleOscVZdKvSyenhepMumZbrbZYF7EkIyLxwAxgg6qOiVQcxpiWJcTH0acwkz6FmXx9mG+aqrJh1z4WbNzNok27WbxpDws27ubNeZu/XC4zOYE+TsLqW+j7269LpjUIGkMieSZzK7AI6BTBGIwxQRIRSnLSKMlJ46wBXb6cXnugniWb97Bo026WbN7Dks17mDhnI8/ur/9ynoLMZPoUZnBs50wneWVwbGEmWan2EGlHE5EkIyIlwHnA/wE/ikQMxhhvZCQnUNYjh7IeOV9OU1W27D7A4s2+xLN0Sy3Lqvfw/Ofr2Hfo8Jfzdc5M5pjOGV8ZCjKS7bJblBJVDf9GRV4CfgdkArf7u1wmIuOAcQCFhYVlEyZMCGpbtbW1ZGRktCHa6GNljg0docwNqmzfp2yobWBjbQMbapVNdb7X+/+be0hLgC7pcRQkH6ZbVhJFGXF0SY+jME1I6OBVrNtynCsrK2eqakS7ug/7mYyIjAGqVXWmiFQEmk9VHwYeBigvL9eKioCzNquqqopgl41WVubY0JHLfOTMZ3l1Lcur97B8ay0rt9axcP0OplUf+nK++DihJCeVnvnp9MxPp1d+Oj3zMyjNT6M4K5W4DpCAov04R+Jy2UnAWBE5F0gBOonI06p6VQRiMca0QyJCl6wUumSlMPrY/C+nV1VVUT5qNKu21rFiay0rt9ayclsdq7bVMX3VDvYe/O/pT1JCHD1y0+iRl07PfN/f0rx0euSlUZydag+ZhknYk4yqjgfGAzhnMrdbgjHGuJWRnMCgEl/LBI2pKtV7DrByqy/prN5ex+ptdazZvpePlm3lQH3Dl/MmxvsqLXTPTaNH3pG/6XTPTaNbbqo98xNCtieNMR2CiFDYKYXCTimM6p131HsNDcqWPftZta2Otdv3smbHXtZu38vq7XXMWrOTPQfqj5o/PyOZbrmpdM/1JaCSnFS6OTXpirJTrP+eVohoklHVKqAqkjEYYzq+uDihKCuVoqxUTux99Huqys69h1izvY51O/exbsde37BzL7PW7mTi3E0cbvhvBak48XW70DUnlZKcVEqyUynJSaNrTipds1Mpyk4hOSE+zCVsv+xMxhgT00SE3PQkctOTGNY95yvv1x9uYFPNftbt3Mv6nftYv8P3d93OvUxdsZ3Nu/fTKAch4quKXZydSnG2LwkVfzmkUJyVSnZaYsxUybYkY4wxzUiIj6NbbhrdctP8vn/ocAOba/b7EtDOvWzYtY8NO/exsWYfCzfu5r2FWzjY6H4QQGpiPEVZKRRnp1KUlULRkb9ZKRRlpdIlK4VOKQkdIhFZkjHGmDZIPCoJ5X3lfVVlW+1BNu7a5xtq9rNp1z421exnY80+Plq2jS179tP0kcW0pHi6ZKVwSc/DVISlJN6wJGOMMR4SEQoykynITGZIt2y/8xw63MDWPQfYVLOfTTX72Fyzn001+9lcs5+MxF1hjji0LMkYY0yEJcbHfXnfBo6+L1RVVRWRmELF6uEZY4zxjCUZY4wxnrEkY4wxxjOWZIwxxnjGkowxxhjPWJIxxhjjGUsyxhhjPGNJxhhjjGci0v1ya4nIVmBNkIvnA9tCGE40sDLHBitzbGhLmXuoakEog2mtqEgybSEiMyLdx3W4WZljg5U5NkR7me1ymTHGGM9YkjHGGOOZWEgyD0c6gAiwMscGK3NsiOoyd/h7MsYYYyInFs5kjDHGRIglGWOMMZ7pEElGRB4XkWoRmR/g/QoRqRGRL5zhjnDHGGoi0k1EJonIQhFZICK3+plHROSvIrJcROaKyPBIxBoqLsvcoY61iKSIyHQRmeOU+Zd+5kkWkeed4zxNRErDH2louCzvdSKytdEx/nYkYg01EYkXkdkiMtHPe1F7jDtKz5hPAvcD/2xmno9UdUx4wgmLeuDHqjpLRDKBmSLynqoubDTPOcCxzjASeMD5G63clBk61rE+AJymqrUikgh8LCJvqerURvPcAOxU1WNE5DLgHuDSSAQbAm7KC/C8qn4/AvF56VZgEdDJz3tRe4w7xJmMqk4BdkQ6jnBS1U2qOst5vQffh7Nrk9kuAP6pPlOBbBEpCnOoIeOyzB2Kc+xqndFEZ2haW+cC4Cnn9UvA6SIiYQoxpFyWt8MRkRLgPODRALNE7THuEEnGpVHOKfhbIjIg0sGEknPqPAyY1uStrsC6RuPr6SA/ys2UGTrYsXYuo3wBVAPvqWrA46yq9UANkBfeKEPHRXkBLnIuAb8kIt3CHKIX7gN+CjQEeD9qj3GsJJlZ+NrwGQL8Dfh3hOMJGRHJAF4GblPV3ZGOJxxaKHOHO9aqelhVhwIlwAgRGRjpmLzkorz/AUpVdTDwHv/9Dz8qicgYoFpVZ0Y6Fi/ERJJR1d1HTsFV9U0gUUTyIxxWmznXrF8GnlHVV/zMsgFo/F9eiTMtarVU5o56rAFUdRcwCTi7yVtfHmcRSQCygO3hjS70ApVXVber6gFn9FGgLNyxhdhJwFgRWQ1MAE4TkaebzBO1xzgmkoyIdDly/VJERuArd1QcoECc8jwGLFLVPwWY7XXgGqeW2QlAjapuCluQIeamzB3tWItIgYhkO69TgTOBxU1mex241nl9MfChRulT1m7K2+S+4lh89+ailqqOV9USVS0FLsN3/K5qMlvUHuMOUbtMRJ4DKoB8EVkP3InvhiGq+iC+g3KTiNQD+4DLouUANeMk4GpgnnP9GuD/Ad3hy3K/CZwLLAf2AtdHIM5QclPmjnasi4CnRCQeX8J8QVUnisivgBmq+jq+xPsvEVmOrwLMZZELt83clPcHIjIWX23DHcB1EYvWQx3lGFuzMsYYYzwTE5fLjDHGRIYlGWOMMZ6xJGOMMcYzlmSMMcZ4xpKMMcYYz1iSMcYY4xlLMsYYYzzT5iQjIt8Rkc1Og4QrROSaUAQmIj8QkUUi8oy/8VasJ1tEbm4y7dNQxBgpInKXiNwexHJRty9EpFQC9BMU5PqC+hx5QURqW57L73JBH7Ngtxkp/j6z4dpOa/ZzuOJ0K5jPiFe/BW1+GFNE7gfmq+qDTjMeb6pqm9uKEpHFwBmqut7feCvWUwpMVFXPGhV0mjERVQ3UgmpIlxeRu4BaVf1DK7dTisf7ItTaErO//draz1Fbj20L665V1YxQr7e9bbMtwvWZbet2Ai3v5ecnaqhqmwZgClDpvC4ANrZy+auA6cAXwENAPPAgcBCYB/zQz/hXlnHWdQ0wF5gD/MuZNgFf8yJfAPc602qdv3cD32sUy13A7YHiahJ3KbAEX0dpC4AeAcpSiq/tpWfwtbH0EpDmb3lnvT8C5jvDbY229z/AUuBj4Dngdmcd8xvNcztwVzD7ItC2nW0sAh5x4nwXSPWzL/zOEyjGRvvlSadczwBnAJ8Ay4ARjZb/yv5r5rPjd7868x/1OWqhzH7X0cx2j3f2dwqQ7iw3MNCxaPI5DLSP0oE3nOXmA5e29fPbaNlfcfTn6/+AW/18P/8NzHTKM86Z9pW4Aq2vrccZ/5/ZQMesxe00U6aWvht+j2Gj9xsv/yL+v9v+tluKn+9OgH3cmjLWNnOsmv1cteW3wO9vfAiSzE6gGBDgl8D1zvScRvO8CRT7WfY4fM12Jzrj/wCucV6vBvIbzbsayA+0DDDA2fH5zvRcf1/gJgdgGDC50fSF+Fo6DRhXkx/WBuCE5srizKfASc70x/lvgvhyeee9Mnw/gOlAhnMghzWanoav17zlNJNkgtwXgbZdiq+NqKHOfC8AV/nZF37naSbGI8sMwnfZdqazbwRfB03/brS8v/3X3P4+ar82iXV1o/3SXJn9riPQdp3XvwH+APwdGO9M83ssmuz7QPvoIuCRRtOz2vr5bbLNWc7rOGAFkOenvEc+O6n4fnDy/MUVaH0hOM5N901Ln9Nmt9NMmY7aTpN9FfAYNvkOzPf32+Biu1/57jSzj92W8Ujs/tbT0ucq6N8Cf0Ob7sk4nQVl4ksi1cBofFkW4M9H5lPVc1V1o59VnO4U6HOnwcPTgV4tbDbQMqcBL6rqNmebLfaUqaqzgc4iUiwiQ/B1b7quFXGt0f92C9vcMutU9RPn9dP49lPT5XGmv6qqdeprrv4V4GRneFVV96qv/5TXWyhaq/dFM9sGWKWqRxqknInvw9aUm3n8LTNPfZcSFgAfqO/TO6/J8v72X3P7u+l+DaS5MgdaR3Pb/RW+VoPLgd8704I5FkfMA84UkXtE5GRVrWn8Zls+v6q6GtguIsOArwGzVdVfa9U/EJE5wFR8CexYf3G1sL62HOemWvqcutmOvzI1J5hj6O/zE2i7/r47gY692zIe4W89zX6uaPtvwVHa2grzIGCKqp4mIjn4svMoEekE9BORn6jqvc0sL8BTqjq+Fdv0u4yI3NLa4B0v4mu5twvwfCvjqnMRVylf7T72yHgdbVPP0ZU3Utq4vkAONHp9GN9/Ym7naS7Gxss0NBpv4OjPpr/919z+but+pZl1NPfZyMP3n18ivnK6jcPvPlLVpSIyHF9L2r8RkQ9U9VdNlm3L5/dRfC0Yd8H3H/FRRKQC3+WYUaq6V0SqgJRm4gq0vrYc59ZocTuBytTK7bhx1LFvYbtf+e7428f4Lr+53ZdA4M+Qi89VIG5+C47S1tplg4HZAKq6E3gWXz/V24CnW0gwAB8AF4tIZwARyRWRHkEu8yHwTRHJOzLdmX8PvrOtQJ7H12z2xfi+sKGOC6C7iIxyXl+B776KPx8BF4pImoikA193pk1xpqeKSCZwvjP/Fnz/yeaJSDIwxpkezL4ItO22ChRja/jbf8Eco6aCKXNz230I+AW+a+X3ONMCHYvG/O4jESkG9qrq08C9wHA/y7bl8/sqvg7Bjgfe8fN+Fr6zo70i0g84oYW4WlpfS/wd56af2bZ+Tv2Wyc92GnNzDFv6nQm0Xb9cHvsW+VuPi3WH9LcgFGcybzUa/w/wF3zXY+ccmSgibwLfbnrJTFUXisj/Au+KSBxwCPgesCbQBgMto6pTReT/gMkichhf8rtOVbeLyCfiqwb7lqr+pMn6Fjg/3BvU6dArlHEBm/HdBPyeiDyO77r5A0BnP+uYJSJP4rthC/Coc0kEEXne2afVwOfO/IfE1+fEdHw95y1uVKZW7YtA23bODIIWKMZW+sr+c76sgfa329haXeZAx1lETgUOqeqz4usL5VMROU1VP/R3LJqsM9A+GgTcKyINznZu8hNP0J9fVT0oIpOAXap62E9x3wa+KyKL8B2DI5d//MblYn0tCXScj/rMtvFz6rdMLXw3/H6fGq+0yfL+OlELtC8DafHYu+RvPc2uO9S/BZ70JyO+DoUuAu5W1ajuta6tJAqrDZvY4CSgWcA3VXVZJNdn35OOy5Mn/lX1dVW9NtYTjDHtlYj0x1dL8YMQJZiQrs90HNYzpjHGGM9Y22XGGGM8Y0nGGGOMZyzJGGOM8YwlGWOMMZ6xJGOMMcYzlmSMMcZ4xpKMMcYYz/x/rJs5xdYIBCIAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"\n",
"Rt = np.linspace(1.5, 4.0)\n",
"Se = 0.7\n",
"rho = 1/14.0\n",
"psi = 0.3\n",
"\n",
"tau = (Rt - 1)*rho/(1 - psi)\n",
"plt.plot(Rt, 1.0/tau)\n",
"\n",
"plt.xlabel('$R_t$: effective reproduction number for exclusively asymptomatic transmission')\n",
"plt.ylabel('testing frequency / days')\n",
"plt.grid(True)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 639
},
"colab_type": "code",
"executionInfo": {
"elapsed": 1993,
"status": "ok",
"timestamp": 1596386957000,
"user": {
"displayName": "Jeffrey Kantor",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gg_n8V7bVINy02QRuRgOoMo11Ri7NKU3OUKdC1bkQ=s64",
"userId": "09038942003589296665"
},
"user_tz": 300
},
"id": "E_Lb57gLbRil",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
},
"outputId": "1a591063-33aa-49a1-dadc-fa9dd2c876d1"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAI4CAYAAAB3HEhGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdd5xdVb3//9fntDnTeybJZEIqJRBCCSFUUUSQ7lWKVFEURLp6lateC+hXxWu513v1609/il4VLCgtgAiKKE1SSEhCmPSZSTK9l1PX94+9J5kME0gyZzIl7+fjcR5n77X3XmudcyaT85m19meZcw4REREREREZvsBod0BERERERGSiUIAlIiIiIiKSIQqwREREREREMkQBloiIiIiISIYowBIREREREckQBVgiIiIiIiIZogBLRGSUmdkPzewLo92P0WZmXWY2axjXrzazMzLYpYwzsw+Z2d9Hqe3TzGzdaLS9P8zsS2b2v6PdDxGRfaUAS0RkGMzsr2bWamZZe3n+m75gO+dudM7dneF+dQ14pM2sd8D+lZlsK1Occ3nOuY3DuP5I59xfM9ilA8YPfvo/n24zc4M+w+n7Uaczszn9+86555xzh2W25zvb+quZ9fl9bTKzB81syki0JSIy1inAEhHZT2Y2AzgNcMCFo9qZQfxgJc85lwdsBS4YUPbL/vPMLDR6vZR+fvDT/3kd6RcXDfjMto5m//bSzX7/DwWKgO+Mcn9EREaFAiwRkf13DfAi8DPg2oEHzKzK/yt+o5k1m9n3zewI4IfASf5f+tv8c39mZvf422vN7PwB9YT8Oo7z9xeb2fNm1mZmr+7rlDgzO8PMas3sM2a2A/ipmRWb2aN+O63+9rQB1/zVzO42s3+YWaeZ/cnMyvxjUTP7X/81tpnZP82sYsB19/j97TKzR8ys1Mx+aWYd/rkzBrSzc8TFzM41szV+e3Vm9im/vMzvX5uZtZjZc2YW8I9tNrN3+9tZZvZdM9vmP77bP8o44D34pJk1mNl2M7vuLd6z6/zPpdPMNprZDUO8n0PW5b/eh/3X+zIwe18+L7+OQjP7iV93nf+eBv1jc8zsWTNr90eOHvDL/+Zf/qr/3l/W39cB9W42s0+Z2Ur/+gfMLDrg+L/6bW4zs+tt0IjYnjjnWoDfA0f59Zzsf9bt/vPJA9qY6r8/LWa23sw+uq/vj4jIWKMAS0Rk/10D/NJ/nD0gsAgCjwJbgBlAJXC/c24tcCPwgj8qUTREnb8GPjhg/2ygyTm3zMwqgceAe4AS4FPA782sfB/7Pdm//hDgY3j/F/zU358O9ALfH3TNFcB1wCQg4rcNXmBZCFQBpf7r6x1w3eXA1f57MBt4wW+rBFgLfHEPffwJcINzLh/vi/ozfvkngVqgHKgA/g1vBHGwzwGLgWOABcAi4POD3oNCv18fAf7bzIr30JcG4HygwH8PvtMf8O5FXf8N9AFTgA/7j331MyAJzAGOBd4DXO8fuxv4E1AMTAP+C8A5d7p/fIH/s/bAHuq+FDgHmAkcDXwIwMzOAe4E3u23e8bedtYPvt8PLDezEryf2f/E+/n4NvCYmZX6p9+P93lOBT4AfM3M3rW3bYmIjEUKsERE9oOZnYoXkPzGObcU2IAXhID3ZX4q8GnnXLdzrs85t7eJDX4FXGhmOf7+FXhBF8BVwBLn3BLnXNo59xTwCnDuPnY/DXzRORdzzvU655qdc793zvU45zqBrwLvGHTNT51zbzjneoHf4AUuAAm8L85znHMp59xS51zHoOs2OOfagceBDc65PzvnksBv8QKGoSSAeWZW4Jxrdc4tG1A+BTjEOZfwp9YNFWBdCXzFOdfgnGsEvowX6A2s/yt+HUuALmDI+5Occ4/5r8E5557FC2hOe7u6/ED7/cC/+z8HrwH37eH1DskP2s8FbvfraMCbenf5gLYPAabu489Zv/90zm3zR50eYdfneineZ7faOdcDfGlv6jJvVPZVYDtegHYeUO2c+4VzLumc+zXwOnCBmVUBpwCf8fu+Avgx3h8uRETGLQVYIiL751rgT865Jn//V+yaJlgFbPGDiH3inFuPN7JzgR9kXejXDd4X6Uv86XFt/pfZU/ECjn3R6Jzr698xsxwz+79mtsXMOoC/AUX909B8OwZs9wB5/vYvgCeB+/2pZN80s/CAc+sHbPcOsZ/H0N6PF1hs8afAneSX3wusB/7kT9f77B6un4o3gthvi1/Wr3nQ5zPwNe3GzN5rZi/609ja/H6V7UVd5UAIqBnUj31xCBAGtg/4zP8v3kgiwL8CBrxsXhbFfR0h29PnOnVQvwdu78mtzrki51ylc+5KP7Ad/Dng71f6x1r8oH7wMRGRcUs3N4uI7CMzy8b7C3/QvPuYALLwgpIFeF9Gp5tZaIgga6jRlsH6pwkGgDV+0IVf7y+cc8O9T2VwHz6JN3pzonNuh5kdAyzH++L+1hU5l8AbHfqyefdTLQHW4U3x2/8OOvdP4CI/WLsZb9Ssyv8y/kngk2Z2FPCMmf3TOff0oCq24QUnq/396X7ZPvHv2/o93qjKQ865hJn9kb14b4BGvKl9VXijNv392Bc1QAwoGypgd87tAD7q9/VU4M9m9rcBPzP7azvelMN+VftZT//nMNB04An/WImZ5Q8IsqYDdfvZlojImKARLBGRfXcxkALm4U2pOgY4AngO74v4y3hfUL9uZrnmJYI4xb+2HphmZpG3qP9+vPtsPs6u0SuA/8Ub2TrbzIJ+vWfYgIQU+ykfbzSpzb9nZk/3Rb2Jmb3TzOb7o10deFPW0sPpjJlFzOxKMyv0A7iO/jrN7Hw/sYMB7Xifw1Dt/Rr4vJmV+/cE/Tve+7evInjBcyOQNLP34n02b8s5lwIeBL7kjxLOY1AylL2oYzvelMT/MLMCMwuY2WwzeweAmV0y4PNvxQue+9+PemB/1xX7DXCdmR3hj6Tu7zptS4BDzewK8xK2XIb37+ZR51wN8Dzwf/yf5aPx7mHT2lciMq4pwBIR2XfX4t2fstU5t6P/gZcY4kq80Y0L8JIDbMW7if8y/9pn8EZVdphZ05ur3vml+gXgZOCBAeU1wEV4iR0a8UY3Ps3wf5d/F8gGmvCyIj6xD9dOBn6HFwStBZ7FmzY4XFcDm/0pizfiva8Ac4E/493n9ALwP865vwxx/T1496etBFYBy/yyfeKPrNyKF3C04t0T9/A+VHEz3rS7HXjJKn66r33AC9ojwBq/D79j17TQE4CXzKzL79dtA9YS+xJwnz+18NJ9adA59zheYoq/4E3JfNE/FNvHeprxEoR8EmjGm9J4/oCptR/ESwSzDfgD3r2Bf96XNkRExhob+t5gEREREY95Swy8BmTtz72FIiIHE41giYiIyJuY2fvMW0+sGPgG8IiCKxGRt6cAS0RERIZyA94aYBvw7nX7+Oh2R0RkfNAUQRERERERkQzRCJaIiIiIiEiGjOl1sAqKi13hpEm7LTZiA5ZvGVxubzqwq+zNC5a4QeVD7++pbHBfdj9ugNvZuhtQ3L/t/HOHGj8c0H1siJ7bHs/d/aw9HwNzA8/cvfu79t3QxwZ2euA5Q7G3OmqDGhzi+JuO2VBPezh3D+WD+zRo397m+G77e9i2tztnZ5nfP/M/rzcdH6J9ERERERl1S5cubXLOlQ8u36sAy8zuAK7H+2q9CrgOL0Xs/UApsBS42jkX9xdl/DlwPF5K1succ5v9eu7CW+Mihbfi+5Nv1W5W0RSC77t3r16gY+9W7xxp4YAjYo78UJKicJKCUJLCUJKCYIL8YIL8UIJcSxAJpAiTJmxpIpYkYGkskMbMec+A69+3lBecBdI4SwPes7MUmCNtKRxp0qRxpEhbihRpUn5ZwoyEGXGDBEYcSJjznnHESRN3jrhLEfMfCZcilk4QSyeJpePEU3Fi6ThpN/TyNkGMsAuSRYiwCxJ2AbJckLALEnFBwgS8Z+c9R1yAcDqw+3MqQNgZ4bQRSQcIp4xwGkL+czgJwTSEko5QCoJJRyiVJphwBBMpAsk0gUSKQCJJIJ7EEkmIJ7B4HBdLQCyGi8eH/yEPCjCHPpBhZhAMYoEAhELec/9+MIj5j/5tQkEsGPK3/fN3KwtiobB3XTgEfrmFQ975A4+FQlg47JWFQt4jEvbLvGOEw7vO6T8WjuzcDkQi4D9bOIxlZWGhMf33HREREZngnHOQSuHSae85lYZ0CtJpryyd9spcetd5flkwP4/wpElbhqr3bb/hmFkl3hog85xzvWb2G+By4FzgO865+83sh3iB0w/851bn3Bwzuxwv89Bl/gKLlwNHAlPxVps/1F+IccJIpI0ERncqwo7YW60jemCYOQpCKQpDSQpDKQpCSfJDSfKDCQqCCcqDCXIDCfICcfICcXIsTi59ZFsfURcj6vrISveSle4hnO6FVA+JdB+JdJJYKERPOJvecBa9oQg94Sx6QmF6A0F6giF6AgG6zegxRzeOHpei2yVpScfpSvXQnYrRlegmns5A0LO374cLUUCUnHSYgnQW+ekIeekwOekQuSnvkZMMkpMMkJ0MEE1ANA5ZcUckniYcSxPqSxDqSxDsi2O9MejuhZ5eXF/fyHXcOUgmvRAuHh8Tf0wYtkAAi0R2PgL921lZ/nOEQCTL249mecezolhWFoFoFhbxy7Oi3nM0imVFvWPR7F3P2VEsGiXgPywy+v8uRUREDgSXTOJSKe87RDKJS6dxiYQfTKR2304mve1kClJJv2zg9oDjae/ZpYYq678mvft5yf5AxjvmXTvgnHQKUmnveWc9A4KfnUGQX97/3Wjw8bd6HlQ2HEWXXLLHY3v7J+QQkG1mCSAH2A68C2/BRYD78BY0/AHeIphf8st/B3zfvPlSFwH3O+diwCYzWw8swlsoUkaIc0Z7IkR7IrOjBWaOyqw4M3L6mJbVQ2Wkh0nBbooCvZRbD3n0kOe6yEl3EU11Ekl0EI63E+hrw5K9u9WVCEbojBbQHc2jIyuPrqxsOsNROkNZdIRCdASCdJrRbmnaXZLOdJz2VB9tiS46E117HFUb8v0waKeP9mAf24OdGX1PslwWZelcSlJRSlLZlCSzKEqEKUiEKIgHyY1BTq8juy9NVneCcHeMYFcvgY5uXEdnZkbXxpN0GtfXtzMwPWB/aQkGvUArJ5tANJtAtvew7AHbOdkEsnO8/ZwcAjn+8Zwcrzwnh0BuLoGc/uPew8LhA/UqRERkhPQHHi6Z9J7jCUgmdi/buZ3E9R/rD1YSid3KdwY3Cf856ZftPC+JSyUHnJsacJ5fX3+A01+Xfw07rx9wfMC2jI63/dbtnKszs28BW4Fe4E94UwLbBqyHUQtU+tuVQI1/bdLM2vGmEVayayX4wdfsZGYfAz4GkFc6mdz9eFEy8pwzavuyqO3LAgr36dr8UJIZ2TGmRXupyuqhItxDRbCLMuukmA6mx9vI7WklGttOqK+JQF/bHutKW4DO7EJac0toixbQGs2lNRylJRyhJRCgxdK0uAQtqT6a4520xttJjdCgacxS1AU7qAt27Nf1hek8KlP5TE7kMikRpTQWoSQWoqAH8rvTZHfGyeroI9jWBa3tuO7uDL+Cg0QqRbq7G7q7Mx7UWSSyK+DKzfWDsMHb/ft53n5eHoG8XecF8/J2nq9plCIy0bhUCheP+4FLfLftdDwOfqCS3u1YfwAT37U9sI5kcs/7gx/JxG7HSAwOmBLeKIfIMOzNFMFivNGnmUAb8FvgnJHqkHPuR8CPAMpnzpsQM6Fkd53JEKs6Q6zq3LvwOTeYZm5uD7Ozu5kZ7aQq1MHkQBvltFCYbCI31sD0zh3MaNzwtnWlLUBrbilNeWU05RTSEM2jMRyhIWg0kKI+2UN9vJ2WWNvORCQHSnugj/ZAH2vCjXt1fqHL45BEIVXxfKbGspnUE6Kk2yjoSJLT1kekpQuaWnCdXSPcc+nn4nFS8Tiptj3/UWBfWDTqBVt5XsAVzPWDr/4grL98Z1C2q3xnmf9swWBG+iQi44tLp3H+PcguHicdi+Piu/a9sv79/qBn8PmDHon4zoBo1zVvfqQTA477wc9wp2WJjAd78+fRdwObnHONAGb2IHAKUGRmIX8UaxpQ559fB1QBtWYWwhveaB5Q3m/gNSJ71J0KsKIjjxUdeUDFHs8rjSQ4Kr+LeTkdzA63URVsYbKrpzixg5yebQS7thNwKUq7GintauSwt2gzHsyivmgK2wrK2ZZdSF0ki20BqEv3UhtrpbGv5YAHYIO1Wx8rI32sjNRDHt448RCK0/kcmihhRl8+VT1RJnUGKG5PkdvcQ7i+FdfQpGkEY5Tr6yPV10equXnYdVl2th+k5e4aURswWrYriBtwfPCjf3QuOzsDr05kYnPO7Qo2YjFcLOYFK4n4zoAnHYvhdgYwsd0DnVhsV9luQU5sV9DTX09/QDSgvH8ESL/fRQ68vQmwtgKLzSwHb4rgmcArwF+AD+BlErwWeMg//2F//wX/+DPOOWdmDwO/MrNv4yW5mAu8nMHXIge55niYZ5uLeba5GDjkTcezgymOKejimLw2Do80MyNYz5TkNgp7a4h0bMZSu+6BiqRiVDVvpqp585BtxUJR6kqq2FpQwdbsPLaGg2x1cbbEWtnR17RP94WNtNZALy9l1fFS/2zOKbsfD7kAhyWmcnismBld2UxtD1DSnCCnoYNAXb1GwCYI19tLqreXVFPT8CsLBr370wZOgfQDr0BuDrYzENsVkPXfr2ZRfzs7e9d2NIpl53gJSTTSJsPkBRyJnaMsuwU5u426DBylGTSCE4vhEgPKBwQ4Qwczsd2vjcW8qWYiclDam3uwXjKz3wHLgCSwHG8K32PA/WZ2j1/2E/+SnwC/8JNYtOBlDsQ5t9rPQLjGr+cTEy2DoIxtvakgL7QW8kJrIYMDsKxAmtNL2jg5r56jwnXMSG2iuPMNQp1DD7JmJfuY1VDNrIbqNx2LhaJsKZ3BpqIKNkVz2RiEjclONvfsIJaKjcRLG5akpVkdaWB1pAHyeVMANj1VxvzeMg7tyqWqNUhpY4ycumZc7Q79ZfRglUqR7uoi3ZX54NvCYW+0LSvrzc/R6JszSGZleRkns/zy/gyU/dko+x/h8Jufw7svN2ChkLfkQP/SBvLmDGRD3WifSHpZwfr344khbuT3b+YfdK+LSwxxn8zge2cG34cz+P6dgfuJxKDlM0REDjxzY/gXUfnMeS73sr1bB0tkJEzP7uOskkaOz97BXKthSt9GctvXYfF9TzCRsiC1pYewvriS6px83gg6quOtbO3ZMaZGvPZWxAU5Jj6ZBV0lzGoNM7k+Tl5NC65mmwIvGf/MdgVcO9eXC+2+5txQ69L5DzPztoMBb9n3/mPWvxC5eevbDbW4+GDODVil3lv10TnnLb3XvyYLDtLO23bpXdv9aYnT/eu7+GXJ5K71X/oDqAEpkPvLRERkaEWXXMLUe+5e6pxbOPiYAiyRfWTmWFzUwTsL6zkmXMPs5HqKOtYS7G7Yr/p6Izm8UTGXdYUVrImEWZvspLq7jkR6fE4viboQJ/ZVckxHEbMaA5TXdhHeWIdr37/siiIiIiJjzVsFWMoBLLKPnLMBUw0PxbstEebnd3N2yXZOjGxmTmIdRa2rsNjbBxXZ8R4W1LzKgppdZYlghDcqDmV18RRWZUV4LdHGxu66cTHS1WdJns3ewrPZW7ycJEd55fMSU1jcUcERTRGm1PaQVV2La81Mtj0RERGRsUIBlkiGrOrMZVXnHGAO8G7MHO8qaeW9hTUcF3iDaV0ribS9fSp5gHAqzpHbXuPIba9xqV/WFS1g1ZTDWVFYzquW4NXuGroS42ctrDXhRtaUNnrZDg8DzoSjEpWc2j6JI+rDVGxqI1i9defCwyIiIiLjkQIskRHinPF0cwlPN5cAC4BLmJ3TywfKazkt8gaze14l2rIG28tRqby+Dk7a9DIn+ftpC1BdcTivlFexNBxgaU8dLbHxNSL0Wrie18rqoQw4ErJckHf0HMqJzUXM2honf20N6abhpygXEREROVB0D5bIKJoWjXFlxVbOiKxldtdSIq1vzkq4L9ZXHMrLk2byUtj4Z9dWOhPjP8X6MfHJnNFSwbwaKF67DVe3fbS7JCIiIgc5JbkQGSfm53dzVfkGTrVXmdL8IoG+1v2uK2VBVlcexfOllTxvfazs2ERqAqyMcHiijLNbKjlqKxStqsHV719yEREREZH9pQBLZBwKWppLJtfz/rzVHNXzEtnNq4dVX0d2Ic9PP4a/5ebxXPdW2uLtGerp6FoYm8pZjRUcviFGzsoNuK7xc1+aiIiIjE8KsEQmgGMKuvjIpHWcknyJ4oaXsGGkcU9ZkFerFvBM6VSeiTdQ07Mjgz0dPREX5JyuWbyjLp+q1Y1QvVmLjoqIiEjGKcASmWCmRmPcNHU9Z/ESkxr+jiWHl3lv3eQjeHryLJ5KtbG+q+btLxgnZidLeF/jdOa/ESdneTWut3e0uyQiIiITgAIskQmsPJLgpsr1nGfPU17/dywVG1Z9GyYdypNT5/JEsoVN3XUZ6uXoy3MRLm6fw6kbI5Qt3Ui6qWW0uyQiIiLjlAIskYPElGic26e+ztnpZymsf2mvU8DvyetT5rFk8kyWxLZT39uUoV6OPnNwbvccztpSQOXSGmUmFBERkX2iAEvkIHR0QRefrljGSe2PEeoY3rS/tAV45ZDjebhkEk91bqAn2ZOhXo4N7+ydwflbSpj+Si2uZttod0dERETGOAVYIgexoKW5cdpWrg7/hYrtz2DDTNXeE8nlqdmL+WMWvNI+vHW7xqJ39czgws0lVL60GbdDKeBFRETkzRRgiQjgrbP1+ckvcULzQwR6Godd39aymTxYNY8/9tbSHNv/NbvGInNwXvcczl2fR/kL1bi2iZHWXkRERIZPAZaI7CY3mOaz09dycepJ8hteGXZ9iUCYv8w9id/kRHip7Y0M9HBsyXJBLm87nDNWG3kvrcHF46PdJRERERlFCrBEZI/OLW/ik0XPMmv7Eiw5/DTmm8pn88C0I3ioewNdiYm36O+kdC4f3n4ox7zSSmDN+tHujoiIiIwCBVgi8ramZ/fxlWmvcFrrHwl2DT/RQ09WHg/NPYVf0c7m7omZOOLEWCUf3FBB5d/X45qV9l1ERORg8VYBVmg0OiQiY8/W3igfqj6V7OBJ3DV9HZfE/0h282v7XV9OrIsPvvYkl2M8N/skfp6fw0vtE2v64EtZdbw0r47IEUGubj2Gdy5PEnllDaSHlx5fRERExi+NYInIHt0wbSs3hh6heMc/MlLf2inz+NmUGfyp7XWSLpmROseaeYlyrttUxYy/bcQ1Tpy1w0RERGQXTREUkWG5uKKBz+YtoaLuKYzh/87YVjydn804mj90rqMvFctAD8eeiAtyTcsRvHNpnPCytTCGf9eKiIjIvnmrACswGh0SkfHlj/WTWLzhQ1yf+1/UTDsPZ8P71TG1dSv/tvxRntzeyvVF88kL52aop2NH3FL8uPQ1rnzPG3zzjioazjsBy88b7W6JiIjICFOAJSJ77enmEk5bfyXXZn+fmmnnDzvQKulu4rblj/FEzXZuKpxPfnhiBiCvZG3j5qOXc/1NsPyaE7AZVaPdJRERERkhCrBEZJ/9raWI09ZfwXXZ/0Vd5Xtx2LDqK+xt4+MrHuPJrXUTOtBqD/TxfyqXc8kHt/P7m44itugosOG9dyIiIjK2KMASkf3215ZiTtlwNZ/I/x6NU9857Pry+9r5+IrHeKKmjhsK55MbyslAL8emBwpf5+ozX+ebd1TRdM5CLDs62l0SERGRDFCAJSLDtqSxjBM2fpTPFX+LzklvutdznxX0tnPzisd4fFsj1xQdTVYwKwO9HJteydrGTceu4NZbsqm+dBGBstLR7pKIiIgMgwIsEcmYX26fyvytd/L9iq8QL5oz7PqKu5v59PJHebSph38pnk/Qghno5di0PdjJ52Yv46rru3npQwuxmdNHu0siIiKyH/YqwDKzIjP7nZm9bmZrzewkMysxs6fMrNp/LvbPNTP7TzNbb2Yrzey4AfVc659fbWbXjtSLEpHR9a0tc5jf8CUemfZJ0tllw65vclsdX172GL/vCnNG0bwM9HDs6rMk/zFlBZdeto1Hb1xAav5ho90lERER2Qd7O4L1PeAJ59zhwAJgLfBZ4Gnn3FzgaX8f4L3AXP/xMeAHAGZWAnwROBFYBHyxPygTkYknlg5wy/rjObnnWyyffi0uA9P8Zje8wX8tf4Kfpss5smBmBno5djmDnxev5oPnb+C+Ww4ntni+EmKIiIiMA28bYJlZIXA68BMA51zcOdcGXATc5592H3Cxv30R8HPneREoMrMpwNnAU865FudcK/AUcE5GX42IjDk7YhHe98bZXBH5Lg1Tz8xInQu3LOXXr/6Nr0XnUJGBEbKx7rG89Vz9zrX85+0z6HznsRCcuFMlRURExru9GcGaCTQCPzWz5Wb2YzPLBSqcc9v9c3YAFf52JVAz4Ppav2xP5bsxs4+Z2Stm9kpfZ+u+vRoRGbNeaC1k0caP8I3y/5OR+7MMxwVrn+GR9a/z8cL5RCdwIox+f4/W8JHFq7jn9sm0nL0QwuHR7pKIiIgMsjcBVgg4DviBc+5YoJtd0wEBcM45wGWiQ865HznnFjrnFkbzNYNQZKL5Qc0hLGj8Ik9X3YKL5A67vux4DzeteIyHm/s4q/jIDPRw7FsZqefG41bwhdtKaTjvBCyqFO8iIiJjxd4EWLVArXPuJX//d3gBV70/9Q//ucE/XgdUDbh+ml+2p3IROcj0poJ8pPokLnTfZVtlZmYKT2mt4dvLHufHVDA7b1pG6hzr1oWbuPno5Xz6ljy2XbgIy84e7S6JiIgc9N42wHLO7QBqzKw/ldWZwBrgYaA/E+C1wEP+9sPANX42wcVAuz+V8EngPWZW7Ce3eI9fJiIHqVWduZy84Rq+Uf41EoWZSVpx4qZ/8tvV/+TO/CPJmcALFQ+0OdTG7Ucu45O35FJ70SIs5+B43SIiImPR3mYRvAX4pZmtBI4BvgZ8HTjLzKqBd/v7AEuAjcB64P8DbgJwzrUAdwP/9B9f8ctE5CD3g5oZHCnUhdUAACAASURBVNf8ZV6quh4XjAy7vnA6wXUrH+ehxs6DZtogwNZgG3fOW8Ydn8im9mIFWiIiIqPBvNunxqbymfNc7mX3jnY3ROQAOrO0he/m/oz8hlcyVudzs0/iq9EkdT31GatzPJiWLOTON2ZT9adVuN7e0e6OiIjIhFF0ySVMvefupc65hYOP7e0IlojIAfF0cwlH19zBQ5WfwmXlZ6TO0za8wB/feI2PFM0nZKGM1Dke1IbauXOeN3Vw+4WLlAxDRETkAFCAJSJjjnPGbRuO4yL3HzROfWdG6owmerl9+WM80B3h6IJZGalzvNgabOO2I5fxmVvyvayDkeFPwxQREZGhKcASkTFrZUceJ2z8KD+f8nnS2SUZqfPQ+tf5xcq/8dm8Iw6aJBj9NoZaufno5Xz+1hKaz14IoYNnNE9ERORAUYAlImPev2+axznxe9lReVZG6gu4NFeuepI/NnVzatHhGalzPFkXbuLjx63gntsq6DjzOAjovwIREZFM0f+qIjIuvNGdzeIN1/HTKV8gHc3MIuRTWmv4wfI/8bXoHAojBRmpczxZGann+kUr+Y/bq+g59RgwG+0uiYiIjHsKsERkXPnypiO4IPVNWiefkrE6L1j7DA/V1R9UKd0Heimrjg+d9ho/vHU28UVHjXZ3RERExjUFWCIy7qzuzOW4LTfx5LTbcMGsjNRZ2tXIt5c9zrciMynJKspInePNMzmbuerM1/nfm48gPf/Q0e6OiIjIuKQAS0TGJeeMG9afyMdzvkWs5LCM1Xv2umf5Y00dZx+ko1kAD+dXc/n5G3n440fD3Bmj3R0REZFxRQGWiIxrTzSWsrDhc6ytujxjdRZ3N/MtfzSrOFKYsXrHm/8tWsNl76/lr9cfh1VNHe3uiIiIjAsKsERk3OtMhnhv9YV8b9I9pLPLMlbv2eue5Q91O3hX8byM1TneOIP/KV/JlVc2s+yaEwiUlY52l0RERMY0BVgiMmF8Z+sszk18neYpp2esztKuRr637Am+Fp1DfjgvY/WON3FL8fXK5Xzk+hjVly3C8vNHu0siIiJjkgIsEZlQXu/KYeHmG3h82u24UDRj9V6w9hkebGhncVHm7vcaj9qtj8/NWsYtHw9Sd9EiLJq591hERGQiUIAlIhOOc8bH1y/ihmhmE2BMbqvjR8v/zF15RxDNUPbC8WpHsIs75i3j324ppOU9CyEYHO0uiYiIjAkKsERkwvpTU0nGE2AYjitWPclv2tMcVTAzY/WOV9WhZm48fgX33lZJz6kLRrs7IiIio04BlohMaLsnwMhcgoaZjRv4xap/8PHC+QRNozf/zNrGh05bzU9uO5TksUeMdndERERGjQIsETkofGfrLC5Ifp32isUZqzOUTnLTise4L1HA9JwpGat3PHsyZyNXnFPNH26aD3M1wiciIgcfBVgictBY3ZnLcVtv5rmqG3GBUMbqXVDzKr+tfo33F8/PWJ3j3a8L13LZ+2u8NbQqFXyKiMjBQwGWiBxUUi7A1dWn87nCb5DMr8xYvTnxbr607DG+GzrkoF6ceKD+NbSuurqFFVedgJWWjHaXRERERpwCLBE5KP1q+xTO6LyH+qnvzmi9Z1Y/x++3N3LyQZ7OfaCYpfha1XKuvz7OhksWYXm5o90lERGREaMAS0QOWrV9WZy48cMsmXYHLoNp18s7dvDD5X/mM3nziAQiGat3vGsP9HHXnGXc8fEoO84/AYvovRERkYlHAZaIHPRuWn8Ct+d9g0ThjIzVaTiuWvUEv+4KMSevKmP1TgS1oXZunb+cL95aSvu7j9caWiIiMqEowBIRAR6qn8RpbV+irvK9Ga330PrXuX/tUq4oPjqj9U4Ea8KNfPSEV/nOrVX0nqz3R0REJgYFWCIivh2xCKdsuJo/TvsULhTNWL1ZyT7uWvYo/x2YRklWccbqnSheiNZy7TvW8P/fepjW0BIRkXFPAZaIyCC3rz+OT2R/k3jRrIzWe/qG53mwdhunFSmIGMoTuRu44pxqHrzpKNxhmX3vRUREDhQFWCIiQ1jSWMaprV+kdtp5Ga23tKuR/1n+JJ/Nm0dWBhNrTCT3F77O5e/byp8/egw2Y9pod0dERGSfKMASEdmDhliYU9dfyYOVn87olEGAK1c9wa86g0qAsQfO4Edlr/HByxt48bqF2ORJo90lERGRvbLXAZaZBc1suZk96u/PNLOXzGy9mT1gZhG/PMvfX+8fnzGgjrv88nVmdnamX4yIyEi4c8OxIzJlsD8BxgeLlOBhT5KW5tuTV3D1hzpYddUiLVYsIiJj3r6MYN0GrB2w/w3gO865OUAr8BG//CNAq1/+Hf88zGwecDlwJHAO8D9mpty8IjIuLGks45SWzE8ZzEr28W/LH+X7wSpKsooyWvdE0mdJ7q5axvXXx6m+bBFWUDDaXRIRERnSXgVYZjYNOA/4sb9vwLuA3/mn3Adc7G9f5O/jHz/TP/8i4H7nXMw5twlYDyzKxIsQETkQGuPelMFMZxkEeMf6f/D7unpOKTo8o/VONO2BPj43axmfuDHAlvcvwnJzR7tLIiIiu9nbEazvAv8KpP39UqDNOZf092uBSn+7EqgB8I+3++fvLB/imp3M7GNm9oqZvdLX2boPL0VE5MDozzKYKMzslMGyznp+sPwpPp03j0ggktG6J5qGYBefPnQZd9wUZduFi7BoZgNeERGR/fW2AZaZnQ80OOeWHoD+4Jz7kXNuoXNuYTRf68WIyNi0pLGMU9q+SO20czNar+G4ZtUT/Ko7wqw8ZdB7O7Whdm4/chmfuSWfhvNOwCIKTEVEZHTtzQjWKcCFZrYZuB9vauD3gCIzC/nnTAPq/O06oArAP14INA8sH+IaEZFxx8syeNWITBk8bMcaHnh9OZcWz89ovRPVxlArNx+9nM/fWkLTOQshHB7tLomIyEHqbQMs59xdzrlpzrkZeEkqnnHOXQn8BfiAf9q1wEP+9sP+Pv7xZ5xzzi+/3M8yOBOYC7ycsVciIjJKRmph4miily8se4zvhQ6hOFKY0bonqnXhJm46dgVfuq2MlvcshFDo7S8SERHJoOGsg/UZ4E4zW493j9VP/PKfAKV++Z3AZwGcc6uB3wBrgCeATzjnUsNoX0RkzOjPMliT4SyDAO+qfo7fb29kcdFhGa97oloTbuTG41dw922TaDvreAVaIiJywJg3uDQ2lc+c53Ivu3e0uyEisk/+Y/YK/qX+v7Bkb0brdRg/P/psvtddTSKdyGjdE938+CRuXjmF4r+8Csnk218gIiLyFoouuYSp99y91Dm3cPCx4YxgiYjIED654Rg+Fr2XWPGhGa3XcFy78gl+3Z3FbCXA2CerIg3csPBVvnJ7BS1n6x4tEREZOQqwRERGwFNNJSxu+jwbp70v43UftmMND6xdxhXFR2NYxuufyF4L13PjcSv499tKaXrvQmUdFBGRjFOAJSIyQloTId61/hJ+NuULuEheRuvOSvZx17JH+YFNoTxaktG6Dwavh5u46ZgV/Nutxew4/wQsW+toiYhIZijAEhEZYV/adARXBO+lp+zojNd9ysYXeXDLVs4qPjLjdR8MqsPN3Dp/OZ+8JY/aixdhebmj3SURERnnFGCJiBwAL7QWcvz2T7Oy6mpchqf1FfW08O1lj/PV6FzywgoQ9sfWYBt3HrGMT3wixIZLFmHFRaPdJRERGacUYImIHCC9qSAXVr+Xb5V/lXROecbrv3Dt0zzY2MWiwswm1ziYNAS6uWvOMq6/IcmqKxdhFZNGu0siIjLOKMASETnA/rtmBmfHvk7zlNMzXveU1hp+vOJpPpM3j2gwK+P1HyzarY+7py/jquvaeeG647EZVaPdJRERGScUYImIjILq7mwWbr6BJ6bdhstwIGQ4rlr1BL9pT3N0wayM1n2wiVmK70x+lUsv386SGxeQnq/RQREReWsKsERERolzxo3rT+SmnHuJFR+W8fpnNm7g5yuf47aCowgHtO7TcDiDnxWv5vLzN3LfLYfTe8oCCOi/UBEReTP97yAiMsoebyxjYePnWFd1acbrDroU17+6hAe6QszLn5Hx+g9Gj+Wt59rTV/ONOyppOmchFlWKdxER2UUBlojIGNCZDHF29cX8T8WXSUeLM17/3Pp1/PK157lFo1kZszSynZuOXcEdt+Sy4ZJFBMq0HpmIiCjAEhEZU765ZS4Xpb5Je8XijNcdSif52KtL+E1XiPm6NytjakPt3DVnGdd8pJcXrjse5s4Y7S6JiMgoUoAlIjLGrOrM5bitN/NM1SdwIzDaNKd+Hb9Y+RyfylemwUzqCSS8hBgfqOX+m+fRd9LRuk9LROQgpN/8IiJjUMoF+HD1Kdyefy/x4rkZrz/oUly78gkebE1wotbNyrgH89/gmjPWcM8dU9h+wQlYfv5od0lERA4QBVgiImPYQ/WTOKHpC6yp+iAOy3j9Vc2b+fGKP/Pl7EMpiCgIyLSVkXpuO2o513/CsfSaE2D2IaPdJRERGWEKsERExrj2RIhzqy/gyyXfIFEwMl/Q/2XNn3morpH3Fh81IvUf7Nqtj29ULufSS+v45S1H0H3aMRAKjXa3RERkBCjAEhEZJ362bRqL274yYqNZZV0NfHPZEn5oU5mWMznj9Yvnobxqrjv1NT57RzEbLlmEVZSPdpdERCSDFGCJiIwjzfEw51ZfwL+XfJN40ewRaeOUjS/yhzdW8dHC+UrpPoI2hlq5a84yPnhdO4/duIDYoqOUFENEZALQb3IRkXHoF9sqOb7pi7wy/cO4QOanmkUTvdy64jF+12lKgjHCkpbmvuLVXH3m63zpzgq2vH8RNqlstLslIiL7SQGWiMg41ZkM8YE33s1Nud+mu/yYEWljVsN6frziz9wbmcWkqL70j7Q14UY+fegyPvjhDh69cYGX6l33aomIjCsKsERExrnHG8s4uvZTLJl2By5rZDIBnrPurzyy8Q0+XKRpgwdC0tL8vHg115yxhs/eUczrly/CDpk22t0SEZG9oABLRGQCSLkAN60/gfPT32Z75dkj0kZOrIs7lj/GH9od7yg6YkTakDfbGGrl32cu45IrdvCzWw+j5T0Lsfy80e6WiIjsgQIsEZEJZHVnLidtuJZvlX+NROHMEWnjkKaNfH/5k/zQpjI7T6MqB9KS3A3cePwKPnyT46/XH0f8hKMgGBztbomIyAAKsEREJqDv18zgmOav8I+qG3Ch7BFp45SNL/K71S/zudzDKckqGpE2ZGidgRj/U76Sq979OnfdWcrqKxbB3JEJqEVEZN8owBIRmaC6k0GurH4H7w9+lx2V7xmRNkLpJJe/9ice27yZDxfNJyuYNSLtyJ5tCLXw5UOWcekHavjuHTOped8ibErFaHdLROSgpQBLRGSCW9aez+INH+Lu0m/QV3L4iLSR19fBHcsf49GmXi4snk/A9N/LaHg+WsMnD1/Gpdc2c98th9N47glYSfFod0tE5KCi/wFFRA4SP6mrYv6OL/Bg5adJ54xMyvXJbbV8ddlj/LY7qkQYo8gZPJa3nk8sWM4HP9bNbz9xJK3vOR4rKhztromITHhvG2CZWZWZ/cXM1pjZajO7zS8vMbOnzKzafy72y83M/tPM1pvZSjM7bkBd1/rnV5vZtSP3skREZCiJtHHnhmNZ3P0f3iLFI3R/1qH1r/P95U/yi2QpJxTOHZE2ZO8kLc1vC9Zxw/GvcuWNffzhpvm0naVgS0RkpJhz7q1PMJsCTHHOLTOzfGApcDHwIaDFOfd1M/ssUOyc+4yZnQvcApwLnAh8zzl3opmVAK8ACwHn13O8c651T22Xz5znci+7d9gvUkREhnZ0QRffq1jCjNqHMZcesXZemLmI7xfksLJj44i1Ifsm4oJc3DmXd26IUv7KRtJNLaPdJRGRcaPokkuYes/dS51zCwcfe9vl4Z1z24Ht/nanma0FKoGLgDP80+4D/gp8xi//ufMitxfNrMgP0s4AnnLOtQCY2VPAOcCvh/XqRERkv63syOOdHZdyVtm7+WrBH5i07ekRaeekTS9zEvC32Sfzg7wwr3VsGpF2ZO/FLcVvCl7nN8dC8FjjvK4jOHNzHlOX1eLqto9290RExq23DbAGMrMZwLHAS0CFH3wB7AD6UxZVAjUDLqv1y/ZUPriNjwEfA8grnUzuvnRQRET2y1NNJTzV9BEum3Ied2X9jqIdz49IO6dveJ7T8QKt/5sX0YjWGJHC8XBeNQ8fBRwFp/bN5LzacmatasbWbYS3me0iIiK77HWAZWZ5wO+B251zHWa285hzzplZRn77Oud+BPwIvCmCmahTRET2zgPbJ/MAN/OhqRdzZ/h3FNS/PCLt9Adaz89azI8KclnaXj0i7cj++Xu0hr/PqYE5MDcxifc1VjF/XYzoq9W43r7R7p6IyJi2VwGWmYXxgqtfOuce9IvrzWyKc267PwWwwS+vA6oGXD7NL6tj15TC/vK/7n/XRURkpPxs2zR+xu18uLKG20J/oLD+xRFp5+SNL3IysGz6cfyktJy/ta0dkXZk/1WHm/nm1GaYCvnvyOKijqM5eXOE8ldrcdt2jHb3RETGnL1JcmF491i1OOduH1B+L9A8IMlFiXPuX83sPOBmdiW5+E/n3CI/ycVSoD+r4DK8JBd7vKtWSS5ERMaGq6fWcXvWI5Ru/9uItvNGxeHcVzmbJe1rSaaTI9qWDN+JsUrO2VHBoeu6iKxaj4vHR7tLIiIHxFsludibAOtU4DlgFdCfYurf8O7D+g0wHdgCXOqca/EDsu/jJbDoAa5zzr3i1/Vh/1qArzrnfvpWbSvAEhEZWy6Y1Mhn859g6rY/YS41Yu3UF07h17OO47c9m+mId45YO5I5hS7K+e0zWVwTZfLqetymraPdJRGRETOsAGs0KcASERmbTizq4Ivlz3LEjoexRPeItdMbyeGRuafwq0A3G7pqR6wdyby5yVLOa5rG/M1pCldtURp4EZlQFGCJiMiImBaNcXfVK5zW9kdCnXUj2taLMxdxf3EJf21bR2oER89kZJzUN40zG8uZuzFGzmubcR0do90lEZH9Nqx1sERERPakti+L66pPIStwEp+aXs1l7vERyzy4eNPLLN4E9YVTeXDmsfw+vp363qYRaUsy74VoLS9U1UIVBN9hnN47h9MbSpi9qY/s1Qq4RGTi0AiWiIhk1HvKWriz+DkOa1iCxUbu/qmUBfnHrBP5fWEBf2t7g6RTUozxKohxau90Tm0qYc6WBPlra0g3NY92t0RE9khTBEVE5IArjST4TNUazo89Tk7TyhFtqzmvnEdnLeQh10l1l5IrTATHxCdzRksFh9cZJesbYFONFjwWkTFDAZaIiIyqf6lo4KaC55hd/wQWH7mkGACvT5nHI5Nn8XhfLY19SqwwUUxK53JWx3QWNGRTubmLyBtbcZ1do90tETlIKcASEZExYVJWgs9MW83Z8afIa1w+om2lLcDLMxbyRHE5T3Ur3ftEYw4Wx6ZxUlsZc7dD6cZm2FgDSU0VFZGRpwBLRETGnHeUtnJrySssaH+aUMfITutLBMK8MPME/lRYzF8UbE1YeS7CaT1VHN9SwIztKQo2NcGWOkgp66SIZJayCIqIyJjzbHMxzzafBZzFv1Q0cE3BMo5sf5Zwx5aMtxVOJzh9w/OcDiQDIf55yHE8XVzOX3q30dCnZAoTRZfFeTx3A4/nAlXAIih02ZzWPY0FrfkcsiNN0ZZm2FSrkS4RGTEawRIRkTHl3PImri1axYKefxBtXjOibTmMNZVH8dfy6Tyb7mBtZ+aDOxl7oi7E4r5Kjm0vYlZDgNK6LsKb6nDtShUvIntHUwRFRGRcOq6wk4+Uv87i1FJKGl7CUrERba+hcAr/qDyS56JhXuzaQmdCSRQOJoclyljYXc5hrdlMrU9SUNuCbdmGi8dHu2siMsZoiqCIiIxLy9rzWdZ+AnACxeHruXbKVs7Oeo3ZnS8TaduY8fYmtW/nfe3beR/eOlurps3nhdJKXqSXlZ2bSaY1rWwiWxduYl1RExQBM72ykAtwXPwQFnSVMKs1zOT6BLm1LVCzDRKJUe2viIxNGsESEZFx6bjCTq4o3cjiwGtMaf0nwe6GEW2vJ5LLsqqjebmghKXpbtZ0btXixgexkAuwIFHB/O4SZrdlMbkpRf72DoI19bgOTTUUmeg0giUiIhOON7q1AFgAXMm7Slu5qGgTx9saprQtJ9i1PaPt5cS7OXXDC5zq7/dk5bFi6pEsLSxjOX2s6tpK3whPYZSxI2lplka2szSyHYrZOeIFMC1ZyjF95RzWmUdlW4DSxhjZO9qwbfW43r5R67OIHBgKsEREZEJ4prmYZ5qLgeOAq1hY2MlFJVtZFKpmes9qoi2vYy5z6bpzYl2cvOklTvb3E4Ewr089ghXFU1kRNlb2NbCjtzFj7cn4URtqpzavnUfzgCnAEV65OZiTquCo3lJmd+UwpT1ASXOcnPoOAtubNPIlMkEowBIRkQnplfZ8Xmk/EjgSuJjSSILzyxo4PXcrR6SrmdS5JqPrb4XTCebXrmR+7Uqu9ssaCqewatIcVucW8JrFWdOznfa4vkQfrJxBdaiZ6vxmyMcLvgaYnCpiXqyM2b35TOsMU96WpqC5j6zGDtjRoNEvkXFCAZaIiBwUmuNh7ttWyX1UAicBMD27j/eUNnJSdi2Huo1M6l5PpH0DlqFkFpPat3Nm+3bOHFBWVzKdtWWHsDangHWWZF2sSSNdAsCOYBc7crp4JgcoffPxaclSDksUM7Mnj6ldYco7oKA1TrSli0BDK66lFcbwvfUiBwsFWCIictDa2hvlx7VV/Jgq+oOu3FCKd5W0cFLeDuYF66hKbqGwawPBzjqM4X95rWzZSmXLVt49oKw9u4jqSbOpzi9jfSTE+nQvG3sbaYu3D7s9mThqQ+3UhtohmyEDsKjLYm6ihFnxQip7s5ncFaKk05HfFiertZtgcweuuUWLLIuMMAVYIiIiA3QngzzSUM4jDeXA/J3lpZEEpxa3sjCnkcNCO5ie2kpJzwbC7VuGfW9XYW8bC7csZXAqqpbcMjaWHcKmvBI2R7LYTIItiXbqehqUwVDepM+SrIo0sCrSAHlA+ZvPCWJUJcuYFS+iMp7D5J4IZd0BCrrS5LbHyWrrIdDagWtuVRp6kf2kAEtERGQvNMfDPFQ/iYeYhHdflyc/lOS04jZOyGtkXmgHVekaivtqiHZuweLDW6i4pLuJku6mNwVeyUCIbSVVbC2cTE12ATXhMHWWpDbRRV1fE93JnmG1KxNXCsfmUBubQ22Qg7fm1x5MThVxSLKQynguk/uilPaFKOqG/K4U2Z1xIu29BNq7oLUd19t7wF6DyFinAEtERGQYOpMhljSWsaSxjJ3p4nzTs/tYkN/JEdltzAq3UGlNlKWbKIjXE+3ZQaCncb9Gv0LpJNObNjG9adOQx9tzitlWOIVteaVsj+ayPRRiu6WoT/WxI95Oc6yVVAYzKsrEtCPYxY5gF2ThJeV4C/npXKpSBUxJ5lIRz6Y0FqGkN0hBL+T2pMnuShDp6iPY2Uugo4t0W4emKsqEpQBLRERkhGztjbK1N8ojQ83VAsIBx+G5PRye28msrE6qwu1UWBulrpXCVAs58WYifY0Eepv3KfFGYU8rhT2tg8K9XVIWpKmggob8MhqyC2nIyqExFKIpAE0uSVOqh8Z4J63xdgVislc6AzHWBBpZE2707hHbC6XpAiYn86hI5lCWjFISD1MUC5EfM3J7Iac3RVZPknBPnFBXH9bVA13duK5uJfOQMU0BloiIyChJpI1Vnbms6swFJu/xPDPHzOwYs3N6qMrqpjLSTUWwizLrpJgO8tId5KbaiCbaCcXbCfa2YMk9T9kKuhQV7duoaN/2lv1LW4DW3FKa8spozi6gOZpLSzhCczBIs0GrS9Ka7qM12UNrvJMeTU2UfdAc6KE50sPqyL5dFyREaTqHimQupalsSpJZFMUjFCSC5CeC5MYgu88RjaWJ9KaI9CYI9sYJ9sSguwe6e3E9PQrSZMQowBIRERnjnDM29kTZ2BMFSvbqmvxQkunZMSqzYkyO9FEe6qUs1ENxoIfC/8fefcdHVeX/H399pqSQhBZqIIig2OhSVBRZUbArgqKigorIWteCuv501V3WuuvqoqJ+7YUVKxZQQQQBRREQREUFqYEAIUAgIWVm7vn9MUMIUqQkmQTeTx73MXPPOffcz03mccln7rnnWiFpFJDiCkj2CkiObCIhkk8glI+/eANWlIfh8DmP9Pwc0vN3bxr5En8iG1Lrsj65NhuTUtmQkExeMJE8f4CNfh8bDTbiscmF2eSVkB8pZmO4kE2hfEKeJlSQ3RPBscZXwJqEgr3uw5yfuq4Gdb1k6kSSqBNJpGY4SGo4EF1CPpJLjOQQJBU7Eos9gsUegZIwgcIQvqISfMUlUFgMhcXRe9A0KYjEKMESERHZD20KB/hxU4AfN6Xs8bZBn6NZUhEHJRfRJHEzDQJFNAgUkO4vIIVialghya6IRFdMoldIgldI0CsiECmkTriQ9PwN2IZsLFSIRYp3a58l/kQ2JdckPymNgoRkChJqkB9MpMCfwOZAgAKfnwKfj81mbDbHZhyFRNjsRSh0YQq9EIVeCYWREgojRRSFi3DlMK2+7J+cQa5tJte3udz+Gk50idRySdTykqgVSSTVC5IaCZIaCVAjHKBGxEdyxEdS2EdSCBLCkBCCYIlHMOQRCHkESiL4SyL4ikP4SsJYSQiKS0oXV1wMEQ3breqUYImIiMg2Qp7x2+ZkftucDNTZp76CPkftQJjawTBpgTA1/VteQ6T6w9TwhUnxhUj2hUi26JJoIRIjYdK8EPUoIcGFCBIi4EIEXQkBF8LvRV99Xgi/K8EXib43rwTzSsALU2J+ivx+igNBigIJFAUSKQwkUhRbL/QHKfb5KfT7KTQfv9QPRgAAIABJREFURT4fxQZFGEXmKMZRjEeR8yhxEYqdR7ELU+yFCbkwxZEQxV4JYS9MiRfS/WoHuGKLsMYKWOMrqMC/sI0El0iaSyTVSyDFBUnxgtTwgiR7AWp4fpI8P0lhP4mej6SIkRjxEYwYCREIRiAYhkDYEQw7AmGHL+zwhz0CoQi+sIeFPXyhMBaOYKEwFopASSg6KUkoDKEQLhTSJCW7oARLREREKkzIM3JKguSUBOMaR61gmPRgmLrBEHWCIWoFQtTyl8QSvRISiJBqEYIWIWgeQcIEzCNAJLZ4BCyCnwgBF8aPh59I6eJzHp5ByGeEfT5CQDj2PmxGxCBsFi0zR8SMMNFXzxxhg4g5wkCE6PsI0eFw0fdblzAeHhDBIwLRfnCEcYTdllePEB5h5wi5CGHnEXYRIrHXcKws4iJEXISwF47WexFd+aviSiyy9epbHJkLkOyC1CCBROenhhckkQCJzkeiFyDR+Un0/CR4PhJcdAl6PhI8H0HPtlkCESPgQcADvwf+SGzxXGzd4Y84fF40IfRFHL6Ih3mx1+2WCEQ8LBx9JVLmNRyJrUdw4XD0fTnfj1fpCZaZnQo8DviB55xzD1Z2DCIiInJgyQsFyAsFWERSvEMpV4k+j5qBCDUDYdICEVIDEdL8IWr5ItTwhwmah8/Aj8NnHn7Abx4+wIcjYB6Gw28Onzl8ODBw5ohguFhyiDmcGZ5Fh9c5wDPAwCPa3rNYUBati/7J6uF8hofDcHhmpQmcs9g7c3ixTZ05IBqLP5bQ+szDZxGMCGYehkfEHB7R7VwswYzGQbTcuej7bV6j5d7WyEr/lb530Zi21kTfey72c3Fumzq21LGD7VzZVtFanIv+LJ0Hzivdb8RtefVKXz0XjcyL1XnOlV4l9WLbEjseL7adK2275SdacZzBZguxmdi9Z/4K32UF8RNwPgL4SCRA0PkJOh9BYq+xJYCfgLPS+s6tasLwHfdYqQmWmfmBJ4FTgCzgWzP7wDn3U2XGISIiIrI/KPZ85JT44n6FUPZO0Oeo4Y+Q6o+Q5PPwG7GEN5qvRHNYh8XKDWNL6hotK9tma91WLrqVbUn+LJbURusww8X62VKPsR23pT1E22xJHS0aU9Ag0R8h0RchyR8hwecImkeCL4Lf55XuzyO6vy2JdiztLI3a27IeO7Cy9ca269FkfMtR/q6N/f4nsfW67JZX266mzM8ldpw+gwSLEPB50SvaFr2S7TOPhKQW2/+gYir7ClYXYKFzbhGAmb0BnAMowRIRERGRA0rIM/K86NVVqV4u6pK507rK/m02AZaXWc8CupZtYGZDgCGx1eK1D535QyXFJge2esDaeAch+z19zqQy6HMmlUWfNakMVfJzFrvH6aAd1VW5dNk59yzwLICZzXTOdYpzSHIA0GdNKoM+Z1IZ9DmTyqLPmlSG6vg581Xy/lYAZa+nNY2ViYiIiIiIVHuVnWB9CxxqZgebWQJwIfBBJccgIiIiIiJSISp1iKBzLmxm1wGfEp0c5QXn3I+72OTZyolMRJ81qRT6nEll0OdMKos+a1IZqt3nzFw5P1hLRERERETkQFXZQwRFRERERET2W0qwREREREREykmVTbDM7FQz+8XMFprZHfGOR/YPZpZpZpPM7Ccz+9HMboyV1zWzCWa2IPZaJ96xSvVnZn4z+87MPoqtH2xm38TOa6Njk/2I7BMzq21mb5vZz2Y238yO1TlNypuZ3RT7f/MHM/ufmSXpnCblwcxeMLM1ZvZDmbIdnsMs6r+xz9z3ZtYxfpHvXJVMsMzMDzwJnAYcCVxkZkfGNyrZT4SBW5xzRwLHANfGPlt3ABOdc4cCE2PrIvvqRmB+mfWHgP845w4B1gNXxiUq2d88DnzinDscaEf0M6dzmpQbM2sC3AB0cs61JjpR2YXonCbl4yXg1N+V7ewcdhpwaGwZAoyspBj3SJVMsIAuwELn3CLnXAnwBnBOnGOS/YBzLts5Nzv2fhPRP0SaEP18vRxr9jJwbnwilP2FmTUFzgCei60bcBLwdqyJPmeyz8ysFtAdeB7AOVfinNuAzmlS/gJAspkFgBpANjqnSTlwzk0B1v2ueGfnsHOAV1zU10BtM2tcOZHuvqqaYDUBlpdZz4qViZQbM2sOdAC+ARo657JjVauAhnEKS/YfjwG3AV5sPR3Y4JwLx9Z1XpPycDCQA7wYG476nJmloHOalCPn3ArgX8AyoolVHjALndOk4uzsHFYtcoSqmmCJVCgzSwXeAf7inNtYts5Fn12g5xfIXjOzM4E1zrlZ8Y5F9nsBoCMw0jnXASjgd8MBdU6TfRW7/+Ucogl9BpDC9kO6RCpEdTyHVdUEawWQWWa9aaxMZJ+ZWZBocvW6c+7dWPHqLZeYY69r4hWf7Be6AWeb2RKiQ5xPInqfTO3Y8BrQeU3KRxaQ5Zz7Jrb+NtGES+c0KU8nA4udcznOuRDwLtHznM5pUlF2dg6rFjlCVU2wvgUOjc1Ok0D0RsoP4hyT7Adi98E8D8x3zj1apuoDYGDs/UDg/cqOTfYfzrm/OueaOueaEz1/fe6cGwBMAvrFmulzJvvMObcKWG5mh8WKegI/oXOalK9lwDFmViP2/+iWz5nOaVJRdnYO+wC4LDab4DFAXpmhhFWGRa+6VT1mdjrRexj8wAvOuX/GOSTZD5jZ8cBUYB5b7425k+h9WG8CzYClwAXOud/fcCmyx8ysB3Crc+5MM2tB9IpWXeA74BLnXHE845Pqz8zaE51MJQFYBFxO9AtUndOk3JjZfUB/orPxfgcMJnrvi85psk/M7H9AD6AesBq4BxjDDs5hsQT/CaJDVDcDlzvnZsYj7l2psgmWiIiIiIhIdVNVhwiKiIiIiIhUO0qwREREREREyokSLBERERERkXKiBEtERERERKScKMESEREREREpJ0qwREREREREyokSLBERERERkXKiBEtERERERKScKMESEREREREpJ0qwREREREREyokSLBERERERkXKiBEtERERERKScKMESEZEqx8wmm9ngvdy2mZnlm5m/vOOqCPtyrCIiUvUowRIRkXJlZkvM7OR47c85t8w5l+qci1TAvpyZFcQSuBVm9mh1SeRERKRyKMESERHZM+2cc6lAT+Bi4Ko4xyMiIlWIEiwREakwZnaImX1hZnlmttbMRpepO87Mvo3VfWtmx+2kj5Zm9rmZ5cb6eN3MasfqXgWaAR/GrirdZmbNY1eaArE2GWb2gZmtM7OFZnZVmb7vNbM3zewVM9tkZj+aWafdOTbn3M/AVKB1rK+rYv2vi+0vY0+PVUREqj8lWCIiUpH+AYwH6gBNgREAZlYXGAv8F0gHHgXGmln6Dvow4AEgAzgCyATuBXDOXQosA86KDQt8eAfbvwFkxbbvB9xvZieVqT871qY28AHwxO4cmJkdCZwAfBfr7wHgAqAxsDTW554eq4iIVHNKsEREpCKFgIOADOdckXNuWqz8DGCBc+5V51zYOfc/4GfgrN934Jxb6Jyb4Jwrds7lEE1QTtydnZtZJtANuD22/znAc8BlZZpNc86Ni92z9SrQ7g+6nW1m64EPY329CAwAXnDOzXbOFQN/BY41s+Z7cqwiIlL9KcESEZGKdBvRK1AzYsPvroiVZxC9ylPWUqDJ7zsws4Zm9kZsUomNwGtAvd3cfwawzjm3aRf7WVXm/WYgacvwwp3o6Jyr45xr6Zy7yznn/f54nHP5QG5sP7t9rCIiUv0pwRIRkQrjnFvlnLvKOZcBXA08ZWaHACuJXtkqqxmwYgfd3A84oI1zriZwCdGkrXQ3uwhhJVDXzNJ2Yz/7YpvjMbMUosMBV/y+rgJjEBGRKkAJloiIVBgzO9/MmsZW1xNNhjxgHNDKzC42s4CZ9QeOBD7aQTdpQD6QZ2ZNgGG/q18NtNjR/p1zy4GvgAfMLMnM2gJXEr0KVp7+B1xuZu3NLJFoUviNc24Je3asIiJSzSnBEhGRitQZ+MbM8olOIHGjc26Rcy4XOBO4hehQutuAM51za3fQx31ARyCP6GQR7/6u/gHgLjPbYGa37mD7i4DmRK8kvQfc45z7bJ+PrIxYf3cD7wDZQEvgwljdnhyriIhUc+bcrkZWiIiIiIiIyO7SFSwREREREZFyogRLRERERESknCjBEhERERERKSdKsERERERERMrJrh6kGHf16tVzzZs3j3cYIiIiIiIi25g1a9Za51z935dX6QSrefPmzJw5M95hiIiIiIiIbMPMlu6oXEMERUREREREyokSLBERERERkXKyTwmWmS0xs3lmNsfMZsbK6prZBDNbEHutEys3M/uvmS00s+/NrGN5HICIiIiIiEhVUR73YP3JObe2zPodwETn3INmdkds/XbgNODQ2NIVGBl73SOhUIisrCyKior2PXIpN0lJSTRt2pRgMBjvUERERERE4qYiJrk4B+gRe/8yMJlognUO8IpzzgFfm1ltM2vsnMvek86zsrJIS0ujefPmmFk5hi17yzlHbm4uWVlZHHzwwfEOR0Sk6nIOV7gBK9kExZtwxQUQLoRwCXhhDC/aDMP8QZwvCIEkLKEGLiEFEmthybXBX6XnqBIROaDt6xnaAePNzAHPOOeeBRqWSZpWAQ1j75sAy8tsmxUr2ybBMrMhwBCAZs2abbfDoqIiJVdVjJmRnp5OTk5OvEMREYmvjdm43IWwfglsWAZ5K2DjCihYDQVrsc3rMBcpbb6z/8lsB/XbtE2sCTXSIaU+pDXCpTbCajeFWk2hdnOo0xxS0svxwEREZHfta4J1vHNuhZk1ACaY2c9lK51zLpZ87bZYkvYsQKdOnXa4rZKrqke/ExE5oBRvwq2cA6vmYat/xK35EVu7EEo27TRpKt/9b4wu6xcDO0nUkmpB3ZZQrxWuXius4ZHQ4Eioc1BlRCgicsDapwTLObci9rrGzN4DugCrtwz9M7PGwJpY8xVAZpnNm8bKREREqjS3diEs/RKWfQMrZ2JrF2DOK62vkl8xFeXBytmwcvbvrn7VgkZtoHE7yGiPy+iI1TskXlGKiOx39jrBMrMUwOec2xR73wv4O/ABMBB4MPb6fmyTD4DrzOwNopNb5O3p/Vc70vyOsfvaxTaWPHjGbrX75z//yahRo/D7/fh8Pp555hm6dt3jOTv+0IYNGxg1ahTXXHNNufdd1uTJk0lISOC4444D4Omnn6ZGjRpcdtllFbpfEZEqadMq3MKJ8NskWDIVy18V74jKT3EeLJ0WXYglh8l1oGlnyOwCzY6FJkdDMDmuYYqIVFf7cgWrIfBebGhYABjlnPvEzL4F3jSzK4GlwAWx9uOA04GFwGbg8n3Yd1xNnz6djz76iNmzZ5OYmMjatWspKSmpkH1t2LCBp556qlISrNTU1NIEa+jQoRW6PxGRqsat+A5+GQe/foyt+gFjj0a4b99fQgqhlAwKEhuwMZDOBl8tcl1N1nsprIsksy6SSF44kU2RAJsjfoo8PyFnOAdmkOBzJFqEGv4INf0hagZKqOMvoa6vkDr+zdSxTdT28qjprSelZC2Jm1djm9fuXdyF62HB+OgC4E+AJkfjDuqGtTgRMrtCIHGffh4iIgeKvU6wnHOLgHY7KM8Feu6g3AHX7u3+qpLs7Gzq1atHYmL0P5t69erx+eefc8011zBmzBgAJkyYwFNPPcV7771Hamoqf/7znxk3bhyNGzfm/vvv57bbbmPZsmU89thjnH322bz00ku899575OXlsWLFCi655BLuuece7rjjDn777Tfat2/PKaecwsMPP8xtt93Gxx9/jJlx11130b9/fyZPnsw999xD7dq1mTdvHhdccAFt2rTh8ccfp7CwkDFjxtCyZUs+/PBDhg8fTklJCenp6bz++usUFhby9NNP4/f7ee211xgxYgQTJ04kNTWVW2+9lYULFzJ06FBycnLw+/289dZbtGzZMp6/AhGRcuGWfws/vAs/f4jlLf/jDX6/vS9ISa0WrK3RgmW+TH4JN+T7zenM3FiTZRuTYGMFBL0LKX6PtjU30TYlj8MScznYv4aM8ArqbF5CcONSzAvtXkeRElg2HVs2Hab+CwLJuMyu2CE94ZCe0PCoij0QEZFqTPO87oVevXrx97//nVatWnHyySfTv39//vSnP3HNNdeQk5ND/fr1efHFF7niiisAKCgo4KSTTuKRRx6hT58+3HXXXUyYMIGffvqJgQMHcvbZZwMwY8YMfvjhB2rUqEHnzp0544wzePDBB/nhhx+YM2cOAO+88w5z5sxh7ty5rF27ls6dO9O9e3cA5s6dy/z586lbty4tWrRg8ODBzJgxg8cff5wRI0bw2GOPcfzxx/P1119jZjz33HM8/PDD/Pvf/2bo0KGlCRXAxIkTS493wIAB3HHHHfTp04eioiI8z0NEpNrK/Q03ZxQ27y1sw9Ld3syZn6K6h5NV40jmRlrwRX4Gn+emU5Dtq8Bg90xBxMf09bWYvr4WsO1MvMn+CMfVzqNbzdW0Da7g4NBv1N74M/6C1X/ccbgQWzwZFk+GCXdDWgYcejIc2gta/AkSUyvicEREqiUlWHshNTWVWbNmMXXqVCZNmkT//v158MEHufTSS3nttde4/PLLmT59Oq+88goACQkJnHrqqQC0adOGxMREgsEgbdq0YcmSJaX9nnLKKaSnR6fVPe+885g2bRrnnnvuNvueNm0aF110EX6/n4YNG3LiiSfy7bffUrNmTTp37kzjxo0BaNmyJb169Srd56RJk4Doc8T69+9PdnY2JSUlf/jcqk2bNrFixQr69OkDRB8oLCJS7ZQU4H54F757BVs+Y7cmpXC+IPn12vFTYnsmF7Xk7dUZ5Kyovg9TL4z4mZhbl4m5dYEjgJMBOCJ1M6enZ3NMwmIOCf1C7fXfY8Wbdt3ZppUw+5Xo4k/ENT8BO/x0OOx0qNm4wo9FRKQqU4K1l/x+Pz169KBHjx60adOGl19+mWeeeYazzjqLpKQkzj//fAKB6I83GAyWTmPu8/lKhxb6fD7C4XBpn7+f6nxPpz7f0u+u9nP99ddz8803c/bZZzN58mTuvffePTtwEZFqxK2eD98+h817Eyv+4/F64ZrNWFjrWD4tbsNrqzLJWVZ9E6rdNT+/BvPzWwItgZPxm0eveus4vdZSOjCfxutn7foqV6QY++0z+O0zGHsLrunR2BFnwxFnQ109fF5EDjxKsPbCL7/8gs/n49BDDwVgzpw5HHTQQWRkZJCRkcHw4cP57LPP9rjfCRMmsG7dOpKTkxkzZgwvvPACaWlpbNq09ZvEE044gWeeeYaBAweybt06pkyZwiOPPMLPP/+8i563ysvLo0mTJgC8/PLLpeVpaWls3Lj9Hx9paWk0bdqUMWPGcO6551JcXEwkEqFGjRp7fHwiIpXCObxfxmHfjMQWT/3D5oX1WjMz+XheXd+a8Wvqbn24yAEq4nx8nFOPj3PqAUcDl3Bi3fWcV2cxXZhHw9wZ+IrW72Rrh2XNhKyZMOFv0angjzwXjuqjZEtEDhjVPsHa3WnVy1N+fj7XX389GzZsIBAIcMghh/Dss88C0fuVcnJyOOKII/a43y5dutC3b1+ysrK45JJL6NSpEwDdunWjdevWnHbaaTz88MNMnz6ddu3aYWY8/PDDNGrUaLcTrHvvvZfzzz+fOnXqcNJJJ7F4cfQhlWeddRb9+vXj/fffZ8SIEdts8+qrr3L11Vfzt7/9jWAwyFtvvUWLFi32+PhERCpUqAj33Wvw9ZP41i3aZdOiukfwdcqfeCqnLTOyalZSgNXXF+vq8MW6OkBH/HYp5zRYS5+aP9OueBZpa7/DvPCON8yeG10m3gcZHaF13+iiYYQish+z6OR+VVOnTp3czJkztymbP3/+XiUvleW6666jQ4cOXHnllXu03UsvvcTMmTN54oknKiiyilfVfzcisp8q2og34/+iV6wKcnbaLJLSkHl1e/P0hs58kpNeiQHu35okFXN5oyWcEviOzNwv8RXm7noD88FB3XBt+2NHngNJSnBFpHoys1nOuU6/L6/2V7CqkqOPPpqUlBT+/e9/xzsUEZH9nivcgPv6aeybkfiKNuy4jflZ2/hE3oj8if8ub0Eod8/ubZU/tqIokeFLDmM4h+G3C7iw0Sr6pc3jqI1TSdiwgyuJzos+vHnJVBh3a3RijPYXQ8uTwOev/AMQESlnuoIl5Ua/GxGpFMWb8KaPxL5+AivK22ETr0Y9Zqafw/2ruzJno6YQj5ee6eu4vO48jt48jeTcH3fdOLURtL0AOlwC9Q+rnABFRPaBrmCJiEj1Fi7GzXgOm/ZvfJt3PAytMP0o3ks8m38uPYqCdVXn+VQHqui08CcCJ3JsnTyurjePrpunkJz7w/aN81fBV/+NLk07Q4dLo/dr6RlbIlLNKMESEZGqzTnc3NHYpH9iect22GRd4xN4KnQmz2VlVnJwsruiD0A+Hjie4+vm8ef0OXTO/5yE9Qu2b5z1bXT59M7oDIRHD4Km231JLCJSJSnBEhGRKsstngbj78Sy525fZz6yM3rxwKbT+HBx/ThEJ3tr2rpaTFsXvbJ1ev21DKk9kzbrP8Ofv3LbhiX58N2r0aVh62ii1ba/JsYQkSpNCZaIiFQ5bt0SGH8X9vOH29eZjxVNTuNv60/n89/qVH5wUq7G5dRjXM6p+K0XlzdZwYCk6TRfMwErKdi24eofopNiTLgH1/o86HQl1qRDfIIWEdmF6p9g3VurnPvb8Q3TZfn9ftq0aVO6PmbMGJo3b77DtqmpqeTn5+9TSIMGDeKLL76gVq1a+Hw+nnzySY499tg96mPw4MHcfPPNHHnkkdx///3ceeedpXXHHXccX3311T7FKCJSLkKFeFP/g++rxyFctE2Vw8hu0ps715/F5IVKrPY3EefjuaxMniOTOsHzuDXzZ87wJlNr1XSMMhNyhQqwLVe1mhwNnQfDUedBMCl+wYuIlFH9ZxGMQ4K1J0lTeSVYZ555Jv369WP8+PHceuutfP/993vdX3nEtCOaRVBE9oX381jskzuwDdvfZ5Xb+ETuye/LRzn14hCZxFPHWpu4tcEsuuR9QmDjju/BI7kudLwUOl0JdQ6q3ABF5IC1s1kENcVSOcjPz6dnz5507NiRNm3a8P7772/XJjs7m+7du9O+fXtat27N1KlTARg/fjzHHnssHTt25Pzzz//DxKd79+4sXLgQgEcffZTWrVvTunVrHnvsMQAKCgo444wzaNeuHa1bt2b06NEA9OjRg5kzZ3LHHXdQWFhI+/btGTBgABBNuAAuvPBCxo4dW7qvQYMG8fbbbxOJRBg2bBidO3embdu2PPPMM/v4ExMR2cptWI4bdRG+Ny7eLrnaXK8tf09/iKMXX63k6gA1Oy+Nixf04NCcBxhe7yGymp6B8ydu26hwHXz5OPy3PfzvIlg0OS6xiojA/jBEMA62JCgABx98MG+99RbvvfceNWvWZO3atRxzzDGcffbZmG19oOWoUaPo3bs3/+///T8ikQibN29m7dq1DB8+nM8++4yUlBQeeughHn30Uf72t7/tdN8ffvghbdq0YdasWbz44ot88803OOfo2rUrJ554IosWLSIjI6M0UcrL2/aK3IMPPsgTTzzBnDlztuu7f//+vPnmm5xxxhmUlJQwceJERo4cyfPPP0+tWrX49ttvKS4uplu3bvTq1YuDDz64PH6cInKg8iJ4Xz+NTb4fK9n2y6VwWhNGpV7OPUuOwDk9HFjAOYsNIRxAs+S+3Nl0Ln8q+ITE9b+UaeTBL+OiS/0joOsQaHshJNSIX+AicsBRgrUXkpOTt0lQQqEQd955J1OmTMHn87FixQpWr15No0aNStt07tyZK664glAoxLnnnkv79u354osv+Omnn+jWrRsAJSUlO723atiwYQwfPpz69evz/PPPM3HiRPr06UNKSgoA5513HlOnTuXUU0/llltu4fbbb+fMM8/khBNO2O3jOu2007jxxhspLi7mk08+oXv37iQnJzN+/Hi+//573n77bSCatC1YsEAJlojsNZc9Dz68Ht/K77YtD6bwZaNL+PPibmzK0X9RsmPLCpMYurAr0JWLG2dzdcoXNFs1Hit7317OfPjoJvjsPlzHy7AuQ6C2pvEXkYqn/73Kweuvv05OTg6zZs0iGAzSvHlzioq2vTm7e/fuTJkyhbFjxzJo0CBuvvlm6tSpwymnnML//ve/P9zHI488Qr9+/UrXJ06cuMN2rVq1Yvbs2YwbN4677rqLnj177vKKWFlJSUn06NGDTz/9lNGjR3PhhRcC4JxjxIgR9O7de7f6ERHZqXAJ3hcP4/vyMfBC21Qtb3oG16w+l3kLUuIUnFRHo7IbM4oLaZrUh7ubzuFP+WNJ2LBwa4OiDdhX/4XpT8IRZ8Gx10Jml/gFLCL7Pd2DVQ7y8vJo0KABwWCQSZMmsXTp0u3aLF26lIYNG3LVVVcxePBgZs+ezTHHHMOXX35Zek9VQUEBv/76627t84QTTmDMmDFs3ryZgoIC3nvvPU444QRWrlxJjRo1uOSSSxg2bBizZ8/ebttgMEgoFNpBr9Fhgi+++GLp1TCA3r17M3LkyNJtfv31VwoKCna4vYjIzngrZuE92x3f1Ee2Sa6K6x7GPXUf4YSFA5i3ScmV7J2sokSuXtiVVqv+zj/SHyK7SW+cr8z3yC4CP42B50+B/+sJP7wDXiR+AYvIfmufr2CZmR+YCaxwzp1pZgcDbwDpwCzgUudciZklAq8ARwO5QH/n3JJ93f/uzPpX0QYMGMBZZ51FmzZt6NSpE4cffvh2bSZPnswjjzxCMBgkNTWVV155hfr16/PSSy9x0UUXUVxcDMDw4cNp1arVH+6zY8eODBo0iC5dot/CDR48mA4dOvDpp58ybNgwfD4fwWCQkSNHbrftkCFDaNu2LR07duT111/fpq5Xr15ceulQpNadAAAgAElEQVSlnHPOOSQkJJT2vWTJEjp27Ihzjvr16zNmzJg9/jmJyAEqXII3+cHo1OteuLTYBVP4vNEVXPNbV4o9fd8n5ef5FZk8z0COSuvHXU2+pcu69/EXrN7aYMVMePsKqHVv9D6tjgP18GIRKTf7PE27md0MdAJqxhKsN4F3nXNvmNnTwFzn3EgzuwZo65wbamYXAn2cc/131fduTdMuVYZ+NyLye27VD/De1djqH7YpX5PRkyFr+zNnY2qcIpMDSaLP47aDfuX8yMfUXPPt9g0S0qDjZXDMUKjdrPIDFJFqqUKmaTezpsAZwHOxdQNOAt6ONXkZODf2/pzYOrH6nlZ2mj0REdl/eB7etMew//vTNslVJKUhTze8ly6LrlRyJZWm2PPxj8WH03bZTVyT9l9+y+yLCyRvbVCyCb5+Eh5vD29dDiu2H14vIrK79nWI4GPAbUBabD0d2OCc2zIGJAtoEnvfBFgO4JwLm1lerP3ash2a2RBgCECzZvoWSUSkunHrl+HGDMW39Mttyn/L7Msly88iOzchTpGJwLiceozL6Uuz5DO4N3MW3Te8T2BTVrTSReDHd6PLQcfDcddDq96g74NFZA/sdYJlZmcCa5xzs8ysR3kF5Jx7FngWokMEy6tfERGpeN68t7Cxt+Ar2np/bLhmMx5OuIZnF+hLM6k6lhUmccWCbgR9x3FL5gIuZhw1V8/Y2mDptOhS7zDcsddi7S6EQOLOOxQRidmXK1jdgLPN7HQgCagJPA7UNrNA7CpWU2BFrP0KIBPIMrMAUIvoZBciIlLdFefjjRuGb+6o0iKH8UvmBQxYejq5JcE4BieycyHPeHBpKx6kFWfWX8sttT6nefbHWCQ6+RRrf8E+vAEm/RO6Xg2droTk2vENWkSqtL2+B8s591fnXFPnXHPgQuBz59wAYBKw5YFNA4H3Y+8/iK0Tq//c7esMGyIiEndu5RzcMydsk1yFa2YyPP1BTl1wjpIrqTY+yqnHnxZeQC+e4qvMIURSGmytzF8NE/8O/zkKPrkT8rLiF6iIVGkVMS/u7cDNZraQ6D1Wz8fKnwfSY+U3A3dUwL5FRKQSedOfwp4/BVu3qLRsUeZ5HJc3nOdXZMYxMpG9t6AgmYsX9KDthkd5PeNOCtNbb60syY9NiNEO985V0ZkyRUTK2Odp2ivS7kzT3ublNuW6z3kD5+2yPjc3l549ewKwatUq/H4/9evXB2DGjBmlz47aFz169CA7O5ukpCRSU1N54YUXOOyww/aoj9NPP51Ro6LfJo8aNYprrrkGgJUrV3LDDTfw9ttv72rzvaJp2kUOHG7zOtyYa/H9Oq60zKtRjyfTbuTfS1vGMTKRijEoI4trkj6lfvYkzHnbVh5yMnS7EQ7uHp/gRCQuKmSa9gNReno6c+bMYc6cOQwdOpSbbrqpdD0hIYFwOPzHneyG119/nblz5zJw4ECGDRu2x9uPGzeO2rVrs2HDBp566qnS8oyMjApJrkTkwOGWfwvPnLhNcpWTcRK9ix9SciX7rZdWNqXLoiu5OOlJfsq8CJeQsrVy4Wfw8lnwbA/4cQx43k77EZH9nxKscjBo0CCGDh1K165due2227j33nv517/+VVrfunVrlixZAsBrr71Gly5daN++PVdffTWRSGSXfXfv3p2FCxfinGPYsGG0bt2aNm3aMHr0aACys7Pp3r077du3p3Xr1kydOhWA5s2bs3btWu644w5+++032rdvz7Bhw1iyZAmtW0eHOhxzzDH8+OOPpfvq0aMHM2fOpKCggCuuuIIuXbrQoUMH3n///e0DE5EDkjf9KezF07C8ZQC4YA3GNL2VzosGs6Ag+Q+2Fqn+pq+vxekLzuK4kieZmHk94bQmWytXfgdvDYQnjoaZL0CoKH6BikjcKMEqJ1lZWXz11Vc8+uijO20zf/58Ro8ezZdffsmcOXPw+/28/vrru+z3ww8/pE2bNrz77rvMmTOHuXPn8tlnnzFs2DCys7MZNWoUvXv3Lq1r3779Nts/+OCDtGzZkjlz5vDII49sU9e/f3/efPNNIJqoZWdn06lTJ/75z39y0kknMWPGDCZNmsSwYcMoKCjYy5+MiOwPXNFGvNGX4vv0r+CFAChMb82ghEf4y8KOcY5OpPJlFyVw5YJjOSr3IV5sfDeb67XbWrluEXx0EzzWBqb+Gwo3xC9QEal0+/qgYYk5//zz8fv9u2wzceJEZs2aRefOnQEoLCykQYMGO2w7YMAAkpOTad68OSNGjODRRx/loosuwu/307BhQ0488US+/fZbOnfuzBVXXEEoFOLcc8/dLsHalQsuuIBevXpx33338eabb9KvX3Tyx/Hjx/PBBx+UXoUrKipi2bJlur9K5ADlVv0Ab12GL/e36DrGD5kXc+Gi0yiI6Hs6ObAVez7uW3wE93EEl2as4LqkT2mQ/Xn0Pq2CNdGZB6f+BzoNgmOugZoZ8Q5ZRCqYEqxykpKydSx2IBDAKzP+uqgoOkTAOcfAgQN54IEH/rC/119/nU6dtrtnbjvdu3dnypQpjB07lkGDBnHzzTdz2WWX7VbMTZo0IT09ne+//57Ro0fz9NNPl8b5zjvv7PHEGiKy//HmvIFv7E0Q2hxdT67H42l/4fEFLeIcmUjV8+rKJrzKFRxbpy9/q/cFh6/6EAsVQMkm+GoEfPMMtLkgOiFG/VbxDldEKoi+eqwAzZs3Z/bs2QDMnj2bxYsXA9CzZ0/efvtt1qxZA8C6detYunTpbvV5wgknMHr0aCKRCDk5OUyZMoUuXbqwdOlSGjZsyFVXXcXgwYNL97tFWloamzZt2mm//fv35+GHHyYvL4+2bdsC0Lt3b0aMGMGWGSa/++67PfsBiEj1FwkR+egWfGOuLk2u8hoew1nhB3h8mZIrkV2Zvr4Wpy04mxNCT/BF5p+JpDSKVkRKYM5r8GQXeGMALP82voGKSIWo9lew/mha9Xjo27cvr7zyCkcddRRdu3alVavot1RHHnkkw4cPp1evXnieRzAY5Mknn+Sggw76wz779OnD9OnTadeuHWbGww8/TKNGjXj55Zd55JFHCAaDpKam8sorr2yzXXp6Ot26daN169acdtppXHvttdvU9+vXjxtvvJG77767tOzuu+/mL3/5C23btsXzPA4++GA++uijcvjJiEh14PJW4t66DH9W9I8/Zz6+bjqYSxZ2J+L0vZzI7soqSmTgghNI8Xfj/x30I+cVjSFp3XzAwc8fRZeDukG3v0CrXvEOV0TKSbV/DpZUHfrdiFR/3pJp2NtXYPmrAYikNOD+pFv00GCRcnJ102UMCY6jbvZUjDJ/gzVsDcfdAK37gr/af/8tckDQc7BERGSXvK+fwffKuaXJ1YZGx3Ja0QNKrkTK0TNZzTh68VCGpI5gUeZ5OH9itGL1D/DeEPhvB/j6aSjZHN9ARWSvKcESETnQhYrw3h2K75PbwAvhzMc3mYM5eum1/KpnW4lUiAlr63LSgn705ilmZF6Jl1w3WpG3DD65Hf5zFEx6AApy4xuoiOyxaplgVeVhjQcq/U5Eqidvw3K8F3vj+/5/0fXkdP5Vbzj9F5yk+61EKsGvBclcsKAnHfIf44OmtxCqFZtEpnAdfPEgPNYaxg2D9bs3KZaIxF+1+98zKSmJ3Nxc/UFfhTjnyM3NJSkpKd6hiMge8JZMw/7vJHwr5wCQX78D50Ue4MnlzeMbmMgBKC8U4IaFR9NqzT8Y0eAfbGzYJVoR2gwznoURHeGdwZD9fXwDFZE/VO0muQiFQmRlZZU+W0qqhqSkJJo2bUowGIx3KCKyGyIz/g//J38FLwTA/MwLOW/RGRRGdv3AdBGpPOc1XMPNaeNpsnI85oW3VrTsGX2WVosT4xeciOx0kotql2CJiMg+iISIjL0V/+yXAHDBFF6udzP3LtYMoCJVVcda+dzbYCpt1ozBiss827Jx+2iideQ54NOXIyKVTQmWiMgBzuXn4L15Kf5l0wEoqd2Ca8M3M2Ft3ThHJiK7o0FiiOGZszhp43sENi7fWlGnORx7HbQfAAk14hafyIFGCZaIyAHMW/kdjL4UX170j7LVGSdzzopLWFWcEOfIRGRPBX2O25v9ykWR90nJmbO1okY6dL4KugyBlPT4BShygFCCJSJygIrMexv/B9dDaDPOfExpejWDFh6Pcxbv0ERkH13YOJsba4yn0crPMBeJFgaSof3FcNx1ULdFfAMU2Y8pwRIROdA4hzfxH/im/RsAL7kuj6QOY+Tyg+IcmIiUt061NnFPgym0XvPB1vu0zAeHnwHH3QiZneMboMh+qNwTLDNLAqYAiUAAeNs5d4+ZHQy8AaQDs4BLnXMlZpYIvAIcDeQC/Z1zS3a1DyVYIiJ7xxVtwnvvavy/jAWgML01l+Zfz8y8tDhHJiIVqVFiCX/PnM1JG8cQ2Lhsa0VmV9yx12GHnwm+aveUHpEqqSISLANSnHP5ZhYEpgE3AjcD7zrn3jCzp4G5zrmRZnYN0NY5N9TMLgT6OOf672ofSrBERPact24xvHExvjU/AbC06dmcuaQfm8KBOEcmIpUl6HPckrmAAe4j0taU+Vuqbgs45hpNiCFSDip0iKCZ1SCaYP0ZGAs0cs6FzexY4F7nXG8z+zT2frqZBYBVQH23iwCUYImI7Blv8RTsrUHY5lycL8jYjOu5buF2534ROYCc13ANN6V9RtOVn2KxZ9+RXAc6XQldroK0RvENUKSa2lmCtU/XiM3Mb2ZzgDXABOA3YINzbsvT8LKAJrH3TYDlALH6PKLDCH/f5xAzm2lmM3NycvYlPBGRA0rk2+fxvXoetjkXr0Z9/lb7fiVXIsK7qxtwwsKLOd03khmZV+Il14PC9TD1X/BYG3jvz7BqXrzDFNlv7FOC5ZyLOOfaA02BLsDh+xqQc+5Z51wn51yn+vXr72t3IiL7v0iYyEe34B97M3gh8ut34JzQ/by6sskfbysiB4z5+TW4YEFP2m16lNEZd1CUfiRESmDuKHj6eHj5LPj1U6jCE6CJVAflMiDfObfBzCYBxwK1zSwQu0rVFFgRa7YCyASyYkMEaxGd7EJERPaSK8jFe3sg/sVTAViY2ZdzFvWhIKKb2EVkxzaFA9y+qC2305ZBGVkMTZ5Aw5WfY4unwOIpkH4IHPNnaHcRJKTEO1yRamev/wc2s/pmVjv2Phk4BZgPTAL6xZoNBN6Pvf8gtk6s/vNd3X8lIiK75q3+CffcSfgXT8X5E3i3yTBOXtBXyZWI7LaXVjblmN8up2/CSL5rNhAvqQ7kLoSxt8CjR8KEv0FeVrzDFKlW9mUWwbbAy4CfaKL2pnPu72bWgug07XWB74BLnHPFsWndXwU6AOuAC51zi3a1D01yISKyY5Gfx+F772qseCOR1MbcGRzG6GzdqC4i+6ZWMMzfmv3AGYUfkrRufrTQ/HDEWdGrWs2OiW+AIlWIHjQsIrKfCE/9N4HPh4Pz2NSgE+evG8rP+ZpuWUTK18CMFVydPJHG2Z9hXmz+sowO0HUoHHUeBBLiG6BInCnBEhGp5lxJIZEPrifww1sA/JLZn3MXnUlhxB/nyERkf9YmrYC7Gn1D59z38W2OzfCc0gA6XQGdLtc073LAUoIlIlKNeXlZMPoSfCu/wwWSGN3gJu5Y1CbeYYnIASTF7zGs2S/0jXy89eHFviAceQ50vRoyu8Q3QJFKpgRLRKSa8pZ9A29ehi9/FeG0JtzmG8a7qxvEOywROYCdXn8tN9WewiGrPsZCBdHCxu2jiVbrvhBIjG+AIpVACZaISDUUnv0qgbG3QKSYDY2Ope+awfy2OTneYYmIANA4qYS7m87l5IKPSFi/IFpYIx06XgadroTamfENUKQCKcESEalOImHCn/6VwIxnAfg+81L6/nYqIc/iHJiIyI5d0WQ5g5Mm0Th7IuaForMPtuoNnQdDy5PAdP6S/YsSLBGRaqLsw4NdMIUX6t3CPxYfHu+wRER2S6uUQu7KmMlxGz4ksCn2DK26LaHzldD+YkiuE98ARcqJEiwRkWogkv09NnoAvg3LKKndgmvDNzNhbd14hyUissf85nFd5hIGBCZRP3sy5iIQSI7eo9X5CmhydLxDFNknSrBERKq48Ly38H9wIxYqYE1GT85ecSmrivWcGRGp/trWzOevDWfSecNYAptWRAsbt4vep9WmHySkxDdAkb2gBEtEpKryPMKf3UPgq//izM+UpkMYtPB4nNP9CiKyf/Gbx/WZS7g4MIn6q76IPsA4sSa0vSD6XK2GR8U7RJHdpgRLRKQK8grW4r1zFYFFn+Ml1+OhlFt5JqtZvMMSEalwR6UVcHuj2RyXN5bAxmXRwqad4ejL4ag+kFAjvgGK/AElWCIiVUwkey42+hJ8G5aRX78DF+f9me83psY7LBGRSmXmGNJkOZclfkHGqs+xSDEk1ope1Tp6IDTSQ9WlalKCJSJShYTmvkHgo5uw0GbmZ15Iv0VnUhDxxTssEZG4ap5cxB1N5tJj83iS1s2PFmZ0jCZarftBor6EkqpDCZaISBXgwiWEP72T4Lf/h0tI4aX0m7lv8RHxDktEpMo5r+Eahtb8kkPXfIoVb4SEVDjqXOhwGTTrGu/wRJRgiYjEm7dxJe6tQfiXf0NxncO4uvgGJq/T82BERHYlLRDmlswFnOM+p/bq6ZjzoN5h0OESaHchpDaId4hygFKCJSISR+HFU/C9Mxhf/mqWNT2LPsv6kVsSjHdYIiLVSvua+dzScDbHbPyUYN5i8AXgkFOiyVar3uDXeVUqz84SrEA8ghEROZCEpv2HwOfDwRfgnSa3ccvC9vEOSUSkWpqzMZVLN3YHujOg8UouT51Oy6UTsF8/hhr1ohNjtL9YE2NIXOkKlohIBfEK1+ONuZbAL2Mpqd2SGyJ/4ZOc9HiHJSKyX0kLhPlL5kLOsSmkr5oWfbZWozbQ7iJocwGk1o93iLKf0hBBEZFKFF4xG3v7cvzrl7C86Zmct+x8cjQkUESkQh2aUsjNjedxYtEkaqydGx1C2LJn9F6tw06HYFK8Q5T9SLknWGaWCbwCNAQc8Kxz7nEzqwuMBpoDS4ALnHPrzcyAx4HTgc3AIOfc7F3tQwmWiFRHoRnPEPj0bvD5ebP+Ddy+qG28QxIROeCcmL6ea+p+R8e8CQQ3Lo0+W+vIs6Ftf2h+PJjFO0Sp5ioiwWoMNHbOzTazNGAWcC4wCFjnnHvQzO4A6jjnbjez04HriSZYXYHHnXO7nGNTCZaIVCdeUR6RD24g+NMYiuoezjXF1/N5rmYJFBGJt/6NVzEodQaH5X6Gb/NaqNkU2vSLJlsNj4x3eFJNVfgQQTN7H3gitvRwzmXHkrDJzrnDzOyZ2Pv/xdr/sqXdzvpUgiUi1UU4axb27pX41y3ml8z+9Ft8BpvCmkdIRKQqCfocg5ss5YLEGTTPmYgVb4KGraPJVuu+ULtZvEOUaqRCZxE0s+ZAB+AboGGZpGkV0SGEAE2A5WU2y4qV7TTBEhGpDkJfP0Vgwj24YAojG97HQwsOjXdIIiKyAyHPGLm8OSNpTkqgL9c1WcQ5gek0/uJh7LP7ILNrNNk6qg+k1It3uFJN7XOCZWapwDvAX5xzG63MeFbnnDOzPbpEZmZDgCEAzZrpWwQRqbq8grVE3r+O4K8fs6HRsVyaewXzlqbEOywREdkNBWE/Dy09lIc4lPSEi7iuyUJOi3xNw/F3YR/fDi1OhKPOgyPOguTa8Q5XqpF9GiJoZkHgI+BT59yjsbLSoX8aIigi+6vQb5PwjbkGX0EOk5oM4aqFxxJxvniHJSIi+6hBYojrM36lt31N/dXTMBy0PCmabB12GiTVjHeIUkVUxCQXBrxMdEKLv5QpfwTILTPJRV3n3G1mdgZwHVsnufivc67LrvahBEtEqhoXLiE8aTjBr0ZQUrslw7xreX91g3iHJSIiFaBRYgnXZiygl31DgzXTMOdwLXtirftEk63EtHiHKHFUEQnW8cBUYB7gxYrvJHof1ptAM2Ap0Wna18USsieAU4lO0365c26X2ZMSLBGpSsJrfoH3rsKf/T3zMy/koiWnkRfSRBYiIgeC+gkh/txkIaf5ZtBoTeyBxof0hCPPiV3ZqhXvEKWS6UHDIiL7IDTjWfwT7sEl1uZfydczcvlB8Q5JRETipFYwzJCMxZwZnEWznC+wcCG06AFHnB19oHFKerxDlEqgBEtEZC9ENq7E++AGggsnsKzpWVyUdR4rihLjHZaIiFQRyf4IgzKyODfpOw5ZNwX/5hxo3i2abB1+BtTMiHeIUkGUYImI7KHQ92/i//h2MB/PpF3PQ0s1/bqIiOycmaNvwzVclPY9bfKnkbB+ITTpGE20Dj8L6reKd4hSjv5/e3ceZldV5//+vVIJJCFASAIIGUwUVJwYjAwOiAMNDu3UrWi3ttra6cG+av9au9W+92d7f9rXbrtVvM3FSyuKNlNkMgoIyIxAyDyHjJWaq07Np+rUmdfvj3MCRSSYoersGt6v5znPHs4+Z3+rns0qPllrr23AkqRDVBpMUb7zi0zbegfN89/Jx1s/xJ7M9KTLkiSNM2+a08en5m7l9bknOT61ljDnJfCKd8HL3w0LXg9TnH12PBvVBw1L0kSR33IHdXd9iSnA/3fq1/m33fZaSZKOzGPdJ/JY90XARSyekeUvjt3FW+vXctrqawlTp8PLLoOXvRNe+lY4xucoThT2YEkSUBrooHz3PzJty23UL3gfH2t6P03eayVJGgUz6kp8/LRm3jtjEy/vf4Jpgy2w+M3w8svhZZfDiQuSLlGHwCGCknQQhQ03U3fPVylPncl/HPvXzhAoSaqpN83p4+NztnN+cTWzU6sJ886EMy+FMy+DhefDlLqkS9TzcIigJB2g2LOPeNeXmLr7fjbM/xM+Vf8OenyulSSpxipDCS8ALmDuMQU+SQN/sG8TL934F0zNp+Glb4Mz/wDOeAfMOjnpcvV72IMladKJpRKFlT9g6kP/wtCJZ/Cl7J9zV2pe0mVJkvQ7Lp7Ty0fn7OD80jrmdK4mzDujErTOeAcsOB/q/IfBpDhEUJKAQtMquOuL1HXX88u5n+F/7DmHUnQWJ0nS2Hfc1BJ/+qJm3jlzG68YXMP0wUbC4jdXerhe+jaYsyTpEicVA5akSa2U6ab04DeZuuYn7Dv9PXym5Q/ZnZmRdFmSJB2xl84c4mOn1vOWqVtY1PsUU6dOhZe8tTIr4ZKLYcZJSZc4oRmwJE1KMUby66+n7jdfpzDjFP5X6VPc0Hpa0mVJkjTi3nhSHx+es5vz2cSpPWuZMnshvOQSeMlbYOGFMM1nOo4kA5akSafQtBru+Qp1nXu4Y86n+NKesx0OKEmaFEKIvHNeF+8/cRfnljczt28zU05+eSVsLb4Y5p8HddOSLnNcM2BJmjSK/W2UH/xfTN10C1tO/2P+quHtNPtMK0nSJDZtSuQPT07x7hN2c3ZpE3P6txNOfRVhyZsrgev0c5wO/jAZsCRNeOXCEMWVVzP10e/SMfcCvtj7QR7rPjHpsiRJGnOmTYm8++QU7z5+D2eXtzB3cCd1J78MXvxGWPwmOP1ce7h+DwOWpAkrlsvkNy9nygPfJD9tDv9a+hg/bTk96bIkSRo3QohcOreH98zey3ls40WDTzN19oJK4HrxG2DBUpjm5FDDGbAkTUi53Q8w5f7/m5jp4yfT/4x/qX9Z0iVJkjQhLD0xzfvnNnB+3Q4WDW3n2BkzCQvPh0VvgIUXwHFzky4xUQcLWD6ZTNK4lG9eDQ98k6nt27njxI/x1Y7Xkis7gYUkSSNldd/xrO57FfAqAOZPz/HBXAtvbvwNLyv8vxxPhrrTXlMJW4suhHlnJlvwGGEPlqRxpdC+hfLD/8rUfU9w30kf5e/rlzJY9KZcSZJqbdqUyOXzOrn0hAbOZienFpqZfuLJleGEC86H+a+DY2clXeaocYigpHGtkNpO+ZH/oG7Pwzw058N8qf719BTshJckaSxZPCPL+05u4Q3H7uPM4g5OmFpg6ikvg/lLK8Fr3sthysQYcTIqASuEcC3wHqAjxvjq6r45wM3AYqAe+HCMsSeEEIArgXcBGeCTMca1L/T9BixJhY5tlB/9DnX1v+WBE/+If9y31GAlSdI48qY5fVx2YhPnTd3LgnITs6YfS92LXlnp4Tr9PJi9MOkSj8hoBayLgQHgp8MC1r8B3THGb4UQvgycFGP8xxDCu4D/g0rAugC4MsZ4wQt9vwFLmrzyreuJj32P0LSWXx//x3yl/hyHAkqSNAEcO6XM2+Z289YTmjl7yl5eFLqZNXMGdae+sjI9/GnnwAmnJV3m7zVqQwRDCIuBXw0LWE8Dl8QYW0MIpwEPxRhfHkL4/6vrNx543MG+24AlTT65vY/C498ndjfx82M+wDf2neXkFZIkTXDHTinz9rndvOX4Fl5bV8+LpvRy/MwZleGFp50NL3rtmOvpquUsgqcOC01twKnV9flA47Djmqr7nhOwQgjLgGUAixYtGoXyJI01sVQiv/0XhCd/QKYwlR+W3s1VzYuTLkuSJNVIrjyFu1LzuCs1D3gtAHWhzJvm9HHJCds4Z9o9zA89nDBzGtNPml8JXC96TWXmwilja4TLqN7IEGOMIYTD6iKLMV4DXAOVHqxRKUzSmFAc6qW0/gZYex3Nx57Fv/V9jF+nJvczNSRJUkUpTuHhrpN4uOsk4Kxn9r9iVoa3n9TB66b/jJdMaWP2jDpOOO44ppxyFrzo1XDqq2D6iYnVPRoBqz2EcNqwIYId1f3NwPB+vQXVfZImmXxqB+U11xJ3PchTM97K17v+gT2Z6UmXJUmSxoHtAzPZPrCYypx6FcfVlbl4TjdvmPUYr552M6cck2X2zGM57sST4ZSzKqFr7plQN/oTZY3GGVYAnwC+VV3+Ytj+vw0h3ERlkou+F7r/StLEUi4VKV7i020AACAASURBVOy4m7j2OgYHhri5fCnfbfm/KJRD0qVJkqRxbrA0hbtT87g7NY/9D0YGOG16nred1MnrZt7Ky6a2M2fGFGbPPJaZs0+pBK+TXwEnLRnRqeOPKmCFEG4ELgHmhRCagK9RCVbLQwifBvYBH64efheVGQR3UZmm/VNHc25J40Oht4HS+uspP30v26e9lm+nPsgTPcl120uSpMmjNXsM17eezvWc/pz9i2dkufikFs6buZaXTO1izoypzD7uWGadOKcSuk5+BZy0+Iju7/JBw5JGXKmQo7jzbsobltM3kOO24pu5svGlzgYoSZLGtBcdm+dNJ/XwupkdnDGti5Nm1DFn1nROnDWTurkvgblnVCbWOOa4ms4iKGmSyjathk0/J9u0mVXhPL7d+kF2DM5IuixJkqRD0pY7hlvaTuWWZyZCrzh2SpkLZvfzulmP8spjb2XBS1970O8wYEk6Krmu3ZS33EZu7xPsKS3kmp7X8evUxUmXJUmSNGJy5Sk80j2bR7pnAy/hoycd/JlcBixJhy3X20h52wpyex6nKXcCN6Rfx41tf06MTlghSZImNwOWpEOS695L3H4ng/vW0jQ0g+Xpc7ih7aOGKkmSpGEMWJKeV4yRbNsGwo576G7ZTf3QCdzY+2p+2fFHSZcmSZI0ZhmwJD2jkBugtPcRCvW/pb2zly1DL+LHqZexvv/VSZcmSZI0LhiwpEksxki2fTPseZiu9gZa+or8ZuBMrm+7gMHi4T/3QZIkabIzYEmTTLZ7D3Hfb+lr3U1Ld4aNg6dwfcdidg4uSbo0SZKkcc+AJU1gMUaynU9D41N0pVpo6Rpkx8Dx3NL5Ytb3vz7p8iRJkiYcA5Y0gRTygxRb1pFv3Uxrd5qW7gxb0idxe+d89mRek3R5kiRJE54BSxqnSqUi+dQ2Sq2b6OjqoaU3Q3NviUf7TuO+rvnkylOSLlGSJGnSMWBJ40Ahn6GY2ka+YyetPYO09QzQ2pdjTf887umcS7p4YtIlSpIkCQOWNKaUSkXyPXsode6mo6eX9r4MrT1DtPYXWdl3Mr/tOYFSPD7pMiVJknQQBiwpAflcmlL3brLdzbT3ZWnrz9DWN0RHf57NfSfy257ZDJZOAE5IulRJkiQdBgOWNEqGMl3Q20C6t4uOgSE6+rKk0jlS/Rna0oE1fbPZNjATmF59SZIkabwzYElHoFgukh9op9zXSu9ghs6BLF39OboGc3Sms3Smc7QMTGN9//G05Y4BpgAzq6+Tki1ekiRJo8aAJQ1TLBfJZzoppztJZzL0ZAr0DOboGczTncnRO7B/WaR+cAbbBmYOm61vCjCj+pIkSdJkZMDShJbNZyhneyhk0vTn8qSHCvRnCvRn8/RlCqRzBXoH8/QPFegbytGXKdOSOZbdmRkUyuGAb5tafc1M4CeRJEnSeFDzgBVCuBy4EqgDfhhj/Fata9D4EGMkW8gQ82nyuSEGs0WG8iUGcgUy1eVgtsRANs9gvsRgLs9AtkB/rsRgtsBAtkA6O4WWoWNJ5ae9wJnqqi/vg5IkSdLRqWnACiHUAVcBlwJNwKoQwooY49Za1qGRUY5lcqUcsZijXMiRK5bIFcqVZalMrlBmqFAkXyiTLZTIFkrkiiWy+SLZ6nvZQomhfCU4De1fL5TJ5ooM5ksM5afSkZvGYOlQH5obeLanyaF6kiRJqq1a92CdD+yKMe4BCCHcBLwPmDQBqxzLlGOZUixRjmViqUQkUi5HSrFMuQzFcmVZipFSuUypVF2WY+W9uP+YSKFUWRbLkWIJCtXji9XjC6XSM+8VyyVKpUi+VKZULpMvRUrlEoVSmWIpkC+VKRZLlWWpTKFUOaZQLFXXyxSKlVe+VCZXiORLdQwWpzBUqhuh39CU6svRq5IkSRp/av1/sfOBxmHbTcAFww8IISwDllU3cyGEzTWqTZPbPKAz6SI04XmdqRa8zlQrXmuqhTF5nVXvcXrx87035roJYozXANcAhBBWxxiXJlySJgGvNdWC15lqwetMteK1ploYj9fZod7YMlKagYXDthdU90mSJEnSuFfrgLUKODOEsCSEcAzwEWBFjWuQJEmSpFFR0yGCMcZiCOFvgXuozIt9bYxxywt85JraVCZ5rakmvM5UC15nqhWvNdXCuLvOQowx6RokSZIkaUKo9RBBSZIkSZqwDFiSJEmSNELGbMAKIVweQng6hLArhPDlpOvRxBBCWBhCeDCEsDWEsCWE8Pnq/jkhhPtCCDury5OSrlXjXwihLoSwLoTwq+r2khDCymq7dnN1sh/pqIQQZocQbgkhbA8hbAshXGSbppEWQvi76t/NzSGEG0MI023TNBJCCNeGEDqGP/v2YG1YqPh+9ZrbGEI4L7nKD25MBqwQQh1wFfBO4JXAR0MIr0y2Kk0QReDvY4yvBC4EPlu9tr4M3B9jPBO4v7otHa3PA9uGbf8r8N0Y4xlAD/DpRKrSRHMl8OsY4yuAs6lcc7ZpGjEhhPnA54ClMcZXU5mo7CPYpmlk/AS4/IB9B2vD3gmcWX0tA66uUY2HZUwGLOB8YFeMcU+MMQ/cBLwv4Zo0AcQYW2OMa6vraSr/IzKfyvV1XfWw64D3J1OhJooQwgLg3cAPq9sBeBtwS/UQrzMdtRDCicDFwI8AYoz5GGMvtmkaeVOBGSGEqcBMoBXbNI2AGOMjQPcBuw/Whr0P+GmseBKYHUI4rTaVHrqxGrDmA43Dtpuq+6QRE0JYDJwLrAROjTG2Vt9qA05NqCxNHN8D/gEoV7fnAr0xxmJ123ZNI2EJkAJ+XB2O+sMQwnHYpmkExRibgX8HGqgEqz5gDbZpGj0Ha8PGRUYYqwFLGlUhhFnArcAXYoz9w9+LlWcX+PwCHbEQwnuAjhjjmqRr0YQ3FTgPuDrGeC4wyAHDAW3TdLSq97+8j0qgPx04jt8d0iWNivHYho3VgNUMLBy2vaC6TzpqIYRpVMLV9THG26q72/d3MVeXHUnVpwnhjcB7Qwj1VIY4v43KfTKzq8NrwHZNI6MJaIoxrqxu30IlcNmmaSS9A9gbY0zFGAvAbVTaOds0jZaDtWHjIiOM1YC1CjizOjvNMVRupFyRcE2aAKr3wfwI2BZj/M6wt1YAn6iufwL4Ra1r08QRY/xKjHFBjHExlfbrgRjjnwIPAn9cPczrTEctxtgGNIYQXl7d9XZgK7ZpGlkNwIUhhJnVv6P7rzPbNI2Wg7VhK4A/q84meCHQN2wo4ZgRKr1uY08I4V1U7mGoA66NMX4z4ZI0AYQQ3gQ8Cmzi2XtjvkrlPqzlwCJgH/DhGOOBN1xKhy2EcAnwxRjje0IIL6HSozUHWAd8LMaYS7I+jX8hhHOoTKZyDLAH+BSVf0C1TdOICSF8HbiCymy864DPULn3xTZNRyWEcCNwCTAPaAe+BtzB87Rh1YD/n1SGqGaAT8UYVydR9wsZswFLkiRJksabsTpEUJIkSZLGHQOWJEmSJI0QA5YkSZIkjRADliRJkiSNEAOWJEmSJI0QA5YkSZIkjRADliRJkiSNEAOWJEmSJI0QA5YkSZIkjRADliRJkiSNEAOWJEmSJI0QA5YkSZIkjRADliRJzyOEEEMIZ9TwfP8cQvjvWp1PkjQ6DFiSpKMWQqgPIQyFEAZCCG0hhJ+EEGYlXddoCSE8FELIVn/ezhDCbSGE05KuS5KUPAOWJGmk/GGMcRZwDnAu8JWE6xltf1v9eV8GzAa+m3A9kqQxwIAlSRpRMcY24B4qQQuAEMKFIYTHQwi9IYQNIYRLhr33UAjhG9X3B0IIvwwhzA0hXB9C6A8hrAohLB52/Buq+/qqyzdU918RQlg9vJYQwt+FEFZU148NIfx7CKEhhNAeQvhBCGHGsGO/FEJoDSG0hBD+/DB+3m7gVuDVL1Rf9b3TQwgrQgjdIYRdIYS/ONTzSJLGBwOWJGlEhRAWAO8EdlW35wN3At8A5gBfBG4NIZw87GMfAT4OzAdeCjwB/Lh6/Dbga9XvmlP9ru8Dc4HvAHeGEOYCvwReHkI4c9j3/glwQ3X9W1R6m84Bzqie639Wv/fyal2XAmcC7ziMn3ce8EfAut9TH8BNQBNwOvDHwL+EEN52qOeSJI19BixJ0ki5I4SQBhqBDqqhCPgYcFeM8a4YYznGeB+wGnjXsM/+OMa4O8bYB9wN7I4x/ibGWAR+TmXIIcC7gZ0xxp/FGIsxxhuB7VSGJ2aAXwAfBagGrVcAK0IIAVgG/F2MsTvGmAb+hUqwA/hwtYbNMcZB4J8P4ef9fgihF9gAtAL/44XqCyEsBN4I/GOMMRtjXA/8EPizQ/nlSpLGBwOWJGmkvD/GeDxwCZVgM6+6/8XAh6rDA3uroeRNwPBJIdqHrQ89z/b+CTNOB/YdcN59VHqjoNJb9dHq+p8Ad1SD18nATGDNsBp+Xd2//3sbD/jO3+dzMcbZMcb5McY/jTGmfk99pwP7w93z1S5JmgAMWJKkERVjfBj4CfDv1V2NwM+qYWT/67gY47eO4OtbqAS24RYBzdX1+4CTQwjnUAla+4cHdlIJaq8aVsOJ1UkqoNIDtfCA7zwSL1RfCzAnhHD8QWqXJE0ABixJ0mj4HnBpCOFs4L+pDJG7LIRQF0KYHkK4pHqv1uG6C3hZCOFPQghTQwhXAK8EfgUQYyxQGVL4bSr3b91X3V8G/gv4bgjhFKjcGxZCuKz6vcuBT4YQXhlCmMmzwxtHrL4YYyPwOPD/VH8HrwU+TeX3I0maIAxYkqQRVx0u91Pgf1aDxfuArwIpKj1aX+II/gbFGLuA9wB/D3QB/wC8J8bYOeywG6hMUvHz6j1c+/0jlYk3ngwh9AO/AV5e/d67qYTCB6rHPHC4tR1ifR8FFlPpzbod+FqM8TdHci5J0tgUYoxJ1yBJkiRJE4I9WJIkSZI0QgxYkiRJkjRCEglY1Zuc14UQfpXE+SVJkiRpNCTVg/V5YFtC55YkSZKkUTG11iesTsv7buCbVJ56f1Dz5s2LixcvrkVZkiRJknTI1qxZ0xljPPnA/TUPWFSmwf0H4PjnezOEsAxYBrBo0SJWr15dw9IkSZIk6fcLIex7vv01HSIYQngP0BFjXHOwY2KM18QYl8YYl5588u8EQkmSJEkas2p9D9YbgfeGEOqBm4C3hRB8gr0kSZKkCaGmASvG+JUY44IY42LgI8ADMcaP1bIGSZIkSRotSdyDdVQKhQJNTU1ks9mkS5mQpk+fzoIFC5g2bVrSpUiSJEnjTmIBK8b4EPDQ4X6uqamJ448/nsWLFxNCGPG6JrMYI11dXTQ1NbFkyZKky5EkSZLGnXHXg5XNZg1XoySEwNy5c0mlUkmXIkmSJNVEJl+kN1OgN1Ogb6hA31C+uhz+KtJfXe/PFrj0rFMP+n3jLmABhqtR5O9WkiRJ41G+WKY3k6c7k6dnsEBvJk9PpkBPJk9vJk9vpkBPphKghq8XSvGwz9W/pHDQ98ZlwJIkSZI0sfUNFegezNM9mKNrIE/3YJ6uwcqyZ3B/kHo2UA3kikmXDEyAgLX4y3eO6PfVf+vdv/eYuro6XvOa11AsFlmyZAk/+9nPmD179ojWMdr++Z//mVmzZvHFL34x6VIkSZI0CRRKZboG8nQO5EgN5OhM5+gazD+7HKgEqa7BHD2DBfKlctIlH5FxH7CSMGPGDNavXw/AJz7xCa666ir+6Z/+KeGqKpNUxBiZMqXWjzeTJEnSZBRjpDdToCOdI5XO0ZHOPrO+/9U5UHn1DhWIhz8ab9wxYB2liy66iI0bNwKwe/duPvvZz5JKpZg5cyb/9V//xSte8Qra29v5q7/6K/bs2QPA1VdfzRve8Aa+853vcO211wLwmc98hi984Qt8+ctfZuHChXz2s58FntvT9O1vf5vly5eTy+X4wAc+wNe//nXq6+u57LLLuOCCC1izZg133XUXy5cv/53jAL75zW9y3XXXccopp7Bw4UJe97rXJfAbkyRJ0njQm8nT3p+jrT9Le3+WVDpHe3W9vf/ZADVee5pGiwHrKJRKJe6//34+/elPA7Bs2TJ+8IMfcOaZZ7Jy5Ur+5m/+hgceeIDPfe5zvOUtb+H222+nVCoxMDDAmjVr+PGPf8zKlSuJMXLBBRfwlre8hSuuuIIvfOELzwSs5cuXc88993Dvvfeyc+dOnnrqKWKMvPe97+WRRx5h0aJF7Ny5k+uuu44LL7zwoMcdd9xx3HTTTaxfv55isch5551nwJIkSZqEyuVIaiBHa1+Wtr6h6jJLW/+zy/b+LNmCwelIGLCOwNDQEOeccw7Nzc2cddZZXHrppQwMDPD444/zoQ996JnjcrkcAA888AA//elPgcr9WyeeeCKPPfYYH/jABzjuuOMA+OAHP8ijjz7K5z73OTo6OmhpaSGVSnHSSSexcOFCrrzySu69917OPfdcAAYGBti5cyeLFi3ixS9+MRdeeCEA99577/Mel06n+cAHPsDMmTMBeO9731ubX5YkSZJqqjeTp6lniJbeIdr6szT3DtHSm6W1txKm2vuzFMuTYKxeQgxYR2D/PViZTIbLLruMq666ik9+8pPMnj37mXuzjsaHPvQhbrnlFtra2rjiiiuAyvjWr3zlK/zlX/7lc46tr69/JqS90HHf+973jrouSZIkJSvGSEc6R1NPhqaeIZp6hmjuHaK5umzpHSKTLyVd5qTmbAhHYebMmXz/+9/nP/7jP5g5cyZLlizh5z//OVC5+Dds2ADA29/+dq6++mqgMqywr6+PN7/5zdxxxx1kMhkGBwe5/fbbefOb3wzAFVdcwU033cQtt9zyTI/YZZddxrXXXsvAwAAAzc3NdHR0/E5NBzvu4osv5o477mBoaIh0Os0vf/nL0f3lSJIk6Yh0DeRY39jLLze0cNWDu/jKbZv4+I9W8tZ/f4iX/5+/5oJ/uZ8/uvoJPn/Ter59z9PcsLKBh3ek2NUxYLgaA8Z9D9ahTKs+ms4991xe+9rXcuONN3L99dfz13/913zjG9+gUCjwkY98hLPPPpsrr7ySZcuW8aMf/Yi6ujquvvpqLrroIj75yU9y/vnnA5VJLvYP63vVq15FOp1m/vz5nHbaaQD8wR/8Adu2beOiiy4CYNasWfz3f/83dXV1z6nnYMedd955XHHFFZx99tmccsopvP71r6/Vr0iSJEnDFEplmnqG2Nc1SEN3hoauTGXZnaGxO8OgIWlcC3EMz5W4dOnSuHr16ufs27ZtG2eddVZCFU0O/o4lSZKOTr5YpqE7Q33nIPVdlde+rgz7ujI09w5R8h6oce2j5y/kW3909poY49ID3xv3PViSJElSEsrlSHPvEHs6B9mbGmBv52BlvXOQlt4hzFCTkwFLkiRJegEDuSK7OwbYnaq89qQG2Z0aoL4rQ77oVOZ6rnEZsGKMhBCSLmNCGstDRiVJkkZTKp1jZ0ea3R0D7OoYYFeqsmzvzyVdmsaRcRewpk+fTldXF3PnzjVkjbAYI11dXUyfPj3pUiRJkkZNKp1jR3uane1pdnQMsLM9zc6OAXozhaRL0wQw7gLWggULaGpqIpVKJV3KhDR9+nQWLFiQdBmSJElHLZ0tsKM9zfa2NDva0jzdnmZH+wDdg/mkS9MENu4C1rRp01iyZEnSZUiSJGmMKJUjezsH2NaaZntbP9tbK6GquXco6dI0CY27gCVJkqTJK50tsL0tzdaWfra29LOtrZ8d7WmyBSeb0NhgwJIkSdKYlErn2NzSx5bmPra29rOlpZ+G7gzOyaWxzIAlSZKkxLX1ZdnY1Mvmln42N/exubmPjrSz92n8MWBJkiSpplLpHBubetnY1Mem5j42NvXROWCY0sRgwJIkSdKoSWcLbGrqY31TLxsb+9jY1EtLXzbpsqRRY8CSJEnSiCiVI9vb+lnX0Mv6xl42NPayOzVA2XumNIkYsCRJknREUukcaxt6WNfQy7qGHjY195HJl5IuS0qUAUuSJEm/V7kc2d6WZk1DD2v39bBmXw8N3Zmky5LGHAOWJEmSfkcmX2RdQy+r63tYva+bdQ29DOSKSZcljXk1DVghhOnAI8Cx1XPfEmP8Wi1rkCRJ0u/qGsixqr6HVfXdrKrvZmtLP0VvnpIOW617sHLA22KMAyGEacBjIYS7Y4xP1rgOSZKkSa21b4in9nazcm83T+3tZlfHQNIlSRNCTQNWjDEC+//rnVZ9+U8jkiRJo6y5d4iVe7p4ck8XT+7p9v4paZTU/B6sEEIdsAY4A7gqxrjygPeXAcsAFi1aVOvyJEmSJoT2/iyP7+7kyd3dPL6nk8buoaRLkiaFmgesGGMJOCeEMBu4PYTw6hjj5mHvXwNcA7B06VJ7tyRJkg5Bz2Cex3d38fjuTp7Y3cWezsGkS5ImpcRmEYwx9oYQHgQuBzb/vuMlSZL0rKF8iafqu3lsZ4rf7upiW1s/0X+alhJX61kETwYK1XA1A7gU+Nda1iBJkjQelcuRTc19PLark0d3pli7r5d8qZx0WZIOUOserNOA66r3YU0BlscYf1XjGiRJksaFlt4hHtmR4tGdnfx2dye9mULSJUn6PWo9i+BG4NxanlOSJGm8yBZKrNzbzcNPp3h4Rwe7U95HJY03id2DJUmSJNiTGuChp1M8tCPFyj1d5IoO+5PGMwOWJElSDWULJZ7Y08VD2zt48OmUz6OSJhgDliRJ0ihr7h3ige0dPLi9g8d3d5It2EslTVQGLEmSpBFWLkfWNfZy/7Z2Htjewfa2dNIlSaoRA5YkSdIIyOSLPLKjk99sa+fB7R10DeaTLklSAgxYkiRJR6ijP8t929q5b2s7j+/uIu8EFdKkZ8CSJEk6DLs60tyzpZ17t7azsamXGJOuSNJYYsCSJEl6ATFW7qe6d0s7925pY0+nz6aSdHAGLEmSpAMUS2VW7u3mni1t3LOljfb+XNIlSRonDFiSJElAvljmsV0p7t7Uxm+2tdOTKSRdkqRxyIAlSZImrWyhxMM7Uty9qZX7t3eQzhaTLknSOGfAkiRJk0q2UOKhp1PctamV+7e1M5gvJV2SpAnEgCVJkiY8Q5WkWjFgSZKkCSlfLPPIjhR3bmrlvq3tDOQc/idp9BmwJEnShFEqRx7f3cmK9S3cs6WNfu+pklRjBixJkjSuxRhZva+HFetbuHtzK50D+aRLkjSJGbAkSdK4tLWln19saOZXG1pp7h1KuhxJAgxYkiRpHGnszvCL9c38Yn0LOzsGki5Hkn6HAUuSJI1pPYN5frWxhTvWt7BmX0/S5UjSCzJgSZKkMSdbKHH/tg5uX9fEwztSFEox6ZIk6ZAYsCRJ0pgQY2Tl3m5uX9vMXZtbSTsDoKRxyIAlSZIStSc1wG1rm7ljfTNNPU5WIWl8M2BJkqSa68sUWLGxhdvWNrGuoTfpciRpxBiwJElSTRRLZR7ekeLWtU38ZlsH+WI56ZIkacQZsCRJ0qh6ui3NLWsauX1dC50DuaTLkaRRZcCSJEkjri9T4BcbmrllTRMbm/qSLkeSasaAJUmSRkS5HHl0VyfLVzdy39Z2hwBKmpRqGrBCCAuBnwKnAhG4JsZ4ZS1rkCRJI2tf1yA/X93ErWubaO3LJl2OJCWq1j1YReDvY4xrQwjHA2tCCPfFGLfWuA5JknQUsoUSd21qZfnqRlbu7Sb6HGBJAmocsGKMrUBrdT0dQtgGzAcMWJIkjQMbm3q5eVUjK9a3kM75IGBJOlBi92CFEBYD5wIrD9i/DFgGsGjRoprXJUmSnqsvU+D2dU3ctKqR7W3ppMuRpDEtkYAVQpgF3Ap8IcbYP/y9GOM1wDUAS5cudcCBJEkJiDHyxJ4ubl7VyK83t5FzwgpJOiQ1D1ghhGlUwtX1Mcbban1+SZJ0cB3pLLesaWL5qkbquzJJlyNJ406tZxEMwI+AbTHG79Ty3JIk6fmVy5GHd6a4cWUDD2zvoFh2AIkkHala92C9Efg4sCmEsL6676sxxrtqXIckSZNea98QN69q5Oerm2juHUq6HEmaEGo9i+BjQKjlOSVJ0rNK5cgD2zu48akGHt6RomRvlSSNqMRmEZQkSbXT3DvEzU81sHx1E239PgxYkkaLAUuSpAlqf2/VDSv38fCOFHZWSdLoM2BJkjTBtPQOcdOqRpavarS3SpJqzIAlSdIEUCpHHnq6gxtWNvCQ91ZJUmIMWJIkjWNtfVmWr27kpqcaaOmzt0qSkmbAkiRpnCmXI4/u6uT6J/dx//YOe6skaQwxYEmSNE50DuRYvrqRG59qoLHb51ZJ0lhkwJIkaYx7fHcn169s4N4tbRRK9lZJ0lhmwJIkaQzqzeS5ZU0TNzzVwJ7UYNLlSJIOkQFLkqQxZHV9NzesbODOTa3kiuWky5EkHSYDliRJCUtnC9y+rpnrn2zg6fZ00uVIko6CAUuSpIRsaurj+pX7WLGhhUy+lHQ5kqQRYMCSJKmGMvkiK9a3cP3KBjY19yVdjiRphBmwJEmqge1t/dywsoHb1zaTzhWTLkeSNEoMWJIkjZJsocSvNrZyw8p9rG3oTbocSVINGLAkSRphuzrSXL+ygdvWNtM3VEi6HElSDRmwJEkaAbliibs3tXHDygaequ9OuhxJUkIMWJIkHYXdqQFuXNnArWub6MnYWyVJk50BS5Kkw5Qrlvj15kpv1cq99lZJkp5lwJIk6RDt6khz41ON3Lq2iV57qyRJz8OAJUnSC8gWSty5sZWbVjWwqr4n6XIkSWOcAUuSpOexrbWfG59q4I51zfRnfW6VJOnQGLAkSaoazBVZsaGFm55qYENTX9LlSJLGIQOWJGnSW7Ovh5tXNfCrja1k8qWky5EkjWMGLEnSpNQ1kOP2dc3cvKqRnR0DSZcjSZogDFiSpEmjVI48siPFzasauX97O4VSTLokSdIEY8CSJE14ezsH+fnqyvTq7f25pMuRJE1gNQ1YIYRrgfcAHTHGV9fy3JKkyWUwV+TO+6mOhgAACqxJREFUja38fE2j06tLkmqm1j1YPwH+E/hpjc8rSZoEYow8saeLW9Y08evNbU5YIUmquZoGrBjjIyGExbU8pyRp4qvvHOTWtU3ctraZ5t6hpMuRJE1iY+4erBDCMmAZwKJFixKuRpI0VvUNFbhzYyu3rW1i9T6HAEqSxoYxF7BijNcA1wAsXbrU6Z0kSc8olMo89HSK29c18ZttHeSL5aRLkiTpOcZcwJIk6UBr9vVwx7pmfrWxhZ5MIelyJEk6KAOWJGlM2tUxwIr1zdyxvoWG7kzS5UiSdEhqPU37jcAlwLwQQhPwtRjjj2pZgyRp7GrtG+KXG1r4xfoWtrT0J12OJEmHrdazCH60lueTJI19nQM57t7Uyi83tLJqXzfRu28lSeOYQwQlSTXXm8lzz5Y2frmhlSf2dFEqm6okSRODAUuSVBN9mQL3bGnjzk2tPL67k0LJUCVJmngMWJKkUdM9mOfeLW3ctbmNJwxVkqRJwIAlSRpRbX1Z7t3axt2b2niqvtvhf5KkScWAJUk6artTA9y7pZ17trSxoanXiSokSZOWAUuSdNjK5ci6xh7u29rBfVvb2J0aTLokSZLGBAOWJOmQDOaKPLqzk/u3tfPA9g66BvNJlyRJ0phjwJIkHdS+rkEe2N7Bg0+neHJPF/liOemSJEka0wxYkqRnZAslVu7t5qGnO3j46RR7Oh36J0nS4TBgSdIkt7M9zSM7O3lkR4qVe7vIFuylkiTpSBmwJGmS6RzI8dtdnTy6s5Pf7uqktS+bdEmSJE0YBixJmuD6swWe2tPN47u7eHx3J0+3p51GXZKkUWLAkqQJpj9bYHV9Nyv3dPPEni62tPT7sF9JkmrEgCVJ41znQI7V9d08tbeHlXu72Nbaj3lKkqRkGLAkaRyJMbI7NcDq+h7W7Ku8nOlPkqSxw4AlSWNYX6bA+qZe1jX0sK6hl/WNvfQNFZIuS5IkHYQBS5LGiKF8ia2tfWxs6mNDYy8bmvrYa++UJEnjigFLkhIwkCuyrbWfzc19bG6uLHelBpyMQpKkcc6AJUmjrKknw/bWNNvb+tna2s+21jT1XYNOlS5J0gRkwJKkEZJK59jZkWZHW5odHQPsaEvzdHuadLaYdGmSJKlGDFiSdBhK5UhTT4Y9qUF2pwbYnRpgV0fl1ZNx8glJkiY7A5YkHaBcjrT2Z9nXOUh9V4b6rkHqOwfZ2znIvq4M+VI56RIlSdIYZcCSNCn1DOZp6hmiqSdDY0+Gpp4hGrozNHRV1g1RkiTpSBiwJE04Q/kSrX1DtPVlaenL0tY3RHNvlpbeoWdeg/lS0mVKkqQJyIAladxIZwt0DuRJpXOk0jk60lk60jk6+ivrbX1Z2vuz9DuphCRJSogBS1IiYoykc0V6BvP0ZAr0DObprr66BvN0D+boGsjTOZinayBH50CObMFhe5IkaWwzYEk6YoVSmXS2yEC2SH+2QH+2QDpbpH+oQH912Tfs1ZvJ0ztUoC9T2S76UF1JkjTB1DxghRAuB64E6oAfxhi/VesapMkmxki2UGaoUKq88tVXoUQmX2QoXyKTL5EplMjkigzm9y+LDOYqx6SzRQZyRQZzlWU6WyRXtEdJkiRpuJoGrBBCHXAVcCnQBKwKIayIMW6tZR3SaCqVI8VymWIpUixFCvvXy2UKpUihVK6+quvFMoVyJF8sUyyVyZfK5IvDlsXnbueeeZUqy8Lw9coyWyiRLZTJFkvPrEuSJGn01boH63xgV4xxD0AI4SbgfcCIBKwYD3+40Qt95IW+7fnOdeCe5/vuOOyog517+P79xz9333NriAd+Lv7uZ4d/5sDjh39P5djnfi7GOOzYyrJc/Z79n62M9KocVx52/nK5snzO52JleeBn9r8Xq+9F4rD9zx5XKsdnfo5SOT7nOyvvQSlW9pfL8ZnPlKv7SuVnj92/v1SOlGKkVKosy/u3y5WQ9Mx6uXJMsRwplcvVZXwmQBWr35ekqXWBWXVTmTU90TIkSZImrPmzZxz0vVoHrPlA47DtJuCC4QeEEJYBy6qbuRDC5hrVpsltHtCZdBGa8LzOVAteZ6oVrzXVwpi8zu6sLF78fO+NuUkuYozXANcAhBBWxxiXJlySJgGvNdWC15lqwetMteK1ploYj9fZlBqfrxlYOGx7QXWfJEmSJI17tQ5Yq4AzQwhLQgjHAB8BVtS4BkmSJEkaFTUdIhhjLIYQ/ha4h8o07dfGGLe8wEeuqU1lkteaasLrTLXgdaZa8VpTLYy76ywcycx7kiRJkqTfVeshgpIkSZI0YRmwJEmSJGmEjNmAFUK4PITwdAhhVwjhy0nXo4khhLAwhPBgCGFrCGFLCOHz1f1zQgj3hRB2VpcnJV2rxr8QQl0IYV0I4VfV7SUhhJXVdu3m6mQ/0lEJIcwOIdwSQtgeQtgWQrjINk0jLYTwd9W/m5tDCDeGEKbbpmkkhBCuDSF0DH/27cHasFDx/eo1tzGEcF5ylR/cmAxYIYQ64CrgncArgY+GEF6ZbFWaIIrA38cYXwlcCHy2em19Gbg/xngmcH91Wzpanwe2Ddv+V+C7McYzgB7g04lUpYnmSuDXMcZXAGdTueZs0zRiQgjzgc8BS2OMr6YyUdlHsE3TyPgJcPkB+w7Whr0TOLP6WgZcXaMaD8uYDFjA+cCuGOOeGGMeuAl4X8I1aQKIMbbGGNdW19NU/kdkPpXr67rqYdcB70+mQk0UIYQFwLuBH1a3A/A24JbqIV5nOmohhBOBi4EfAcQY8zHGXmzTNPKmAjNCCFOBmUArtmkaATHGR4DuA3YfrA17H/DTWPEkMDuEcFptKj10YzVgzQcah203VfdJIyaEsBg4F1gJnBpjbK2+1QacmlBZmji+B/wDUK5uzwV6Y4zF6rbtmkbCEiAF/Lg6HPWHIYTjsE3TCIoxNgP/DjRQCVZ9wBps0zR6DtaGjYuMMFYDljSqQgizgFuBL8QY+4e/FyvPLvD5BTpiIYT3AB0xxjVJ16IJbypwHnB1jPFcYJADhgPapuloVe9/eR+VQH86cBy/O6RLGhXjsQ0bqwGrGVg4bHtBdZ901EII06iEq+tjjLdVd7fv72KuLjuSqk8TwhuB94YQ6qkMcX4blftkZleH14DtmkZGE9AUY1xZ3b6FSuCyTdNIegewN8aYijEWgNuotHO2aRotB2vDxkVGGKsBaxVwZnV2mmOo3Ei5IuGaNAFU74P5EbAtxvidYW+tAD5RXf8E8Ita16aJI8b4lRjjghjjYirt1wMxxj8FHgT+uHqY15mOWoyxDWgMIby8uuvtwFZs0zSyGoALQwgzq39H919ntmkaLQdrw1YAf1adTfBCoG/YUMIxI1R63caeEMK7qNzDUAdcG2P8ZsIlaQIIIbwJeBTYxLP3xnyVyn1Yy4FFwD7gwzHGA2+4lA5bCOES4IsxxveEEF5CpUdrDrAO+FiMMZdkfRr/QgjnUJlM5RhgD/ApKv+AapumERNC+DpwBZXZeNcBn6Fy74ttmo5KCOFG4BJgHtAOfA24g+dpw6oB/z+pDFHNAJ+KMa5Oou4XMmYDliRJkiSNN2N1iKAkSZIkjTsGLEmSJEkaIQYsSZIkSRohBixJkiRJGiEGLEmSJEkaIQYsSZIkSRohBixJkiRJGiH/G+9duCa+fUOIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"from scipy.integrate import solve_ivp\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"\n",
"# time horizon in days\n",
"d = 15 * 7 \n",
"\n",
"# disease dynamics\n",
"Rt = 4.0\n",
"theta = 1/3.0 # 1/incubation time in days\n",
"rho = 1.0/14.0 # 1/time to recovery in days\n",
"mu = 1.0/1.0 # 1/time to false-postive return in days\n",
"p_si = 0.20 # probability of symptoms given infection\n",
"p_fs = 0.0005 # probability of fataility given symptoms\n",
"\n",
"sigma = rho * p_si / (1 - p_si) # rate of symptom development\n",
"beta = (sigma + rho)*Rt\n",
"delta = rho * (p_fs/p_si) / (1 - (p_fs/p_si))\n",
"\n",
"# testing protocols\n",
"Sp = 0.98 # test specificity\n",
"Se = 0.70 # test sensitivity\n",
"tau = 1000 # testing period\n",
"\n",
"# population parameters\n",
"x = 10.0 # weekly exogeneous infections\n",
"y = 10.0\n",
"IC = [8200-y, 0, y, 0, 0, 0, 0, 0]\n",
"\n",
"# SEIR model differential equations.\n",
"def deriv(t, X):\n",
" U, E, A, S, Tp, Fp, R, D = X\n",
" exog = x*((t + 1) % 7 < 1)\n",
" dU = -beta*U*A/(U + E + A + R) - (1 - Sp)*U/tau + mu*Fp - exog\n",
" dE = beta*U*A/(U + E + A + R) - theta*E + exog\n",
" dA = theta*E - (sigma + rho + Se/tau)*A\n",
" dS = -(rho + delta)*S + sigma*(Tp + A)\n",
" dTp = -(sigma + rho)*Tp + Se*A/tau\n",
" dFp = -mu*Fp + (1 - Sp)*U/tau\n",
" dR = rho*(Tp + S + A)\n",
" dD = delta*S\n",
" return np.array([dU, dE, dA, dS, dTp, dFp, dR, dD,])\n",
"\n",
"t = np.linspace(0, d, 10*d + 1)\n",
"soln = solve_ivp(deriv, [0, max(t)], IC, t_eval = t, atol=1e-8, rtol=1e-8)\n",
"U, E, A, S, Tp, Fp, R, D = soln.y\n",
"\n",
"fix, ax = plt.subplots(3, 1, figsize=(12, 8))\n",
"ax[0].stackplot(t, U, E, A, R)\n",
"ax[0].set_ylim(0, sum(IC))\n",
"ax[0].set_title('Active Transmission and Testing Pool')\n",
"\n",
"ax[1].stackplot(t, S, Tp, Fp)\n",
"ax[1].legend(['Symptomatic', 'False Positive', 'True Positive'], loc=\"upper left\")\n",
"ax[1].set_title('Isolation Pool')\n",
"\n",
"ax[2].stackplot(t, D)\n",
"ax[2].set_title('Removed Pool')\n",
"ax[2].legend(['Recovered', 'Dead'], loc=\"upper left\")\n",
"\n",
"for a in ax:\n",
" a.set_xlim(0, d)\n",
"\n",
"plt.tight_layout()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "gXw3CAB3rt3u",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [2.2 Campus SEIR Modeling](https://jckantor.github.io/CBE40455-2020/02.02-Campus-SEIR-modeling.html) | [Contents](toc.html) | [2.4 Linear Analysis of Campus Reopening](https://jckantor.github.io/CBE40455-2020/02.04-Linear-Analysis-of-Campus-Reopening.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "eAbATGsb5fwf",
"nbpages": {
"level": 1,
"link": "[2.3 Campus Re-opening Model](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3-Campus-Re-opening-Model)",
"section": "2.3 Campus Re-opening Model"
}
},
"source": [
"# 2.3 Campus Re-opening Model\n",
"\n",
"Following [Paltiel, et al. (2020)](https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2768923). \n",
"\n",
"\n",
"\n",
"(Figure e1 from Paltiel, et al., 2020)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "fmDN0ArmBQ5C",
"nbpages": {
"level": 3,
"link": "[2.3.1 Active transmission and testing pool. ](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.1-Active-transmission-and-testing-pool.)",
"section": "2.3.1 Active transmission and testing pool. "
}
},
"source": [
"\n",
"### 2.3.1 Active transmission and testing pool. \n",
"\n",
"This pool consists of individuals in the campus population subject to testing and the transmission of virus.\n",
"\n",
"* $U$ uninfected, susceptible individuals\n",
"* $E$ exposed, asymptomatic, non-infectious\n",
"* $A$ infected, asymptomatic\n",
"\n",
"\\begin{align*}\n",
"\\frac{dU}{dt} & = -\\beta U \\frac{A}{U + E + A} - \\tau (1-S_p) U + \\mu F_p - x(t) \\\\\n",
"\\frac{dE}{dt} & = \\beta U \\frac{A}{U + E + A} - \\theta E + x(t) \\\\\n",
"\\frac{dA}{dt} & = \\theta E - (\\sigma + \\rho + \\tau S_e)A\n",
"\\end{align*} \n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "H3sOz0YPBYOW",
"nbpages": {
"level": 3,
"link": "[2.3.2 Isolation pool](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.2-Isolation-pool)",
"section": "2.3.2 Isolation pool"
}
},
"source": [
"### 2.3.2 Isolation pool\n",
"\n",
"* $S$ infected, symptomatic with a true positive test result.\n",
"* $T_p$ infected, asymptomatic with a true positive test result\n",
"* $F_p$ uninfected with a false positive result.\n",
"\n",
"\\begin{align*}\n",
"\\frac{dF_p}{dt} & = -\\mu F_p + \\tau(1-S_p) U \\\\\n",
"\\frac{dT_p}{dt} & = -(\\sigma + \\rho) T_p + \\tau S_e A\\\\\n",
"\\frac{dS}{dt} & = -(\\rho + \\delta)S + \\sigma (T_p + A)\n",
"\\end{align*} "
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "D64CeE2hCIdC",
"nbpages": {
"level": 3,
"link": "[2.3.3 Removed pool](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.3-Removed-pool)",
"section": "2.3.3 Removed pool"
}
},
"source": [
"### 2.3.3 Removed pool\n",
"\n",
"* $R$ recovered. These individuals assumed to be immune for the remainder of the simulation, and not returned to the campus population.\n",
"* $D$ dead.\n",
"\n",
"\\begin{align*}\n",
"\\frac{dR}{dt} & = \\rho (T_p + A + S)\\\\\\\n",
"\\frac{dD}{dt} & = \\delta S\n",
"\\end{align*} "
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "Yso2VSWXrssr",
"nbpages": {
"level": 3,
"link": "[2.3.4 Parameter estimates](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4-Parameter-estimates)",
"section": "2.3.4 Parameter estimates"
}
},
"source": [
"### 2.3.4 Parameter estimates\n",
"\n",
"Given:\n",
"\n",
"* $\\rho$ recovery rate \n",
"* $R_t$ basic reproductive number for asymptomatic transmission \n",
"* $p_{si}$ probability that an infected individual will become symptomatic.\n",
"\n",
"\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "6SpT6hhJ5lmU",
"nbpages": {
"level": 4,
"link": "[2.3.4.1 Odds of becoming symptomatic if infected](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.1-Odds-of-becoming-symptomatic-if-infected)",
"section": "2.3.4.1 Odds of becoming symptomatic if infected"
}
},
"source": [
"#### 2.3.4.1 Odds of becoming symptomatic if infected\n",
"\n",
"Based on the compartmental relationships and rates, the probability of symptom development for infected individuals is given by\n",
"\n",
"$$p_{si} = \\frac{\\sigma}{\\sigma + \\rho}$$\n",
"\n",
"Inverting this relationship\n",
"\n",
"$$\\sigma = \\frac{p_{si}}{1 - p_{si}}\\rho$$\n",
"\n",
"where $\\frac{p_{si}}{1 - p_{si}}$ is the 'odds' that an infected individual becomes symptomatic.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "-N4_RCNk5xPJ",
"nbpages": {
"level": 4,
"link": "[2.3.4.2 Effective reproductive number with isolation of symptomatic individuals](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.2-Effective-reproductive-number-with-isolation-of-symptomatic-individuals)",
"section": "2.3.4.2 Effective reproductive number with isolation of symptomatic individuals"
}
},
"source": [
"#### 2.3.4.2 Effective reproductive number with isolation of symptomatic individuals\n",
"\n",
"For an initially uninfected population with no testing regime, where transmission is solely due to non-isolated, asymptomatic individuals, the effective reproductive number is\n",
"\n",
"$$R_t = \\frac{\\beta}{\\sigma + \\rho}$$\n",
"\n",
"Expressed in terms of recovery rate and probability of becoming symptomatic\n",
"\n",
"$$R_t = \\frac{\\beta}{\\rho}(1 - p_{si})$$"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "8e0Q1QYCAtcK",
"nbpages": {
"level": 4,
"link": "[2.3.4.3 Testing threshold](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.3-Testing-threshold)",
"section": "2.3.4.3 Testing threshold"
}
},
"source": [
"#### 2.3.4.3 Testing threshold\n",
"\n",
"With a testing regime, for effective herd immunity requires\n",
"\n",
"$$\\beta \\leq \\sigma + \\rho + \\tau S_e $$\n",
"\n",
"where $\\tau$ is the testing rate and $S_e$ is the test sensitivity. With some manipulation using the above relationships, the testing treshhold becomes\n",
"\n",
"$$\\tau S_e \\geq \\frac{(R_t - 1) \\rho}{1 - p_{si}}$$\n",
"\n",
"or \n",
"\n",
"$$\\frac{1}{\\tau} \\leq S_e \\left(\\frac{1 - p_{si}}{R_t - 1}\\right)\\frac{1}{\\rho} $$"
]
},
{
"cell_type": "markdown",
"metadata": {
"colab_type": "text",
"id": "DM1O_lhAEPEN",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
}
},
"source": [
"#### 2.3.4.4 Parameter values\n",
"\n",
"| parameter | value |\n",
"| :--: | :--: |\n",
"| $p_{si}$ | 0.3 |\n",
"| $R_t$ | [1.5, 2.5, 3.5] |\n",
"| $\\frac{1}{\\rho}$ | 14 d |\n",
"| $S_e$ | 0.7 |\n",
"\n",
"\n",
"t"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 283
},
"colab_type": "code",
"executionInfo": {
"elapsed": 594,
"status": "ok",
"timestamp": 1596387599982,
"user": {
"displayName": "Jeffrey Kantor",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gg_n8V7bVINy02QRuRgOoMo11Ri7NKU3OUKdC1bkQ=s64",
"userId": "09038942003589296665"
},
"user_tz": 300
},
"id": "Nlvxm2wvE-hm",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
},
"outputId": "cab1ce50-2134-4b13-f688-59a4ebaed9a1"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAZkAAAEKCAYAAADAVygjAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd3gc1dX48e9Rr1a3LFm2ZRts425L2BgMSJTQjCGB0GsITiAhkIQU/943QMqbQEghCQm9JRTTAzG9WDbNNi64997lKltylXV+f+yYyGJXGq12drXa83meebQzO+Xcmd09mpk794qqYowxxnghLtIBGGOM6bgsyRhjjPGMJRljjDGesSRjjDHGM5ZkjDHGeCYh0gG4kZ+fr6WlpUEtW1dXR3p6emgDaueszLHByhwb2lLmmTNnblPVghCH1CpRkWRKS0uZMWNGUMtWVVVRUVER2oDaOStzbLAyx4a2lFlE1oQ2mtbz7HKZiHQTkUkislBEFojIrc70XBF5T0SWOX9zvIrBGGNMZHl5T6Ye+LGq9gdOAL4nIv2BnwMfqOqxwAfOuDHGmA7IsySjqptUdZbzeg+wCOgKXAA85cz2FHChVzEYY4yJLAlHszIiUgpMAQYCa1U125kuwM4j402WGQeMAygsLCybMGFCUNuura0lIyMjuMCjlJU5NliZY0NbylxZWTlTVctDHFLrqKqnA5ABzAS+4YzvavL+zpbWUVZWpsGaNGlS0MtGKytzbLAyx4a2lBmYoR7/xrc0ePqcjIgkAi8Dz6jqK87kLSJS5LxfBFR7GYMxxpjI8bJ2mQCPAYtU9U+N3noduNZ5fS3wmlcxGGOMiSwvz2ROAq4GThORL5zhXOBu4EwRWQac4Yx7ompJNRNXHPRq9cYYY1rg2cOYqvoxIAHePt2r7Tb26YrtvLr8EL88UE96clQ8d2qMMR1Kh267rKJPAYfVl2yMMcaEX4dOMmWlOSTHw+SlVrfAGGMioUMnmeSEePrnxVO1ZOuR6tLGGGPCqEMnGYBB+fGs37mPldvqIh2KMcbEnJhIMgCTl2yNcCTGGBN7OnySKUiLo1dBOlVLLckYY0y4dfgkA3BqnwKmrdzO/kOHIx2KMcbElJhIMhV9O3OgvoHPVlpVZmOMCaeYSDIje+aSnBBn92WMMSbMYiLJpCTGc0KvPKbYfRljjAmrmEgyABV9C1i5rY612/dGOhRjjIkZMZNkTu1TANjT/8YYE04xk2R65qfTPTeNyXbJzBhjwiZmkoyIcGqfAj5dsZ0D9VaV2RhjwiFmkgz4LpntPXiYGat3RjoUY4yJCV72jPm4iFSLyPxG04aKyFSnA7MZIjLCq+37M6p3HknxcVQtsfsyxhgTDl6eyTwJnN1k2u+BX6rqUOAOZzxs0pMTOL5njt2XMcaYMPEsyajqFGBH08lAJ+d1FrDRq+0HUtGnM0u31LJx175wb9oYY2JOuO/J3AbcKyLrgD8A48O8fU7te6Qqs53NGGOM18TLzrxEpBSYqKoDnfG/ApNV9WURuQQYp6pnBFh2HDAOoLCwsGzChAlBxVBbW0tGRsaX46rKjyfvo2dWHLcMSwlqne1d0zLHAitzbLAyt05lZeVMVS0PcUito6qeDUApML/ReA3/TWwC7HaznrKyMg3WpEmTvjLt5y/P0YF3vK0H6w8Hvd72zF+ZOzorc2ywMrcOMEM9/I13M4T7ctlG4FTn9WnAsjBvH4DKvp3Zc6Cez1ZYq8zGGOOlBK9WLCLPARVAvoisB+4EbgT+IiIJwH6cy2HhdkqfAjKSE5g4dyOnOM3NGGOMCT3PkoyqXh7grTKvtulWSmI8Z/Yv5O35m/nNhYNISoipZ1KNMSZsYvbX9fwhRezeX8/Hy62WmTHGeCVmk8zoYwrISk1k4pxNkQ7FGGM6rJhNMkkJcZw1oJB3F25h/yFrMNMYY7wQs0kGYMzgYmoP1FNl3TIbY4wnYjrJnNg7j9z0JCbODXvrNsYYExNiOskkxMdx9sAufLComr0H6yMdjjHGdDgxnWQAxgwuYt+hw3y42Jr/N8aYUIv5JDOyZx4FmclWy8wYYzwQ80kmPk44b1ARk5ZUU3vALpkZY0woxXySAd8lswP1Dby/cEukQzHGmA7FkgwwvHsORVkp/GeO1TIzxphQsiQDxDmXzKYs20rN3kORDscYYzoMSzKOMUOKOXRYeWfh5kiHYowxHYYlGceQkiy65aYyca7VMjPGmFCxJOMQEcYMLuaT5dvYUXcw0uEYY0yHYEmmkfMHF3O4Qa0CgDHGhEiLSUZEbhWRTuLzmIjMEpGvuVjucRGpFpH5TabfIiKLRWSBiPy+LcGHWv/iTgzqmsVz09fi6x7bGGNMW7g5k/mWqu4GvgbkAFcDd7tY7kng7MYTRKQSuAAYoqoDgD+0KtowuGJkdxZv3sOstTsjHYoxxkQ9N0lGnL/nAv9S1QWNpgWkqlOAHU0m3wTcraoHnHnaXYNhY4cUk5GcwDPT1kY6FGOMiXrS0mUhEXkC6Ar0BIYA8UCVqpa1uHKRUmCiqg50xr8AXsN3hrMfuF1VPw+w7DhgHEBhYWHZhAkT3JWoidraWjIyMlq1zD8XHOCjDfX8uSKNjKQW82m7E0yZo52VOTZYmVunsrJypqqWhzik1lHVZgd8ZzvDgWxnPA8Y3NJyzrylwPxG4/OBv+E7ExoBrMJJdM0NZWVlGqxJkya1epkFG2q0x88m6qMfrQx6u5EUTJmjnZU5NliZWweYoS5+q70c3FwuexEoAnY7SWm7qs4NMqetB15xyj8daADyg1yXZ/oXd2JY92yenbbGKgAYY0wbuEkyDwBXAMtE5G4R6duG7f0bqAQQkT5AErCtDevzzBUjurNiax3TVzW9rWSMMcatFpOMqr6vqlfiu2S2GnhfRD4VketFJDHQciLyHPAZ0FdE1ovIDcDjQC+nWvME4Fptp6cKYwYXk5liFQCMMaYtEtzMJCJ5wFX4qi/PBp4BRgPXAhX+llHVywOs7qpWRxkBqUnxXDS8hGenrWVH3UFy05MiHZIxxkQdNw9jvgp8BKQB56vqWFV9XlVvATp0NY8rR3bn4OEGXpq5LtKhGGNMVHJzT+avqtpfVX+nqke1HqmRrhrnsWMLMzm+NIdnp62loaFdXtUzxph2zc09mUkiMlBELhGRa44M4QiuPbhyZA9Wb9/LZyu3RzoUY4yJOm4ul92J79mWv+GrGfZ7YKzHcbUbZw/sQk5aIs9aBQBjjGk1N5fLLgZOBzar6vX4nvrP8jSqdiQlMZ6Ly0p4Z8Fmtu45EOlwjDEmqrhJMvtUtQGoF5FOQDXQzduw2pfLR3SnvkF5/nM7mzHGmNZwk2RmiEg28AgwE5iF7/mXmNGrIINT+xTw5Ker2X/ocKTDMcaYqOHmxv/NqrpLVR8EzsT3AOX13ofWvtxU0ZtttQd5cYZVZzbGGLcCPowpIsObe09VZ3kTUvs0smcuw7tn89CUlVw+ojsJ8dapqDHGtKS5J/7/6PxNAcqBOfhaTx4MzABGeRta+yIi3FxxDN/+5wz+M3cjXx9WEumQjDGm3Qv477iqVqpqJbAJGK6q5errQ2YYsCFcAbYnp/XrTN/CTB6oWmEPZxpjjAturvn0VdV5R0ZUdT5wnHchtV9xccJ3K3qxdEstHy5ud516GmNMu+MmycwVkUdFpMIZHgGC7U8m6p0/uJiSnFT+UbXc+poxxpgWuEky1wMLgFudYaEzLSYlxMfxnVN6MWvtLqZZXzPGGNMsN1WY96vqn1X1687wZ1XdH47g2qtvlncjPyOJf1StiHQoxhjTrnlWD1dEHheRaqeDsqbv/VhEVETaXdfLbqQkxnP9ST2ZsnQr8zfURDocY4xpt7x82ONJ4OymE0WkG/A1IKrbaLl6VA8ykxN4wM5mjDEmoIBJRkTGi8iwYFesqlMAfzct/gz8FIjqu+adUhK5alQP3py/iZVbayMdjjHGtEsSqIaUiFwKnIOv1eU5wFvAu6q60/XKRUqBiao60Bm/ADhNVW8VkdVAuapuC7DsOGAcQGFhYdmECRPcbvYotbW1ZGR404FnzQHlx5P3MqoogRsGJXuyjWB4Web2ysocG6zMrVNZWTkz4p1LqmqLA74HMMcDk4ApwB3ACBfLlQLznddpwDQgyxlfDeS72X5ZWZkGa9KkSUEv68adr83XXuPf0GVbdnu6ndbwusztkZU5NliZWweYoS5+Y70cXN2TUdXZ6ut+uRIYg69K87dbmc96Az2BOc5ZTAkwS0S6tHI97cotpx1DamI897y9JNKhGGNMu9PqG/+qultVX1bVca1cbp6qdlbVUlUtBdbja65mc2tjaE/yMpL57qm9eG/hFj5fbc/NGGNMY15WYX4OX78zfUVkvYjc4NW2Iu2G0b0o7JTMb99cZK0AGGNMI54lGVW9XFWLVDVRVUtU9bEm75dqgJv+0SY1KZ4fndmH2Wt38fb8qD4xM8aYkGoxyYjIKyJynohYByrNuGh4Ccd2zuD37yzh0OGGSIdjjDHtgpvE8Q/gCmCZiNwtIn09jikqJcTH8fNz+rFqWx0Tpkf1c6bGGBMybtoue19VrwSG46t2/L6IfCoi14tIotcBRpPT+nVmZM9c7nt/GbUH6iMdjjHGRJyrS2Aikgdch6/a8mzgL/iSznueRRaFRITx5x7H9rqDPDzZmpsxxhg392ReBT7C9zDl+ao6VlWfV9VbgNh69NaFod2yOW9wEY98tIrq3THdWLUxxrg6k/mrqvZ3Hsbc1PgNjXRzBe3UT8/qS31DA39+f1mkQzHGmIhyk2T6i0j2kRERyRGRmz2MKer1yEvnypE9eP7ztcxbb10BGGNil5skc6Oq7joyor4GMm/0LqSO4Ydn9iEvI5nxr86l3qo0G2NilJskEy8icmREROKBJO9C6hiyUhO58/z+zN+wm39+tibS4RhjTES4STJvA8+LyOkicjrwnDPNtOC8QUVU9C3gj+8uYeOufZEOxxhjws5NkvkZvib+b3KGD/B1OmZaICL8+oKBHFblrtcXRDocY4wJOzcPYzao6gOqerEzPKSqh8MRXEfQLTeNW0/vw7sLt/DOAmvXzBgTW9w8J3OSiLwnIktFZKWIrBKRleEIrqP49sk96VuYyV2vL7CWAIwxMcXN5bLHgD8Bo4HjgXLnr3EpMT6O335jEJtq9vOnd5dGOhxjjAkbN0mmRlXfUtVqVd1+ZPA8sg6mrEcOV47szpOfrrJnZ4wxMcNNkpkkIveKyCgRGX5kaGkhEXlcRKpFZH6jafeKyGIRmSsirzZ+yDMW/PTsfuSm27MzxpjY4SbJjMR3iey3wB+d4Q8ulnsSOLvJtPeAgao6GFgKjHcdaQeQlZrIXWN9z848UGUNaBpjOr6ElmZQ1cpgVqyqU0SktMm0dxuNTgUuDmbd0ey8QUW8O2QL932wjJP7FDC0W0ydzBljYoy01Ce9iBTiO4spVtVzRKQ/MKppd8oBli0FJqrqQD/v/Qd4XlWfDrDsOGAcQGFhYdmECRNa2pxftbW1ZGS0r8ai6w4pd3yyj4Q4+OWJqaQkSMsLtUJ7LLPXrMyxwcrcOpWVlTMj3pCxqjY7AG8BlwBznPEEYF5LyznzlgLz/Uz/H+BVnCTX0lBWVqbBmjRpUtDLemnqim1a+vOJ+tMX54R83e21zF6yMscGK3PrADPUxW+sl4ObezL5qvoC0OAkpXog6IcxReQ6YAxwpbMTYtLIXnncXNGb52es4+35m1pewBhjopCbJFPn9IypACJyAhBUHVwRORtfkzRjVXVvMOvoSG47ow+DS7L4+Svz2FxjHZwZYzoeN0nmR8DrQG8R+QT4J3BLSwuJyHPAZ0BfEVkvIjcA9wOZwHsi8oWIPBh86NEvMT6O+y4dyoFDDdz+4hwaGmL2xM4Y00G5qV02S0ROBfoCAixR1UMulrvcz+QWKwvEml4FGdxxfn/GvzKPxz9ZxbdP7hXpkIwxJmRaTDIick2TScNFBFX9p0cxxZzLju/GpMXV/P7tJZzQK4+BXbMiHZIxxoSEm8tlxzcaTgbuAsZ6GFPMERHuvmgwuelJfPfpmeysOxjpkIwxJiTcNPV/S6PhRmA4EFsV1cMgNz2JB68uo3rPAW55brY1O2OM6RDcnMk0VQf0DHUgBoZ2y+Y3Fw7k4+XbuPedJZEOxxhj2szNPZn/4FRfxpeU+gMveBlULLukvBvz1tfw0JSVDOiaxdghxZEOyRhjgtZikuHoxjDrgTWqut6jeAzwizH9Wbx5Nz99aQ7HFGTQv7hTpEMyxpiguLknM7nR8IklGO8lJcTx9yuHk52axHeenmEVAYwxUctN98t7RGS3n2GPiOwOR5CxqHNmCg9cNZwtNQf4wQSrCGCMiU5ubvzfB/wc6AqUAD8D7lPVTFW16zgeGtY9h19fOICPlm3jd28tjnQ4xhjTam7uyYxV1SGNxh8QkTnAHR7FZBq59PjuLNq0h8c+XkVRVoq1CGCMiSpuG8i8UkTiRSRORK7EV43ZhMkvxvTn3EFd+M0bi3h9zsZIh2OMMa65STJX4OtPZoszfNOZZsIkPk740yVDGdEzlx+/8AWfLt8W6ZCMMcYVN7XLVqvqBaqar6oFqnqhqq4OQ2ymkZTEeB65upye+emM+9dMFm60OhfGmPbPTe2yPiLygYjMd8YHi8j/eh+aaSorLZGnvjWCzJQErntiOut2xHyXPMaYds7N5bJHgPHAIQBVnQtc5mVQJrCirFSe+tYI9h86zLVPTLdnaIwx7ZqbJJOmqtObTKtvaSEReVxEqo+cATnTckXkPRFZ5vzNaW3ABvoUZvLotcezfuc+rn/yc/bsb7F7H2OMiQg3SWabiPTmv90vXwy46ZT+SeDsJtN+DnygqscCHzjjJggjeuZy/+XDmL+hhmsfn26JxhjTLrlJMt8DHgL6icgG4Dbguy0tpKpTgB1NJl8APOW8fgq40H2opqmvDejC/VcMZ+76Gq574nNqD7R4gmmMMWElqoH7lReReOAeVb1dRNKBOFXd43rlIqXARFUd6IzvUtVs57UAO4+M+1l2HDAOoLCwsGzChAluN3uU2tpaMjI6dvc3n2+u54E5B+idFcePylM4vL+uw5e5qVg4zk1ZmWNDW8pcWVk5U1XLQxxSqzT7xL+qHhaR0c7rkD6AqaoqIgEznKo+DDwMUF5erhUVFUFtp6qqimCXjRYVwMABm/j+c7N5fHky3zqGDl/mpmLhODdlZY4N0V5mN83KzBaR14EXafSkv6q+EsT2tohIkapuEpEioDqIdRg/zhlUxN+AW56bTU2NcMrJ9aQnuzm8xhjjHTf3ZFKA7cBpwPnOMCbI7b0OXOu8vhZ4Lcj1GD/OHVTEXy8bxvJdDVz/hNU6M8ZEXsB/dUXkHlX9GfCmqr7Y2hWLyHP4ruTki8h64E7gbuAFEbkBWIOvuRoTQucNLmLBgmQenreTSx+aypPfOp7OmSmRDssYE6OaO5M517k5Pz6YFavq5apapKqJqlqiqo+p6nZVPV1Vj1XVM1S1ae0zEwIjihJ47LrjWb29josf+Iw12609U2NMZDSXZN4GdgKDrbOy6HNqnwKevfEE9uw/xEUPfMr8DTWRDskYE4MCJhlV/YlTvfgNVe3UaLDOyqLE0G7ZvPjdE0lOiOeyh6da683GmLBz0wrzBeEIxHjjmM4ZvHzTiRRnp3DdE5/z5jw3jTUYY0xouKldZqJcl6wUXvzOiQwuyeJ7z87i4SkraO4hXGOMCRVLMjEiKy2Rf90wknMHFvHbNxfz4xfnsP/Q4UiHZYzp4CzJxJDUpHjuv2IYPzyjD6/M2sDlj0yles/+SIdljOnA3HRaNk9E5jYZPhKRP4tIXjiCNKEjItx6xrE8cOVwFm/awwX3f2I1z4wxnnFzJvMW8AZwpTP8B5gBbMbXnL+JQucMKuKlm0YhwMUPfsobc61CgDEm9Nw0bnWGqg5vND5PRGap6nARucqrwIz3BhRn8dr3R/Odf83ge8/OYv7G3vz4zD4kxNtVVGNMaLj5NYkXkRFHRkTkeCDeGbUOTKJcQWYyz407gctHdOOBqhVc8cg0NtfYfRpjTGi4STLfBh4TkVUishp4DLjR6V/md14GZ8IjOSGe331jMPddOpT5G2s4968fMXnp1kiHZYzpANw8jPm5qg4ChgJDVHWwqk5X1TpVfcH7EE24XDisK69/fzQFGclc98R0/vjuEg432PM0xpjgtXhPRkSSgYuAUiDB12YmqOqvPI3MRMQxnTP49/dO4q7XF/C3D5fz+eod/PWyYXTuZC05G2Naz83lsteAC/Ddf6lrNJgOKjUpnnsuHswfvzmEOetqOOu+KdYcjTEmKG5ql5Wo6tmeR2LanYvKShjaPZsfPf8FNz8zi68P68pdYweQlZoY6dCMMVHCzZnMpyIyKJQbFZEfisgCEZkvIs+JiF2Laad6F2Tw0k0nctsZx/L6nI2cfd8UPl5mrTkbY9xxk2RGAzNFZInztP88EZkb7AZFpCvwA6BcVQfiqw59WbDrM95LjI/jtjP68OrNJ5KWFM9Vj03jrtcXsO+gtX1mjGmem8tl53i03VQROQSkARs92IYJscEl2bzxg5O5+63FPPnpaqYs3cpvvzGIE3pZ60LGGP8CnsmIyJGOyfYEGIKiqhuAPwBrgU1Ajaq+G+z6THilJMZz19gBPPPtkdQ3KJc9PJWfvTSXXXsPRjo0Y0w7JIH6FRGRiao6RkRWAQpIo7dVVXsFtUGRHOBl4FJgF/Ai8JKqPt1kvnHAOIDCwsKyCRMmBLM5amtrycjICGrZaBWuMh84rLy2/BBvrz5ERiJceVwyI7rEc6SaezjZcY4NVubWqaysnKmq5SEOqVUCJhnPNijyTeBsVb3BGb8GOEFVbw60THl5uc6YMSOo7VVVVVFRURHUstEq3GVesLGG8a/MY+76Gir7FvDrCwdSkpMWtu2DHedYYWVuHRGJeJJx09T/B26mtcJa4AQRSRPfv7ynA4vasD4TYQOKs3j15pP4xZj+TFu1gzP/NIW/T1punaIZY5q9J5MiIrlAvojkiEiuM5QCXYPdoKpOA14CZgHznBgeDnZ9pn2IjxNuGN2Td394Cqf2KeDed5bwtT9P4b2FW6yrZ2NiWHNnMt8BZgL9nL9HhteA+9uyUVW9U1X7qepAVb1aVQ+0ZX2m/SjJSePBq8t4+oaRJCfEceM/Z3DN49NZXh10XRFjTBQLmGRU9S+q2hO4XVV7qWpPZxiiqm1KMqbjG31sPm/eejJ3jOnPF+t2cfZ9H/HriQup2Xso0qEZY8LIzcOYm0UkE0BE/ldEXhGR4S0tZExifBzfGt2TSbdXcHFZCY9/sopT7p3Ew1NW2P0aY2KEmyTzC1XdIyKjgTPw9SfzgLdhmY4kPyOZuy8azBu3nMzQbtn89s3FnP7Hybw8c711JWBMB+cmyRz5l/M84GFVfQNI8i4k01H1L+7EU98awbPfHkluehI/fnEO5/31IyYtqbbKAcZ0UG6SzAYReQjfw5NvOv3LWCfwJmgnHpPPa987ifuvGMa+Q4e5/onPueShz/h0+TZLNsZ0MG6SxSXAO8BZqroLyAV+4mlUpsOLixPGDC7mvR+eyq8vGMC6Hfu44tFpXPrwVD5bsT3S4RljQsRN98t7gWp8rTGDr/OyZV4GZWJHUkIcV48qpeonFfxy7ADWbK/j8kemculDnzF1pSUbY6Kdmyf+7wR+Box3JiUCTwdewpjWS0mM59oTS5n8k0ruPL8/q7bVcdnDU7nkoc/sno0xUczN5bKvA2NxulxW1Y1AppdBmdiVkhjP9Sf1ZMpPK7ljTH/W7djL9U98zjl/+YjXvthA/eGGSIdojGkFN0nmoPr+jVQAEUn3NiRjfMnmW6N7Mvknlfzhm0Oob1BunfAFFX+o4p+frbYO04yJEm6SzAtO7bJsEbkReB941NuwjPFJSojj4rIS3r3tFB6+uoyCzGTueG0BJ93zIX98dwlbdu+PdIjGmGa02DOmqv5BRM4EdgN9gTtU9T3PIzOmkbg44WsDunBm/0Kmr9rBox+v4v5Jy3lw8grOG1TEkNTDVEQ6SGPMV7SYZETkHlX9GfCen2nGhJWIMLJXHiN75bFmex1PfrqaF2es598H6pm48VOuP6mUswZ0ITHeHuUypj1w800808+0c0IdiDGt1SMvnTvPH8Bn40/jin5JbKs9wPefnc2Jd/supW3YtS/SIRoT8wKeyYjITcDNQC8RmdvorUzgE68DM8atzJREvlaayK+vOZXJS6t5Zupa7p+0nL9PWs5p/Tpz5cgenNKngPi48HcLbUysa+5y2bPAW8DvgJ83mr5HVXd4GpUxQYiPE07rV8hp/QpZv3MvE6avY8Ln63h/0ed0zU7lkvJuXFxeQtfs1EiHakzMCJhkVLUGqAEuD/VGRSQbXw21gfiqRn9LVT8L9XZM7CrJSeP2s/ryg9OP5b2FW3h2+hr+/P5S7vtgKaOPyeeb5d34Wv9CUhLjIx2qMR1aizf+PfIX4G1VvVhEkoC0CMVhOrikhDjOG1zEeYOLWLdjLy/NXM9LM9fzg+dm0yklgQuGduXishIGl2QhYpfTjAm1sCcZEckCTgGuA1DVg8DBcMdhYk+33DR+eGYfbj39WD5buZ0XZqzj+Rnr+NfUNfTKT+fCYV25cGhXuufZ/zzGhIqEu00oERkKPAwsBIYAM4FbVbWuyXzjgHEAhYWFZRMmTAhqe7W1tWRkZLQp5mhjZXav7pAyY0s9n22sZ/EOX5M1x2THcWJxAsd3SSAzqf2e3dhxjg1tKXNlZeVMVS0PcUitEokkUw5MBU5S1Wki8hdgt6r+ItAy5eXlOmPGjKC2V1VVRUVFRVDLRisrc3A27NrH619s5NXZ61m6pZb4OOGkY/IZM6iIswZ0ISstMTTBhogd59jQljKLSMSTTCTuyawH1qvqNGf8JY6uvWZMRHTNTuWmit5899ReLNq0h//M3cgbczfx05fn8j//nsfoY/I5b3AxZ/YvJCu1fSUcY9qrsCcZVd0sIutEpK+qLgFOx3fpzJh2QUToX9yJ/sWd+OlZfZm/YTcT5xjRRIwAABQuSURBVG5k4txNTHpxDonxwom98znLaeamIDM50iEb025FqnbZLcAzTs2ylcD1EYrDmGaJCINKshhUksXPz+nHnPU1vDlvE+8s2Mz/e3Ue//PveZT3yOGsAV04a0AXuuVapQFjGotIklHVL4CIXic0prVEhKHdshnaLZvx5/Rj8eY9vLNgM2/P38xv3ljEb95YRL8umZx+XGdO61fI0G7Z1sqAiXmROpMxJqqJCMcVdeK4ok7cdkYf1myv490FW3h/0RYenLySv09aQV56EpX9OnPGcZ0ZfWwBGcn2dTOxxz71xoRAj7x0bjylFzee0ouavYeoWlrNB4uqeXfBZl6auZ6EOKG8NIeKvp2p6FtA38JMe/jTxARLMsaEWFZaIhcM7coFQ7ty6HADM1bvpGppNZOXbOXutxZz91uL6dIphVP7FHBKnwJOOiaP7LSkSIdtjCcsyRjjocT4OEb1zmNU7zzGn3Mcm2v2M3lpNZOXbuXN+Zt4fsY6RGBQ1yxGH5PP6GPzKeuRQ3KCtalmOgZLMsaEUZesFC49vjuXHt+d+sMNzFm/i4+WbePjZdt4aMpK/lG1gpTEOI4vzeXE3vmM6p3HwOJOJFgnbCZKWZIxJkIS4uMo65FLWY9cbjujD3v2H2Lqyh18vGwrn67Yzj1vLwYgMzmBET1zGdU7jxN65XFcUSertWaihiUZY9qJzJREzuxfyJn9CwGo3rOfqSt38NmK7UxduZ0PFlc78yVwfGku+Q0H6dRrJ4O6Zll306bdsiRjTDvVOTOFsUOKGTukGIBNNfuYunI701ftZPqq7Xy49RAvLP2U1MR4hvfIpqxHLuU9chjWPZvMFGv2xrQPlmSMiRJFWal8fVgJXx9WAsBr70wiqbgf01btYNqqHdz/4TIaFOIE+nbpRHmPHMpLcxjePYeSnFSrMm0iwpKMMVEqK1moGFTEOYOKANiz/xCz1+5ixpqdzFyzg5dnredfU9cAkJ+RzLDu2Qzrns3w7jkMLskiLcm+/sZ79ikzpoPITEnkFOfZG4D6ww0s3ryH2et2MXvNTmav28V7C7cAEB8n9CnMZGi3LAaXZDOkJJs+hRlWi82EnCUZYzqohPg4BnbNYmDXLK4+oQcAO+sO8sW6Xcxau9Np7HMzz01fB0BKYhwDi32NgQ4uyWJQ1yx65mdYTTbTJpZkjIkhOU57apX9OgOgqqzZvpc563cxZ10Nc9bv4rnpa3niE18voWlJ8Qwo7sTArr6kM6A4i94F6XbGY1yzJGNMDBMRSvPTKc1P54KhXQHfZbYVW+uYt6GG+RtqmLehxpd4DvkST1JCHP26ZDKguBP9i7MYUNyJfl0y7R6P8cs+FcaYoyTEx9G3SyZ9u2RycZmvJlv94QZWbqtjwcYaFmzYzYKNu3lj7qYvL7WJQGleOscVZdKvSyenhepMumZbrbZYF7EkIyLxwAxgg6qOiVQcxpiWJcTH0acwkz6FmXx9mG+aqrJh1z4WbNzNok27WbxpDws27ubNeZu/XC4zOYE+TsLqW+j7269LpjUIGkMieSZzK7AI6BTBGIwxQRIRSnLSKMlJ46wBXb6cXnugniWb97Bo026WbN7Dks17mDhnI8/ur/9ynoLMZPoUZnBs50wneWVwbGEmWan2EGlHE5EkIyIlwHnA/wE/ikQMxhhvZCQnUNYjh7IeOV9OU1W27D7A4s2+xLN0Sy3Lqvfw/Ofr2Hfo8Jfzdc5M5pjOGV8ZCjKS7bJblBJVDf9GRV4CfgdkArf7u1wmIuOAcQCFhYVlEyZMCGpbtbW1ZGRktCHa6GNljg0docwNqmzfp2yobWBjbQMbapVNdb7X+/+be0hLgC7pcRQkH6ZbVhJFGXF0SY+jME1I6OBVrNtynCsrK2eqakS7ug/7mYyIjAGqVXWmiFQEmk9VHwYeBigvL9eKioCzNquqqopgl41WVubY0JHLfOTMZ3l1Lcur97B8ay0rt9axcP0OplUf+nK++DihJCeVnvnp9MxPp1d+Oj3zMyjNT6M4K5W4DpCAov04R+Jy2UnAWBE5F0gBOonI06p6VQRiMca0QyJCl6wUumSlMPrY/C+nV1VVUT5qNKu21rFiay0rt9ayclsdq7bVMX3VDvYe/O/pT1JCHD1y0+iRl07PfN/f0rx0euSlUZydag+ZhknYk4yqjgfGAzhnMrdbgjHGuJWRnMCgEl/LBI2pKtV7DrByqy/prN5ex+ptdazZvpePlm3lQH3Dl/MmxvsqLXTPTaNH3pG/6XTPTaNbbqo98xNCtieNMR2CiFDYKYXCTimM6p131HsNDcqWPftZta2Otdv3smbHXtZu38vq7XXMWrOTPQfqj5o/PyOZbrmpdM/1JaCSnFS6OTXpirJTrP+eVohoklHVKqAqkjEYYzq+uDihKCuVoqxUTux99Huqys69h1izvY51O/exbsde37BzL7PW7mTi3E0cbvhvBak48XW70DUnlZKcVEqyUynJSaNrTipds1Mpyk4hOSE+zCVsv+xMxhgT00SE3PQkctOTGNY95yvv1x9uYFPNftbt3Mv6nftYv8P3d93OvUxdsZ3Nu/fTKAch4quKXZydSnG2LwkVfzmkUJyVSnZaYsxUybYkY4wxzUiIj6NbbhrdctP8vn/ocAOba/b7EtDOvWzYtY8NO/exsWYfCzfu5r2FWzjY6H4QQGpiPEVZKRRnp1KUlULRkb9ZKRRlpdIlK4VOKQkdIhFZkjHGmDZIPCoJ5X3lfVVlW+1BNu7a5xtq9rNp1z421exnY80+Plq2jS179tP0kcW0pHi6ZKVwSc/DVISlJN6wJGOMMR4SEQoykynITGZIt2y/8xw63MDWPQfYVLOfTTX72Fyzn001+9lcs5+MxF1hjji0LMkYY0yEJcbHfXnfBo6+L1RVVRWRmELF6uEZY4zxjCUZY4wxnrEkY4wxxjOWZIwxxnjGkowxxhjPWJIxxhjjGUsyxhhjPGNJxhhjjGci0v1ya4nIVmBNkIvnA9tCGE40sDLHBitzbGhLmXuoakEog2mtqEgybSEiMyLdx3W4WZljg5U5NkR7me1ymTHGGM9YkjHGGOOZWEgyD0c6gAiwMscGK3NsiOoyd/h7MsYYYyInFs5kjDHGRIglGWOMMZ7pEElGRB4XkWoRmR/g/QoRqRGRL5zhjnDHGGoi0k1EJonIQhFZICK3+plHROSvIrJcROaKyPBIxBoqLsvcoY61iKSIyHQRmeOU+Zd+5kkWkeed4zxNRErDH2louCzvdSKytdEx/nYkYg01EYkXkdkiMtHPe1F7jDtKz5hPAvcD/2xmno9UdUx4wgmLeuDHqjpLRDKBmSLynqoubDTPOcCxzjASeMD5G63clBk61rE+AJymqrUikgh8LCJvqerURvPcAOxU1WNE5DLgHuDSSAQbAm7KC/C8qn4/AvF56VZgEdDJz3tRe4w7xJmMqk4BdkQ6jnBS1U2qOst5vQffh7Nrk9kuAP6pPlOBbBEpCnOoIeOyzB2Kc+xqndFEZ2haW+cC4Cnn9UvA6SIiYQoxpFyWt8MRkRLgPODRALNE7THuEEnGpVHOKfhbIjIg0sGEknPqPAyY1uStrsC6RuPr6SA/ys2UGTrYsXYuo3wBVAPvqWrA46yq9UANkBfeKEPHRXkBLnIuAb8kIt3CHKIX7gN+CjQEeD9qj3GsJJlZ+NrwGQL8Dfh3hOMJGRHJAF4GblPV3ZGOJxxaKHOHO9aqelhVhwIlwAgRGRjpmLzkorz/AUpVdTDwHv/9Dz8qicgYoFpVZ0Y6Fi/ERJJR1d1HTsFV9U0gUUTyIxxWmznXrF8GnlHVV/zMsgFo/F9eiTMtarVU5o56rAFUdRcwCTi7yVtfHmcRSQCygO3hjS70ApVXVber6gFn9FGgLNyxhdhJwFgRWQ1MAE4TkaebzBO1xzgmkoyIdDly/VJERuArd1QcoECc8jwGLFLVPwWY7XXgGqeW2QlAjapuCluQIeamzB3tWItIgYhkO69TgTOBxU1mex241nl9MfChRulT1m7K2+S+4lh89+ailqqOV9USVS0FLsN3/K5qMlvUHuMOUbtMRJ4DKoB8EVkP3InvhiGq+iC+g3KTiNQD+4DLouUANeMk4GpgnnP9GuD/Ad3hy3K/CZwLLAf2AtdHIM5QclPmjnasi4CnRCQeX8J8QVUnisivgBmq+jq+xPsvEVmOrwLMZZELt83clPcHIjIWX23DHcB1EYvWQx3lGFuzMsYYYzwTE5fLjDHGRIYlGWOMMZ6xJGOMMcYzlmSMMcZ4xpKMMcYYz1iSMcYY4xlLMsYYYzzT5iQjIt8Rkc1Og4QrROSaUAQmIj8QkUUi8oy/8VasJ1tEbm4y7dNQxBgpInKXiNwexHJRty9EpFQC9BMU5PqC+hx5QURqW57L73JBH7Ngtxkp/j6z4dpOa/ZzuOJ0K5jPiFe/BW1+GFNE7gfmq+qDTjMeb6pqm9uKEpHFwBmqut7feCvWUwpMVFXPGhV0mjERVQ3UgmpIlxeRu4BaVf1DK7dTisf7ItTaErO//draz1Fbj20L665V1YxQr7e9bbMtwvWZbet2Ai3v5ecnaqhqmwZgClDpvC4ANrZy+auA6cAXwENAPPAgcBCYB/zQz/hXlnHWdQ0wF5gD/MuZNgFf8yJfAPc602qdv3cD32sUy13A7YHiahJ3KbAEX0dpC4AeAcpSiq/tpWfwtbH0EpDmb3lnvT8C5jvDbY229z/AUuBj4Dngdmcd8xvNcztwVzD7ItC2nW0sAh5x4nwXSPWzL/zOEyjGRvvlSadczwBnAJ8Ay4ARjZb/yv5r5rPjd7868x/1OWqhzH7X0cx2j3f2dwqQ7iw3MNCxaPI5DLSP0oE3nOXmA5e29fPbaNlfcfTn6/+AW/18P/8NzHTKM86Z9pW4Aq2vrccZ/5/ZQMesxe00U6aWvht+j2Gj9xsv/yL+v9v+tluKn+9OgH3cmjLWNnOsmv1cteW3wO9vfAiSzE6gGBDgl8D1zvScRvO8CRT7WfY4fM12Jzrj/wCucV6vBvIbzbsayA+0DDDA2fH5zvRcf1/gJgdgGDC50fSF+Fo6DRhXkx/WBuCE5srizKfASc70x/lvgvhyeee9Mnw/gOlAhnMghzWanoav17zlNJNkgtwXgbZdiq+NqKHOfC8AV/nZF37naSbGI8sMwnfZdqazbwRfB03/brS8v/3X3P4+ar82iXV1o/3SXJn9riPQdp3XvwH+APwdGO9M83ssmuz7QPvoIuCRRtOz2vr5bbLNWc7rOGAFkOenvEc+O6n4fnDy/MUVaH0hOM5N901Ln9Nmt9NMmY7aTpN9FfAYNvkOzPf32+Biu1/57jSzj92W8Ujs/tbT0ucq6N8Cf0Ob7sk4nQVl4ksi1cBofFkW4M9H5lPVc1V1o59VnO4U6HOnwcPTgV4tbDbQMqcBL6rqNmebLfaUqaqzgc4iUiwiQ/B1b7quFXGt0f92C9vcMutU9RPn9dP49lPT5XGmv6qqdeprrv4V4GRneFVV96qv/5TXWyhaq/dFM9sGWKWqRxqknInvw9aUm3n8LTNPfZcSFgAfqO/TO6/J8v72X3P7u+l+DaS5MgdaR3Pb/RW+VoPLgd8704I5FkfMA84UkXtE5GRVrWn8Zls+v6q6GtguIsOArwGzVdVfa9U/EJE5wFR8CexYf3G1sL62HOemWvqcutmOvzI1J5hj6O/zE2i7/r47gY692zIe4W89zX6uaPtvwVHa2grzIGCKqp4mIjn4svMoEekE9BORn6jqvc0sL8BTqjq+Fdv0u4yI3NLa4B0v4mu5twvwfCvjqnMRVylf7T72yHgdbVPP0ZU3Utq4vkAONHp9GN9/Ym7naS7Gxss0NBpv4OjPpr/919z+but+pZl1NPfZyMP3n18ivnK6jcPvPlLVpSIyHF9L2r8RkQ9U9VdNlm3L5/dRfC0Yd8H3H/FRRKQC3+WYUaq6V0SqgJRm4gq0vrYc59ZocTuBytTK7bhx1LFvYbtf+e7428f4Lr+53ZdA4M+Qi89VIG5+C47S1tplg4HZAKq6E3gWXz/V24CnW0gwAB8AF4tIZwARyRWRHkEu8yHwTRHJOzLdmX8PvrOtQJ7H12z2xfi+sKGOC6C7iIxyXl+B776KPx8BF4pImoikA193pk1xpqeKSCZwvjP/Fnz/yeaJSDIwxpkezL4ItO22ChRja/jbf8Eco6aCKXNz230I+AW+a+X3ONMCHYvG/O4jESkG9qrq08C9wHA/y7bl8/sqvg7Bjgfe8fN+Fr6zo70i0g84oYW4WlpfS/wd56af2bZ+Tv2Wyc92GnNzDFv6nQm0Xb9cHvsW+VuPi3WH9LcgFGcybzUa/w/wF3zXY+ccmSgibwLfbnrJTFUXisj/Au+KSBxwCPgesCbQBgMto6pTReT/gMkichhf8rtOVbeLyCfiqwb7lqr+pMn6Fjg/3BvU6dArlHEBm/HdBPyeiDyO77r5A0BnP+uYJSJP4rthC/Coc0kEEXne2afVwOfO/IfE1+fEdHw95y1uVKZW7YtA23bODIIWKMZW+sr+c76sgfa329haXeZAx1lETgUOqeqz4usL5VMROU1VP/R3LJqsM9A+GgTcKyINznZu8hNP0J9fVT0oIpOAXap62E9x3wa+KyKL8B2DI5d//MblYn0tCXScj/rMtvFz6rdMLXw3/H6fGq+0yfL+OlELtC8DafHYu+RvPc2uO9S/BZ70JyO+DoUuAu5W1ajuta6tJAqrDZvY4CSgWcA3VXVZJNdn35OOy5Mn/lX1dVW9NtYTjDHtlYj0x1dL8YMQJZiQrs90HNYzpjHGGM9Y22XGGGM8Y0nGGGOMZyzJGGOM8YwlGWOMMZ6xJGOMMcYzlmSMMcZ4xpKMMcYYz/x/rJs5xdYIBCIAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"\n",
"Rt = np.linspace(1.5, 4.0)\n",
"Se = 0.7\n",
"rho = 1/14.0\n",
"psi = 0.3\n",
"\n",
"tau = (Rt - 1)*rho/(1 - psi)\n",
"plt.plot(Rt, 1.0/tau)\n",
"\n",
"plt.xlabel('$R_t$: effective reproduction number for exclusively asymptomatic transmission')\n",
"plt.ylabel('testing frequency / days')\n",
"plt.grid(True)"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 639
},
"colab_type": "code",
"executionInfo": {
"elapsed": 1993,
"status": "ok",
"timestamp": 1596386957000,
"user": {
"displayName": "Jeffrey Kantor",
"photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gg_n8V7bVINy02QRuRgOoMo11Ri7NKU3OUKdC1bkQ=s64",
"userId": "09038942003589296665"
},
"user_tz": 300
},
"id": "E_Lb57gLbRil",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
},
"outputId": "1a591063-33aa-49a1-dadc-fa9dd2c876d1"
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAI4CAYAAAB3HEhGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdd5xdVb3//9fntDnTeybJZEIqJRBCCSFUUUSQ7lWKVFEURLp6lateC+hXxWu513v1609/il4VLCgtgAiKKE1SSEhCmPSZSTK9l1PX94+9J5kME0gyZzIl7+fjcR5n77X3XmudcyaT85m19meZcw4REREREREZvsBod0BERERERGSiUIAlIiIiIiKSIQqwREREREREMkQBloiIiIiISIYowBIREREREckQBVgiIiIiIiIZogBLRGSUmdkPzewLo92P0WZmXWY2axjXrzazMzLYpYwzsw+Z2d9Hqe3TzGzdaLS9P8zsS2b2v6PdDxGRfaUAS0RkGMzsr2bWamZZe3n+m75gO+dudM7dneF+dQ14pM2sd8D+lZlsK1Occ3nOuY3DuP5I59xfM9ilA8YPfvo/n24zc4M+w+n7Uaczszn9+86555xzh2W25zvb+quZ9fl9bTKzB81syki0JSIy1inAEhHZT2Y2AzgNcMCFo9qZQfxgJc85lwdsBS4YUPbL/vPMLDR6vZR+fvDT/3kd6RcXDfjMto5m//bSzX7/DwWKgO+Mcn9EREaFAiwRkf13DfAi8DPg2oEHzKzK/yt+o5k1m9n3zewI4IfASf5f+tv8c39mZvf422vN7PwB9YT8Oo7z9xeb2fNm1mZmr+7rlDgzO8PMas3sM2a2A/ipmRWb2aN+O63+9rQB1/zVzO42s3+YWaeZ/cnMyvxjUTP7X/81tpnZP82sYsB19/j97TKzR8ys1Mx+aWYd/rkzBrSzc8TFzM41szV+e3Vm9im/vMzvX5uZtZjZc2YW8I9tNrN3+9tZZvZdM9vmP77bP8o44D34pJk1mNl2M7vuLd6z6/zPpdPMNprZDUO8n0PW5b/eh/3X+zIwe18+L7+OQjP7iV93nf+eBv1jc8zsWTNr90eOHvDL/+Zf/qr/3l/W39cB9W42s0+Z2Ur/+gfMLDrg+L/6bW4zs+tt0IjYnjjnWoDfA0f59Zzsf9bt/vPJA9qY6r8/LWa23sw+uq/vj4jIWKMAS0Rk/10D/NJ/nD0gsAgCjwJbgBlAJXC/c24tcCPwgj8qUTREnb8GPjhg/2ygyTm3zMwqgceAe4AS4FPA782sfB/7Pdm//hDgY3j/F/zU358O9ALfH3TNFcB1wCQg4rcNXmBZCFQBpf7r6x1w3eXA1f57MBt4wW+rBFgLfHEPffwJcINzLh/vi/ozfvkngVqgHKgA/g1vBHGwzwGLgWOABcAi4POD3oNCv18fAf7bzIr30JcG4HygwH8PvtMf8O5FXf8N9AFTgA/7j331MyAJzAGOBd4DXO8fuxv4E1AMTAP+C8A5d7p/fIH/s/bAHuq+FDgHmAkcDXwIwMzOAe4E3u23e8bedtYPvt8PLDezEryf2f/E+/n4NvCYmZX6p9+P93lOBT4AfM3M3rW3bYmIjEUKsERE9oOZnYoXkPzGObcU2IAXhID3ZX4q8GnnXLdzrs85t7eJDX4FXGhmOf7+FXhBF8BVwBLn3BLnXNo59xTwCnDuPnY/DXzRORdzzvU655qdc793zvU45zqBrwLvGHTNT51zbzjneoHf4AUuAAm8L85znHMp59xS51zHoOs2OOfagceBDc65PzvnksBv8QKGoSSAeWZW4Jxrdc4tG1A+BTjEOZfwp9YNFWBdCXzFOdfgnGsEvowX6A2s/yt+HUuALmDI+5Occ4/5r8E5557FC2hOe7u6/ED7/cC/+z8HrwH37eH1DskP2s8FbvfraMCbenf5gLYPAabu489Zv/90zm3zR50eYdfneineZ7faOdcDfGlv6jJvVPZVYDtegHYeUO2c+4VzLumc+zXwOnCBmVUBpwCf8fu+Avgx3h8uRETGLQVYIiL751rgT865Jn//V+yaJlgFbPGDiH3inFuPN7JzgR9kXejXDd4X6Uv86XFt/pfZU/ECjn3R6Jzr698xsxwz+79mtsXMOoC/AUX909B8OwZs9wB5/vYvgCeB+/2pZN80s/CAc+sHbPcOsZ/H0N6PF1hs8afAneSX3wusB/7kT9f77B6un4o3gthvi1/Wr3nQ5zPwNe3GzN5rZi/609ja/H6V7UVd5UAIqBnUj31xCBAGtg/4zP8v3kgiwL8CBrxsXhbFfR0h29PnOnVQvwdu78mtzrki51ylc+5KP7Ad/Dng71f6x1r8oH7wMRGRcUs3N4uI7CMzy8b7C3/QvPuYALLwgpIFeF9Gp5tZaIgga6jRlsH6pwkGgDV+0IVf7y+cc8O9T2VwHz6JN3pzonNuh5kdAyzH++L+1hU5l8AbHfqyefdTLQHW4U3x2/8OOvdP4CI/WLsZb9Ssyv8y/kngk2Z2FPCMmf3TOff0oCq24QUnq/396X7ZPvHv2/o93qjKQ865hJn9kb14b4BGvKl9VXijNv392Bc1QAwoGypgd87tAD7q9/VU4M9m9rcBPzP7azvelMN+VftZT//nMNB04An/WImZ5Q8IsqYDdfvZlojImKARLBGRfXcxkALm4U2pOgY4AngO74v4y3hfUL9uZrnmJYI4xb+2HphmZpG3qP9+vPtsPs6u0SuA/8Ub2TrbzIJ+vWfYgIQU+ykfbzSpzb9nZk/3Rb2Jmb3TzOb7o10deFPW0sPpjJlFzOxKMyv0A7iO/jrN7Hw/sYMB7Xifw1Dt/Rr4vJmV+/cE/Tve+7evInjBcyOQNLP34n02b8s5lwIeBL7kjxLOY1AylL2oYzvelMT/MLMCMwuY2WwzeweAmV0y4PNvxQue+9+PemB/1xX7DXCdmR3hj6Tu7zptS4BDzewK8xK2XIb37+ZR51wN8Dzwf/yf5aPx7mHT2lciMq4pwBIR2XfX4t2fstU5t6P/gZcY4kq80Y0L8JIDbMW7if8y/9pn8EZVdphZ05ur3vml+gXgZOCBAeU1wEV4iR0a8UY3Ps3wf5d/F8gGmvCyIj6xD9dOBn6HFwStBZ7FmzY4XFcDm/0pizfiva8Ac4E/493n9ALwP865vwxx/T1496etBFYBy/yyfeKPrNyKF3C04t0T9/A+VHEz3rS7HXjJKn66r33AC9ojwBq/D79j17TQE4CXzKzL79dtA9YS+xJwnz+18NJ9adA59zheYoq/4E3JfNE/FNvHeprxEoR8EmjGm9J4/oCptR/ESwSzDfgD3r2Bf96XNkRExhob+t5gEREREY95Swy8BmTtz72FIiIHE41giYiIyJuY2fvMW0+sGPgG8IiCKxGRt6cAS0RERIZyA94aYBvw7nX7+Oh2R0RkfNAUQRERERERkQzRCJaIiIiIiEiGjOl1sAqKi13hpEm7LTZiA5ZvGVxubzqwq+zNC5a4QeVD7++pbHBfdj9ugNvZuhtQ3L/t/HOHGj8c0H1siJ7bHs/d/aw9HwNzA8/cvfu79t3QxwZ2euA5Q7G3OmqDGhzi+JuO2VBPezh3D+WD+zRo397m+G77e9i2tztnZ5nfP/M/rzcdH6J9ERERERl1S5cubXLOlQ8u36sAy8zuAK7H+2q9CrgOL0Xs/UApsBS42jkX9xdl/DlwPF5K1succ5v9eu7CW+Mihbfi+5Nv1W5W0RSC77t3r16gY+9W7xxp4YAjYo78UJKicJKCUJLCUJKCYIL8YIL8UIJcSxAJpAiTJmxpIpYkYGkskMbMec+A69+3lBecBdI4SwPes7MUmCNtKRxp0qRxpEhbihRpUn5ZwoyEGXGDBEYcSJjznnHESRN3jrhLEfMfCZcilk4QSyeJpePEU3Fi6ThpN/TyNkGMsAuSRYiwCxJ2AbJckLALEnFBwgS8Z+c9R1yAcDqw+3MqQNgZ4bQRSQcIp4xwGkL+czgJwTSEko5QCoJJRyiVJphwBBMpAsk0gUSKQCJJIJ7EEkmIJ7B4HBdLQCyGi8eH/yEPCjCHPpBhZhAMYoEAhELec/9+MIj5j/5tQkEsGPK3/fN3KwtiobB3XTgEfrmFQ975A4+FQlg47JWFQt4jEvbLvGOEw7vO6T8WjuzcDkQi4D9bOIxlZWGhMf33HREREZngnHOQSuHSae85lYZ0CtJpryyd9spcetd5flkwP4/wpElbhqr3bb/hmFkl3hog85xzvWb2G+By4FzgO865+83sh3iB0w/851bn3Bwzuxwv89Bl/gKLlwNHAlPxVps/1F+IccJIpI0ERncqwo7YW60jemCYOQpCKQpDSQpDKQpCSfJDSfKDCQqCCcqDCXIDCfICcfICcXIsTi59ZFsfURcj6vrISveSle4hnO6FVA+JdB+JdJJYKERPOJvecBa9oQg94Sx6QmF6A0F6giF6AgG6zegxRzeOHpei2yVpScfpSvXQnYrRlegmns5A0LO374cLUUCUnHSYgnQW+ekIeekwOekQuSnvkZMMkpMMkJ0MEE1ANA5ZcUckniYcSxPqSxDqSxDsi2O9MejuhZ5eXF/fyHXcOUgmvRAuHh8Tf0wYtkAAi0R2PgL921lZ/nOEQCTL249mecezolhWFoFoFhbxy7Oi3nM0imVFvWPR7F3P2VEsGiXgPywy+v8uRUREDgSXTOJSKe87RDKJS6dxiYQfTKR2304mve1kClJJv2zg9oDjae/ZpYYq678mvft5yf5AxjvmXTvgnHQKUmnveWc9A4KfnUGQX97/3Wjw8bd6HlQ2HEWXXLLHY3v7J+QQkG1mCSAH2A68C2/BRYD78BY0/AHeIphf8st/B3zfvPlSFwH3O+diwCYzWw8swlsoUkaIc0Z7IkR7IrOjBWaOyqw4M3L6mJbVQ2Wkh0nBbooCvZRbD3n0kOe6yEl3EU11Ekl0EI63E+hrw5K9u9WVCEbojBbQHc2jIyuPrqxsOsNROkNZdIRCdASCdJrRbmnaXZLOdJz2VB9tiS46E117HFUb8v0waKeP9mAf24OdGX1PslwWZelcSlJRSlLZlCSzKEqEKUiEKIgHyY1BTq8juy9NVneCcHeMYFcvgY5uXEdnZkbXxpN0GtfXtzMwPWB/aQkGvUArJ5tANJtAtvew7AHbOdkEsnO8/ZwcAjn+8Zwcrzwnh0BuLoGc/uPew8LhA/UqRERkhPQHHi6Z9J7jCUgmdi/buZ3E9R/rD1YSid3KdwY3Cf856ZftPC+JSyUHnJsacJ5fX3+A01+Xfw07rx9wfMC2jI63/dbtnKszs28BW4Fe4E94UwLbBqyHUQtU+tuVQI1/bdLM2vGmEVayayX4wdfsZGYfAz4GkFc6mdz9eFEy8pwzavuyqO3LAgr36dr8UJIZ2TGmRXupyuqhItxDRbCLMuukmA6mx9vI7WklGttOqK+JQF/bHutKW4DO7EJac0toixbQGs2lNRylJRyhJRCgxdK0uAQtqT6a4520xttJjdCgacxS1AU7qAt27Nf1hek8KlP5TE7kMikRpTQWoSQWoqAH8rvTZHfGyeroI9jWBa3tuO7uDL+Cg0QqRbq7G7q7Mx7UWSSyK+DKzfWDsMHb/ft53n5eHoG8XecF8/J2nq9plCIy0bhUCheP+4FLfLftdDwOfqCS3u1YfwAT37U9sI5kcs/7gx/JxG7HSAwOmBLeKIfIMOzNFMFivNGnmUAb8FvgnJHqkHPuR8CPAMpnzpsQM6Fkd53JEKs6Q6zq3LvwOTeYZm5uD7Ozu5kZ7aQq1MHkQBvltFCYbCI31sD0zh3MaNzwtnWlLUBrbilNeWU05RTSEM2jMRyhIWg0kKI+2UN9vJ2WWNvORCQHSnugj/ZAH2vCjXt1fqHL45BEIVXxfKbGspnUE6Kk2yjoSJLT1kekpQuaWnCdXSPcc+nn4nFS8Tiptj3/UWBfWDTqBVt5XsAVzPWDr/4grL98Z1C2q3xnmf9swWBG+iQi44tLp3H+PcguHicdi+Piu/a9sv79/qBn8PmDHon4zoBo1zVvfqQTA477wc9wp2WJjAd78+fRdwObnHONAGb2IHAKUGRmIX8UaxpQ559fB1QBtWYWwhveaB5Q3m/gNSJ71J0KsKIjjxUdeUDFHs8rjSQ4Kr+LeTkdzA63URVsYbKrpzixg5yebQS7thNwKUq7GintauSwt2gzHsyivmgK2wrK2ZZdSF0ki20BqEv3UhtrpbGv5YAHYIO1Wx8rI32sjNRDHt448RCK0/kcmihhRl8+VT1RJnUGKG5PkdvcQ7i+FdfQpGkEY5Tr6yPV10equXnYdVl2th+k5e4aURswWrYriBtwfPCjf3QuOzsDr05kYnPO7Qo2YjFcLOYFK4n4zoAnHYvhdgYwsd0DnVhsV9luQU5sV9DTX09/QDSgvH8ESL/fRQ68vQmwtgKLzSwHb4rgmcArwF+AD+BlErwWeMg//2F//wX/+DPOOWdmDwO/MrNv4yW5mAu8nMHXIge55niYZ5uLeba5GDjkTcezgymOKejimLw2Do80MyNYz5TkNgp7a4h0bMZSu+6BiqRiVDVvpqp585BtxUJR6kqq2FpQwdbsPLaGg2x1cbbEWtnR17RP94WNtNZALy9l1fFS/2zOKbsfD7kAhyWmcnismBld2UxtD1DSnCCnoYNAXb1GwCYI19tLqreXVFPT8CsLBr370wZOgfQDr0BuDrYzENsVkPXfr2ZRfzs7e9d2NIpl53gJSTTSJsPkBRyJnaMsuwU5u426DBylGTSCE4vhEgPKBwQ4Qwczsd2vjcW8qWYiclDam3uwXjKz3wHLgCSwHG8K32PA/WZ2j1/2E/+SnwC/8JNYtOBlDsQ5t9rPQLjGr+cTEy2DoIxtvakgL7QW8kJrIYMDsKxAmtNL2jg5r56jwnXMSG2iuPMNQp1DD7JmJfuY1VDNrIbqNx2LhaJsKZ3BpqIKNkVz2RiEjclONvfsIJaKjcRLG5akpVkdaWB1pAHyeVMANj1VxvzeMg7tyqWqNUhpY4ycumZc7Q79ZfRglUqR7uoi3ZX54NvCYW+0LSvrzc/R6JszSGZleRkns/zy/gyU/dko+x/h8Jufw7svN2ChkLfkQP/SBvLmDGRD3WifSHpZwfr344khbuT3b+YfdK+LSwxxn8zge2cG34cz+P6dgfuJxKDlM0REDjxzY/gXUfnMeS73sr1bB0tkJEzP7uOskkaOz97BXKthSt9GctvXYfF9TzCRsiC1pYewvriS6px83gg6quOtbO3ZMaZGvPZWxAU5Jj6ZBV0lzGoNM7k+Tl5NC65mmwIvGf/MdgVcO9eXC+2+5txQ69L5DzPztoMBb9n3/mPWvxC5eevbDbW4+GDODVil3lv10TnnLb3XvyYLDtLO23bpXdv9aYnT/eu7+GXJ5K71X/oDqAEpkPvLRERkaEWXXMLUe+5e6pxbOPiYAiyRfWTmWFzUwTsL6zkmXMPs5HqKOtYS7G7Yr/p6Izm8UTGXdYUVrImEWZvspLq7jkR6fE4viboQJ/ZVckxHEbMaA5TXdhHeWIdr37/siiIiIiJjzVsFWMoBLLKPnLMBUw0PxbstEebnd3N2yXZOjGxmTmIdRa2rsNjbBxXZ8R4W1LzKgppdZYlghDcqDmV18RRWZUV4LdHGxu66cTHS1WdJns3ewrPZW7ycJEd55fMSU1jcUcERTRGm1PaQVV2La81Mtj0RERGRsUIBlkiGrOrMZVXnHGAO8G7MHO8qaeW9hTUcF3iDaV0ribS9fSp5gHAqzpHbXuPIba9xqV/WFS1g1ZTDWVFYzquW4NXuGroS42ctrDXhRtaUNnrZDg8DzoSjEpWc2j6JI+rDVGxqI1i9defCwyIiIiLjkQIskRHinPF0cwlPN5cAC4BLmJ3TywfKazkt8gaze14l2rIG28tRqby+Dk7a9DIn+ftpC1BdcTivlFexNBxgaU8dLbHxNSL0Wrie18rqoQw4ErJckHf0HMqJzUXM2honf20N6abhpygXEREROVB0D5bIKJoWjXFlxVbOiKxldtdSIq1vzkq4L9ZXHMrLk2byUtj4Z9dWOhPjP8X6MfHJnNFSwbwaKF67DVe3fbS7JCIiIgc5JbkQGSfm53dzVfkGTrVXmdL8IoG+1v2uK2VBVlcexfOllTxvfazs2ERqAqyMcHiijLNbKjlqKxStqsHV719yEREREZH9pQBLZBwKWppLJtfz/rzVHNXzEtnNq4dVX0d2Ic9PP4a/5ebxXPdW2uLtGerp6FoYm8pZjRUcviFGzsoNuK7xc1+aiIiIjE8KsEQmgGMKuvjIpHWcknyJ4oaXsGGkcU9ZkFerFvBM6VSeiTdQ07Mjgz0dPREX5JyuWbyjLp+q1Y1QvVmLjoqIiEjGKcASmWCmRmPcNHU9Z/ESkxr+jiWHl3lv3eQjeHryLJ5KtbG+q+btLxgnZidLeF/jdOa/ESdneTWut3e0uyQiIiITgAIskQmsPJLgpsr1nGfPU17/dywVG1Z9GyYdypNT5/JEsoVN3XUZ6uXoy3MRLm6fw6kbI5Qt3Ui6qWW0uyQiIiLjlAIskYPElGic26e+ztnpZymsf2mvU8DvyetT5rFk8kyWxLZT39uUoV6OPnNwbvccztpSQOXSGmUmFBERkX2iAEvkIHR0QRefrljGSe2PEeoY3rS/tAV45ZDjebhkEk91bqAn2ZOhXo4N7+ydwflbSpj+Si2uZttod0dERETGOAVYIgexoKW5cdpWrg7/hYrtz2DDTNXeE8nlqdmL+WMWvNI+vHW7xqJ39czgws0lVL60GbdDKeBFRETkzRRgiQjgrbP1+ckvcULzQwR6Godd39aymTxYNY8/9tbSHNv/NbvGInNwXvcczl2fR/kL1bi2iZHWXkRERIZPAZaI7CY3mOaz09dycepJ8hteGXZ9iUCYv8w9id/kRHip7Y0M9HBsyXJBLm87nDNWG3kvrcHF46PdJRERERlFCrBEZI/OLW/ik0XPMmv7Eiw5/DTmm8pn88C0I3ioewNdiYm36O+kdC4f3n4ox7zSSmDN+tHujoiIiIwCBVgi8ramZ/fxlWmvcFrrHwl2DT/RQ09WHg/NPYVf0c7m7omZOOLEWCUf3FBB5d/X45qV9l1ERORg8VYBVmg0OiQiY8/W3igfqj6V7OBJ3DV9HZfE/0h282v7XV9OrIsPvvYkl2M8N/skfp6fw0vtE2v64EtZdbw0r47IEUGubj2Gdy5PEnllDaSHlx5fRERExi+NYInIHt0wbSs3hh6heMc/MlLf2inz+NmUGfyp7XWSLpmROseaeYlyrttUxYy/bcQ1Tpy1w0RERGQXTREUkWG5uKKBz+YtoaLuKYzh/87YVjydn804mj90rqMvFctAD8eeiAtyTcsRvHNpnPCytTCGf9eKiIjIvnmrACswGh0SkfHlj/WTWLzhQ1yf+1/UTDsPZ8P71TG1dSv/tvxRntzeyvVF88kL52aop2NH3FL8uPQ1rnzPG3zzjioazjsBy88b7W6JiIjICFOAJSJ77enmEk5bfyXXZn+fmmnnDzvQKulu4rblj/FEzXZuKpxPfnhiBiCvZG3j5qOXc/1NsPyaE7AZVaPdJRERERkhCrBEZJ/9raWI09ZfwXXZ/0Vd5Xtx2LDqK+xt4+MrHuPJrXUTOtBqD/TxfyqXc8kHt/P7m44itugosOG9dyIiIjK2KMASkf3215ZiTtlwNZ/I/x6NU9857Pry+9r5+IrHeKKmjhsK55MbyslAL8emBwpf5+ozX+ebd1TRdM5CLDs62l0SERGRDFCAJSLDtqSxjBM2fpTPFX+LzklvutdznxX0tnPzisd4fFsj1xQdTVYwKwO9HJteydrGTceu4NZbsqm+dBGBstLR7pKIiIgMgwIsEcmYX26fyvytd/L9iq8QL5oz7PqKu5v59PJHebSph38pnk/Qghno5di0PdjJ52Yv46rru3npQwuxmdNHu0siIiKyH/YqwDKzIjP7nZm9bmZrzewkMysxs6fMrNp/LvbPNTP7TzNbb2Yrzey4AfVc659fbWbXjtSLEpHR9a0tc5jf8CUemfZJ0tllw65vclsdX172GL/vCnNG0bwM9HDs6rMk/zFlBZdeto1Hb1xAav5ho90lERER2Qd7O4L1PeAJ59zhwAJgLfBZ4Gnn3FzgaX8f4L3AXP/xMeAHAGZWAnwROBFYBHyxPygTkYknlg5wy/rjObnnWyyffi0uA9P8Zje8wX8tf4Kfpss5smBmBno5djmDnxev5oPnb+C+Ww4ntni+EmKIiIiMA28bYJlZIXA68BMA51zcOdcGXATc5592H3Cxv30R8HPneREoMrMpwNnAU865FudcK/AUcE5GX42IjDk7YhHe98bZXBH5Lg1Tz8xInQu3LOXXr/6Nr0XnUJGBEbKx7rG89Vz9zrX85+0z6HznsRCcuFMlRURExru9GcGaCTQCPzWz5Wb2YzPLBSqcc9v9c3YAFf52JVAz4Ppav2xP5bsxs4+Z2Stm9kpfZ+u+vRoRGbNeaC1k0caP8I3y/5OR+7MMxwVrn+GR9a/z8cL5RCdwIox+f4/W8JHFq7jn9sm0nL0QwuHR7pKIiIgMsjcBVgg4DviBc+5YoJtd0wEBcM45wGWiQ865HznnFjrnFkbzNYNQZKL5Qc0hLGj8Ik9X3YKL5A67vux4DzeteIyHm/s4q/jIDPRw7FsZqefG41bwhdtKaTjvBCyqFO8iIiJjxd4EWLVArXPuJX//d3gBV70/9Q//ucE/XgdUDbh+ml+2p3IROcj0poJ8pPokLnTfZVtlZmYKT2mt4dvLHufHVDA7b1pG6hzr1oWbuPno5Xz6ljy2XbgIy84e7S6JiIgc9N42wHLO7QBqzKw/ldWZwBrgYaA/E+C1wEP+9sPANX42wcVAuz+V8EngPWZW7Ce3eI9fJiIHqVWduZy84Rq+Uf41EoWZSVpx4qZ/8tvV/+TO/CPJmcALFQ+0OdTG7Ucu45O35FJ70SIs5+B43SIiImPR3mYRvAX4pZmtBI4BvgZ8HTjLzKqBd/v7AEuAjcB64P8DbgJwzrUAdwP/9B9f8ctE5CD3g5oZHCnUhdUAACAASURBVNf8ZV6quh4XjAy7vnA6wXUrH+ehxs6DZtogwNZgG3fOW8Ydn8im9mIFWiIiIqPBvNunxqbymfNc7mX3jnY3ROQAOrO0he/m/oz8hlcyVudzs0/iq9EkdT31GatzPJiWLOTON2ZT9adVuN7e0e6OiIjIhFF0ySVMvefupc65hYOP7e0IlojIAfF0cwlH19zBQ5WfwmXlZ6TO0za8wB/feI2PFM0nZKGM1Dke1IbauXOeN3Vw+4WLlAxDRETkAFCAJSJjjnPGbRuO4yL3HzROfWdG6owmerl9+WM80B3h6IJZGalzvNgabOO2I5fxmVvyvayDkeFPwxQREZGhKcASkTFrZUceJ2z8KD+f8nnS2SUZqfPQ+tf5xcq/8dm8Iw6aJBj9NoZaufno5Xz+1hKaz14IoYNnNE9ERORAUYAlImPev2+axznxe9lReVZG6gu4NFeuepI/NnVzatHhGalzPFkXbuLjx63gntsq6DjzOAjovwIREZFM0f+qIjIuvNGdzeIN1/HTKV8gHc3MIuRTWmv4wfI/8bXoHAojBRmpczxZGann+kUr+Y/bq+g59RgwG+0uiYiIjHsKsERkXPnypiO4IPVNWiefkrE6L1j7DA/V1R9UKd0Heimrjg+d9ho/vHU28UVHjXZ3RERExjUFWCIy7qzuzOW4LTfx5LTbcMGsjNRZ2tXIt5c9zrciMynJKspInePNMzmbuerM1/nfm48gPf/Q0e6OiIjIuKQAS0TGJeeMG9afyMdzvkWs5LCM1Xv2umf5Y00dZx+ko1kAD+dXc/n5G3n440fD3Bmj3R0REZFxRQGWiIxrTzSWsrDhc6ytujxjdRZ3N/MtfzSrOFKYsXrHm/8tWsNl76/lr9cfh1VNHe3uiIiIjAsKsERk3OtMhnhv9YV8b9I9pLPLMlbv2eue5Q91O3hX8byM1TneOIP/KV/JlVc2s+yaEwiUlY52l0RERMY0BVgiMmF8Z+sszk18neYpp2esztKuRr637Am+Fp1DfjgvY/WON3FL8fXK5Xzk+hjVly3C8vNHu0siIiJjkgIsEZlQXu/KYeHmG3h82u24UDRj9V6w9hkebGhncVHm7vcaj9qtj8/NWsYtHw9Sd9EiLJq591hERGQiUIAlIhOOc8bH1y/ihmhmE2BMbqvjR8v/zF15RxDNUPbC8WpHsIs75i3j324ppOU9CyEYHO0uiYiIjAkKsERkwvpTU0nGE2AYjitWPclv2tMcVTAzY/WOV9WhZm48fgX33lZJz6kLRrs7IiIio04BlohMaLsnwMhcgoaZjRv4xap/8PHC+QRNozf/zNrGh05bzU9uO5TksUeMdndERERGjQIsETkofGfrLC5Ifp32isUZqzOUTnLTise4L1HA9JwpGat3PHsyZyNXnFPNH26aD3M1wiciIgcfBVgictBY3ZnLcVtv5rmqG3GBUMbqXVDzKr+tfo33F8/PWJ3j3a8L13LZ+2u8NbQqFXyKiMjBQwGWiBxUUi7A1dWn87nCb5DMr8xYvTnxbr607DG+GzrkoF6ceKD+NbSuurqFFVedgJWWjHaXRERERpwCLBE5KP1q+xTO6LyH+qnvzmi9Z1Y/x++3N3LyQZ7OfaCYpfha1XKuvz7OhksWYXm5o90lERGREaMAS0QOWrV9WZy48cMsmXYHLoNp18s7dvDD5X/mM3nziAQiGat3vGsP9HHXnGXc8fEoO84/AYvovRERkYlHAZaIHPRuWn8Ct+d9g0ThjIzVaTiuWvUEv+4KMSevKmP1TgS1oXZunb+cL95aSvu7j9caWiIiMqEowBIRAR6qn8RpbV+irvK9Ga330PrXuX/tUq4oPjqj9U4Ea8KNfPSEV/nOrVX0nqz3R0REJgYFWCIivh2xCKdsuJo/TvsULhTNWL1ZyT7uWvYo/x2YRklWccbqnSheiNZy7TvW8P/fepjW0BIRkXFPAZaIyCC3rz+OT2R/k3jRrIzWe/qG53mwdhunFSmIGMoTuRu44pxqHrzpKNxhmX3vRUREDhQFWCIiQ1jSWMaprV+kdtp5Ga23tKuR/1n+JJ/Nm0dWBhNrTCT3F77O5e/byp8/egw2Y9pod0dERGSfKMASEdmDhliYU9dfyYOVn87olEGAK1c9wa86g0qAsQfO4Edlr/HByxt48bqF2ORJo90lERGRvbLXAZaZBc1suZk96u/PNLOXzGy9mT1gZhG/PMvfX+8fnzGgjrv88nVmdnamX4yIyEi4c8OxIzJlsD8BxgeLlOBhT5KW5tuTV3D1hzpYddUiLVYsIiJj3r6MYN0GrB2w/w3gO865OUAr8BG//CNAq1/+Hf88zGwecDlwJHAO8D9mpty8IjIuLGks45SWzE8ZzEr28W/LH+X7wSpKsooyWvdE0mdJ7q5axvXXx6m+bBFWUDDaXRIRERnSXgVYZjYNOA/4sb9vwLuA3/mn3Adc7G9f5O/jHz/TP/8i4H7nXMw5twlYDyzKxIsQETkQGuPelMFMZxkEeMf6f/D7unpOKTo8o/VONO2BPj43axmfuDHAlvcvwnJzR7tLIiIiu9nbEazvAv8KpP39UqDNOZf092uBSn+7EqgB8I+3++fvLB/imp3M7GNm9oqZvdLX2boPL0VE5MDozzKYKMzslMGyznp+sPwpPp03j0ggktG6J5qGYBefPnQZd9wUZduFi7BoZgNeERGR/fW2AZaZnQ80OOeWHoD+4Jz7kXNuoXNuYTRf68WIyNi0pLGMU9q+SO20czNar+G4ZtUT/Ko7wqw8ZdB7O7Whdm4/chmfuSWfhvNOwCIKTEVEZHTtzQjWKcCFZrYZuB9vauD3gCIzC/nnTAPq/O06oArAP14INA8sH+IaEZFxx8syeNWITBk8bMcaHnh9OZcWz89ovRPVxlArNx+9nM/fWkLTOQshHB7tLomIyEHqbQMs59xdzrlpzrkZeEkqnnHOXQn8BfiAf9q1wEP+9sP+Pv7xZ5xzzi+/3M8yOBOYC7ycsVciIjJKRmph4miily8se4zvhQ6hOFKY0bonqnXhJm46dgVfuq2MlvcshFDo7S8SERHJoOGsg/UZ4E4zW493j9VP/PKfAKV++Z3AZwGcc6uB3wBrgCeATzjnUsNoX0RkzOjPMliT4SyDAO+qfo7fb29kcdFhGa97oloTbuTG41dw922TaDvreAVaIiJywJg3uDQ2lc+c53Ivu3e0uyEisk/+Y/YK/qX+v7Bkb0brdRg/P/psvtddTSKdyGjdE938+CRuXjmF4r+8Csnk218gIiLyFoouuYSp99y91Dm3cPCx4YxgiYjIED654Rg+Fr2XWPGhGa3XcFy78gl+3Z3FbCXA2CerIg3csPBVvnJ7BS1n6x4tEREZOQqwRERGwFNNJSxu+jwbp70v43UftmMND6xdxhXFR2NYxuufyF4L13PjcSv499tKaXrvQmUdFBGRjFOAJSIyQloTId61/hJ+NuULuEheRuvOSvZx17JH+YFNoTxaktG6Dwavh5u46ZgV/Nutxew4/wQsW+toiYhIZijAEhEZYV/adARXBO+lp+zojNd9ysYXeXDLVs4qPjLjdR8MqsPN3Dp/OZ+8JY/aixdhebmj3SURERnnFGCJiBwAL7QWcvz2T7Oy6mpchqf1FfW08O1lj/PV6FzywgoQ9sfWYBt3HrGMT3wixIZLFmHFRaPdJRERGacUYImIHCC9qSAXVr+Xb5V/lXROecbrv3Dt0zzY2MWiwswm1ziYNAS6uWvOMq6/IcmqKxdhFZNGu0siIjLOKMASETnA/rtmBmfHvk7zlNMzXveU1hp+vOJpPpM3j2gwK+P1HyzarY+7py/jquvaeeG647EZVaPdJRERGScUYImIjILq7mwWbr6BJ6bdhstwIGQ4rlr1BL9pT3N0wayM1n2wiVmK70x+lUsv386SGxeQnq/RQREReWsKsERERolzxo3rT+SmnHuJFR+W8fpnNm7g5yuf47aCowgHtO7TcDiDnxWv5vLzN3LfLYfTe8oCCOi/UBEReTP97yAiMsoebyxjYePnWFd1acbrDroU17+6hAe6QszLn5Hx+g9Gj+Wt59rTV/ONOyppOmchFlWKdxER2UUBlojIGNCZDHF29cX8T8WXSUeLM17/3Pp1/PK157lFo1kZszSynZuOXcEdt+Sy4ZJFBMq0HpmIiCjAEhEZU765ZS4Xpb5Je8XijNcdSif52KtL+E1XiPm6NytjakPt3DVnGdd8pJcXrjse5s4Y7S6JiMgoUoAlIjLGrOrM5bitN/NM1SdwIzDaNKd+Hb9Y+RyfylemwUzqCSS8hBgfqOX+m+fRd9LRuk9LROQgpN/8IiJjUMoF+HD1Kdyefy/x4rkZrz/oUly78gkebE1wotbNyrgH89/gmjPWcM8dU9h+wQlYfv5od0lERA4QBVgiImPYQ/WTOKHpC6yp+iAOy3j9Vc2b+fGKP/Pl7EMpiCgIyLSVkXpuO2o513/CsfSaE2D2IaPdJRERGWEKsERExrj2RIhzqy/gyyXfIFEwMl/Q/2XNn3morpH3Fh81IvUf7Nqtj29ULufSS+v45S1H0H3aMRAKjXa3RERkBCjAEhEZJ362bRqL274yYqNZZV0NfHPZEn5oU5mWMznj9Yvnobxqrjv1NT57RzEbLlmEVZSPdpdERCSDFGCJiIwjzfEw51ZfwL+XfJN40ewRaeOUjS/yhzdW8dHC+UrpPoI2hlq5a84yPnhdO4/duIDYoqOUFENEZALQb3IRkXHoF9sqOb7pi7wy/cO4QOanmkUTvdy64jF+12lKgjHCkpbmvuLVXH3m63zpzgq2vH8RNqlstLslIiL7SQGWiMg41ZkM8YE33s1Nud+mu/yYEWljVsN6frziz9wbmcWkqL70j7Q14UY+fegyPvjhDh69cYGX6l33aomIjCsKsERExrnHG8s4uvZTLJl2By5rZDIBnrPurzyy8Q0+XKRpgwdC0tL8vHg115yxhs/eUczrly/CDpk22t0SEZG9oABLRGQCSLkAN60/gfPT32Z75dkj0kZOrIs7lj/GH9od7yg6YkTakDfbGGrl32cu45IrdvCzWw+j5T0Lsfy80e6WiIjsgQIsEZEJZHVnLidtuJZvlX+NROHMEWnjkKaNfH/5k/zQpjI7T6MqB9KS3A3cePwKPnyT46/XH0f8hKMgGBztbomIyAAKsEREJqDv18zgmOav8I+qG3Ch7BFp45SNL/K71S/zudzDKckqGpE2ZGidgRj/U76Sq979OnfdWcrqKxbB3JEJqEVEZN8owBIRmaC6k0GurH4H7w9+lx2V7xmRNkLpJJe/9ice27yZDxfNJyuYNSLtyJ5tCLXw5UOWcekHavjuHTOped8ibErFaHdLROSgpQBLRGSCW9aez+INH+Lu0m/QV3L4iLSR19fBHcsf49GmXi4snk/A9N/LaHg+WsMnD1/Gpdc2c98th9N47glYSfFod0tE5KCi/wFFRA4SP6mrYv6OL/Bg5adJ54xMyvXJbbV8ddlj/LY7qkQYo8gZPJa3nk8sWM4HP9bNbz9xJK3vOR4rKhztromITHhvG2CZWZWZ/cXM1pjZajO7zS8vMbOnzKzafy72y83M/tPM1pvZSjM7bkBd1/rnV5vZtSP3skREZCiJtHHnhmNZ3P0f3iLFI3R/1qH1r/P95U/yi2QpJxTOHZE2ZO8kLc1vC9Zxw/GvcuWNffzhpvm0naVgS0RkpJhz7q1PMJsCTHHOLTOzfGApcDHwIaDFOfd1M/ssUOyc+4yZnQvcApwLnAh8zzl3opmVAK8ACwHn13O8c651T22Xz5znci+7d9gvUkREhnZ0QRffq1jCjNqHMZcesXZemLmI7xfksLJj44i1Ifsm4oJc3DmXd26IUv7KRtJNLaPdJRGRcaPokkuYes/dS51zCwcfe9vl4Z1z24Ht/nanma0FKoGLgDP80+4D/gp8xi//ufMitxfNrMgP0s4AnnLOtQCY2VPAOcCvh/XqRERkv63syOOdHZdyVtm7+WrBH5i07ekRaeekTS9zEvC32Sfzg7wwr3VsGpF2ZO/FLcVvCl7nN8dC8FjjvK4jOHNzHlOX1eLqto9290RExq23DbAGMrMZwLHAS0CFH3wB7AD6UxZVAjUDLqv1y/ZUPriNjwEfA8grnUzuvnRQRET2y1NNJTzV9BEum3Ied2X9jqIdz49IO6dveJ7T8QKt/5sX0YjWGJHC8XBeNQ8fBRwFp/bN5LzacmatasbWbYS3me0iIiK77HWAZWZ5wO+B251zHWa285hzzplZRn77Oud+BPwIvCmCmahTRET2zgPbJ/MAN/OhqRdzZ/h3FNS/PCLt9Adaz89azI8KclnaXj0i7cj++Xu0hr/PqYE5MDcxifc1VjF/XYzoq9W43r7R7p6IyJi2VwGWmYXxgqtfOuce9IvrzWyKc267PwWwwS+vA6oGXD7NL6tj15TC/vK/7n/XRURkpPxs2zR+xu18uLKG20J/oLD+xRFp5+SNL3IysGz6cfyktJy/ta0dkXZk/1WHm/nm1GaYCvnvyOKijqM5eXOE8ldrcdt2jHb3RETGnL1JcmF491i1OOduH1B+L9A8IMlFiXPuX83sPOBmdiW5+E/n3CI/ycVSoD+r4DK8JBd7vKtWSS5ERMaGq6fWcXvWI5Ru/9uItvNGxeHcVzmbJe1rSaaTI9qWDN+JsUrO2VHBoeu6iKxaj4vHR7tLIiIHxFsludibAOtU4DlgFdCfYurf8O7D+g0wHdgCXOqca/EDsu/jJbDoAa5zzr3i1/Vh/1qArzrnfvpWbSvAEhEZWy6Y1Mhn859g6rY/YS41Yu3UF07h17OO47c9m+mId45YO5I5hS7K+e0zWVwTZfLqetymraPdJRGRETOsAGs0KcASERmbTizq4Ivlz3LEjoexRPeItdMbyeGRuafwq0A3G7pqR6wdyby5yVLOa5rG/M1pCldtURp4EZlQFGCJiMiImBaNcXfVK5zW9kdCnXUj2taLMxdxf3EJf21bR2oER89kZJzUN40zG8uZuzFGzmubcR0do90lEZH9Nqx1sERERPakti+L66pPIStwEp+aXs1l7vERyzy4eNPLLN4E9YVTeXDmsfw+vp363qYRaUsy74VoLS9U1UIVBN9hnN47h9MbSpi9qY/s1Qq4RGTi0AiWiIhk1HvKWriz+DkOa1iCxUbu/qmUBfnHrBP5fWEBf2t7g6RTUozxKohxau90Tm0qYc6WBPlra0g3NY92t0RE9khTBEVE5IArjST4TNUazo89Tk7TyhFtqzmvnEdnLeQh10l1l5IrTATHxCdzRksFh9cZJesbYFONFjwWkTFDAZaIiIyqf6lo4KaC55hd/wQWH7mkGACvT5nHI5Nn8XhfLY19SqwwUUxK53JWx3QWNGRTubmLyBtbcZ1do90tETlIKcASEZExYVJWgs9MW83Z8afIa1w+om2lLcDLMxbyRHE5T3Ur3ftEYw4Wx6ZxUlsZc7dD6cZm2FgDSU0VFZGRpwBLRETGnHeUtnJrySssaH+aUMfITutLBMK8MPME/lRYzF8UbE1YeS7CaT1VHN9SwIztKQo2NcGWOkgp66SIZJayCIqIyJjzbHMxzzafBZzFv1Q0cE3BMo5sf5Zwx5aMtxVOJzh9w/OcDiQDIf55yHE8XVzOX3q30dCnZAoTRZfFeTx3A4/nAlXAIih02ZzWPY0FrfkcsiNN0ZZm2FSrkS4RGTEawRIRkTHl3PImri1axYKefxBtXjOibTmMNZVH8dfy6Tyb7mBtZ+aDOxl7oi7E4r5Kjm0vYlZDgNK6LsKb6nDtShUvIntHUwRFRGRcOq6wk4+Uv87i1FJKGl7CUrERba+hcAr/qDyS56JhXuzaQmdCSRQOJoclyljYXc5hrdlMrU9SUNuCbdmGi8dHu2siMsZoiqCIiIxLy9rzWdZ+AnACxeHruXbKVs7Oeo3ZnS8TaduY8fYmtW/nfe3beR/eOlurps3nhdJKXqSXlZ2bSaY1rWwiWxduYl1RExQBM72ykAtwXPwQFnSVMKs1zOT6BLm1LVCzDRKJUe2viIxNGsESEZFx6bjCTq4o3cjiwGtMaf0nwe6GEW2vJ5LLsqqjebmghKXpbtZ0btXixgexkAuwIFHB/O4SZrdlMbkpRf72DoI19bgOTTUUmeg0giUiIhOON7q1AFgAXMm7Slu5qGgTx9saprQtJ9i1PaPt5cS7OXXDC5zq7/dk5bFi6pEsLSxjOX2s6tpK3whPYZSxI2lplka2szSyHYrZOeIFMC1ZyjF95RzWmUdlW4DSxhjZO9qwbfW43r5R67OIHBgKsEREZEJ4prmYZ5qLgeOAq1hY2MlFJVtZFKpmes9qoi2vYy5z6bpzYl2cvOklTvb3E4Ewr089ghXFU1kRNlb2NbCjtzFj7cn4URtqpzavnUfzgCnAEV65OZiTquCo3lJmd+UwpT1ASXOcnPoOAtubNPIlMkEowBIRkQnplfZ8Xmk/EjgSuJjSSILzyxo4PXcrR6SrmdS5JqPrb4XTCebXrmR+7Uqu9ssaCqewatIcVucW8JrFWdOznfa4vkQfrJxBdaiZ6vxmyMcLvgaYnCpiXqyM2b35TOsMU96WpqC5j6zGDtjRoNEvkXFCAZaIiBwUmuNh7ttWyX1UAicBMD27j/eUNnJSdi2Huo1M6l5PpH0DlqFkFpPat3Nm+3bOHFBWVzKdtWWHsDangHWWZF2sSSNdAsCOYBc7crp4JgcoffPxaclSDksUM7Mnj6ldYco7oKA1TrSli0BDK66lFcbwvfUiBwsFWCIictDa2hvlx7VV/Jgq+oOu3FCKd5W0cFLeDuYF66hKbqGwawPBzjqM4X95rWzZSmXLVt49oKw9u4jqSbOpzi9jfSTE+nQvG3sbaYu3D7s9mThqQ+3UhtohmyEDsKjLYm6ihFnxQip7s5ncFaKk05HfFiertZtgcweuuUWLLIuMMAVYIiIiA3QngzzSUM4jDeXA/J3lpZEEpxa3sjCnkcNCO5ie2kpJzwbC7VuGfW9XYW8bC7csZXAqqpbcMjaWHcKmvBI2R7LYTIItiXbqehqUwVDepM+SrIo0sCrSAHlA+ZvPCWJUJcuYFS+iMp7D5J4IZd0BCrrS5LbHyWrrIdDagWtuVRp6kf2kAEtERGQvNMfDPFQ/iYeYhHdflyc/lOS04jZOyGtkXmgHVekaivtqiHZuweLDW6i4pLuJku6mNwVeyUCIbSVVbC2cTE12ATXhMHWWpDbRRV1fE93JnmG1KxNXCsfmUBubQ22Qg7fm1x5MThVxSLKQynguk/uilPaFKOqG/K4U2Z1xIu29BNq7oLUd19t7wF6DyFinAEtERGQYOpMhljSWsaSxjJ3p4nzTs/tYkN/JEdltzAq3UGlNlKWbKIjXE+3ZQaCncb9Gv0LpJNObNjG9adOQx9tzitlWOIVteaVsj+ayPRRiu6WoT/WxI95Oc6yVVAYzKsrEtCPYxY5gF2ThJeV4C/npXKpSBUxJ5lIRz6Y0FqGkN0hBL+T2pMnuShDp6iPY2Uugo4t0W4emKsqEpQBLRERkhGztjbK1N8ojQ83VAsIBx+G5PRye28msrE6qwu1UWBulrpXCVAs58WYifY0Eepv3KfFGYU8rhT2tg8K9XVIWpKmggob8MhqyC2nIyqExFKIpAE0uSVOqh8Z4J63xdgVislc6AzHWBBpZE2707hHbC6XpAiYn86hI5lCWjFISD1MUC5EfM3J7Iac3RVZPknBPnFBXH9bVA13duK5uJfOQMU0BloiIyChJpI1Vnbms6swFJu/xPDPHzOwYs3N6qMrqpjLSTUWwizLrpJgO8tId5KbaiCbaCcXbCfa2YMk9T9kKuhQV7duoaN/2lv1LW4DW3FKa8spozi6gOZpLSzhCczBIs0GrS9Ka7qM12UNrvJMeTU2UfdAc6KE50sPqyL5dFyREaTqHimQupalsSpJZFMUjFCSC5CeC5MYgu88RjaWJ9KaI9CYI9sYJ9sSguwe6e3E9PQrSZMQowBIRERnjnDM29kTZ2BMFSvbqmvxQkunZMSqzYkyO9FEe6qUs1ENxoIfC/8fefcdHVeX/H399pqSQhBZqIIig2OhSVBRZUbArgqKigorIWteCuv501V3WuuvqoqJ+7YUVKxZQQQQBRREQREUFqYEAIUAgIWVm7vn9MUMIUqQkmQTeTx73MXPPOffcz03mccln7rnnWiFpFJDiCkj2CkiObCIhkk8glI+/eANWlIfh8DmP9Pwc0vN3bxr5En8iG1Lrsj65NhuTUtmQkExeMJE8f4CNfh8bDTbiscmF2eSVkB8pZmO4kE2hfEKeJlSQ3RPBscZXwJqEgr3uw5yfuq4Gdb1k6kSSqBNJpGY4SGo4EF1CPpJLjOQQJBU7Eos9gsUegZIwgcIQvqISfMUlUFgMhcXRe9A0KYjEKMESERHZD20KB/hxU4AfN6Xs8bZBn6NZUhEHJRfRJHEzDQJFNAgUkO4vIIVialghya6IRFdMoldIgldI0CsiECmkTriQ9PwN2IZsLFSIRYp3a58l/kQ2JdckPymNgoRkChJqkB9MpMCfwOZAgAKfnwKfj81mbDbHZhyFRNjsRSh0YQq9EIVeCYWREgojRRSFi3DlMK2+7J+cQa5tJte3udz+Gk50idRySdTykqgVSSTVC5IaCZIaCVAjHKBGxEdyxEdS2EdSCBLCkBCCYIlHMOQRCHkESiL4SyL4ikP4SsJYSQiKS0oXV1wMEQ3breqUYImIiMg2Qp7x2+ZkftucDNTZp76CPkftQJjawTBpgTA1/VteQ6T6w9TwhUnxhUj2hUi26JJoIRIjYdK8EPUoIcGFCBIi4EIEXQkBF8LvRV99Xgi/K8EXib43rwTzSsALU2J+ivx+igNBigIJFAUSKQwkUhRbL/QHKfb5KfT7KTQfv9QPRgAAIABJREFURT4fxQZFGEXmKMZRjEeR8yhxEYqdR7ELU+yFCbkwxZEQxV4JYS9MiRfS/WoHuGKLsMYKWOMrqMC/sI0El0iaSyTVSyDFBUnxgtTwgiR7AWp4fpI8P0lhP4mej6SIkRjxEYwYCREIRiAYhkDYEQw7AmGHL+zwhz0CoQi+sIeFPXyhMBaOYKEwFopASSg6KUkoDKEQLhTSJCW7oARLREREKkzIM3JKguSUBOMaR61gmPRgmLrBEHWCIWoFQtTyl8QSvRISiJBqEYIWIWgeQcIEzCNAJLZ4BCyCnwgBF8aPh59I6eJzHp5ByGeEfT5CQDj2PmxGxCBsFi0zR8SMMNFXzxxhg4g5wkCE6PsI0eFw0fdblzAeHhDBIwLRfnCEcYTdllePEB5h5wi5CGHnEXYRIrHXcKws4iJEXISwF47WexFd+aviSiyy9epbHJkLkOyC1CCBROenhhckkQCJzkeiFyDR+Un0/CR4PhJcdAl6PhI8H0HPtlkCESPgQcADvwf+SGzxXGzd4Y84fF40IfRFHL6Ih3mx1+2WCEQ8LBx9JVLmNRyJrUdw4XD0fTnfj1fpCZaZnQo8DviB55xzD1Z2DCIiInJgyQsFyAsFWERSvEMpV4k+j5qBCDUDYdICEVIDEdL8IWr5ItTwhwmah8/Aj8NnHn7Abx4+wIcjYB6Gw28Onzl8ODBw5ohguFhyiDmcGZ5Fh9c5wDPAwCPa3rNYUBati/7J6uF8hofDcHhmpQmcs9g7c3ixTZ05IBqLP5bQ+szDZxGMCGYehkfEHB7R7VwswYzGQbTcuej7bV6j5d7WyEr/lb530Zi21kTfey72c3Fumzq21LGD7VzZVtFanIv+LJ0Hzivdb8RtefVKXz0XjcyL1XnOlV4l9WLbEjseL7adK2275SdacZzBZguxmdi9Z/4K32UF8RNwPgL4SCRA0PkJOh9BYq+xJYCfgLPS+s6tasLwHfdYqQmWmfmBJ4FTgCzgWzP7wDn3U2XGISIiIrI/KPZ85JT44n6FUPZO0Oeo4Y+Q6o+Q5PPwG7GEN5qvRHNYh8XKDWNL6hotK9tma91WLrqVbUn+LJbURusww8X62VKPsR23pT1E22xJHS0aU9Ag0R8h0RchyR8hwecImkeCL4Lf55XuzyO6vy2JdiztLI3a27IeO7Cy9ca269FkfMtR/q6N/f4nsfW67JZX266mzM8ldpw+gwSLEPB50SvaFr2S7TOPhKQW2/+gYir7ClYXYKFzbhGAmb0BnAMowRIRERGRA0rIM/K86NVVqV4u6pK507rK/m02AZaXWc8CupZtYGZDgCGx1eK1D535QyXFJge2esDaeAch+z19zqQy6HMmlUWfNakMVfJzFrvH6aAd1VW5dNk59yzwLICZzXTOdYpzSHIA0GdNKoM+Z1IZ9DmTyqLPmlSG6vg581Xy/lYAZa+nNY2ViYiIiIiIVHuVnWB9CxxqZgebWQJwIfBBJccgIiIiIiJSISp1iKBzLmxm1wGfEp0c5QXn3I+72OTZyolMRJ81qRT6nEll0OdMKos+a1IZqt3nzFw5P1hLRERERETkQFXZQwRFRERERET2W0qwREREREREykmVTbDM7FQz+8XMFprZHfGOR/YPZpZpZpPM7Ccz+9HMboyV1zWzCWa2IPZaJ96xSvVnZn4z+87MPoqtH2xm38TOa6Njk/2I7BMzq21mb5vZz2Y238yO1TlNypuZ3RT7f/MHM/ufmSXpnCblwcxeMLM1ZvZDmbIdnsMs6r+xz9z3ZtYxfpHvXJVMsMzMDzwJnAYcCVxkZkfGNyrZT4SBW5xzRwLHANfGPlt3ABOdc4cCE2PrIvvqRmB+mfWHgP845w4B1gNXxiUq2d88DnzinDscaEf0M6dzmpQbM2sC3AB0cs61JjpR2YXonCbl4yXg1N+V7ewcdhpwaGwZAoyspBj3SJVMsIAuwELn3CLnXAnwBnBOnGOS/YBzLts5Nzv2fhPRP0SaEP18vRxr9jJwbnwilP2FmTUFzgCei60bcBLwdqyJPmeyz8ysFtAdeB7AOVfinNuAzmlS/gJAspkFgBpANjqnSTlwzk0B1v2ueGfnsHOAV1zU10BtM2tcOZHuvqqaYDUBlpdZz4qViZQbM2sOdAC+ARo657JjVauAhnEKS/YfjwG3AV5sPR3Y4JwLx9Z1XpPycDCQA7wYG476nJmloHOalCPn3ArgX8AyoolVHjALndOk4uzsHFYtcoSqmmCJVCgzSwXeAf7inNtYts5Fn12g5xfIXjOzM4E1zrlZ8Y5F9nsBoCMw0jnXASjgd8MBdU6TfRW7/+Ucogl9BpDC9kO6RCpEdTyHVdUEawWQWWa9aaxMZJ+ZWZBocvW6c+7dWPHqLZeYY69r4hWf7Be6AWeb2RKiQ5xPInqfTO3Y8BrQeU3KRxaQ5Zz7Jrb+NtGES+c0KU8nA4udcznOuRDwLtHznM5pUlF2dg6rFjlCVU2wvgUOjc1Ok0D0RsoP4hyT7Adi98E8D8x3zj1apuoDYGDs/UDg/cqOTfYfzrm/OueaOueaEz1/fe6cGwBMAvrFmulzJvvMObcKWG5mh8WKegI/oXOalK9lwDFmViP2/+iWz5nOaVJRdnYO+wC4LDab4DFAXpmhhFWGRa+6VT1mdjrRexj8wAvOuX/GOSTZD5jZ8cBUYB5b7425k+h9WG8CzYClwAXOud/fcCmyx8ysB3Crc+5MM2tB9IpWXeA74BLnXHE845Pqz8zaE51MJQFYBFxO9AtUndOk3JjZfUB/orPxfgcMJnrvi85psk/M7H9AD6AesBq4BxjDDs5hsQT/CaJDVDcDlzvnZsYj7l2psgmWiIiIiIhIdVNVhwiKiIiIiIhUO0qwREREREREyokSLBERERERkXKiBEtERERERKScKMESEREREREpJ0qwREREREREyokSLBERERERkXKiBEtERERERKScKMESEREREREpJ0qwREREREREyokSLBERERERkXKiBEtERERERKScKMESEZEqx8wmm9ngvdy2mZnlm5m/vOOqCPtyrCIiUvUowRIRkXJlZkvM7OR47c85t8w5l+qci1TAvpyZFcQSuBVm9mh1SeRERKRyKMESERHZM+2cc6lAT+Bi4Ko4xyMiIlWIEiwREakwZnaImX1hZnlmttbMRpepO87Mvo3VfWtmx+2kj5Zm9rmZ5cb6eN3MasfqXgWaAR/GrirdZmbNY1eaArE2GWb2gZmtM7OFZnZVmb7vNbM3zewVM9tkZj+aWafdOTbn3M/AVKB1rK+rYv2vi+0vY0+PVUREqj8lWCIiUpH+AYwH6gBNgREAZlYXGAv8F0gHHgXGmln6Dvow4AEgAzgCyATuBXDOXQosA86KDQt8eAfbvwFkxbbvB9xvZieVqT871qY28AHwxO4cmJkdCZwAfBfr7wHgAqAxsDTW554eq4iIVHNKsEREpCKFgIOADOdckXNuWqz8DGCBc+5V51zYOfc/4GfgrN934Jxb6Jyb4Jwrds7lEE1QTtydnZtZJtANuD22/znAc8BlZZpNc86Ni92z9SrQ7g+6nW1m64EPY329CAwAXnDOzXbOFQN/BY41s+Z7cqwiIlL9KcESEZGKdBvRK1AzYsPvroiVZxC9ylPWUqDJ7zsws4Zm9kZsUomNwGtAvd3cfwawzjm3aRf7WVXm/WYgacvwwp3o6Jyr45xr6Zy7yznn/f54nHP5QG5sP7t9rCIiUv0pwRIRkQrjnFvlnLvKOZcBXA08ZWaHACuJXtkqqxmwYgfd3A84oI1zriZwCdGkrXQ3uwhhJVDXzNJ2Yz/7YpvjMbMUosMBV/y+rgJjEBGRKkAJloiIVBgzO9/MmsZW1xNNhjxgHNDKzC42s4CZ9QeOBD7aQTdpQD6QZ2ZNgGG/q18NtNjR/p1zy4GvgAfMLMnM2gJXEr0KVp7+B1xuZu3NLJFoUviNc24Je3asIiJSzSnBEhGRitQZ+MbM8olOIHGjc26Rcy4XOBO4hehQutuAM51za3fQx31ARyCP6GQR7/6u/gHgLjPbYGa37mD7i4DmRK8kvQfc45z7bJ+PrIxYf3cD7wDZQEvgwljdnhyriIhUc+bcrkZWiIiIiIiIyO7SFSwREREREZFyogRLRERERESknCjBEhERERERKSdKsERERERERMrJrh6kGHf16tVzzZs3j3cYIiIiIiIi25g1a9Za51z935dX6QSrefPmzJw5M95hiIiIiIiIbMPMlu6oXEMERUREREREyokSLBERERERkXKyTwmWmS0xs3lmNsfMZsbK6prZBDNbEHutEys3M/uvmS00s+/NrGN5HICIiIiIiEhVUR73YP3JObe2zPodwETn3INmdkds/XbgNODQ2NIVGBl73SOhUIisrCyKior2PXIpN0lJSTRt2pRgMBjvUERERERE4qYiJrk4B+gRe/8yMJlognUO8IpzzgFfm1ltM2vsnMvek86zsrJIS0ujefPmmFk5hi17yzlHbm4uWVlZHHzwwfEOR0Sk6nIOV7gBK9kExZtwxQUQLoRwCXhhDC/aDMP8QZwvCIEkLKEGLiEFEmthybXBX6XnqBIROaDt6xnaAePNzAHPOOeeBRqWSZpWAQ1j75sAy8tsmxUr2ybBMrMhwBCAZs2abbfDoqIiJVdVjJmRnp5OTk5OvEMREYmvjdm43IWwfglsWAZ5K2DjCihYDQVrsc3rMBcpbb6z/8lsB/XbtE2sCTXSIaU+pDXCpTbCajeFWk2hdnOo0xxS0svxwEREZHfta4J1vHNuhZk1ACaY2c9lK51zLpZ87bZYkvYsQKdOnXa4rZKrqke/ExE5oBRvwq2cA6vmYat/xK35EVu7EEo27TRpKt/9b4wu6xcDO0nUkmpB3ZZQrxWuXius4ZHQ4Eioc1BlRCgicsDapwTLObci9rrGzN4DugCrtwz9M7PGwJpY8xVAZpnNm8bKREREqjS3diEs/RKWfQMrZ2JrF2DOK62vkl8xFeXBytmwcvbvrn7VgkZtoHE7yGiPy+iI1TskXlGKiOx39jrBMrMUwOec2xR73wv4O/ABMBB4MPb6fmyTD4DrzOwNopNb5O3p/Vc70vyOsfvaxTaWPHjGbrX75z//yahRo/D7/fh8Pp555hm6dt3jOTv+0IYNGxg1ahTXXHNNufdd1uTJk0lISOC4444D4Omnn6ZGjRpcdtllFbpfEZEqadMq3MKJ8NskWDIVy18V74jKT3EeLJ0WXYglh8l1oGlnyOwCzY6FJkdDMDmuYYqIVFf7cgWrIfBebGhYABjlnPvEzL4F3jSzK4GlwAWx9uOA04GFwGbg8n3Yd1xNnz6djz76iNmzZ5OYmMjatWspKSmpkH1t2LCBp556qlISrNTU1NIEa+jQoRW6PxGRqsat+A5+GQe/foyt+gFjj0a4b99fQgqhlAwKEhuwMZDOBl8tcl1N1nsprIsksy6SSF44kU2RAJsjfoo8PyFnOAdmkOBzJFqEGv4INf0hagZKqOMvoa6vkDr+zdSxTdT28qjprSelZC2Jm1djm9fuXdyF62HB+OgC4E+AJkfjDuqGtTgRMrtCIHGffh4iIgeKvU6wnHOLgHY7KM8Feu6g3AHX7u3+qpLs7Gzq1atHYmL0P5t69erx+eefc8011zBmzBgAJkyYwFNPPcV7771Hamoqf/7znxk3bhyNGzfm/vvv57bbbmPZsmU89thjnH322bz00ku899575OXlsWLFCi655BLuuece7rjjDn777Tfat2/PKaecwsMPP8xtt93Gxx9/jJlx11130b9/fyZPnsw999xD7dq1mTdvHhdccAFt2rTh8ccfp7CwkDFjxtCyZUs+/PBDhg8fTklJCenp6bz++usUFhby9NNP4/f7ee211xgxYgQTJ04kNTWVW2+9lYULFzJ06FBycnLw+/289dZbtGzZMp6/AhGRcuGWfws/vAs/f4jlLf/jDX6/vS9ISa0WrK3RgmW+TH4JN+T7zenM3FiTZRuTYGMFBL0LKX6PtjU30TYlj8MScznYv4aM8ArqbF5CcONSzAvtXkeRElg2HVs2Hab+CwLJuMyu2CE94ZCe0PCoij0QEZFqTPO87oVevXrx97//nVatWnHyySfTv39//vSnP3HNNdeQk5ND/fr1efHFF7niiisAKCgo4KSTTuKRRx6hT58+3HXXXUyYMIGffvqJgQMHcvbZZwMwY8YMfvjhB2rUqEHnzp0544wzePDBB/nhhx+YM2cOAO+88w5z5sxh7ty5rF27ls6dO9O9e3cA5s6dy/z586lbty4tWrRg8ODBzJgxg8cff5wRI0bw2GOPcfzxx/P1119jZjz33HM8/PDD/Pvf/2bo0KGlCRXAxIkTS493wIAB3HHHHfTp04eioiI8z0NEpNrK/Q03ZxQ27y1sw9Ld3syZn6K6h5NV40jmRlrwRX4Gn+emU5Dtq8Bg90xBxMf09bWYvr4WsO1MvMn+CMfVzqNbzdW0Da7g4NBv1N74M/6C1X/ccbgQWzwZFk+GCXdDWgYcejIc2gta/AkSUyvicEREqiUlWHshNTWVWbNmMXXqVCZNmkT//v158MEHufTSS3nttde4/PLLmT59Oq+88goACQkJnHrqqQC0adOGxMREgsEgbdq0YcmSJaX9nnLKKaSnR6fVPe+885g2bRrnnnvuNvueNm0aF110EX6/n4YNG3LiiSfy7bffUrNmTTp37kzjxo0BaNmyJb169Srd56RJk4Doc8T69+9PdnY2JSUlf/jcqk2bNrFixQr69OkDRB8oLCJS7ZQU4H54F757BVs+Y7cmpXC+IPn12vFTYnsmF7Xk7dUZ5Kyovg9TL4z4mZhbl4m5dYEjgJMBOCJ1M6enZ3NMwmIOCf1C7fXfY8Wbdt3ZppUw+5Xo4k/ENT8BO/x0OOx0qNm4wo9FRKQqU4K1l/x+Pz169KBHjx60adOGl19+mWeeeYazzjqLpKQkzj//fAKB6I83GAyWTmPu8/lKhxb6fD7C4XBpn7+f6nxPpz7f0u+u9nP99ddz8803c/bZZzN58mTuvffePTtwEZFqxK2eD98+h817Eyv+4/F64ZrNWFjrWD4tbsNrqzLJWVZ9E6rdNT+/BvPzWwItgZPxm0eveus4vdZSOjCfxutn7foqV6QY++0z+O0zGHsLrunR2BFnwxFnQ109fF5EDjxKsPbCL7/8gs/n49BDDwVgzpw5HHTQQWRkZJCRkcHw4cP57LPP9rjfCRMmsG7dOpKTkxkzZgwvvPACaWlpbNq09ZvEE044gWeeeYaBAweybt06pkyZwiOPPMLPP/+8i563ysvLo0mTJgC8/PLLpeVpaWls3Lj9Hx9paWk0bdqUMWPGcO6551JcXEwkEqFGjRp7fHwiIpXCObxfxmHfjMQWT/3D5oX1WjMz+XheXd+a8Wvqbn24yAEq4nx8nFOPj3PqAUcDl3Bi3fWcV2cxXZhHw9wZ+IrW72Rrh2XNhKyZMOFv0angjzwXjuqjZEtEDhjVPsHa3WnVy1N+fj7XX389GzZsIBAIcMghh/Dss88C0fuVcnJyOOKII/a43y5dutC3b1+ysrK45JJL6NSpEwDdunWjdevWnHbaaTz88MNMnz6ddu3aYWY8/PDDNGrUaLcTrHvvvZfzzz+fOnXqcNJJJ7F4cfQhlWeddRb9+vXj/fffZ8SIEdts8+qrr3L11Vfzt7/9jWAwyFtvvUWLFi32+PhERCpUqAj33Wvw9ZP41i3aZdOiukfwdcqfeCqnLTOyalZSgNXXF+vq8MW6OkBH/HYp5zRYS5+aP9OueBZpa7/DvPCON8yeG10m3gcZHaF13+iiYYQish+z6OR+VVOnTp3czJkztymbP3/+XiUvleW6666jQ4cOXHnllXu03UsvvcTMmTN54oknKiiyilfVfzcisp8q2og34/+iV6wKcnbaLJLSkHl1e/P0hs58kpNeiQHu35okFXN5oyWcEviOzNwv8RXm7noD88FB3XBt+2NHngNJSnBFpHoys1nOuU6/L6/2V7CqkqOPPpqUlBT+/e9/xzsUEZH9nivcgPv6aeybkfiKNuy4jflZ2/hE3oj8if8ub0Eod8/ubZU/tqIokeFLDmM4h+G3C7iw0Sr6pc3jqI1TSdiwgyuJzos+vHnJVBh3a3RijPYXQ8uTwOev/AMQESlnuoIl5Ua/GxGpFMWb8KaPxL5+AivK22ETr0Y9Zqafw/2ruzJno6YQj5ee6eu4vO48jt48jeTcH3fdOLURtL0AOlwC9Q+rnABFRPaBrmCJiEj1Fi7GzXgOm/ZvfJt3PAytMP0o3ks8m38uPYqCdVXn+VQHqui08CcCJ3JsnTyurjePrpunkJz7w/aN81fBV/+NLk07Q4dLo/dr6RlbIlLNKMESEZGqzTnc3NHYpH9iect22GRd4xN4KnQmz2VlVnJwsruiD0A+Hjie4+vm8ef0OXTO/5yE9Qu2b5z1bXT59M7oDIRHD4Km231JLCJSJSnBEhGRKsstngbj78Sy525fZz6yM3rxwKbT+HBx/ThEJ3tr2rpaTFsXvbJ1ev21DKk9kzbrP8Ofv3LbhiX58N2r0aVh62ii1ba/JsYQkSpNCZaIiFQ5bt0SGH8X9vOH29eZjxVNTuNv60/n89/qVH5wUq7G5dRjXM6p+K0XlzdZwYCk6TRfMwErKdi24eofopNiTLgH1/o86HQl1qRDfIIWEdmF6p9g3VurnPvb8Q3TZfn9ftq0aVO6PmbMGJo3b77DtqmpqeTn5+9TSIMGDeKLL76gVq1a+Hw+nnzySY499tg96mPw4MHcfPPNHHnkkdx///3ceeedpXXHHXccX3311T7FKCJSLkKFeFP/g++rxyFctE2Vw8hu0ps715/F5IVKrPY3EefjuaxMniOTOsHzuDXzZ87wJlNr1XSMMhNyhQqwLVe1mhwNnQfDUedBMCl+wYuIlFH9ZxGMQ4K1J0lTeSVYZ555Jv369WP8+PHceuutfP/993vdX3nEtCOaRVBE9oX381jskzuwDdvfZ5Xb+ETuye/LRzn14hCZxFPHWpu4tcEsuuR9QmDjju/BI7kudLwUOl0JdQ6q3ABF5IC1s1kENcVSOcjPz6dnz5507NiRNm3a8P7772/XJjs7m+7du9O+fXtat27N1KlTARg/fjzHHnssHTt25Pzzz//DxKd79+4sXLgQgEcffZTWrVvTunVrHnvsMQAKCgo444wzaNeuHa1bt2b06NEA9OjRg5kzZ3LHHXdQWFhI+/btGTBgABBNuAAuvPBCxo4dW7qvQYMG8fbbbxOJRBg2bBidO3embdu2PPPMM/v4ExMR2cptWI4bdRG+Ny7eLrnaXK8tf09/iKMXX63k6gA1Oy+Nixf04NCcBxhe7yGymp6B8ydu26hwHXz5OPy3PfzvIlg0OS6xiojA/jBEMA62JCgABx98MG+99RbvvfceNWvWZO3atRxzzDGcffbZmG19oOWoUaPo3bs3/+///T8ikQibN29m7dq1DB8+nM8++4yUlBQeeughHn30Uf72t7/tdN8ffvghbdq0YdasWbz44ot88803OOfo2rUrJ554IosWLSIjI6M0UcrL2/aK3IMPPsgTTzzBnDlztuu7f//+vPnmm5xxxhmUlJQwceJERo4cyfPPP0+tWrX49ttvKS4uplu3bvTq1YuDDz64PH6cInKg8iJ4Xz+NTb4fK9n2y6VwWhNGpV7OPUuOwDk9HFjAOYsNIRxAs+S+3Nl0Ln8q+ITE9b+UaeTBL+OiS/0joOsQaHshJNSIX+AicsBRgrUXkpOTt0lQQqEQd955J1OmTMHn87FixQpWr15No0aNStt07tyZK664glAoxLnnnkv79u354osv+Omnn+jWrRsAJSUlO723atiwYQwfPpz69evz/PPPM3HiRPr06UNKSgoA5513HlOnTuXUU0/llltu4fbbb+fMM8/khBNO2O3jOu2007jxxhspLi7mk08+oXv37iQnJzN+/Hi+//573n77bSCatC1YsEAJlojsNZc9Dz68Ht/K77YtD6bwZaNL+PPibmzK0X9RsmPLCpMYurAr0JWLG2dzdcoXNFs1Hit7317OfPjoJvjsPlzHy7AuQ6C2pvEXkYqn/73Kweuvv05OTg6zZs0iGAzSvHlzioq2vTm7e/fuTJkyhbFjxzJo0CBuvvlm6tSpwymnnML//ve/P9zHI488Qr9+/UrXJ06cuMN2rVq1Yvbs2YwbN4677rqLnj177vKKWFlJSUn06NGDTz/9lNGjR3PhhRcC4JxjxIgR9O7de7f6ERHZqXAJ3hcP4/vyMfBC21Qtb3oG16w+l3kLUuIUnFRHo7IbM4oLaZrUh7ubzuFP+WNJ2LBwa4OiDdhX/4XpT8IRZ8Gx10Jml/gFLCL7Pd2DVQ7y8vJo0KABwWCQSZMmsXTp0u3aLF26lIYNG3LVVVcxePBgZs+ezTHHHMOXX35Zek9VQUEBv/76627t84QTTmDMmDFs3ryZgoIC3nvvPU444QRWrlxJjRo1uOSSSxg2bBizZ8/ebttgMEgoFNpBr9Fhgi+++GLp1TCA3r17M3LkyNJtfv31VwoKCna4vYjIzngrZuE92x3f1Ee2Sa6K6x7GPXUf4YSFA5i3ScmV7J2sokSuXtiVVqv+zj/SHyK7SW+cr8z3yC4CP42B50+B/+sJP7wDXiR+AYvIfmufr2CZmR+YCaxwzp1pZgcDbwDpwCzgUudciZklAq8ARwO5QH/n3JJ93f/uzPpX0QYMGMBZZ51FmzZt6NSpE4cffvh2bSZPnswjjzxCMBgkNTWVV155hfr16/PSSy9x0UUXUVxcDMDw4cNp1arVH+6zY8eODBo0iC5dot/CDR48mA4dOvDpp58ybNgwfD4fwWCQkSNHbrftkCFDaNu2LR07duT111/fpq5Xr15ceulQpNadAAAgAElEQVSlnHPOOSQkJJT2vWTJEjp27Ihzjvr16zNmzJg9/jmJyAEqXII3+cHo1OteuLTYBVP4vNEVXPNbV4o9fd8n5ef5FZk8z0COSuvHXU2+pcu69/EXrN7aYMVMePsKqHVv9D6tjgP18GIRKTf7PE27md0MdAJqxhKsN4F3nXNvmNnTwFzn3EgzuwZo65wbamYXAn2cc/131fduTdMuVYZ+NyLye27VD/De1djqH7YpX5PRkyFr+zNnY2qcIpMDSaLP47aDfuX8yMfUXPPt9g0S0qDjZXDMUKjdrPIDFJFqqUKmaTezpsAZwHOxdQNOAt6ONXkZODf2/pzYOrH6nlZ2mj0REdl/eB7etMew//vTNslVJKUhTze8ly6LrlRyJZWm2PPxj8WH03bZTVyT9l9+y+yLCyRvbVCyCb5+Eh5vD29dDiu2H14vIrK79nWI4GPAbUBabD0d2OCc2zIGJAtoEnvfBFgO4JwLm1lerP3ash2a2RBgCECzZvoWSUSkunHrl+HGDMW39Mttyn/L7Msly88iOzchTpGJwLiceozL6Uuz5DO4N3MW3Te8T2BTVrTSReDHd6PLQcfDcddDq96g74NFZA/sdYJlZmcCa5xzs8ysR3kF5Jx7FngWokMEy6tfERGpeN68t7Cxt+Ar2np/bLhmMx5OuIZnF+hLM6k6lhUmccWCbgR9x3FL5gIuZhw1V8/Y2mDptOhS7zDcsddi7S6EQOLOOxQRidmXK1jdgLPN7HQgCagJPA7UNrNA7CpWU2BFrP0KIBPIMrMAUIvoZBciIlLdFefjjRuGb+6o0iKH8UvmBQxYejq5JcE4BieycyHPeHBpKx6kFWfWX8sttT6nefbHWCQ6+RRrf8E+vAEm/RO6Xg2droTk2vENWkSqtL2+B8s591fnXFPnXHPgQuBz59wAYBKw5YFNA4H3Y+8/iK0Tq//c7esMGyIiEndu5RzcMydsk1yFa2YyPP1BTl1wjpIrqTY+yqnHnxZeQC+e4qvMIURSGmytzF8NE/8O/zkKPrkT8rLiF6iIVGkVMS/u7cDNZraQ6D1Wz8fKnwfSY+U3A3dUwL5FRKQSedOfwp4/BVu3qLRsUeZ5HJc3nOdXZMYxMpG9t6AgmYsX9KDthkd5PeNOCtNbb60syY9NiNEO985V0ZkyRUTK2Odp2ivS7kzT3ublNuW6z3kD5+2yPjc3l549ewKwatUq/H4/9evXB2DGjBmlz47aFz169CA7O5ukpCRSU1N54YUXOOyww/aoj9NPP51Ro6LfJo8aNYprrrkGgJUrV3LDDTfw9ttv72rzvaJp2kUOHG7zOtyYa/H9Oq60zKtRjyfTbuTfS1vGMTKRijEoI4trkj6lfvYkzHnbVh5yMnS7EQ7uHp/gRCQuKmSa9gNReno6c+bMYc6cOQwdOpSbbrqpdD0hIYFwOPzHneyG119/nblz5zJw4ECGDRu2x9uPGzeO2rVrs2HDBp566qnS8oyMjApJrkTkwOGWfwvPnLhNcpWTcRK9ix9SciX7rZdWNqXLoiu5OOlJfsq8CJeQsrVy4Wfw8lnwbA/4cQx43k77EZH9nxKscjBo0CCGDh1K165due2227j33nv517/+VVrfunVrlixZAsBrr71Gly5daN++PVdffTWRSGSXfXfv3p2FCxfinGPYsGG0bt2aNm3aMHr0aACys7Pp3r077du3p3Xr1kydOhWA5s2bs3btWu644w5+++032rdvz7Bhw1iyZAmtW0eHOhxzzDH8+OOPpfvq0aMHM2fOpKCggCuuuIIuXbrQoUMH3n///e0DE5EDkjf9KezF07C8ZQC4YA3GNL2VzosGs6Ag+Q+2Fqn+pq+vxekLzuK4kieZmHk94bQmWytXfgdvDYQnjoaZL0CoKH6BikjcKMEqJ1lZWXz11Vc8+uijO20zf/58Ro8ezZdffsmcOXPw+/28/vrru+z3ww8/pE2bNrz77rvMmTOHuXPn8tlnnzFs2DCys7MZNWoUvXv3Lq1r3779Nts/+OCDtGzZkjlz5vDII49sU9e/f3/efPNNIJqoZWdn06lTJ/75z39y0kknMWPGDCZNmsSwYcMoKCjYy5+MiOwPXNFGvNGX4vv0r+CFAChMb82ghEf4y8KOcY5OpPJlFyVw5YJjOSr3IV5sfDeb67XbWrluEXx0EzzWBqb+Gwo3xC9QEal0+/qgYYk5//zz8fv9u2wzceJEZs2aRefOnQEoLCykQYMGO2w7YMAAkpOTad68OSNGjODRRx/loosuwu/307BhQ0488US+/fZbOnfuzBVXXEEoFOLcc8/dLsHalQsuuIBevXpx33338eabb9KvX3Tyx/Hjx/PBBx+UXoUrKipi2bJlur9K5ADlVv0Ab12GL/e36DrGD5kXc+Gi0yiI6Hs6ObAVez7uW3wE93EEl2as4LqkT2mQ/Xn0Pq2CNdGZB6f+BzoNgmOugZoZ8Q5ZRCqYEqxykpKydSx2IBDAKzP+uqgoOkTAOcfAgQN54IEH/rC/119/nU6dtrtnbjvdu3dnypQpjB07lkGDBnHzzTdz2WWX7VbMTZo0IT09ne+//57Ro0fz9NNPl8b5zjvv7PHEGiKy//HmvIFv7E0Q2hxdT67H42l/4fEFLeIcmUjV8+rKJrzKFRxbpy9/q/cFh6/6EAsVQMkm+GoEfPMMtLkgOiFG/VbxDldEKoi+eqwAzZs3Z/bs2QDMnj2bxYsXA9CzZ0/efvtt1qxZA8C6detYunTpbvV5wgknMHr0aCKRCDk5OUyZMoUuXbqwdOlSGjZsyFVXXcXgwYNL97tFWloamzZt2mm//fv35+GHHyYvL4+2bdsC0Lt3b0aMGMGWGSa/++67PfsBiEj1FwkR+egWfGOuLk2u8hoew1nhB3h8mZIrkV2Zvr4Wpy04mxNCT/BF5p+JpDSKVkRKYM5r8GQXeGMALP82voGKSIWo9lew/mha9Xjo27cvr7zyCkcddRRdu3alVavot1RHHnkkw4cPp1evXnieRzAY5Mknn+Sggw76wz779OnD9OnTadeuHWbGww8/TKNGjXj55Zd55JFHCAaDpKam8sorr2yzXXp6Ot26daN169acdtppXHvttdvU9+vXjxtvvJG77767tOzuu+/mL3/5C23btsXzPA4++GA++uijcvjJiEh14PJW4t66DH9W9I8/Zz6+bjqYSxZ2J+L0vZzI7soqSmTgghNI8Xfj/x30I+cVjSFp3XzAwc8fRZeDukG3v0CrXvEOV0TKSbV/DpZUHfrdiFR/3pJp2NtXYPmrAYikNOD+pFv00GCRcnJ102UMCY6jbvZUjDJ/gzVsDcfdAK37gr/af/8tckDQc7BERGSXvK+fwffKuaXJ1YZGx3Ja0QNKrkTK0TNZzTh68VCGpI5gUeZ5OH9itGL1D/DeEPhvB/j6aSjZHN9ARWSvKcESETnQhYrw3h2K75PbwAvhzMc3mYM5eum1/KpnW4lUiAlr63LSgn705ilmZF6Jl1w3WpG3DD65Hf5zFEx6AApy4xuoiOyxaplgVeVhjQcq/U5Eqidvw3K8F3vj+/5/0fXkdP5Vbzj9F5yk+61EKsGvBclcsKAnHfIf44OmtxCqFZtEpnAdfPEgPNYaxg2D9bs3KZaIxF+1+98zKSmJ3Nxc/UFfhTjnyM3NJSkpKd6hiMge8JZMw/7vJHwr5wCQX78D50Ue4MnlzeMbmMgBKC8U4IaFR9NqzT8Y0eAfbGzYJVoR2gwznoURHeGdwZD9fXwDFZE/VO0muQiFQmRlZZU+W0qqhqSkJJo2bUowGIx3KCKyGyIz/g//J38FLwTA/MwLOW/RGRRGdv3AdBGpPOc1XMPNaeNpsnI85oW3VrTsGX2WVosT4xeciOx0kotql2CJiMg+iISIjL0V/+yXAHDBFF6udzP3LtYMoCJVVcda+dzbYCpt1ozBiss827Jx+2iideQ54NOXIyKVTQmWiMgBzuXn4L15Kf5l0wEoqd2Ca8M3M2Ft3ThHJiK7o0FiiOGZszhp43sENi7fWlGnORx7HbQfAAk14hafyIFGCZaIyAHMW/kdjL4UX170j7LVGSdzzopLWFWcEOfIRGRPBX2O25v9ykWR90nJmbO1okY6dL4KugyBlPT4BShygFCCJSJygIrMexv/B9dDaDPOfExpejWDFh6Pcxbv0ERkH13YOJsba4yn0crPMBeJFgaSof3FcNx1ULdFfAMU2Y8pwRIROdA4hzfxH/im/RsAL7kuj6QOY+Tyg+IcmIiUt061NnFPgym0XvPB1vu0zAeHnwHH3QiZneMboMh+qNwTLDNLAqYAiUAAeNs5d4+ZHQy8AaQDs4BLnXMlZpYIvAIcDeQC/Z1zS3a1DyVYIiJ7xxVtwnvvavy/jAWgML01l+Zfz8y8tDhHJiIVqVFiCX/PnM1JG8cQ2Lhsa0VmV9yx12GHnwm+aveUHpEqqSISLANSnHP5ZhYEpgE3AjcD7zrn3jCzp4G5zrmRZnYN0NY5N9TMLgT6OOf672ofSrBERPact24xvHExvjU/AbC06dmcuaQfm8KBOEcmIpUl6HPckrmAAe4j0taU+Vuqbgs45hpNiCFSDip0iKCZ1SCaYP0ZGAs0cs6FzexY4F7nXG8z+zT2frqZBYBVQH23iwCUYImI7Blv8RTsrUHY5lycL8jYjOu5buF2534ROYCc13ANN6V9RtOVn2KxZ9+RXAc6XQldroK0RvENUKSa2lmCtU/XiM3Mb2ZzgDXABOA3YINzbsvT8LKAJrH3TYDlALH6PKLDCH/f5xAzm2lmM3NycvYlPBGRA0rk2+fxvXoetjkXr0Z9/lb7fiVXIsK7qxtwwsKLOd03khmZV+Il14PC9TD1X/BYG3jvz7BqXrzDFNlv7FOC5ZyLOOfaA02BLsDh+xqQc+5Z51wn51yn+vXr72t3IiL7v0iYyEe34B97M3gh8ut34JzQ/by6sskfbysiB4z5+TW4YEFP2m16lNEZd1CUfiRESmDuKHj6eHj5LPj1U6jCE6CJVAflMiDfObfBzCYBxwK1zSwQu0rVFFgRa7YCyASyYkMEaxGd7EJERPaSK8jFe3sg/sVTAViY2ZdzFvWhIKKb2EVkxzaFA9y+qC2305ZBGVkMTZ5Aw5WfY4unwOIpkH4IHPNnaHcRJKTEO1yRamev/wc2s/pmVjv2Phk4BZgPTAL6xZoNBN6Pvf8gtk6s/vNd3X8lIiK75q3+CffcSfgXT8X5E3i3yTBOXtBXyZWI7LaXVjblmN8up2/CSL5rNhAvqQ7kLoSxt8CjR8KEv0FeVrzDFKlW9mUWwbbAy4CfaKL2pnPu72bWgug07XWB74BLnHPFsWndXwU6AOuAC51zi3a1D01yISKyY5Gfx+F772qseCOR1MbcGRzG6GzdqC4i+6ZWMMzfmv3AGYUfkrRufrTQ/HDEWdGrWs2OiW+AIlWIHjQsIrKfCE/9N4HPh4Pz2NSgE+evG8rP+ZpuWUTK18CMFVydPJHG2Z9hXmz+sowO0HUoHHUeBBLiG6BInCnBEhGp5lxJIZEPrifww1sA/JLZn3MXnUlhxB/nyERkf9YmrYC7Gn1D59z38W2OzfCc0gA6XQGdLtc073LAUoIlIlKNeXlZMPoSfCu/wwWSGN3gJu5Y1CbeYYnIASTF7zGs2S/0jXy89eHFviAceQ50vRoyu8Q3QJFKpgRLRKSa8pZ9A29ehi9/FeG0JtzmG8a7qxvEOywROYCdXn8tN9WewiGrPsZCBdHCxu2jiVbrvhBIjG+AIpVACZaISDUUnv0qgbG3QKSYDY2Ope+awfy2OTneYYmIANA4qYS7m87l5IKPSFi/IFpYIx06XgadroTamfENUKQCKcESEalOImHCn/6VwIxnAfg+81L6/nYqIc/iHJiIyI5d0WQ5g5Mm0Th7IuaForMPtuoNnQdDy5PAdP6S/YsSLBGRaqLsw4NdMIUX6t3CPxYfHu+wRER2S6uUQu7KmMlxGz4ksCn2DK26LaHzldD+YkiuE98ARcqJEiwRkWogkv09NnoAvg3LKKndgmvDNzNhbd14hyUissf85nFd5hIGBCZRP3sy5iIQSI7eo9X5CmhydLxDFNknSrBERKq48Ly38H9wIxYqYE1GT85ecSmrivWcGRGp/trWzOevDWfSecNYAptWRAsbt4vep9WmHySkxDdAkb2gBEtEpKryPMKf3UPgq//izM+UpkMYtPB4nNP9CiKyf/Gbx/WZS7g4MIn6q76IPsA4sSa0vSD6XK2GR8U7RJHdpgRLRKQK8grW4r1zFYFFn+Ml1+OhlFt5JqtZvMMSEalwR6UVcHuj2RyXN5bAxmXRwqad4ejL4ag+kFAjvgGK/AElWCIiVUwkey42+hJ8G5aRX78DF+f9me83psY7LBGRSmXmGNJkOZclfkHGqs+xSDEk1ope1Tp6IDTSQ9WlalKCJSJShYTmvkHgo5uw0GbmZ15Iv0VnUhDxxTssEZG4ap5cxB1N5tJj83iS1s2PFmZ0jCZarftBor6EkqpDCZaISBXgwiWEP72T4Lf/h0tI4aX0m7lv8RHxDktEpMo5r+Eahtb8kkPXfIoVb4SEVDjqXOhwGTTrGu/wRJRgiYjEm7dxJe6tQfiXf0NxncO4uvgGJq/T82BERHYlLRDmlswFnOM+p/bq6ZjzoN5h0OESaHchpDaId4hygFKCJSISR+HFU/C9Mxhf/mqWNT2LPsv6kVsSjHdYIiLVSvua+dzScDbHbPyUYN5i8AXgkFOiyVar3uDXeVUqz84SrEA8ghEROZCEpv2HwOfDwRfgnSa3ccvC9vEOSUSkWpqzMZVLN3YHujOg8UouT51Oy6UTsF8/hhr1ohNjtL9YE2NIXOkKlohIBfEK1+ONuZbAL2Mpqd2SGyJ/4ZOc9HiHJSKyX0kLhPlL5kLOsSmkr5oWfbZWozbQ7iJocwGk1o93iLKf0hBBEZFKFF4xG3v7cvzrl7C86Zmct+x8cjQkUESkQh2aUsjNjedxYtEkaqydGx1C2LJn9F6tw06HYFK8Q5T9SLknWGaWCbwCNAQc8Kxz7nEzqwuMBpoDS4ALnHPrzcyAx4HTgc3AIOfc7F3tQwmWiFRHoRnPEPj0bvD5ebP+Ddy+qG28QxIROeCcmL6ea+p+R8e8CQQ3Lo0+W+vIs6Ftf2h+PJjFO0Sp5ioiwWoMNHbOzTazNGAWcC4wCFjnnHvQzO4A6jjnbjez04HriSZYXYHHnXO7nGNTCZaIVCdeUR6RD24g+NMYiuoezjXF1/N5rmYJFBGJt/6NVzEodQaH5X6Gb/NaqNkU2vSLJlsNj4x3eFJNVfgQQTN7H3gitvRwzmXHkrDJzrnDzOyZ2Pv/xdr/sqXdzvpUgiUi1UU4axb27pX41y3ml8z+9Ft8BpvCmkdIRKQqCfocg5ss5YLEGTTPmYgVb4KGraPJVuu+ULtZvEOUaqRCZxE0s+ZAB+AboGGZpGkV0SGEAE2A5WU2y4qV7TTBEhGpDkJfP0Vgwj24YAojG97HQwsOjXdIIiKyAyHPGLm8OSNpTkqgL9c1WcQ5gek0/uJh7LP7ILNrNNk6qg+k1It3uFJN7XOCZWapwDvAX5xzG63MeFbnnDOzPbpEZmZDgCEAzZrpWwQRqbq8grVE3r+O4K8fs6HRsVyaewXzlqbEOywREdkNBWE/Dy09lIc4lPSEi7iuyUJOi3xNw/F3YR/fDi1OhKPOgyPOguTa8Q5XqpF9GiJoZkHgI+BT59yjsbLSoX8aIigi+6vQb5PwjbkGX0EOk5oM4aqFxxJxvniHJSIi+6hBYojrM36lt31N/dXTMBy0PCmabB12GiTVjHeIUkVUxCQXBrxMdEKLv5QpfwTILTPJRV3n3G1mdgZwHVsnufivc67LrvahBEtEqhoXLiE8aTjBr0ZQUrslw7xreX91g3iHJSIiFaBRYgnXZiygl31DgzXTMOdwLXtirftEk63EtHiHKHFUEQnW8cBUYB7gxYrvJHof1ptAM2Ap0Wna18USsieAU4lO0365c26X2ZMSLBGpSsJrfoH3rsKf/T3zMy/koiWnkRfSRBYiIgeC+gkh/txkIaf5ZtBoTeyBxof0hCPPiV3ZqhXvEKWS6UHDIiL7IDTjWfwT7sEl1uZfydczcvlB8Q5JRETipFYwzJCMxZwZnEWznC+wcCG06AFHnB19oHFKerxDlEqgBEtEZC9ENq7E++AGggsnsKzpWVyUdR4rihLjHZaIiFQRyf4IgzKyODfpOw5ZNwX/5hxo3i2abB1+BtTMiHeIUkGUYImI7KHQ92/i//h2MB/PpF3PQ0s1/bqIiOycmaNvwzVclPY9bfKnkbB+ITTpGE20Dj8L6reKd4hSjv5/e3ceZldV5//+vVIJJCFASAIIGUwUVJwYjAwOiAMNDu3UrWi3ttra6cG+av9au9W+92d7f9rXbrtVvM3FSyuKNlNkMgoIyIxAyDyHjJWaq07Np+rUmdfvj3MCRSSYoersGt6v5znPHs4+Z3+rns0qPllrr23AkqRDVBpMUb7zi0zbegfN89/Jx1s/xJ7M9KTLkiSNM2+a08en5m7l9bknOT61ljDnJfCKd8HL3w0LXg9TnH12PBvVBw1L0kSR33IHdXd9iSnA/3fq1/m33fZaSZKOzGPdJ/JY90XARSyekeUvjt3FW+vXctrqawlTp8PLLoOXvRNe+lY4xucoThT2YEkSUBrooHz3PzJty23UL3gfH2t6P03eayVJGgUz6kp8/LRm3jtjEy/vf4Jpgy2w+M3w8svhZZfDiQuSLlGHwCGCknQQhQ03U3fPVylPncl/HPvXzhAoSaqpN83p4+NztnN+cTWzU6sJ886EMy+FMy+DhefDlLqkS9TzcIigJB2g2LOPeNeXmLr7fjbM/xM+Vf8OenyulSSpxipDCS8ALmDuMQU+SQN/sG8TL934F0zNp+Glb4Mz/wDOeAfMOjnpcvV72IMladKJpRKFlT9g6kP/wtCJZ/Cl7J9zV2pe0mVJkvQ7Lp7Ty0fn7OD80jrmdK4mzDujErTOeAcsOB/q/IfBpDhEUJKAQtMquOuL1HXX88u5n+F/7DmHUnQWJ0nS2Hfc1BJ/+qJm3jlzG68YXMP0wUbC4jdXerhe+jaYsyTpEicVA5akSa2U6ab04DeZuuYn7Dv9PXym5Q/ZnZmRdFmSJB2xl84c4mOn1vOWqVtY1PsUU6dOhZe8tTIr4ZKLYcZJSZc4oRmwJE1KMUby66+n7jdfpzDjFP5X6VPc0Hpa0mVJkjTi3nhSHx+es5vz2cSpPWuZMnshvOQSeMlbYOGFMM1nOo4kA5akSafQtBru+Qp1nXu4Y86n+NKesx0OKEmaFEKIvHNeF+8/cRfnljczt28zU05+eSVsLb4Y5p8HddOSLnNcM2BJmjSK/W2UH/xfTN10C1tO/2P+quHtNPtMK0nSJDZtSuQPT07x7hN2c3ZpE3P6txNOfRVhyZsrgev0c5wO/jAZsCRNeOXCEMWVVzP10e/SMfcCvtj7QR7rPjHpsiRJGnOmTYm8++QU7z5+D2eXtzB3cCd1J78MXvxGWPwmOP1ce7h+DwOWpAkrlsvkNy9nygPfJD9tDv9a+hg/bTk96bIkSRo3QohcOreH98zey3ls40WDTzN19oJK4HrxG2DBUpjm5FDDGbAkTUi53Q8w5f7/m5jp4yfT/4x/qX9Z0iVJkjQhLD0xzfvnNnB+3Q4WDW3n2BkzCQvPh0VvgIUXwHFzky4xUQcLWD6ZTNK4lG9eDQ98k6nt27njxI/x1Y7Xkis7gYUkSSNldd/xrO57FfAqAOZPz/HBXAtvbvwNLyv8vxxPhrrTXlMJW4suhHlnJlvwGGEPlqRxpdC+hfLD/8rUfU9w30kf5e/rlzJY9KZcSZJqbdqUyOXzOrn0hAbOZienFpqZfuLJleGEC86H+a+DY2clXeaocYigpHGtkNpO+ZH/oG7Pwzw058N8qf719BTshJckaSxZPCPL+05u4Q3H7uPM4g5OmFpg6ikvg/lLK8Fr3sthysQYcTIqASuEcC3wHqAjxvjq6r45wM3AYqAe+HCMsSeEEIArgXcBGeCTMca1L/T9BixJhY5tlB/9DnX1v+WBE/+If9y31GAlSdI48qY5fVx2YhPnTd3LgnITs6YfS92LXlnp4Tr9PJi9MOkSj8hoBayLgQHgp8MC1r8B3THGb4UQvgycFGP8xxDCu4D/g0rAugC4MsZ4wQt9vwFLmrzyreuJj32P0LSWXx//x3yl/hyHAkqSNAEcO6XM2+Z289YTmjl7yl5eFLqZNXMGdae+sjI9/GnnwAmnJV3m7zVqQwRDCIuBXw0LWE8Dl8QYW0MIpwEPxRhfHkL4/6vrNx543MG+24AlTT65vY/C498ndjfx82M+wDf2neXkFZIkTXDHTinz9rndvOX4Fl5bV8+LpvRy/MwZleGFp50NL3rtmOvpquUsgqcOC01twKnV9flA47Djmqr7nhOwQgjLgGUAixYtGoXyJI01sVQiv/0XhCd/QKYwlR+W3s1VzYuTLkuSJNVIrjyFu1LzuCs1D3gtAHWhzJvm9HHJCds4Z9o9zA89nDBzGtNPml8JXC96TWXmwilja4TLqN7IEGOMIYTD6iKLMV4DXAOVHqxRKUzSmFAc6qW0/gZYex3Nx57Fv/V9jF+nJvczNSRJUkUpTuHhrpN4uOsk4Kxn9r9iVoa3n9TB66b/jJdMaWP2jDpOOO44ppxyFrzo1XDqq2D6iYnVPRoBqz2EcNqwIYId1f3NwPB+vQXVfZImmXxqB+U11xJ3PchTM97K17v+gT2Z6UmXJUmSxoHtAzPZPrCYypx6FcfVlbl4TjdvmPUYr552M6cck2X2zGM57sST4ZSzKqFr7plQN/oTZY3GGVYAnwC+VV3+Ytj+vw0h3ERlkou+F7r/StLEUi4VKV7i020AACAASURBVOy4m7j2OgYHhri5fCnfbfm/KJRD0qVJkqRxbrA0hbtT87g7NY/9D0YGOG16nred1MnrZt7Ky6a2M2fGFGbPPJaZs0+pBK+TXwEnLRnRqeOPKmCFEG4ELgHmhRCagK9RCVbLQwifBvYBH64efheVGQR3UZmm/VNHc25J40Oht4HS+uspP30v26e9lm+nPsgTPcl120uSpMmjNXsM17eezvWc/pz9i2dkufikFs6buZaXTO1izoypzD7uWGadOKcSuk5+BZy0+Iju7/JBw5JGXKmQo7jzbsobltM3kOO24pu5svGlzgYoSZLGtBcdm+dNJ/XwupkdnDGti5Nm1DFn1nROnDWTurkvgblnVCbWOOa4ms4iKGmSyjathk0/J9u0mVXhPL7d+kF2DM5IuixJkqRD0pY7hlvaTuWWZyZCrzh2SpkLZvfzulmP8spjb2XBS1970O8wYEk6Krmu3ZS33EZu7xPsKS3kmp7X8evUxUmXJUmSNGJy5Sk80j2bR7pnAy/hoycd/JlcBixJhy3X20h52wpyex6nKXcCN6Rfx41tf06MTlghSZImNwOWpEOS695L3H4ng/vW0jQ0g+Xpc7ih7aOGKkmSpGEMWJKeV4yRbNsGwo576G7ZTf3QCdzY+2p+2fFHSZcmSZI0ZhmwJD2jkBugtPcRCvW/pb2zly1DL+LHqZexvv/VSZcmSZI0LhiwpEksxki2fTPseZiu9gZa+or8ZuBMrm+7gMHi4T/3QZIkabIzYEmTTLZ7D3Hfb+lr3U1Ld4aNg6dwfcdidg4uSbo0SZKkcc+AJU1gMUaynU9D41N0pVpo6Rpkx8Dx3NL5Ytb3vz7p8iRJkiYcA5Y0gRTygxRb1pFv3Uxrd5qW7gxb0idxe+d89mRek3R5kiRJE54BSxqnSqUi+dQ2Sq2b6OjqoaU3Q3NviUf7TuO+rvnkylOSLlGSJGnSMWBJ40Ahn6GY2ka+YyetPYO09QzQ2pdjTf887umcS7p4YtIlSpIkCQOWNKaUSkXyPXsode6mo6eX9r4MrT1DtPYXWdl3Mr/tOYFSPD7pMiVJknQQBiwpAflcmlL3brLdzbT3ZWnrz9DWN0RHf57NfSfy257ZDJZOAE5IulRJkiQdBgOWNEqGMl3Q20C6t4uOgSE6+rKk0jlS/Rna0oE1fbPZNjATmF59SZIkabwzYElHoFgukh9op9zXSu9ghs6BLF39OboGc3Sms3Smc7QMTGN9//G05Y4BpgAzq6+Tki1ekiRJo8aAJQ1TLBfJZzoppztJZzL0ZAr0DOboGczTncnRO7B/WaR+cAbbBmYOm61vCjCj+pIkSdJkZMDShJbNZyhneyhk0vTn8qSHCvRnCvRn8/RlCqRzBXoH8/QPFegbytGXKdOSOZbdmRkUyuGAb5tafc1M4CeRJEnSeFDzgBVCuBy4EqgDfhhj/Fata9D4EGMkW8gQ82nyuSEGs0WG8iUGcgUy1eVgtsRANs9gvsRgLs9AtkB/rsRgtsBAtkA6O4WWoWNJ5ae9wJnqqi/vg5IkSdLRqWnACiHUAVcBlwJNwKoQwooY49Za1qGRUY5lcqUcsZijXMiRK5bIFcqVZalMrlBmqFAkXyiTLZTIFkrkiiWy+SLZ6nvZQomhfCU4De1fL5TJ5ooM5ksM5afSkZvGYOlQH5obeLanyaF6kiRJqq1a92CdD+yKMe4BCCHcBLwPmDQBqxzLlGOZUixRjmViqUQkUi5HSrFMuQzFcmVZipFSuUypVF2WY+W9uP+YSKFUWRbLkWIJCtXji9XjC6XSM+8VyyVKpUi+VKZULpMvRUrlEoVSmWIpkC+VKRZLlWWpTKFUOaZQLFXXyxSKlVe+VCZXiORLdQwWpzBUqhuh39CU6svRq5IkSRp/av1/sfOBxmHbTcAFww8IISwDllU3cyGEzTWqTZPbPKAz6SI04XmdqRa8zlQrXmuqhTF5nVXvcXrx87035roJYozXANcAhBBWxxiXJlySJgGvNdWC15lqwetMteK1ploYj9fZod7YMlKagYXDthdU90mSJEnSuFfrgLUKODOEsCSEcAzwEWBFjWuQJEmSpFFR0yGCMcZiCOFvgXuozIt9bYxxywt85JraVCZ5rakmvM5UC15nqhWvNdXCuLvOQowx6RokSZIkaUKo9RBBSZIkSZqwDFiSJEmSNELGbMAKIVweQng6hLArhPDlpOvRxBBCWBhCeDCEsDWEsCWE8Pnq/jkhhPtCCDury5OSrlXjXwihLoSwLoTwq+r2khDCymq7dnN1sh/pqIQQZocQbgkhbA8hbAshXGSbppEWQvi76t/NzSGEG0MI023TNBJCCNeGEDqGP/v2YG1YqPh+9ZrbGEI4L7nKD25MBqwQQh1wFfBO4JXAR0MIr0y2Kk0QReDvY4yvBC4EPlu9tr4M3B9jPBO4v7otHa3PA9uGbf8r8N0Y4xlAD/DpRKrSRHMl8OsY4yuAs6lcc7ZpGjEhhPnA54ClMcZXU5mo7CPYpmlk/AS4/IB9B2vD3gmcWX0tA66uUY2HZUwGLOB8YFeMcU+MMQ/cBLwv4Zo0AcQYW2OMa6vraSr/IzKfyvV1XfWw64D3J1OhJooQwgLg3cAPq9sBeBtwS/UQrzMdtRDCicDFwI8AYoz5GGMvtmkaeVOBGSGEqcBMoBXbNI2AGOMjQPcBuw/Whr0P+GmseBKYHUI4rTaVHrqxGrDmA43Dtpuq+6QRE0JYDJwLrAROjTG2Vt9qA05NqCxNHN8D/gEoV7fnAr0xxmJ123ZNI2EJkAJ+XB2O+sMQwnHYpmkExRibgX8HGqgEqz5gDbZpGj0Ha8PGRUYYqwFLGlUhhFnArcAXYoz9w9+LlWcX+PwCHbEQwnuAjhjjmqRr0YQ3FTgPuDrGeC4wyAHDAW3TdLSq97+8j0qgPx04jt8d0iWNivHYho3VgNUMLBy2vaC6TzpqIYRpVMLV9THG26q72/d3MVeXHUnVpwnhjcB7Qwj1VIY4v43KfTKzq8NrwHZNI6MJaIoxrqxu30IlcNmmaSS9A9gbY0zFGAvAbVTaOds0jZaDtWHjIiOM1YC1CjizOjvNMVRupFyRcE2aAKr3wfwI2BZj/M6wt1YAn6iufwL4Ra1r08QRY/xKjHFBjHExlfbrgRjjnwIPAn9cPczrTEctxtgGNIYQXl7d9XZgK7ZpGlkNwIUhhJnVv6P7rzPbNI2Wg7VhK4A/q84meCHQN2wo4ZgRKr1uY08I4V1U7mGoA66NMX4z4ZI0AYQQ3gQ8Cmzi2XtjvkrlPqzlwCJgH/DhGOOBN1xKhy2EcAnwxRjje0IIL6HSozUHWAd8LMaYS7I+jX8hhHOoTKZyDLAH+BSVf0C1TdOICSF8HbiCymy864DPULn3xTZNRyWEcCNwCTAPaAe+BtzB87Rh1YD/n1SGqGaAT8UYVydR9wsZswFLkiRJksabsTpEUJIkSZLGHQOWJEmSJI0QA5YkSZIkjRADliRJkiSNEAOWJEmSJI0QA5YkSZIkjRADliRJkiSNEAOWJEmSJI0QA5YkSZIkjRADliRJkiSNEAOWJEmSJI0QA5YkSZIkjRADliRJzyOEEEMIZ9TwfP8cQvjvWp1PkjQ6DFiSpKMWQqgPIQyFEAZCCG0hhJ+EEGYlXddoCSE8FELIVn/ezhDCbSGE05KuS5KUPAOWJGmk/GGMcRZwDnAu8JWE6xltf1v9eV8GzAa+m3A9kqQxwIAlSRpRMcY24B4qQQuAEMKFIYTHQwi9IYQNIYRLhr33UAjhG9X3B0IIvwwhzA0hXB9C6A8hrAohLB52/Buq+/qqyzdU918RQlg9vJYQwt+FEFZU148NIfx7CKEhhNAeQvhBCGHGsGO/FEJoDSG0hBD+/DB+3m7gVuDVL1Rf9b3TQwgrQgjdIYRdIYS/ONTzSJLGBwOWJGlEhRAWAO8EdlW35wN3At8A5gBfBG4NIZw87GMfAT4OzAdeCjwB/Lh6/Dbga9XvmlP9ru8Dc4HvAHeGEOYCvwReHkI4c9j3/glwQ3X9W1R6m84Bzqie639Wv/fyal2XAmcC7ziMn3ce8EfAut9TH8BNQBNwOvDHwL+EEN52qOeSJI19BixJ0ki5I4SQBhqBDqqhCPgYcFeM8a4YYznGeB+wGnjXsM/+OMa4O8bYB9wN7I4x/ibGWAR+TmXIIcC7gZ0xxp/FGIsxxhuB7VSGJ2aAXwAfBagGrVcAK0IIAVgG/F2MsTvGmAb+hUqwA/hwtYbNMcZB4J8P4ef9fgihF9gAtAL/44XqCyEsBN4I/GOMMRtjXA/8EPizQ/nlSpLGBwOWJGmkvD/GeDxwCZVgM6+6/8XAh6rDA3uroeRNwPBJIdqHrQ89z/b+CTNOB/YdcN59VHqjoNJb9dHq+p8Ad1SD18nATGDNsBp+Xd2//3sbD/jO3+dzMcbZMcb5McY/jTGmfk99pwP7w93z1S5JmgAMWJKkERVjfBj4CfDv1V2NwM+qYWT/67gY47eO4OtbqAS24RYBzdX1+4CTQwjnUAla+4cHdlIJaq8aVsOJ1UkqoNIDtfCA7zwSL1RfCzAnhHD8QWqXJE0ABixJ0mj4HnBpCOFs4L+pDJG7LIRQF0KYHkK4pHqv1uG6C3hZCOFPQghTQwhXAK8EfgUQYyxQGVL4bSr3b91X3V8G/gv4bgjhFKjcGxZCuKz6vcuBT4YQXhlCmMmzwxtHrL4YYyPwOPD/VH8HrwU+TeX3I0maIAxYkqQRVx0u91Pgf1aDxfuArwIpKj1aX+II/gbFGLuA9wB/D3QB/wC8J8bYOeywG6hMUvHz6j1c+/0jlYk3ngwh9AO/AV5e/d67qYTCB6rHPHC4tR1ifR8FFlPpzbod+FqM8TdHci5J0tgUYoxJ1yBJkiRJE4I9WJIkSZI0QgxYkiRJkjRCEglY1Zuc14UQfpXE+SVJkiRpNCTVg/V5YFtC55YkSZKkUTG11iesTsv7buCbVJ56f1Dz5s2LixcvrkVZkiRJknTI1qxZ0xljPPnA/TUPWFSmwf0H4PjnezOEsAxYBrBo0SJWr15dw9IkSZIk6fcLIex7vv01HSIYQngP0BFjXHOwY2KM18QYl8YYl5588u8EQkmSJEkas2p9D9YbgfeGEOqBm4C3hRB8gr0kSZKkCaGmASvG+JUY44IY42LgI8ADMcaP1bIGSZIkSRotSdyDdVQKhQJNTU1ks9mkS5mQpk+fzoIFC5g2bVrSpUiSJEnjTmIBK8b4EPDQ4X6uqamJ448/nsWLFxNCGPG6JrMYI11dXTQ1NbFkyZKky5EkSZLGnXHXg5XNZg1XoySEwNy5c0mlUkmXIkmSJNVEJl+kN1OgN1Ogb6hA31C+uhz+KtJfXe/PFrj0rFMP+n3jLmABhqtR5O9WkiRJ41G+WKY3k6c7k6dnsEBvJk9PpkBPJk9vJk9vpkBPphKghq8XSvGwz9W/pHDQ98ZlwJIkSZI0sfUNFegezNM9mKNrIE/3YJ6uwcqyZ3B/kHo2UA3kikmXDEyAgLX4y3eO6PfVf+vdv/eYuro6XvOa11AsFlmyZAk/+9nPmD179ojWMdr++Z//mVmzZvHFL34x6VIkSZI0CRRKZboG8nQO5EgN5OhM5+gazD+7HKgEqa7BHD2DBfKlctIlH5FxH7CSMGPGDNavXw/AJz7xCa666ir+6Z/+KeGqKpNUxBiZMqXWjzeTJEnSZBRjpDdToCOdI5XO0ZHOPrO+/9U5UHn1DhWIhz8ab9wxYB2liy66iI0bNwKwe/duPvvZz5JKpZg5cyb/9V//xSte8Qra29v5q7/6K/bs2QPA1VdfzRve8Aa+853vcO211wLwmc98hi984Qt8+ctfZuHChXz2s58FntvT9O1vf5vly5eTy+X4wAc+wNe//nXq6+u57LLLuOCCC1izZg133XUXy5cv/53jAL75zW9y3XXXccopp7Bw4UJe97rXJfAbkyRJ0njQm8nT3p+jrT9Le3+WVDpHe3W9vf/ZADVee5pGiwHrKJRKJe6//34+/elPA7Bs2TJ+8IMfcOaZZ7Jy5Ur+5m/+hgceeIDPfe5zvOUtb+H222+nVCoxMDDAmjVr+PGPf8zKlSuJMXLBBRfwlre8hSuuuIIvfOELzwSs5cuXc88993Dvvfeyc+dOnnrqKWKMvPe97+WRRx5h0aJF7Ny5k+uuu44LL7zwoMcdd9xx3HTTTaxfv55isch5551nwJIkSZqEyuVIaiBHa1+Wtr6h6jJLW/+zy/b+LNmCwelIGLCOwNDQEOeccw7Nzc2cddZZXHrppQwMDPD444/zoQ996JnjcrkcAA888AA//elPgcr9WyeeeCKPPfYYH/jABzjuuOMA+OAHP8ijjz7K5z73OTo6OmhpaSGVSnHSSSexcOFCrrzySu69917OPfdcAAYGBti5cyeLFi3ixS9+MRdeeCEA99577/Mel06n+cAHPsDMmTMBeO9731ubX5YkSZJqqjeTp6lniJbeIdr6szT3DtHSm6W1txKm2vuzFMuTYKxeQgxYR2D/PViZTIbLLruMq666ik9+8pPMnj37mXuzjsaHPvQhbrnlFtra2rjiiiuAyvjWr3zlK/zlX/7lc46tr69/JqS90HHf+973jrouSZIkJSvGSEc6R1NPhqaeIZp6hmjuHaK5umzpHSKTLyVd5qTmbAhHYebMmXz/+9/nP/7jP5g5cyZLlizh5z//OVC5+Dds2ADA29/+dq6++mqgMqywr6+PN7/5zdxxxx1kMhkGBwe5/fbbefOb3wzAFVdcwU033cQtt9zyTI/YZZddxrXXXsvAwAAAzc3NdHR0/E5NBzvu4osv5o477mBoaIh0Os0vf/nL0f3lSJIk6Yh0DeRY39jLLze0cNWDu/jKbZv4+I9W8tZ/f4iX/5+/5oJ/uZ8/uvoJPn/Ter59z9PcsLKBh3ek2NUxYLgaA8Z9D9ahTKs+ms4991xe+9rXcuONN3L99dfz13/913zjG9+gUCjwkY98hLPPPpsrr7ySZcuW8aMf/Yi6ujquvvpqLrroIj75yU9y/vnnA5VJLvYP63vVq15FOp1m/vz5nHbaaQD8wR/8Adu2beOiiy4CYNasWfz3f/83dXV1z6nnYMedd955XHHFFZx99tmccsopvP71r6/Vr0iSJEnDFEplmnqG2Nc1SEN3hoauTGXZnaGxO8OgIWlcC3EMz5W4dOnSuHr16ufs27ZtG2eddVZCFU0O/o4lSZKOTr5YpqE7Q33nIPVdlde+rgz7ujI09w5R8h6oce2j5y/kW3909poY49ID3xv3PViSJElSEsrlSHPvEHs6B9mbGmBv52BlvXOQlt4hzFCTkwFLkiRJegEDuSK7OwbYnaq89qQG2Z0aoL4rQ77oVOZ6rnEZsGKMhBCSLmNCGstDRiVJkkZTKp1jZ0ea3R0D7OoYYFeqsmzvzyVdmsaRcRewpk+fTldXF3PnzjVkjbAYI11dXUyfPj3pUiRJkkZNKp1jR3uane1pdnQMsLM9zc6OAXozhaRL0wQw7gLWggULaGpqIpVKJV3KhDR9+nQWLFiQdBmSJElHLZ0tsKM9zfa2NDva0jzdnmZH+wDdg/mkS9MENu4C1rRp01iyZEnSZUiSJGmMKJUjezsH2NaaZntbP9tbK6GquXco6dI0CY27gCVJkqTJK50tsL0tzdaWfra29LOtrZ8d7WmyBSeb0NhgwJIkSdKYlErn2NzSx5bmPra29rOlpZ+G7gzOyaWxzIAlSZKkxLX1ZdnY1Mvmln42N/exubmPjrSz92n8MWBJkiSpplLpHBubetnY1Mem5j42NvXROWCY0sRgwJIkSdKoSWcLbGrqY31TLxsb+9jY1EtLXzbpsqRRY8CSJEnSiCiVI9vb+lnX0Mv6xl42NPayOzVA2XumNIkYsCRJknREUukcaxt6WNfQy7qGHjY195HJl5IuS0qUAUuSJEm/V7kc2d6WZk1DD2v39bBmXw8N3Zmky5LGHAOWJEmSfkcmX2RdQy+r63tYva+bdQ29DOSKSZcljXk1DVghhOnAI8Cx1XPfEmP8Wi1rkCRJ0u/qGsixqr6HVfXdrKrvZmtLP0VvnpIOW617sHLA22KMAyGEacBjIYS7Y4xP1rgOSZKkSa21b4in9nazcm83T+3tZlfHQNIlSRNCTQNWjDEC+//rnVZ9+U8jkiRJo6y5d4iVe7p4ck8XT+7p9v4paZTU/B6sEEIdsAY4A7gqxrjygPeXAcsAFi1aVOvyJEmSJoT2/iyP7+7kyd3dPL6nk8buoaRLkiaFmgesGGMJOCeEMBu4PYTw6hjj5mHvXwNcA7B06VJ7tyRJkg5Bz2Cex3d38fjuTp7Y3cWezsGkS5ImpcRmEYwx9oYQHgQuBzb/vuMlSZL0rKF8iafqu3lsZ4rf7upiW1s/0X+alhJX61kETwYK1XA1A7gU+Nda1iBJkjQelcuRTc19PLark0d3pli7r5d8qZx0WZIOUOserNOA66r3YU0BlscYf1XjGiRJksaFlt4hHtmR4tGdnfx2dye9mULSJUn6PWo9i+BG4NxanlOSJGm8yBZKrNzbzcNPp3h4Rwe7U95HJY03id2DJUmSJNiTGuChp1M8tCPFyj1d5IoO+5PGMwOWJElSDWULJZ7Y08VD2zt48OmUz6OSJhgDliRJ0ihr7h3ige0dPLi9g8d3d5It2EslTVQGLEmSpBFWLkfWNfZy/7Z2Htjewfa2dNIlSaoRA5YkSdIIyOSLPLKjk99sa+fB7R10DeaTLklSAgxYkiRJR6ijP8t929q5b2s7j+/uIu8EFdKkZ8CSJEk6DLs60tyzpZ17t7azsamXGJOuSNJYYsCSJEl6ATFW7qe6d0s7925pY0+nz6aSdHAGLEmSpAMUS2VW7u3mni1t3LOljfb+XNIlSRonDFiSJElAvljmsV0p7t7Uxm+2tdOTKSRdkqRxyIAlSZImrWyhxMM7Uty9qZX7t3eQzhaTLknSOGfAkiRJk0q2UOKhp1PctamV+7e1M5gvJV2SpAnEgCVJkiY8Q5WkWjFgSZKkCSlfLPPIjhR3bmrlvq3tDOQc/idp9BmwJEnShFEqRx7f3cmK9S3cs6WNfu+pklRjBixJkjSuxRhZva+HFetbuHtzK50D+aRLkjSJGbAkSdK4tLWln19saOZXG1pp7h1KuhxJAgxYkiRpHGnszvCL9c38Yn0LOzsGki5Hkn6HAUuSJI1pPYN5frWxhTvWt7BmX0/S5UjSCzJgSZKkMSdbKHH/tg5uX9fEwztSFEox6ZIk6ZAYsCRJ0pgQY2Tl3m5uX9vMXZtbSTsDoKRxyIAlSZIStSc1wG1rm7ljfTNNPU5WIWl8M2BJkqSa68sUWLGxhdvWNrGuoTfpciRpxBiwJElSTRRLZR7ekeLWtU38ZlsH+WI56ZIkacQZsCRJ0qh6ui3NLWsauX1dC50DuaTLkaRRZcCSJEkjri9T4BcbmrllTRMbm/qSLkeSasaAJUmSRkS5HHl0VyfLVzdy39Z2hwBKmpRqGrBCCAuBnwKnAhG4JsZ4ZS1rkCRJI2tf1yA/X93ErWubaO3LJl2OJCWq1j1YReDvY4xrQwjHA2tCCPfFGLfWuA5JknQUsoUSd21qZfnqRlbu7Sb6HGBJAmocsGKMrUBrdT0dQtgGzAcMWJIkjQMbm3q5eVUjK9a3kM75IGBJOlBi92CFEBYD5wIrD9i/DFgGsGjRoprXJUmSnqsvU+D2dU3ctKqR7W3ppMuRpDEtkYAVQpgF3Ap8IcbYP/y9GOM1wDUAS5cudcCBJEkJiDHyxJ4ubl7VyK83t5FzwgpJOiQ1D1ghhGlUwtX1Mcbban1+SZJ0cB3pLLesaWL5qkbquzJJlyNJ406tZxEMwI+AbTHG79Ty3JIk6fmVy5GHd6a4cWUDD2zvoFh2AIkkHala92C9Efg4sCmEsL6676sxxrtqXIckSZNea98QN69q5Oerm2juHUq6HEmaEGo9i+BjQKjlOSVJ0rNK5cgD2zu48akGHt6RomRvlSSNqMRmEZQkSbXT3DvEzU81sHx1E239PgxYkkaLAUuSpAlqf2/VDSv38fCOFHZWSdLoM2BJkjTBtPQOcdOqRpavarS3SpJqzIAlSdIEUCpHHnq6gxtWNvCQ91ZJUmIMWJIkjWNtfVmWr27kpqcaaOmzt0qSkmbAkiRpnCmXI4/u6uT6J/dx//YOe6skaQwxYEmSNE50DuRYvrqRG59qoLHb51ZJ0lhkwJIkaYx7fHcn169s4N4tbRRK9lZJ0lhmwJIkaQzqzeS5ZU0TNzzVwJ7UYNLlSJIOkQFLkqQxZHV9NzesbODOTa3kiuWky5EkHSYDliRJCUtnC9y+rpnrn2zg6fZ00uVIko6CAUuSpIRsaurj+pX7WLGhhUy+lHQ5kqQRYMCSJKmGMvkiK9a3cP3KBjY19yVdjiRphBmwJEmqge1t/dywsoHb1zaTzhWTLkeSNEoMWJIkjZJsocSvNrZyw8p9rG3oTbocSVINGLAkSRphuzrSXL+ygdvWNtM3VEi6HElSDRmwJEkaAbliibs3tXHDygaequ9OuhxJUkIMWJIkHYXdqQFuXNnArWub6MnYWyVJk50BS5Kkw5Qrlvj15kpv1cq99lZJkp5lwJIk6RDt6khz41ON3Lq2iV57qyRJz8OAJUnSC8gWSty5sZWbVjWwqr4n6XIkSWOcAUuSpOexrbWfG59q4I51zfRnfW6VJOnQGLAkSaoazBVZsaGFm55qYENTX9LlSJLGIQOWJGnSW7Ovh5tXNfCrja1k8qWky5EkjWMGLEnSpNQ1kOP2dc3cvKqRnR0DSZcjSZogDFiSpEmjVI48siPFzasauX97O4VSTLokSdIEY8CSJE14ezsH+fnqyvTq7f25pMuRJE1gNQ1YIYRrgfcAHTHGV9fy3JKkyWUwV+TO+6mOhgAACqxJREFUja38fE2j06tLkmqm1j1YPwH+E/hpjc8rSZoEYow8saeLW9Y08evNbU5YIUmquZoGrBjjIyGExbU8pyRp4qvvHOTWtU3ctraZ5t6hpMuRJE1iY+4erBDCMmAZwKJFixKuRpI0VvUNFbhzYyu3rW1i9T6HAEqSxoYxF7BijNcA1wAsXbrU6Z0kSc8olMo89HSK29c18ZttHeSL5aRLkiTpOcZcwJIk6UBr9vVwx7pmfrWxhZ5MIelyJEk6KAOWJGlM2tUxwIr1zdyxvoWG7kzS5UiSdEhqPU37jcAlwLwQQhPwtRjjj2pZgyRp7GrtG+KXG1r4xfoWtrT0J12OJEmHrdazCH60lueTJI19nQM57t7Uyi83tLJqXzfRu28lSeOYQwQlSTXXm8lzz5Y2frmhlSf2dFEqm6okSRODAUuSVBN9mQL3bGnjzk2tPL67k0LJUCVJmngMWJKkUdM9mOfeLW3ctbmNJwxVkqRJwIAlSRpRbX1Z7t3axt2b2niqvtvhf5KkScWAJUk6artTA9y7pZ17trSxoanXiSokSZOWAUuSdNjK5ci6xh7u29rBfVvb2J0aTLokSZLGBAOWJOmQDOaKPLqzk/u3tfPA9g66BvNJlyRJ0phjwJIkHdS+rkEe2N7Bg0+neHJPF/liOemSJEka0wxYkqRnZAslVu7t5qGnO3j46RR7Oh36J0nS4TBgSdIkt7M9zSM7O3lkR4qVe7vIFuylkiTpSBmwJGmS6RzI8dtdnTy6s5Pf7uqktS+bdEmSJE0YBixJmuD6swWe2tPN47u7eHx3J0+3p51GXZKkUWLAkqQJpj9bYHV9Nyv3dPPEni62tPT7sF9JkmrEgCVJ41znQI7V9d08tbeHlXu72Nbaj3lKkqRkGLAkaRyJMbI7NcDq+h7W7Ku8nOlPkqSxw4AlSWNYX6bA+qZe1jX0sK6hl/WNvfQNFZIuS5IkHYQBS5LGiKF8ia2tfWxs6mNDYy8bmvrYa++UJEnjigFLkhIwkCuyrbWfzc19bG6uLHelBpyMQpKkcc6AJUmjrKknw/bWNNvb+tna2s+21jT1XYNOlS5J0gRkwJKkEZJK59jZkWZHW5odHQPsaEvzdHuadLaYdGmSJKlGDFiSdBhK5UhTT4Y9qUF2pwbYnRpgV0fl1ZNx8glJkiY7A5YkHaBcjrT2Z9nXOUh9V4b6rkHqOwfZ2znIvq4M+VI56RIlSdIYZcCSNCn1DOZp6hmiqSdDY0+Gpp4hGrozNHRV1g1RkiTpSBiwJE04Q/kSrX1DtPVlaenL0tY3RHNvlpbeoWdeg/lS0mVKkqQJyIAladxIZwt0DuRJpXOk0jk60lk60jk6+ivrbX1Z2vuz9DuphCRJSogBS1IiYoykc0V6BvP0ZAr0DObprr66BvN0D+boGsjTOZinayBH50CObMFhe5IkaWwzYEk6YoVSmXS2yEC2SH+2QH+2QDpbpH+oQH912Tfs1ZvJ0ztUoC9T2S76UF1JkjTB1DxghRAuB64E6oAfxhi/VesapMkmxki2UGaoUKq88tVXoUQmX2QoXyKTL5EplMjkigzm9y+LDOYqx6SzRQZyRQZzlWU6WyRXtEdJkiRpuJoGrBBCHXAVcCnQBKwKIayIMW6tZR3SaCqVI8VymWIpUixFCvvXy2UKpUihVK6+quvFMoVyJF8sUyyVyZfK5IvDlsXnbueeeZUqy8Lw9coyWyiRLZTJFkvPrEuSJGn01boH63xgV4xxD0AI4SbgfcCIBKwYD3+40Qt95IW+7fnOdeCe5/vuOOyog517+P79xz9333NriAd+Lv7uZ4d/5sDjh39P5djnfi7GOOzYyrJc/Z79n62M9KocVx52/nK5snzO52JleeBn9r8Xq+9F4rD9zx5XKsdnfo5SOT7nOyvvQSlW9pfL8ZnPlKv7SuVnj92/v1SOlGKkVKosy/u3y5WQ9Mx6uXJMsRwplcvVZXwmQBWr35ekqXWBWXVTmTU90TIkSZImrPmzZxz0vVoHrPlA47DtJuCC4QeEEJYBy6qbuRDC5hrVpsltHtCZdBGa8LzOVAteZ6oVrzXVwpi8zu6sLF78fO+NuUkuYozXANcAhBBWxxiXJlySJgGvNdWC15lqwetMteK1ploYj9fZlBqfrxlYOGx7QXWfJEmSJI17tQ5Yq4AzQwhLQgjHAB8BVtS4BkmSJEkaFTUdIhhjLIYQ/ha4h8o07dfGGLe8wEeuqU1lkteaasLrTLXgdaZa8VpTLYy76ywcycx7kiRJkqTfVeshgpIkSZI0YRmwJEmSJGmEjNmAFUK4PITwdAhhVwjhy0nXo4khhLAwhPBgCGFrCGFLCOHz1f1zQgj3hRB2VpcnJV2rxr8QQl0IYV0I4VfV7SUhhJXVdu3m6mQ/0lEJIcwOIdwSQtgeQtgWQrjINk0jLYTwd9W/m5tDCDeGEKbbpmkkhBCuDSF0DH/27cHasFDx/eo1tzGEcF5ylR/cmAxYIYQ64CrgncArgY+GEF6ZbFWaIIrA38cYXwlcCHy2em19Gbg/xngmcH91Wzpanwe2Ddv+V+C7McYzgB7g04lUpYnmSuDXMcZXAGdTueZs0zRiQgjzgc8BS2OMr6YyUdlHsE3TyPgJcPkB+w7Whr0TOLP6WgZcXaMaD8uYDFjA+cCuGOOeGGMeuAl4X8I1aQKIMbbGGNdW19NU/kdkPpXr67rqYdcB70+mQk0UIYQFwLuBH1a3A/A24JbqIV5nOmohhBOBi4EfAcQY8zHGXmzTNPKmAjNCCFOBmUArtmkaATHGR4DuA3YfrA17H/DTWPEkMDuEcFptKj10YzVgzQcah203VfdJIyaEsBg4F1gJnBpjbK2+1QacmlBZmji+B/wDUK5uzwV6Y4zF6rbtmkbCEiAF/Lg6HPWHIYTjsE3TCIoxNgP/DjRQCVZ9wBps0zR6DtaGjYuMMFYDljSqQgizgFuBL8QY+4e/FyvPLvD5BTpiIYT3AB0xxjVJ16IJbypwHnB1jPFcYJADhgPapuloVe9/eR+VQH86cBy/O6RLGhXjsQ0bqwGrGVg4bHtBdZ901EII06iEq+tjjLdVd7fv72KuLjuSqk8TwhuB94YQ6qkMcX4blftkZleH14DtmkZGE9AUY1xZ3b6FSuCyTdNIegewN8aYijEWgNuotHO2aRotB2vDxkVGGKsBaxVwZnV2mmOo3Ei5IuGaNAFU74P5EbAtxvidYW+tAD5RXf8E8Ita16aJI8b4lRjjghjjYirt1wMxxj8FHgT+uHqY15mOWoyxDWgMIby8uuvtwFZs0zSyGoALQwgzq39H919ntmkaLQdrw1YAf1adTfBCoG/YUMIxI1R63caeEMK7qNzDUAdcG2P8ZsIlaQIIIbwJeBTYxLP3xnyVyn1Yy4FFwD7gwzHGA2+4lA5bCOES4IsxxveEEF5CpUdrDrAO+FiMMZdkfRr/QgjnUJlM5RhgD/ApKv+AapumERNC+DpwBZXZeNcBn6Fy74ttmo5KCOFG4BJgHtAOfA24g+dpw6oB/z+pDFHNAJ+KMa5Oou4XMmYDliRJkiSNN2N1iKAkSZIkjTsGLEmSJEkaIQYsSZIkSRohBixJkiRJGiEGLEmSJEkaIQYsSZIkSRohBixJkiRJGiH/G+9duCa+fUOIAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"import numpy as np\n",
"from scipy.integrate import solve_ivp\n",
"import matplotlib.pyplot as plt\n",
"import seaborn as sns\n",
"\n",
"# time horizon in days\n",
"d = 15 * 7 \n",
"\n",
"# disease dynamics\n",
"Rt = 4.0\n",
"theta = 1/3.0 # 1/incubation time in days\n",
"rho = 1.0/14.0 # 1/time to recovery in days\n",
"mu = 1.0/1.0 # 1/time to false-postive return in days\n",
"p_si = 0.20 # probability of symptoms given infection\n",
"p_fs = 0.0005 # probability of fataility given symptoms\n",
"\n",
"sigma = rho * p_si / (1 - p_si) # rate of symptom development\n",
"beta = (sigma + rho)*Rt\n",
"delta = rho * (p_fs/p_si) / (1 - (p_fs/p_si))\n",
"\n",
"# testing protocols\n",
"Sp = 0.98 # test specificity\n",
"Se = 0.70 # test sensitivity\n",
"tau = 1000 # testing period\n",
"\n",
"# population parameters\n",
"x = 10.0 # weekly exogeneous infections\n",
"y = 10.0\n",
"IC = [8200-y, 0, y, 0, 0, 0, 0, 0]\n",
"\n",
"# SEIR model differential equations.\n",
"def deriv(t, X):\n",
" U, E, A, S, Tp, Fp, R, D = X\n",
" exog = x*((t + 1) % 7 < 1)\n",
" dU = -beta*U*A/(U + E + A + R) - (1 - Sp)*U/tau + mu*Fp - exog\n",
" dE = beta*U*A/(U + E + A + R) - theta*E + exog\n",
" dA = theta*E - (sigma + rho + Se/tau)*A\n",
" dS = -(rho + delta)*S + sigma*(Tp + A)\n",
" dTp = -(sigma + rho)*Tp + Se*A/tau\n",
" dFp = -mu*Fp + (1 - Sp)*U/tau\n",
" dR = rho*(Tp + S + A)\n",
" dD = delta*S\n",
" return np.array([dU, dE, dA, dS, dTp, dFp, dR, dD,])\n",
"\n",
"t = np.linspace(0, d, 10*d + 1)\n",
"soln = solve_ivp(deriv, [0, max(t)], IC, t_eval = t, atol=1e-8, rtol=1e-8)\n",
"U, E, A, S, Tp, Fp, R, D = soln.y\n",
"\n",
"fix, ax = plt.subplots(3, 1, figsize=(12, 8))\n",
"ax[0].stackplot(t, U, E, A, R)\n",
"ax[0].set_ylim(0, sum(IC))\n",
"ax[0].set_title('Active Transmission and Testing Pool')\n",
"\n",
"ax[1].stackplot(t, S, Tp, Fp)\n",
"ax[1].legend(['Symptomatic', 'False Positive', 'True Positive'], loc=\"upper left\")\n",
"ax[1].set_title('Isolation Pool')\n",
"\n",
"ax[2].stackplot(t, D)\n",
"ax[2].set_title('Removed Pool')\n",
"ax[2].legend(['Recovered', 'Dead'], loc=\"upper left\")\n",
"\n",
"for a in ax:\n",
" a.set_xlim(0, d)\n",
"\n",
"plt.tight_layout()"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"colab": {},
"colab_type": "code",
"id": "gXw3CAB3rt3u",
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.3.4.4 Parameter values](https://jckantor.github.io/CBE40455-2020/02.03-Campus-reopening.html#2.3.4.4-Parameter-values)",
"section": "2.3.4.4 Parameter values"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"\n",
"< [2.2 Campus SEIR Modeling](https://jckantor.github.io/CBE40455-2020/02.02-Campus-SEIR-modeling.html) | [Contents](toc.html) | [2.4 Linear Analysis of Campus Reopening](https://jckantor.github.io/CBE40455-2020/02.04-Linear-Analysis-of-Campus-Reopening.html) > 
 "
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "Campus-reopening.ipynb",
"provenance": [
{
"file_id": "1ddb_0swsq9MRKyHrzflCzeF8Tqqmp24H",
"timestamp": 1596290235744
}
],
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 4
}
"
]
}
],
"metadata": {
"colab": {
"collapsed_sections": [],
"name": "Campus-reopening.ipynb",
"provenance": [
{
"file_id": "1ddb_0swsq9MRKyHrzflCzeF8Tqqmp24H",
"timestamp": 1596290235744
}
],
"toc_visible": true
},
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.7.4"
}
},
"nbformat": 4,
"nbformat_minor": 4
}

