This notebook contains material from CBE40455-2020; content is available on Github.
7.9 Log-Optimal Portfolios¶
This notebook demonstrates the Kelly criterion and other phenomena associated with log-optimal growth.
7.9.1 Initializations¶
%matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
import random
7.9.2 Kelly's Criterion¶
In a nutshell, Kelly's criterion is to choose strategies that maximize expected log return.
$$\max E[\ln R]$$where $R$ is total return. As we learned, Kelly's criterion has properties useful in the context of long-term investments.
7.9.3 Example 1. Maximizing Return for a Game with Arbitrary Odds¶
Consider a game with two outcomes. For each \$1 wagered, a successful outcome with probability $p$ returns $b+1$ dollars. An unsuccessful outcome returns nothing. What fraction $w$ of our portfolio should we wager on each turn of the game?
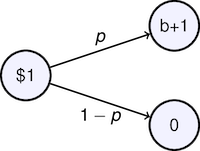
There are two outcomes with returns
\begin{align*} R_1 & = w(b+1) + 1 - w = 1+wb & \mbox{with probability }p\\ R_2 & = 1-w & \mbox{with probability }1-p \end{align*}The expected log return becomes
\begin{align*} E[\ln R] & = p \ln R_1 + (1-p) \ln R_2 \\ & = p\ln(1+ wb) + (1-p)\ln(1-w) \end{align*}Applying Kelly's criterion, we seek a value for $w$ that maximizes $E[\ln R]$. Taking derivatives
\begin{align*} \frac{\partial E[\ln R]}{\partial w} = \frac{pb}{1+w_{opt}b} - \frac{1-p}{1-w_{opt}} & = 0\\ \end{align*}Solving for $w$
$$w_{opt} = \frac{p(b+1)-1}{b}$$The growth rate is then the value of $E[\ln R]$ when $w = w_{opt}$, i.e.,
$$m = p\ln(1+ w_{opt}b) + (1-p)\ln(1-w_{opt})$$You can test how well this works in the following cell. Fix $p$ and $b$, and let the code do a Monte Carlo simulation to show how well Kelly's criterion works.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from numpy.random import uniform
p = 0.5075
b = 1
# Kelly criterion
w = (p*(b+1)-1)/b
# optimal growth rate
m = p*np.log(1+w*b) + (1-p)*np.log(1-w)
# number of plays to double wealth
K = int(np.log(2)/m)
# monte carlo simulation and plotting
for n in range(0,100):
W = [1]
for k in range(0,K):
if uniform() <= p:
W.append(W[-1]*(1+w*b))
else:
W.append(W[-1]*(1-w))
plt.semilogy(W,alpha=0.2)
plt.semilogy(np.linspace(0,K), np.exp(m*np.linspace(0,K)),'r',lw=3)
plt.title('Kelly Criterion w = ' + str(round(w,4)))
plt.xlabel('k')
plt.grid()
7.9.4 Example 2. Betting Wheel¶
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
w1 = np.linspace(0,1)
w2 = 0
w3 = 0
p1 = 1/2
p2 = 1/3
p3 = 1/6
R1 = 1 + 2*w1 - w2 - w3
R2 = 1 - w1 + w2 - w3
R3 = 1 - w1 - w2 + 5*w3
m = p1*np.log(R1) + p2*np.log(R2) + p3*np.log(R3)
plt.plot(w1,m)
plt.grid()
def wheel(w,N = 100):
w1,w2,w3 = w
7.9.5 Example 3. Stock/Bond Portfolio in Continuous Time¶
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime
from pandas_datareader import data, wb
from scipy.stats import norm
import requests
def get_symbol(symbol):
"""
get_symbol(symbol) uses Yahoo to look up a stock trading symbol and
return a description.
"""
url = "http://d.yimg.com/autoc.finance.yahoo.com/autoc?query={}®ion=1&lang=en".format(symbol)
result = requests.get(url).json()
for x in result['ResultSet']['Result']:
if x['symbol'] == symbol:
return x['name']
symbol = '^GSPC'
# end date is today
end = datetime.datetime.today().date()
# start date is three years prior
start = end-datetime.timedelta(1.5*365)
# get stock price data
S = data.DataReader(symbol,"yahoo",start,end)['Adj Close']
rlin = (S - S.shift(1))/S.shift(1)
rlog = np.log(S/S.shift(1))
rlin = rlin.dropna()
rlog = rlog.dropna()
# plot data
plt.figure(figsize=(10,6))
plt.subplot(3,1,1)
S.plot(title=get_symbol(symbol))
plt.ylabel('Adjusted Close')
plt.grid()
plt.subplot(3,1,2)
rlin.plot()
plt.title('Linear Returns (daily)')
plt.grid()
plt.tight_layout()
plt.subplot(3,1,3)
rlog.plot()
plt.title('Log Returns (daily)')
plt.grid()
plt.tight_layout()
print('Linear Returns')
mu,sigma = norm.fit(rlin)
print(' mu = {0:12.8f} (annualized = {1:.2f}%)'.format(mu,100*252*mu))
print('sigma = {0:12.8f} (annualized = {1:.2f}%)'.format(sigma,100*np.sqrt(252)*sigma))
print()
print('Log Returns')
nu,sigma = norm.fit(rlog)
print(' nu = {0:12.8f} (annualized = {1:.2f}%)'.format(nu,100*252*nu))
print('sigma = {0:12.8f} (annualized = {1:.2f}%)'.format(sigma,100*np.sqrt(252)*sigma))
mu = 252*mu
nu = 252*nu
sigma = np.sqrt(252)*sigma
rf = 0.04
mu = 0.08
sigma = 0.3
w = (mu-rf)/sigma**2
nu_opt = rf + (mu-rf)**2/2/sigma/sigma
sigma_opt = np.sqrt(mu-rf)/sigma
print(w,nu_opt,sigma_opt)
7.9.6 Volatility Pumping¶
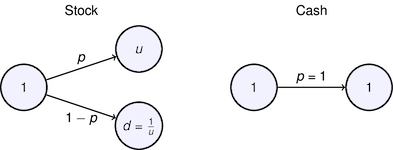
# payoffs for two states
u = 1.059
d = 1/u
p = 0.54
rf = 0.004
K = 100
ElnR = p*np.log(u) + (1-p)*np.log(d)
print("Expected return = {:0.5}".format(ElnR))
Z = np.array([float(random.random() <= p) for _ in range(0,K)])
R = d + (u-d)*Z
S = np.cumprod(np.concatenate(([1],R)))
ElnR = lambda alpha: p*np.log(alpha*u +(1-alpha)*np.exp(rf)) + \
(1-p)*np.log(alpha*d + (1-alpha)*np.exp(rf))
a = np.linspace(0,1)
plt.plot(a,map(ElnR,a))
from scipy.optimize import fminbound
alpha = fminbound(lambda(alpha): -ElnR(alpha),0,1)
print alpha
#plt.plot(alpha, ElnR(alpha),'r.',ms=10)
R = alpha*d + (1-alpha) + alpha*(u-d)*Z
S2 = np.cumprod(np.concatenate(([1],R)))
plt.figure(figsize=(10,4))
plt.plot(range(0,K+1),S,range(0,K+1),S2)
plt.legend(['Stock','Stock + Cash']);
