{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 0,
"link": "[](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html)",
"section": ""
}
},
"source": [
"\n",
"*This notebook contains material from [cbe30338-2021](https://jckantor.github.io/cbe30338-2021);\n",
"content is available [on Github](https://github.com/jckantor/cbe30338-2021.git).*\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 0,
"link": "[](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html)",
"section": ""
}
},
"source": [
"\n",
"< [2.0 Linear Process Models](https://jckantor.github.io/cbe30338-2021/02.00-Process-Modeling.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.2 Properties of Scalar First Order Linear Systems](https://jckantor.github.io/cbe30338-2021/02.02-Properties-of-Scalar-First-Order-Linear-Systems.html) >
"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.1 One Compartment Pharmacokinetics](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1-One-Compartment-Pharmacokinetics)",
"section": "2.1 One Compartment Pharmacokinetics"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"# 2.1 One Compartment Pharmacokinetics"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.1.1 Learning Goals](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.1-Learning-Goals)",
"section": "2.1.1 Learning Goals"
}
},
"source": [
"## 2.1.1 Learning Goals\n",
"\n",
"The notebook introduces a single, linear, first-order differential equation in the general form\n",
"\n",
"$$\\frac{dx}{dt} = a x + b u$$\n",
"\n",
"as mathematical model to describe the dynamic response of a system to a changing input. \n",
"\n",
"In any particular application, the **state variable** $x$ corresponds to a process variable such as temperature, pressure, concentration, or position. The **input variable** $u(t)$ corresponds to a changing input such as heater power, flowrate, or valve position. This notebook uses this equation to describe a one-compartment model for a pharmacokinetics in the which the state is the concentration of an antimicrobrial, and the input is a rate of intraveneous administration.\n",
"\n",
"This notebook demonstrates features of this model that can be used in a wide range of process applications:\n",
"\n",
"* Simulate response from a known initial condition.\n",
"* Simulate response to a changinig input.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.1.2 Pharamacokinetics](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.2-Pharamacokinetics)",
"section": "2.1.2 Pharamacokinetics"
}
},
"source": [
"## 2.1.2 Pharamacokinetics\n",
"\n",
"Pharmacokinetics is a branch of pharmacology that studies the fate of chemical species in living organisms. The diverse range of applications includes the administration of drugs and anesthesia in humans. This notebook introduces a one compartment model for pharmacokinetics and shows how it can be used to determine strategies for the intravenous administration of an antimicrobial."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.2.1 One-Compartment Model](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.2.1-One-Compartment-Model)",
"section": "2.1.2.1 One-Compartment Model"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"### 2.1.2.1 One-Compartment Model\n",
"\n",
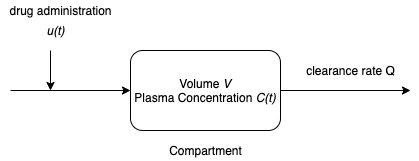
"For the purposes of drug administration, for a one-compartment model of the human body is assumed to consist of a single compartment of a constant volume $V$ containing all the plasma of the body. The plasma is assumed to be sufficiently well mixed that any drug is uniformly distributed with concentration $C(t)$. The drug enters the plasma by direct injection into the plasma at rate $u(t)$. The drug leaves the body as a component of the plasma where $Q$ is the constant plasma clearance rate.\n",
"\n",
"\n",
"\n",
"A generic mass balance for a single species is given by\n",
"\n",
"$$\\fbox{Rate of Accumulation} = \\fbox{Inflow} - \\fbox{Outflow} + \\fbox{Production by reaction} - \\fbox{Consumption by reaction}$$\n",
"\n",
"Assuming the drug is neither produced or consumed by reaction in the body, this generic mass balance can be translated to differential equation\n",
"\n",
"$$\\begin{align*}\n",
"\\underbrace{\\fbox{Rate of Accumulation}}_{V \\frac{dC}{dt}} & = \\underbrace{\\fbox{Inflow}}_{u(t)} - \\underbrace{\\fbox{Outflow}}_{Q C} + \\underbrace{\\fbox{Production by reaction}}_0 - \\underbrace{\\fbox{Consumption by reaction}}_0\n",
"\\end{align*}$$\n",
"\n",
"or, summarizing,\n",
"\n",
"$$V \\frac{dC}{dt} = u(t) - Q C(t)$$\n",
"\n",
"This model is characterized by two parameters, the plasma volume $V$ and the clearance rate $Q$."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.2.2 Antimicrobials](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.2.2-Antimicrobials)",
"section": "2.1.2.2 Antimicrobials"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"### 2.1.2.2 Antimicrobials\n",
"\n",
"Let's consider the administration of an antimicrobial to a patient. Concentration $C(t)$ refers to the concentration of the antibiotic in blood plasma in units of [mg/L or $\\mu$g/mL]. There are two concentration levels of interest in the medical use of an antimicrobrial:\n",
"\n",
"**Minimum Inhibitory Concentration (MIC)** The minimum concentration of the antibiotic that prevents visible growth of a particular microorganism after overnight incubation. This is generally not enough to kill the microorganism, only enough to prevent further growth.\n",
"\n",
"**Minimum Bactricidal Concentration (MBC)** The lowest concentration of the antimicrobrial that prevents the growth of the microorganism after subculture to antimicrobrial-free media. MBC is generally the concentration needed \"kill\" the microorganism.\n",
"\n",
"Extended exposure to an antimicrobrial at levels below MBC leads to [antimicrobrial resistance](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4378521/)."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.2.3 What questions can we ask and answer with this model?](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.2.3-What-questions-can-we-ask-and-answer-with-this-model?)",
"section": "2.1.2.3 What questions can we ask and answer with this model?"
}
},
"source": [
"### 2.1.2.3 What questions can we ask and answer with this model?\n",
"\n",
"There are multiple reasons to create mathematical models. In research and development, for example, a mathematical model forms a testable hypothesis of one's understanding of a system. The model guides the design of experiments to either validate or falsify the assumptions incorporated in the model. \n",
"\n",
"In the present context of control systems, a model is used to answer operating questions. In pharmacokinetics, for example, the operational questions might include:\n",
"\n",
"* What values for the parameters $V$ and $Q$ provide accurate predictions of system response?\n",
"* How long will it take to clear the antimicrobial from the body?\n",
"* What rate of antimicrobial addition is required to achieve the minimum bactricidal concentration?\n",
"* If doses are administered periodically, how large should each dose be, and how frequently should the doses be administered?\n",
"\n",
"Questions like these can be answered through simulation, regression to experimental data, and mathematical analysis. We'll explore several of these techniques below.\n",
"\n",
"* Simulation\n",
" * Known initial condition\n",
" * Time dependent input\n",
"* Steady state analysis\n",
"* Alternative model formulations\n",
" * State space model\n",
" * Gain and Time Constant"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.1.3 Simulation](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3-Simulation)",
"section": "2.1.3 Simulation"
}
},
"source": [
"## 2.1.3 Simulation"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.1 Simulation from a Known Initial Condition](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1-Simulation-from-a-Known-Initial-Condition)",
"section": "2.1.3.1 Simulation from a Known Initial Condition"
}
},
"source": [
"### 2.1.3.1 Simulation from a Known Initial Condition"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.1 Problem Statement ](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.1-Problem-Statement)",
"section": "2.1.3.1.1 Problem Statement "
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.1.1 Problem Statement \n",
"\n",
"Assume the minimum inhibitory concentration (MIC) of a particular organism to a particular antimicrobial is 5 mg/liter, and the minimum bactricidal concentration (MBC) is 8 mg/liter. Further assume the plasma volume $V$ is 4 liters with a clearance rate $Q$ of 0.5 liters/hour. \n",
"\n",
"An initial intravenous antimicrobial dose of 64 mg in 4 liters of plasm results in a plasma concentration $C_{initial}$ of 16 mg/liter. How long will the concentration stay above MBC? Above MIC?"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.2 Step 1. Import libraries](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.2-Step-1.-Import-libraries)",
"section": "2.1.3.1.2 Step 1. Import libraries"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.1.2 Step 1. Import libraries\n",
"\n",
"For this first simulation we compute the response of the one compartment model due starting with an initial condition $C_{initial}$, and assuming input $u(t) = 0$. We will use the [`solve_ivp`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html) function for solving differential equations from the `scipy.integrate` library.\n",
"\n",
"The first steps to a solution are:\n",
"\n",
"1. Initialize the plotting system.\n",
"2. Import the `numpy` library for basic mathematical functions.\n",
"3. Import the `matplotlib.pyplot` library for plotting.\n",
"4. Import the any needed mathematical functions or libraries."
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.2 Step 1. Import libraries](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.2-Step-1.-Import-libraries)",
"section": "2.1.3.1.2 Step 1. Import libraries"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"from scipy.integrate import solve_ivp"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.3 Step 2. Enter Parameter Values](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.3-Step-2.-Enter-Parameter-Values)",
"section": "2.1.3.1.3 Step 2. Enter Parameter Values"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.1.3 Step 2. Enter Parameter Values"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.3 Step 2. Enter Parameter Values](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.3-Step-2.-Enter-Parameter-Values)",
"section": "2.1.3.1.3 Step 2. Enter Parameter Values"
}
},
"outputs": [],
"source": [
"V = 4 # liters\n",
"Q = 0.5 # liters/hour\n",
"MIC = 5 # mg/liter\n",
"MBC = 8 # mg/liter\n",
"\n",
"C_initial = 16 # mg/liter"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.4 Step 3. Write the differential equation in standard form](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.4-Step-3.-Write-the-differential-equation-in-standard-form)",
"section": "2.1.3.1.4 Step 3. Write the differential equation in standard form"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.1.4 Step 3. Write the differential equation in standard form\n",
"\n",
"The most commonly solvers for systems of differential equations require a function evaluating the right hand sides of the differential equations when written in a standard form\n",
"\n",
"$$\\frac{dC}{dt} = \\frac{1}{V}u(t) - \\frac{Q}{V}C$$\n",
"\n",
"Here we write two functions. One function returns values of the input $u(t)$ for a specified point in time, the second returns values of the right hand side as a function of time and state."
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.4 Step 3. Write the differential equation in standard form](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.4-Step-3.-Write-the-differential-equation-in-standard-form)",
"section": "2.1.3.1.4 Step 3. Write the differential equation in standard form"
}
},
"outputs": [],
"source": [
"def u(t):\n",
" return 0\n",
"\n",
"def deriv(t, C):\n",
" return u(t)/V - (Q/V)*C"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.5 Step 4. Solution and Visualization](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.5-Step-4.-Solution-and-Visualization)",
"section": "2.1.3.1.5 Step 4. Solution and Visualization"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.1.5 Step 4. Solution and Visualization"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.5 Step 4. Solution and Visualization](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.5-Step-4.-Solution-and-Visualization)",
"section": "2.1.3.1.5 Step 4. Solution and Visualization"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
" message: 'A termination event occurred.'\n",
" nfev: 26\n",
" njev: 0\n",
" nlu: 0\n",
" sol: None\n",
" status: 1\n",
" success: True\n",
" t: array([0. , 0.48979592, 0.97959184, 1.46938776, 1.95918367,\n",
" 2.44897959, 2.93877551, 3.42857143, 3.91836735, 4.40816327,\n",
" 4.89795918, 5.3877551 , 5.87755102, 6.36734694, 6.85714286,\n",
" 7.34693878, 7.83673469, 8.32653061, 8.81632653, 9.30612245])\n",
" t_events: [array([5.53942584]), array([9.31072423])]\n",
" y: array([[16. , 15.049792 , 14.15601545, 13.31532006, 12.5243503 ,\n",
" 11.779541 , 11.07848539, 10.41894155, 9.79872358, 9.21570167,\n",
" 8.66780203, 8.15300696, 7.6693548 , 7.21493994, 6.78791284,\n",
" 6.38648 , 6.00890398, 5.65350342, 5.31865298, 5.00287861]])\n",
" y_events: [array([[8.]]), array([[5.]])]\n"
]
}
],
"source": [
"# specify time span and evaluation points\n",
"t_span = [0, 24]\n",
"t_eval = np.linspace(0, 24, 50)\n",
"\n",
"# initial conditions\n",
"IC = [C_initial]\n",
"\n",
"# add events\n",
"def cross_mbc(t, y):\n",
" return y[0] - MBC\n",
"cross_mbc.direction = -1.0\n",
"\n",
"def cross_mic(t, y):\n",
" return MIC-y[0]\n",
"cross_mic.terminal = True\n",
"\n",
"# compute solution\n",
"soln = solve_ivp(deriv, t_span, IC, t_eval=t_eval, events=[cross_mbc, cross_mic])\n",
"\n",
"# display solution\n",
"print(soln)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.5 Step 4. Solution and Visualization](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.5-Step-4.-Solution-and-Visualization)",
"section": "2.1.3.1.5 Step 4. Solution and Visualization"
}
},
"source": [
"The decision on how to display or visualize a solution is problem dependent. Here we create a simple function to visualize the solution and relevant problem specifications. "
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.5 Step 4. Solution and Visualization](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.5-Step-4.-Solution-and-Visualization)",
"section": "2.1.3.1.5 Step 4. Solution and Visualization"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEWCAYAAABhffzLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAABAl0lEQVR4nO3dd3xUZfb48c9JI4QOoYWAASlKgISOgBRBFhBwRcSuoIIia9mv3d1VdP2pq6xiV1wVREAUBQUBBaQIKBh6kV5DEQjSW8r5/XFvMKROymQmyXm/XvPKzH1uOXNz58yd5z73eURVMcYYU3IE+DoAY4wxhcsSvzHGlDCW+I0xpoSxxG+MMSWMJX5jjClhLPEbY0wJY4nfFGsi0kVE4j2cd4SIfJbP7d0qIj8URDzFnYi8LyL/yqb8aRH5n4frGiMiLxRcdHknIjtFpLv7PNv3kNPx4i1FPvGLyCARWSsip0XkgIi8JyIVvbi9NiIyQ0SOisgREVkmIoO9tb2CIiJRIqIiEuSj7ef4wXTj+z1tjCISJCIHRaRI3HCiquNVtUfqa/c91c/r+kRkvojck+Z1FxH5Q0Ruym+s3pA+3uyo6n2q+m93uQxfiKr6oqp6tC4P4qopIh+JyH4ROSEiG0XkOREpUxDrz0ra95DZZzD98VJYinTiF5FHgP8AjwEVgHbAJcBsEQnxwvauAH4EFgD1gSrAMKBXQW+rIPkq2efRUS7en72BP3wTin8RkR7AVOAuVf3cx+EUGSJSGfgZKA1coarlgKuBisClPgzNd1S1SD6A8sBJYGC66WWBgzgfDoARwBfAp8AJYD3QKs38EcBXwCFgB/BgNttcBLyTQ1xDgK3AEeBbICJNmQL3A1vcWP6Nc+D9DBx34wxx5+0CxANPA4eBncCtadZ1DbDSXW4PMCJNWZS7rbuB3cBC96+6++wkcAUwCFgMvI6TcLcD7d3pe9z9eGea9ZYCRrrr+h14HyidLt5H3OX2A4PdsqFAInDe3fa0LPadAv8EvkwzbTLwD+dQveh/9q27j7cCQ9KUlQbG4HxZbMA5KYj35P/tHiufZRHbAuB693lHN9be7uvuwCr3+SBgkft8oTvfKfd935jdfspiu/OBe4A+7v+odyb77D6cY+oP4B1A3LIAd3/ucrf1KVDBLRsLPOI+r+Wu5373dX1330pe483pmHDLxwAvAGWAM0AKfx6fEen/H8CXwAHgmLtvo9OvK4uYXgDWAgHZxN0e+NVd969A+3Tv6d84n5UTwA9AeJry2919nIBzrO4Euqc/psj6M7ioIOLIzaMon/G3B0KBr9NOVNWTwEycb/RU/YDPcb7hvwXeBhCRAGAasBrn4O8GPCwif0m/MREJw/lHTc4qIBG5CngJGAjUxDkY0p+Z9QRa4vw6eRwYDdwK1AaaADenmbcGEO7GdicwWkQauWWngDvc93QNMExE/ppuW52By4G/AJ3caRVVtayq/uy+bguswfn1MsGNtzXOh/824G0RKevO+x+gIRDrltcCnkkXbwV3+t3AOyJSSVVHA+OBV9xt981s/7mmAp1EpKJbZXcl8E26eSbiJJQIYADwooh0c8uexfkyvdR933emLpSb/3cmFuAkMnD25Xac/Zv6ekH6BVQ1dZ/HuO97kvs60/2Uzbb7Ap8BA1R1RiblfXD+ZzE4x17q+xnkProC9XBOit7O5P10zuT9/KRutslDvGnluKyqnsL5lbfP3U9lVXVfJuuaCTQAqgErcI4pT3QHvlbVlMwK3V8E3wFv4nwOXgO+E5EqaWa7BRjsbjsEeNRdtjHwHk7yj3CXj8wijqw+g/mOI7eKcuIPBw6ralImZfvd8lSLVHWGqiYD43A+IOB8WKqq6vOqel5VtwMfApnVn1bC2V/7s4npVuBjVV2hqueAp4ArRCQqzTz/UdXjqroeWAf8oKrbVfUYzoHdPN06/6Wq51R1Ac5BMRBAVeer6lpVTVHVNTjJsHO6ZUeo6ilVPZNNzDtU9RN330zC+QJ63t3mDzhn6fVFRHB+zfxdVY+o6gngxXT7KtFdNtFNUCeBRuTOWZzkfKO77m/daQCISG2cM+4nVPWsqq4C/ofzwQNn//w/N8Y9OB+iVLn5f6e3gIsT40tpXncmk8Sfjdzup67AZpwzvcy8rKpHVXU3MA/nixmc4/E19/g6iXM83uRW/S0ArnS/DDsBrwAdsng/+fm/FsQxAYCqfqyqJ9zP1gggRkQqeLBoFbL/3F4DbFHVcaqapKoTgY04X7ipPlHVze5n6Qv+3McDgOmqutCN6184v1zyIj9x5EpRTvyHgfAs6q9ruuWpDqR5fhoIdZe7BIhwL9QeFZGjOFUr1TNZ5x84/9Ca2cQUgXOWD1z49ZGAc7aT6vc0z89k8rpsmtd/uGdDqXa520BE2orIPBE5JCLHcH7up/2yA6e6Jifpt4+qZhZTVSAMWJ5mX81yp6dKSPdFfDrd+/HUpzi/Zu5wn6cVAaR+8aTaxZ/7OIKL3/euNM9z8/9O72egoYhUx/mwfQrUFpFwoA1O1YOncruf/gWcA6aKSKlMytMf36nruuh4dJ8HAdVVdRtOEo7F+VU1Hdjn/qJMn/jz838tkGNCRAJF5GUR2SYix3GqUyDjMZ9pDOTic+tKe0xB9vv4wvHmfl4TPIipoOPIlaKc+H/G+TD0TzvRvUrfC5jrwTr24JzxVkzzKKeqvdPPqKqn3W1en8369uEkl7SxVAH2ehBLZiqla3VQx90GONUy3wK1VbUCTn27pA87i+d5cRjnSyA6zb6qoKqeHni52f5POB/U6jjXVdLaB1QWkXJpptXhz328H+dXS9qyVB7/vzME7/z/lwMPAetU9TywBPg/YJuqHs5u+Xw6hXORuwIwWUSCPVzuouMRZ18k8eeX/QKcM9YQVd3rvr4D59ftqvyHnSs5HR+3ANfiVNtUwLmOBRmP+czMAa5zf91kJv1+gouPqexcdLy5VcJVspg3p/eYnzhypcgmfrdq5DngLRHpKSLBbpXKlzj1v+M8WM0y4LiIPCEipd2ziiYi0jqL+R8HBonIY6n1biISIyKp9fgTgMEiEuuemb0ILFXVnXl+o/CciISIyJU4dblfutPL4Zz5nhWRNjgfjOwcwvnFUi8vQbj1ox8Cr4tINQARqeVh/Tg4ycajbbt1y32BfmnqmVPL9uAk3JdEJFREmuHUHafW934BPCUilUQkEnggzeK5/X+ntwD4G3+eDc9P9zozHr/v7Li/cHrinBVOEJFADxabCPxdROq612leBCalOQNPfT+pv1bm4+yvRW7VX2H6HaiSTdVNOZwTvQScX54v5mLdr+E0BhkrIpfAhWP3Nff4mYHza+4WcZoP3wg0xvkVlJPJQB8R6ei2JHyerPNqTp/B/MSRK0U28QOo6is4P9VH4rRuWYpzVtfNrW/LaflknAQTi9PC4zBOfXGmB5+qLgGuch/bReQIzsXZGW75XJyf5V/hnAlcimf1x1k5gFPFtA8nsd2nqhvdsvuB50XkBM4F1i+yW5F7xvr/gMVuNUe7PMTzBE4rml/cn9tz8Ly+9iOgsbvtqTnNrKrr3esgmbkZ54xvHzAFeFZVZ7tlz+H8PN6B0+rhwglAbv/fmViAk4AWZvE6MyNwEs5RERno4XYypapHcRotNAQ+zeYMNtXHOO9/Ic77PcvFX4Tp41+Ek1RzU21VINzjeiLO5+qoiESkm+VTnP/rXpzWWr/kYt1HcBqDJAJL3c/MXJyWM1tVNQHnpOoRnC+Wx4E+nvyKc4/R4TgnfftxPq+Z3qCX02cwP3HklqQ7oTJ+QkS64DQDy6qFgDHG5EmRPuM3xhiTe5b4jTGmhLGqHmOMKWHsjN8YY0qYItF5V3h4uEZFRfk6DGOMKVKWL19+WFWrpp9eJBJ/VFQUcXFxvg7DGGOKFBFJfycwYFU9xhhT4ljiN8aYEsYSvzHGlDBFoo7fmKImMTGR+Ph4zp49m/PMxuRTaGgokZGRBAd71n+fJX5jvCA+Pp5y5coRFRWFM5SBMd6hqiQkJBAfH0/dunU9WsZrVT0i8rE4g2SvSzf9ARHZJCLrReQVb23fGF86e/YsVapUsaRvvE5EqFKlSq5+XXqzjn8MTjeyF4hIV5w+tZupajROr5rGFEuW9E1hye2x5rXEr6oLcQZsTmsYzjBx59x5DnqyrhNnEws4OmOMKbkKu1VPQ5xxPpeKyILsBsAQkaEiEicicTsTTjNrXXZDZhpjMjNlyhREhI0bN+Y8MzBq1ChOnz594XXv3r05evQoO3fupEmTJpkuc88997Bhw4Zs1/viixePm9K+fXuP4kn16aef0qRJE6Kjo2ncuDEjR/q2smDVqlXMmJHZuPfZ27lzJxMmTLjwOi4ujgcffLAgQ/OMqnrtgTNYxro0r9fhDH4tOOOU7sDtKC67R8U6jbTeU9/pN6v2qjFFwYYNG3wdgqqq3nDDDdqxY0d99tlnPZr/kksu0UOHDmWYvmPHDo2Ojs5zHGXKlMnzsjNmzNDmzZvr3r3O5//MmTM6evToPK+vIHzyySc6fPjwTMsSExOzXG7evHl6zTXXeCWmzI45IE4zy82ZTSyoRyaJfxbQJc3rbUDVnNbTvEULveH9JVr3yen6ZdyeAtxVxniHPyT+EydOaEREhG7atEkbNWp0Yfq8efO0c+fOev3112ujRo30lltu0ZSUFH3jjTc0ODhYmzRpol26dFHVP78IduzYoY0aNdI77rhDmzZtqtdff72eOnVKVVU7d+6sv/76q6qqTpgwQZs0aaLR0dH6+OOPq6rqE088oQEBARoTE6O33HKLql78RfCf//xHmzRpos2aNdMnnngiw/u48sorde7cuZm+x5UrV2rbtm21adOm+te//lWPHDlyIabHH39cW7durQ0aNNCFCxeqqmpSUpI+8sgj2qRJE23atKm++eabqqoaFxennTp10hYtWmiPHj103759Wa7n3LlzWrt2bQ0PD9eYmBj9/PPP9dlnn9UhQ4bo1VdfrTfffLPu2LFDO3bsqM2bN9fmzZvr4sWLVVW1bdu2Wr58eY2JidHXXnvtoi+ChIQEvfbaa7Vp06batm1bXb16taqqPvvsszp48GDt3Lmz1q1bV994441M90VuEn9hN+ecijNs4XwRaQiE4Ax/l60AEcYObsOQT+N4bPJqzielcEvbOjktZoxfeG7aejbsO16g62wcUZ5n+0ZnO8/UqVPp2bMnDRs2pHLlyqxYsYIWLVoAsHLlStavX09ERAQdOnRg8eLFPPjgg7z22mvMmzeP8PDwDOvbtGkTH330ER06dOCuu+7i3Xff5dFHH71Qvm/fPp544gmWL19OpUqV6NGjB1OnTuXll1/m7bffZtWqVRnWOXPmTKZOncrSpUsJCwvjyJH0lwVh3bp1tGzZMtP3eMcdd/DWW2/RuXNnnnnmGZ577jlGjRoFQFJSEsuWLWPGjBk899xzzJkzh9GjR7Njxw5WrlxJUFAQR44cITExkQceeIBvvvmGqlWrMmnSJP7xj3/w8ccfZ7me559/nri4ON5++20ARowYwfLly1m0aBGlS5fm9OnTzJ49m9DQULZs2cLNN99MXFwcL7/8MiNHjmT6dGcY3fnz5194L88++yzNmzdn6tSp/Pjjj9xxxx0X9tnGjRuZN28eJ06coFGjRgwbNszjNvuZ8WZzzonAz0AjEYkXkbtxxgCt5zbx/By40/1WylHpkED+d2crujSsytNT1jJm8Q5vhW5MsTBx4kRuuskZ8vmmm25i4sSJF8ratGlDZGQkAQEBxMbGsnPnzhzXV7t2bTp06ADAbbfdxqJFiy4q//XXX+nSpQtVq1YlKCiIW2+9lYULsx++d86cOQwePJiwsDAAKleu7PH7O3bsGEePHqVz584A3HnnnRdtr3///gC0bNnywvubM2cO9913H0FBQRe2t2nTJtatW8fVV19NbGwsL7zwAvHx8dmuJzP9+vWjdOnSgHMD35AhQ2jatCk33HBDjtdAABYtWsTtt98OwFVXXUVCQgLHjh0D4JprrqFUqVKEh4dTrVo1fv/9d092UZa8dsavqjdnUXRbXtcZGhzI+7e35IEJKxkxbQPnklK4t/OleV2dMYUipzNzb0hISODHH39k3bp1iAjJycmICK+84tw6U6pUqQvzBgYGkpSUlOM60zcZTP/aw3O4DMvk1BQxOjqa5cuXc9VVV+Vq3anvMe37y2x7qkp0dDQ///yzx+vJTJkyZS48f/3116levTqrV68mJSWF0NDQHOPNbP+lxpqX/1d2ilxfPaWCAnnn1hb0aVaTl2Zu5M25W3wdkjF+Z/Lkydxxxx3s2rWLnTt3smfPHurWrZvhLD29cuXKceLEiUzLdu/efSE5Tpw4kY4dO15U3rZtWxYsWMDhw4dJTk5m4sSJF87Gg4ODSUzM2Cy7R48efPzxxxdaEmVW1fPUU0/x+OOPc+DAAQDOnTvHm2++SYUKFahUqRI//fQTAOPGjbuwvaz06NGD999//0LiPHLkCI0aNeLQoUMX3ltiYiLr16/Pdj3Z7Sdwfo3UrFmTgIAAxo0bR3Jyco7LderUifHjxwNOFVB4eDjly5fPNo68KnKJHyA4MIA3bmpO/xa1eG32ZkZ+vylPZxvGFFcTJ07kuuuuu2ja9ddff1FTwswMHTqUXr160bVr1wxll19+OWPHjqVZs2YcOXKEYcOGXVRes2ZNXnrpJbp27UpMTAwtWrTg2muvvbDeZs2aceutt160TM+ePenXrx+tWrUiNjY202aavXv3Zvjw4XTv3p3o6Ghatmx5IXGPHTuWxx57jGbNmrFq1SqeeeaZbN/fPffcQ506dWjWrBkxMTFMmDCBkJAQJk+ezBNPPEFMTAyxsbEsWbIk2/V07dqVDRs2EBsby6RJkzKU33///YwdO5Z27dqxefPmC78GmjVrRlBQEDExMbz++usXLTNixAji4uJo1qwZTz75JGPHjs02hvwoEmPutmrVSjMbiCUlRXl6ylo+/3UPQ66sy9O9L7e7JY1f+O2337j88st9HYYpQTI75kRkuaq2Sj9vke6kLSBAePG6ppQKCuDDn3ZwLimFEX2jCQiw5G+MMVkp0okfnOQ/ol80IW7yP5+UwovXNbXkb4wxWSjyiR+cK99P976c0OBA3vpxK+eTUnhlQDOCAovkJQxjjPGqYpH4wUn+j/RoREhgAP+dvZlzySmMujGWYEv+xhhzkWKT+FM90K0BpYIDeHHGRs4npfD2Lc0pFRTo67CMMcZvFMvT4aGdLuW5ftHM3vA7945bztnEZF+HZIwxfqNYJn6AO9tH8eJ1TVmw+RD3jI3j9Pn83elmTFEjIhe6AACnz5mqVavSp08fAMaMGcPf/va3C+X+1vWx8Z5im/gBbmlbh1cHxLBk22EGffyrDehiSpQyZcqwbt06zpw5A8Ds2bOpVatWpvPOnDmTUaNG8cMPP7B+/XpWrFhBhQoVCjNcU4iKdeIHGNAykjduas7y3X9w84e/cPjkOV+HZEyh6dWrF9999x3g3M17882Zd6H10ksvMXLkSCIiIgAIDQ1lyJAhhRanKVzF7uJuZvrGRFC2VBDDxi9nwHtLGHd3W2pXDvN1WKYE6TKmS4ZpA6MHcn/r+zmdeJre43tnKB8UO4hBsYM4fPowA74YcFHZ/EHzPdruTTfdxPPPP0+fPn1Ys2YNd91114W+bdLKrutjU/wU+zP+VF0vq8b4e9rxx+lE+r+3hN/2F2z/6Mb4o2bNmrFz504mTpxI794Zv1xMyVQizvhTtbykEl/edwV3fLSMgR/8zEd3tqZNXc/7/zYmr7I7Qw8LDsu2PDws3OMz/Mz069ePRx99lPnz55OQkJDpPHnt+tgUTSXmjD9Vw+rl+Or+9lQtV4rbP1rK7A35G9DAGH9311138cwzz9C0adMs58mq62NTPJW4xA9Qq2JpJt/XnstqlufecXF88eseX4dkjNdERkby0EMPZTtPdl0fm+KnSHfLnF+nziUxbPwKFm4+xOM9GzGs86XWrbMpENYtsylsuemWuUSe8acqUyqI/93Rin4xEbwyaxP/nv4bKSn+/0VojDH5UaIu7mYmJCiAUTfGUqVsCB8v3sGRU+d49YYY69zNGFNslfjED06f/s/0aUx42VK8+v0m/jidyHu3tSAsxHaPMab4sdNal4gwvGt9Xu7flJ+2HOKWD5fyx6nzvg7LGGMKnCX+dG5qU4f3bmvJhv3HueGDn9l39IyvQzLGmAJliT8Tf4muwbi72vD7sbNc/94Stvx+wtchGWNMgbHEn4W29aow6d4rSEpRbvjgZ1bs/sPXIRmTK550y1y1alViY2OJjo5mwIABnD59+sL8I0eO5LLLLqNJkybExMTw6aefFvp7MN5hiT8bjSPK89V97alYOphbP1zKvE0HfR2SMR7zpFvmG2+8kVWrVrF+/XpCQkKYNGkSAO+//z6zZ89m2bJlrFu3joULF1IU7vkxnrHEn4M6VcL48r721KtahiFj45iyMt7XIRnjMU+7ZU5KSuLUqVNUqlQJgBdffJF3332X8uXLA1ChQgXuvPPOwgnaeJ3XEr+IfCwiB0VkXSZlj4qIiki4t7ZfkKqWK8XnQ9vRpm5l/j5pNW/N3WJnPyZ3unTJ+Hj3Xafs9OnMy8eMccoPH85Y5qGbbrqJzz//nLNnz7JmzRratm17UfmkSZOIjY2lVq1aHDlyhL59+3LixAlOnDjBpZdemue3a/ybN8/4xwA9008UkdrA1cBuL267wJULDeaTwa3p37wW/529mUe/XMP5pBRfh2VMtnLqljm1qufAgQM0bdqUV199FVW1rkuKOa/doaSqC0UkKpOi14HHgW+8tW1vKRUUyH8HxhAVXobXZm9m79HTvH9bSyqGhfg6NOPv5s/PuiwsLPvy8PDsy3PgSbfMIkLfvn156623ePLJJylTpgzbt2+nXr16ed6u8V+FWscvIv2Avaq62oN5h4pInIjEHTp0qBCi84yI8GC3BrxxUywrdh2l/7tL2JVwytdhGZMlT7plBli0aNGF6p2nnnqK4cOHc/y4M2DR8ePHGT16tNdjNYWj0PokEJEw4B9AD0/mV9XRwGhweuf0Ymh5cm1sLSIqlmbop3H89Z3FfHhHK1pF2aAuxv9k1y3zpEmTWLRoESkpKURGRjLGva4wbNgwTp48SevWrQkODiY4OJhHHnmkEKM23uTVbpndqp7pqtpERJoCc4HUhsKRwD6gjaoeyG493uqWuSDsPHyKwWN+Ze8fZ3j1hmZcG1sr54VMsWfdMpvC5pfdMqvqWlWtpqpRqhoFxAMtckr6/i4qvAxfD2tPbJ2KPPT5KmvxY4zxe95szjkR+BloJCLxInK3t7bla5XKhDDu7jZcZy1+jDFFQJZ1/CJyPIdlBdivqg0zK1TVzO8U+bM8KsfoipBSQYG8NjCGqCpleH2OtfgxWLNIU2hyW8uQ3Rn/NlUtn82jHGDNWdIQER7q3oBRN1qLn5IuNDSUhIQEq/YzXqeqJCQkEBoa6vEyWV7cFZF6qro924U9mKcg+PPF3aws23GEoePiELAWPyVQYmIi8fHxnD171tehmBIgNDSUyMhIgoODL5qe1cXdbFv1iEgg8L2qdi/wSHOhKCZ+gB2HT3GXtfgxxvhInlr1qGoycFpEKngtsmKsbmqLn9rW4scY4z88uYHrLLBWRGaTpk5fVR/0WlTFSKUyIYy7pw1PfrWW/87ezM6E07zUvykhQdYxqjHGNzxJ/N+5D5NHqS1+LqkSxqg5W4j/4zQf3G4tfowxvpFj4lfVsSJSGqijqpsKIaZiSUR4uHtDLqkSxhOT13Kt281Dw+rlfB2aMaaEybG+QUT6AquAWe7rWBH51stxFVvXNY9kwpC2nDqXzHXvLGbWuiJ947IxpgjypKJ5BNAGOAqgqquAul6LqARoFVWZ6Q90pH61stz32XJem72ZlBS76GuMKRyeJP4kVT2WbpplqXyqUSGUSfdewfUtInlz7haGjlvOibOJvg7LGFMCeJL414nILUCgiDQQkbeAJV6Oq0QIDQ5k5A3NeLZvY+ZtOshf31nM9kMnfR2WMaaY8yTxPwBEA+eACcAxIPPOvU2uiQiDO9Rl3N1tOHLqPNe+s5h5Gw/6OixjTDHmSeK/RlX/oaqt3cc/gX7eDqykaX9pON/+rSO1K4Vx19hfeXf+VrvZyxjjFZ4k/qc8nGbyqXblML4a1p5rmtbklVmb+NuElZw+n+TrsIwxxUx23TL3AnoDtUTkzTRF5QHLRl5SOiSQt25uTpNaFfjPrI1sO3SSD+9oRe3KYb4OzRhTTGR3xr8PiMPpsmF5mse3wF+8H1rJJSLc1/lSPhnUmn1Hz9D37UUs3nrY12EZY4qJHMfcFZEgVfXpGX5R7Z2zIOw4fIqhn8ax/fApnu59OXd1iLLBPYwxHsl175wi8oX7dKWIrEn/8Fqk5iJ1w8swZXgHul1WjX9P38AjX6zmbGKyr8MyxhRh2fXVk9pks09hBGKyVrZUEO/f1pK3ftzK63M2s/XQSd6/rSURFUv7OjRjTBGU5Rm/qu53/+7K7FF4IRqAgABnWMfRt7dk28GT9Ht7Eb/uPOLrsIwxRVB2VT0nROR4mr/H074uzCDNn3pE12Dq8A6UCw3m5tG/8NGiHdbe3xiTK9md8ZdLHVQ9/SDrqlq+MIM0F2tQvRxTh3egSyOn3v/+8Ss4bv38GGM8lN0Zf5yIvCEiPUXE8+HbTaGoUDqYD+9oydO9L+OHDb/T761FrN+Xvi89Y4zJKLt2/O2AKUAXYIGIzBCRh0SkYaFEZnIkIgztdCmThrbjbGIK1727hInLdlvVjzEmW9lV9SSp6nxVfVJV2wJ3AyeAF0RkpYi8W2hRmmy1iqrMdw92pG3dyjz19Voe+WK1dfVgjMmSxyN+q+p+Vf1YVQcCLYHx3gvL5FaVsqUYM7gNf+/ekCmr9nLt24vZ8vsJX4dljPFDOY65KyLTyDjwyjEgzr0r7KxXIjO5Fug2+WwVVYmHPl9Jv7cX81L/pvy1eS1fh2aM8SOenPFvB04CH7qP48DvQEP3daZE5GMROSgi69JMe1VENrp3/04RkYr5it5kqkP9cL578Eqa1qrAw5NW8dTXa+1uX2PMBZ4k/uaqeouqTnMftwFtVHU40CKb5cYAPdNNmw00UdVmwGase2evqV4+lAlD2nJf50uZuGw3/d9dwq6EU74OyxjjBzxJ/FVFpE7qC/d5uPvyfFYLqepC4Ei6aT+k6fDtFyAyd+Ga3AgKDODJXpfx0Z2t2Hv0DH3eXMSsdft9HZYxxsc8SfyPAItEZJ6IzAd+Ah4TkTLA2Hxs+y5gZlaFIjLUvZcg7tChQ/nYjOl2eXWmP9CRelXLcN9nK3h+2gbOJ6X4OixjjI/k2C0zgIiUAi4DBNjo6QVdEYkCpqtqk3TT/wG0AvqrBwGU5G6ZC9L5pBRenPEbY5bspHmdirxzSwvr6M2YYizX3TKnWTAQZ+CVzsBVwP0i8n/5COROnB4/b/Uk6ZuCExIUwIh+0bxzSwu2/H6Sa978iXmbbGB3Y0oaT6p6pgGDgCpAuTSPXBORnsATQD9VPZ2XdZj8u6ZZTb79Wweqlw9l8Ce/8sqsjSQmW9WPMSVFju34gUi3FU6uiMhEnO4ewkUkHngWpxVPKWC2O4rUL6p6X27XbfKvXtWyTB3egRHfrufd+dtYvC2BN2+K5ZIqZXwdmjHGyzwZevE/wFxV/aFwQsrI6vi967s1+3nq6zUkpygj+kUzoGWkDe9oTDGQ5zp+nGaXU0TkjPXHXzxd06wmsx7uRJNaFXhs8hr+NnElx05bN8/GFFeeJP7/AlcAYdYff/EVUbE0E4a047G/NOL7dQfo9cZClm5P8HVYxhgv8CTxbwHWWQuc4i8wQBjetT6Th7UnJCiAmz/8hZHfb7ILv8YUM55c3N0PzBeRmcC51Imq+prXojI+FVu7It89eCUjvl3P2/O2smjrYd6wC7/GFBuenPHvAOYCIeSzOacpOsqUCuLVG2J455YWbD90kt5v/MTk5fE2yIsxxYBHd+76mrXq8a29R8/w90mrWLbjCH2a1eT/XdeUCqWDfR2WMSYHuW7VIyIjPFhpjvOYoq9WxdJMdC/8zlx3gN5v/MSyHUdyXtAY45eyPON3b7rKrh5fgCGqepk3AkvLzvj9x6o9R3no85XsOXKa4V3r82C3BgQHejyQmzGmEOWlHf+HXFynn/5RlmwGYjHFU+qF3/4tInnrx63c8P7P1s+/MUWM1fGbPJu2eh9PT1lLSory3LVNuL5FLbvj1xg/kp87d43JVN+YCGY93InoiAo8+uVq7h+/goST53Je0BjjU5b4Tb7UqliaiUPb8XjPRsz97SA9Xl/IzLU2ypcx/swSv8m3wADh/i71mfZAR2pWDGXY+BU8OHElf5zKcmROY4wP5XjnrohUBYYAUWnnV9W7vBeWKYoa1SjHlPs78P78bbz54xaWbEvgpf5NubpxdV+HZoxJw5Mz/m+ACsAc4Ls0D2MyCA4M4IFuDfhmeEeqlivFkE/j+L9Jq6y3T2P8iCd99YSp6hNej8QUK40jyvPN8A68PW8r78zbyuJth3m5fzO6XlbN16EZU+J5csY/XUR6ez0SU+yEBAXwf1c3ZOr9HahYOoTBY37l8cmrOX7Wzv6N8SVPEv9DOMn/rDsIiw3EYnKlaWQFvn2gA/d3uZTJy+Pp+fpCftpyyNdhGVNi5Zj43YFXAlQ11H1uA7GYXCsVFMjjPS/j6/s7UDokkNs/WsbTU9Zy8lySr0MzpsTxqDmniPQTkZHuo4+3gzLFV2qXD0M71WPist385fWFLNl62NdhGVOi5Jj4ReRlnOqeDe7jIXeaMXkSGhzI070vZ/J9VxASFMAt/1vKM9+s4/R5O/s3pjDk2FePiKwBYlU1xX0dCKxU1WaFEB9gffUUZ2fOJ/Pq95v4ZMkOalcK49UBzWhbr4qvwzKmWMhvXz0V0zyvUCARGQOUDgnkmb6N+XxIOwBuHP0L/5iylmNnrOWPMd7iSeJ/CVgpImNEZCywHHjRu2GZkqZtvSrMevhK7ulYl4nLdnP1awuYuXa/DfVojBd41C2ziNQEWuMMvrJUVQ94O7C0rKqnZFkbf4wnv17D+n3H6X55dZ6/NpqIiqV9HZYxRU5ehl68zP3bAqgJxAN7gAh3mjFe0TSyAt8M78A/el/O4q2Hufq1BYxZvIPkFDv7N6YgZDf04mhVHSoi8zIpVlW9yruh/cnO+EuuPUdO88+p61iw+RAxtSvycv+mXF7TbiMxxhNZnfF70qonVFXP5jQtk+U+BvoAB1W1iTutMjAJp6fPncBAVf0jp+At8Zdsqsq3q/fx/LQNHD2TyJAr6/FQtwaUDgn0dWjG+LX8tOpZ4uG09MYAPdNNexKYq6oNgLnua2OyJSJcG1uLuY90ZkCLSN5fsI2/jLJuH4zJq+zq+GuISEugtIg0F5EW7qMLEJbTilV1IXAk3eRrgbHu87HAX/MStCmZKoaF8J8BzZg4pB1BAcLtHy3j/yatsuEejcml7Or47wQGAa2AtPUsJ4Axqvp1jisXiQKmp6nqOaqqFdOU/6GqlbJYdigwFKBOnTotd+3a5cHbMSXF2cRk3p23lfcWbKNsqSD+eU1j+ttg78ZcJD91/Ner6ld53GgUeUz8aVkdv8nK5t9P8NTXa1m+6w861K/C//trU6LCy/g6LGP8QlaJP8eBWFT1KxG5BogGQtNMfz4PcfwuIjVVdb97b8DBPKzDmAsaVi/Hl/dewYRlu/nPzI38ZdRCHuzWgKGd6hEcaENKG5MZTzppex+4EXgA5wauG4BL8ri9b4E73ed34gzraEy+BAQIt7W7hDmPdOaqy6rx6veb6P3GTyzZZr1+GpMZT06J2qvqHcAfqvoccAVQO6eFRGQi8DPQSETiReRu4GXgahHZAlztvjamQFQvH8p7t7Xkf3e04mxSMrd8uJThE1aw/9gZX4dmjF/xZMzd1Pb6p0UkAkgA6ua0kKrenEVRNw9jMyZPujeuTscG4XywYDvvzt/Kj78d5IFu9bm7Y11KBVnbf2M8OeOfJiIVgVeBFTg3Xk30YkzG5FtocCAPdW/AnP/rzJUNwnll1iZ6jvqJ+ZvsspIx2bbqEZEAoJ2qLnFflwJCVfVYIcUHWKsek3/zNx3kuWkb2HH4FD0aV+dffRpTu3KOt6MYU6Tl6c5dd/CV/6Z5fa6wk74xBaFLo2rMevhKnuh5GYu2Hqb7awsYNWczZxOTfR2aMYXOk6qeH0TkerE7Y0wRVyookGFdLmXuI525unF1Rs3ZQvfXFvDD+gPW778pUTy5gesEUAZIwrnQKzi9cxZaF4lW1WO8Ycm2wzz7zXq2HDxJl0ZVebZvNHXt5i9TjOT5zl1/YInfeEticgpjl+xk1JwtnE9K4Z4r6/K3q+oTFuJJgzdj/Fuee+cUkbmeTDOmKAoODOCeK+vx46Od6RNTk3fnb6Pbfxfw3Rob9tEUX9n1zhnq9p8fLiKVRKSy+4gCIgotQmMKQbVyobw2MJbJ911BpbAQhk9Ywa3/W8pv+4/7OjRjClx2Z/z34gysfpn7N/XxDfCO90MzpvC1iqrMtAc68u9ro1m/7zjXvPkTT0xew8Hj2Y47ZEyR4snF3QdU9a1CiidTVsdvfOHo6fO89eNWPv15J8GBAdzb6VKGdKpr9f+myMjXxV0RaY8zXOKFI15VPy3IALNjid/40s7Dp/jPrI3MXHeA6uVL8WiPRlzfIpKAAGvhbPxbfvrjHwdcCqwCUu92UVV9sKCDzIolfuMPft15hBe++43Ve47SuGZ5/nnN5bSvH+7rsIzJUn4S/29AY/VhEwdL/MZfpKQo09bs45VZm9h79AzdLqvGU70vp361sr4OzZgM8jPY+jqgRsGHZEzRExDw58Dvj/dsxNIdR/jLqIX8a+o6G/vXFBmenPHPA2KBZcCFI1tV+3k1sjTsjN/4q8Mnz/HGnC1MWLabsOBA7u9an8EdoggNtu6fje/lp6qnc2bTVXVBAcWWI0v8xt9tPXiCl2ZsZO7Gg9SqWJrHezaiX0yEDf5ufCrPVT1ugt8JBLvPf8Xpl98Y46pfrRwfDWrN+HvaUr50MA99voq/vruEuJ1HfB2aMRl40mXDEGAy8IE7qRYw1YsxGVNkdagfzvQHOvLKgGbsP3qGAe//zH3jlrP14Elfh2bMBZ5c3B0OdACOA6jqFqCaN4MypigLDBAGtqrN/Me68HD3Bvy05RA9Xl/AY1+uJv6P074OzxiPEv85VT2f+kJEggDrvcqYHISFBPFw94YsfLwrgzvU5ZvV+7hq5AJGfLueQyesBZDxHU8S/wIReRooLSJXA18C07wbljHFR5WypfhXn8bMf7QL/VvUYtwvu+j0yjxe/X4jx84k+jo8UwJ50qonALgb6IEzCMv3wP8K84Yua9VjipPth07y2uzNTF+zn/KhQdzX5VIGtY+yPoBMgctPc84ywFlVTXZfBwKlVLXQKist8ZviaP2+Y4z8fhPzNh2iarlSPHBVfW5qXYeQIE9+iBuTs/zcuTsXKJ3mdWlgTkEFZkxJFR1RgU8Gt+HL+66gbpUyPPPNeq7673y+Wh5PcopdRjPe40niD1XVC23R3Odh3gvJmJKldVRlJt3bjjGDW1OhdDCPfLmanqMWMmudDQJvvMOTxH9KRFqkvhCRlsAZ74VkTMkjInRpVI1pf+vIO7e0IFmV+z5bzl/fWcyiLYftC8AUKE/q+FsDnwP73Ek1gRtVdbmXY7vA6vhNSZOUnMLXK/Yyas5m9h07yxX1qvBIj4a0iqrs69BMEZLfgViCgUY4rXo2qmq+2qCJyN+Be3DuB1gLDFbVLMe2s8RvSqpzSclMWLqbd+Zt5fDJ83SoX4UHr2pA23pVfB2aKQL8ZgQuEakFLMLp4/+MiHwBzFDVMVktY4nflHSnzycx/pfdfLBwO4dPnqNt3co81L0BV9SrYh3BmSxllfhzbDic1QhcQH6GXgzCuSEsEedC8b5s5960Cbp0uXjawIFw//1w+jT07p1xmUGDnMfhwzBgQMbyYcPgxhthzx64/faM5Y88An37Otu+996M5f/8J3TvDqtWwcMPZyx/8UVo3x6WLIGnn85YPmoUxMbCnDnwwgsZyz/4ABo1gmnT4L//zVg+bhzUrg2TJsF772UsnzwZwsNhzBjnkd6MGRAWBu++C198kbF8/nzn78iRMH36xWWlS8PMmc7zf/8b5s69uLxKFfjqK+f5U0/Bzz9fXB4ZCZ995jx/+GFnH6bVsCGMHu08HzoUNm++uDw21tl/ALfdBvHxF5dfcQW89JLz/PrrISHh4vJu3eBf/3Ke9+oFZ9JdsurTBx591Hme/rgDnxx7YcAQ4C5VZl93D88cLsULL0zk1cWfUKtSaSqUDuZC+rdjz3lux17Gcpcnd4y0ogBH4FLVvSIyEtiNc5H4B1X9If18IjIUGArQrFSpgti0MUVeoAg9m9SkS+eu/DD+POcWJLNx/3HKhgYRWTGMCmFpvgCMyYInF3e/BB5U1f0FskGRSsBXwI3AUZwuICar6mdZLWNVPcZk7lxSMl/GxfPe/G3sPXqGmMgKPNitAVddVs2qgEzeq3qAcGCDiBTUCFzdgR2qesgN7GugPZBl4jfGZK5UUCC3tbuEga1q89WKeN6Zt5W7x8YRHVGeB7s1oEfj6vYFYDLwJPGPKOBt7gbaiUgYTlVPN8BO543Jh5CgAG5uU4cBLSOZsnIv78zbyr3jlnN5zfI8eFV9/hJdg4AA+wIwDk9b9VQHWrsvl6nqwXxtVOQ5nKqeJGAlcI+qZtlPrVX1GJM7SckpfLNqH2/P28qOw6doVL0cD3SrT68mNQm0L4ASIz+dtA0EXgXm47TjvxJ4TFUneyHOTFniNyZvklOU6Wv28ebcLWw7dIr61cpyb6d6XBtbyzqDKwHyk/hXA1ennuWLSFVgjqrGeCXSTFjiNyZ/klOUGWv38868rWw8cIKaFUK5u2NdbmpTh7KlrDvo4io/iX+tqjZN8zoAWJ12mrdZ4jemYKgq8zcf4oMF2/hl+xHKhwZx+xWXMKh9XaqWs2bTxU1+WvXMEpHvgYnu6xuBmQUZnDGmcIgIXRtVo2ujaqzc/QejF27n3fnb+PCnHQxoGcnQK+sRFV7G12EaL/P04m5/oCNOHf9CVZ3i7cDSsjN+Y7xn+6GTfPjTdr5avpfElBR6NanBfZ0vpVlkRV+HZvIp11U9IlIfqK6qi9NN7wTsVdVtXok0E5b4jfG+g8fP8smSnXz2yy5OnE2i/aVVuLfzpXRqEG73AhRReRmBaxRwIpPpp90yY0wxUq18KE/0vIwlT17F070vY9uhk9z58TKueXMR36zaS1Jyiq9DNAUkuzP+daraJIuytXZx15ji7VxSMt+s2scHC7ax7dApIiuVZsiV9RjYqjalQwJ9HZ7xQF6qeraqav3clnmDJX5jfCclRZnz2++8v2AbK3YfpVJYMHdcEcWt7epQrVyor8Mz2chL4p8I/KiqH6abfjfQQ1Vv9EqkmbDEb4x/+HXnEd6fv425Gw8SEhhAn5ia3NWhLk1qVfB1aCYTeUn81YEpwHkgdZjFVkAIcJ2qHvBSrBlY4jfGv2w/dJKxS3by5fJ4Tp9Ppk1UZe7qGMXVjWtYlxB+JD83cHUFUuv616vqj16IL1uW+I3xT8fOJPJl3B7GLNlJ/B9nqFWxNIPaRzGwdW0qlA72dXglXr6GXvQ1S/zG+LfkFGX2ht/5ZPEOlu44QlhIIANaRjKofRT1qpb1dXglliV+Y0yhWL/vGJ8s3sm3q/ZxPjmFro2qMrhDXa60+wEKnSV+Y0yhOnTiHBOW7mbcL7s4fPIcDaqVZVCHKPo3j7TmoIXEEr8xxifOJSXz3Zr9fLx4B+v2HqdiWDA3ta7DHVdcQkTF0r4Or1izxG+M8SlVJW7XH3y8aAffrz+AiHD15dW5rd0ltL+0io0Q5gX56Z3TGGPyTURoHVWZ1lGVif/jNON+3sUXcXuYtf4AdcPLcGvbOlzfIpJKZUJ8HWqxZ2f8xhifOZuYzKx1B/jsl13E7fqDkKAA+jSryW3tLqF57Yp2MTifrKrHGOPXftt/nPFLdzFlxV5OnU+mcc3y3NquDn+NrUUZGyUsTyzxG2OKhJPnkpi6ci+f/bKLjQdOULZUENc1r8Vt7S6hUY1yvg6vSLHEb4wpUlSVFbuPMv6XXUxfu5/zSSm0jqrEbe0uoWeTGpQKsiahObHEb4wpso6cOs/k5XsYv3Q3uxJOU7lMCDe0iuTWNpdQp0qYr8PzW5b4jTFFXkqKsmjrYcYv3cWc3w6SosqVDapyU+vadLu8mv0KSMcSvzGmWNl/7AyfL9vDF3F72H/sLJXCgrmueSQDW0dyWY3yvg7PL1jiN8YUS8kpyk9bDvFlXDw/bDhAYrISE1mBG1rVpl9sBOVDS24voZb4jTHF3pFT55m6ci9fxO1h44EThAYH0LtJTW5oVZt29SqXuPsCLPEbY0oMVWVN/DG+iNvDt6v2ceJcEpdUCeOGlpEMaFmbGhVKxpCRfpX4RaQi8D+cAV4UuEtVf85qfkv8xpi8OnM+mVnr9zPp1z38sv0IAQKdGlblxla16XZ5dUKCAnwdotf4W+IfC/ykqv8TkRAgTFWPZjW/JX5jTEHYlXCKL+Pimbw8ngPHz1K5TAjXNa/FwFa1i+XNYX6T+EWkPLAaqKcebtwSvzGmICWnKAu3HOLLuD3M3vA7iclKs8gKXNe8Fn1jIggvW8rXIRYIf0r8scBoYAMQgzOQ+0OqeirdfEOBoQB16tRpuWvXrkKN0xhTMiScPMfUVfv4ekU86/cdJzBA6NQgnOtaRNKjcXVCg4vuvQH+lPhbAb8AHVR1qYi8ARxX1X9ltYyd8RtjCsPm30/w9Yq9fLNqL/uPnaVsqSB6NanBdS1q0a5u0RszwJ8Sfw3gF1WNcl9fCTypqtdktYwlfmNMYUpJUX7ZkcCUFXuZue4AJ88lUbNCKNfG1qJ/i1o0rF40rgf4TeJ3g/kJuEdVN4nICKCMqj6W1fyW+I0xvnLmfDKzf/udqSv3smDzIZJTlMY1y9O/RS36xUZQrZz/Ng31t8Qfi9OcMwTYDgxW1T+ymt8SvzHGHxw+eY5pq/cxZeVe1sQfI0CgY4Oq9G9eix7R1QkL8a9xA/wq8eeWJX5jjL/ZevAkU1fuZcrKvew9eoawkEB6Rtegb2wEHeuHExzo+/sDLPEbY4wXpKQov+48wpSVe/lu7X5OnE2iYlgwvZrUoG+zCNrWq0Kgjy4KW+I3xhgvO5eUzMLNh5m+Zh+zN/zO6fPJhJctRe+mNegbE0HLOpUKtWWQJX5jjClEZ84nM2/TQaav2cfc3w5yLimFmhVCuaZpTfrERBATWcHrncZZ4jfGGB85eS6Jub/9zrTV+1iw+RCJyUrtyqXp0yyCPs1q0rhmea98CVjiN8YYP3DsTCI/rD/AtDX7Wbz1MMkpSr2qZejTLIK+zWrSoADvEbDEb4wxfubIqfPMXLef6av388uOBFThshrluKZpTXo1rUH9avn7ErDEb4wxfuzg8bPMWLufaWv2s3yXc1vTpVXL0KtJTXo2qUF0RO6rgyzxG2NMEXHg2Fl+2HCAmWsPsHRHAikKkZVK0zO6Br2a1qB5bc9aB1niN8aYIujIqfPM3nCAWesOsGjrYRKTlWrlSvGX6Br0bFKDtnUrE5TFzWKW+I0xpog7fjaReRsPMnPtAeZvPsjZxBQqhgVz9eXV6dW0Bh3qh1Mq6M9upC3xG2NMMXLmfDILNh9k1roDzP3tICfOJVG2VBBdL6tGryY16NywKmVDgzNN/P7Vo1AWNiVsosuYLhdNGxg9kPtb38/pxNP0Ht87wzKDYgcxKHYQh08fZsAXAzKUD2s1jBub3MieY3u4fcrtGcofueIR+jbqy6bDm7h3+r0Zyv/Z6Z90r9edVQdW8fCshzOUv9jtRdrXbs+SPUt4eu7TGcpH9RxFbI1Y5myfwwsLX8hQ/kGfD2gU3ohpm6bx35//m6F83HXjqF2hNpPWTeK9uPcylE8eOJnwsHDGrBrDmFVjMpTPuHUGYcFhvPvru3yx/osM5fMHzQdg5JKRTN88/aKy0sGlmXnrTAD+veDfzN0x96LyKmFV+GrgVwA8Necpfo6/eDjlyPKRfNb/MwAenvUwqw6suqi8YZWGjO47GoCh04ayOWHzReWxNWIZ1XMUALd9fRvxx+MvKr8i8gpe6v4SANd/cT0JpxMuKu9Wtxv/6uwM/9BrfC/OJJ65qLxPwz482v5RgAzHHdixZ8feKMAPjr0Jfx57laMg8EwitUJ6snhrO6au/o2EUi9nWD6V73sRMsYYky8iUDEsmBta1WbZ090YfXsrqpXLevhIq+oxxphiKqs6fjvjN8aYEsYSvzHGlDCW+I0xpoSxxG+MMSWMJX5jjClhLPEbY0wJY4nfGGNKGEv8xhhTwhSJG7hE5ASwyddx+LFw4LCvg/Bjtn+yZ/sne0V5/1yiqlXTTywSffUAmzK7+8w4RCTO9k/WbP9kz/ZP9orj/rGqHmOMKWEs8RtjTAlTVBL/aF8H4Ods/2TP9k/2bP9kr9jtnyJxcdcYY0zBKSpn/MYYYwqIJX5jjClh/Drxi0hPEdkkIltF5Elfx+NPRKS2iMwTkd9EZL2IPOTrmPyRiASKyEoRmZ7z3CWLiFQUkckistE9jq7wdUz+RET+7n621onIRBEJ9XVMBcVvE7+IBALvAL2AxsDNItLYt1H5lSTgEVW9HGgHDLf9k6mHgN98HYSfegOYpaqXATHYfrpARGoBDwKtVLUJEAjc5NuoCo7fJn6gDbBVVber6nngc+BaH8fkN1R1v6qucJ+fwPnQ1vJtVP5FRCKBa4D/+ToWfyMi5YFOwEcAqnpeVY/6NCj/EwSUFpEgIAzY5+N4Cow/J/5awJ40r+OxxJYpEYkCmgNLfRyKvxkFPA6k+DgOf1QPOAR84laF/U9Eyvg6KH+hqnuBkcBuYD9wTFV/8G1UBcefE79kMs3anqYjImWBr4CHVfW4r+PxFyLSBzioqst9HYufCgJaAO+panPgFGDX0VwiUgmnhqEuEAGUEZHbfBtVwfHnxB8P1E7zOpJi9FOrIIhIME7SH6+qX/s6Hj/TAegnIjtxqgmvEpHPfBuSX4kH4lU19VfiZJwvAuPoDuxQ1UOqmgh8DbT3cUwFxp8T/69AAxGpKyIhOBdWvvVxTH5DRASnfvY3VX3N1/H4G1V9SlUjVTUK59j5UVWLzRlbfqnqAWCPiDRyJ3UDNvgwJH+zG2gnImHuZ60bxejit9/2zqmqSSLyN+B7nCvqH6vqeh+H5U86ALcDa0VklTvtaVWd4buQTBHzADDePbHaDgz2cTx+Q1WXishkYAVOC7qVFKOuG6zLBmOMKWH8uarHGGOMF1jiN8aYEsYSvzHGlDCW+I0xpoSxxG+MMSWMJX5jjClhLPGbYktEqojIKvdxQET2us9Pisi7XtjeGBHZISL3pXk9IB/rGy8iR/KzDmMy47c3cBmTX6qaAMQCiMgI4KSqjvTyZh9T1cmeziwigaqanFmZqt4qImMKLDJjXHbGb0ocEemSOjCLiIwQkbEi8oOI7BSR/iLyioisFZFZbn9IiEhLEVkgIstF5HsRqenh5jqJyBIR2Z565u5uf56ITMC587qMiHwnIqvdQT9u9M47N8Zhid8YuBSn3/5rgc+AearaFDgDXOMm/7eAAaraEvgY+H8errsm0BHoA7ycZnob4B+q2hjoCexT1Rh30I9ZBfCejMmSVfUYAzNVNVFE1uL0C5WaeNcCUUAjoAkw2+mvi0CcPto9MVVVU4ANIlI9zfRlqrojzXZGish/gOmq+lO+3o0xObDEbwycA1DVFBFJ1D87sErB+YwIsF5V8zIm7bk0z9OOMXEq9YmqbhaRlkBv4CUR+UFVn8/DtozxiFX1GJOzTUDV1MHIRSRYRKILauUiEgGcVtXPcEZ9sn7xjVfZGb8xOVDV8+6F2TdFpALO52YUUFDdhDcFXhWRFCARGFZA6zUmU9YtszEFxG16OT03zTl9sU5jrKrHmIJzDPh36g1c+SUi44HOwNmCWJ8xqeyM3xhjShg74zfGmBLGEr8xxpQwlviNMaaEscRvjDElzP8HfYSB4U/ozd8AAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"def plotConcentration(soln):\n",
" fig, ax = plt.subplots(1, 1)\n",
" ax.plot(soln.t, soln.y[0])\n",
" ax.set_xlim(0, max(soln.t))\n",
" ax.plot(ax.get_xlim(), [MIC, MIC], 'g--', ax.get_xlim(), [MBC, MBC], 'r--')\n",
" ax.legend(['Antibiotic Concentration','MIC','MBC'])\n",
" ax.set_xlabel('Time [hrs]')\n",
" ax.set_ylabel('Concentration [mg/liter]')\n",
" ax.set_title('One Compartment Model with Known Initial Condition');\n",
" \n",
"plotConcentration(soln)\n",
"\n",
"# save solution to a file for reuse in documents and reports\n",
"plt.savefig('./figures/Pharmaockinetics1.png')"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.1.6 Step 5. Analysis of the Results](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.1.6-Step-5.-Analysis-of-the-Results)",
"section": "2.1.3.1.6 Step 5. Analysis of the Results"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
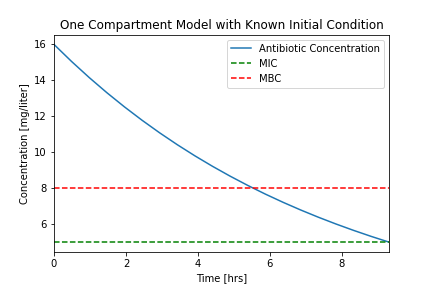
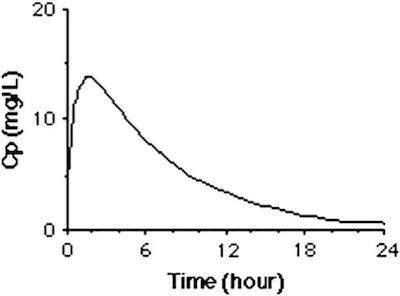
"#### 2.1.3.1.6 Step 5. Analysis of the Results\n",
"\n",
"Let's compare our results to a typical experimental result. \n",
"\n",
"| | |\n",
"| :-: | :-: |\n",
"|||\n",
"\n",
"We see that that the assumption of a fixed initial condition is questionable. Can we fix this?\n",
"\n",
"[Levison, Matthew E., and Julie H. Levison. “Pharmacokinetics and Pharmacodynamics of Antibacterial Agents.” Infectious disease clinics of North America 23.4 (2009): 791–vii. PMC. Web. 8 May 2017.](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3675903/)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2-Example-2:-Improving-Simulation-using-Time-Dependent-Input)",
"section": "2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"### 2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input\n",
"\n",
"For the next simulation we will assume the dosing takes place over a short period of time $\\delta t$. To obtain a total dose $U_{dose}$ in a time period $\\delta t$, the mass flow rate rate must be\n",
"\n",
"$$u(t) = \n",
"\\begin{cases}\n",
"U/ \\delta t \\qquad \\mbox{for } 0 \\leq t \\leq \\delta t \\\\\n",
"0 \\qquad \\mbox{for } t \\geq \\delta t\n",
"\\end{cases}\n",
"$$\n",
"\n",
"Before doing a simulation, we will write a Python function for $u(t)$. "
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2-Example-2:-Improving-Simulation-using-Time-Dependent-Input)",
"section": "2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"# parameter values\n",
"dt = 1.5 # length hours\n",
"Udose = 64 # mg\n",
"\n",
"# function defintion\n",
"def u(t):\n",
" if t <= 0:\n",
" return 0\n",
" elif t <= dt:\n",
" return Udose/dt\n",
" else:\n",
" return 0"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2-Example-2:-Improving-Simulation-using-Time-Dependent-Input)",
"section": "2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"This code cell demonstrates the use of a list comprehension to apply a function to each value in a list."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2-Example-2:-Improving-Simulation-using-Time-Dependent-Input)",
"section": "2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input"
}
},
"outputs": [
{
"data": {
"text/plain": [
"Text(0.5, 1.0, 'Dosing function u(t) for of total dose 64 mg')"
]
},
"execution_count": 7,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEWCAYAAABrDZDcAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAih0lEQVR4nO3debgcVbnv8e/PMCkkQphMgBAZnEDGiCI8iiAKioI4ABe9gCiOCOqVQc454AioIMgRPaBolEmuoiAiiggiDkgCyCAiCGGQJAxhCMiYvOePtZp0Nru7a+9d1d27+vd5nv307u6qVW91dddba62qVYoIzMxscD2v1wGYmVlvORGYmQ04JwIzswHnRGBmNuCcCMzMBpwTgZnZgHMi6EOSHpW0XgXlStL3JD0o6S9ll99h2b+UtE83l9m07LMk7dbm/eMlfbhDGe+QdFfeNpuXHuTSy+rZdsrLny4pJC1TcPrvS/pi1XFZdZwIRknSHEmPS1oo6SFJf5T0YUlj/kwjYqWIuK2MOIfYFtgRWDsitqqgfAAkHSXp9ObXImLniJhZ1TLbxLIJsClwXn6+r6Qrhkz2VeAIScu1KeprwMfztrmmmmif1XY7tViHlkY6/XggaXVJZ+bf3oOSzhhmmsmS7qvbulfBiWBs3hYRE4F1gWOAQ4Hv9jakttYF5kTEY70OpIs+BJwRba6cjIi5wN+Bt7cpZ13gxtEEIGnCCGcZxO00UucC80if1RqkRD3UscBN3Qxq3IoI/43iD5gDvHHIa1sBi4GN8/MXAj8A7gPuAP4DeF5+bwPgd8DDwP3Aj5rKCWCD/P/3gW8CvwAWAlcC6zdN+ybg5lzOybnMDwwT7/7AE8Ai4FHgc8C+wBVDphvJsjcCLgYWAPOBzwI7AU8BT+fl/DVPe1kjLtIByH/kz+Te/Bm9ML83PcewD3Bn/myOaLMdni03P19qnYDbgG3z/y8f8hk81DTdEcD3hil/+TxtAI8B/2wq6zLgIVKCeHvTPN8HvgVcmOd54zDlTgXOz5/drcAHW22nIfMNuw60+K61mf6twDXAI8BdwFFNy2hsg2VafOabA1fn78SPgLOBLza9/8G8TgvyOk7Nrwv4et7mDwPXseS3sjxpZ34n6bv0beD5LZb/JtLvb0Kb78XWwJ+A/RjyHR8y3XbA3cAhOa65wG7AW4B/5HX4bNP0zwdmAg+SkswhwN293h+N9a/nAYzXP4ZJBPn1O4GP5P9/QGqSmJh/XP8A9s/vnUXa+TwPWIG8s8rvDd0ZLyAlmWWAM4Cz83ur5R/y7vm9g0g74Ockgjz9viy9k1zq+QiXPTH/aD6d458IvDq/dxRw+pByL2NJInh/3lGsB6xEOrr7YX5veo7h1Pyj2xR4Enh5i3V6ttyh6wSsmMtavd0659d3B65us72bP5dlc/yfBZYDtiftFF/a9Lk9DGzT2L7DlPc7UuJeAdiMtAPfoV2MHbZbu+/acNNvB7wyx7cJaee725Bt8JxEkNf3DuCT+XN4F+k798X8/vak5L0Faed+EnB5fu/NwGxgZVJSeDkwJb93AilpTM7r8HPg6Bbr/1/Ar4DTgQeAq4DXN70/gZSotizwWW4HPJPLXJaUxO4DzsxxbERKpOvl6Y/J224VYG1SMhv3icBNQ+W7B5icmwP2AA6PiIURMQc4Dnhfnu5pUrV2akQ8ERHt2jHPjYi/RMQzpJ3xZvn1twA3RsS5+b1vkKrLZWq17F2AeRFxXI5/YURcWbDMvYHjI+K2iHgUOBzYc0jn5Oci4vGI+CvwV1JCGKmV8+PCAtMubJq+k9eQEtgxEfFURPwWuADYq2ma8yLiDxGxOCKeaJ5Z0jqkfoBD82d3LfAdlnw3RqTAd+05IuKyiLg+x3cd6cDk9QUW9xrSDvOEiHg6In5M2hE37A2cFhFXR8STpG27taTppO/8ROBlgCLipoiYK0mkHfAnI2JBRCwEvgzs2SKGtUm1gkuBF+V1PU/Savn9TwBXRsTsAutDjutLEfE0qXazGnBi/ixvJNX4NsnTvgf4ckQ8GBF3k35z454TQfnWIh1Fr8aSo6eGO/L7kKqUAv4i6UZJ729TZvPO/d+knRCk5oW7Gm9EOmS5e0zRF1/2OsA/R1nmVJ77uSwDrFlguSPxUH6cWGDaiU3TdzIVuCsiFje91rxtoWm7tJi/scNrNf9IdPquPYekV0u6NHemPgx8OJfTyVTgX/m71rys5veffZ4T/QPAWjlh/jepuXG+pFMkTQJWB14AzM6dvw8BF+XXh/M4qQ/luzkZnU36vLeRNJWUCI4osC4ND0TEoqayIdWQmpc37G+O9tt53HAiKJGkV5F+fFeQqseNo/6GacC/ACJiXkR8MCKmkjo0T5a0wQgXOZd0dNRYvpqfF/AY6QfYmP9FI5j3LmD9Fu91GtL2Hp77uTzD0j++opZaB9IRYgoidbb+E3hJgdheTqp5FHEPsM6QM8Se3bYdltOYf7Kk5gQ1dP52hpbd9rvWIpYzSU0x60TEC0lt8iqw7LnAWvm71ryshqW2raQVgVVZ8r3/RkRsSWpyeQnwmRz/48BGEbFy/nthRLRK/te1WCdIzZhTgL9JmgecCGwlad4oOu2Hs9RvjnRANO45EZRA0iRJu5CqlafnKvci4BzgS5ImSloX+BSpXRNJ75bU+EI9SPpiLxqm+HZ+AbxS0m65WeVjNO0IC/grsJGkzSStQGrbL+oC4EWSDpa0fF7HV+f35gPT25xKexbwSUkvlrQSqRngR7n5aaSuBXaX9IKcSPcf8v6FLN3kMR9Ye5hTRV8P/LLgMq8kJaBDJC0raTvgbaTt31FE3AX8ETha0gr5FNf9SU1vRSy1Dp2+a0OnzyaSaiVPSNoK+D8Fl/0nUtL+hKRlJO1O2vk2nAnsl79Ty5O27ZURMUfSq3JNZFnS5/cEsCjXrE4Fvi5pDQBJa0l6c4sYfgqsImkfSRMkvYt0APYH0jacTmrC3IzU9n8NsFnTUf9YnAMcLmkVSWsBHy+hzJ5zIhibn0taSDo6PgI4nnSWQsOBpC/8baRawpnAafm9VwFXSnqUdGR2UETcPpKFR8T9wLuBr5Cq368AZpE6V4vM/w/g88BvgFtyjEWXvZB0rvvbSM04twBvyG////z4gKSrh5n9NOCHwOXA7aQdwoFFlz3E10lnKc0nnc0xdGd6CrB30xHsb0ltvvMk3Q8gaQrps/tZkQVGxFOkU013Jh3Nngz834j4+wji3ou0w7qHtGM7MiIuLjjvc9aB9t+14ab/KPD5/P39L9IOrqO87ruTOmEfJPVNnNv0/iXAfwI/IR09r8+Stv5JpB3+g6TmowdYctrnoaQO+D9LeoT0nXxpixgWkD7//0fqlD8M2DUi7o+IJ3Nte15EzMvvP53/L8PnSc2vt+cYf0zB31s/09JNfTae5SPwu4G9I+LSXsfTLySdCZwTET9r8f5xpNNCT+5qYDbuSfoIsGdEFOlo71tOBONcrj5fSWpj/QypeWi9iHi87YxmNmK59rgeqYlsQ1Lz7H9HxAm9jGusCo0lYn1ta1IzwHLA30jngjsJmFVjOeB/gBeTzjI7m9Q0OK65RmBmNuDcWWxmNuDGRdPQaqutFtOnT+91GGZm48rs2bPvj4hWF+Y9a1wkgunTpzNr1qxeh2FmNq5IuqPzVG4aMjMbeE4EZmYDzonAzGzAORGYmQ04JwIzswHnRGBmNuCcCMzMBty4uI5gtJ54ehHf+8McHn9qNMPcP9dr1luV125Q5CZOZmbjR60TwVVzFnDsRWmIeBW591IbEXDpzffx8wO3LSEyM7P+UetEsGhxGlDv3I++li2mrTKmsj4wcxb3PORBPc2sfmrdR1D2uKoep9XM6qjWicDMzDobiEQwxu6BVEYZhZiZ9aF6J4KS23J8Ex8zq6N6JwIzM+uo1okgcpVAJbTruGXIzOqq1onAzMw6qzwRSJog6RpJF+TnkyVdLOmW/Di2E/yLxFBGGa4SmFlNdaNGcBBwU9Pzw4BLImJD4JL8vBJl9+26r9jM6qjSRCBpbeCtwHeaXt4VmJn/nwnsVmUMZmbWXtU1ghOAQ4DFTa+tGRFzAfLjGlUtvHEEX0azjtxdbGY1VVkikLQLcG9EzB7l/AdImiVp1n333VdydKMTHmTCzGqoyhrBNsDbJc0Bzga2l3Q6MF/SFID8eO9wM0fEKRExIyJmrL766mMKpIyjeXcWm1ldVZYIIuLwiFg7IqYDewK/jYj3AucD++TJ9gHOqyyGsstzhcDMaqgX1xEcA+wo6RZgx/zczMx6pCv3I4iIy4DL8v8PADt0Y7kNpXQWu2nIzGqq1lcWlz1InFuGzKyOap0IyuTTR82srmqdCMrvLHadwMzqp9aJwMzMOhuIRFBKR69bhsyspmqdCEofdK7c4szM+kKtE0FDKVcWlxCHmVk/qnkicJXAzKyTmicCMzPrZCASQTlXFrtxyMzqqdaJwJ3FZmad1ToRNJRzYxozs3qqdSLwlcVmZp21HH1U0u4F5n8iIi4sMR4zM+uydsNQn0q6aUy7VpHXAX2fCHyHMjOz1tolgl9GxPvbzZxvPdm33FlsZtZZyz6CiHivpOdJem27aaoJq1zuLDYza61tZ3FELAaO61IspQsfw5uZdVTkrKFfS3qnfEWVb15vZrVU5J7FnwJWBJ6R9ASplSQiYlKlkZWolFGonQfNrKY6JoKImNiNQKpQfmexqwRmVj9FagRIWgtYt3n6iLi8qqD6kesDZlZXHROBpGOBPYC/AYvyywH0fSJoHL+7VcfMrLUiNYLdgJdGxJMVx9L33FlsZnVU5Kyh24Blqw6kWr6QwMyslXZjDZ1Eal35N3CtpEuAZ2sFEfGJ6sMbm7IHiXONwMzqqF3T0Kz8OBs4vwux9LUyxisyM+tH7RLBNsAvgd9ExMIuxVMJdxabmbXWro/gNGBT4EJJl0g6VNKmXYrLzMy6pGWNICL+DPwZOErSqsCbgE9L2gS4GrgoIs7pTphjU86VxSUUYmbWhwpdUBYRDwBn5T8kbQnsVGFcpSj9ymL3FptZDRW5oOxTw7z8MPCL8sPpX64QmFldFbmOYAbwYWCt/HcAsB1wqqRDqgutPB4wzsystSJNQ6sCW0TEowCSjgR+TLpN5WzgK9WFNzZlDxLnhiEzq6MiNYJpwFNNz58G1o2Ix2m6wKyfubPYzKy1IjWCM4E/SzovP38bcJakFUkD0fWt8juLyy3PzKwfFLkfwRckXQhsSzq4/nBENK463rvK4MzMrHqFTh8lDTz3dGN6SVtExNWVRVWycm5e77YhM6unIqePfgHYF/gnS/pLA9i+w3wrkO5ZsHxezo8j4khJk4EfAdOBOcB7IuLB0YXfnu9QZmbWWZEawXuA9SPiqY5TLu1JYPuIeFTSssAVkn4J7A5cEhHHSDoMOAw4dIRlj0gZR/PuLDazuipy1tANwMojLTiSR/PTZfNfALsCM/PrM0k3vqmEj9/NzDorUiM4GrhG0g0sfT+Ct3eaUdIE0rUGGwDfjIgrJa0ZEXNzGXMlrdFi3gNIF68xbdq0AmFWz2cNmVkdFUkEM4FjgeuBxSMpPCIWAZtJWhn4qaSNRzDvKcApADNmzBjTLriUzmI3DZlZTRVJBPdHxDfGspCIeEjSZaSB6uZLmpJrA1OAe8dSdoflllteqaWZmfWHIn0EsyUdLWlrSVs0/jrNJGn1XBNA0vOBNwJ/J93tbJ882T7AecMW0HdcJTCzeipSI9g8P76m6bWOp48CU4CZuZ/gecA5EXGBpD8B50jaH7gTePcIYy7MR/BmZp0VubL4DaMpOCKuY0kSaX79AWCH0ZTZa+4sNrM6atk0JGmXTjMXmaYfuLPYzKy1djWCr0r6F+0bx78MXFBuSCUq/QjeVQIzq592iWA+cHyH+W8pMZbKlHFjGlcIzKyu2t28frsuxlEJjw1kZtZZkdNHLXNnsZnV0UAkAt+hzMystVongvKHoTYzq5+OiUDSCyT9p6RT8/MNx8tpow2+MY2ZWWtFagTfI406unV+fjfwxcoiMjOzriqSCNaPiK+QblVJRDzOODmbsuymnLIHsTMz6wdFEsFTedC4AJC0Pk33JRgPfIcyM7PWigw6dxRwEbCOpDOAbYD9qgyqLO4sNjPrrMigc7+WNJs0+qiAgyLi/soj6zOuEJhZXRU5a+iSiHggIn4RERdExP2SLulGcGVxs46ZWWstawSSVgBeAKwmaRWWHBRPAqZ2IbYxK3uICfcVm1kdtWsa+hBwMGmnP5slieAR4JvVhlWucq4sdrXCzOqp3aBzJwInSjowIk7qYkyl8RG8mVlnRTqLT5K0MfAKYIWm139QZWD9yNcRmFkddUwEko4EtiMlgguBnYErgPGTCNyqY2bWUpELyt5FusfwvIjYD9gUWL7SqEpS+pXFJZdnZtYPiiSCxyNiMfCMpEnAvcB61YZVLl9ZbGbWWpEri2dJWhk4lXT20KPAX6oMqjRu0zcz66hIZ/FH87/flnQRMCkirqs2rP4j5LYhM6ultk1DkiZIWq3ppXuA10i6qdqwyuVmHTOz1lomAkl7AguA6yT9TtIbgNtIZw3t3aX4xsSdxWZmnbVrGvoPYMuIuFXSFsCfgD0j4qfdCa08vmexmVlr7ZqGnoqIWwEi4mrg9vGWBNxXbGbWWbsawRqSPtX0fKXm5xFxfHVh9R/hK4vNrJ7aJYJTgYltno8bHjDOzKy1doPOfa6bgVSh7CN41wfMrI6KXFk87rmz2MystVonAh/Bm5l1VutEUCZJPgvJzGqpyDDUywPvBKY3Tx8Rn68urHK5WcfMrLUig86dBzxMGnDuyWrDKVfZR/Bl3wPZzKwfFEkEa0fETpVHUqFShqEuIQ4zs35UpI/gj5JeWXkkFfDxu5lZZ0USwbbAbEk3S7pO0vWSOg5DLWkdSZdKuknSjZIOyq9PlnSxpFvy4ypjXYmukIesMLN6KtI0tPMoy34G+HREXC1pIimZXAzsC1wSEcdIOgw4DDh0lMsoxu06ZmYtdawRRMQdwMrA2/Lfyvm1TvPNzYPVERELgZuAtYBdgZl5spnAbqMJvAiPDWRm1lnHRJCbdM4A1sh/p0s6cCQLkTQd2By4ElgzIuZCSha5zOHmOUDSLEmz7rvvvpEsbpiyxjR7KgO5z8HMaqlI09D+wKsj4jEASceS7k1wUpEFSFoJ+AlwcEQ8UnQAuIg4BTgFYMaMGd4Hm5lVpEhnsYBFTc8XUbDVXdKypCRwRkScm1+eL2lKfn8KcG/xcHvM6cjMaqhIjeB7wJWSGjel2Q34bqeZlA79vwvcNOTeBecD+wDH5MfzRhLwaHjQOTOz1jomgog4XtJlpNNIBewXEdcUKHsb4H3A9ZKuza99lpQAzpG0P3An8O5RxF2I+4rNzDprmQgkTcpt+pOBOfmv8d7kiFjQruCIuILWB+M7jDzU0SvjxjTCQ0yYWT21qxGcCexCGmOoeQ+o/Hy9CuMyM7MuaXeHsl3y44u7F065yj6Cd1OTmdVRkesILinyWj9zZ7GZWWvt+ghWAF4ArJbHA2rsCicBU7sQ25j5CN7MrLN2fQQfAg4m7fRnsyQRPAJ8s9qw+o+vLDazumrXR3AicKKkAyOi0FXE/crNOmZmrRW5juAkSRsDrwBWaHr9B1UGVoayj+A9iJ2Z1VGRexYfCWxHSgQXkoalvgLo+0TQUModylyrMLOaKjLW0LtIF4DNi4j9gE2B5SuNqiQ+gDcz66xIIng8IhYDz0iaRBokbuAuJmtcRWdmVjdFBp2bJWll4FTS2UOPAn+pMqiyuVnHzKy1tokgjyB6dEQ8BHxb0kXApIjoeM/ifuCxgczMOmvbNBTpNJmfNT2fM16SQOkk9zmYWS0V6SP4s6RXVR5JBbzjNjPrrEgfwRuAD0m6A3iM3G8aEZtUGlmfcTeDmdVVkUSwc+VRVMydxWZmrRVpGvpiRNzR/Ad8serAzMysO4okgo2an0iaAGxZTTjVKPPKYg8zYWZ10zIRSDpc0kJgE0mP5L+FpAvKKr/hfBm80zYz66xlIoiIoyNiIvDViJiU/yZGxKoRcXgXY+wLjVqFc4uZ1U2RpqELJK0IIOm9ko6XtG7FcZXKncVmZq0VSQTfAv4taVPgEOAOxsnIoz56NzPrrEgieCZfYbwrcGK+Yc3EasMqV5n3LHZuMbO6KXIdwUJJhwPvBV6XzxpattqwzMysW4rUCPYAngT2j4h5wFrAVyuNqiRlHr03ahU+E8nM6qbIrSrnAcc3Pb+TcdJH0CD3FpuZtdQyEUi6IiK2zdcONB8GN8YamlR5dGPkg3czs85aJoKI2DY/jquO4eG4s9jMrLUincWNYSXWbJ4+NxGZmdk41zERSDoQOBKYDyzOLwfQ98NQl3mHskY/g5ubzKxuitQIDgJeGhEPVB1MVdxXbGbWWpHTR+8CHq46kCr46N3MrLMiNYLbgMsk/YJ0PQEAEXF861n6S5mnj5bZ3GRm1g+KJII7899y+c/MzGqkyAVln+tGIFUo9cpi9zOYWU21u6DshIg4WNLPGWafGhFvrzSyPuV+BzOrm3Y1gh/mx691I5BKeK9tZtZRuyuLZ+fH342mYEmnAbsA90bExvm1ycCPgOnAHOA9EfHgaMovHkdJ5ZRyfbKZWf/pePqopF0kXSNpQeO+xZIeKVD294Gdhrx2GHBJRGwIXJKfm5lZDxW5juAEYB9g1ab7FncccC4iLgcWDHl5V2Bm/n8msFvxUEfOncVmZp0VvaDshihnIP41I2IuQH5co4Qy2yp7/+1uBzOrmyLXERwCXCjpd3TxgjJJBwAHAEybNm1UZXinbWbWWZEawZeAfwMrkO5V3PgbjfmSpgDkx3tbTRgRp0TEjIiYsfrqq49yceV59g5lvrLYzGqmSI1gckS8qaTlnU/qbzgmP55XUrkt+e5kZmbtFakR/EbSiBOBpLOAPwEvlXS3pP1JCWBHSbcAO+bnlSl3GOrSijIz6ytFagQfAw6R9CTwNAVvVRkRe7V4a4eRhTg27iw2M2uvyFhD4/ZWld5pm5l11m6soS3azRgRV5cfTv9qXFns3GJmddOuRnBcflwBmAH8ldTSsglwJbBttaGVw237Zmbttewsjog3RMQbgDuALfKpnFsCmwO3divAsfDRu5lZZ0XOGnpZRFzfeBIRNwCbVRZRycoaLK5RsyjnAmszs/5R5KyhmyR9BziddJD9XuCmSqMyM7OuKZII9gM+AhyUn18OnFxZRCWq4uDd9QEzq5uOTUMR8UREfD0i3hER7wCuAsbNjet9GwEzs/aK1AiQtBmwF7AHcDtwboUxlcbjApmZddbuOoKXAHuSEsADpDuLKZ9JNG6UVSFojFnkvmIzq5t2NYK/A78H3hYRtwJI+mRXojIzs65p10fwTmAecKmkUyXtwHhrcS/x6H18rbiZWXHtLij7aUTsAbwMuAz4JLCmpG+NZjTSXin9ymI3DZlZzRQ5a+ixiDgjInYB1gauZZzcdN77bDOzzopcWfysiFgQEf8TEdtXFVDZSr+y2OnFzGpmRInAzMzqp9aJoMxxgdxZbGZ1VetEAOV3Fvs6AjOrm1onAu+0zcw6q3UigAquLC6pPDOzflH7RGBmZu3VOhGUefTuW16aWV3VOhHAkiadsvgOZWZWN7VOBN5nm5l1VutEACV2FudH5xYzq5vaJwIzM2uv1omg1HGB3FtsZjVV60QAlD42hPsdzKxuap0IvNM2M+us1okAqugsdnYxs3qpfSIwM7P2nAgKcl+xmdVV7RNB2VcWu2XIzOqm9onAzMzaq3UiKPcOZW4bMrN6qnUigAruUFZucWZmPVfrROBhqM3MOqt1IoDybzrvi9TMrG56kggk7STpZkm3SjqsFzGYmVnS9UQgaQLwTWBn4BXAXpJeUcWyyjx6d8uQmdXVMj1Y5lbArRFxG4Cks4Fdgb9VsbCyryPY69Q/s8zznBbMrDu+vPsredX0yZUuoxeJYC3grqbndwOvHjqRpAOAAwCmTZs2qgVtvNYknnxm0ajmHWqbDVZjt82m8tSixaWUZ2ZWxPOXnVD5MtTte/BKejfw5oj4QH7+PmCriDiw1TwzZsyIWbNmdStEM7NakDQ7ImZ0mq4XncV3A+s0PV8buKcHcZiZGb1JBFcBG0p6saTlgD2B83sQh5mZ0YM+goh4RtLHgV8BE4DTIuLGbsdhZmZJLzqLiYgLgQt7sWwzM1ta7a8sNjOz9pwIzMwGnBOBmdmAcyIwMxtwXb+gbDQk3QfcMcrZVwPuLzGc8WaQ19/rPrgGef2b133diFi90wzjIhGMhaRZRa6sq6tBXn+v+2CuOwz2+o9m3d00ZGY24JwIzMwG3CAkglN6HUCPDfL6e90H1yCv/4jXvfZ9BGZm1t4g1AjMzKwNJwIzswFX60QgaSdJN0u6VdJhvY6nmyTNkXS9pGsl1f6uPpJOk3SvpBuaXpss6WJJt+THVXoZY1VarPtRkv6Vt/+1kt7SyxirImkdSZdKuknSjZIOyq8PyrZvtf4j2v617SOQNAH4B7Aj6WY4VwF7RUQl90buN5LmADMiYiAuqpH0OuBR4AcRsXF+7SvAgog4Jh8IrBIRh/Yyziq0WPejgEcj4mu9jK1qkqYAUyLiakkTgdnAbsC+DMa2b7X+72EE27/ONYKtgFsj4raIeAo4G9i1xzFZRSLicmDBkJd3BWbm/2eSfiC102LdB0JEzI2Iq/P/C4GbSPdFH5Rt32r9R6TOiWAt4K6m53czig9oHAvg15JmSzqg18H0yJoRMRfSDwZYo8fxdNvHJV2Xm45q2TTSTNJ0YHPgSgZw2w9ZfxjB9q9zItAwr9WzHWx420TEFsDOwMdy84ENjm8B6wObAXOB43oaTcUkrQT8BDg4Ih7pdTzdNsz6j2j71zkR3A2s0/R8beCeHsXSdRFxT368F/gpqals0MzPbaiNttR7exxP10TE/IhYFBGLgVOp8faXtCxpJ3hGRJybXx6YbT/c+o90+9c5EVwFbCjpxZKWA/YEzu9xTF0hacXccYSkFYE3ATe0n6uWzgf2yf/vA5zXw1i6qrETzN5BTbe/JAHfBW6KiOOb3hqIbd9q/Ue6/Wt71hBAPmXqBGACcFpEfKm3EXWHpPVItQBI96U+s+7rLuksYDvSELzzgSOBnwHnANOAO4F3R0TtOlVbrPt2pGaBAOYAH2q0mdeJpG2B3wPXA4vzy58ltZMPwrZvtf57MYLtX+tEYGZmndW5acjMzApwIjAzG3BOBGZmA86JwMxswDkRmJkNOCcCM7MB50RgtSVp1aZheOc1Dcv7qKSTK1je9yXdLunDTc/fNYbyzpC0YCxlmBWxTK8DMKtKRDxAuqimm8MyfyYiflx0YkkTImLRcO9FxN6Svl9aZGYtuEZgA0fSdpIuyP8fJWmmpF/nm/nsLukr+aY+F+VxXJC0paTf5dFcfzXkEv52Xifpj5JuaxzZ5+VfKulM4Po8JMgvJP1V0g2S9qhmzc2G50RglkZpfCtpDPvTgUsj4pXA48BbczI4CXhXRGwJnAYUHbJjCrAtsAtwTNPrWwFHRMQrgJ2AeyJi03xjmYtKWCezwtw0ZAa/jIinJV1PGpeqsSO+HpgOvBTYGLg4jfHFBNLQvkX8LI8A+TdJaza9/peIuL1pOV+TdCxwQUT8fkxrYzZCTgRm8CRARCyW9HQsGYBrMek3IuDGiNh6tGVnzffIeKzxT0T8Q9KWwFuAoyX9OiI+P4plmY2Km4bMOrsZWF3S1pDGf5e0UVmFS5oK/DsiTge+BmxRVtlmRbhGYNZBRDyVO3q/IemFpN/NCcCNJS3ilcBXJS0GngY+UlK5ZoV4GGqzkuRTPS8YyemjvSjTbCg3DZmV52HgC40LysZK0hnA64EnyijPrBXXCMzMBpxrBGZmA86JwMxswDkRmJkNOCcCM7MB97/tZAlA6dzmcQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# visualization\n",
"t = np.linspace(0, 24, 1000) # create a list of time steps\n",
"y = np.array([u(tau) for tau in t]) # list comprehension\n",
"\n",
"fig, ax = plt.subplots(1, 1)\n",
"ax.plot(t, y)\n",
"ax.set_xlabel('Time [hrs]')\n",
"ax.set_ylabel('Administration Rate [mg/hr]')\n",
"ax.set_title('Dosing function u(t) for of total dose {0} mg'.format(Udose))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2-Example-2:-Improving-Simulation-using-Time-Dependent-Input)",
"section": "2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"Simulation"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2-Example-2:-Improving-Simulation-using-Time-Dependent-Input)",
"section": "2.1.3.2 Example 2: Improving Simulation using Time-Dependent Input"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEWCAYAAABhffzLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAABGc0lEQVR4nO3dd3hUZfbA8e9JJ5AESEINvbcQIIKCCthFsBfsHbvr/tZddV0VXVddRWXti2XBhigqimJBpIjYQpEmRQEhQAg1CYSElPP7497EkDKZhEwmyZzP88yTmVvP3Nw588573/u+oqoYY4wJHEH+DsAYY0ztssRvjDEBxhK/McYEGEv8xhgTYCzxG2NMgLHEb4wxAcYSv2nQRGSEiKR6uex4EXnzCPd3qYh8WRPxNHQi8pKI3Odh/t9F5BUvtzVZRB6uueiqT0Q2ichJ7nOP76Gy88VX6n3iF5GrRGSFiGSLSJqIvCgiTX24v8EiMktE9onIHhH5UUSu9tX+aoqIdBQRFZEQP+2/0g+mG9+OkjGKSIiIpItIvbjhRFXfUtVTil6776lrdbcnIvNE5LoSr0eIyF4RGXuksfpC6Xg9UdUbVfWf7nplvhBV9RFV9WpbXsTVWkReFZHtIpIlImtE5EERaVwT269IyfdQ3mew9PlSW+p14heRvwD/Bv4KxABHAx2A2SIS5oP9HQN8DcwHugKxwE3A6TW9r5rkr2RfTfs4/HiOAvb6J5S6RUROAWYA16jqO34Op94QkebAd0Aj4BhVjQJOBpoCXfwYmv+oar18ANHAfuDCUtObAOk4Hw6A8cC7wOtAFrAKSC6xfBvgfWAnsBG43cM+FwLPVxLX9cCvwB7gY6BNiXkK3Aysd2P5J86J9x2Q6cYZ5i47AkgF/g7sAjYBl5bY1hnAUne9LcD4EvM6uvu6FtgMLHD/qnvM9gPHAFcB3wJP4yTcDcBQd/oW9zheWWK74cAEd1s7gJeARqXi/Yu73nbganfeOCAPOOTue2YFx06BfwDvlZg2HbjXOVUP+5997B7jX4HrS8xrBEzG+bJYjVMoSPXm/+2eK29WENt84Dz3+bFurKPc1ycBy9znVwEL3ecL3OUOuO/7Ik/HqYL9zgOuA0a7/6NR5RyzG3HOqb3A84C484Lc4/m7u6/XgRh33hTgL+7ztu52bnZfd3WPrVQ33srOCXf+ZOBhoDFwECjkj/OzTen/B/AekAZkuMe2T+ltVRDTw8AKIMhD3EOBn9xt/wQMLfWe/onzWckCvgTiSsy/3D3Gu3HO1U3ASaXPKSr+DC6siTiq8qjPJf6hQATwQcmJqrof+AznG73ImcA7ON/wHwPPAYhIEDAT+Bnn5D8RuENETi29MxGJxPlHTa8oIBE5AXgUuBBojXMylC6ZnQYMwvl18jdgEnAp0A7oC1xcYtlWQJwb25XAJBHp4c47AFzhvqczgJtE5OxS+xoO9AJOBY53pzVV1Saq+p37egiwHOfXy9tuvEfhfPgvA54TkSbusv8GugNJ7vy2wP2l4o1xp18LPC8izVR1EvAW8Li77zHlHT/XDOB4EWnqVtkdB3xUapmpOAmlDXA+8IiInOjOewDny7SL+76vLFqpKv/vcszHSWTgHMsNOMe36PX80iuoatEx7+++72nu63KPk4d9jwHeBM5X1VnlzB+N8z/rj3PuFb2fq9zHSKAzTqHouXLez/By3s836mabasRbUqXrquoBnF9529zj1ERVt5Wzrc+AbkALYAnOOeWNk4APVLWwvJnuL4JPgWdwPgdPAZ+KSGyJxS4Brnb3HQbc6a7bG3gRJ/m3cddPqCCOij6DRxxHVdXnxB8H7FLV/HLmbXfnF1moqrNUtQB4A+cDAs6HJV5VH1LVQ6q6AXgZKK/+tBnO8druIaZLgddUdYmq5gL3AMeISMcSy/xbVTNVdRWwEvhSVTeoagbOiT2g1DbvU9VcVZ2Pc1JcCKCq81R1haoWqupynGQ4vNS641X1gKoe9BDzRlX9n3tspuF8AT3k7vNLnFJ6VxERnF8zf1bVPaqaBTxS6ljluevmuQlqP9CDqsnBSc4Xudv+2J0GgIi0wylx36WqOaq6DHgF54MHzvH5lxvjFpwPUZGq/L9Lm8/hifHREq+HU07i96Cqx2kksA6npFeex1R1n6puBubifDGDcz4+5Z5f+3HOx7Fu1d984Dj3y/B44HFgWAXv50j+rzVxTgCgqq+papb72RoP9BeRGC9WjcXz5/YMYL2qvqGq+ao6FViD84Vb5H+qus79LL3LH8f4fOATVV3gxnUfzi+X6jiSOKqkPif+XUBcBfXXrd35RdJKPM8GItz1OgBt3Au1+0RkH07VSstytrkX5x/a2kNMbXBK+UDxr4/dOKWdIjtKPD9YzusmJV7vdUtDRX5394GIDBGRuSKyU0QycH7ul/yyA6e6pjKl94+qlhdTPBAJLC5xrD53pxfZXeqLOLvU+/HW6zi/Zq5wn5fUBij64inyO38c4zYc/r5/L/G8Kv/v0r4DuotIS5wP2+tAOxGJAwbjVD14q6rH6T4gF5ghIuHlzC99fhdt67Dz0X0eArRU1d9wknASzq+qT4Bt7i/K0on/SP6vNXJOiEiwiDwmIr+JSCZOdQqUPefLjYEqfG5dJc8p8HyMi8839/O624uYajqOKqnPif87nA/DuSUnulfpTwfmeLGNLTgl3qYlHlGqOqr0gqqa7e7zPA/b24aTXErGEgts9SKW8jQr1eqgvbsPcKplPgbaqWoMTn27lA67gufVsQvnS6BPiWMVo6rennhV2f83OB/UljjXVUraBjQXkagS09rzxzHejvOrpeS8Il7/v8sE7/z/FwN/Alaq6iFgEfB/wG+qusvT+kfoAM5F7hhguoiEerneYecjzrHI548v+/k4JdYwVd3qvr4C59ftsiMPu0oqOz8uAc7CqbaJwbmOBWXP+fJ8BZzj/ropT+njBIefU54cdr65VcKxFSxb2Xs8kjiqpN4mfrdq5EHgWRE5TURC3SqV93Dqf9/wYjM/ApkicpeINHJLFX1F5KgKlv8bcJWI/LWo3k1E+otIUT3+28DVIpLklsweAX5Q1U3VfqPwoIiEichxOHW577nTo3BKvjkiMhjng+HJTpxfLJ2rE4RbP/oy8LSItAAQkbZe1o+Dk2y82rdbtzwGOLNEPXPRvC04CfdREYkQkUScuuOi+t53gXtEpJmIJAC3lVi9qv/v0uYDt/JHaXheqdfl8fp9e+L+wjkNp1T4togEe7HaVODPItLJvU7zCDCtRAm86P0U/VqZh3O8FrpVf7VpBxDroeomCqegtxvnl+cjVdj2UziNQaaISAcoPnefcs+fWTi/5i4Rp/nwRUBvnF9BlZkOjBaRY92WhA9RcV6t7DN4JHFUSb1N/ACq+jjOT/UJOK1bfsAp1Z3o1rdVtn4BToJJwmnhsQunvrjck09VFwEnuI8NIrIH5+LsLHf+HJyf5e/jlAS64F39cUXScKqYtuEkthtVdY0772bgIRHJwrnA+q6nDbkl1n8B37rVHEdXI567cFrRfO/+3P4K7+trXwV6u/ueUdnCqrrKvQ5SnotxSnzbgA+BB1R1tjvvQZyfxxtxWj0UFwCq+v8ux3ycBLSggtflGY+TcPaJyIVe7qdcqroPp9FCd+B1DyXYIq/hvP8FOO83h8O/CEvHvxAnqVal2qpGuOf1VJzP1T4RaVNqkddx/q9bcVprfV+Fbe/BaQySB/zgfmbm4LSc+VVVd+MUqv6C88XyN2C0N7/i3HP0FpxC33acz2u5N+hV9hk8kjiqSkoVqEwdISIjcJqBVdRCwBhjqqVel/iNMcZUnSV+Y4wJMFbVY4wxAcZK/MYYE2DqReddcXFx2rFjR3+HYYwx9crixYt3qWp86en1IvF37NiRlJQUf4dhjDH1ioiUvhMYsKoeY4wJOJb4jTEmwFjiN8aYAFMv6viNqW/y8vJITU0lJyen8oWNOUIREREkJCQQGupd/32W+I3xgdTUVKKioujYsSPOUAbG+Iaqsnv3blJTU+nUqZNX61hVjzE+kJOTQ2xsrCV943MiQmxsbJV+XVriN8ZHLOmb2lLVcy3gEn/2oXze+uF3cvJqu7txY4ypGwIu8c9ds5N7P1zJfTNWYv0UmYbuww8/RERYs2ZN5QsDEydOJDs7u/j1qFGj2LdvH5s2baJv377lrnPdddexevVqj9t95JHDx00ZOnSoV/EUef311+nbty99+vShd+/eTJgwoUrr17Rly5Yxa1Z54957tmnTJt5+++3i1ykpKdx+++01GZpXAi7xb89wxh1/b3Eqb3xf7k1txjQYU6dO5dhjj+Wdd96pfGHKJv5Zs2bRtGlTj+u88sor9O7d2+MypRP/okWLvIoH4LPPPmPixIl8+eWXrFq1iiVLlhAT4+3YOb7hKfHn5+eXOx3KJv7k5GSeeeaZGo+vMj5L/CLymoiki8jKcubdKSLqDlRdq7Zn5NAoNJgTerbgoZmr+WFDdcdFNqZu279/P99++y2vvvrqYYl/3rx5jBgxgvPPP5+ePXty6aWXoqo888wzbNu2jZEjRzJy5EjA6S5l1y5nAKj8/HyuvPJKEhMTOf/884u/IEaMGFHcpcrUqVPp168fffv25a677gLg7rvv5uDBgyQlJXHppZcC0KTJH0M1P/744/Tr14/+/ftz9913l3kfjz76KBMmTKBNG2dQroiICK6//nrAScBHH300iYmJnHPOOezdu7c4prvuuovBgwfTvXt3vvnmGwAKCgq488476devH4mJiTz77LMALF68mOHDhzNo0CBOPfVUtm/fXuF2Dh06xP3338+0adNISkpi2rRpjB8/nnHjxnHKKadwxRVXsGnTJo477jgGDhzIwIEDi7/o7r77br755huSkpJ4+umnmTdvHqNHjwZgz549nH322SQmJnL00UezfPlyAMaPH88111zDiBEj6Ny5c418UfiyOedk4DmcIdOKiUg7nOHjNvtw3xVKy8ihddMInr4oibOf/5Zb3l7Cx7ceS5umjfwRjgkAD85cxeptmTW6zd5tonlgTB+Py8yYMYPTTjuN7t2707x5c5YsWcLAgQMBWLp0KatWraJNmzYMGzaMb7/9lttvv52nnnqKuXPnEhdXtky2du1aXn31VYYNG8Y111zDCy+8wJ133lk8f9u2bdx1110sXryYZs2accoppzBjxgwee+wxnnvuOZYtW1Zmm5999hkzZszghx9+IDIykj179pRZZuXKlQwaNKjc93jFFVfw7LPPMnz4cO6//34efPBBJk6cCDhfVD/++COzZs3iwQcf5KuvvmLSpEls3LiRpUuXEhISwp49e8jLy+O2227jo48+Ij4+nmnTpnHvvffy2muvVbidhx56iJSUFJ577jnASc6LFy9m4cKFNGrUiOzsbGbPnk1ERATr16/n4osvJiUlhccee4wJEybwySfOMLrz5s0rfi8PPPAAAwYMYMaMGXz99ddcccUVxcdszZo1zJ07l6ysLHr06MFNN93kdZv98visxK+qC4Cy/0V4GmcsSb9UsG/POEjrmAhiGoUy6fJBHDxUwE1vLraLvabBmTp1KmPHOkM+jx07lqlTpxbPGzx4MAkJCQQFBZGUlMSmTZsq3V67du0YNmwYAJdddhkLFy48bP5PP/3EiBEjiI+PJyQkhEsvvZQFCzwP3/vVV19x9dVXExkZCUDz5s29fn8ZGRns27eP4cOHA3DllVcetr9zzz0XgEGDBhW/v6+++oobb7yRkJCQ4v2tXbuWlStXcvLJJ5OUlMTDDz9Mamqqx+2U58wzz6RRI6cAmZeXx/XXX0+/fv244IILKr0GArBw4UIuv/xyAE444QR2795NRkYGAGeccQbh4eHExcXRokULduzY4c0hqlCt3sAlImcCW1X158qaH4nIOGAcQPv27Wsshu0ZOQzt4pRmurWM4qmLkrjhjcX8Y8ZKnjg/0ZrgmRpXWcncF3bv3s3XX3/NypUrEREKCgoQER5//HEAwsPDi5cNDg72WC9dpPRno/Tr6jSWUNVKP3N9+vRh8eLFnHDCCVXadtF7LPn+ytufqtKnTx++++47r7dTnsaNGxc/f/rpp2nZsiU///wzhYWFREREVBpvecevKNbq/L88qbWLuyISCdwL3O/N8qo6SVWTVTU5Pr5Md9LVkl9QSHpWLq1j/vgnnNqnFbef0JXpi1N5/Tu72GsahunTp3PFFVfw+++/s2nTJrZs2UKnTp3KlNJLi4qKIisrq9x5mzdvLk6ORReNSxoyZAjz589n165dFBQUMHXq1OLSeGhoKHl5eWW2ecopp/Daa68VXy8or6rnnnvu4W9/+xtpaWkA5Obm8swzzxATE0OzZs2K6+/feOON4v1V5JRTTuGll14qTpx79uyhR48e7Ny5s/i95eXlsWrVKo/b8XScwPk10rp1a4KCgnjjjTcoKCiodL3jjz+et956C3CqgOLi4oiOjvYYR3XVZqueLkAn4GcR2QQkAEtEpFVtBbBr/yEKCpVWMYd/+95xUndO7NmCf35iF3tNwzB16lTOOeecw6add955h7UoKc+4ceM4/fTTiy/ultSrVy+mTJlCYmIie/bs4aabbjpsfuvWrXn00UcZOXIk/fv3Z+DAgZx11lnF201MTCy+uFvktNNO48wzzyQ5OZmkpKRym2mOGjWKW265hZNOOok+ffowaNCg4sQ9ZcoU/vrXv5KYmMiyZcu4/37P5crrrruO9u3bk5iYSP/+/Xn77bcJCwtj+vTp3HXXXfTv35+kpKRKWx2NHDmS1atXF1/cLe3mm29mypQpHH300axbt67410BiYiIhISH079+fp59++rB1xo8fT0pKComJidx9991MmTLFYwxHwqdj7opIR+ATVS3TANhN/smququy7SQnJ2tNDMSydPNeznlhEa9emcyJvVoeNi8zJ4+zn/uWzJw8Zv95OM0ahx3x/kzg+uWXX+jVq5e/wzABpLxzTkQWq2py6WV92ZxzKvAd0ENEUkXkWl/ty1tpGU5fFq1jyrbgiY4I5flLB7I3O4/Hv1hb26EZY0yt8dnFXVW9uJL5HX2174psL0785V9o6dU6mquHduTVbzdyQXICA9s3q83wjDGmVgTUnbtpmTmEhwTRNLLi9q93nNydFlHh3DdjJQWF1qWDMabhCajEvz0jh9YxER6bjzUJD+G+0b1ZtS2TN61LB2NMAxRQiT8t42CZFj3lOaNfa47rFseEL9aSnmUjKBljGpaASvxOib/yrhlEhAfP7ENufiGPfPpLLURmjDG1J2ASf2GhsiMzx6sSP0Dn+CbcMLwzM5ZtY9FvlbY4NabOEZHiLgDA6XMmPj6+uFOwyZMnc+uttxbPr2tdHxvfCZjEv/vAIfIKtMIWPeW5ZWRX2jVvxP0freJQfqEPozOm5jVu3JiVK1dy8KDTFfns2bNp27ZtucvWxa6Pje8ETOIv6oe/VbT3iT8iNJjxY/rwa/p+Xl240VehGeMzp59+Op9++ing3M178cXlt7L21PWxaXhqtZM2f9ru4eYtT07s1ZJTerfkmTnrGdO/NQnNIn0RnmngRkweUWbahX0u5OajbiY7L5tRb40qM/+qpKu4KukqdmXv4vx3zz9s3ryr5nm137Fjx/LQQw8xevRoli9fzjXXXFPct01Jnro+Ng1PwJT4i+/abep9ib/I/WN6oygPzqy8a1Vj6pLExEQ2bdrE1KlTGTWq7JeLCUwBVeIPCw6ieWTV++BJaBbJHSd157HP1vDZiu2c3q+1DyI0DZmnEnpkaKTH+XGRcV6X8Mtz5plncueddzJv3jx27y6/E8Lqdn1s6qcAKvEfpGVMOEFB1etv/7pjO9GnTTT3fbSKfdmHajg6Y3znmmuu4f7776dfv34VLlNR18emYQqYxL89I4fW0dUfXjEkOIh/n5fI3uxD/Mva9pt6JCEhgT/96U8el/HU9bFpeHzaLXNNqYlumYc/MZf+CU155uIBR7Sdf3++hhfn/cYb1w7muG41M0CMaXisW2ZT2+pEt8x1iaoW99NzpP50Yjc6xzXmng9WkH3ISkTGmPonIBL/3uw8DuUXen3XricRocE8dl4iqXsPMuGLdTUQnTHG1K6ASPxFN2/VRIkfYHCn5lx2dHv+t2gjSzbvrZFtGmNMbQmIxF/Uhr9VFW/e8uSu03rSKjqCu6YvJze/oMa2a4wxvhYQib+ykbeqIyoilH+d05f16ft5Ye5vNbZdY4zxtQBJ/AcJCRLimoTX6HZP6NmSs5La8MK8X1mbllWj2zbGGF/x5WDrr4lIuoisLDHtCRFZIyLLReRDEWnqq/2XtD0jh5bREQRX8+YtT+4f3ZuoiFD+Ov1n8gqsB09Td3jTLXN8fDxJSUn06dOH888/n+zs7OLlJ0yYQM+ePenbty/9+/fn9ddfr/X3YHzDlyX+ycBppabNBvqqaiKwDrjHh/svlpbhfT/8VRXbJJyHz+7L8tQMq/IxdYo33TJfdNFFLFu2jFWrVhEWFsa0adMAeOmll5g9ezY//vgjK1euZMGCBdSHe36Md3yW+FV1AbCn1LQvVbWo8fv3QIKv9l+SLxM/wKh+rTk7qQ3Pfr2e5an7fLYfY6rK226Z8/PzOXDgAM2aNQPgkUce4YUXXiA6OhqAmJgYrrzyytoJ2vicP+v4rwE+q2imiIwTkRQRSdm5c2e1d1J881YV+uGvjgfP7Etck3D+792fycmzVj6mlBEjyj5eeMGZl51d/vzJk535u3aVneelsWPH8s4775CTk8Py5csZMmTIYfOnTZtGUlISbdu2Zc+ePYwZM4asrCyysrLo0qVLtd+uqdv8kvhF5F4gH3iromVUdZKqJqtqcnx89btGyDyYz8G8Ap+W+AFiIkN54oJEfk3fzxNfrPXpvozxVmXdMhdV9aSlpdGvXz+eeOIJVBWRmr8eZuqOWu+WWUSuBEYDJ2otVBpuzyy6eavm2vBX5Lhu8VxxTAdeXbiRE3u1YGiXOJ/v09QT8+ZVPC8y0vP8uDjP8yvhTbfMIsKYMWN49tlnufvuu2ncuDEbNmygc+fO1d6vqbtqtcQvIqcBdwFnqmp2ZcvXhO3FN2/5tsRf5O7Te9IprjF/fW85WTl5tbJPYzzxpltmgIULFxZX79xzzz3ccsstZGZmApCZmcmkSZN8HqupHb5szjkV+A7oISKpInIt8BwQBcwWkWUi8pKv9l8kzQc3b3kSGRbCkxf2Z3vGQR6yEbtMHeCpW+aiOv7ExESWLl3KfffdB8BNN93EyJEjOeqoo+jbty/Dhw8nMtKGHW0oGny3zE/NXsdzX69n3cOnExJcez9wJnyxlufm/sqkywdxSp9WtbZfUzdYt8ymtlm3zCWkZRykRVRErSZ9gNtP7Ebv1tHc88EKdu3PrdV9G2OMJw0+8W/3cRv+ioSFBPH0RUlk5eRz1/TldvOLMabOqDDxi0hmJY8sEanzHdLX1AAs1dGjVRT3jOrJnDXpTF60yS8xGP+xL3tTW6p6rnkq8f+mqtEeHlHAgSOKthb4+q7dylw1tCMn9WrBo7PWsHJrht/iMLUrIiKC3bt3W/I3Pqeq7N69m4gI7/Ocp3b853mxvjfL+E1WTh77c/P9VuIHp3304+f35/T/LOD2qUuZeduxNA6v9dsnTC1LSEggNTWVI7nr3BhvRUREkJDgfQ84FWYgVd0gIsHAF6p6UkXLVD3E2uOLAViqo3njMCZeNIBLXvme+z9axZMX9vdrPMb3QkND6dSpk7/DMKZcHi/uqmoBkC0iMbUUT43yxQAs1XVMl1huG9mV95ekMmPpVn+HY4wJYN7UOeQAK0RkNiXq9FX1dp9FVUOKS/w+7qDNW7ef2I3vNuzm3g9XkNSuKR3jGvs7JGNMAPKmOeenwH3AAmBxiUedtz0jBxFoWUcSf0hwEBPHDiAkOIjb31nKoXwbuMUYU/sqTfyqOgV4F/heVacUPXwf2pFLyzxIXJNwwkLqzu0KbZs24t/nJbI8NYMnvljj73CMMQGo0owoImOAZcDn7uskEfnYx3HVCH+24ffktL6tuOzo9rz8zUa+XrPD3+EYYwKMN0Xh8cBgYB+Aqi4D6kVzhbSMnDpTv1/aP87oTa/W0dzxzjK27KmVjkqNMQbwLvHnq2rpO4/qxV0pdbXEDxARGsxLlw1EgRvfXGyjdhljao03iX+liFwCBItINxF5Fljk47iOWPahfDIO5vm9Db8nHWIbM/GiJFZty+T+j1b6OxxjTIDwJvHfBvQBcoG3gQyg/M6965C61IbfkxN7teTWkV15NyWVd37c7O9wjDEBwJvEf4aq3quqR7mPfwBn+jqwI5VWyyNvHYk/n9yd47rFcf/Hq1iRav35GGN8y5vEf4+X0+qU+lLiBwgOEv4zdgBxjcO48c3F7Ms+5O+QjDENmKdumU936/PbisgzJR6Tgfxai7Ca0jKcQdbrys1blWneOIwXLhvEzqxc7pi2jMLCenH93BhTD3kq8W8DUnC6bCh5x+7HwKmVbVhEXhORdBFZWWJacxGZLSLr3b/Njiz8im3PyKF54zAiQoN9tYsal9SuKfeP6c28tTt55uv1/g7HGNNAVZj4VfVn9w7dLiXv2FXVD1R1rxfbngycVmra3cAcVe0GzHFf+0RaHW7K6cmlQ9pz7sC2/GfOer5abTd3GWNqnqeqnnfdp0tFZHnpR2UbVtUFwJ5Sk88Cirp7mAKcXY2YvVKX2/B7IiI8ck4/+raJ4U/vLGVtWpa/QzLGNDCeqnqKmmyOBsaU86iOlqq6HcD926KiBUVknIikiEhKdQazSMv078hbRyIiNJiXr0imcXgI173+E3sO2MVeY0zN8VTVU5Sgfy/v4evAVHWSqiaranJ8fHyV1s3JK2DPgUO0rsM3b1WmVUwEk65IZkdmLje9udh68jTG1BhPVT1ZJQZVLz3IemY197dDRFq7228NpFdzO553kuk05awvLXoqktSuKY+fl8gPG/cwfuYqG7/VGFMjPA29GOWD/X0MXAk85v79yAf7qHMDsByJswe0Ze2OLF6c9xs9W0VxxTEd/R2SMaae81TiTxGR/4jIaSJS5QwqIlOB74AeIpIqItfiJPyTRWQ9cLL7usalZRbdtRvui83Xur+e0oOTerXgwZmr+fbXXf4OxxhTz3m6uHs08CEwApgvIrNE5E8i0t2bDavqxaraWlVDVTVBVV9V1d2qeqKqdnP/lm71UyMaSlVPkaAgYeLYAXSNb8LNby1h464Dla9kjDEV8HRxN19V56nq3ao6BLgWyAIeFpGlIvJCrUVZRTsyc4kMC6ZJuDdDCtcPTcJDeOXKZIIErp3yExnZef4OyRhTT3k9JqGqblfV11T1QmAQ8JbvwjoyaZnOACwi4u9QalS75pG8dNkgUvcc5Po3UsjNtz78jTFV583QizNF5OOSD5ybr5KrU/dfG3Zk5DSYap7ShnSO5YkLEvlx4x7ufG+59eljjKkyb0r8G4D9wMvuIxPYAXR3X9c5O7JyaBndMC7sluespLbcdVpPZv68jce/WOvvcIwx9Yw3leADVPX4Eq9nisgCVT1eRFb5KrDqUlV2ZObSsp7eteutG4d3Zuu+bF6a/xttmzXi8qM7+DskY0w94U2JP15E2he9cJ/HuS/rXF8Ce7PzOJRf2CDa8HsiIowf04cTe7bggY9WWoduxhiveZP4/wIsFJG5IjIP+Ab4q4g05o8O1+qMhtaU05OQ4CCevWQAfdvGcNvUpfy8ZZ+/QzLG1AOVJn5VnQV0A+5wHz1U9VNVPaCqE30aXTWkBVDiB4gMC+HVK48iLiqMa6f8xObd2f4OyRhTx3nTqicYZ+CV4cAJwM0i8n++Dqy6dtSjsXZrSnxUOJOvHkx+oXLl/35k1/5cf4dkjKnDvKnqmQlcBcQCUSUeddKOTCfpxTdpuK16ytMlvgmvXpnM9oyDXPHqj2Tm2A1expjyedOqJ0FVE30eSQ1Jy8whrkkYYSFe35vWYAzq0Jz/Xp7MdVN+4trJP/H6NUNoFFZ/hp40xtQOb7LjZyJyis8jqSE7MhvuzVveGN49nqcvSiLl973c9Jb142+MKcubxP898KGIHKyB/vh9LtATP8DoxDY8ck4/5q3dyf+9u4wCu7vXGFOCN1U9TwLHACu0HowEsiMzh8SEpv4Ow+8uHtyezIN5PPrZGqIbhfKvs/s2uL6LjDHV403iXw+srA9J/1B+Ibv2H2rQ3TVUxQ3Du7DvYB4vzvuNmEah3HVaT3+HZIypA7xJ/NuBeSLyGVDcTlBVn/JZVNW0023G2NDv2q2Kv53agww3+UdHhHLTiC7+DskY42feJP6N7iPMfdRZRUMuNvR+eqpCRPjnWX3Zn5PPvz9fQ0iQcP3xnf0dljHGjypN/Kr6YG0EUhOKu2uIssRfUnCQ8NSF/SkoVP416xdE4LrjLPkbE6g8jbk7vrKVvVmmNu3IDLy7dr0VEhzExLFJjOrXioc//YXXFm70d0jGGD/xVOK/rpJmmwKMBcZXdaci8mfgOkCBFcDVqppT1e2UlpaZQ1hwEM0iQ490Uw1SaHAQ/xk7gMLCpTz0yWqCg4Qrh3b0d1jGmFrmqR3/yxzeRUPpRxOqMRCLiLQFbgeSVbUvEIzzBXLEdmTk0CI63JotehAaHMQzFw/glN4teeDjVbz+3SZ/h2SMqWUVlvh9XLcfAjQSkTwgEtjmcem1a2HEiMOnXXgh3HwzZGfDqFEAjNueyfUKfBYNV13lPHbtgvPPL7vNm26Ciy6CLVvg8svLzv/LX2DMGGffN9xQdv4//gEnnQTLlsEdd5Sd/8gjMHQoLFoEf/972fkTJ0JSEnz1FTz8cNn5//0v9OgBM2fCk0+Wnf/GG9CuHUybBi++WHb+9OkQFweTJzuPEsKA5z7+hJsV1j3wODt2LSl709u8ec7fCRPgk08On9eoEXz2mfP8n/+EOXMOnx8bC++/7zy/5x747rvD5yckwJtvOs/vuMM5hiV17w6TJjnPx42DdesOn5+U5Bw/gMsug9TUw+cfcww8+qjz/LzzYPfuw+efeCLcd5/z/PTT4eDBw+ePHg133uk8L33eQbnn3mHs3Kvw3ANg1iyIjIQXXoB33y07384957kvzj1XrXdoo6pbgQnAZpymohmq+mXp5URknIikiEhKXp53HY4dyi8kNAD76KmOsJAgnr90AD1bRbFx14Hi7qyNMQ2f1PZ9WSLSDHgfuAjYB7wHTFfVNytaJzk5WVNSUjxuV1Xp88AXjD2qPfeP6V2DETdsufkF3PzmEuasSeee03tyw3Br529MQyEii1U1ufR0fxSPTwI2qupOVc0DPgCGHulG9+fmk32ogFYxdtduVYSHBPPS5YM4I7E1j362hqdmr6Me3KRtjDkClbbjF5F44HqgY8nlVfWaau5zM3C0iEQCB4ETAc/FeS8E0pCLNS00OIhnxg6gcVgwz8xZz4HcfP5xRi+7SG5MA+XNnbsf4Yyz+xVQcKQ7VNUfRGQ6sATIB5YCk450u2kZTncNlvirJzhIeOzcRGcox4UbyT6Uz8Nn9yM4yJK/MQ2NN4k/UlXvqsmdquoDwAM1uc3im7cs8VdbUJDwwJjeNAkP4bm5v5J9qIAJF/QnNNgumBvTkHiT+D8RkVHuoOt1VqANsu4rIsKdp/YgMjyYxz9fS/ahAp69eAARoTaSlzENhTdFuT/hJP8cdxCWOjkQS3pmDtERITbUYA25eURXHjqrD7NX7+DK134k46CN4WtMQ1Fp4lfVKFUNUtUI93mUqkbXRnBVkZaZY3301LArjunIf8YmsWTzXi586Tu2ZxysfCVjTJ3nVeWtiJwpIhPcx2hfB1UdaZm5Vs3jA2cltWXK1YPZuu8g576wiHU7svwdkjHmCFWa+EXkMZzqntXu40/utDol3cba9ZmhXeN494ZjKChUzn9xET9u3OPvkIwxR8CbEv8o4GRVfU1VXwNOc6fVGQWFSnpWrrXo8aHebaL54OahxEeFc9mrPzBrxXZ/h2SMqSZv2+k1LfE8xgdxHJHd+3MpKFQba9fHEppF8v5NQ+nXNoZb3l7C5G+tT39j6iNvEv+jwFIRmSwiU4DFwCO+DatqdmTazVu1pWlkGG9dN4STe7Vk/MzVPDhzFfkFhf4OyxhTBd606pkKHI3Tp84HwDGq+o6vA6uKNBt5q1ZFhAbz4mWDuPbYTvzv201c93oKmTnW3NOY+sLT0Is93b8DgdZAKrAFaONOqzPs5q3aFxwk3De6N4+c04+F63dx3guL2LIn299hGWO84OnO3f8DxgHljMSAAif4JKJqSM/MIThIiGtidfy17ZIh7ekYG8lNby3hrOe/5b+XD+Kojs39HZYxxoMKS/yqOs59erqqjiz5oI616knLyCG+Sbh1KOYnQ7vGMeOWYTRtFMolL3/P9MWpla9kjPEbby7uLvJymt+kZeZYix4/6xTXmA9vHsbgTs25872fefSzXygotH79jamLKqzqEZFWQFucsXEHAEXF6WiccXLrjPTMXDrE1qmQAlJMZCiTrx7M+I9X8d/5G1i9LZNnxg6gWeMwf4dmjCnBUx3/qcBVQALwVInpWUA5Izj7T1pmDkM6W71yXRAaHMS/zulHv7Yx3P/RKsY8t5CXLhtE37Z17vYPYwKWpzr+KW59/lWl6vjPVNUPajFGj3LyCsg4mGcteuqYsYPb8+6NTjcP5724yOr9jalDKu2PX1XfF5EzgD5ARInpD/kyMG/ZkIt1V1K7psy87Vhue3spd773Mz9v2cd9o3sTFmIDuxjjT9500vYScBFwG049/wVABx/H5bW0DBt5qy6LaxLOG9cOZtzxnXnj+98ZO+m74i9rY4x/eFP0GqqqVwB7VfVB4Big3ZHsVESaish0EVkjIr+IyDHV3dYfN29Zq566KiQ4iL+P6sVzlwxgTVoWZzzzDd+s3+nvsIwJWN4k/qLiWbaItAHygE5HuN//AJ+rak+gP/BLdTeUXtRPj3XXUOeNTmzDR7cMo3njMK547Uee+GKN9fNjjB94k/hnikhT4AlgCbAJmFrdHYpINHA88CqAqh5S1X3V3V5aZg6RYcFEhXszfLDxt24to/jolmO5KLkdz8/9jbGTvmfbPhvZy5ja5DHxi0gQMEdV96nq+zh1+z1V9f4j2GdnYCfwPxFZKiKviEjjcvY9TkRSRCRl586KqwXS3AFYROyu3fqiUVgwj52XyH/GJvHL9kxGPfMNs1fv8HdYxgQMj4lfVQsp0VePquaqasYR7jMEGAi8qKoDgAPA3eXse5KqJqtqcnx8fIUbS7e7duuts5La8sntx9G2aSOufz2Fh2au5lC+Vf0Y42veVPV8KSLnSc0VqVOBVFX9wX09HeeLoFrSMnOsRU891imuMR/cPJSrhnbktW83cs4L37LexvU1xqe8Sfz/B7wH5IpIpohkiUhmdXeoqmnAFhHp4U46EWcs3+psix02yHq9Fx4SzPgz+zDp8kFsz8jhjGcX8trCjRRaXz/G+IQ3N3BF+WC/twFviUgYsAG4ujob2Zedx6H8Qkv8DcQpfVoxoH0z7n5/OQ99spo5a3Yw4YL+tI5p5O/QjGlQvLmBa44306pCVZe59feJqnq2qu6tznZsAJaGJz4qnFeuTObRc/uxdPM+Tn16AR8t2+rvsIxpUDyNwBUhIs2BOBFpJiLN3UdHoE2tRejBH0Mu2sXdhkREuHhwe2bdfhxdWjThT+8s49a3l7Av+5C/QzOmQfBU4r8BZ2D1nu7fosdHwPO+D61y6Vbib9A6xjXmvRuO4c5TuvP5yjROemoBn69M83dYxtR7nnrn/I+qdgLuVNXOqtrJffRX1edqMcYKpWU4d+22iLLE31CFBAdx6wndmHHLMFpEhXPjm4u55a0l7Nqf6+/QjKm3vLm4+6yIDAU6llxeVV/3YVxeScvMIbZxmPX2GAD6to3ho1uH8d/5v/HMnF9Z9NsuHhjTh7OS2tjNe8ZUkTcXd98AJgDHAke5j2Qfx+WVdPeuXRMYQt3S/6e3H0vHuMbcMW0Z101JKe6h1RjjHW86uEkGeqtqnWtUbWPtBqZuLaOYfuNQJi/axBNfrOHkp+bzt9N7csng9gQHWenfmMp4U0eyEmjl60CqY0dmDq2sV86AFBwkXHtsJ76443gS28Vw34yVnPvCt6zceqQ9ihjT8HlT4o8DVovIj0DxFTVVPdNnUZWydvdaRkwecdi083pdwO4DHWkaqWXmAVyVdBVXJV3FruxdnP/u+WXm35R8Exf1vYgtGVu4/MPLy8z/yzF/YUyPMazdtZYbPrmhzPx/HP8PTup8EsvSlnHH53eUmf/IiY8wtN1QFm1ZxN/nlB2ieOJpE0lqlcRXG77i4QUPl5n/39H/pUdcD2auncmT3z1ZZv4b57xBu5h2TFs5jRdTXiwzf/qF04mLjGPysslMXja5zPxZl84iMjSSF356gXdXvVtm/ryr5gEwYdEEPln3yWHzGoU24rNLPwPgn/P/yZyNh9/WERsZy/sXvg/APV/dw3ep3x02PyE6gTfPfROAOz6/g2Vpyw6b3z22O5PGTAJg3MxxrNu97rD5Sa2SmHjaRADunX8DW0NSaZKQy9e7szlqUiGDWg9h1lUvEh0Rynnvnsfu7N2HrX9ipxO5b/h9AJz+1ukczDu8d9DR3Udz59A7Aco9ty7scyE3H3Uz2XnZjHprVJn5du4Fxrl32QeXkZp5+JCixyQcw6MnPQpQJ8+9It4k/vFeLFPr9ufmoQrx0eFgLfwCXlyTcJpGhpG6J5uVWzM46cn53De6N9S5Ckpj/E+8qboXkQ5AN1X9SkQigWBVrbWetJKTkzUlJeWwaT9v2cdZz3/Ly1ckc3LvlrUViqkHft6yj3tnrGDl1kyO6xbHA2P60LVFE3+HZUytE5HFqlqmMY43rXqux+lB87/upLbAjBqNrhrSs4ra8NvFXXO4/u2a8tEtxzJ+TG+Wbd7HaRMX8NDM1WQczPN3aMbUCd5c3L0FGAZkAqjqeqCFL4PyRnqW04SvhbXqMeUIDhKuGtaJuX8dwQXJ7fjfoo2MnDCPt374nQLr9dMEOG8Sf66qFneSIiIh1IGa0/TMXEScul1jKhLXJJxHz+3HzFuPpWuLJtz74UpGP7uQ7zfsrnxlYxoobxL/fBH5O9BIRE7G6Zt/pm/Dqlx6Vi7NI8MIDba7dk3l+raNYdq4o3n+koFkHsxj7KTvufmtxWzadcDfoRlT67zJmnfjjJG7AqfjtlnAP3wZlDd2ZuUQb/X7pgpEhDMSWzPnL8P580ndmbtmJyc9NZ8HPlppff+YgOJNc85GwGuq+jKAiAS707J9GVhl0rNs5C1TPRGhwfzppG5cPLgdE+es580fNvP+kq3ccHxnrj2uE5Fh3nwsjKm/vCnxz8FJ9EUaAV/5JhzvpWfmWosec0RaREfwyDn9+OKO4xnWNZYnZ69jxBPzmPrjZvILbNB303B5k/gjVHV/0Qv3eaTvQqpcYaGyc3+utegxNaJriyb89/Jkpt94DO2aR3LPBys4ZeICZv68zcb9NQ2SN4n/gIgMLHohIoOAgx6W97ndBw5RUKjWD7+pUckdmzP9xmP47+WDCAkSbpu6lFHPfMMXq9Kog30UGlNt3lRm3gG8JyLb3NetgYuOdMfutYIUYKuqjq7KusVt+K2qx9QwEeHUPq04qVdLPlm+jf98tZ4b3lhMv7Yx/N/J3RnRI976/zf1njcDsfwkIj2BHoAAa1S1Jm6B/BPwCxBd1RWL79q1qh7jI8FBwllJbTmjX2tmLNvGf+as4+rJPzGwfVP+fHJ3ju0aZ18Apt7ythH8UUAiMAC4WESuOJKdikgCcAbwSnXW35lpQy6a2hESHMT5gxL4+i8jeOScfmzPyOHyV3/k7BcW8dXqHVYFZOqlSkv87ghcXYBlQIE7WYEjGXpxIvA3IMrDfscB4wDat29/2Lyiqh5rx29qS2hwEJcMac95g9ry/uKtvDj/V657PYWeraK49YSunN63tQ0CY+qNWh+BS0RGA+mqulhERlS0nKpOAiaB0ztnyXnpWblER4QQERpcEyEZ47XwkGAuGdKeC5MT+PjnbTw/91dufXspnePXcfOIrpyV1MbuJjd1nj9G4BoGnCkim4B3gBNE5M2qbCA9M5cWdvOW8aOQ4CDOHZjAl38ezvOXDCQ8JJg73/uZ4Y/P5ZVvNrA/N9/fIRpToVofgUtV7wHuAXBL/Heq6mVV2UZ6Vo616DF1QnCQ0w3EqH6t+HpNOpMWbODhT3/hP3PWc8mQ9lwzrJPdYW7qnHo5Ald6Vi7JHZr5OwxjiokIJ/ZqyYm9WrJsyz5eXrCBlxds4LWFGzkrqS3XH9eZHq0qvKRlTK3ypjnnfBFpidOyB+BHVU2viZ2r6jxgXhXXIT3LqnpM3ZXUrinPXzqQzbuzeXXhBt5NSWX64lSO6xbHVUM7MrJHC4LsQrDxI29G4LoQ+BG4ALgQ+EFEKh7F18cyD+ZzKL/QqnpMndc+NpIHz+rLortP4K+n9mD9jv1cOyWFkU/O45VvNtiIYMZvvKnquRc4qqiULyLxOJ20TfdlYBWxppymvmnWOIxbRnZl3PGd+XLVDiYv2sjDn/7CU7PXcd7ABK4c2oGuLawayNQebxJ/UKmqnd14f+NXjftjrF2r6jH1S2hwEGcktuaMxNas3JrB5EWbmJayhTe+/52jOzfnkiEdOLVPS8JDrJmy8S1vEv/nIvIFMNV9fRHwme9C8szG2jUNQd+2MUy4oD/3nN6TaSlbmPrjZm6fupTmjcO4YFACFw9uT8e4xv4O0zRQ3lzc/auInAsci9NXzyRV/dDnkVUg3e2uwZrImYYgtkk4N4/oyo3Hd2Hhr7t464ffeWXhRv67YAPDusZyyeAOnNS7hf0KMDWqwsQvIl2Blqr6rap+AHzgTj9eRLqo6m+1FWRJ6Vm5RIYF0yTcRkkyDUdQkHB893iO7x7Pjswc3v1pC+/8tIVb3l5C08hQzk5qy/mDEujbNsbfoZoGwFP2nAj8vZzp2e68MT6Ip1I7Mu3mLdOwtYyO4LYTu3HzyK4s/HUX76Vs4e0fNzN50SZ6tY7mgkEJnD2gLc0bh/k7VFNPeUr8HVV1eemJqpoiIh19F5Jn6Vm5dmHXBITgIGF493iGd49nX/YhZv68jfcWp/LQJ6t59LNfOKFnC84Z0JYRPVpYv1WmSjwlfk/ZtZGHeT61MyuX3m2q3IW/MfVa08gwLj+mI5cf05E1aZlMT0llxrJtfLFqB1ERIYzq25qzBrTh6E6xdnOYqZSnxP+TiFyvqi+XnCgi1wKLfRtWxdIzcxjRI95fuzfG73q2iuYfo3tz9+k9WfTbbmYs28ony7cxLWULraIjODOpDWf2b0OfNtE2WIwpl6fEfwfwoYhcyh+JPhkIA87xcVzlOpCbz4FDBVbVYwxOD6FFF4QPnl3A7F928NHSrby2cCOTFmygY2wko/o59w30bm1fAuYPFSZ+Vd0BDBWRkUBfd/Knqvp1rURWjj9u3rKLu8aU1CgsmDP7OyX9PQcO8cWqND5dvp3/LtjAC/N+o1NcY0b1a8UZ/drQq3WUfQkEOG/a8c8F5tZCLJVKz7Sbt4ypTPPGYVw8uD0XD27P7v25fLFqB5+u2MaL837j+bm/0SE2klP7tOLUPi0Z0K6ZXRMIQPWqMbx112BM1cQ2CeeSIe25ZEh7du3P5YtVaXyxagf/+9apDoprEs7JvVtySp+WDO0SazeKBYh6mvitxG9MVcU1CefSIR24dEgHMnPymLsmnS9X7eDjZVuZ+uNmmoSHcHz3OE7o2ZIRPeKJa2Kfs4aqniX+HMKCg2gaGervUIyp16IjQjkrqS1nJbUlJ6+A737bzZer05jzSzqzVqQhAv0TmnJizxac0KuFXRxuYOpV4t+ZmUt8VLidgMbUoIjQYEb2bMHIni1QVVZty+TrNenMWZPOk7PX8eTsdbSKjuD47nEc3z2eY7vG0TTS7hquz+pV4k/PyrV++I3xIRGhb9sY+raN4fYTu7EzK5d5a9OZuzadz1em8W5KKkECiQlNOb57PMO7x9E/oSkhwX7rqd1UQ60nfhFpB7wOtAIKcXr7/I8366Zn5dAx1rqqNaa2xEeFc0FyOy5Ibkd+QSE/p2awYN1OFqzfyXNfr+eZOeuJigjh6M6xDOsSy7CucXRt0cR+lddx/ijx5wN/UdUlIhIFLBaR2aq6urIV07NyGdypue8jNMaUERIcxKAOzRjUoRl/Prk7+7IPsfDXXSxcv4tvf9vF7NU7AKfxxdAusQztGsfQLrEkNIv0c+SmtFpP/Kq6HdjuPs8SkV+AtoDHxJ+bX8C+7DxrymlMHdE0MozRiW0YndgGgC17svn21118+9tuFv66ixnLtgHQtmkjhnRuztGdYhnSuTntm0faLwI/82sdv9vL5wDgh3LmjQPGAbRv356dWUUDsFgdvzF1UbvmkYwd3J6xg9ujqqzdkcX3v+3mh417mL92Jx8s2QpAq+gIhnRuzlEdm5PcsRndW0TZTWS1zG+JX0SaAO8Dd6hqZun5qjoJmASQnJysOzLt5i1j6gsRoWeraHq2iuaqYZ1QVX5N38/3G/fw48Y9fPfbbj5yfxFERYQwqEMzkjs0Y1CH5iS1a0qjMLuRzJf8kvhFJBQn6b/lju5VqZ3uWLvWqseY+kdE6NYyim4to7j86A6oKlv2HOSnTXtI+X0vi3/fw4S1OwEICRJ6t4kmqV1TBrRvyoB2zegQa9VDNckfrXoEeBX4RVWf8na94rt2rarHmHpPRGgfG0n72EjOG5QAQEZ2Hks27yXl9z0s3byP9xen8vp3vwPQLDKUpHZNSWrXjP7tYkhMaGojkB0Bf5T4hwGXAytEZJk77e+qOsvTSumZuQQJxDa2xG9MQxQTGVp8IxlAQaGyPj2LpZv3sXTzXpZt2ce8dTtRdZZPaNaIxATnSyCxbQx9E2KIjrC7+r3hj1Y9C4Eq/2ZLz8ohrkk4wXYRyJiAEBz0x3WCiwe3ByArJ48VWzNYkZrB8tQMlm/dx6wVacXrdIiNpG+bGHq3iaZv2xj6tIm2PofKUW/u3E3PyrVqHmMCXFREKEO7xDG0S1zxtD0HDrlfBvtYtS2T5Vv38emK7cXzW0VH0KdNNL1aR9OzdRS9WkfTMbZxQBci60/iz8ylVYy16DHGHK5547DiQemLZGTnsWp7Bqu3ZbJqWyartmUwb91OCgqdeqKI0CB6tIxyflG0jqJHyyi6t4oKmF8H9SfxZ+WSmBDj7zCMMfVATGTZXwa5+QWs37GfNWlZ/LI9kzVpmcz+ZQfTUrYUL9O8cRjdWzYp/iLo1iKKri2aNLgLyfUi8Suw50Cu9cNvjKm28JDg4g7oiqgqu/YfYt2OLNamZTl/d2QxfXEqBw4VFC/XvHEYXeOb0LVlE+dviyZ0jm9Mm5hG9fLms3qR+PMLFFWIj7aqHmNMzRER4qPCiY8KZ1jXP34dqCpb9x1kffp+fkvfz6/uY9aK7ezLziteLiI0iI6xjekS34ROcY3pHN+YzvFN6BTbmJg6PG5IPUn8hYCNvGWMqR0iQkKzSBKaRTKyR4vi6arK7gOH+DV9Pxt2HmDDzv1s2HWAVdsy+HxVWvE1BICmkaF0iG1Mp9hIOsQ2pmOc87dD80iaNw7z6w1p9SPxF1riN8b4n4gQ1yScuCbhHN059rB5h/IL2bwnmw079/P77mw27T7A77uz+WnTXj76eVvx/QcAjcOCadc8kg6xkbRv7jzaNY90v2waERHq2y4r6kXizytwjlgLq+oxxtRRYSFBdG3h1P+XlptfwJY9B/l99wE278l2Hruz2bDzAPPW7iQ3v/Cw5eOjwklo1qj4i6BtU/fRrBFtmjaiSfiRpe56kfjzC5QgID5AmloZYxqW8JDgCr8UVJWdWbls3pNN6t6DpO4t+nuQ5an7+Hzl9uLCb5HoiBDaNoukbdMIWsc0onXTCFrHuM9jImgVE0F4SMW/GupF4s8rLKRVZChhITa8mzGmYRERWkRH0CI6guSOZecXFDpfDFv3HWTrvoNsK/FI3XuQnzbtJeNgXpn1Yj00Qa0XiT+/QK07ZmNMQAoOElq5pfhBHZqVu0z2oXy2Z+SwfV8O2zMOOs8zDrKkgm3Wi8SfV1Bo3TUYY0wFIsNC6BLfhC7xh1clPVbB8vWi7iS/0Er8xhhTU+pH4rcSvzHG1Jh6kfgVa8NvjDE1pV4kfrCxdo0xpqbUn8RvVT3GGFMj6k/it6oeY4ypEfUo8VtVjzHG1AS/JH4ROU1E1orIryJyd2XLB4nQKMy3nRYZY0ygqPXELyLBwPPA6UBv4GIR6e1pndDg+jfQgTHG1FX+KPEPBn5V1Q2qegh4BzjL0wohQfWmRsoYY+o8f2TUtsCWEq9T3WmHEZFxIpIiIilBBbm1FpwxxjR0/kj85dXbaJkJqpNUNVlVkzu2al4LYRljTGDwR+JPBdqVeJ0AbPNDHMYYE5D8kfh/ArqJSCcRCQPGAh/7IQ5jjAlItd4ts6rmi8itwBdAMPCaqq6q7TiMMSZQ+aU/flWdBczyx76NMSbQWTtJY4wJMJb4jTEmwFjiN8aYAGOJ3xhjAoyolrl3qs4RkSxgrb/jqIPigF3+DqKOsWNSPjsu5Wvox6WDqsaXnuiXVj3VsFZVk/0dRF0jIil2XA5nx6R8dlzKF6jHxap6jDEmwFjiN8aYAFNfEv8kfwdQR9lxKcuOSfnsuJQvII9Lvbi4a4wxpubUlxK/McaYGmKJ3xhjAkydTvxVHZQ9UIjIJhFZISLLRCTF3/H4i4i8JiLpIrKyxLTmIjJbRNa7f5v5M0Z/qOC4jBeRre45s0xERvkzxtomIu1EZK6I/CIiq0TkT+70gDxf6mzir86g7AFmpKomBWIb5BImA6eVmnY3MEdVuwFz3NeBZjJljwvA0+45k+T2kBtI8oG/qGov4GjgFjefBOT5UmcTP9UYlN0EFlVdAOwpNfksYIr7fApwdm3GVBdUcFwCmqpuV9Ul7vMs4Becsb4D8nypy4nfq0HZA5QCX4rIYhEZ5+9g6piWqrodnA870MLP8dQlt4rIcrcqKCCqNMojIh2BAcAPBOj5UpcTv1eDsgeoYao6EKca7BYROd7fAZk670WgC5AEbAee9Gs0fiIiTYD3gTtUNdPf8fhLXU78Nih7BVR1m/s3HfgQp1rMOHaISGsA92+6n+OpE1R1h6oWqGoh8DIBeM6ISChO0n9LVT9wJwfk+VKXE78Nyl4OEWksIlFFz4FTgJWe1wooHwNXus+vBD7yYyx1RlFyc51DgJ0zIiLAq8AvqvpUiVkBeb7U6Tt33SZnE/ljUPZ/+Tci/xORzjilfHB6V307UI+LiEwFRuB0rbsDeACYAbwLtAc2AxeoakBd6KzguIzAqeZRYBNwQ1HddiAQkWOBb4AVQKE7+e849fwBd77U6cRvjDGm5tXlqh5jjDE+YInfGGMCjCV+Y4wJMJb4jTEmwFjiN8aYAGOJ3xhjAowlftNgiUhsiW6I00p0S7xfRF7wwf4mi8hGEbmxxOvzj2B7b4nIniPZhjHlCfF3AMb4iqruxrlpCREZD+xX1Qk+3u1fVXW6twuLSLCqFpQ3T1UvFZHJNRaZMS4r8ZuAIyIjROQT9/l4EZkiIl+6A9ycKyKPuwPdfO7274KIDBKR+W6PqF+U6gLBk+NFZJGIbCgqubv7nysibwMr3G44PhWRn0VkpYhc5Jt3bozDEr8xTq+VZ+D0zf4mMFdV+wEHgTPc5P8scL6qDgJeA7ztJqM1cCwwGnisxPTBwL2q2htn0JRtqtpfVfsCn9fAezKmQlbVYwx8pqp5IrICp1+oosS7AugI9AD6ArOdvr4Ixuna2Bsz3B4xV4tIyxLTf1TVjSX2M0FE/g18oqrfHNG7MaYSlviNgVwAVS0UkTz9owOrQpzPiACrVPWY6m7bVXKMiQNFT1R1nYgMAkYBj4rIl6r6UDX2ZYxXrKrHmMqtBeJF5Bhw+nUXkT41tXERaQNkq+qbwARgYE1t25jyWInfmEqo6iH3wuwzIhKD87mZCKyqoV30A54QkUIgD7iphrZrTLmsW2Zjaojb9PKTqjTn9Mc2jbGqHmNqTgbwz6IbuI6UiLwFDAdyamJ7xhSxEr8xxgQYK/EbY0yAscRvjDEBxhK/McYEGEv8xhgTYP4f9lI4mfhlkfQAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# specify time span and evaluation points\n",
"t_span = [0, 24]\n",
"t_eval = np.linspace(0, 24, 50)\n",
"\n",
"# initial conditions\n",
"C_initial = 0\n",
"IC = [C_initial]\n",
"\n",
"# compute solution\n",
"soln = solve_ivp(deriv, t_span, IC, t_eval=t_eval)\n",
"\n",
"# display solution\n",
"plotConcentration(soln)\n",
"plt.savefig('./figures/Pharmaockinetics2.png')"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.2.1 Analysis of the Results](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.2.1-Analysis-of-the-Results)",
"section": "2.1.3.2.1 Analysis of the Results"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.2.1 Analysis of the Results\n",
"\n",
"Let's compare our results to a typical experimental result. \n",
"\n",
"| | |\n",
"| :-: | :-: |\n",
"|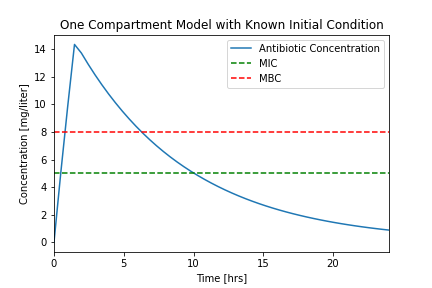||\n",
"\n",
"While it isn't perfect, this is a closer facsimile of actual physiological response.\n",
"\n",
"[Levison, Matthew E., and Julie H. Levison. “Pharmacokinetics and Pharmacodynamics of Antibacterial Agents.” Infectious disease clinics of North America 23.4 (2009): 791–vii. PMC. Web. 8 May 2017.](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3675903/)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.3.3 Example 2: Periodic Dosng](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3-Example-2:-Periodic-Dosng)",
"section": "2.1.3.3 Example 2: Periodic Dosng"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"### 2.1.3.3 Example 2: Periodic Dosng\n",
"\n",
"The minimum inhibitory concentration (MIC) of a particular organism to a particular antibiotic is 5 mg/liter, the minimum bactricidal concentration (MBC) is 8 mg/liter. Assume the plasma volume $V$ is 4 liters with a clearance rate $Q$ of 0.5 liters/hour. \n",
"\n",
"Design an antibiotic therapy to keep the plasma concentration above the MIC level for a period of 96 hours. "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"#### 2.1.3.3.1 Solution\n",
"\n",
"We consider the case of repetitive dosing where a new dose is administered every $t_{dose}$ hours. A simple Python \"trick\" for this calculation is the `%` operator which returns the remainder following division. This is a useful tool worth remembering whenever you need to functions that repeat in time."
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
},
"slideshow": {
"slide_type": "-"
}
},
"outputs": [],
"source": [
"# parameter values\n",
"dt = 2 # length of administration for a single dose\n",
"tdose = 8 # time between doses\n",
"Udose = 42 # mg\n",
"\n",
"# function defintion\n",
"def u(t):\n",
" if t <= 0:\n",
" return 0\n",
" elif t % tdose <= dt:\n",
" return Udose/dt\n",
" else:\n",
" return 0"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
}
},
"outputs": [
{
"data": {
"text/plain": [
"Text(0.5, 1.0, 'Dosing function u(t) for of total dose 42 mg')"
]
},
"execution_count": 10,
"metadata": {},
"output_type": "execute_result"
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAYUAAAEWCAYAAACJ0YulAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAA+SUlEQVR4nO2dd7wkVZX4v4c4hBlymhlgAMkICCNBUUEMoCCIssKKiywr6howfBbFiBhABQRd0R8ogpJ0WRQkCSJBVgVnkCg5h4EZ0jADTGDm/P6o6p5+71VVV78+91RXvfv9fN6nX1d133NuVXXduiddUVUikUgkEgFYqmoFIpFIJDI4xEEhEolEIm3ioBCJRCKRNnFQiEQikUibOChEIpFIpE0cFCKRSCTSJg4KA4iIzBWRjQO0KyLyCxF5XkRusm6/i+zLReRQT5kdss8Tkf0L9p8kIh/r0sZ7ReSx9Ny8zlzJobIqO0+p/CkioiKyTMnPnyki3wqtV8SHOCiMEhF5WEReEZE5IvKCiPxFRD4mIn0fU1VdWVUftNBzGLsBbwcmq+pOAdoHQESOEZGzO7ep6t6qelYomQW6bAtsB1yUvv+wiNww7GPfB74sIssVNHUC8Mn03PwjjLZtCs9TTh9y6fXzdSIdPFVEXtOx7QQRuS/9bd4tIv9WpY51Iw4K/bGvqo4HNgSOB74A/LxalQrZEHhYVV+qWhFHPgqcowVZmqo6A7gbeE9BOxsCd45GARFZusevjMXz1DMishuwScaul4B9gVWAQ4FTROQNnrrVGlWNf6P4Ax4G3jZs207AYmCb9P0qwC+BWcAjwFeApdJ9rwGuA2YDzwC/7mhHgdek/58J/Bi4FJgD3Ahs0vHZdwD3pO2cmrb5Hxn6Hg7MAxYBc4FvAB8Gbhj2uV5kbw1cBTwHPA18CdgLWAAsTOXcmn722pZeJA8jX0mPycz0GK2S7puS6nAo8Gh6bL5ccB7a7abvh/QJeBDYLf1/y2HH4IWOz30Z+EVG+8unn1WSm80DHW1dC7xAMli8p+M7ZwI/AS5Lv/O2jHYnAhenx+5+4CN552nY9zL7QM61VvD5dwP/AF4EHgOO6ZDROgfL5Bzz1wE3p9fEr4HzgW917P9I2qfn0j5OTLcL8IP0nM8GbmPJb2V5ktnYoyTX0k+BFQrO+zKp/tvScc3mfPZi4PM5+3YHHgeOSvWaAewPvAu4N+3Dlzo+vwJwFvA8cFf6vcervh9Z/lWuQF3/yBgU0u2PAh9P//8lidlifPpDuxc4PN13HsmNaClgHOmNK903/Mb8HMmAswxwDnB+um/N9Ed9QLrvSJKb8YhBIf38hxl6wxzyvkfZ49Mf0OdT/ccDO6f7jgHOHtbutSwZFP49vWlsDKwMXAj8Kt03JdXh9PQHuB0wH9gyp0/tdof3CVgpbWutoj6n2w8Abi44353HZdlU/y8BywFvJblBbt5x3GYDb2yd34z2riMZxMcB25PczPcs0rHLeSu61rI+vzvw2lS/bUluxPsPOwcjBoW0v48An02Pw/tJrrlvpfvfSjKQ70Byo/8RcH26753AdGBVkgFiS2C9dN/JJDfv1dM+/B44ruAY/BdwyvBzk/G5FUiu071y9u8OvAp8Le3PR9JzcW6qx9Ykg+rG6eePT8/dasBkkoGtUYNCNB/Z8ySwemoy+ABwtKrOUdWHgROBD6WfW0hiJpioqvNUtcjme6Gq3qSqr5LcmLdPt78LuFNVL0z3/RB4yrg/ebL3AZ5S1RNT/eeo6o0l2/wgcJKqPqiqc4GjgYOGOTa/oaqvqOqtwK0kg0OvrJq+zinx2Tkdn+/GLiSD2fGqukBV/wRcAhzc8ZmLVPX/VHWxqs7r/LKIrE/iN/hCeuxuAX7GkmujJ0pcayNQ1WtV9fZUv9tIHlLeUkLcLiQ3z5NVdaGqXgD8vWP/B4EzVPVmVZ1Pcm53FZEpJNf8eGALQFT1LlWdISJCcjP+rKo+p6pzgO8AB+X0d30Ss+DXSuj7U5Lr5w8Fn1kIfFtVF5LMetYkGXDmqOqdJDPBbdPP/gvwHVV9XlUfJ/nNNYo4KNgzieTpek2WPFW1eCTdD8m0U4CbROROEfn3gjY7b/Qvk9yQIDFBPNbaocmjzON9aV9e9vrAA6NscyIjj8sywDol5PbCC+nr+BKfHd/x+W5MBB5T1cUd2zrPLXScl5zvt25+ed/vhW7X2ghEZGcRuUZEZonIbOBjaTvdmAg8kV5rnbI697ffp4P+s8CkdPD8bxKT5NMicpqITADWAlYEpqdBGy8AV6TbszgZOFZVZxcpKiLfB7YB/mWYvsN5VlUXpf+/kr4+3bH/FXJ+cxSf51oSBwVDROT1JD/EG0im0K3ZQIsNgCcAVPUpVf2Iqk4keeo5tTOCoiQzSKawLfnS+b4EL5H8GFvfX7eH7z5GtpMPkul8EU8y8ri8ytAfYlmG9AFo90ETR+0DwGYldNuS5ImyDE8C6w+LNGuf2y5yWt9fXUQ6B6vh3y9ieNuF11qOLueSmGvWV9VVSJ6opYTsGcCk9FrrlNViyLkVkZWANVhy3f9QVXckMctsRmIGeobkxru1qq6a/q2iqnkPAnsC3xeRp0Sk9fDwVxH51w653wD2Bt6hqi+W6FdZhvzmSB6OGkUcFAwQkQkisg/J1PPsdFq+CPgN8G0RGS8iGwKfA85Ov3OgiLQurudJfriLMpov4lLgtSKyf2p6+QQdN8US3ApsLSLbi8g4El9AWS4B1hWRz4jI8mkfd073PQ1MKQjPPQ/4rIhsJCIrk5gKfp2aqHrlFuAAEVkxHVQPH7b/MoaaRZ4GJmeEn74FuLykzBtJBqOjRGRZEdmdJNrl/DJfVtXHgL8Ax4nIuDRs9nAS81wZhvSh27U2/PMp40lmK/NEZCfgXynHX0kG8E+LyDIicgCJz6nFucBh6TW1PMm5vVFVHxaR16czlGVJjt88YFE64zod+IGIrA0gIpNE5J05OmxGYk7cniXmzH2B36bfPTrtz9tV9dmS/SrLb4CjRWQ1EZkEfNK4/cqJg0J//F5E5pA8NX8ZOAk4rGP/p0gu/gdJZg/nAmek+14P3Cgic0me2I5U1Yd6Ea6qzwAHAt8jmaJvBUwjccyW+f69wLHAH4H7Uh3Lyp5DEku/L4mp5z5gj3T3/6Svz4rIzRlfPwP4FXA98BDJzeFTZWUP4wck0U5Pk0SFDL+xngZ8sOPJ9k8kNuKnROQZABFZj+TY/a6MQFVdQBK+ujfJU+6pwL+p6t096H0wiUP3SZKb2ddV9aqS3x3RB4qvtazP/ydwbHr9fo3kZteVtO8HkDivnyfxZVzYsf9q4KvA/5I8VW/CEt/ABJKb//MkJqZnSSKOIAnnvh/4m4i8SHJNbp6jw8x0pv2UqrZmCs+oasv08x2S2ct9kiQbzhWRL5XpXwmOJTHRPpTqeAElf291QYpNbZE6kT6ZPw58UFWvqVqfQUFEzgV+o6q/y9l/Ikmo6amuikVqj4h8HDhIVcs46WtBHBRqTjrFvpHEJvtfJCakjTuemiKRiBHprHJjEjPapiQm3P9W1ZOr1MuSUrVNIgPNriSmguWAf5LEmscBIRIJw3LA/wM2IolWO5/EfNgY4kwhEolEIm2iozkSiUQibWphPlpzzTV1ypQpVasRiUQitWL69OnPqGpeEmAmtRgUpkyZwrRp06pWIxKJRGqFiDzS/VNDieajSCQSibSJg0IkEolE2sRBIRKJRCJt4qAQiUQikTZxUIhEIpFImzgoRCKRSKRNHBQikUgk0qYWeQqjZd7CRfzi/x7mlQUjy/RPWXMlDtihl/Vo8rnolid4YObckTtEeM926/Gatcss/FXMbY+/wB//mb0GzbaTV+VtW62Tua8Xnp07n3NvfJSFixaP2LfKistx2BumsNRSZdZhyUdV+eVfH+HZuSOrDS+91FIctNP6rDNhXF8yAB577mUumP44WWVcJq22Ah94/QYZ3+qN+a8u4sz/e5iX5o+8vpZfdmk+tOuGTBi3bN9yLrntSe59KntF0XdvO5HN1+3/+rrjidlceWf2Sq5bTVyFvbbpZZmOfM698VGemj2yNJeIcODUyUxebcWMb/XGXx94lr8+8Ezmvl02WYM3bFJmgblinnjhFf5n2mMsXjzy+lp3lRX41537v76efOEVzr/pUd67w2Q2WnOlvtsrS6MHhb8//BzfvSIpcd+5TpRq8n6/7SexdJ83OYDP/+ZWXl2sQ2S05Dwzdz7fee9r+5bxw6vv4493zcyUMWnVFUwGhcvveIoTr7oXGHm8AN606Zpstk5/N6AnXniFr198Z66MFZZbiiPenLegW3nOvelRfnLtA5nHC5Kb6crL93f53/rYbI67PPv6Apiyxkq8e9v1+pIBcNQFt/HygkWZfXly9jxOOHA0y1cP5SfXPsClt8/IlLHmysuZDArPv7SAL/32doDc8/LZt29Gvxx/xd3c+tgLmTKuu3cWF31yt75l/M+0xzj5j/fl9mPvbdZltZWGr+PUGzNmz+OHf7qfHaesHgcFKxalo/iF//kGdthgtfb2H159HyelNz8TOap8es9N+dywC3rn7/wx80liVDIWK9tOXoWLh13QX7jgNq67d5aJjMXpFT39K29jjZWXb2+/4o4ZfOzsm9vHsy8Z6STkxAO34307LpmpzVu4iC2+egUZk5RRylHGLbsUd39z7yHbf/bnB/nWpXe1+9oPreNx/hG7sMvGa7S3PzBrLnueeB2LjIpNLlqsfPQtG3P03lsO2f6m7/3J9PraYt3xXPGZNw/Z/rWL7uD3tz5pIyM9Ht/cb2s+tOuUIfs2+dJlJucEknP/1i3W5owPv37I9sPP/DtPz5lnJmMpgQePe/eQ7b/62yN89Xd3mJ37Kmi0T6HbabGqEFvUjNW1UdSMdu1pSRldmrHoSzddzfrSbb9HX6yur1Hu601GfktmMhyuL+jSF4ffo52cagaWRg8KkUgkUnf6N3D3xpgYFIYf1BAHOatNMZaUKSNAZ2REo/ZChosI0o8MvUf2zUJO8XsbGRl9cbhdBJGQcQ6s5Xj8VrKuJUsRVVmgmj0odJuuuqhQIxNVl4Ys+uJmQugqyEKIQRt9yqmXCdTJdOjyW+my3/DiCPHAVESwQUFE1heRa0TkLhG5U0SOTLevLiJXich96etq3dqKRCKRiA8hZwqvAp9X1S2BXYBPiMhWwBeBq1V1U+Dq9H0QWqP18Gle662Js1FbMkbuEzF2bGVNV8XS2Zi2mSEDrJyzQ9tsyzA2ILTCjofT2mQy62m1OeL6krYOFigjw50TObbnPtMcImI2G2kpm2fasXyKz366FlPHfKGJyvC34k2wQUFVZ6jqzen/c4C7gEnAfsBZ6cfOAvYPpUMkEonUHQ/fUScuPgURmQK8DrgRWEdVZ0AycABrB5c/Up8AMqpxnrk4gc0ljDxeYRzNGduCOOa7y+1bRslt1jJCkD2DC98be0dzllQ7IY11NIvIysD/Ap9R1Rd7+N4RIjJNRKbNmjW65CwPZ5CHPzOR4xB77XARdnVmO8T2J3IMZDg5G6t2nFqbJ6uU4+GY76ZDrzTG0QwgIsuSDAjnqOqF6eanRWS9dP96wMys76rqaao6VVWnrrVWT+tORyKRSGSUhIw+EuDnwF2qelLHrouBQ9P/DwUuCqVDazTPG2lDOk6TbcZ5CjnORqvnkiWO5mzHqSV5JhdbZ2O+Sc8mIlWHtNmWYeiYT+TkX192T6T5zmxrMk0spo7mnL7YNJ/IIC8PpqWDgYyK7Echax+9EfgQcLuI3JJu+xJwPPAbETkceBQ4MKAOlVPjEigjsBxEIzWiRubJJuKd0RxsUFDVG8jvz56h5GZRlVPTQ0aYjFMHGcNFOmQaB5MTOLw2r01z16yLA7g4VNhMRkm51kKsZyNV0OiMZpeMZYcs4ETO6Pb1JmMAMpr7ltBqJ7xDexCys10ymk0k+GU0F8qoYUaz91Sh0YNCJBKJRHpjTAwKedP78I7m/tsf2l7YjObONove28gYZtJLX02f5ArOiW3po5yMeQMZrXYyz4F1RrNDbD8UmHYCZzQLYliavTij2SPkORSNHhSq8t4PVcKqmer7Uuca8ZHR4xXbH8mmkRnNg4ZPuekAM4XMbeEdtB5Pi25PpPZiXJKLXDKaHRzA+XKMw7ebkNEcF9mxp3sGZY0cp4WO5vpkabo66PrQo1wbTtnZhSm6JiKKndk2IhwzmsNn/3uW5W9URnMkEolE6sWYGBRCZs8WPZWYT4lzHKfWT1gjncAOsf3W5aZVs3MSWnIsS2dni7Cd8+SVtTbMZncrIJhj2rGcWbmUGi9IVDDpS3Q02zMIjq0mOelMYvsN9Ij44rYaXiQT74zmRg8KLTwymjPlmjuaw2e1ZrbpVf/GWoaT49QDt2z24TJqmv7vlZ0dkpjRHIRuGZQGEroV3TOQkbQT3nk2GI5mG7q2Y5iokLfymsnqW12d2f3LaLeTcxF7ZOVLl/09ySnUwaovxUX3LCdFQQbmAho+KEQikUikF8bEoNCUgmXZGboeBd7scckALynXWk6jjpetiHw51mXmQ1ery2nOsh8xozkA3QuWNaMAV61WK+sa4F2jnAuHAm9uRfccZPSjQ0/teORcON6wY55CADxq+WTLtX768cFlkR3zFjNkZC6yUy9nY4vsmWhFqdT9NllRCnjdznzMaA6ARwaln6N5dPt6kuHgne3qbOxbQiqna+lsAxk55960KFrX/WEdp2V0KC8jf5+Xo9muFlneQ0e6v8bRt7mL7IjIASW+P09VLzPUJxKJRCIdeM9wilZeO51k/eQind4MDPyg4BITX3JbXzIcnI1Zbfo5TsOb2zwydN1WK3NxNDuZDmvmBM6XYdd+VbONokHhclX996Ivi8jZxvqY4uGk81jhKxWU/8MxE+Fncgkpo5ScmhRD9MpTKBZi1Ux4x3za0Gh29SbC4fpqMTCOZlU9RESWEpE3FH0mjFq25NXZCS/YurlqnI1hDlfMaO6FqvT2mImGoMjeXxcGMqNZVRcDJzrpYk738EcDGV0czR7UMcwui8TRXKfw2oRqHc02JEXkqruIa5fRjObkDbXkmIiphDLRR1eKyPukyiumxnhF03jgEdsfGTw8ylxEivC99Rb5FFp8DlgJeFVE5tEa1FUnBNXMEJeMU4eM5uoczfV0nGadgapWSeu7zaoc86YS0jYbEmQQ2jFfVVXZroOCqo73UCQELs7Gvj9QUo5DRnM/Oli1Ua/ifk3KaC7IAvbIHzBkEDKaLfvqbaMpM1NARCYBG3Z+XlWvD6VUaGqb0ezkOPUoNe6T0Zwlt55W0Kocp16L7JjLaFCQgTddBwUR+S7wAeCfwKJ0swIDPyjkOQLb+02efLVQhgceNWM8EMTwCSt8qHDu9WXqaPZxNeetVuaF6cprRfsML/HMgbp97h2sEIEoM1PYH9hcVecH1qWReEXTeFD1oBGphqY8dNQV77G6TPTRg8CyoRUJy/CM0yqkWrTn4zj1yWgOP7/3yJxNmgyf0Zwpt6Z5MB6mHZeM5tCnedAymkXkRyRqvQzcIiJXA+3Zgqp+Orx6/dHdEWggo6sOBkLo4jyrlXO2v/2DJGesHC+30uwmUrr0xbCAYOF+EykJ3tkAReajaenrdOBiB13c8DrI5k9yDqF8kPGU1ShHcz3xCkeuQkYImpDRXBVFg8IbgcuBP6rqHCd9gpDvaLYLGawyt68pfgvTjGaXzmQHGbTfeyziZNZOdoauFyJSu/DaIhOVT5BBGIp8CmcA2wGXicjVIvIFEdnOSa/GULcY7yLqfKFHRk9TyqjUFe+xOnemoKp/A/4GHCMiawDvAD4vItsCNwNXqOpvfNTsjxERg2718BzisUO0OewAeTkbzWVkOubraUSorBhiiDYdzoFXkEFIBrF0dhtVfRY4L/1DRHYE9gqolwkuWYct81Hu7vDmkKaUm5bEfmRCpSuvtXWwk5G/3zBPYZQ69CAld4+X6dDyt1Lst7C7ow9cRrOIfC5j82zgUnt1fHALSTV3NPt4Tj1mVlU5SWv2sNimKkdzCCEu56BB2ezelMlTmAp8DJiU/h0B7A6cLiJHhVPNjrzpqqWNvBEZzRXb+y0zmj3rXo0sC+LnbLQ794OQ0WzTlofZRdHConseIc+hKGM+WgPYQVXnAojI14ELSJbinA58L5x6/VH1TQ6a5Wg2WX+i/yYiNSU6mkeH9wynzExhA2BBx/uFwIaq+godyWyDzMi4+3pOI0OX6m236ZHRXJGTtKan3q2stYeM6oIMwsu1ZJBrH50L/E1ELkrf7wucJyIrkRTJG1g8Haf5jmYjitM0g4uwElPkGPUqipboYSCjm6PZMA9mtPvLCyqOClLVvqOGilW1LIZYoIOlY77Ab2Gb0WzYWAm6zhRU9ZvAR4AXSBzMH1PVY1X1JVX9YN73ROQMEZkpInd0bDtGRJ4QkVvSv3cZ9CESiUQiRpQxH0FSFO8aknLZi0VkhxLfOZPssNUfqOr26d9lJeX3Ra45xNBGnl1GN3wBLhH7jOYReQpOCyoIDiGDLUeghYxWkEFQGUPbHC7IMsjAbWW/HNOOZZ2wvMgzS8d81kVs62iuxoBUJiT1m8CHgQdYckwVeGvR91T1ehGZ0qd+fTEIjq0mOZo9FqKPDCYW6y0Mwu8x0p0yPoV/ATZR1QVdP1mOT4rIv5EU3Pu8qj6f9SEROYIk/JUNNtigL4EeK4llyw3fXk1D1SuLGK9rrLrHGuBl5fbdpoujuRq5llQ1hpYxH90BrGok7yfAJsD2wAzgxLwPquppqjpVVaeutdZaoxLW1dk4qlaHtTEIK681pDiNGJtDCvebFkMcur3tbHQwIYR2nHph6Z4tasXWPDly+5Js9vpOi8rMFI4D/pE6jDvXU3hPr8JU9enW/yJyOnBJr23Uj/Cp+154LEQfGUwsfTCR3hi4MhfAWcB3gduBxf0IE5H1VHVG+va9JLOQ4AR9kmu32V1uv+Q5TkNntXoVRbN0NJP3JBfACTziCDk5mi2vL8Uvtj/vtxL+KV4MB6axndH8jKr+sNeGReQ8knIYa4rI48DXgd1FZHuSa/Bh4KO9ttsLg7AmrEeNeC9s+lJ9PyK9k/yW+sxTiKd+VHj7wcoMCtNF5DiS1dc6zUc3F31JVQ/O2Pzz3tQLg5uj2XqmkLnNOOw1a1tNHc11cyz2SsxoLpDRgIzmqh6gygwKr0tfd+nY1jUkdRDo7mg2tJFXufKaobOxUgLkXOTuN3QC5628VqeM5rzYfi+Emq28luuYtzNNV0XXQUFV9/BQpKk0JDAo0cGijQHoR6R34rmvjoEpcyEi+3T7cpnPDAL5tWn6bzsvqzXZ5pXRbEOS1eqTDZGbcWr55Fu48prdHWpERrNZy7TVzMuYDz2zCnNDyguYCFyXyPK3osUmqjpH6hXNFL4vIk9QfI1/h0EOKx2AJ5PGmHYwMocY6BHxJ67PXR2DFJL6NHBSl+/fZ6hLMEbW8vGSa95iiS3WEvzq35jLcAqv9aC6bPaaZjQX2PvrQlVDaO6goKq7O+oRBJdVq3KyWj2p04pVRVjegHwczclrXgFBl5XXTB2n1V3EpqbDon2GzuzCjOYaT4rKVkmNjBLbqozVEp2NY5c628jrziCuvFZ7RjoCW09yYW3k5qadwLYd34zmHB0sa/kUyPUo22C6iFOe49Th6dqavOvJNlIvzwlcHx9fVYNoowcFz4OaN5pbRtNUTuACb/VLLkoIGn3kSJHeoS+/Kk1XoyX7oaOePphOug4KIrKiiHw1LWCHiGxal1DUFiMOqtdBtl5kp+S2/mQUhXFayglPdn2l+t18wCfkOVNuiCADh7tcE4IMqorWKjNT+AVJeYtd0/ePA98KppEjIdfp9cYjezY0gp8PJugazZZF0brut/M0V38Nm7UUXEZias2PBqz6t9QPZQaFTVT1e8BCAFV9hZoMuoNwXgZBBytMbOQGekTqSZ1vlFXifbMtMygsEJEVSH/PIrIJHYXx6sCIldcM2y66UXo4mm2fSrO9s05JrYkOphnNGWIdM05torVa9ZWyT0xoR3OQlddydQgfZOBVdqbO0VplCuIdA1wBrC8i5wBvBA4LqZQVvo7mPB3qE+3goUNRG3V0NkLWQ0dd+5FP6JyLmp76EYTxwdi3WUSZgnhXish0kiqpAhypqs8E1ywgXjcf+9LZ4R2nTcpodpv1OFCV47SuN7m8RXYi3SkTfXS1qj6rqpeq6iWq+oyIXO2hnBX5MfH9tz0wjuaBaWT0JI7msAXe2vsNncDVOpptqDyj2TDKoDij2er6yslodjz3ocidKYjIOGBFkpXTVmPJg8kEYKKDbn3TpAJcg9CXWBRt7FJnG3n98R2si8xHHwU+QzIATGeJZi8CPw6rli2VpSlYt1fwZBJUhlPpbHMZFckNQa7jNHRSWYg2Xc59XkZzfagqYbWoIN4pwCki8ilV/ZGjTma4RAikr1XbK03W0LVRZdSY3uS6nfvA2dmJCg5P15YF3myaGhWCGJrCCvIUjGSgxQ9Qlr+lQXQ0/0hEtgG2AsZ1bP9lSMVC4lc623CJwdyL0JbihUMMaPlgLNrqgteCQS7kZmeHHcpD2Mhj2fTBpuugICJfB3YnGRQuA/YGbgDqMygEdTQ73uWK9LBoo3Kjr+HTokexuvQ1rKM5fD8g/6HDi2SWGD7IwDSjuSC8rfrf0ugpk7z2fmBP4ClVPQzYDlg+qFZGDMJp8Yqm8SCuvDZ2acZDRz0ZxIzmV1R1MfCqiEwAZgIbh1XLlhHJRV7mI/P2wjvPPE1rwWVkyg0uNghV9SWIqaeyIIN6nfxBzmieJiKrAqeTRCHNBW4KqZQZXR2BdiKqvtxCZxt7YLo+gIOjecmqewEzmj360W6nwjwFfEpQ2FUY6LLymomUtE3nwayMo/k/039/KiJXABNU9bawaoXFK1LI9iaXU5fIozy3oaPZM9mvSc5Gj3DkIrmWpsPqggwiZSg0H4nI0iKyZsemJ4FdROSusGrZEnqVr0RGxSGpDahgahnM57IyVqrriDyYADfS0e7vRU61jmbLSL3wIal5AeCe63OHIndQEJGDgOeA20TkOhHZA3iQJProg0769UXVNzmwjXaomjpf6JH+sJwlRnrDe6wuMh99BdhRVe8XkR2AvwIHqepvfVSzI+9JLrzc8KYda7xWK3Ppi9Mqch54FEP0oqpzULdTP4hrNC9Q1fsBVPVm4KG6DQg+9e6T16qvt+hoHkrX+H7D4zUiTyGAjPz9ho5Tk5ZGh6mjedQ7e5CRU0BwyZb6TouKZgpri8jnOt6v3PleVU8Kp1ZDEENzSd5FaB2SmrWtvdGubEN0NPdGdY5mOxs5OT6YEDSpdPYglbk4HRhf8L425E1Xo418KIPQF7eQVAfHvE3Ua/iw6kHBLPCjKCTVRoJPafZBy1NQ1W94KhICzwzKkGs2wGD8+EPXiK/tk9yI5Mia9qNI7dA3uRoeMq+EQu/fRZmM5toz0tHslKfg0J75BeNmpojOxl6oSu0QcmPp7HJU9SDY6EGh+0Gtl428jB5Vt9EPYuiD8ZzeV+to7l9Gq50qZ2pejmZLx3x2PTzLbJtqaPSgkIfXpZ/c5GzITav3cDQbXuitH6Wnk3TotvByQ5B97h3qR7Wz2S0zmv30HrItuNQwDJKjGQARWR54HzCl8/Oqemw4tWwJukZz/02YMAhOYgv8HM0GMhzLc492f3k5A3D91CyjuVgHAxmDtvJaBxcBs0mK4c0Pq44tnsc09+knOpqHtlGwr7ZPcsPf17QjRXqHNoXV0Tnv5Wj2psygMFlV9wquSUCqK51taSnNM+3Y4mVy8cloztpWz19tdkazh9wAbbo4mquRa8kgO5r/IiKv7bVhETlDRGaKyB0d21YXkatE5L70dbVe2+0FlzhyRxt5sR4WbVQ7HxGxW3mt29k1KVa3xEg+BNOiaE6e5spXXsMnyMByDfCijOaqf0v9UGZQ2A2YLiL3iMhtInK7iJQpnX0mMHyG8UXgalXdFLg6fe+Oa+ls0+USHTKaCxx0Jn1pR+xU42ys6UTBMVR4uIwAQQYGbXWjKsd8CAbO0UxSFbVnVPV6EZkybPN+JOs9A5wFXAt8YTTt98SYcDQPRhv9Ui9Hs4MMh35YttMPHufebjbikGle0UnpOlNQ1UeAVYF9079V022jYR1VnZG2OwNYO++DInKEiEwTkWmzZs0albA6T+Ei9aGuforhVJqnUMNDmKlyCP+b88HpOiiIyJHAOSQ38LWBs0XkU6EVU9XTVHWqqk5da621+mprRHKRl6NZLMtcZFex9CjPvWTRmP7bz1uYJgSNilUvuc1cbvvcG4bXVpWjEl6sKVWFCZcxHx0O7KyqLwGIyHdJ1lb40SjkPS0i66nqDBFZD5g5ijbMMIkjd7SRF+th6DitiLplNFMQZCBiJaSUCgbtZGfoeiEYrrxWcPZNM8CLMpprbKQo42gWYFHH+0WM/vK5GDg0/f9QkhyIRmOX0WzUUD86WLQxAP2I9E4899XhPVaXmSn8ArhRRH6bvt8f+Hm3L4nIeSRO5TVF5HHg68DxwG9E5HDgUeDAUejcMyOSi9JXyxrx2XL9itVZZehmz3jsL8vciZXhk2/xymv1yDYumokmIbxhZ1ZB8hRyWjWN1MsW7PaQZmmF8KbroKCqJ4nItSShqQIcpqr/KPG9g3N27dmThn3gm9Ec6Zc6OhuhOnu/NVXqXMdz71WJdWBCUkVkgqq+KCKrAw+nf619q6vqc+HVs2H4U5avo9ny6cchtj9rm6WzsfXkG4ui9URlA49lIl4ryKCiVOymRImFpmimcC6wD0nNo85LolW7YeOAerkQsnyyN40onY1dRrNPwbLkNde0Y3gj7aaDgaABCJYwamfUO3uRkVO12FBOVT/HopXX9klfN/JTx5ZBqPxYvQaDRTwe9cQymz3SGwO38pqIXF1m2yCTF7HsUdrYksLUfaPfrJfJJb+ceVhno6ljvouutiHPI/fZ5sFkE8bR3JsOPZNjarUuO9NFheAyQlHkUxgHrEgSPbQaS87lBGCig259MxClsyOlqdoEN1qio9lAdl1P/jBC9GNgHM3AR4HPkAwA01lyzbwI/DisWmHxczQbJuRoXkazNflhnLWrxJqZ1VrPm0/2NevorDe0HlVVDLGeZ96fIp/CKcApIvIpVR1N9vLAEHTltQGxk9Y5LnqIDk7teBRDdJHRv4iknQE4+bXKaO623yHIIBRl8hR+JCLbAFsB4zq2/zKkYhZUbe+31KH6n2x4H0xdn+Q81s72oHDlNYP2C1deM2jfmyYtSNVJmTWav06SmbwVcBlJKe0bgIEfFFqMWHnNsO2iG6X1ySy6+VhlZ1fvaLZpP9fcFiDnInd/3xKW6JnrOLVyzOdsD2Fuy79xhg8yiBnN3SlT++j9JFnIT6nqYcB2wPJBtTIiZjTXi7o6G7OXyqxfX2JGc280JcBgOGUGhVdUdTHwqohMIKlsWuvENa+bj2WlzLyMZvPZSNY2w9lIzGgeHVX1pVll02t69gco+qjFNBFZFTidJAppLnBTSKWsGRuOZoM2BqAvXirYFBDssr9G+V4Dce4dnMB2DvXwmeYDl9EMIMkj9XGq+gLwUxG5ApigqmXWaK4cT+99Hae/g0ZtD2FD7AhVmu/q+PvxCjAYqIxmTYbV33W8f7guA0IRS0KvwzqDWkWiLMittdLOIbDpS/iFQ4qLooXOaMbUFOaX0ZyF9cp+mTK67O9JRpc6YZbhtfkZzVYyuuz3EBKIMj6Fv4nI64NrEgDfY1rDR51Bo6aHsCm+i0odzTU8YlUlFIamjE9hD+CjIvII8BLpA7CqbhtUs4DUM6PZZ7paVCPe0m/hcQ6y1+mt54+2qr7YOprbrfbfWBeaMlDDYJW5aLF3cC0CE9TRPBBpZVaO0+r7Ymlu62e/kRLBG/Eq8OZB6JyLRIaJiBJBBmETPUNSxnz0LVV9pPMP+FZoxepGHR1lg0ZdD2FRGG+tqFDnOh4vt5XX7JsspMygsHXnGxFZGtgxjDphGJHR7GU+wvBJrt3iSBmWFJY6MHz6qXoVubpRVV/aQQYGbbWzs130ztpYr5M/cBnNInK0iMwBthWRF9O/OSTJaxe5adgH3aNDLGQkr1Vfbk3IuRDD8JCufbFMxMux93vkjpj6rCq8ik0j9Twsg1pcEmYArHGjJndQUNXjVHU88H1VnZD+jVfVNVT1aEcdzfG6+E1DBnMczdZPP4UZzQbt+zqaM7aFFxuEyoruWdaKGtpkWDIH6nrinT9Sxnx0iYisBCAih4jISSKyYWC9TAkdEz8I1G0VuTxqtTJW16zW8OdkEM6ZFV4/RxcnsEMeTCjKDAo/AV4Wke2Ao4BHqEmFVN/1XOr6HDI41PUINsV3UanONTxg2efdvh+D6Gh+Nc1s3g84JV18Z3xYtWwZcVDdjrJdngL4rLyWXSPezn7kWhStYBW5ulFVJda2jdywWJTLymtZ22p26gey9lHKHBE5GjgEeHMafbRsWLV8aJKj2dJxWhUeZRva+00dzSP3ibGM/P1W5rbshw4vrBzNZY5Hrn+uJzkU+i0GIedntJSZKXwAmA8crqpPAZOA7wfVyoi80+J18VvXWqnK2ehZ/8aUqpyzAcgOMvCQayckls4eHQOX0ZwOBCd1vH+UmvgUWuRd2DGjeXgb1ffFMlqrcL+DY97FmW0gw7KdfvBYDQ+szkv/enSVUdFJyR0UROQGVd0tzU3oVK9V+2hCcO36xNfR7CerqdT2Sa4hvosqVa7h4XLzW3j/LnIHBVXdLX2tlVM5i+GH1G3lNWzruXg4G0OvA+1aFK3ktjpQVV8sHc2uOSpOJShCMsiO5lZpi3U6P5+akWqOz3TVA8vokCqxLAtSdA/wcQKHl+GWAV4TynQjeVDrb4ToWi2hxsez66AgIp8Cvg48DSxONysw8KWzuy0cYkloJ3BuWr1xZwoX2TFov6j+jUtfQkzvHTKnixZYMpNRWDbdMMigohpePjKC2I9cKTNTOBLYXFWfDa1MKMKWzh4MGpPRbOk5Lfgx+TiBw89E7Q5X9WffYzU88LnOvcJrQ1AmJPUxYHZoRULg6miurbU6EoQaXg7VOprrd8DcHM0DOFN4ELhWRC4lyVcAQFVPyv/KYDH8gvMrnW248ho+zsZCE4LhIFtVRnMt79ZAlt6e8f6Ws+qqSmfXcNyphDKDwqPp33LpX2Oo8xRvOF5T79DYmkPy7wIeMfEeeTB2Gc0mzfSng5MJtE6Z5lVQJnntGx6KhCA/o9nHGWTvOA0fZudVbrqwxpKZjHLbgsjxkOEYZBCaWjrmHUPbPSlKXjtZVT8jIr8n4/6qqu8JqpkDHo7mepWC7ra/Hk/XpeTYiAmOn6M5vByPMM5yGc0WM5LwmeYDl9EM/Cp9PcFDkSA4HtVoruyfuh7DpmQ0V3kG6ni4muq3KMponp6+XmctVEQeBuYAi0hKc0+1lrFEVrltoWTbPfnm5VxYx6rnb7S0kVdXFK2eVJbR3D73dvZ+n1X36nqmR+LdlzLJa/sA3wQ2TD9vVftoD1V9ps82+sKrAJcHzemLXUZzaDHdzSHhD6iXuc0DrwKVtclmr8jIWSb66GTgAOB2rZlLPd/RbE/e4u22MrI2mopw6Ucip9y2vmQ4mXV8nMDVOOZDUNmCQTV1zHvPecomr91hPCAocKWITBeRI7I+ICJHiMg0EZk2a9asUQsqrH8z6lbLt+LmCHRxmhvIcHM0NyPb2KMEeKul0e8tKcGhL37rPHf9hIOMMJSZKRwFXCYi12GXvPZGVX1SRNYGrhKRu1X1+s4PqOppwGkAU6dOHdXh8c1ojvRLXc3ATUmRq1TnGh6wJlRizaLMTOHbwMvAOJK1mVt/o0ZVn0xfZwK/BXbqp72e8TpxYmhXVqdCYlnbWhsN/RZVmQvq+putztGcSLG5jPOLIVoTV14bPWVmCqur6jusBIrISsBSqjon/f8dwLFW7WfIy91X59WRQjAILqNGmdtcMpr7l2HZTh10qMt5qeqUlJkp/FFEzAYFknUZbhCRW4GbgEtV9QrD9tvkl852cjZ6yLD3zpbZ1L+Yip7kwmQ0V+QErm02e3g5LqYdr4z5QVl5rYNPAEeJyHxgIX2GpKrqg8B2o/nuaCh2NIevtdKoJ9/+RZToh1MGuEdYYp0ywA0+0bWFAXDMJ3Ka05cQlKl9VNvlOGPp7HpRVyddcxzN1WY0D4IJqxeyz3sdz/xQimof7VD0RVW92V4dH/wymsVsqqCqTqWzM7YZOhs9/RZeORceVG1uMy2dHYMMemKQHM0npq/jgKnArSTHdVvgRmC3sKrZUHhAG+RoNolXH4C+1KrAW4OcjYMQZGBzCTtlNNPFNF3jjOZcR7Oq7qGqewCPADuo6lRV3RF4HXC/l4L94HlI62r6GCTqegirrK9lSaUrr9Xw7DflvA+nTPTRFqp6e+uNqt4BbB9MI2OKYvttnEH5rYiRDNJ2ii5CqyeTbJNLS0b4omh2azTnmNssC7y5OBvT2P6caBozx3zO9pZcS8dp7rk3dAAXnvu+pXRvpE7Z2cMpE310l4j8DDib5FAcAtwVVKtIJBKJVEKZQeEw4OPAken764FTg2lkSN5IG6QoWqYc2xBLl5XXsrYFeMLKPAd1LfDmkkQQXEKXmVX/7ReVTa9jsTqPCgPgb5Lqaj5S1Xmq+gNVfa+qvhf4O9BP3SNfCg5onRyB3ahzXPQQHZza8cm5cJDRv4iknUE4906/RxszqE+meRWUmSkgItsDBwMfAB4CLgyokxmu3vsGOJiqpkmHsI4OxyoXpqnn8Sq3rW85g5LRLCKbAQeRDAbPAr8GJI1Iqg3F5pCwziBbR3NenkIrh8CmL0XTbo+V10zNbRnbLc0h3RsJ7zgNv7Jfut+yL7mO5v7p5pi3k9Nlv4mMaqYbRTOFu4E/A/uq6v0AIvJZF60ikUgkUglFPoX3AU8B14jI6SKyJ3Wb4ec5mgOIclnly2G6mjlVDTEl9uhLVavhEcAJXFF2dhizTnXnJbyMAEEsg+JoVtXfquoHgC2Aa4HPAuuIyE+Mq6YGpeiA1qWEbpl2XDJ0LWQ4zYi7mzvsci5y9zsExFv5zQbCaW6YB1Msp28xPn2pyFldJvroJVU9R1X3ASYDtwBfDK2YBTGjuV7U8RDm6VzH66HSjOY6Hi+nlde8D02ZjOY2qvqcqv4/VX1rKIWsCe1wKmokcTTbPckVTbGtSkEXZ00bZjTn9MVyZhU87r7b7M1QRmhHc/5lahhk0HICB3U05+8Twx++hxO4qqjWngaFSCQSiTSbRg8K+aO5T0azy8pYDvNuryxNj9XKPJzZ4OM49QgyqKs5pKiGl52MjG3GMhI5vgakRg8K0M3RXBdnYwlBDo5TCzxWKysnx0CGgxPYLaO5634Hc4lHmjlO58XBPBmKRg8Kriuv1dFTNmDU8QhGR7OV7BoesAya0I9GDwoQvsBbcUazGK6hW7zymp2jOT/fwiejuX8ZiZxsKabZ2a6O5uyz75bRbNmXnBun5eyt8iADk9lI8W8lFI0fFCKRSCRSnkYPCn5uZi+npoOMkttCCKrl8XLLaC4ve9QyMuX6BGXU0Qns4cxO5ARotIBGDwrQ5aJ2yGi2wsNx6pE962FySdpphhO4ezCET0azjYzwJ79MEx7+7OhoHlDqXNM8EolEqqDRgwJUPyW2XEM3e6Unv3h4y5oxLn0pua0/GTl5CtY5FyW39SWjwORi62guJ7sfPH73Rc5sC9q/lZin4EedF9ceTp2nq0N0GBBznEUbPoXX+pdh2U5fOji1YfKg1s08OQDHc7Q0elDIu8FER3OPMrzKAdfweLnFC1aUne21kpiLE7imvxVvGj0oAIVXW73W0G2G49TrCasxGc0uAQYD0henQnUujmYDGVVNNxo9KNR5CheJRCJV0OhBAcI7g4ok2WY0V+c4DeNozpJtS14WsK2MnO0exeo8HPMhzn2mKcwhYMJUgs+9pYqqGY0fFIrwmq560JS+uJlDamI7dOkHgzGr9jCBgleQgU9fQjAmBwUvx6m9U7Ma51kIKnMEemU017Av2ctz+1wQLv5/89lI+GNThdu68YNC0YnzcTj5PMn5PPg6hPDWKMTSx9noIKNEOx7Z2V5h1ZbF6vL390/MaI5EIpFI5TR6UMgtBxwk9jq8nJzc2eAy3I6XR3a2qYSCjOamZGeHOPdVmVqtRZQT25+MCjzNjR4UoPgkeTgbvaaATYkjNzO3ddXDQEZXc4hD7oiT/agufSl1/XiYqbz6EoBGDwqehzR7RPerSxRSSF0d89nhteHPSdH20cuppi9hsv+rCRX2cf77hDyHpNGDAhQfVJ+sVgMZZbI0HRzNFvjV8hmADN2+JfiEPoLPdeziNPeZKPisvDaWHM0ispeI3CMi94vIF6vQIRKJRCIjcR8URGRp4MfA3sBWwMEislUIWXkjbX0dzc1wniVyHIqvVZTVGkSOgx0h+9wHMB1myjGW4ZJz4VHYz7jBEizjL5KdgPtV9UEAETkf2A/4ZwhhRRf1MRffyQl/uKev9l+a/2rh/udeWsDbT7quLxllZpEfP2c645ZZui85T7zwCputMz53/xk3PMTv/vFEXzKef3lh4f7bn5jd9/ECePS5l9livQm5+4+//G5OveaBvmTMmju/cP+f7prZd19eXrCocP+c+a+aHK+Fi4qvsk+f9w9WWLa/62v2K8Xn/oGZc/vuy6uLu/9aDjrtbyyzVH9320eee5mJq66Qu//EK+/lZ39+qC8Zz3S5vkJRxaAwCXis4/3jwM7DPyQiRwBHAGywwQajErTNpAnMf3Xkj2qTtVbm4J3W73qRluVNyy/L5uuOvJnuv/0kZr+80MS+uMW643nH1uuM2L7jhqtxwA6TmLew+OZRhk3XWZm3bzVSxrJLL8Un93gNDz4zt28ZAJNWXYEJK4y89A7ZeUNWWWFZExmbrrMyB+44ecT2yautwCG7bMBzLy0wkbHNpFUy9/3HmzbmLw8807cMgDe+Zg22zBjg9t1uIrPmzDe5vjZbdzzveu16I7ZvN3kV3r/jZF5eUPzwU5a1Vl6edSeMG7H94J3WZ9mlbR6Lt528Cm96zVojtr9p0zXZb/uJLFy0uG8Zm66zMu/bYeT1te6EcXz4DVOYOWeeiYwt1s1/sAmFeNe7EZEDgXeq6n+k7z8E7KSqn8r7ztSpU3XatGleKkYikUgjEJHpqjq1l+9U4Wh+HFi/4/1k4MkK9IhEIpHIMKoYFP4ObCoiG4nIcsBBwMUV6BGJRCKRYbj7FFT1VRH5JPAHYGngDFW901uPSCQSiYykCkczqnoZcFkVsiORSCSST+MzmiORSCRSnjgoRCKRSKRNHBQikUgk0iYOCpFIJBJp4568NhpEZBbwyCi/viZgk1paT8Zy/2Pfxy5juf+dfd9QVUemdxdQi0GhH0RkWq8ZfU1iLPc/9n1s9h3Gdv/77Xs0H0UikUikTRwUIpFIJNJmLAwKp1WtQMWM5f7Hvo9dxnL/++p7430KkUgkEinPWJgpRCKRSKQkcVCIRCKRSJtGDwoispeI3CMi94vIF6vWJyQisr6IXCMid4nInSJyZLp9dRG5SkTuS19Xq1rXUIjI0iLyDxG5JH0/lvq+qohcICJ3p9fArmOl/yLy2fSav0NEzhORcU3uu4icISIzReSOjm25/RWRo9N74D0i8s5u7Td2UBCRpYEfA3sDWwEHi8hW1WoVlFeBz6vqlsAuwCfS/n4RuFpVNwWuTt83lSOBuzrej6W+nwJcoapbANuRHIfG919EJgGfBqaq6jYk5fgPotl9PxPYa9i2zP6m94CDgK3T75ya3htzaeygAOwE3K+qD6rqAuB8YL+KdQqGqs5Q1ZvT/+eQ3BQmkfT5rPRjZwH7V6JgYERkMvBu4Gcdm8dK3ycAbwZ+DqCqC1T1BcZI/0mWAFhBRJYBViRZybGxfVfV64Hnhm3O6+9+wPmqOl9VHwLuJ7k35tLkQWES8FjH+8fTbY1HRKYArwNuBNZR1RmQDBzA2hWqFpKTgaOAzlXZx0rfNwZmAb9IzWc/E5GVGAP9V9UngBOAR4EZwGxVvZIx0Pdh5PW35/tgkwcFydjW+PhbEVkZ+F/gM6r6YtX6eCAi+wAzVXV61bpUxDLADsBPVPV1wEs0y1ySS2o73w/YCJgIrCQih1Sr1UDR832wyYPC48D6He8nk0wrG4uILEsyIJyjqhemm58WkfXS/esBM6vSLyBvBN4jIg+TmAnfKiJnMzb6Dsm1/riq3pi+v4BkkBgL/X8b8JCqzlLVhcCFwBsYG33vJK+/Pd8Hmzwo/B3YVEQ2EpHlSJwtF1esUzBEREhsynep6kkduy4GDk3/PxS4yFu30Kjq0ao6WVWnkJznP6nqIYyBvgOo6lPAYyKyebppT+CfjI3+PwrsIiIrpr+BPUn8aWOh753k9fdi4CARWV5ENgI2BW4qbElVG/sHvAu4F3gA+HLV+gTu624k08LbgFvSv3cBa5BEI9yXvq5eta6Bj8PuwCXp/2Om78D2wLT0/P8OWG2s9B/4BnA3cAfwK2D5JvcdOI/Ef7KQZCZweFF/gS+n98B7gL27tR/LXEQikUikTZPNR5FIJBLpkTgoRCKRSKRNHBQikUgk0iYOCpFIJBJpEweFSCQSibSJg0IkEolE2sRBIdJYRGQNEbkl/XtKRJ5I/58rIqcGkHemiDwkIh/reP/+Pto7R0Se66eNSKRXlqlagUgkFKr6LElSFyJyDDBXVU8ILPa/VPWCsh8WkaVVdVHWPlX9oIicaaZZJFKCOFOIjDlEZPeOhXiOEZGzRORKEXlYRA4Qke+JyO0ickVaTwoR2VFErhOR6SLyh1admRK8WUT+IiIPtp74U/nXiMi5wO0ispKIXCoit6YLxXwgTM8jke7EQSESgU1I1mLYDzgbuEZVXwu8Arw7HRh+BLxfVXcEzgC+XbLt9UhKkOwDHN+xfSeS0itbkSx+8qSqbqfJQjFXGPQpEhkV0XwUicDlqrpQRG4nWbmrdVO+HZgCbA5sA1yV1FxjaZLaM2X4naouBv4pIut0bL9Jk0VPWnJOEJHvktRt+nNfvYlE+iAOCpEIzAdQ1cUislCXFARbTPIbEeBOVd11tG2ndNa2f6n1j6reKyI7khQwPE5ErlTVY0chKxLpm2g+ikS6cw+wlojsCsm6FSKytVXjIjIReFlVzyZZRWwHq7YjkV6JM4VIpAuquiB1Ev9QRFYh+d2cDNxpJOK1wPdFZDFJOeSPG7UbifRMLJ0diRiRho9e0ktIahVtRiJFRPNRJGLHbOCbreS1fhGRc4C3APMs2otEyhBnCpFIJBJpE2cKkUgkEmkTB4VIJBKJtImDQiQSiUTaxEEhEolEIm3+P/keRHMrUmmnAAAAAElFTkSuQmCC\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# visualization\n",
"t = np.linspace(0, 96, 1000) # create a list of time steps\n",
"y = np.array([u(tau) for tau in t]) # list comprehension\n",
"\n",
"fig, ax = plt.subplots(1, 1)\n",
"ax.plot(t, y)\n",
"ax.set_xlabel('Time [hrs]')\n",
"ax.set_ylabel('Administration Rate [mg/hr]')\n",
"ax.set_title('Dosing function u(t) for of total dose {0} mg'.format(Udose))"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"The dosing function $u(t)$ is now applied to the simulation of drug concentration in the blood plasma. A fourth argument is added to `odeint(deriv, Cinitial, t, tcrit=t)` indicating that special care must be used for every time step. This is needed in order to get a high fidelity simulation that accounts for the rapidly varying values of $u(t)$."
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"None\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEWCAYAAABhffzLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAABqtElEQVR4nO2deZxcVZX4v6d63/fudNLZ970Twr6FRQcQ0VEGdFBBVEZxw2UE3AbUHy7DKKOOOowygGLAwY1V2QIYQCCBACEhAZJA9r33tbrO74/3XnV1dS2vqt6r7k7f7+dTn+6qV1Xnvlf3nXvuOeeeK6qKwWAwGMYPgZFugMFgMBiyi1H8BoPBMM4wit9gMBjGGUbxGwwGwzjDKH6DwWAYZxjFbzAYDOMMo/gNRzUislJEdrp873Ui8psM5V0iIg950Z6jHRH5hYh8I8Hxr4rIL11+160i8h3vWpc+IrJdRM62/094Dsn6i1+MecUvIpeJyCsi0iUie0Xk5yJS6aO840TkARFpEZHDIvKciHzUL3leISLTRERFJHeE5Ce9Me327Ytso4jkish+ERkTC05U9Q5Vfafz3D6nWel+n4g8LiIfj3i+UkSOiMgHMm2rH0S3NxGq+klV/bb9uWEDoqreoKquvstFuxpF5FciskdE2kXkNRG5XkRKvPj+eESeQ6x7MLq/ZIsxrfhF5EvA94F/BSqAE4CpwMMiku+DvBOBx4AngFlADfAp4FyvZXnJSCn7NGlh6PU8DzgyMk0ZXYjIO4E/AZer6p0j3Jwxg4hUA88ARcCJqloGvAOoBGaOYNNGDlUdkw+gHOgALop6vRTYj3VzAFwH/A64HWgHXgVWRLx/IvB74ACwDfhcAplrgP9K0q5PAG8Ah4F7gIkRxxS4Enjdbsu3sTreM0Cb3c58+70rgZ3AV4GDwHbgkojvehfwov25HcB1Ecem2bI+BrwNPGn/VfuadQAnApcBTwE/wlK4W4GT7Nd32Nfx0ojvLQButL9rH/ALoCiqvV+yP7cH+Kh97AqgH+izZd8b59op8HXg/yJeuxv4mtVVh/xm99jX+A3gExHHioBbsQaLjVhGwU43v7fdV34Tp21PAO+3/z/Fbut59vOzgfX2/5cBa+z/n7Tf12mf98WJrlMcuY8DHwfOt3+j82Jcs09i9akjwH8BYh8L2NfzLVvW7UCFfew24Ev2/5Ps77nSfj7LvraSbnuT9Qn7+K3Ad4ASoBsIMdg/J0b/HsD/AXuBVvvaLoz+rjht+g7wChBI0O6TgOft734eOCnqnL6Nda+0Aw8BtRHHP2xf40NYfXU7cHZ0nyL+PbjGi3ak8hjLFv9JQCHwh8gXVbUDeBBrRHe4ALgTa4S/B/gpgIgEgHuBl7A6/1nAVSLyD9HCRKQY64e6O16DRORM4LvARUAjVmeItszOAY7Bmp18BbgZuASYDCwCPhjx3glArd22S4GbRWSufawT+Ih9Tu8CPiUi742SdTowH/gH4DT7tUpVLVXVZ+znxwMvY81efmu391ism/9DwE9FpNR+7/eBOUCzfXwS8M2o9lbYr38M+C8RqVLVm4E7gB/Yst8d6/rZ/Ak4TUQqbZfdqcCfo96zCkuhTAQuBG4QkbPsY/+GNZjOtM/7UudDqfzeMXgCS5GBdS23Yl1f5/kT0R9QVeeaL7XP+y77eczrlED2u4HfABeq6gMxjp+P9Zstxep7zvlcZj/OAGZgGUU/jXE+p8c4n7+prW3SaG8kST+rqp1Ys7zd9nUqVdXdMb7rQWA2UA+8gNWn3HA28AdVDcU6aM8I7gd+jHUf/BC4X0RqIt72z8BHbdn5wJftzy4Afo6l/Cfan2+K045492DG7UiVsaz4a4GDqhqMcWyPfdxhjao+oKoDwK+xbhCwbpY6Vf2Wqvap6lbgf4BY/tMqrOu1J0GbLgFuUdUXVLUXuBY4UUSmRbzn+6rapqqvAhuAh1R1q6q2YnXsZVHf+Q1V7VXVJ7A6xUUAqvq4qr6iqiFVfRlLGZ4e9dnrVLVTVbsTtHmbqv6vfW3uwhqAvmXLfAjLSp8lIoI1m/mCqh5W1Xbghqhr1W9/tt9WUB3AXFKjB0s5X2x/9z32awCIyGQsi/tqVe1R1fXAL7FuPLCuz/+z27gD6yZySOX3juYJhirG70Y8P50Yij8BqV6nM4AtWJZeLL6nqi2q+jawGmtgBqs//tDuXx1Y/fEDtuvvCeBUezA8DfgBcHKc88nkd/WiTwCgqreoart9b10HLBWRChcfrSHxffsu4HVV/bWqBlV1FfAa1oDr8L+qusW+l37H4DW+ELhPVZ+02/UNrJlLOmTSjpQYy4r/IFAbx3/daB932BvxfxdQaH9uKjDRDtS2iEgLlmulIcZ3HsH6QRsTtGkilpUPhGcfh7CsHYd9Ef93x3heGvH8iG0NObxly0BEjheR1SJyQERasab7kYMdWO6aZETLR1VjtakOKAbWRVyrv9ivOxyKGoi7os7HLbdjzWY+Yv8fyUTAGXgc3mLwGk9k6Hm/FfF/Kr93NM8Ac0SkAetmux2YLCK1wHFYrge3pHqdvgH0An8SkYIYx6P7t/NdQ/qj/X8u0KCqb2Ip4WasWdV9wG57Rhmt+DP5XT3pEyKSIyLfE5E3RaQNy50Cw/t8zDaQwn1rE9mnIPE1Dvc3+3495KJNXrcjJcay4n8G62Z4X+SLdpT+XOBRF9+xA8virYx4lKnqedFvVNUuW+b7E3zfbizlEtmWGmCXi7bEoioq62CKLQMst8w9wGRVrcDyt0t0s+P8nw4HsQaBhRHXqkJV3Xa8VOT/DetGbcCKq0SyG6gWkbKI16YweI33YM1aIo85uP69hzXe+v3XAZ8HNqhqH/A08EXgTVU9mOjzGdKJFeSuAO4WkTyXnxvSH7GuRZDBwf4JLIs1X1V32c8/gjW7XZ95s1MiWf/4Z+A9WG6bCqw4Fgzv87F4BPhHe3YTi+jrBEP7VCKG9DfbJVwT573JzjGTdqTEmFX8tmvkeuAnInKOiOTZLpX/w/L//trF1zwHtInI1SJSZFsVi0Tk2Djv/wpwmYj8q+N3E5GlIuL48X8LfFREmm3L7AbgWVXdnvaJwvUiki8ip2L5cv/Pfr0My/LtEZHjsG6MRBzAmrHMSKcRtn/0f4AfiUg9gIhMcukfB0vZuJJt+5bfDVwQ4Wd2ju3AUrjfFZFCEVmC5Tt2/L2/A64VkSoRaQI+G/HxVH/vaJ4APsOgNfx41PNYuD7vRNgznHOwrMLfikiOi4+tAr4gItPtOM0NwF0RFrhzPs5s5XGs67XGdv1lk31ATQLXTRmWoXcIa+Z5Qwrf/UOsZJDbRGQqhPvuD+3+8wDWbO6fxUofvhhYgDULSsbdwPkicoqdSfgt4uvVZPdgJu1IiTGr+AFU9QdYU/UbsbJbnsWy6s6y/W3JPj+ApWCasTI8DmL5i2N2PlV9GjjTfmwVkcNYwdkH7OOPYk3Lf49lCczEnf84HnuxXEy7sRTbJ1X1NfvYlcC3RKQdK8D6u0RfZFus/w94ynZznJBGe67GyqL5uz3dfgT3/tpfAQts2X9K9mZVfdWOg8Tig1gW327gj8C/qerD9rHrsabH27CyHsIGQKq/dwyewFJAT8Z5HovrsBROi4hc5FJOTFS1BStpYQ5wewIL1uEWrPN/Eut8exg6EEa3fw2WUk3FbeUJdr9ehXVftYjIxKi33I71u+7Cytb6ewrffRgrGaQfeNa+Zx7Fypx5Q1UPYRlVX8IaWL4CnO9mFmf30U9jGX17sO7XmAv0kt2DmbQjVSTKoDKMEkRkJVYaWLwMAYPBYEiLMW3xGwwGgyF1jOI3GAyGcYZx9RgMBsM4w1j8BoPBMM4YE8W7amtrddq0aSPdDIPBYBhTrFu37qCq1kW/PiYU/7Rp01i7du1IN8NgMBjGFCISvRIYMK4eg8FgGHcYxW8wGAzjDKP4DQaDYZxhFL/BYDCMM4ziNxgMhnGGUfwGg8EwzjCK32AwGMYZRvEbDAbDCNLTP8Bv/v4WbT39WZNpFL/BYBj1vHWok20HO5O/0QM6eoPc+NfNtHZlRxHf8tQ2vv6nDax69u2syAOj+A0GwxjgfT97mjNufJyefv83BnvglT38dPUbfOu+jb7LAnhzvzWgvbKrNSvywCh+g8EwyunuG+BQZx8Am/e2+y7vVVsB72vr8V0WWLMZIGszGvBR8YvILSKyX0Q2xDj2ZRFREan1S77BYDg6ONA+uIvqln3+K/7drZbCz5YiPtBhnd/OI91ZkQf+Wvy3Ym0OPQQRmYy1b2j2HFoGg2HM0to96Gt/+3CX7/L22wPNntZu+gdCvss73GHNZlq7+7MW4PVN8avqk8DhGId+hLWJsNkBxnDU0trdT0dvcKSbcVTQ0t0X/j8bVvFBW/GHFPa2+uvu6Q0O0N4bZH5jOQA7D2fH6s+qj19ELgB2qepL2ZRrMGSb9/3sKU79/mOEQsa+yZQWO7umpiSfHVmw+A919oYV8a4WfxXxkU7r3JY2VQCw44j/5wdZVPwiUgx8Dfimy/dfISJrRWTtgQMH/G3cKKR/IOR7pzP4w5HOPt480MmRrn62H8pewO5opcV29SyaVOG7YuwNDtDTH2KBo/h9nmG0RpwbZM/Pn02LfyYwHXhJRLYDTcALIjIh1ptV9WZVXaGqK+rqhm0gc9TzHw9t4eTvPcbbh7JjARztdPcN8L9PbcvKYLo1Iii4aY//wcijnTZbOS6cWM6+tl56g/6ldLZ1W+65+Y1lgP8Wv+PTn1pTTEl+DjuPNotfVV9R1XpVnaaq04CdwHJV3ZutNowl7n1pNwCPvbZvhFtydPDghj1cf+9G/mv1G77Lao3wSWcjGDkSrN1+mGXfeohXd/ufe97S1UdRXg4z60oBf61wRxHXlRVQX1bAWz4bXs4isYqiPCZXF2fFlQX+pnOuAp4B5orIThH5mF+yjkZyAgLAmwey4yp4+1AX696KFYs/OnCm0NmYQWU7C2Uk+N+nt3Okq5971u/2XVZLVz+VxZZiBH/dIc7sorwwjxl1JWw92OGbLBgcaMoL85hWU5K1FFI/s3o+qKqNqpqnqk2q+quo49NU9aBf8sc6jvLwu+M5fPI363j/z59hexYXkWQTx0rMxlTaseKmZNGCyzaH7Nzz1/f73z9bu/upKMqjqaoI8Hcwde678qJcZtaVsvVAJ6r+BejDA02RNdC8dagrKymkZuXuKGQgpGFLwO/gksPGPW0AvLSzJSvyss3+distb+eRbgZ8zrQZDEaW89bh7Ayk2w52cs5NT/LgK3uyIm+HnXaYDUOhxVb8E8oLKcwL+GoVt/VYPv6Kojxm1JXS2t0fXjXsp7yyQmugCYY0K7NEo/hHIe09/ahCfm6A3S09vqcERtY/ycaS+JHAseSCIWVPq/+ZGqUFucyoLWV3S09WLLg7n3+b1/a288OHt/guC6yUR7Cs76DP59dqu3oCAWFGbSlvHvBvlhHp6plZVwLAmz7Oalq7+ynJzyEvJ8DM+lLf5TkYxT8KCad4TSynbyAUXtLttzzInk/6zufe5uGN2Qtct3ZbygP8P0fHNTGlupiBkLKnxf+aLy++3QJYrpfDPlqoMJjyOK2mmGBIfU9BbOnuo6LI+u1m1vur+FsjXC9OMHmrnzOM7n7K7XObYQ80fspzMIp/FOIsWFk40cnt9V9ROWTDJ90XDHHNH17hE7ev9d1adGjtDrLYzpX2+xydm3lKjRWMzMZg+vahLurLCgD/Z21Of2meXAnANp/XKliDdj4As+pK2Xmk27cqnW09/eTnBijMy2FSZREFuQFfLfC2nn7KCy3FX16YR31ZgbH4xystEXnL4P+iDmegmVpTnBUlFRmwfisL8lSVtu5+5k0oIy9H2HbQX5ktXf1U2hY/+K/4e/oH2NvWw1nz6wF4w0eLGAbdIWHF72PmWU+/NbsYtPhLUIWtPsls6w6GFXEgIEyvLfF9huGcG8DMOn9nNA5G8Y9CWrqsqfripgoC4n9Kp2PBLZ5UwZEu/wtFOcvUAV7f538n7+kP0TcQoqokn2k1Jbzhs0Xl3MwN5YXk5wR8D/A6rp3Fkyopyc/x3WJ0+sv0ulLKCnJ9XZ3syHLcdI77xS/laM3WcsPPZ9aX+uzqCQ6RN6OuhDd9ziQCo/hHJY5F1VBeyJTq4qzdyNlyhUS6lt7KQkmD1oiA3SyffcSOvIqiPHICQlN1EW/5PMM4YhsK1SX5zKov9X1ga4lYdDS9zt/c80hZANNrSxDxUfH3DLfAdxzu8tW15MwwHHl+ZxKBUfyjksjOPqu+lNf3++uzDc8wsugDd8iGq8dR/BVFecyuL+WtQ52+Lvtv7e6nwrZQZ9WV+u56cWZQVcV5TK0p8X2GEXk9/V50FLb4iywff2FeDk1VRb7Ngtu6oxVxCSHFtxW8kcFdIGuZPUbxp0BP/4DvGRNg+fidFK9Z9WVsO9jpaxC0rbsfkcFgst/L1J0yu7PqS7O6kraiKI+Z9aWE1L9NNnr6B+gNDvqkZzeUsv1gJ31B/36/wxEWf1NVEXtaenxdqzBE8deWsLul27eB1DFKHFcP2IOpT4qxrSc4VBE7mT0+DN6hkNLeGy0vO5k9RvGnwHt++hTLv/2w73KGZDHUl9I/oL5axq22lVNRnEd1Sb7vy8Zbu/vJCQjzG8uzEkxu6x46gwJ8UxyRShGs3y8YUl9dWo5yrCrJZ1JVEcGQhhes+cGg6yyXGbWWRezXLLEl6noC9oraDl/Wt1huukGf+/RaO5ffB8Xf3htE1bqODhMriijM8zeTCIziT4nN9rZv7T4HP1u6Bqd/fisqGFwZ6cjzexm+4wOfWl3Mrhb/dzkaYvHXlSKSPcU/u96q8ujnNXVmoZVFeUyqtMoa+Lniu7W7n7KCXHJzAkyzFaNfmVLhQbt4qDukN+h92XIn+yvS1VNSkMvEikJfXEuR5RocsrFIDYzid01kcMf/LJs+KrOo+CMXN81pKOX1fe2+ZhW0dgetdMcaa4HTbp9L30Yq48K8HCZXFWdN8fs90IBV/7+80FLETj0bP8sJt0YYJtNrHMXvz/m1dFmzw7KCiEwbnzJ7uvsHCIZ0iCIGmGHPMLwmuq8MyivxXccYxe+SyEyUbGRNOIq4tCCXxopC3xV/pIXa1hMM7zvqBy1dfdYCJzvP3ffSt1GWlZ+ZL05g3vn9ivKthUB+WvxHuvqpLrFcgxNti9/PtR+R/WXQPeiXq8datSsi4df8MobiKeKZPqVYRlbmHCqvlB1H/MskAqP4XZNNxR9pgYO/igqGWnCz7ZvKz/z6NltxzPDRfxqJ45pwSl3PsnOz/QiAxlIes+utWZRfHOnqC8eEivNzqS7Jz5riB5hWU+xbsTZnMVwk1SX5VBXneW4VO5uwDFPE9aV09HpvDIXlRcQUHHmq+Lo+wih+l2RL8asqLVEpXk7uuV/F2lq7B2+u2Q2OT9o/ReUojrqyAiqK8tji8yKu6JS5WXWl9AVDvgQkYyr+hjLfBhqwFL9j8QNMqizy19UTrfhr/UvpbI367Rz8WOEatsCjFXGdPymW8S1+pzicUfwjjjOFt3KI/VNUPf0h+oKhcN4yWIq/q2+A3T5UlXQGGudGri3Np7LYX2XcYs9oRIS5DWW+WsMwXFHNavAvbtJqp8aWFQ4duP0aaMDK468qjlL8PtZ3ip6RzqwrZW9bjy9JD9GyImV6rYidfRSiFbEzC97icT+NFbgGmFFrxYX8NL6M4neJY8kdM7XK1wVATo57dN4y+KOoOvsGGAhpWJ6IMLu+lDd86nShkIZdPWDluW/xPZgcpfgdH7EfAbuuviFupUh5fvn5D3f2URXRX5qqLIvfr2vaEnU959qzRD+MhViuHrCu6aHOPo54uK7GscCjffx1ZQVUFuex2ePzc9bPlOYPnWEU5ecwtbrYV3erUfwuiVT8IYXtPgWzBlcqDnUVgH8WKgx3TWzZ1+GL4ujoCxLSQXlzGqxg8r42/4LJ0YrfqYLo1/WMtuAGFb/3g2lP/wDd/QNURbp6qoro6Q/5suy/p3+AvmBoiPtl7gRH8Xt/ftG/nYMza/NyMI2VXgmWMTSnocx7i78nSFlBLoEII8FhTkNZOH3cD4zid0l0KVq/s0IiO3t1ST7VJfm+yHQW/0QHI1u7+33ZByA8nY5Q/OCP0gjLjCq8Bf6tV4ilqMoLrd2j3vDBgosuYgbQVOXf3rSxDIVJlUUU5+d4/hs6O9FVRLixHJxZxua9bZ7Ja+0e3A0rljyvZ6axjISwvAnWin2/PAt+brZ+i4jsF5ENEa/9u4i8JiIvi8gfRaTSL/leYy3syPU9rz6s+KOtRp+WqQ/eyIM3l7PoyFdFFVb8/vhPo2VGK+PZ9ZaP2OtZjRUoH66oZtX7U7MnnD4aIXNytZXSma3gdSAg9izR29/Q2YkulqunsaKQssJcT63itp7BUinRzGkopb0nyN4271ZERy8Wi2R2QxkDIfWt/LSfFv+twDlRrz0MLFLVJcAW4Fof5XtKS1cfFcV5FOfnMqnSvwBva9jHP1R5zGqwLFTPc4lj3MhzfJhGO0QrjprSAmpK8n1T/NG1cxxm2Sl6XruYov3fkfLe2O99ZlasGdtk2+Lf4UOAN16u+5z6Ujbv9ba/RK+JiMRJDNjioczo7K9I5oRnGN4ONPEU/1yfZ8K+KX5VfRI4HPXaQ6oatJ/+HWjyS77XRFqNfubVx/LxQ4T7xeNc4lgzjLqyAsoLc33z2UbLm2PHFPwg1sAGg3ETr/2o8ZTH7AZ/MrNiuXpKCqxcfmdDdE/lxVHGcyeUcbCjl0MeugfjDTIOcyaU8dreNs+MoUSK2A+XZHQt/kim15aQGxDfdlMbSR//5cCD8Q6KyBUislZE1h44cCCLzYpNpOKf02BN2/2omNnS1U9uQCjOzxnyuhNAe83jjhBroHGCWdmw+MHfMhGDudlDb+h5E7z3Eatq3GCkXzV7YhUxA5hcVeTLlp3x5M3xIbOnJcagFsm8Cd4mBsT77cAqgFdXVuDp+SWSl58bYEZdydiz+BMhIl8DgsAd8d6jqjer6gpVXVFXV5e9xsUh8keaO6GcvmCI7T6UGojMcY9k3gRrG0avLYDW7tgDzewGf2Y1sXzSsxvK6Owb8GXRUTyrsbI4nwnlhby2x7vr2d0/QP+AxlRU4ViGx79fvFzwydXFWfPxgz+ZPYNurOExE4hwv3gkM5EFDoMBXq9INMMAf2fCWVf8InIpcD5wifq9v5iHtHYHwx1wXtj69s5aDMvpim0FVJfkU19WwCaPZcYbaGbVl3G4s4+DHmf2tHb3k58ToDBvsOs5SsOPvOVE7oK5E8o8nUHFyshyqCzOp7Gi0PMZW0tXP4EYueCT7cqnXq8Wdq5nWZTCqg+vwvbu/JK5esJ+cI+uqRtF/Po+b+I0/QMhuvoG4sYUwDq/tw930dUXjPuedMmq4heRc4CrgQtU1f9C7B7hlGuN9PHn+OR/SzT9mzuhzBeLP1bn88tCdeRFDjRz6v3NA4fYymNeYxlv7O/wrCx0MkU1b0IZm/Z4PXBbRcyic8EnVxXTP6Ds8zALBawZRlnh0AVqEBFs9dQHnvh6VtnGkFeDabx7wWHuhFK6+wc8SZNt77GUebxzg4jyKT4YRH6mc64CngHmishOEfkY8FOgDHhYRNaLyC/8ku8l3f0D9A0MZoYU5uUwo7aETR66CRycGzkW8xvLeX2/t7GFtjgDjeNa2uS54u8bstEFWG6Keo/9p2F5CazweRPK6BsIeVZgLF5gPiyvsZw3D3R4uhuXNRMdLs9J6fR6o5tEhsnshlI27/UuVtPa3U9RXg75ufHV1NwJ3gw2oZDSEbUbVjReJgQMVoxN4Fqa4E8CAvib1fNBVW1U1TxVbVLVX6nqLFWdrKrN9uOTfsn3kliW3Fw7o8APWdGpnGGZDWV2bMG73N54ucR1ZQXUlhZ4bqHGOz+vbuDh8pwKiDFcPQ3eDm4tXbEDyQ7zJpTRP6Bs9bB2vZVmPPx6hlM6PVb8LV19cYOtcz0OtibzuYPtftnfnrFLK9ZuWNF4WbMnvEo4gWtpSnUxBbkBz2fdYFbuuiJWytz8xnJ2Hun2vDBVW3cwbueb12hZAF7ONBJNb+c3ej+4Jcp6eX1/u+d57q3d8RflzKx3Uua8OcdkrglnFuVlQDnejG1iZRE5AfF8r4NEFr/XwdZEshzmTiijpz+U8cwmXrmGSMoKrR3OvHC3xss2iyQnINYsKpsWv4i0JXm0i8gWz1s0ConlLpjnQxZDyFmiHqcz+BFbaOsJDnO9OMxvLGfLPm9dS/Fu5nmN1g3s9d7CiZRHQW4OM+pKPLuesdYoRDKjroS8HPE0QN/SHbuIWX5ugOm13qcDulH82Qq2QmTphsxkJovPOMyxiwpmint5/syEE1n8b6pqeYJHGeBfwehRRGuMadm8RttN4KH11tFnTzcTKaraEs+s8Fh7jEYyv9FyLW31sNZ6S5yspQX29dy42/sZRiKrat6Ecs9+Q2cT+chtAiPJywkwq77MU4s/Xtli8E5JDZUXO6YAVuZZncfB1mSKcbZHJT/i1caPZu4Eb+I08TZ9GSavoYx9bb3h1FavSKT43+/i827eM+ZpixGBn+jUCvHS+nbh95vX6J2i6uqz9hhNFEwGPPPzD4SU9p7YimNWfSm5AWHjnlZPZDkkWoYPlqtgV0t3+MbPhJZua+/b6NTYSOZ7GBsKheIvGAPLWnzrsHdb+IUNhQTXc35juWf9pa0nsSywdhybUl2c8X0YbzesaBZMLKd/QDNe4xJv05doHANzo8extriKX1W3ikiOiDyS6D2etmaUEst3KyLM8zjAG703bCzmeaiokvkZZ9SWWq4Jjwaa9jj1zsHKlJpVX+p5plQyq3F+o3fuiUTWsMO8RsuCO+xByeT2HmuGmEjxq3pXUDA6uy0WCxrLeX1/uyeZS/HWtEQzb0JZxu6zZPEZhwUeKeK27n7ycoSivJyE7/NrJpwwuKuqA0CXiFR4KnWM4Sjk0qig67wJ5bzmYfqaG6sjHFvwRFEl7uz5uZZrwisLLpm8+Y3lvrh6Et3Mc52Aq0fXM6niD8vL/DyT1rLxuLDYYLpq7Kwz8M4iDoWU9t74iQ7RMrcd7MxooZObYCtYNXQK8wIZ99NW28WaaHYIVnZdfVlB9iz+CHqAV0TkVyLyY+fhaStGOW09/cN2VQLLemvvCbK71ZtFMm4CPl7W7HHjZ/QysyfRylawrJu9bT2eFvpKFCyHQZedV4o4VmplJE5mlhd+/pY4lVwdptVY6YBeKQ03/dMrizicXunC4l/QWI5qZvG2eLthRZMTEOZNKM/YJdnWk3jNQCQLJnpvELlR/PcD3wCeBNZFPMYNVj5x7AVAAK956NOExIp4UmURZQXeKSpIfCPPn1DumWsiVlpsJAsmehswd5bFJzo/x2XnhVXc2hV/8Z1DnV2GOhu/X25OgIUTy3l5Z0vGsiDxYjiH6bUlFOXlZKyo3KRXOiycZDkkNu5OXxk7Fnis3bCicRRxJjN9Z38PNyxoLOeN/R2ebsqSVPGr6m3A74C/q+ptzsOzFowB4gWZnKm0V1kMbjq7iDCvscwT5TgoL34H9DLA68bV45UsN/Ii5W7ak/kaAsvVk/hmdn4/L/pMonr1DkuaKnllV6snKblurmdOwDq/VzNQwpGykmW9gDVrqyzOy2iWYVng7hVxW08wo6KCybLNIlk4sYJgSD0t3ZBU8YvIu4H1wF/s580ico9nLRgDtMYZncsK85hSXezZNMyZbsZLB3RYOLGCTXvaMl6t6OZGHlw0lvk5xivp61BdYlXMzKZrAmDRxAo6eoMZrSFQVdp6ggn93w7zJpSzeW/mq03dKMfmyZX09Ic8KQft9nouaCxn454MLeIEiQDRiAgLJ5bzagb3YaK05mgW2jPTjOS5yFhycGbCXrp73Lh6rgOOA1oAVHU9MN2zFowBEqWwLZpUzoYMrZuwnASbL0eycGI5XX0DbMswv965uaIrLUZSW1pAXVmBxzOMBD5iD/2ZbhXVwknWjbVhV/q/Y0dvkIEEqbGRLGgspzcYyngXt47e5MkAS5osN8hLO1oykgUpKP6J5bT3BDMqZuY2vTIss9FKtEi34J6bwLzDvAnlBCQzRWyt0Hcnb2p1MSX5OZ4GeN0o/qCqRt8RY6acshe098T/kRZOrOCtQ13hmyITEm2+HMki26fpxXQ6VtA6Gq9ys1u7+ynMC1CYIIVtQWM5bxzo8CT33E16LFjlIvJzAhkN4MkC15EstpVxJgMNWOmxASFhSuC0mhLKC3N5aWfmxkmrMyNN4pteONH2uWfienE5yETK7MtgMHWzStihKD+H6bUlGbqW3A80gYAwv7E84/t9yHe6eM8GEflnIEdEZovIT4CnPWvBGCBePRSAxR4pYUeOm843u76UgtxAxoojXtA6Gic3O9Pgkpu87PmN5QyEMk8HBPfKIz83wNwJZby6K/0b2e0gAzDDTgl8JcPfr6MnSGlB4gVjgYCwpKnSM4vfzYx0bkNZ5haxy/RKh4UZukPcFISLZMHEirRl9fQP0BcMpSjPmziUgxvF/1lgIdAL/BZoBT7vifQxwICTTxznRwr7+zJQGg6tLhV/bk6AeY3lbMhQptsA0+JJFfQPaMaZL4lKTjt46c90U/rWwXHZpeuXdrsSE6zfb0FjecZ9pr0nmNBN57B0cgWb97VnPItqd5mCWJSfw4y60ox84K3dsTeYiceMulIK8wJpy0zF1QOWMbSrpTuc6ZQKblbox5LX0Rtkh0fbabpR/O9S1a+p6rH24+vABZ5IHwO0J0mxrCktYGJFYcbWG6Q2/Vs0MTNF5chzk1Lm+IkzPcfW7v6kwc+p1cUUe+TPdJN+6LBwYgUtXf1pZ2o4Pmm3v9/iSRW8urs1IwuuvTeY1O0CsLSpkoGQZjwrbbdnGG5YkKF70NrwxV16JVjZRHMnpOcO6QuG6O4fSE0RT0x/vUKqs5lIeZkMppG4UfzXunztqKQtQT13h0WTKjwJ8FoWuLsba9GkCtp7guw4nEkAzZ3F31RVREVRXsaupVYXriXHn5mpLEueFVMoyE28LB4G4ybpzqLcFvlyWDipgs6+AbZlsLdCe0+/O8U/uRKAl3ZkHlNIJfNlV0t32sXFUrXAHZnp5Ne3p6OIM1io5jZIHsmchjJyAuJZ4kOisszn2v78SZErdkXkVqyN0scFbtLKFk2qYNvBznCWRdqyXNR6Ccu0A2iZDDiJYheRiAiLJ1XwcoYBwjaXA5tlDbdlnHueWqaGdWOlaxU7W+m5VR6LJ2Ue4O3odWeBN5QXMqG8kJcyXMhluZZcWvyZ+txTyKt3WDjRyq9PNZuorSe1DCIYLKXwahq/3+CKeffyCvNymFVX6lmAN5HFvxtYi1WyIXLF7j3AP3gifQwwmCsd/0daNMlaMp7JaJzqdHPOBKuaZSaKoy1BtlI0i5sq2LIvswCvW1fW0skVdPcP8OaBzNJVU1H8hXk5zK4vTft6ul2D4TCrvpT8DAP0HS59/GC56zIN8Hb0BofVq4qHY5ik6x5Mz+J3Ei1Suw/TscDBGrzTGUzTcfWAlXb8yq7M1kc4JKrO+ZK9Qndm5IpdVf2Dqh5J9sUicouI7BeRDRGvVYvIwyLyuv23KuMz8Bk3ueeLPLDeUu0MBbk5zGkoY0Oag01wIERHr/sZRqYBXmdPUzeKavGkSoCMLdRUYiZgKY50r2dbTz+l+ckzXhzycgLMbyzPKG7S3uNeES+dXMn2Q10Z1XV361oCayP0ydVFaf+GqSyockh31pZOsBWsVdFbD3amvAtfqqmqDkubKjnY0cseD2qDJXL1/M7+90UReTn64eK7bwXOiXrtGuBRVZ0NPGo/H9W4Ucj1ZYXUlxVk7HaB1DrDokmWLzwdC6A9xemt45pI193jZk9Thxm1JZQW5GZcY8ZNmeRIFk0q50B7L/vbUr+x3KbGDpE30crsSTfA6za4C5bSgPR/P1V1nUXkYKWRZs/iL8yzjKFU1yyka4EvmVyBaupxIWeG4fa3C8trcu7BlpQ+F4tErh4nZfN84N0xHglR1SeBw1Evvwdw6vzcBrw3hbaOCG6zNRZNqsjI4k8l9TBS5uHOvrQsgFSnt01VRVQWpx/gTaXoViAgLJpUziuexBRSUfzpx03aUrCGHRZPqqC9N5jWfrG9QSsX3K1raXGGSqM3GCIYUtdZPQBLmyrY1dKdVrXVVEoaRNI82XJppWIMpevqGRxMW1L6XFtP0HXSQSTzG8vJDYgni/ESuXr22H/fivVIU15DxPfuAerjvVFErhCRtSKy9sCBA2mKyxwnn7gkP/GPtGhSBW/s76C7Lz0feKxdvpKxMAM/aqpZKJkGeMMzjBQs1E17MtvQI1WrcX5jOSLwys40UvRSHGRgcKBJ5/frsK+nWwu8oiiPGbUlrE/TAh/sL+4V/5I0Zxm9wQF6+hNv+BKPpU2VtHb3p7TJvNttEKOpLsmnqaoo5fNLx40F1oxmXmOZvxa/vZl6W8TfyE3WvS0OHQNVvVlVV6jqirq6Or/FxcWxPJJtmLBoYjkhJe063eku6sgJSFqWcbKNwWOxaJIV4E1nIVCqA83ipgr6BkJpxxRSjWEAlBbkMrOuNM2AnftAucOchvRLRTgDaUoW+ORKXtqZmjXskOpAA9aMJiCpx2rSyXpxcAabVGS29Vi7YRXmucluH8rSpsrUzy/F2FMkS5oqeXlHZus/ILHFX+Zsqh69ybqqlqcpb5+INALYf/en+T1Zw+3o7ORKp2tRpbLk36EoP4d5E8pYn0a2RjpWzpJJVnnYdJRxKq4eGJxGpx0cTGMGBVY1y/UpugrAznFPMf3QKRXxchp9xkkddhvcBcv1cqC9l71pxDDSGWhKCnKZVV+askWczr3gMKfBWsGbSmzBmRkmM+5isaSpgp1HUnNnpVKSOZrmpkrae4MZrf+AxBb/WhH5TxE5R0QKM5IyyD3Apfb/lwJ/9uh7faMtzubg0TSUFzKxojAtJWzJSc/P2DzZqsOSqgWQjl/TcU28nIZrYtDV4z6mUFWcl7afP12/bfPkSg539qW8MC7d6fuyKZW8vLMl5RLNg5VVU3C9ZLCQqz1s8acakLTOL5WBNN1gK1jlMFJNs0z3t4MId1YK94RVmTP12QxYAWXIPMCbaG5zAvBHYCXwhIg8ICKfF5E5br5YRFYBzwBzRWSniHwM+B7wDhF5HXiH/XxUk8pq2uYplazfkTTTNa6c/JwABbmpTTebJ1sWwNaDqRU1S6W2jIOjjF9OZ4aRoqISERanMY12SGUjj0iabeX4Ygq/Yyr7w8aS19k3kHJRurDrpSA116AVHGxJSRZAR2/sfaeTsbSpgoMdfSmVwkh30HZY0lTJhl2trks0t/UEKUtT1uKmCkRIadaWiatnVl0pRXk5Ga/CTuTqCarq46p6jaoeD3wMaAe+IyIvisjPEn2xqn5QVRtVNU9Vm1T1V6p6SFXPUtXZ9t/orJ9RRyrWQPPkSnYc7uZgOlkMdjpgqtPNZVMqAXjh7ZaUPtfabfk1E5X0jUZEWDalihczcC2lZKFOquD1NAPm6cQwwMoFL8wLpDRz6+hzvz9sNMumWEtZXnw7NYMhHQvcCQ6ms5CrLcUZm0M6Ad508+odlk6upDcYYss+dy5JtyvYY+HEhVKxwDNx9eTmBFg0KfPtNF2bl6q6R1VvUdWLgGOAOzKSPEZIpU63cxOvT1EJg/tyBtHMqC2lrDA3ZReTM6ClPNBMruSN/R0p7z/Q1tNPSX4OuTnuZzRLmioYCGlaAfN0rUbHVZDK9cxEUU2rKaayOI8XU+wz6fj4wYqdvLIz9eBguq6eeY1l5OWkNstIp4RCJM1OfMilVZzK/rexWNJUwUs73a2nUdWMXEuWvEpe3d2W9qYz4G7rxXtF5J7IB1YO/goPff+jlrbuoGurcdHECnICkpKbICwnhQEmkkBAWNpUmfJgk84CGYDlU+3BLcWBpj2NvGwnYJ6qUnTkQXrKuHmydWO5TSVNdbeoSESE5smVKfcZR/GnqoiXNqXnGnRcSyUpBHfBWmE+v7E8NVdIhhb/5GrLJel2ZpPumgGHVFbUdvYNENL0BzWwBppUZjSxcGN+bQU6gP+xH23APmCO/fyoZbB+jrsfqSg/h/mN6WbZpD/dbJ5cyeZ97Sm5RNL1ay6xfZqpuibaut2vMnVoKC9kUmVRWoq/I00LFaB5chV9wZDrssKppqpGs2xyFa/v70hp6X9bjxMTSm0R0PKplUDqrsH2nn6K8nLIS2HG5rCkqYJXdrW6DmC3dfdTkJt4p7ZEiNibz7iYZVgWeOqpuJEMVj9NLi/dcg1D5KU4o4mFm19xmar+s6reaz8+BBynqp8GlqcteQyQTnaBlWXjvpM7ZOL3WzbFqreeykKgdKe3ZYV5zG0oS1lxpDujWT61inVvpT6D6ugNIgLFSRbexaLZjpu4HcBTrcwZzbIplaim5gfvSKFSZiQzakupKMrjhRSvaSqVOaNZPqWKjt4gr+93Z6GmOxuNZOnkSrbsa6erL3HF3J7+EH0D6S0Wc1jQWE5+bsBVP0036SCSqTXFVJfk80KKxlckbhR/nYhMcZ7Y/9faT9Ov+DQGSGfKuWyy1clT3fvTShtN06cZdom47wiZzDCWTalk/dtHUvITpzudPmZKJXvbetid4gYpzqYh6eRmT6wopK6swLXi9yIYCan9fqkUaIskEBCWT6lMeTBNpTJnNMfY7kG3MjN1vYAViwppcqs4ney2aPJzAyxtqmCdi98v1fUssRARlk+pSnnwjsSN4v8SsEZEVovI48DfgH8VkRIG6+6MCL/821Z+tWabb9+fziIgx1pM5SZWVdfbLsaiprSAydVFqQUkM7i5lk2poq0nNT+xtWF96jfXMVOrAfdKI1Ke2zo20Th+d9eKP42c+kgqivKYWVeSWiaRy1r8sThmquVaSmXbQKsWUXr9ZUp1MbWl+azb7u439MLid7Ld1r2VOHEw00HbYfnUKjbsak26qj3dhYXRHDO1iq0HO9OqgwQuFL+qPgDMBq6yH3NV9X5V7VTVm9KS6hHfuX8T375vY0b1XBKRTuG06TUllKeYZdPVN8BASDOyAponV7mW6Qw06Xa+5WmkkDpb6aXKvEYrvTJ1CzV9RQXWLGrbwU5XZYzTSVWNZtmUKl582/1Cp1RKJEfjBOhfSCGg3JHmOgWwBtJjpla5soghswVODpXF+cyuL2Vtkn6T6ZoBhxVTq+kfSO5u9cLVA7Bimv0bphH/AndZPTlYG6+cDpwJXCkiX0xLmoe0RQTCMoluJ5SRxo8UCAjN9k3sWk6aq3YjWTa5kj2tPexpTe4S6ekP0T+gaXe+GbWllBfmup7VqGpaOyqBVbd+aVNlyv7MdF0hDsvCM7eWpO9NJ1U1lrxDKawYtlxZabqWmirJCUhKroJU9tuNxTFTq3jrUBcH2pNbqF5Y/GApxxfeSuySzGSVcCTLwzOMxNe0LQ1jMhaLJ1WQlyOsTTKjiYebnnovcBlQA5RFPEaUQx2DlphX+1BGk26nWD7FyrJpc5ml4YUV4FgAa11MpzO1clId3MIzmjTP75ipVWzc3ZZS1lImrhCwYjW5AeH57clvrHQqc8aSB7ge4NJ1nYGVkjm/sSylWVQmMwxIzWXnhY/fkdnWE+T1BKuiMykIF0lNaQHTa0uS3n+DbsHMzq8wL4dFkyrS9vO7UfxNqvo+Vf03Vb3eeaQlzUMiU9+82ocyGre1+KM5dlo1qikEszLIA3dY0FhOcX6OO0XlQUDLGdzcpCBmmvVyzNQqgiFNabViulkvDkX51o3l5nq2p1GZM5q5E8ooK8h1JQ8yC7YCHDPFcg263de4I4MZBlib3OTnBpIObKGQZpR4EMkK26WVyCr2ytUDVj994e0jCd11bd1W7CnH5U5tCeVNqeKlna1pbYfqRvE/KCLvTL1Z/uIoE8CTjQlikW79nGVTKi1rcZu7m9iLzpebE2D5lCqecyHTC3nLp1Sh6i7lMdPgp7Mi2q2PGFLbnSoex02v5qUdbgJ26a26jiQnICyfWuVK8as621hmMHBPraKrb4DXXFRaHQgpnX0DGckryM1hyaQK1iY5v86+oLXAKcOBFKy0x2RBZcf1kqkFDpbiP9zZx/YEewFkkrYdzYpp1nqTVPcYBneK/+/AH0WkO5v1+JPhWJor59axYVdr0nzddHBu6FRTAovzc1no0loE7zILjp1WzeZ97UnLKXghb/nUKgKCq8EtU3nVJfnMqC1J0Sfdn5GrByyLsW8glDRgl+4ahWiOm17Nln0dHOlMHFDu7rdcZ5lY4E6KpRvXUiaL4aJlbtjVlnAgzbRcQyQiwoqp1QkDvG32wrT8FI27WDjXNNHgls5ObfFY7hhELrOlInFztv8BnAgUe1CP3zOcDnLW/AaCIU1rdWdSGRmMzsdNq3JlLYJ3081jp1tWeDIF6UVAq7Qgl0WTKnjWheLP1NUD1kDzgsusl/6BED39oYwUI8CKaZZfOtksKp1VybE41paXzGAI18bPQOakyiIaygtcDabtvZnN2ByOsQfSRNt3emmBg2UVv324K+4+ym0p7suciFl1VtJDosHUKzcWQH15IZOri9Ja4OhG8b8ObNB0tu3xEaeDnDG3joDAs1sPeS4jk9z6Y6dV0zcQcrUaM1NXiIMTkHwuieLwIv0Q4Lhp1by4o8WVKyRTeSvsabSbhXGdadaxiaa6JJ9Z9aVJ3RNeBSOXNFWQnxtwofhT3wYxGifF8nkX1uJggbbMc90hcewr3WJw8Qhb4XFkplJ2PRkB212XKMDrpasHCM9oUlXPbhT/HuBxEblWRL7oPNJqpYc4HaSxosi15ZkqVgpi+oofkltvYJ1LcYbpgBARkExyLdo9GmiOn1FDXzD54OaFa+n4GTUA/H2r+xlGJhaxw7HTrBsrXgkOL6otOhTm5dDcVMlzSZSxV8rx+Ok17GrpZkeSzd7T2X0rFrV25kuiwaaj11uLf+HECgpyA3GVsVduOocV9uK4w3HcdV4kAkSyfGoVBzt6U9pjGNwp/m3Ao0A+oyids70nSEl+DjkBCVue6US3E8rIoFxrVUk+cxpKXQVbM02Vi+S46dW8vDOxi6m9J0h+buoFvqI51k4hfW5b4tlWmweKalpNMQ3lBSm5ltJduRvJsdOqaO8Jxt1u0otqi0PkTa/i1V2t4VlLLLyywE+wB9Nk17TDI1cPwPHTq3lu26G4A6nXFn9+boClkyvjZvZ4NVtzcK5pvHsi3fLrceVNtwzMZ5Pcg9G4Wbl7faxHes30jvaIJeTHTa92ZXmmSiY75YBlLb6QwFp0sApgedP53LiY2jLIAY+ksjifeRPKkiqOtp7Mqi2C5Zo4YUYNf996KOm0drBkcebX1Jm5xVMcmZR/jicvWczKK+U4u76UquI8/p7ETerVQAOWYmzrCcatfOqFkRDN8dOreXV3W8zUY68WizksaaqkMC8Qc2Y6YO/U5qW8WfWl1Jbm88ybHil+Ebku2YfdvMcvIqsFHusyCJcKTrnWTDr7cdOrae+N38kdMql8GI2Tu5zIxdTu4fT2uOnVrHvrSMJNITK9jg7HT6/hQHsvWw8m3mjaucG9cPU0VRUxobwwbt8aXIPhzfU8xs6WShSnafdoEVAgIBw/vSapteilFX5C2GUXW6bXAynAiTNqGAhpzHvCi/IQkeTnBlgxtTrm+flxbiLC8TNq+PvWwyn5+RNZ/B+P9OnHeHwJ+ECajf2CiLwqIhtEZFU6G7q09w66R6pK8pnbUJbUckmF3qBVrjWTzu4+SyOzujKRuHExeTnQHD+9hq6+gYS5xF7kuQOcMMOe1ibx84d3p/LA1SMiHDu9mue2xb6xvArMO5QV5rFgYnnCOI23iriaHYe72Xkkvo/YS3kTKgqZXluSQPEHycuRlNfOJGL51CrycwLDrOJQSNPaICgZJ86s4bW97cP8/F4bCWF5M2rY29aTkp8/0dX9H4b69KMfpaSxEYuITAI+B6xQ1UVADmkMINHukeNnWJan25WIbr4fMsucmFhZRFNVUVJF5aUiBksZr91+OK4V7uVAc+z05H5+r4Kf02tLqC8rcO2a8MqSO3FGDfvbe3nzwPCZhldrMCI5dlo1L+44Erf4YHtPPyJQmu+B4p9p+/kT9NGO3n5yAqntz5xQ5oxqnt12OKYL1Omb6ZTTjkdhXg7LplTydJTi77AXi3npeoFBAyX6nvCiJldsedZv+EwKhm+izdZj+vajHv+RZltzgSIRyQWKgd2pfkG0sjxuenVSyzO17/dmOn3SzBqe2Ro/mAXe+dwdTp5VQ2ffQNwdgbwcaOrLCplRW5JQcbRnkB0ViePnf3ZbYj9/uvvRxuMkWzk+8+bBYce8KvIVyQkzaujpD8UtgtfeG6Q0P5eAB8v+59SXJfXzZ7K3QSxOmFFDe08wZo0tr40ghxNn1rBxT9uQaqt+DNoAiydVUpSXM8zPPyjP2/ObWVdCnQuDKBLvr3ASVHWXiNwIvA10Aw+p6kMJP7R5M6xcOeSlfyhbTOtHr4CuLjjvPN45EOLOt45Q95diqCyCyy6zHgcPwoUXDv/OT30KLr4YduyAD3942GG59F+Acup3b4cvXDL881//Opx9NqxfD1ddNfz4DTfASSdxfsd23verr9P9l4qhroebboLmZnjkEf7rf77IhPJC+HHx4PH//m+YOxfuvRf+I8b4+utfw+TJcNdd8POfDzl0dkipXvYvPPXGIVY8fg/ceuuQ499/+wi///Z/W09+9jP43e+Gf//jj1t/b7wR7rtv6LGiInjwQev/b3+bX951D4c6etFbqxGAmhr4/e+t49dey3W/e5Digly4vdR6rakJfvMb6/+rrrKuYSRz5sDNN1v/X3EFbNkSPvS1th7uDzSw/YoTmV5bAh/6EOzcOeTjzQ1zCMx4j2Whvv/9cCjqhjjrLPjGN6z/zz0XuqMqYp5/Pnz5y9b/K1cyFfjD2y2U/jkHGsrgoovgyiuhq4sTP3Yhdx7spOmpKnDScTPse6d85vMEJJ+Njz/P8Zd/b9jxCad+kLLiWUn7Hk8/DV/96vDjEX0v8J3vcOe+drr6BuC/Kq3jUX3vI/s7+MeeIKy+wTqeoO8BcPfdUFtr9buovgdwwp1/AKD1P/4TXnxs6KXZ286XP32T9cRF3+PRR4cej+p7PPMMAJf39HPC7ja6XrmFyvus40X/+mXufOhvzHm0DEryrc8k6HuAdd1ustsXo+9x4onkf/e7rJhWxdnfuBJ+ODhYzu3s47OFMyj//KnWCy763jAi+h7nnQeAAL/d30FbTz/afRXy0Y/G73s23jnSXCIiVcB7gOnARKBERD4U431XiMhaEVnb3z88Gt/THxoycubnBCjKz0larsAt3X3WNLukILPp7aIma5FzW5x29Q+EUFVPijY55AaE+RPKeSqGhQoQzHC5fzTlhXlWPZc4KYgDISXXo/NzLOtE1k3/QMhTC1WAiqJcWruDRM8zggPWKzkB726lkoJcFicoRd3Vl1mBtmjKC/Po7R+gN45raSDkbf9sKLdmidsODXedDYSUMg/7poPTHw5GbFzSZ7tCvTw3B2dWE+ludWb9Xvv4wZpF9AdDHHC7MYuqZvUB/BPwq4jnHwF+lugzxxxzjEbS0x/UqVffpz95dMuQ16+7Z4PO/foD2t0X1Ex58JXdOvXq+/TVXa0Zf9c7fvi4fuiXf4957FBHr069+j69Zc3WjOVEcsP9G3XWV+/Xzt7+Ia/3Bwd06tX36Y8e3uyZrIPtPTF/D4fZX3tAb3hgoyeyQqGQrvjOw/q5VS/Efc8X7npRT/ruo57Ic/jjCzt16tX36Ss7W4a8/v/u36jzvv6gp7JUVb//4Cadce392tbdN+zYB29+Rt/3s6c8k7Vxd6tOvfo+/f26HTGPX/SLp/Wffv60Z/JUVa/5/cu66Jt/0f7gwJDX/+FHT+jHb3veU1kO//w/z+g//OiJ8PO/bNgT8zf1grXbD+vUq+/TB17eHX7t5ife1KlX36ftPf0JPpkeb+5v16lX36d3/P2tIa8DazWGTnWzEUudiHxVRG4WkVucR9pDk+XiOUFEisUyyc4CNqXyBfHyik+ZVUtPfyijvSiHy8jcsjppZi3Pbz8cc4GZV7GEYTJn1dI/oMNWLHqZ4+5QU1rAgsZy1rwxfIbR0z9AXzDkmR9VRDhpZg1PvRHfz++Hn/hE28//VNQ5er0gx+GUWbUMhDRmdpbX5ze3wfLzP/VG7FlUppVAY3HizBrae4NsjEp19svHD1aQ/rW97eHtCts8LMkczZKmCorzc4YEXFu7+wkIlOR7EySPxG3ig4Ob+emfgQrgEeD+iEdaqOqzwN3AC8ArdhtuTuU7Bgs5De0gx8+oITcgMRVQqnip+E8OD0gtvsqJ5NhpVeTlyDB3j1/yTp1dy7q3jgyrkup1ho0lq46DHb1xSwp3ZLhbVCwayguZVV/KU28Oz9TwetAGKwWxIDcQUxl7mZUFVj7/ybNq+dvrB2IOppnuZhYLJ/Ml+l71uoRCJM7g7Sw4HKwE6r28vJwAx06rHpJJ5KwS9jJjycExiJ5+82DCHccc3Cj+YlW9WlV/p6q/dx6ZNFKtTV3mqeoiVf2wqqa0Y3A8i7+0IJdlUyo9VfxeKJDjZ1STExCeTpAV4rUiLs7PZdmUKp5+I3ZKmdeZBSfbM4xoC9WPrJdTZ9cC8OSWAzGP+2GhApw8s4bntx0ekmbp9QIgh8K8HI6dVj1shgH+WMWnza5jf3svW/YNL4Lnx/WsLytk3oSyIb9hKJT5PgOJWNJUSUl+TviatnZbabFelPaIxamza3ljf0d4O1QvK3PGllfHwY6+YbOoWLhR/PeJyHmZN8s7ElmRJ8+q5ZVdra42yU4sw6rTnWnhNLCCZ0uaKuLexM57vObkmbVs2D30Wni5/D6S46ZXk58bYM3rsWcYXp5fQ3khcxvK+NvrsQd4a3cq76/niTNr6e4fGLL5jNe1XiI5aVYNm/e1s799aElhLzaZiebUObEHU1W19zbw/hxPn1PHureOhJMCOvuCqHpvBDnk5QQ4cWZN2DBs67b2bPAiLTYWJ8+yrqkza2vzuEBbNOHf8PXYBlEkbrTa57GUf4+9CcuIb8SSyC9+yqxaVBm2WCNVvLY8Tp5Zy0s7W4fVC/HL9QKW4lAdmgHjl7zCvBxWTK0aPnWP45bLlFNn1/Lc9sMx9+H1YhOWWJw4o4aADPXze7U4LRan2IojcsVpb9DbmIlDY0URs+tLhymN3mCI/gH1pX+eNqeO/gENn59fRkkkp8yq5a1DXbx1qDPjWlzJmNtQRm1pPmvsa+plCehY1JcVMr+xPO5MOBI3RdrKVDWgqoX2/yO+EUsi5bV0ciWlBbkZu3u8nk6fNMuqFxK9qMOv4C5As30tnoywjP2Ud/KsWl7b286B9kHPnR+uHoBT59TRFwzFrGnjV4CwojiPxZOGztz8DEYunFhBeWHukFmUV3spxOLU2XU8t+3wkMqufsRoHFZMq6IoLyc82HR4tI9CIk6dUwfA314/6OugDYOxkzV2IoLf8gBOs2Ntiaq7gss8fhG5QERutB/ne9LCDEjkF8/LCXDCjNi+0VRleOkuOGZqFSX5OTy+ef+Q1/20+PNyApw8q4bHX9sfDtr5eSM7vvfIWEa4PonXrqVplmvpb1HWTV8wRG8w5Jvf9pTZtby4o8VaLKPqeXXHSHICwimza3kyIuh6xHbbVTsLjjzktDm19AZDQ+I0Xq+CjqQgN4cTZlSHLVQ/jRKHGbUlTKosYs3rB634jI8WOFjG0MGOXjbva/d9hgGDs6hk2T1u0jm/h+Xu2Wg/Pm+/NmIkK8IVOZ3LRIaXyrEgN4eTZ9Xy+OahmRPtPf0U5gXI8yCWEIsz5tazu7WH1/d3hOWBPzfXwokVVBbn8eSW4TMMr2+wovwcjptWPczP76eiAssqHggpf3/zEN39AwRD6puPH2Dl3Hr2tfWGA3aHOmzFX+y94j9+eg35OQH+FuHuCfcXH3z8YCmq7Ye6ePtQly8lmaMREU6dXctTbx7kcFef7xa4465b8/pBz3ffikV4FpXE3eNG25wHvENVb1HVW4Bz7NdGjI4kO1atnFsPwGOv7Y953A1+TOHPmFfPrpbusBIelOOv4gBYbV+L9p4gBbkBTzaXjiYnIJw2u44ntuwPp5S19Xhb4CuSU2fXsnlfO3tbB4OffuZmg7XBdXF+ju0q8C8w77DSdk08vtm6kR2Lv8oHi78oP4djp1cNGUy93M0sFqfZ5/fk6wd8nY1GcursOtp7gryxv8N3C3xiZREz6kpYvXn/sGoDfhCeRcVJfHBwe/dXRvxfkW6jvKI9SZ72tNoSZtSVZKj4+z23clbOtTr56oh2+ekjBqsM7rwJZay2XUx+5Z07nDmvnoMdfbxsb6jtpDv6kbt86uxBpeEwmK7qzznm5wY4YYaVGdLm02wmkvryQhZNKg/3GafUb40Pih+sa/ra3nb22ZuTO/L8cC3BoOvlyS0HsuLqAauIodMd/ZYFltXvZPb4PdCANZhuO9iZcEtNN4r/u8CLInKriNwGrANu8KiNaeEm4+bMufU8u/Vw0iBHXBk+LFpprCgaooTBf0UM1kxj7fYjtPf0e14JNJrT59QREHhs0z7A33TH+Y1lNJQX8NimiOvpU83zSE6ZVcu2g53h6pJ+uwvOnFvPC28foaWrL6yIK31w9YD1+wHDBhq/FL+IcNqcOp5+8xCHbTeWn4YQWNeu0u4fEyoKfJUFg+4e8LdfOjizqMcTuHvcZPWsAk4A/mA/TlTVO71pYnq0u8jTPnNePX0DobSyewZCSmffgC8dMFIJg7P5sr8d/Yy59QRDylNvHPR9hlFVks/yKVU85swwfMxkEBHOnNfA314/EC6HkQ0r/DQ7X/r+V/bYsvy9mVfOqyek8OTrBznc2UdZYa4vrjqAeRPKmFRZxCP2YHqosw8RqPJpoAFrsOnoDfLIa/vJzw344haMxrl+TVXFSd6ZOcfYu+KBZfz5zYzaEiZXFw3xLESTaOvFefbf5UAjsBPYAUy0XxsxLDdM4ht7xbRqygpyE558PDp8zCeOVMLg7Ubr8Vg+pZKywlxWv3bA8+X+sThzfj0bdrWxr63HmmH4qITPnl9PZ99AOE3WrxrrkcysK6WxopCHN+6zZfn7+y1tqqS6JJ/Vr+3ncGefb9Y3WIPp2fPrWfPGAXr6Bzjc2UtlUZ4vFSwdTpldS35OgJd2tFBV7E9Jg2g+e+ZsABY0+p+ZXlM6OKtoqvJf8Vu/YUNCozeR2fBF++9/xHjc6FUj06HDhdWanxvg1Dm1PBaRyuiWcLqoDymBkUoYbLeVTxkTDrk5AU6bXcfjW/bT1u3/QHPmvMGAst+5yyfPqqUwL8CjEa4l8NcKF5Eh03e//bY5AeH0OXU8seUABzt6fbW+Ac6a30BPf4in3jjo+0ADVnaeYxVXFvkry+FDJ0zl1ev/gWm1JVmR9y+nz2BJUwUN5SnvMpsW75jfEHcHN0i8A9cV9r/nquoZkQ9GOKsnWXDX4cx5Dexv7015Vy4/F5Lk5gQ4bU4dqzfvt/f89Nf14rBybh372qztA/2WN7fBchc89tp+25Xln2IszMvhlFm1PLppv71IJuhbBcRInIVAkJ0A4cq5dRzu7OPpNw8xsdJf5XH8jGpK8nN4ZNN+DnX4r/gBmqdUAlZmUbYo8WmtRyyuPXc+93zmFF9nTpEcO706oUHixlH4tMvXsoZViyX5j7Zybh0iqad1+r10/Kx59exv72X9zha6+gayojjOmFeftUwGEeGMeXWseeMgBzt6fV8kc9b8Bna1dPPa3nZfKyBGcrJd6RHwzd8eyelz6sK/35Rqf63UgtwcTp9bx2Ov7eNQFix+gCWTrGTByFXDhvTJywnw9DVnxj2eyMc/QUSOwdobd5mILLcfK7H2yR0RBiv4JVdetaUFLGmqDLsB3OIEXv3KXT5zXj05AeEPL+z0VU4ktaUFLJxo+TP9zkIBOGteA1199gInn+WdZbuWHt20LyvL4sHy2/7LaTP47JmzfJcFViZKo+0mmNNQ6ru8s+Y1sK+tlzf2d1Bd4n/my7IplqvnY6dM913WeCHRjCaRxvkH4DKgCfhhxOvtQIyNPLNDh13v3a3//Z0LGvj3v25md0s3EyvdBVb8rhlSWZzPcdOq+cMLu3yVE42jEKfV+j9unxhhEfud9VJfXsjSpgoe2bSfquI832cYDteeNz8rchx+cOFS/v2vr/GOBQ2+yzrDHkwBplT7318mVBSy+TvnUJCbPVfPeCaRj/82259/WZSP/wJV/UMW2ziEjhSXdZ+7aAIAf9mw17WMbCwdf8cCyyIGwjnFfnPZSdMAK+PJbwrzcsIKIxsD21nzG3hpZwuv7m6jttR/C3UkOGV2LX/+zClZcQ1Wl+QzudoylGbV+z/DAIzSzyJu8vh/LyLvEpGviMg3nUc2GheLVGuxzKgrZW5DWUqK3+/6JDC4ihcsaycbvHPhBLZ/711McjnzyZT3L28CrHKxfvPOhQ2owv72XiZkKXPiaOf771vCZSdN4+RZNcnfbBhTJNWeIvILLJ/+GcAvgQuB53xuV1zC/vcUIvLnLJrAjx97nf3tPa6UUEdPkNyAUJjnX9BuWs1ggC5bKV7Z5nNnzeKcRROYnQWL0ckk2tXSTf1Rej2zzUmzajkpIm3VcPTgRrOdpKofAY6o6vXAicBkf5sVn3Qybs5dPAFVeOhVd0FeJ8XSz8yQQECYN6EM4Kh1TYgIcyeU+bbDUbSsFdOsAOHSphEvJ2UwjGrcmM1O6cMuEZkIHAIyCr2LSCXW7GERoMDlqvqMm8+mE3id21DG9NoS/rJhLx86YWrS97f39Gcl0+bez57CgfberOX2Hu188/wFNE+uDFckNRgMsXFj8d9rK+p/B14AtgOrMpT7n8BfVHUesBTY5PaD6WxcIiKcs2gCz2w95Gov3vYe/1fTgpVr6zbTyJCcmtICPnrydDOQGgxJSKj4RSQAPKqqLar6e2AqME9V0w7uikg5cBrwKwBV7VPVFrefd7J6Ut1T9dxFExgIKQ9tTO7u8WMza4PBYBgtJFT8qhrCqs3jPO9V1dYMZc4ADgD/KyIvisgvRWTYUkQRuUJE1orI2gMHInYE6g0iAiX5qSnmxZMqmFJdzL0v7U763myVUTAYDIaRwI2r5yEReb94F+nMBZYDP1fVZUAncE30m1T1ZlVdoaor6uoGUx/be/opzc9NOWAoIry3eSJPvXGQ/W09Cd+bjQqWBoPBMFK4UfxfBP4P6BWRNhFpF5HUqp4NZSewU1WftZ/fjTUQuCKTDVLes2wSIYV7klj9bjZ6MRgMhrGKmwVcZaoaUNV8VS23n6ddxFpV9wI7RGSu/dJZWJu4u8JtZc5YzKwrZfGkCv60flei9hlXj8FgOKpJqvhF5FE3r6XIZ4E7RORloJkUtnLM1Bp/77JJbNjVxhsRG55H0t0/wEBIKc1CVo/BYDCMBImqcxaKSDVQKyJVIlJtP6YBEzMRqqrrbf/9ElV9r6oecftZN9suJuLdSxsJCPw5jtWfai0gg8FgGGsksvj/BWtj9Xn2X+fxZ+C//G9abDLdqrC+rJCTZ9Xyp/W7Yu7MlY0CbQaDwTCSJKrO+Z+qOh34sqrOUNXp9mOpqv40i20cQkdPMOMtEd/bPIkdh7t5btvhYcfCBdqM4jcYDEcpboK7PxGRk0Tkn0XkI84jG42LRUdv+sFdh3MXT6CsIJe7nt8x7Jjfu28ZDAbDSOMmuPtrrM3VTwGOtR8rfG5XTIIDIU+2KizOz+WC5onc/8oeWrv6hxzzexMWg8FgGGncaLcVwAKN5RDPMp291sYlXhRQ++BxU7jj2bf580u7+MiJ08Kvp1P22WAwGMYSbhZwbQAm+N0QN7T3OhukZK6UF02qYOHEclY9t2NIkNe4egwGw9GOG8VfC2wUkb+KyD3Ow++GxSKdypyJ+MBxU9i0p41Xdg2WH2pPswicwWAwjBXcaLfr/G5EMjYf2szKW1fS3hNkb34rX11TzraeS7jy2Cvp6u/ivDvOG/aZy5ov47LmyzjYdZALf3fhsOOfWvEp3tP8Pq67/wnOv/MdzKi16sS9daiLA4U9PPB6iHfPfTebD27mX+77l2Gf//ppX+fsGWezfu96rvrLVcOO33DWDZw0+SSe3vE0X310+N70N51zE80Tmnlk6yN858nvDDv+3+f/N3Nr53Lv5nv5j2f+Y9jxX//jr5lcMZm7NtzFz9f+fNjxuy+6m9riWm5dfyu3rr912PEHLnmA4rxifvb8z/jdq78bdvzxyx4H4Manb+S+LfcNOVaUV8SDlzwIwLef+DaPbhu6nq+muIbfX/R7AK595Fqe2Tl0q4Wm8iZ+877fAHDVX65i/d71Q47PqZnDze++GYAr7r2CLYe2DDnePKGZm865CYAP/eFD7GzbOeT4iU0n8t2zvwvA+3/3fg51HRpy/KzpZ/GN078BwLl3nEt3f/eQ4+fPOZ8vn/RlAFbeupJoLlp4UcZ97+JFF7OjdQcf/uOHhx3/0olfMn0P0/f86HsObrJ6nsCqwZ9n//88Vl3+rDMQslwyXtVbLy/M46z5DRzq6CVof3cwFDL13A0Gw1GNJIvZisgngCuAalWdKSKzgV+o6lnZaCDAihUrdO3atfx5/S4+f+d6Hvni6czyaB/XDbtaOf8na/j6u+bz8VNn8KnfrOON/R08/MXTPfl+g8FgGClEZJ2qDsvCdOPj/zRwMtAGoKqvAyOyt50fqZaLJlVw7LQqbntmOwMhq0BbNrZdNBgMhpHCjeLvVdXwfoUikou1T27W8Tq46/DRk6ez43A3j27aZ2rxGwyGox43iv8JEfkqUCQi78CqzX+vv82KTUdPkJyAUJSX4+n3vnNBAxMrCvnfp7abkswGg+Gox43ivwZrq8RXsAq3PQB83c9GxcMp1+DdZmAWuTkBPnziNJ7ZeoitBzs9WSdgMBgMoxU3ir8IuEVV/0lVLwRusV/LOm09/b7l13/wuMkU5lmXw1j8BoPhaMaN4n+UoYq+CHjEn+YkpsNHN0xlcT7HTqsGoLFiRMY1g8FgyApuFH+hqoa3q7L/L/avSfHxey/c0+dYm7ovmlThmwyDwWAYadxo0U4RWa6qLwCIyDFAd5LP+EJ7T5Da0nzfvv/yk6dz3PRqljRV+ibDYDAYRho3iv8q4P9EZLf9vBG4OFPBIpIDrAV2qer5bj7T0Rtkml1awQ8CATFK32AwHPUkVfyq+ryIzAPmAgK8pqr9ST7mhs8Dm4Bytx8wqZYGg8GQOW58/GBtvrIEWAZ8MNMduESkCXgX8MtUPtfe029SLQ0GgyFDkmpReweumcB6YMB+WYHbM5B7E/AVoCyB3CuwagQxZcoU+oIheoMhY/EbDAZDhmR9By4ROR/Yr6rrRGRlvPep6s3AzWAVaevsNXXyDQaDwQtGYgeuk4ELRGQ7cCdwpoj8JtmHnDo9JUbxGwwGQ0a40aLODlzPAb3Oi6p6QToCVfVa4FoA2+L/sqp+KNnnzCboBoPB4A1jYgcugM4+Y/EbDAaDF7hJ53xCRBqwMnsAnlPV/V4IV9XHgcfdvNex+I3iNxgMhsxI6uMXkYuA54B/Ai4CnhWR+Js5+oQJ7hoMBoM3uNGiXwOOdax8EanDKtJ2t58Ni6bTWPwGg8HgCW6yegJRrp1DLj/nKR291hKC0nyj+A0GgyET3GjRv4jIX4FV9vOLgQf9a1JsBi1+b3ffMhgMhvGGm+Duv4rI+4BTsGr13Kyqf/S9ZVF09gYpyA2Qm5P1yYbBYDAcVcRV/CIyC2hQ1adU9Q/AH+zXTxORmar6ZrYaCYPbLhoMBoMhMxJp0puAr8Z4vcs+9m4f2hOXzt7gkMBuf38/O3fupKenJ5vNMIxTCgsLaWpqIi8vb6SbYjBkTCLFP01VX45+UVXXisg0/5oUm47egSGKf+fOnZSVlTFt2jTPN183GCJRVQ4dOsTOnTuZPn36SDfHYMiYRA7zwgTHsr4pbWdvkNKIwG5PTw81NTVG6Rt8R0Soqakxs0vDUUMixf+8iHwi+kUR+Riwzr8mxaYjytVjtyXbzTCMU0xfMxxNJHL1XAX8UUQuYVDRrwDygX/0uV3D6OwNMrVmRPZ4NxgMhqOKuBa/qu5T1ZOA64Ht9uN6VT1RVfdmp3mDjNasnj/+8Y+ICK+99pqr99900010dXWFn5933nm0tLSwfft2Fi1aFPMzH//4x9m4cWPC773hhhuGPD/ppJNctcfh9ttvZ9GiRSxcuJAFCxZw4403pvR5r1m/fj0PPPBAyp/bvn07v/3tb8PP165dy+c+9zkvm2YwjHmSJsWr6mpV/Yn9eCwbjYpFdFbPaGHVqlWccsop3Hnnna7eH634H3jgASorKxN+5pe//CULFixI+J5oxf/000+7ag/Agw8+yE033cRDDz3Eq6++ygsvvEBFRYXrz/tBIsUfDAbjfi5a8a9YsYIf//jHnrfPYBjLjD5NGofOvoG4iv/6e19l4+42T+UtmFjOv717YcL3dHR08NRTT7F69WouuOACrrvuOgAef/xxrrvuOmpra9mwYQPHHHMMv/nNb/jJT37C7t27OeOMM6itrWX16tVMmzaNtWvXApZCu/TSS3nxxReZM2cOt99+O8XFxaxcuZIbb7yRFStWsGrVKm644QZUlXe96118//vf55prrqG7u5vm5mYWLlzIHXfcQWlpKR0dHQD84Ac/4Ne//jWBQIBzzz2X733ve0PO47vf/S433ngjEydOBKzUxU98wgrvrF+/nk9+8pN0dXUxc+ZMbrnlFqqqqli5ciXHH388q1evpqWlhV/96leceuqpDAwMcPXVV/PXv/4VEeETn/gEn/3sZ1m3bh1f/OIX6ejooLa2lltvvZXGxsaY33P88cfzzW9+k+7ubtasWcO1117Lpk2b2L17N9u3b6e2tpYbbriBD3/4w3R2dgLw05/+lJNOOolrrrmGTZs20dzczKWXXsqyZcu48cYbue+++zh8+DCXX345W7dupbi4mJtvvpklS5Zw3XXX8fbbb7N161befvttrrrqKjNLMBzVjIllsCF718fSUVau4U9/+hPnnHMOc+bMobq6mhdeeCF87MUXX+Smm25i48aNbN26laeeeorPfe5zTJw4kdWrV7N69eph37d582auuOIKXn75ZcrLy/nZz3425Pju3bu5+uqreeyxx1i/fj3PP/88f/rTn/je975HUVER69ev54477hjymQcffJA//elPPPvss7z00kt85StfGSbXGZxi8ZGPfITvf//7vPzyyyxevJjrr78+fCwYDPLcc89x0003hV+/+eab2bZtGy+++CIvv/wyl1xyCf39/Xz2s5/l7rvvZt26dVx++eV87Wtfi/s9+fn5fOtb3+Liiy9m/fr1XHzxxQCsW7eOP//5z/z2t7+lvr6ehx9+mBdeeIG77rorrKi/973vceqpp7J+/Xq+8IUvDDmXf/u3f2PZsmW8/PLL3HDDDXzkIx8JH3vttdf461//ynPPPcf1119Pf39/zOthMBwNjAmLfyBk/Y1n8SezzP1i1apVXHXVVQB84AMfYNWqVSxfvhyA4447jqamJgCam5vZvn07p5xySsLvmzx5MieffDIAH/rQh/jxj3/Ml7/85fDx559/npUrV1JXVwfAJZdcwpNPPsl73/veuN/5yCOP8NGPfpTiYiswXl1d7fr8WltbaWlp4fTTTwfg0ksv5Z/+6Z/Cx9/3vvcBcMwxx7B9+/awvE9+8pPk5uaG5W3YsIENGzbwjne8A4CBgQEaGxsTfk8sLrjgAoqKrEzi/v5+PvOZz7B+/XpycnLYsmVL0vNZs2YNv//97wE488wzOXToEK2trQC8613voqCggIKCAurr69m3b1/49zMYjjbGhOIftPhHT3MPHTrEY489xoYNGxARBgYGEBF+8IMfAFBQUBB+b05OTkK/tEN0ymD083T2u1fVpKmICxcuZN26dZx55pkpfbdzjpHnF0ueqrJw4UKeeeYZ198Ti5KSkvD/P/rRj2hoaOCll14iFApRWJho2clgO6Jx2prO72UwjFXGhqsnZN2wJaOoJPPdd9/NRz7yEd566y22b9/Ojh07mD59OmvWrEn4ubKyMtrb22Mee/vtt8PK0QkaR3L88cfzxBNPcPDgQQYGBli1alXYGs/Ly4vpnnjnO9/JLbfcEg4oHz58eNh7rr32Wr7yla+wd6+VrNXb28uPf/xjKioqqKqq4m9/+xsAv/71r8Py4vHOd76TX/ziF2HFefjwYebOncuBAwfC59bf38+rr76a8HsSXSewZiONjY0EAgF+/etfMzAwkPRzp512WtgV9vjjj1NbW0t5eXnCdhgMRyNZV/wiMllEVovIJhF5VUQ+n+wzA7alNpqyelatWsU//uPQ5Qzvf//7h2SUxOKKK67g3HPP5Ywzzhh2bP78+dx2220sWbKEw4cP86lPfWrI8cbGRr773e9yxhlnsHTpUpYvX8573vOe8PcuWbKESy65ZMhnzjnnHC644AJWrFhBc3NzzDTN8847j09/+tOcffbZLFy4kGOOOSasuG+77Tb+9V//lSVLlrB+/Xq++c1vJjy/j3/840yZMoUlS5awdOlSfvvb35Kfn8/dd9/N1VdfzdKlS2lubk6adXTGGWewceNGmpubueuuu4Ydv/LKK7nttts44YQT2LJlS3g2sGTJEnJzc1m6dCk/+tGPhnzmuuuuY+3atSxZsoRrrrmG2267LWEbDIajFUnHfZCRQJFGoFFVXxCRMqzFYe9V1biJ6nMWLdW+82/g3s+cwuImK81w06ZNzJ8/PzuNNhgwfc4w9hCRdaq6Ivr1rFv8qrpHVV+w/28HNgGTEn0mFA7ujq6sHoPBYBiLjKiP367yuQx4NtH7RmNw12AwGMYqI6b4RaQU+D1wlaoOW30lIleIyFoRWdvWbi1EGk0+foPBYBirjIjiF5E8LKV/h7271zBU9WZVXaGqK4qKixGB4nzj6jEYDIZMGYmsHgF+BWxS1R+6+UxIrVROUxrXYDAYMmckLP6TgQ8DZ4rIevtxXqIPDITUBHYNBoPBI0Yiq2eNqoqqLlHVZvuRsP5uSHVU+vdFhA9/+MPh58FgkLq6Os4//3wAbr31Vj7zmc+Ej4+20scGg2F8MmZW7o7GjJ6SkhI2bNhAd3c3AA8//DCTJsXOTB2NpY8NBsP4ZPRp0xgMqCYt17Dy1pXDXrto4UVceeyVdPV3cd4dw71JlzVfxmXNl3Gw6yAX/u7CIccev+xxV20799xzuf/++7nwwgtZtWoVH/zgB8MlDiJJVPrYYDAYsskYsfhHbyrnBz7wAe688056enp4+eWXOf7442O+L1HpY4PBYMgmo1ObRhFSTVqLP5GFXpxXnPB4bXGtaws/miVLlrB9+3ZWrVrFeecljFEbDAbDqGBMWPwDqpQWjt4x6oILLuDLX/4yH/zgB+O+xyl9bDAYDCPNmFD8odDozOpxuPzyy/nmN7/J4sWL474nXuljg8FgyDajV5tGoEDpKKrFH01TUxOf/3zi6tLnnXce+/bt4+yzzw5vVnL55ZdnqYUGg8EwSNbLMqdDQeNs/fn/PcTlp0wPv2ZK5BqyjelzhrHGqCnLnC6jMY/fYDAYxiJjRvGPZh+/wWAwjCXGkOI3tXoMBoPBC8aM4jeuHoPBYPCGMaP4javHYDAYvGHMKH5j8RsMBoM3jBnFPxotfjdlmevq6mhubmbhwoVceOGFdHV1hd9/4403Mm/ePBYtWsTSpUu5/fbbs34OBoNh/DGGFP/oC+66Kct88cUXs379el599VXy8/O56667APjFL37Bww8/zHPPPceGDRt48sknGQtrKgwGw9hn9JnRMRCgIDeJ4l+5cvhrF10EV14JXV0Qq4DaZZdZj4MH4cKhZZl5/HFXbXNbljkYDNLZ2UlVVRUAN9xwA6tXr6a8vByAiooKLr30UlcyDQaDIRPGhMUfCIzevXaTlWW+6667aG5uZtKkSRw+fJh3v/vdtLe3097ezsyZM0eo1QaDYTwzJiz+gJtN1hNZ6MXFiY/X1rq28KNJVpb54osv5qc//Smqyqc//Wn+/d//nSuvvNJsHG8wGEaMEbH4ReQcEdksIm+IyDXJ3p8zypWkm7LMIsK73/1unnzyScrLyykpKWHr1q1ZbKXBYDBYZF3xi0gO8F/AucAC4IMisiDRZwKj3CHlpiwzwJo1a8LunWuvvZZPf/rTtLW1AdDW1sbNN9/se1sNBoNhJFw9xwFvqOpWABG5E3gPsDHeB1y5ekaQRGWZ77rrLtasWUMoFKKpqYlbb70VgE996lN0dHRw7LHHkpeXR15eHl/60pey2GqDwTBeyXpZZhG5EDhHVT9uP/8wcLyqfibqfVcAVwDUTJp+zMGdQ90ipkSuIduYPmcYa4ymssyxzPdho4+q3qyqK1R1xbQJ1VlolsFgMIwPRkLx7wQmRzxvAnaPQDsMBoNhXDISiv95YLaITBeRfOADwD3pfJFZ6WrIFqavGY4msq74VTUIfAb4K7AJ+J2qvprq9xQWFnLo0CFzQxp8R1U5dOgQhYWFI90Ug8ETRmQBl6o+ADyQyXc0NTWxc+dODhw44FGrDIb4FBYW0tTUNNLNMBg8YUys3I1FXl4e06dPT/5Gg8FgMAxhlC+NMhgMBoPXGMVvMBgM4wyj+A0Gg2GckfWVu+kgIu3A5pFuxyikFjg40o0YZZhrEhtzXWJztF+XqapaF/3iWAnubo617Hi8IyJrzXUZirkmsTHXJTbj9boYV4/BYDCMM4ziNxgMhnHGWFH8plB9bMx1GY65JrEx1yU24/K6jIngrsFgMBi8Y6xY/AaDwWDwCKP4DQaDYZwxqhV/qpuyH62IyGQRWS0im0TkVRH5vP16tYg8LCKv23+rRrqtI4GI5IjIiyJyn/183F8XEakUkbtF5DW735w43q+LiHzBvn82iMgqESkcr9dk1Cr+dDZlP4oJAl9S1fnACcCn7WtxDfCoqs4GHrWfj0c+j1Xi28FcF/hP4C+qOg9YinV9xu11EZFJwOeAFaq6CMjB2gtkXF6TUav4idiUXVX7AGdT9nGHqu5R1Rfs/9uxbuJJWNfjNvtttwHvHZEGjiAi0gS8C/hlxMvj+rqISDlwGvArAFXtU9UWxvl1wVqwWiQiuUAx1s5/4/KajGbFPwnYEfF8p/3auEZEpgHLgGeBBlXdA9bgANSPYNNGipuArwChiNfG+3WZARwA/td2gf1SREoYx9dFVXcBNwJvA3uAVlV9iHF6TUaz4ne1Kft4QkRKgd8DV6lq20i3Z6QRkfOB/aq6bqTbMsrIBZYDP1fVZUAn48SFEQ/bd/8eYDowESgRkQ+NbKtGjtGs+M2m7BGISB6W0r9DVf9gv7xPRBrt443A/pFq3whxMnCBiGzHcgWeKSK/wVyXncBOVX3Wfn431kAwnq/L2cA2VT2gqv3AH4CTGKfXZDQrfs82ZR/riIhg+Ws3qeoPIw7dA1xq/38p8Odst20kUdVrVbVJVadh9Y/HVPVDmOuyF9ghInPtl84CNjK+r8vbwAkiUmzfT2dhxcrG5TUZ1St3ReQ8LB9uDnCLqv6/kW3RyCAipwB/A15h0Jf9VSw//++AKVgd+59U9fCINHKEEZGVwJdV9XwRqWGcXxcRacYKeOcDW4GPYhl64/a6iMj1wMVYWXIvAh8HShmH12RUK36DwWAweM9odvUYDAaDwQeM4jcYDIZxhlH8BoPBMM4wit9gMBjGGUbxGwwGwzjDKH6DwWAYZxjFbzhqEZEaEVlvP/aKyC77/w4R+ZkP8m4VkW0i8smI5xdm8H13iMjhTL7DYIhF7kg3wGDwC1U9BDQDiMh1QIeq3uiz2H9V1bvdvllEclR1INYxVb1ERG71rGUGg42x+A3jDhFZGbFpy3UicpuIPCQi20XkfSLyAxF5RUT+YtdIQkSOEZEnRGSdiPzVqe/igtNE5GkR2epY7rb81SLyW+AVESkRkftF5CV7k5CL/Tlzg8HCKH6DAWZi1fR/D/AbYLWqLga6gXfZyv8nwIWqegxwC+C2fEgjcApwPvC9iNePA76mqguAc4DdqrrU3iTkLx6ck8EQF+PqMRjgQVXtF5FXsOpCOYr3FWAaMBdYBDxs1fciB6umuxv+pKohYKOINES8/pyqbouQc6OIfB+4T1X/ltHZGAxJMIrfYIBeAFUNiUi/DhawCmHdIwK8qqonpvvdNpF7THQ6/6jqFhE5BjgP+K6IPKSq30pDlsHgCuPqMRiSsxmoE5ETwdobQUQWevXlIjIR6FLV32DtErXcq+82GGJhLH6DIQmq2mcHZn8sIhVY981NwKseiVgM/LuIhIB+4FMefa/BEBNTltlg8Ag79fK+VNI5R+I7DQbj6jEYvKMV+LazgCtTROQO4HSgx4vvMxgcjMVvMBgM4wxj8RsMBsM4wyh+g8FgGGcYxW8wGAzjDKP4DQaDYZzx/wEEvDVeymqkkQAAAABJRU5ErkJggg==\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# specify time span and evaluation points\n",
"t_span = [0, 96]\n",
"t_eval = np.linspace(0, 96, 1000)\n",
"\n",
"# initial conditions\n",
"C_initial = 0\n",
"IC = [C_initial]\n",
"\n",
"# compute solution\n",
"soln = solve_ivp(deriv, t_span, IC, t_eval=t_eval)\n",
"\n",
"# display solution\n",
"plotConcentration(soln)\n",
"plt.savefig('./figures/Pharmaockinetics3.png')\n",
"\n",
"print(soln.t_events)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
}
},
"source": [
"This looks like a unevem. The problem here is that the solver may be using time steps that are larger than the dosing interval, and missing important changes in the input. The fix is to specify the `max_step` option for the solver. As a rule of thumb, your simulations should always specify a `max_step` shorter than the minimum feature in the input sequence. In this case, we will specify a `max_step` of 0.1 hr which is short enough to not miss a change in the input."
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"nbpages": {
"level": 4,
"link": "[2.1.3.3.1 Solution](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.3.3.1-Solution)",
"section": "2.1.3.3.1 Solution"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"None\n"
]
},
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEWCAYAAABhffzLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAABqTElEQVR4nO2dd5wcxZX4v28257zSSquwygEUkEBkRLCPbPvMgW1sgxM/GyfO2GAcwfYBtrHN+ZyOO3NkGYwNNhiMydmABAKEEiCUUF5pkzbN7rzfH909Ozs7oWeme3aXre/nM5/dmZ7pV11d/erVq1evRFUxGAwGw9ghMNwFMBgMBkN2MYrfYDAYxhhG8RsMBsMYwyh+g8FgGGMYxW8wGAxjDKP4DQaDYYxhFL/hPY2ILBeR7S6/e6WI3JahvPNF5B9elOe9joj8TkS+m+D4t0Tkf12e6yYR+ZF3pUsfEdksIqfY/ye8hmTtxS9GveIXkQtF5HUR6RSRXSLyWxGp9FHeESLygIi0iMh+EXlRRD7llzyvEJGpIqIikjtM8pM+mHb5dkeWUURyRWSPiIyKBSeqeruqvt95b1/TjHTPJyJPiMhnI94vF5EDIvKRTMvqB9HlTYSqfl5Vf2j/bkiHqKpXq6qrc7koV4OI/F5EdopIu4isF5GrRKTEi/PHI/IaYj2D0e0lW4xqxS8ilwI/Br4BVABHAlOAh0Uk3wd5RwGPAU8CM4Aa4AvAaV7L8pLhUvZp0sLg+jwdODA8RRlZiMj7gXuBT6vqH4a5OKMGEakGngeKgKNUtQx4H1AJTB/Gog0fqjoqX0A50AGcG/V5KbAH6+EAuBK4C7gFaAfeAJZGfH8C8CdgL/AO8JUEMp8Bfp2kXJ8D3gL2A38FJkQcU+Bi4E27LD/EanjPA212OfPt7y4HtgPfAvYBm4HzI851BvCK/bttwJURx6basj4DbAWesv+qXWcdwFHAhcCzwC+wFO4m4Gj78212PV4Qcd4C4Dr7XLuB3wFFUeW91P7dTuBT9rGLgCDQa8u+L07dKfAd4I8Rn90NfNtqqoPu2V/tOn4L+FzEsSLgJqzOYi2WUbDdzf2228ptccr2JPBh+/9j7bKebr8/BVht/38h8Iz9/1P29w7a131eonqKI/cJ4LPAmfY9Oj1GnX0eq00dAH4NiH0sYNfnFlvWLUCFfexm4FL7/4n2eS6238+w61bSLW+yNmEfvwn4EVACdAEhBtrnhOj7AfwR2AW02nU7P/pcccr0I+B1IJCg3EcDL9nnfgk4Ouqafoj1rLQD/wBqI45/wq7jZqy2uhk4JbpNEf8ZfMaLcqTyGs0W/9FAIfDnyA9VtQN4EKtHdzgb+ANWD/9X4FcAIhIA7gNexWr8JwOXiMi/RAsTkWKsG3V3vAKJyEnANcC5QANWY4i2zE4FlmCNTi4DbgDOByYBhwAfjfjueKDWLtsFwA0iMts+dhD4pH1NZwBfEJEPRsk6AZgL/AtwvP1ZpaqWqurz9vtlwGtYo5c77PIejvXwfxz4lYiU2t/9MTALWGQfnwh8L6q8FfbnnwF+LSJVqnoDcDvwE1v2WbHqz+Ze4HgRqbRddscBf4n6zgoshTIBOAe4WkROto99H6sznW5f9wXOj1K53zF4EkuRgVWXm7Dq13n/ZPQPVNWp84X2dd9pv49ZTwlknwXcBpyjqg/EOH4m1j1biNX2nOu50H6dCEzDMop+FeN6TohxPU+rrW3SKG8kSX+rqgexRnk77HoqVdUdMc71IDATqAdexmpTbjgF+LOqhmIdtEcEfwN+ifUc/Bz4m4jURHztY8CnbNn5wNft384Dfoul/CfYv2+MU454z2DG5UiV0az4a4F9qtoX49hO+7jDM6r6gKr2A7diPSBgPSx1qvoDVe1V1U3A/wCx/KdVWPW1M0GZzgduVNWXVbUHuAI4SkSmRnznx6rapqpvAGuAf6jqJlVtxWrYi6PO+V1V7VHVJ7EaxbkAqvqEqr6uqiFVfQ1LGZ4Q9dsrVfWgqnYlKPM7qvp/dt3cidUB/cCW+Q8sK32GiAjWaObfVXW/qrYDV0fVVdD+bdBWUB3AbFKjG0s5n2ef+6/2ZwCIyCQsi/tyVe1W1dXA/2I9eGDVz3/YZdyG9RA5pHK/o3mSwYrxmoj3JxBD8Scg1Xo6EdiIZenF4lpVbVHVrcDjWB0zWO3x53b76sBqjx+xXX9PAsfZneHxwE+AY+JcTyb31Ys2AYCq3qiq7fazdSWwUEQqXPy0hsTP7RnAm6p6q6r2qeoKYD1Wh+vwf6q60X6W7mKgjs8B7lfVp+xyfRdr5JIOmZQjJUaz4t8H1MbxXzfYxx12RfzfCRTav5sCTLAnaltEpAXLtTIuxjkPYN3QhgRlmoBl5QPh0UczlrXjsDvi/64Y70sj3h+wrSGHLbYMRGSZiDwuIntFpBVruB/Z2YHlrklGtHxUNVaZ6oBiYFVEXf3d/tyhOaoj7oy6HrfcgjWa+aT9fyQTAKfjcdjCQB1PYPB1b4n4P5X7Hc3zwCwRGYf1sN0CTBKRWuAILNeDW1Ktp+8CPcC9IlIQ43h0+3bONag92v/nAuNU9W0sJbwIa1R1P7DDHlFGK/5M7qsnbUJEckTkWhF5W0TasNwpMLTNxywDKTy3NpFtChLXcbi92c9rs4syeV2OlBjNiv95rIfhXyM/tGfpTwMedXGObVgWb2XEq0xVT4/+oqp22jI/nOB8O7CUS2RZaoB3XZQlFlVRUQeTbRlguWX+CkxS1Qosf7tEFzvO/+mwD6sTmB9RVxWq6rbhpSL/aawHdRzWvEokO4BqESmL+GwyA3W8E2vUEnnMwfX9HlJ46/6vAr4KrFHVXuA54GvA26q6L9HvM+Qg1iR3BXC3iOS5/N2g9ohVF30MdPZPYlms+ar6rv3+k1ij29WZFzslkrWPjwEfwHLbVGDNY8HQNh+LR4AP2aObWETXEwxuU4kY1N5sl3BNnO8mu8ZMypESo1bx266Rq4D/EpFTRSTPdqn8Ecv/e6uL07wItInI5SJSZFsVh4jI4XG+fxlwoYh8w/G7ichCEXH8+HcAnxKRRbZldjXwgqpuTvtC4SoRyReR47B8uX+0Py/Dsny7ReQIrAcjEXuxRizT0imE7R/9H+AXIlIPICITXfrHwVI2rmTbvuWzgLMj/MzOsW1YCvcaESkUkQVYvmPH33sXcIWIVIlII/DliJ+ner+jeRL4EgPW8BNR72Ph+roTYY9wTsWyCu8QkRwXP1sB/LuINNnzNFcDd0ZY4M71OKOVJ7Dq6xnb9ZdNdgM1CVw3ZViGXjPWyPPqFM79c6xgkJtFZAqE2+7P7fbzANZo7mNihQ+fB8zDGgUl427gTBE51o4k/AHx9WqyZzCTcqTEqFX8AKr6E6yh+nVY0S0vYFl1J9v+tmS/78dSMIuwIjz2YfmLYzY+VX0OOMl+bRKR/ViTsw/Yxx/FGpb/CcsSmI47/3E8dmG5mHZgKbbPq+p6+9jFwA9EpB1rgvWuRCeyLdb/AJ613RxHplGey7GiaP5pD7cfwb2/9vfAPFv2vcm+rKpv2PMgsfgolsW3A7gH+L6qPmwfuwprePwOVtRD2ABI9X7H4EksBfRUnPexuBJL4bSIyLku5cREVVuwghZmAbcksGAdbsS6/qewrrebwR1hdPmfwVKqqbitPMFu1yuwnqsWEZkQ9ZVbsO7ru1jRWv9M4dz7sYJBgsAL9jPzKFbkzFuq2oxlVF2K1bFcBpzpZhRnt9EvYhl9O7Ge15gL9JI9g5mUI1UkyqAyjBBEZDlWGFi8CAGDwWBIi1Ft8RsMBoMhdYziNxgMhjGGcfUYDAbDGMNY/AaDwTDGGBXJu2pra3Xq1KnDXQyDwWAYVaxatWqfqtZFfz4qFP/UqVNZuXLlcBfDYDAYRhUiEr0SGDCuHoPBYBhzGMVvMBgMYwyj+A0Gg2GMYRS/wWAwjDGM4jcYDIYxhlH8BoPBMMYwit9gMBjGGEbxGww+EQqZdChe8eq2FlZva8mavJ2tXXT2xtrV9b2BUfyGMcGTG/cy9Zt/Y0dLou2HveMnf1/PtG89kDXlHwopXb3Z2zvl4bW7+e69a7Im7wO/fpYP/jrelsPec9Q1j3Hef7tO+Z8xzR099Palu1Vv6hjFbxgWQiHljhe2Zs2q+sOLWwF48Z39WZH3P09vAmBz88Ek3/SGr//xVeZ+7+8cONibFXmfu2Ult/5zC93B7G7UlY2kkn39lgJ+/d1W32UBHDjYy5IfPcJnbn4pK/LAKH7DMPH4hj18657X+fk/NmZFXnG+lZ2ktSuYFXkTKosAWLezPck3veHPr1jbsq7flR15DluaO32XEans92ehY4tsI9kYse1otUahT7/p57bNgzGK3zAsbNtvKYx9HUl3yPSEgL0ldzYUFUBlcT4Am/Z2ZEVefo71KG/alx15Du/s839E09EzMCrcnIX7d6BzQPHvbu/2XV5LhLyevuyMoIziNwDQ3h3kPx95k81ZeJABdrZZD1R3MDt+TcdS3JIl10uP7QLJhmIEKMyzHuV39vovL9K9k43rO3BwQDFmo322dA6MKjZloT4PRMjbmiXDxCh+A2BNfv7ikY38+O/rk3/ZA1rshzlbPnDn4Xony/I2ZUFR9YeUdtsqzoa8SAs1G4o4UjFmo+OOtPizXZ/ZkAc+Kn4RuVFE9ojIkKl/Efm6iKiI1Pol35AazqRgtizUli5L3ubmg1nxo7bYfttt+zvp91meqoaVx6a9Hb5PSLZ1BXFEZOP+OfcOstORtkT43LPj6om4vixY/JEjjGw9f35a/DcBp0Z/KCKTgPcBW32UbUgRx+rIxuQZDFhV3cEQu9qy40fNDQjBfvU9pLM7GKK3L0RdWQFt3X2+16mjqCZWFrF1f6fvYYGO62ViZVFWXS8TKgqzMkJ05E2pKeadLMyZHOgMUpyfQ21pQdbmhHxT/Kr6FBArdu4XwGWAWd0ygnAU8Z72nqzEg7d09lJWaEXa+K08QiGlpbOXRZMqLXk+Kw9HER822ZLntxXnWMSHTamiP6RsO+CvVdxqW/yLJleyp72Hgz3+huQ6RsmiyZW8s++g7yOoA51B8nKEQyZUZMX1cqCzl6rifKbVlrwnLP4hiMjZwLuq+qqL714kIitFZOXevXuzULqRxyNrd2ctTnrQ8D1Lfs3Fk6sA//2aHb19hJQBxe+zPEfxL5liX5/P7oKW6I7GZ3mOkbA4yx3pwsZK2rv7Bvng/aCls5fK4nym1ZWwLQsjqNbOIJXFeUyrK8nKZDJkUfGLSDHwbeB7br6vqjeo6lJVXVpXN2TLyPc8b+5u57O3rORbf349K/IcVwjA2z4PN1WVls4gc8eXUZgX8F0ROxPJs8aXUZyfw9u+K2JL3iETKsjLEd87Nsf1cli4I/X3/jmK2Om4N+/zd4TR0hmkrCCXWePKAP9DZA8cDFJlK+KQwtb9/l7fgc5eKovzaKotoflgL60+d2yQXYt/OtAEvCoim4FG4GURGZ/FMowa2rqt4fPjG/ZkRd4B2xUi4r+F2hXsp7c/RFVJPlNrSny3GJ3RTLVtxfmuiG3FWFNawJSaEt/9xI68qTUl1JTk+z5ia+0MUpAbYM54SxH7ff9au4JUluQxva4U8N8wOWBb/E21ljy/O5qWzqA9wrDlZWFeIWuKX1VfV9V6VZ2qqlOB7cBhqrorW2UYTTh+VL+HtWF5nUHGVxQyoaIoCxajdU2VRZaV478ituUVW8rj7T3Zub4q24rzuyNt7QoSECgrzKWptsT3EY1joZYU5DKuvMD36zvQ2UtlUT4Tq4rIzw1kZcRWVZxHU00J4L/r0/LxW20lG/LA33DOFcDzwGwR2S4in/FL1nuRyNjebIQ7Og9zNvyMjk+6sjifqbWWH9XJj+KvvDym1Zayo7XL1wnsloMD1zetroQtzf6GkB7o7KWiKI9AQJhW5/8EoaUYrZXJ0+tKfbfAW2wfeE5AaKop8d/VY3c0FcV5vo+gQiGltcuqz8nVxeQEJCt+fj+jej6qqg2qmqeqjar6+6jjU1U1e8kpRhmRlr6Ty8MvIhvf9LpS32PPWyIs8Gm1JQT7lW0H/LtGJ/dKZXE+0+tLUPXXqjrQGaQkP4f83ADTakvo7Q/5GkJ6IEIRN9WWsre9h/Zu/0aKjiKGAcXvb3vpDafAmF7v74jGmX+qLLGuz2/XYHu3FXhQUZRHfm6ASVVFo9viN2RGa8Sijrd8dk1ENr7pdSUc7O1nd5t/OXRawq6QfGbUW35NP6/Rmfy0rs9/P3GkonL8xP7LG1BU4HfHZlnEANPrSmjv7mNvu4/tpctyvVjyStm6v9O3nDadvfb8U/j++TsCduZnIuX5PYICo/hHLJEWfzZ8tmA1vvAEk4+N70CE62V6FhR/S1cvZQW55OUEaKotQcRfRXygs5eqkiwq4oMDFv8020/sp7Jq6QqGr29GvTXB+5ZP9dlvj0YriwYUf39IfctpM/AsWPKaakvZ19FDm08jqLC8cHspzcpqdqP4RygtXUGaakuoKs7z34dqu0KqSvLCiuptHxXVgOslj/LCPOrLCny9xtbOIBX2g1yYl0NjVZGvnWmk66WmJJ+ywlxfFX9rVzA8wphcU0xA/FsbYblCeqkoGnC9AL5NmLd3W+koKiPmFMC/jnvADTlggYN/az9iyesOhsJJDP3CKP4RSos9YZedKBTL6qgoymd8eSHF+Tn+WvwHeynOz6EgNweAGfWl/rp6IlwhgO912toVpMK2UEXE9xWZkddXkJtDY1Wxb/evs7efYL+GLeLx5YWU+Lg2IjIiC6DJMUx8kzfY9TK9zt8RlBNqHB6xOSNEn0f5RvGPUJyQsmxETbRGhB+KSBb8mgNDd7AU/9t7/JsgbOkasMABptWW8s4+/4bTLfYS/LC8ulLf6rOnr5/O3v6wIrbk+dfRRCtGEWF6vX9tNDIiC6C0IJfx5YW+yYscjYI1grLWtvgjz5l/cp6HabXZieU3in+E4iwimVFfyr6O3kEZ/PyQBQPDzWk+dzatXQOTn2BZ4O09/k0QtnQOWOBguSe6gv2+DKedCKnIEca02hLebfFn8+5oVwFY7gK/cto48iqiRlB+jdhauoZen5+RPS2dgxVxQW4Ok6qKfXN9tnT2IgLltrxx5QX2iNtY/GMSJ39H2IfqswUuQlg5Tq+zFJVfeYIOdA5WjH5H9kRb4GE/sQ/y2nsGIqQcZo5z5Hl/DyMjpBym1ZXS2dvvS9bTWPJm1Jeys7V70E5Z3smzjZKiwR3NJp9GiI7FXx55/+pLeWu3Txa/bZTk2OlSwiNun0M6jeIfgQT7Q7T39FFZlO+rknJo7eylvHCg8U2rK0XVv6X48RSxH5EhsSxwPycI27oGQkcdnMiXN/d4vx/ugShXCMCMOv860ljyBvzg3suL1dH4OUJs7QpSmBegMC8n/NmMcaVs2tfhyyLDaDck2HNeu/3dO9ko/hFIpJ+xsarYXqbu5+TnUNcE+DihFRFlA9bwtrQg1x8LvHuoBV5bmk95Ya4vdRp2hUTIm1JTTF6O8KYP1xftA4eBEcZGH6zUligfOAyM2PyoT2c0Wl4Uq+P2YwQ1sEbBYVZ9GcF+9WUTGCeIY5C8cWXsaO32dRGeUfwjkMiVrTkBKyrE1wVAEeGAMBBZ4IciVtVBC3JgYILQD4s/OmoiUp4frpfWGD5pZ/3Am34o4hg+/trSAqpL8nnLhxFGOB1FhHKcXF1CTkB8GWFEj0Yhon361HFHK2KnI/WjPp08PZFkY1GjUfwjkJaoyVYrssfHBTmdvYN8qMX5uUysLPJFEbf39NEf0iFW1fS6Ep9cE0MtVEteqS+RE05HEy1vZn2ZP4q4a/BkpMOM+lJfLP7IdBQO+bkBptQU+9KRRo9GgXDIsR+Kv7Vr8GgUBkYYfnTcrVFGFxBOP+3HCNHBKP4UuPSuV7n/tR2+y2mJCK8EmF5fypbmg74tU3dCRyOZNa6UDbu8V1StcRTxjPpSdrd5n2MmuhN1mFZX4pO8oa4esKzGrfs7PZ8wb+2ydosqzs8Z9PmscaVs3N3u+QRoS1REloNfYcfRo1EgnIzOlxFGV3BIJ1pSYBlCfiji1hgjjMnVlnv3TR/9/Ebxu6Q/pPzp5e186Y5XfJcVnkCLyIcSUtji4zL1WFbHpr0HPZ/Qig4ddZjhk982Oi47Wp7XyqM1xuQuWBZ/SL13TziuCREZ9PnM+jLau/vY4/EEaEsMCxwsxb+52fv2Ej0adZhZX+aLKzJy8d0geeNKPVf8/SGlrbtv0PwFQE5AmF7nvbxIjOJ3yQEf4+ijCSuPiMRU4I/Pr68/RHt3XwwLtYze/hBbPN59KHo04+BXzp4DB4eGA0LEcNrj4XusqBCI9BN7K6+tKzhEcUTK2+ix1RgdkeUwo76UYL96vltVrNEoWNe3o7Xb8xw68Tq2mfYiNS/TazujzdgdW6kvriUHo/hd0twxoPj9zB0PVuMLCJQVWJuRT68rRcQfH6Oz01d0Y59tK8aNHrt7YoUDgjW8zcsR7y3iOBb4pOpiCvMCbPBBMcayGKfWWBOgfnQ08Sxi8L7NxLf4rQlXr63UlhijURhon166Q3r6+ukK9se2+OvL6O0Lsc3Dji2eWxAsV927LV2+bWRvFL9LmjsGhsxeW8HRtNpWXMCOZCjKz2FqTQkbdrf5IguGNr4Z9VZn4/UEYawoFLAiX6bUeB/50tIZpKwwl9ycwU09JyDMrC/z3CK2FPFQRZWfG2BqTbHnsfwtXbE7mtrSfKqK83yQF88V4r2h0Ncfoi3GaBQGRmwbdnnXXgZG2kPvnzOC8rJji/fsQUTWU5/cPUbxuyQyTbKfQzCIbcX5Ntkap/EV5VtL1Td6rTgSWDmzx3mviOO5JsBSHl7XafQahUhm1pd5bhHHigoBK2R1Zn2Zp21VdehiOIfSglwmVRd5OoJyRqOxXD0TK4soyc/xtL2EAw9iKmLvXWfx5p/Aet69lheJUfwucW4S+BPPGy0rWjHOHlfG5mZ/okIgfuPzOrKgpauXUjs3fjSzx5exdX+np8PbljiKypJXyp72nvA8gBfEmxwEqz63NHu7iUisuHOHmR5H9nTYobjx5M32uCONFwgAVmTPTI8NhUQWeFlhHg0VhZ5a4PHckDAQ2TPqLH4RuVFE9ojImojPfioi60XkNRG5R0Qq/ZLvNU6jqC3N93W23ZEVPWE3a3wZ/SH13AeeqLE7kT29fd7NaSRSjLPH2+4CDx/mAwkUo+Mu8Fp5xLIYAWaMs+6hV5kz+0NKe4yoEIeZ9aW0ebg7VqK2Atb9e2efd2HHLXFCfx2ckFWvSCZvRn2pp66zRPWZm2Nt2zkaLf6bgFOjPnsYOERVFwAbgSt8lO8pLV295OcGOGRihS8LYyKJpRzn+KAUHVlATOUxa1wZfSH1NGdPvCgU8OcaWxO4evzoaBJa4PXeLgRKFBUCkR2bN/KSKX6nvXiV6iPeGoxIefs6etnX4U3HlsgCB2cRXodn6bzbEjx7YF2fX0amn5utPwXsj/rsH6rqjOP/CTT6Jd9r2mxlPHtcGW/v9Sdhk0MsxT+lpoT8nICnk1kwsLdvvNhl8N4irijKjXlsUlUxRXk5rPfQXZDI1TO+vJCywlzP/NJOVEg8eU21JQTEuwnCRPMlYCUXA++SwyUyEgDmjC8HvGsv8UJ/HbzuuMNuzxiT82A9D93BEO+2dHkir6WzN2bob1hefSnbD/gT2TOcPv5PAw/GOygiF4nIShFZuXfv3iwWKzaOMp7TYIV1+ZW50plAi36Y83ICTKsrYcMubyN7nLhzZzesSKbXlRIQbyM1Erl6AgHxdBI7FLVfazQiYk0oe9SZJooKAWvbxyk1JZ7VZzILvK60gMriPM8s/rYkirGptoTcgHjWcSezwL0OOW61c+OXFcY2TJwJV6/aZ7wIMAcnUsqPFdHDovhF5NtAH3B7vO+o6g2qulRVl9bV1WWvcHEIK37bqlm30x/f28He/rgTaLPHl3nuZkqkiAvzrDBSL2UmkgfWNXr1YLV396EaXxGDNXeycY83E6CtSSxwsNxZXo0wEk3MgxPZ490EffTCwmjycwNMryv1tGMTgfLCOB1bmdWxbfDQlVVeOBBGHY3jOlvvkfGV7FnwM8tq1hW/iFwAnAmcr37ttecDjuU4va7Utmq8j6l35EDsh3n2+DLebenyNL9Mcquj1NOQzuSKv5zmg72eTEg6qzrL41hwYFmNLZ1BT+QNuAoSKf5yNjcf9GQ3rmQWMdghqx5F9iQbYYDVkXpl8bd1BSktyI2riEXE8oN75VpK4BYEK7JnUnUR67wa0SSYDwKYUl1MQW6A9Tu91zVZVfwicipwOXC2qvq7CspjnJuUnxtgRn0p632y+BNZjbN9ikJJqIjHlbF530FPwkh7+vrpDoaSygNvrtGVonIWAnkgL1lUCMDchjJUvXEXuLm+uQ3ltHf3sf1A5n7p1q4gOQGhJD+2TxqsEY1XxklbdzCute8wa1ypZx1bS2d8t6DDnPHlniniWJlAI8nNCTDbw440Ej/DOVcAzwOzRWS7iHwG+BVQBjwsIqtF5Hd+yfeayBDLOT7dDBhI6xsvyga8Xa3Y0hk/ygYsP6NXycXcKCpnws6L+k0WNQHe+m3dKmLw5vqciflE1+fIW+eBsoqXEC4SL1MKtyUxSsAyFNq7+zzZZjJWGHU0cxvKeccjQ8jN9c0ZX8a6nW2eZ1mNq/hFpC3Jq11ENsb7vap+VFUbVDVPVRtV9feqOkNVJ6nqIvv1eU+vxieceGnnJs1pKOfdlq5Bi7q8ItbWfQ7OakUvJ3iTNb65DbYi9mCE40YR15UVUFOS78k1hqNQEliNNaUF1JbmezLCGMiNH9911lhVRGlBrieKOF5CuEjmjC9DxJs5qWSjQxgYsXnRkbZ19VEeJwLMYZaH8uKtgo5k7njLEPKqvSSrz7kN3rk+I0lk8b+tquUJXmWAP6EtIwxn2FoRYfGDd7P7kSSyGgMBYZaHk4OOvESNr6m2lMK8AGs9UlSQ2CIG7yZ4HR9/ouE0eJe6IVlUCFh+6TnjyzzpSN0o4pKCXKZUF3vW0SSziBuriijOz/FMEbtpK+DNs2gl2Evc0YRHbBnev2B/iM7e/qSuJUeeF89fJIkU/4dd/N7Nd0Y90QprYLievaRpDs6yeC+GfsH+EAd748edg5XMbPa4Ms8UB7hT/Bt3Z75Qpq3LmkBNNLkLlt92w+72jFPuJosKCctrKGPdrsyH75ZPOrGFCrZf2oO26sY14aRS8KrjTubjryzOp6GiMOP2ORD6m7g+J1dba00yVcTJIqQc5voURRhX8avqJhHJEZFHEn3H09KMUKIn7erLCqgqzvMlpNOZQCstiK2sZo8v44BHUSiJ3EqRzJtQzloP/IyuFf+4MrqC/Ww7kNn8f2uXld46Xl06zJtQTncwxDsZbsWYLCrEwZlwzXQhkBuL2JG3xYMcSG7lzfEokijRKu9I5jWUZ6yIO3r7CGniiXmwOjZrwjUzeckW3zlUFOcxsbLIE8MrkoSTu6raD3SKSIWnUkcZ0QrLGq57Y0XFkpVoAm2ePdp4Y0f2LPB5DeW0dAbZ2ZrZBJqbOHfwboK3rdtSHIkmIwHmT/CmTpOF5zl4tRbEjesFBiKJMq3PRKuuI5nTUMb+g70Z7f7ljEbd1Of8CeW8vTezCVenbbqrz3LWZzjqdvvsgRNMkkXFb9MNvC4ivxeRXzovT0sxwol1k+Y0WMNZr/J2DMiKnX/cYe4E73x+buLAwbvIkFbH9eJC8YvA2gwVseN6Scb0ulLyczKfx3BtETsdmwfy3I4wILP7p6pxc+NHM3+CZSe+saM1bXnt3e7cdGCN2PpDmpF7yc0aDIe5Ddbaj0wiidyOti15mXds0bhR/H8Dvgs8BayKeI0ZYin+uePL6ezN3B0RTUtnb0LFWF6Yx+Tq4oweKodkuVcc5jgTTB4o4pL8nJgpmSMpzs9lWm1Jxha4G580WCtOZ44r9eT6kkWFgD3hWlPskQWe/Poaq4ooK8wskshJyexmTsGJBHvj3fTlufWBA8xrsDqaTDput64XGBixZTLB64Rtu1X8/SH1NEVz0u5UVW8WkSJgsqpu8EzyKCKWgpxjN+51O9uZUlPimay2rmDCFANgDW29cPW4tTpKC3KZWlOcNYsYLKvxpc37k38xAdZG1sktRkteOY+u24OqJnUNxcOtKwQG4rPTpbfPigpxU58iwtzx5Rl1NKm4JsoK85haU5xRGw2H/roYsTVWFVFWkJtRxz2wYt7FZLnz7O9q48Q59enJi7MTXSycjnTtzjYOmeiN1z2pxS8iZwGrgb/b7xeJyF89kT5KaO0KUpA7OF56Zn0ZAfFmYUy0rGQP1/wJ5Wxp7sx4o+lkuV4imdtQ7oGrx51PGuCQieXsbO1mfwabpKTS0cyz46XT9UuHQmrtD+vCIgZ7IVDzQbp60xu+p3LvwFJW63e2pe2adDs6dJg/oYI3dqY/Kg2n23AhLxAQ5jaUZzQKdixwN/VZXuhMuGbSkbp3ZU2pKaEoL8dTXePG1XMlcATQAqCqq4Emz0owCmiNscF0UX4OTR64I4bIcmE1Oj7UdZm6JlIY3s5rKGdzcycdGUSGtLn0SYM3fuI2lz5+gHkZynMbFeIwZ3y5lbohzTUZqVjgYHU0BzNwTaYqb96EcrbtT3+RYzry1u9KPyQ3nfrMZI7G2Ykuei/oWOTY63e8TBPjRvH3qWr00zBqkqt5QTzL8dCJFax5N3Nfu4MzgZbMapzn0QRvS1eQYhc+90iZmTT21Fw9lrw1GfqJ3Vqo4eF0mp1pKlEhMHB9actLwUcMmU/wpmIkQObXN7AGw73i7+ztZ0ua6dJbO4eO6hPKa7D25chkxOa2Lh15Xqz9cHCj+NeIyMeAHBGZKSL/BTznifRRQrybdMjECna1dXu2nDrZnqYO9WVWmoFMRxupND4vIkNSkVdZnM/EyqK0LfDuYD89fYkTwkVSVpjHlAzmMVKJCgHLL11RlMfraRoOqVqos8dZrsn0Oxr3k62Q+YgtZYs/wxWuLTFG9YmYP7GCkKYvr9Vl6K/DXI9Cqh3cKP4vA/OBHuAOoBX4qifSRwmJFD/AGg8ibBw5kLyxiwjzJlRkVfE3VBRSWZyX0SgjVStn/oTytBVVKuGADvMa0p80TyUqBKx7eMjE8rRHjKkqxqL8HGbUl7ImU8XvUl5dWQH1ZQVpt5e27iB5OUJhnrs8kjPHWenS071/qbbNBY32s5/B/Uulo3F0TbqGQjRuavUMVf22qh5uv74DnO2J9FFCPJdBeOGPRzejJQV3wfwJ5by5uz2jja1TaewiYq2QTPPB6u0L0RV0F4XiMH9CBZv2HUxrXiHVyUhLnjVpnk5K4VSiQhwOmVjBhl3taW1m35JCVEikvNe2t6blLnCTkjmaTDpuZw2G2wirgtwcZo4rS1teS5f7iXmwtu2sLc3PaMSWmqunnJyA8Pr27Cn+WBuij5pN0r0gXg6PssI8mmpLPOuFU1nUMX9COX0hzWjjbrdx7pEy1+1qJ5jGfsOpWoxgRfZAeu6lVKJCHMLzGGmEPaYSFeJw6MQKevtDaWV6HMg86n5Es2BiBfs6etjdlrprMtmK8ljMn1DBm3s60lp4lGrbhMxSN7R29aXUVqwRW/pzfG4yc0ZSmJfDzPpS/y1+ETnN9udPjFyxKyI3YW2bOCbo6w/R0RN/xaJ1873bmAHcR9lAZouqUrU6Dm2spLcvQ0WVosUP6Y2o3KRkjsZZCJSJvJTq0x6+v5aGFddq707lJiokLK/RkdeSlrxUFfF8e0VtOu2lrbuPslQV/4Ry9rb3sKc9dT94a2dvSp02WPcv3Y4t2SYs8eS9/m56I7ZoErWaHcBKrJQNkSt2/wr8S8aSRwlttq84XojlIROs3PyZxJs7pBKbPbWmhJL8nMxil1OcYFqQoaKC1BTjuHIrN386fttURk+R8qzhe+ryWjuD5KcQFQJWpsfywty0rLhUJwfB6tgCkp5fOpUIKYeBCd406jONjuYQe8SWjjskVQscLKOvP6QpjzK6g/30phB44LCgsYL9B3vZ4cEEb6LsnK+q6s3AdFW9OeL1Z1U9kLHkUUKyaAbHavMirDMV5RgICPMmlKc9WZeOz31KjaWo0lH86ShiaxI7vWt0Omy3K3cdeQsaK9OyiNu6k2/bF0teuu6CdBRjUX4Os8aV8Voa8tq6Ur++SdVWqoh0jJP2rmBKbiywFHFA4NUU26eTGz/V+kz32U81EMAhPMGbRvuMJpGr5y7731dE5LXoV8aSRwktnYnjped7ONve2hUkNyAUu5xAO3RiJW/saM3M557CcDMTxZiOxQ9WY09nEjuVJf+RLGis4K29HSlPKLel6CN2OLQxvQnedCxUINzRpOouSKejEREOmVCRlgWejrySglxm1pel3D7TiQADK9KtpiQ/5esbCP11P5kMVkhnbkA80TWJXD1OyOaZwFkxXgkRkRtFZI+IrIn4rFpEHhaRN+2/VRmUPSskU1gVRd4lTWtJcQJt4aQKuoOZ+dzTGW5u2NWesl8zbXkTK+gLacrL49tipNlww8LGSlRTt+KsTUNSUxyQ/gRvquGADgsaK9jX0ZtyPHg6ihhg4aRK1u5sS6njthYypu5aAuv6Uo1ccrMlaCycEVuqijjdZ6Ewzx6xeRDZk8jVs9P+uyXWy8W5bwJOjfrsm8CjqjoTeNR+P6IZuEnxe+dD07j58WSl0hgWTaoE4NVt2fG5g/Vg9YU05ciXdCZ3wVIcAK9ua0lZXrqKIx15bjcNiebQNEeM6SridOLBnd2p0pG3aFIFwf7UOu7uYIhgv6Y8WgNYMKmS/Qd72X7A/SY34QiwNOSlM8GbzIuQTF46I7ZoErl62iM2VY/eZD2p01VVnwKi0yt+ALjZ/v9m4IPpFjxbuPFNHzKxgm37u8I3NBNZqSiPydXFVBbnpaykHFmQjuKvBFKPDHGbkjmahopC6soKUlfE3ekpqprSAhqrilK2qtq6+9JSHOlM8KpqWpO7kF48uJOHKF2LH1LrSNM1SgAWNqYegNDmcp+IWKQzwZtqgr1IDm2s4EBnMKWOLRaJLP4yZ1P16E3WVbU8TXnjIkYSO4G4OU1F5CIRWSkiK/fu3ZumuMxx0widePNMrf5Uh+8iwsLGSl5Nw+eeSj7wSBoqrIUrqSrGVCOIHJxrXJ2yBd6XlusFSKtOrU47dXnpTPB2B0P09odSDgeEAXdBKm011Tw9kYwvL6Q+xY57YA1G6vU5Z3w5+TmBlAyTTOQdmsYK3nRHv+BdMEkii3+liPyniJwqIoUZSUkDVb1BVZeq6tK6urpsiw/T0hmkKC+H/Nz4lqpjBadjeUeSznB6YWMFG3e309mb2mRkug9zuhO86bpeABZPrmTTvoPhMruVl46iAsvds/1AF80d7hY6hX3SaVj8YD3M63e6n8DOxDVhyStPKR48E0UlIiycVMnqFNpLJhZ/fm6AuQ1lKXXc6QYCAEywJ3hTG2EEEYGyJHtBx2JOQxl5OZJWZFYkicbdRwL3AMuBJ0XkARH5qojMykDebhFpALD/7sngXFnBjQKpKMpjRn0pr2xt8V1WNAsnVRLS1LNYOvnA0/UzvrWnI6XNu9NZiemw0HEvvdviXl6ak4MQ6c5y93CFfdJpyls0qZLe/pBrP3i6bjqHQxstP7jbzd4zlbewsYJNew+6TtGciSIG6/6tedf93gPprPJ2CHdsKY1o+igryCUQSH3Dn4Jce8SW4QRvIldPn6o+oarfVNVlwGeAduBHIvKKiPwmDXl/BS6w/78A+Esa58gq7S53cVo8qZJXtrWkPekSCmlayjHd0UY6Kz8HZFqZCVNZmJOJBX5oGhOubvfbjSdPBNdWY6YW+OLJVnDbK1vdLY9x5JWl6cpaZLcZt8oqEwscBvz8bpVVJooYrPbZ0dPHpn3u0pm0dfUREFLKQxTJ4kmVvLWnw33HloFRAlZ9vrqtJaP9vl0/9aq6U1VvVNVzgSXA7Ym+LyIrgOeB2SKyXUQ+A1wLvE9E3gTeZ78f0bR1Bylz8UAvmmxZUVv3p7fRRXtPehNodWUFTKwsStkn7YUiTsXdk4m8iqI8ptWVsNpl9JJqep2oQ2lBLjPqSl1b/APhgOkp4vEVhTRUFLoeMWYyGQmWu6AwL8DLW9zJS2fNRyQLJlYC7jvSTOYUIHJC2X1HU55iHqJIDptSZctrcSevq8+VTokrb3IV7T19vLU3/TxdSVuqiNzH0I1XWoGVIrJKVWMGBKvqR+Oc8uTUiji8tHf3UVuafKHF4knWzV+9rSWtPXjTjSUGy1WQjuJP12KsLytkQkVhSsPbTBQ/WNf41MZ9rvbEPdjbT0jTV8RgjaSe2OBuD95MLX6w5jFeTtHiT1deXk6ABRPdy8vU4q8ozmNabYnr9uKsuk63fU6vK6U4P4fXtrfw4SWNyeVlMDoEa4QhAq9sbeH4WcnnI9Nd8+Fw2ORKAF7ecoBZ48rSOocbi38T0AH8j/1qA3YDs+z372naXVr8s8ZZjS1dP38mD9eCRiuc1O1kJFjXlYkiPmxKletrTSc9RDSLJlWyr6PHVZ6STBUVWIvjml36wTO1wMEyHLYf6HKVYCzTEQbA4imVrN3hbmGVs6I8XVcIWFa42xFiuqG/DjkB4dCJFax27Vpy586NR1lhHrPqy9x33BkEOgA01ZZQWZyX0Zyim5pdrKofU9X77NfHgSNU9YvAYWlLHiW0dfe5sjxycwIsaKxw7aeNpj0DK8cZ2qYUWdCd2XBzyZQq3m3pYmdrcsWYqasABiZ43QynM50chIHFcW4ergELPAMrboolb7UrealtSxhT3uQqevtDroICnIisdF0hYE3w7m7rYZeLjjtTxQjWvMnaHa2uFlZlavFb8qwJXjd+9/Y013w4iAiLJ7kfscXCjeKvE5HJEUInA7X228xTUo5gVJX2FCZiFk2qYu3OtvTyj2e4ejAg7icHIf24c4fD7AlJN35iLyzwOQ1l5OcEXCn+TMIPHeY2lFOUl8OqLcnrNBM3ncP8CRXk5QivuOnYulPPBBrNYttd4KbNtHXHT0vuloXhjtSNvMwV8ZIpVQT71ZUx5IW8xZMrae0K8o6LPX8zffbAev7eTGFCORo3iv9S4BkReVxEngCeBr4hIiUMrMIdFh58fSd/X7PLt/P39Flhem6t8MWTKwn2a9bSCDuUFOQyt6GclS6UVFheho193oRyCvMC7hSjBz7wgtwc5k0od2eBe9DR5OUEWDipwuX1ZeaTBmth1byGcneKsSszixGseZrGqiJXVqPl7sxMUc2bUE5+rrv2kul8EFiKH3DZcWfm6oHIyKyWhN8LhZSO3szvnyMv3bVDSRW/qj4AzAQusV+zVfVvqnpQVa9PS6pHfOH2l/n8bat8O/9A2Jy7m7Q4BasmmkxcPQBLp1SxelsLfS4ydYZCSkdPetkkHfJyAixorGSVK8WRuQ8crGt8dXtLUr+0F64QS141a3e2JV2v0NYVpDAvQEFu+hY4WA/zq9tak97DTCcHHQ6b7G6exgtXSEFuDgsbK1wZJ14o4uqSfKbVlrBqS3TWmBjyPLD4Z9SVUlaQm7Qjbe/pQzUzIwGsOSgR0nb3JFX8IpKDtfHKCcBJwMUi8rW0pPnEAQ82QYlFeNLO5U2qLy9kYmVRyukFYKCTKU1jNR/AkqnVdPb2u1oE1NFrNb5MlceSKe78qAM+98zkLZ1aRU9fcr+0F64lgCVTq+gPadKIKS8UB1gjxq5gPxuSZOps6wqmvDtVPHk7W7uTztO4XcuSjKVTq1nzbitdvYnbSyarvCNZMqWKVVsOJFxb4+Tiz1ReICAsmlyZtCP1wi0IljE6e1wZL6c5wevG1XMfcCFQA5RFvIaVyJv5yjZ/9oVpT8NF4ebmx5bVl/aCKoDDp1pDv5VuLBwPJj/BshiD/Zo070umC3IclkypBmDl5sTX6FxfaYYdzWF2iO6qzYnbV7q5+IfIc+kusBLCeWPxQ/J5mrbuIGUFmV/f0ilV9GWxI10ypYoDnUE27Yvvd083F38sFk+qZMOuxCNEL9yeYXmTK1m99UBaC7ncaJlGVf1XVf2+ql7lvFIvprd0RlgNbvx46ZCO+2WpHe2yw+VyeIe2DOLqARoqiphYWeRqKN2exu5UsXDiiZPVf6ZuLIe6sgKaakt4KYkidtYo5KSxJD6SiuI8Zo0rTerO8sr10lhVRG1pfnJ3gUcW8dyGcgpyA0nleeF6AXd+dy/ckA5LpyaX55UFDparLqSJF6oNhP560NFMrqKt2/0K5UjcKP4HReT9qRfLXw5EpEB2uwIxVVL18QMcPtWySl9KYpXGkuVFJMPKzfuTpo1wGnsm4ZxgpTBuqi1Jqvjb7DjwogyiUByWTqli1ZbE1+iVxQhWnb68JbFV5UX4IVhheodNrmJlshFGhuGADvm5VghyIsUf7LfWYHghr7I4n5n1pQlHbO3dlhsyUzcdwLTaUiqK8hKO2Ly0wA+bXIUICe+f1/IgPf3nRvH/E7hHRLpSycfvN07POa68wPWkZqqkYxnPbSinrCCXF95JTfG3u1wvkIilU6vY3daTNFe3V5OfYDW+l5P4UZ1ryyQO3OHwqdUc6Azy9t74w3evXC9guZfauhMvj/dKEQMc0VTN1v2dCePdrRQDmVuMYF1fIr+7V6M1h6VTLb97vI7UizURDoGAcNjkxAEIXiy+c6gotvzuLyZ49r2IOHOYVltCVXEeL6ZoZII7xf8z4Cig2IN8/J7h+N9PmlNPV7A/5Z3uU5GRimWcExCWTK3ipRQVf6aJm8B9CFt47sID5XHYlEqaD/aypTl+jiIvrs1hiTOXkaCxW3l6PFJUUxx58eu01YO4bIdlTTUAcR/m7mA/vX0hzzqaZU3VBPs1biSal64QGOhI39wTuyP1amLeYenUat7a0xF3k6RMcvHHYllTNau2HIi7D7aXHWkgIBw+tTphRxP3ty6+8yawRjPd68tjHKv1lLnjAHhhU+oXn1RGmln7Dp9azZt7OtifQrRRJhuHOMwZX05pQW7SCV6vJnfBCnmExK4tL8IBHabVllBdkp/Qz++lq2dKTTE1Jflx69RJCOeVvLkNZZQW5PLiO80xj3s1Ue6wZGoVASHuCHVAUXkjL1kQgtcdTdgdkqxj82zEVkNXsD/uRimZRu9Fs2xaDVv3d7paQR+JG8W/E3hCRK4Qka85r7RK6SHODZtRX0pTbQkvxHlQMsHJ05Oqi+KIptT9/G5zAiUiJyAsnlzpykcMmUe9AMysL6W6JJ9/Juh4vXBjOYhI2M8fDy8WAEXKc8ICY9EV7KcvlH4u/mhycwIsmVIV14pLNcQ4GeWFecybUB5fnoeuF7C2mqwtLYjbRr30gYOVeiM3ILz4ThJ5Ht2/w5usjibes9/WlVn0XjTLbF2TqtXvRvo7WBuj5zOCwjkj3TDLmqzhTn8G+aljy0hPYS1orCA/N+Da3WPt4ORd5MSG3e3hBh2Ltq4gxRkkwYokEBCWNVXzz03xO14vLXCwRlSbmzvjJjTzarLV4YimarY0x/a7Dyhib+Vt3B17xOi1YgQ4YmoNL289EHNhnNcWuNNxx7P4vcjrFElRfg4LGiviGoaZ5uKPpr6skGm1JQk7Uq86URiYU0xkeMXCzcrdq2K90i6pR0Quk182zfIbrt/lrZ/fbS7+aApyc1g0qdL1pEtXsJ/+kHryMB/RVI0qCTudTJNERbOsqZp3W7rYFmcvAi8tfoj08w+14vr6Qxzs9SYKxeHIaZbfPVbn5rWPGAasuFhWoxeZOYfIm1ZNT18o5kYpXk/uAhzeVM22/bFDnr0e0QAcNb2G17a3xoyvzzQXfyyOsA3RWBPYXhslOQFh6dSquK7BeCTac/fKZD928x2/iLRanQkxr/38bjNzxuKIqdW8saONDhfbEzqN3Qs/6mGTq8jPDfD824ktcC8f5COn2/Uf1z3hbWM/ZEIFRXk5vBBTETtbSnp3ffMayqkoyotZp177iMHa6KYgNxDTamz3MCLLwQlBjnX/vHaFABw5zZIXqyNt7QoSEO984Ja8GvpDGrcj9bIuwVL8bd19MVdgez36BcvP//beg+xtd5+WPZHF/9lIn36M16XARzIudZpEKq8JlUVMqi7y3M+fiWV8RFM1/SHl5VSSmHmgrArzcjhsciXPJ3O9ePggz6ovo6o4L6Yi9sMCz88NcHhTNc8lUsQeXl8gIBzRVM0/Y7QvPxRjQW4OiydXxlT8fsirLsln9riy2Irf3hi8NN9D98T4ciqL82LfPx8s8CVTqsjLkZjuEK9crJEckcDv7vXoN1JeKnOKiRT//zDYpx/9KmUYN2KJVsrLmmriDq/Sl5G+P+6wKVa0hJubkU7YaCKOmlbL2p1tcUPY2j1a8u+QSDE6Ix6vG/vR02t4c0/HECvH63BAh6Om1bCluXOIe8IP1wRY0SFv7GgNt42h8ry3Uldt3j9kPUybnUoknY3B4xEICEc21cQcQXk5Me9QnJ/LwsbK2K46Hyz+xqpiJlYWxe24vey0wUrLHm8EHI9Em63H9O1HvX6WTkFF5N9F5A0RWSMiK0SkMNVzRFfgsiZrYU+8+OB0yCSNQmlBLodOrEjochmQ463yOHpGDaqJXS9edTIOR06rYdv+riE7Vnm5QCaSo2y/e/TIxg+LGOL7+f2Sd8TUakI6dE1GW3eQvByhMM+bqJCwvKZqDvb2D0kp7odrAqw2GmteyA9FDNb9e/3d1iGuV7+u74imal54Z+gKcy/CtqPJsyPBUlk06m3rcYGITAS+AixV1UOAHNJwGVkbFg9UYKIJuHRQzTxnyDEzalm9rSWpn99r5bGwsZKivJy4nY4fw9uBeZbYitFri3/+hHLKCnN5/u19g+X5ZBHPGV9GZfFQP/9A+gtvr++wKZXk5UhMeemEGCfDmVCOdpdamTm9V4xOx/1c9P3zoW2CNcEby8/vVR6iaI6cVs2+jh7eijBEQ6HUNnZKhWVN1WzY3R53lB+N91fsjlygSESCQDGwI+G3N2yA5csHfXRS1SLeOfcC6OyE009nEvDnrS2U/iUHxpXBhRdar3374Jxzhp7zC1+A886DbdvgE58Ycrj7K5cQ0jwa92yF5f9v6O+/8x045RRYvRouuWTo8auv5pgZs/jnbfcTPO5HUBy1Yfv118OiRfDIIyy77Dv8Yd9BJj1bBU6I5X//N8yeDffdBz+LMbC69VaYNAnuvBN++9tBh/KB5R+8wlIaN91kvWwU+O07+3n2P+09dH7zG7jrrqHnf+IJ6+9118H99w8+VlQEDz5o/f/DH8KjjzIX+OPmA1TflwdzpsCf/gRA5Q+/xx8eeIy5j5eD0+AbG+G226z/L7nEqsNIZs2CG26w/r/oIti4cfDxRYvIvf56ljXVcOKPLoVfDrhDlrb1cFlBIxVXnGx98OEPQ3NUB3jyyfDd71r/n3YadEVFl5x5Jnz969b/drsLAHfubreSA+69CC6+GDo7OeuS8zmitZuCf/504PcZtj0uvZTis87ijPw2zvjqx+AnFQOn3tNB97EfAd6XsO1x9NHw3HPwrW8NPR7R9vjRjwCoB+7d1kLBvTnwlzvCbe+SH33f+s09EYv1E7Q9AO6+G2prh7S9MA88wIz6Uj7/xkMs+ev3ob40fOh721v476t+b71x2fYGUVMTbntccQU8/zwAR6py5+YDlLw4BR67zzp+ySX88t7HGFdWCL8qtj5z0fa4/nrr/49/HLZvH3z8qKPgmms4ZkYtv73nakof+iFUWA6NUEj5ok6i/LQfWN912fYGce654bbH6aeHP76wu4/Dd7SyteRNKr9zSfy2Z5N1i19V3wWuA7ZiLQ5rVdV/RH9PRC4SkZUisjIYHBqT3t3XP6SnLi/Kpa27Dy+8/J22lV6SQXTBkilV5OcKrV2JLX5n/UGuh37UpVOteP6OKB9xSBVV7xYcOQgD9R9Jb5/lM87N8dZCBcuKO9jTR0/fgF+6P2T974cVV1GYR0+wf1CCwP5+zTgLaDyWTq2is6ePYP9Ai+4PKcUeTrRGUlGUR3tXkN6IeP7+kHraLh1EhGl1JbR2BQc9r3393oQ1R5MjQmlBLvs6Iu6dKqGQP/evsaqY4vyc8IgQBp5zP9pmSYGVjXbjbpeubrUVQbwXUAd8C7gBuNF5JftdgvNVAY/Z580D7gU+nug3S5Ys0UhCoZBOv+Jveu2D6wZ9fs/L23XK5ffra9taNFPW72zTKZffr/e9+m5G5zn/f/6p//KLJxN+55oH1unMbz2QkZxoVm3Zr1Muv1/vf3XHoM93tXbplMvv19v+udlTeaqq//fMJp1y+f26Zd/B8Gd3vbRVp1x+v25tPpjgl+mxdkerTrn8fv3jym3hz659cJ3O+NbfNBQKeS5v3c6h8r5w20o9+WdPeC5LVfVl+x5GtsEP/foZPf9//umLvH+8sUunXH6/PvfWvvBnx1z7qP77na/4Iu/2f27RKZffr2/taQ9/NuvbD+jVf1vri7yfPbRep13xN23r6lVV1eaOHp1y+f36f89s8kXet/78ms7/3t+1t69fVQfa699e25Hkl+nxmZte1ON/8tigz4CVGkOnurH4/wJUAI8Af4t4pcspwDuquldVg8CfgaNTOUF4mXyUZXDMDGsP+Kfe3JtB8SzS2YQlFkfPqGH9rva4q0zB22yLDodOrKAkP4fnN0X7wL2PO3c4blYdAE+/NVD/XmYCjWb2uDKqS/IH+YmdyUGvfeBgha1Wl+Tz3FuR8ryfrHM4dGIFZYW5PPNmhDyffOBgLeTKCQjPRN4/nyZbwRqxAeF5jO5gPz19IV984Ja8WvpDGg7r9CP0N5JjZ9TS0dPHa3Z+fj/WYETL29LcGXchZSRuFH+xql6uqnep6p+cVwbl2wocKSLFYj2dJwPrUjlBvHTJdWUFzG0oH/SgpItXk5LH2p1RwgVVPjxceTkBjmiq5rm3oidb/YmyASuB2sTKIp7eOFD/TgfqRV6gaAIB4chp1Tz/dnM4eqLNp8lIR96xM2p56s194bBhP8LzHHJzAhw1rYan39w3cH0+KuLywjwWTarkGbvNhEJKe49/HdvUmmIaKgrDHbeXu2HF4rAplRTn5/DURqtj8yP9RSRHTa9BBJ5506pPP1ZdR3LsTNvwcqH/3Cj++0Xk9ORfc4eqvgDcDbwMvG6X4YZUzpFoI5HjZtayassBOnuTr5hNhFdZCedPqKC8MJdn34p/M/xY1AFw3Mw6Nu07OMgC8CvKBiy/7XEza3n27X3heHAnKZVffvCjpteys7U7vL2eV/u1xuP4WXXs6+hhnZ0exE9FDHDszFrebeliq30P/exowDJUXt/eQmtnkIO9zsbg/sgTsTrSZ99qpq8/FF6D4df1FeTmcOS0Gp62PQJ+hRo7VBbnc+jEivAIyu+OZnpdCePLCweN2OLhRvF/FUv5d9ubsGS8EYta2zjOUdVDVPUTqup+rTGJMwYeN7OW3v5QyhuhDJXhzRZpOQHh6OlW43astqGy/HmYT5htWQBPbhw8dAf/Gt9xM+to7+7jVTvvSyaL4Nxwgm3lPLnBeZj9lXf8TNudaI9q/HS9wMCI8Zm39tHT1093MESZh+kMojluZi0htcIsvXoGEnHC7Dpau4K8ur3VtzURkRw/s5bNzZ1sbe70Jc9SNMfMqOWVrVZIt9+uJRHh2Jm1PPd2c9KElW6StJWpakBVC+3/h30jlkTuisOnVpOfG8jY3eOVjx/gGNtq2xxnsxK/rMZptSU0VhUNUvxe7bcbj2NmWMPbsFXlQbrpREyuKWZabUn4Gtt8WPkZSX15IXPGl/HUxr2e5+KPRVNtCRMqCnnmzX0R984/eQsnVVJakMvTb+3z3UgAq2MLiGWc+LXqOpLj7XmoJ9/cm7Xr6wspL77TPCixpF8cN7OWls4gb+yIvR+Ag6twThE5W0Sus19nelLCDBi4YUMrsDAvhyOmVocVT/oy+sjLEQpyM494day2eGXyy9UjIhw/q47n324Oh1X6PdysLM5nQWNl2M/o1wKZSE6YXcc/NzXTHez33RUCcMKsOlZu2c++jl5Pc/HHQkQ4ZoZlxbV0+m+h5uUEOHJaNc++tc/zTVhiUVmcz6JJlTy5MTuKuMk2hp7auDcrI4wlU6ooyA3w9Jv7PE2HHo+jpzu6JrHhm7QEInItlrtnrf36qv3ZsJEsUuS4mbVs3N3B7rb4kTTJSHcTllg01ZYwtaaYx9bviXncT2V1wqw6Onr6wjsQtXX1kZ8ToNCDjc/jcfxMa8Vya1eQ9h5/LX6wrrGnL8Q/NzXbUTb+yjt+Vh3BfuUfa3cB/ioqsPz8rV3B8DyR7/Ls6BDHavS74z5+Vh2vbW8Jb9/pp7xIY6j5YK+nufhjUZiXwxFN1eGOxk9rH6wAlznjy5J6PNx0PacD71PVG1X1RuBU+7NhI1lSs2Nnuuv1EsvwNpph+ex6nn+7ecim1r19IV/9tkdPryE3IGFXSLsPoaPRHDezjv6Q8vzbzb6GOzocOa2GgtwAD72xi97+kK+uArAWVhXl5XD/qzuBLCjGmXUEBP6y+l1bnv8dG8B9r1oL6v3uaE6YVYcq/O21nVmRd/xMK8zyyQ17Pc8EGosTZ9fz9t6DrN3Z5vu1wcCINFGqGLdjjsqI/yvifSlbtHf3kRuIn6hq7vhy6ssKeHxDbAvbDV77pk+aUx+2SiNp93m4WVaYx5IpVREhbP5bxIsnV1KSn8OTG/d6sqVkMgrzrGiN+7KkiK3okOpwgji/67OqJJ/Fk6t4eWtLVuQ11ZYwpaY4LM9vK3VBYyWVxXls2N1OQa6/o1GAo2fUkhMQ1u9q991IADhxTj0Aa95t873TBsvIDPZrwkhCN4r/GuAVEblJRG4GVgFXe1TGtOjo7qO0MDduTx0ICCfNqeepDXvDvu1U8drvfkRTNUV5OUPcPdmInDh+Vh1v7GhjT3t3RhlH3ZKXE+CYGbU8sWGP71EvDo5LC/ydHHRwrGKw8tn7zfIIeX7fPxHhxNn1EfL8rc+cgHCcHZ3ltyywOs7FkyoBqMnCvXM6UvD/3oE1Ii0tyOWJDfHnOd1E9awAjsRaYftn4ChV/YNnpUyDdhe+spPnjqO9p4+VKWxOEC3DS8uqMC+HY2bU8PiGPYPCOsNuqwL/GvwJttJ4auM+37IDRnPy3Hp2tnZ7tqVkMpbPHlCM2RpOO9SVFfguz7EaAWpL/ZcXWZ/5HgQ4JMOpz30dKUV2p03k9WVFnn19dVm4d3k5AY6baRle8Ui09eIc++9hQAOwHdgGTLA/GzY6evqSKspjZtSQnxvgkXXpuXui0z57wYlz6tl+oIu39w4kUvJ7EQlYWwfWlxXw+Po9WXH1AFm1GMGyqhyy0bFNqxvIKJkNi39ew0AEdTYUsZPmPBuyAI6fVZsVOQ5OR/qm26RmGbLU3t4yk6SPqXDibMvwikeiUnwNuAiItdmKAidlVrT0abNdPYkozs/l6Ok1PLp+N989c27KEzh++KaX28rwsfV7mFFfBvizWXc0gYBw8tx67nt1J3k5Qrm9Wbmf1JcXUpSXQ1dwaBZVPxARxpcXsqut29P9WhPxwUUTuHf1Dl/D8xwCAeGXH12MTwugh1CYl8NDlxzvS6qNWNSXFVJVnMe8CdlZIjSvoZz3zRvHvy1pzIq80w4Zz2WnzuZjR0zOirx/mT+e7/5lTdzjiXbgusj+9zRVPTHyxbBH9biLFDl57ji2NHfy9t6DKZ0/vE+sxwprYmURs8eV8fj6yAVV3m67GI+T54yjo6ePA53+T7Y6XHbqbKpL8pnbkJ2H+Q8XHcn5yyYz1fan+s3Pz13E21dn71E4e+EEzlwwIWvyZo8vY2JlUdbkvfTtU7jtM8uyIktE+J9PLuX988dnRV5uToCLl8+gMnpfDp+oKM7j7s/Hz33pxlR5zuVnWaOjJ+jKqjtpjmNh707x/P4tXDlxTj0vbd5Pq70Yx689W6NxMpdCdiY/AT51TBMvf/d9TI9wi/jJ1NoS/uNDh5KbBQscLCvcrxxEY5HcnIDvoZVjiUMb4wdgJvLxjxeRJVg7ZS0WkcPs13KsXbOGDSviJrnymlhZxNyGch5N0c/f7uPS6n+ZP46+kPLYht22rCAiUOLT5hoORfk5jC+3dgKaFuEPNxgMY49EptG/YO2U1Qj8HMvX/zMs33+M/dyyg6rSkUKo5clz6lm55YDrvSghcRK4TFnYWMm48gL+vmaXLauPsoJcAlmwHM9fZvkXZ44r812WwWAYuSTy8d9s+/MvjPLxn62qf85iGQfRHQzRF1LXk07vnz+O/pDy8Fr37h4/N0wIBIR/mT+eJzfupbPXytiXjSgUgC+dNIPHLj2BGfXZcb0YDIaRiZs4/j+JyBkicpmIfM95ZaNwsWjvSW0y9NCJFUysLOJB28J2Q6J8/15w6vzxdAdDdv4Od24rL7D2OTVK32AY67hJ0vY74Dzgy1h7av8bMMXncsUl7H93GbInIpx+6HiefnMgG59rGT5NuB7RVE1lcR5/X7PLStCWpZA5g8FgAHdRPUer6ieBA6p6FXAUMMnfYsUnHaV82qENBPuVR9e5c/f4nT8nNyfA++aO49F1e2ju6MmaxW8wGAzgTvE7y786RWQCEASa/CtSYjrSyBG+qLGShopCHnjdnbsnGxsmnHrIeNp7+nh770GqS4ziNxgM2cON4r9PRCqBn2Ltk7sZWJGJUBGpFJG7RWS9iKwTkaPc/ja8eXcKqzMDAeHUQ8aHs0W6kVGYF/B1ReYxM2optvOA12Qhf4fBYDA4JNRsIhIAHlXVFlX9E5Zvf46qZjq5+5/A31V1DrAQWOf2h+096VnjZxzaQG9fKO5mKINkZGHC1dmgAbK3oMpgMBggieJX1RARuXpUtUdVE2/mmAQRKQeOB35vn7NXVVvc/j7didfDJldRX1bAA6/vTPrdbE24njJ3HABx9mA3GAwGX3Cj3f4hIh8G/qzqiYqaBuwF/k9EFmLl9/+qqg5KqCMiF2EliWPy5IHERo6PP9VEXIGAcPqhDdzx4lZak2zInQ2LH+CjdsKmDy2e6Lssg8FgcHDjxP4a8EegR0TaRKRdRNoykJkLHAb8VlUXAweBb0Z/SVVvUNWlqrq0rm4gd3Z7t7VhcTr5WD60eCK9fSEeTGL1t/m0+Xk0OQHh40dOyVqqVoPBYAB3C7jKVDWgqvmqWm6/zyTd4nZgu6q+YL+/G6sjcEV7d1/aaXcXNFYwra6Ee155N4mM7K2mNRgMhmzjZgHXo24+c4uq7gK2ichs+6OTgbVuf9/Rk741LiJ8aNFEXnhnP9sPdMb9XjY2CDcYDIbhIlF2zkIRqQZqRaRKRKrt11Qg06TgXwZuF5HXgEWksIdvW3eQ0gz87x+0/el/Wb0j7neysUG4wWAwDBeJzNr/B1yCpeRXYaVrAGgDfp2JUFVdDSxN57cdPZlZ45Oqizl8ahX3vPIuFy+fPiT/d09fPz19IdcpIQwGg2G0kSg753+qahPwdVWdpqpN9muhqv4qi2UcRLsHE68fWtzIW3s6eGPH0DnqcGZO4+M3GAzvUdxM7v6XiBwtIh8TkU86r2wULhYdGUzuOpxxaAP5OQH+uHLbkGN+J2gzGAyG4cbN5O6tWBuyHAscbr/SctN4gRf+94riPE47dDz3vPIuXb39Q84P/u+BazAYDMOFG7N2KTDPo8VbGdEfUg729mds8YO1eOovq3fwwOs7+fCSxvDn2doD12AwGIYLN6ug1gDZ2Yo+CR1p5umJxbKmaqbVlrDixa2DPjcWv8FgeK/jRvHXAmtF5CER+avz8rtgsQjnyfdAKYsIHz1iMiu3HGDj7vYIGcbHbzAY3tu40W5X+l0ItzgWv9v9dpPx4SWN/PShDax4cSvfP2s+ELHRuonqMRgM71GSalBVfVJEpgAzVfURESkGcvwv2gAbmjew/KbltHf3sSu/lW8/U87m7vO5+PCL6Qx2cvrtpw/5zYWLLuTCRReyr3Mf59x1zpDjX1j6Bc475DyOmqX89OWP8ei+SgIibD/Qxa78Th7f0s8H55zNhn0b+H/3/78hv//O8d/hlGmnsHrXai75+yVDjl998tUcPelontv2HN969FtDjl9/6vUsGr+IRzY9wo+e+tGQ4/995n8zu3Y29224j589/7Mhx2/90K1MqpjEnWvu5Lcrfzvk+N3n3k1tcS03rb6Jm1bfNOT4A+c/QHFeMb956Tfc9cZdQ44/ceETAFz33HXcv/H+QceK8op48PwHAfjhkz/k0XcGL+SuKa7hT+f+CYArHrmC57c/P+h4Y3kjt/3rbQBc8vdLWL1r9aDjs2pmccNZNwBw0X0XsbF546Dji8Yv4vpTrwfg43/+ONvbtg86flTjUVxzyjUAfPiuD9Pc2Tzo+MlNJ/PdE74LwGm3n0ZXsGvQ8TNnncnXj/46AMtvWk40584/15O2t611G5+45xNDjl961KWcNfss0/ZM2yOaTNueg5uons9h5dP5b/ujicC9yX7nB/0ha345JyBJvumeDy1upK8/RHNHLwB9oRA5ASFHvJNhMBgMIwlJFqwjIquBI4AX7GyaiMjrqnqo/8WzWLp0qa5cuZK/rH6Xr/5hNY987QRm1Jd6cm5V5bT/fBqAB796HN+4+zWefWsfz19xsifnNxgMhuFCRFap6pDwezeTuz2q2htxolxgWEI7w6tqPZx4FRE+fWwT63e189zbzbR1BT2ZPDYYDIaRihvF/6SIfAsoEpH3YeXmv8/fYsXG68ldh7MXTqC2NJ8bn3nHk5QQBoPBMJJxo/i/ibVj1utYidseAL7jZ6Hi0d4dJCcgFOV5O7dcmJfD+cum8Oj6Pbz+bqtR/AaD4T2NG8VfBNyoqv+mqucAN9qfZR0nT090Rk0vOP/IyeTnBKzsnyaU02AwvIdxo/gfZbCiLwIe8ac4ifHTDVNfVsjZi6xtBoL9IV9kGAwGw0jAjeIvVNUO5439f7F/RYpPm8+boH/+hOkA5Kexn6/BYDCMFtyYzwdF5DBVfRlARJYAXUl+4wsdPUFfN0iZUV/K3Z8/iml13oSKGgwGw0jEjRa9BPijiDh7FTYA5/lWogS0d/cxvrzQVxlLp1b7en6DwWAYbtykbHhJROYAs7G2X1yvqsFMBYtIDrASeFdVz3Tzm46ePs9DOQ0Gg2Gs4VaLHg5Mtb+/WERQ1VsylP1VYB1Q7vYHJsbeYDAYMiepFrV34JoOrAac7aoUSFvxi0gjcAbwH8DX3P6uw+fJXYPBYBgLDNcOXNcDlwFl8b4gIhcBFwFMnjyZ7mA/vf0hT3bfMhgMhrFM1nfgEpEzgT2quirR91T1BlVdqqpL6+rqfMnTYzAYDGMRN1rU2YHrRaDH+VBVz05T5jHA2SJyOlAIlIvIbar68UQ/cvL0lBiL32AwGDIi6ztwqeoVwBUAIrIc+HoypQ9w0EnQZhS/wWAwZITbHbjGYUX2ALyoqnv8LdZQOoziNxgMBk9wswPXucCLwL8B5wIviEj8Pb1SQFWfcBvDf9CnlMwGg8Ew1nCjRb8NHO5Y+SJSh5Wk7W4/CxaN8fEbDAaDN7iJ6glEuXaaXf7OU4yrx2AwGLzBjRb9u4g8BKyw358HPOhfkWJz0Fj8BoPB4AluJne/ISL/ChyLlavnBlW9x/eSRdHRYy0aLvZ49y2DwWAYa8RV/CIyAxinqs+q6p+BP9ufHy8i01X17WwVEgZ23woEvN99y2AwGMYSiSz+64Fvxfi80z52lg/licvBnj5KCgas/WAwyPbt2+nu7s5mMQxjlMLCQhobG8nLM7miDKOfRIp/qqq+Fv2hqq4Ukan+FSk2Hb19g/z727dvp6ysjKlTp/qyB6/B4KCqNDc3s337dpqamoa7OAZDxiSKzkm040nWN1s/2NM3KKKnu7ubmpoao/QNviMi1NTUmNGl4T1DIsX/koh8LvpDEfkMkDDBmh84Pv6osmS7GIYximlrhvcSiVw9lwD3iMj5DCj6pUA+8CGfyzWEjp4+JpUMyx7vBoPB8J4irsWvqrtV9WjgKmCz/bpKVY9S1V3ZKd4AB3uHWvwjgXvuuQcRYf369a6+f/3119PZ2Rl+f/rpp9PS0sLmzZs55JBDYv7ms5/9LGvXrk143quvvnrQ+6OPPtpVeRxuueUWDjnkEObPn8+8efO47rrrUvq916xevZoHHngg5d9t3ryZO+64I/x+5cqVfOUrX/GyaAbDqCfpClxVfVxV/8t+PZaNQsXiYE//oKiekcKKFSs49thj+cMf/uDq+9GK/4EHHqCysjLhb/73f/+XefPmJfxOtOJ/7rnnXJUH4MEHH+T666/nH//4B2+88QYvv/wyFRUVrn/vB4kUf19fX9zfRSv+pUuX8stf/tLz8hkMo5mRZ0LHwfLxxw6lu+q+N1i7o81TefMmlPP9s+YnLlNHB88++yyPP/44Z599NldeeSUATzzxBFdeeSW1tbWsWbOGJUuWcNttt/Ff//Vf7NixgxNPPJHa2loef/xxpk6dysqVKwFLoV1wwQW88sorzJo1i1tuuYXi4mKWL1/Oddddx9KlS1mxYgVXX301qsoZZ5zBj3/8Y775zW/S1dXFokWLmD9/PrfffjulpaV0dHQA8JOf/IRbb72VQCDAaaedxrXXXjvoOq655hquu+46JkyYAFihi5/7nDW9s3r1aj7/+c/T2dnJ9OnTufHGG6mqqmL58uUsW7aMxx9/nJaWFn7/+99z3HHH0d/fz+WXX85DDz2EiPC5z32OL3/5y6xatYqvfe1rdHR0UFtby0033URDQ0PM8yxbtozvfe97dHV18cwzz3DFFVewbt06duzYwebNm6mtreXqq6/mE5/4BAcPHgTgV7/6FUcffTTf/OY3WbduHYsWLeKCCy5g8eLFXHfdddx///3s37+fT3/602zatIni4mJuuOEGFixYwJVXXsnWrVvZtGkTW7du5ZJLLjGjBMN7mqzn3EkHVextF0eWxX/vvfdy6qmnMmvWLKqrq3n55ZfDx1555RWuv/561q5dy6ZNm3j22Wf5yle+woQJE3j88cd5/PHHh5xvw4YNXHTRRbz22muUl5fzm9/8ZtDxHTt2cPnll/PYY4+xevVqXnrpJe69916uvfZaioqKWL16Nbfffvug3zz44IPce++9vPDCC7z66qtcdtllQ+Q6nVMsPvnJT/LjH/+Y1157jUMPPZSrrroqfKyvr48XX3yR66+/Pvz5DTfcwDvvvMMrr7zCa6+9xvnnn08wGOTLX/4yd999N6tWreLTn/403/72t+OeJz8/nx/84Aecd955rF69mvPOOw+AVatW8Ze//IU77riD+vp6Hn74YV5++WXuvPPOsKK+9tprOe6441i9ejX//u//Puhavv/977N48WJee+01rr76aj75yU+Gj61fv56HHnqIF198kauuuopgMBizPgyG9wKjwuIP2dv9xsvTk8wy94sVK1ZwySWXAPCRj3yEFStWcNhhhwFwxBFH0NjYCMCiRYvYvHkzxx57bMLzTZo0iWOOOQaAj3/84/zyl7/k61//evj4Sy+9xPLly6mrqwPg/PPP56mnnuKDH/xg3HM+8sgjfOpTn6K42JoYr66udn19ra2ttLS0cMIJJwBwwQUX8G//9m/h4//6r/8KwJIlS9i8eXNY3uc//3lyc3PD8tasWcOaNWt43/veB0B/fz8NDQ0JzxOLs88+m6IiK5I4GAzypS99idWrV5OTk8PGjRuTXs8zzzzDn/70JwBOOukkmpubaW1tBeCMM86goKCAgoIC6uvr2b17d/j+GQzvNUaF4u8PJVb8w0FzczOPPfYYa9asQUTo7+9HRPjJT34CQEFBQfi7OTk5Cf3SDtEhg9Hv09nvXlWThiLOnz+fVatWcdJJJ6V0bucaI68vljxVZf78+Tz//POuzxOLkpKS8P+/+MUvGDduHK+++iqhUIjCwkTLTgbKEY1T1nTul8EwWhkVrh7H4i8bQYr/7rvv5pOf/CRbtmxh8+bNbNu2jaamJp555pmEvysrK6O9vT3msa1bt4aVozNpHMmyZct48skn2bdvH/39/axYsSJsjefl5cV0T7z//e/nxhtvDE8o79+/f8h3rrjiCi677DJ27bKCtXp6evjlL39JRUUFVVVVPP300wDceuutYXnxeP/738/vfve7sOLcv38/s2fPZu/eveFrCwaDvPHGGwnPk6iewBqNNDQ0EAgEuPXWW+nv70/6u+OPPz7sCnviiSeora2lvLw8YTkMhvcio0rxjySLf8WKFXzoQ4OXM3z4wx8eFFESi4suuojTTjuNE088ccixuXPncvPNN7NgwQL279/PF77whUHHGxoauOaaazjxxBNZuHAhhx12GB/4wAfC512wYAHnn3/+oN+ceuqpnH322SxdupRFixbFDNM8/fTT+eIXv8gpp5zC/PnzWbJkSVhx33zzzXzjG99gwYIFrF69mu9973sJr++zn/0skydPZsGCBSxcuJA77riD/Px87r77bi6//HIWLlzIokWLkkYdnXjiiaxdu5ZFixZx5513Djl+8cUXc/PNN3PkkUeycePG8GhgwYIF5ObmsnDhQn7xi18M+s2VV17JypUrWbBgAd/85je5+eabE5bBYHivIum4DzISKDIJuAUYD4Sw0jz/Z6LfzD5kkfac+R/86QtHs2RKFQDr1q1j7ty5vpfXYHAwbc4w2hCRVaq6NPrz4TCh+4BLVfVlESkDVonIw6oad4WSY/GPxAVcBoPBMNrIuqtHVXeq6sv2/+3AOmBiot+E7Mlds9G6wWAwZM6w+vjt9M6LgRdiHLtIRFaKyMq2dmshUmm+UfwGg8GQKcOm+EWkFPgTcImqDll2q6o3qOpSVV1aZE/cjcSUDQaDwTDaGBbFLyJ5WEr/dntbx4SEQkpBboDcnFERhGQwGAwjmqxrUrFWzPweWKeqP3fzm35Vyox/32AwGDxhOEzoY4BPACeJyGr7dXqiH4RCOqJi+B1EhE984hPh9319fdTV1XHmmWcCcNNNN/GlL30pfHykpT42GAxjk6xrU1V9BkhpO6OQKiUjcGK3pKSENWvW0NXVRVFREQ8//DATJ8YOUIpMfTxhwgS6u7u59dZbs1xig8FgGDW5epLH8C+/afmQz86dfy4XH34xncFOTr996KDiwkUXcuGiC9nXuY9z7jpn0LEnLnzCVdlOO+00/va3v3HOOeewYsUKPvrRj4ZTHESSKPWxwWAwZJNRMVsaUh2xMfwf+chH+MMf/kB3dzevvfYay5Yti/m9RKmPDQaDIZuMTG0aRb8m9/EnstCL84oTHq8trnVt4UezYMECNm/ezIoVKzj99IRTFQaDwTAiGB0Wf0hH3CYskZx99tl8/etf56Mf/Wjc7zipjw0Gg2G4GR2KXxmRk7sOn/70p/ne977HoYceGvc78VIfGwwGQ7YZudo0gpHs4wdobGzkq1/9asLvnH766ezevZtTTjklvFnJpz/96SyV0GAwGAbIelrmdChomKm/vushPnvctPBnJkWuIduYNmcYbcRLyzwqXD0wsjZhMRgMhtGMUfwGg8Ewxhg1in8k7bdrMBgMo5lRo/iNxW8wGAzeMIoU/8iN4zcYDIbRxKhR/Ga/XYPBYPCGUaP4R6Krx01a5rq6OhYtWsT8+fM555xz6OzsDH//uuuuY86cORxyyCEsXLiQW265JevXYDAYxh6jRvGPRIs/Mi0zEDMt83nnncfq1at54403yM/P58477wTgd7/7HQ8//DAvvvgia9as4amnnmI0rKkwGAyjn5GnTWMgQEFukj5q+fKhn517Llx8MXR2QqwEahdeaL327YNzBqdl5oknXJXNbVrmvr4+Dh48SFVVFQBXX301jz/+OOXl5QBUVFRwwQUXuJJpMBgMmTAqLP6ACNaOjSOPZGmZ77zzThYtWsTEiRPZv38/Z511Fu3t7bS3tzN9+vRhKrXBYBjLjAqLPxBwofQTWejFxYmP19a6tvCjSZaW+bzzzuNXv/oVqsoXv/hFfvrTn3LxxReP2I7MYDC89xkWi19EThWRDSLyloh8M9n3c0a4knSTlllEOOuss3jqqacoLy+npKSETZs2ZbGUBoPBYJF1xS8iOcCvgdOAecBHRWReot8ERrhDyk1aZoBnnnkm7N654oor+OIXv0hbWxsAbW1t3HDDDb6X1WAwGIbD1XME8JaqbgIQkT8AHwDWxvtBYIRb/InSMt95550888wzhEIhGhsbuemmmwD4whe+QEdHB4cffjh5eXnk5eVx6aWXZrHUBoNhrJL1tMwicg5wqqp+1n7/CWCZqn4p6nsXARcB1ExsWrJv+2C3iEmRa8g2ps0ZRhsjKS1zLPN9SO+jqjeo6lJVXTp1fHUWimUwGAxjg+FQ/NuBSRHvG4Edw1AOg8FgGJMMh+J/CZgpIk0ikg98BPhrOicyK10N2cK0NcN7iawrflXtA74EPASsA+5S1TdSPU9hYSHNzc3mgTT4jqrS3NxMYWHhcBfFYPCEYVnApaoPAA9kco7Gxka2b9/O3r17PSqVwRCfwsJCGhsbh7sYBoMnjIqVu7HIy8ujqalpuIthMBgMo44RvjTKYDAYDF5jFL/BYDCMMYziNxgMhjFG1lfupoOItAMbhrscI5BaYN9wF2KEYeokNqZeYvNer5cpqloX/eFomdzdEGvZ8VhHRFaaehmMqZPYmHqJzVitF+PqMRgMhjGGUfwGg8Ewxhgtit8kqo+NqZehmDqJjamX2IzJehkVk7sGg8Fg8I7RYvEbDAaDwSOM4jcYDIYxxohW/Kluyv5eRUQmicjjIrJORN4Qka/an1eLyMMi8qb9t2q4yzociEiOiLwiIvfb78d8vYhIpYjcLSLr7XZz1FivFxH5d/v5WSMiK0SkcKzWyYhV/Olsyv4epg+4VFXnAkcCX7Tr4pvAo6o6E3jUfj8W+SpWim8HUy/wn8DfVXUOsBCrfsZsvYjIROArwFJVPQTIwdoLZEzWyYhV/ERsyq6qvYCzKfuYQ1V3qurL9v/tWA/xRKz6uNn+2s3AB4elgMOIiDQCZwD/G/HxmK4XESkHjgd+D6CqvarawhivF6wFq0UikgsUY+38NybrZCQr/onAtoj32+3PxjQiMhVYDLwAjFPVnWB1DkD9MBZtuLgeuAwIRXw21utlGrAX+D/bBfa/IlLCGK4XVX0XuA7YCuwEWlX1H4zROhnJit/VpuxjCREpBf4EXKKqbcNdnuFGRM4E9qjqquEuywgjFzgM+K2qLgYOMkZcGPGwffcfAJqACUCJiHx8eEs1fIxkxW82ZY9ARPKwlP7tqvpn++PdItJgH28A9gxX+YaJY4CzRWQzlivwJBG5DVMv24HtqvqC/f5urI5gLNfLKcA7qrpXVYPAn4GjGaN1MpIVv2ebso92RESw/LXrVPXnEYf+Clxg/38B8Jdsl204UdUrVLVRVaditY/HVPXjmHrZBWwTkdn2RycDaxnb9bIVOFJEiu3n6WSsubIxWScjeuWuiJyO5cPNAW5U1f8Y3hINDyJyLPA08DoDvuxvYfn57wImYzXsf1PV/cNSyGFGRJYDX1fVM0WkhjFeLyKyCGvCOx/YBHwKy9Abs/UiIlcB52FFyb0CfBYoZQzWyYhW/AaDwWDwnpHs6jEYDAaDDxjFbzAYDGMMo/gNBoNhjGEUv8FgMIwxjOI3GAyGMYZR/AaDwTDGMIrf8J5FRGpEZLX92iUi79r/d4jIb3yQd5OIvCMin494f04G57tdRPZncg6DIRa5w10Ag8EvVLUZWAQgIlcCHap6nc9iv6Gqd7v9sojkqGp/rGOqer6I3ORZyQwGG2PxG8YcIrI8YtOWK0XkZhH5h4hsFpF/FZGfiMjrIvJ3O0cSIrJERJ4UkVUi8pCT38UFx4vIcyKyybHcbfmPi8gdwOsiUiIifxORV+1NQs7z58oNBguj+A0GmI6V0/8DwG3A46p6KNAFnGEr//8CzlHVJcCNgNv0IQ3AscCZwLURnx8BfFtV5wGnAjtUdaG9ScjfPbgmgyEuxtVjMMCDqhoUkdex8kI5ivd1YCowGzgEeNjK70UOVk53N9yrqiFgrYiMi/j8RVV9J0LOdSLyY+B+VX06o6sxGJJgFL/BAD0AqhoSkaAOJLAKYT0jAryhqkele26byD0mDjr/qOpGEVkCnA5cIyL/UNUfpCHLYHCFcfUYDMnZANSJyFFg7Y0gIvO9OrmITAA6VfU2rF2iDvPq3AZDLIzFbzAkQVV77YnZX4pIBdZzcz3whkciDgV+KiIhIAh8waPzGgwxMWmZDQaPsEMv708lnHM4zmkwGFePweAdrcAPnQVcmSIitwMnAN1enM9gcDAWv8FgMIwxjMVvMBgMYwyj+A0Gg2GMYRS/wWAwjDGM4jcYDIYxxv8Hfxb5RnKGuAwAAAAASUVORK5CYII=\n",
"text/plain": [
""
]
},
"metadata": {
"needs_background": "light"
},
"output_type": "display_data"
}
],
"source": [
"# specify time span and evaluation points\n",
"t_span = [0, 96]\n",
"t_eval = np.linspace(0, 96, 1000)\n",
"\n",
"# initial conditions\n",
"C_initial = 0\n",
"IC = [C_initial]\n",
"\n",
"# compute solution\n",
"soln = solve_ivp(deriv, t_span, IC, t_eval=t_eval, max_step=0.1)\n",
"\n",
"# display solution\n",
"plotConcentration(soln)\n",
"plt.savefig('./figures/Pharmaockinetics4.png')\n",
"\n",
"print(soln.t_events)"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.1.4 Assignment 2](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.4-Assignment-2)",
"section": "2.1.4 Assignment 2"
}
},
"source": [
"## 2.1.4 Assignment 2"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.4.1 Exercise 1](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.4.1-Exercise-1)",
"section": "2.1.4.1 Exercise 1"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"### 2.1.4.1 Exercise 1\n",
"\n",
"The purpose of the dosing regime is to maintain the plasma concentration above the MBC level for at least 96 hours. Assuming that each dose is 64 mg, modify the simulation and find a value of $t_{dose}$ that satisfies the MBC objective for a 96 hour period. Show a plot concentration versus time, and include Python code to compute the total amount of antibiotic administered for the whole treatment."
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"jupyter": {
"outputs_hidden": true
},
"nbpages": {
"level": 3,
"link": "[2.1.4.1 Exercise 1](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.4.1-Exercise-1)",
"section": "2.1.4.1 Exercise 1"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.4.2 Exercise 2](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.4.2-Exercise-2)",
"section": "2.1.4.2 Exercise 2"
},
"slideshow": {
"slide_type": "-"
}
},
"source": [
"### 2.1.4.2 Exercise 2\n",
"\n",
"Consider a continous antibiotic injection at a constant rate designed to maintain the plasma concentration at minimum bactricidal level. Your solution should proceed in three steps:\n",
"\n",
"1. First, by hand, set up and solve the steady state equation to find the desired constant dosage rate. \n",
"2. Modify the Python function for $u(t)$ to simulate the desired flowrate.\n",
"3. Verify your result by repeating the above simulation using your function for $u(t)$. "
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {
"collapsed": true,
"jupyter": {
"outputs_hidden": true
},
"nbpages": {
"level": 3,
"link": "[2.1.4.2 Exercise 2](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.4.2-Exercise-2)",
"section": "2.1.4.2 Exercise 2"
}
},
"outputs": [],
"source": []
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.1.4.2 Exercise 2](https://jckantor.github.io/cbe30338-2021/02.01-One-Compartment-Pharmacokinetics.html#2.1.4.2-Exercise-2)",
"section": "2.1.4.2 Exercise 2"
}
},
"source": [
"\n",
"< [2.0 Linear Process Models](https://jckantor.github.io/cbe30338-2021/02.00-Process-Modeling.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [2.2 Properties of Scalar First Order Linear Systems](https://jckantor.github.io/cbe30338-2021/02.02-Properties-of-Scalar-First-Order-Linear-Systems.html) >