![\"Open](\"https://colab.research.google.com/assets/colab-badge.svg\" "\\"Open"){kind=icon}
![\"Download\"](\"https://img.shields.io/badge/Github-Download-blue.svg\" "\\"Download"){kind=icon}
"
]
},
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"# IMPORT DATA FILES USED BY THIS NOTEBOOK\n",
"import os, requests\n",
"\n",
"file_links = [(\"data/Model_Data.csv\", \"https://jckantor.github.io/cbe30338-2021/data/Model_Data.csv\")]\n",
"\n",
"# This cell has been added by nbpages. Run this cell to download data files required for this notebook.\n",
"\n",
"for filepath, fileurl in file_links:\n",
" stem, filename = os.path.split(filepath)\n",
" if stem:\n",
" if not os.path.exists(stem):\n",
" os.mkdir(stem)\n",
" if not os.path.isfile(filepath):\n",
" with open(filepath, 'wb') as f:\n",
" response = requests.get(fileurl)\n",
" f.write(response.content)\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.3 First Order Model for a Single Heater](https://jckantor.github.io/cbe30338-2021/02.03-First-Order-Model-for-a-Single-Heater.html#2.3-First-Order-Model-for-a-Single-Heater)",
"section": "2.3 First Order Model for a Single Heater"
}
},
"source": [
"# 2.3 First Order Model for a Single Heater"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 1,
"link": "[2.3 First Order Model for a Single Heater](https://jckantor.github.io/cbe30338-2021/02.03-First-Order-Model-for-a-Single-Heater.html#2.3-First-Order-Model-for-a-Single-Heater)",
"section": "2.3 First Order Model for a Single Heater"
}
},
"source": [
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.3.1 Learning Goals](https://jckantor.github.io/cbe30338-2021/02.03-First-Order-Model-for-a-Single-Heater.html#2.3.1-Learning-Goals)",
"section": "2.3.1 Learning Goals"
}
},
"source": [
"## 2.3.1 Learning Goals\n",
"\n",
"Mathematical modeling is an integral part of process control. Process models come in many forms for different purposes, ranging from the barest of information about a process to sophisticated simulation involving millions of computational nodes. \n",
"\n",
"Our purpose here is to demonstrate simple approaches that provide with insight about the qualitative nature of process dynamics. We show how to construct simple models from first-principles understanding of the processes, and how to fit those models to experimental data.\n",
"\n",
"In this notebook we will:\n",
"\n",
"* Construct a first-order lumped model for a single heater/sensor assembly on the Temperature Control Laboratory/\n",
"* Relate this model to the previously enountered first-order linear systems\n",
"* Demonstrate how to estimate parameters from step test experiments."
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 2,
"link": "[2.3.2 First-order model for one heater/sensor assembly](https://jckantor.github.io/cbe30338-2021/02.03-First-Order-Model-for-a-Single-Heater.html#2.3.2-First-order-model-for-one-heater/sensor-assembly)",
"section": "2.3.2 First-order model for one heater/sensor assembly"
}
},
"source": [
"## 2.3.2 First-order model for one heater/sensor assembly"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[2.3.2.1 Energy Balance](https://jckantor.github.io/cbe30338-2021/02.03-First-Order-Model-for-a-Single-Heater.html#2.3.2.1-Energy-Balance)",
"section": "2.3.2.1 Energy Balance"
}
},
"source": [
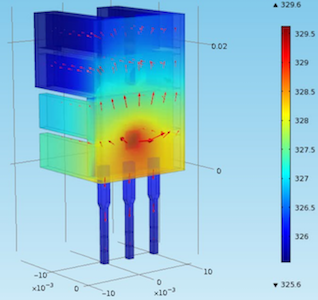
"### 2.3.2.1 Energy Balance\n",
"\n",
"We'll be begin by developing a model for one of the heater/sensor assemblies located on the Temperature Control Laboratory. The basic outline of an energy balaance is given by\n",
"\n",
"$$\\fbox{Rate of energy accumulation} = \\fbox{Rate of energy in flow} - \\fbox{Rate of energy outflow}$$\n",
"\n",
"In the absence of any material flows, changes in kinetic or potential energy, or any chemical changes, changes in sensible temperature is the only form of energy accumulation. If we assume the heater/sensor assembly is at single uniform temperature $T_1$, has mass $m$, and a constant and average specific heat capacity $\\hat{C}_p$,\n",
"\n",
"$$\\fbox{Rate of energy accumulation} = m \\hat{C}_p \\frac{dT_1}{dt}$$\n",
"\n",
"For the purposes of this model we will lump the mass and specific heat capacity into a single parameter representing the overall heat capacity of the assembly\n",
"\n",
"$$C_p = m \\hat{C}_p$$\n",
"\n",
"The final expression for the rate of energy accumulation becomes\n",
"\n",
"$$\\fbox{Rate of energy accumulation} = C_p \\frac{dT_1}{dt}$$\n",
"\n",
"
"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.8.5"
}
},
"nbformat": 4,
"nbformat_minor": 4
}