
\n",
"\n",
"**Study Question:** Carefully exammine the results of this experiment. The PI velocity algorithm is given by an equation\n",
"\n",
"\\begin{align}\n",
"MV_{k} & = MV_{k-1} - K_p(e_{k} - e_{k-1}) - h K_i e_{k}\n",
"\\end{align}\n",
"\n",
"Looking at the period from 0 to 100 seconds, is this equation being satisfied? Why or why not? \n",
"\n",
"**Study Question:** Carefully examine the code for the PI controller. How is it possible for $MV$ to be different from the actual input applied to the device?\n",
"\n",
"
\n",
"\n",
"**Integral (aka Reset) windup is a consequence the controller computing values for the manipulable input that are outside the range of feasible values. The difference is due to the presence of upper and lower bounds on the manipulated variable.**"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.1 Anti-reset windup - Version 1](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.1-Anti-reset-windup---Version-1)",
"section": "3.7.3.1 Anti-reset windup - Version 1"
}
},
"source": [
"### 3.7.3.1 Anti-reset windup - Version 1\n",
"\n",
"There several common strategies for avoiding integral (aka reset) windup. The first of these, which should be part of any practical implementation, is to limit computed values of manipulated variable to the range of values that can be implemented in the actual process. This will avoid $MV$ 'winding up' due to range limits.\n",
"\n",
"\\begin{align}\n",
"\\hat{MV}_{k} & = MV_{k-1} - K_p(e_{k} - e_{k-1}) - \\delta t K_i e_{k} \n",
"\\end{align}\n",
"\n",
"\\begin{align}\n",
"MV_k & = \\begin{cases}\n",
"MV^{min} & \\text{if } \\hat{MV}_k \\leq MV^{min}\\\\\n",
"\\hat{MV}_k & \\text{if } MV^{min} \\leq \\hat{MV}_k \\leq MV^{max}\\\\\n",
"MV^{max} & \\text{if} \\hat{MV_k} \\geq MV^{max}\n",
"\\end{cases}\n",
"\\end{align}"
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.1 Anti-reset windup - Version 1](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.1-Anti-reset-windup---Version-1)",
"section": "3.7.3.1 Anti-reset windup - Version 1"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmsAAAHYCAYAAAAS+q+iAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAxOAAAMTgF/d4wjAAA8ZUlEQVR4nO3de5Tdd13v/+d70txDSE47bTWhFwoo114kCtqfENEmKoqKvyBghS4Ru4iw/OUgcJC1QJd6enQRz6KWpVUsBAvYlpzjQZA5P/ylatEegi2tLR4olBAaoaSYNidpM0ln3r8/Zu92z86+zuy9v9/vnudjrazM/u7b5/v97Mx+5XONzESSJEnlNFF0ASRJktSeYU2SJKnEDGuSJEklZliTJEkqMcOaJElSiRnWJEmSSsywJkmSVGJnFF2AQVu+fHmec845RRdDfZienmblypVFF0N9sM6qxzqrHuuseg4dOnQyMwdeaWMX1jZs2MADDzxQdDHUh6mpKbZt21Z0MdQH66x6rLPqsc6qJyIOD+N17QaVJEkqsbFrWVtKZmaTI4+e7Pt5G9esYNlEDKFEkiRp0AxrFTUzm+y88Q4OPfxY389dvXwZ177mUpZNhMFNkqSSM6xV1JFHTy4oqAE8dmqGN3zo8wBs2rCa6157mYFNkqSSMqxVTL3r88jxJ7s/d++4mI1rV/T03Dd/5E4eOzXzxLFDDz/GkUdPctY6ZxxJklRGhrUKadf1uXHtip7D1kff+KInwt6um+4CeCL4jVOXaD/j+cbpvNW/Xj4rfkYkFcmwViGtuj43bVjNxjXdW9Xqlk3EacGuHtrGpUu03/F843Le6l+vnxU/I5KKZFirqHrX50L/x79xzQo2bVg970vq0MOPcf/hY/O6VKvYotDveL5W5w3VPHfN163V7Mjx3j4rjZ8RPxeSRs2wVlH9dH22smwiuO61l53WJVr/u66MLQq9fAHXdRrP1+m8YTxnzfa73EvZz7vT+bQao9lJq89Kq89I4+eiruzXSVK1lSKsRcS7gfcAz8/MeyLibGAPcBEwDVydmbcVWMSxVO8SbdXKVle2CQj9dnF2CrWdzhvGb9bsQpZ7KfN5L2b5mmabNqzm6ZPrTjvPVp+Rxs9F4/PLep0kVV/hYS0iLgNeBBxsOHwNcHtmbo+ILcAtEXFRZj5eSCHHXGMrW11ji0JZzMwm9x8+1tdYtE7j+Vqdd/19Ws2arUIXcaeWpl67/Bq16yI+ejJ56Nj0vGPDvh7N59br+bRqCWvWruyNn5FOLXVV+Xw0Wuii2u2U/Xy7ab4eVT+fUejnmjU+ttXj/Dx2VmhYi4iVwHXAa4B9DXftAC4EyMz9EfEgcDlw66jLWJRWH9zG7r1BazXxoAzq16HVF2W3JUt6+cfa7rxbzZptDq9FdJMOqtuv27Xr1kX8yNEZ9hzYP+9YL6Golfq1W8y5dTqfxdZN42ek/rmo6/XzMcjydNLpGjYG7H67iHux0Povg1bXY5Tn0+7fQKv/FJVFP9es+bHNjxuHz+OwvwOKbln7beAvMvNrEXMnGRFnAhOZ2bgZ6gHgvNEXrxiD7N4ZhKKW9uh0Hdp1Ww1KL13Ejd1hwxjH1PyLe1C/0Hq5dt26iFtp1T3Yi9XLl/Fff+ESfv1jX1jQuQ37s9CoOdz3+vloNKwvkW6fj1YBe5AWWv9lNcrzafdvYNh1Nmi9XrNRXNtRfx5vuGrLUBs8IjOH9uId3zjixcDvAi/LzIyIA8DLgW8CBzNzbcNjbwY+kZl7WrzOLmBX/faaNWs27d27d9jFH6qjJ5Nr727/pXXmquCNz51gIob35dSqDMN63xMnTrBq1aqeyrBiAn7luctYv4Khnn+j2UyOnWq8DX967wwnZzs/bzHXazaT6++d5Tsn+v/3Wb9G7bLAuuW9Xbvm8240PT3NypUra4/r7XoMQqtz6/V8hmWhn49Ry9kkmj4U3T4rvSjr+S7Eign45ecs4wNfLMf5tKqzsunnmi2vncqpNr/Wqvx5fPMLlrF+RbB9+/ZDmbl50K9fZFh7B/AWoN50sBl4EHgDcAtwQb11LSI+B7wtM2/t9rqTk5N5+PDhbg8rtYeOTXPVDXP/m2rVvTOKFq52rVqLXTKklampKbZt2zbvvZu7IIfxvovRqXu2Ua+7SzTrNGawW8vMKK5Ruzrrx0K6nspS/920uh7D6Opppd013LdvH1u3bp13bFDXc9DjjYrSS5f8IHX7N9Cqzsqmn2tWH0Pc7nFV/jzWyx4RQwlrhXWDZuY1zE0kAKDeslabDXozsBN4T22CwbnAkpwNutglOhaq29Iew5r9NohdGkZhoeOYFqI58JUxsCx0zGPztSvjuS1Et7GQw9TuGq5fMbxxqWUd87pQozyfTv8Ghllng9bPNRv2OY3b5xGKH7PWztuBD0fEfcy1vF3pTNDR6zRua1hLegxil4ZR62ccU79GOR6rCOP4S7WTpXa+6s7PhHpRmrCWmRc0/PwgcEVxpSnOzGwOddbnQrRrZWsuZ6+tIp1mPLVa0LZqrS3tlgRZiKqduyRp8EoT1lS+WaCNOu0pWtfLLLdWYzTazXgqW9dnP/zfsiRpUAxrJdLcBVjG7r+FLFWwEGU8d0mSimBYK6ndOy4u5VilVl18C5nldvqMpy3z7rf7T5KkOYa1EmhcqqJu49ryhpVWXXz9znKr6ownSZJGzbBWsDKPU+uHY7QkSRqOiaILsNRVcakKSZI0OraslUhVl6qQJEnDY1grkSovVSFJkobDblBJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRiLoo7YvVN2+saN2+XJElqZlgboXHZtF2SJI2O3aAj1GrT9jo3b5ckSa3YslaQ+qbtdW7eLkmSWjGsFcRN2yVJUi/sBpUkSSoxW9ZGoD4D1JmfkiSpX4a1IXMGqCRJWgy7QYes1QxQZ35KkqRe2bI2QvUZoM78lCRJvTKsjZAzQCVJUr/sBpUkSSqxoYS1iPjQMF5XkiRpqRlWy9rWIb2uJEnSkrLgMWsR8e12dwEbFvq6kiRJetJiJhgE8DLgkRbHP7uI1x0LLoQrSZIGYTFh7Z+BMzPz7uY7IuJbi3jdynMhXEmSNCiLCWuvBE61uiMzv28Rr1t5LoQrSZIGZTFh7c8y89UDK8mYciFcSZK0GIsJa987sFKMMRfClSRJi7GYpTtysW8eEf8zIu6OiC9ExD9ExCW142dHxKcj4r6IuCciLl/se0mSJFXRYlrWnt9m+Y4AMjPP7uE1dmTmwwAR8TPAnwOXAdcAt2fm9ojYAtwSERdl5uOLKK8kSVLlLCasfRn4icW8eT2o1TwVmK39vAO4sPaY/RHxIHA5cOti3k+SJKlqFhPWpjPz64stQETs4ckdD7ZHxJnARGYebnjYAeC8xb6XJElS1UTmwoaeRcSdmXnpwAoS8TrgVcCVwMHMXNtw383AJzJzT4vn7QJ21W+vWbNm0969ewdVrAU5ejK59u4ZAN78gmWsX+Es0E5OnDjBqlWrii6G+mCdVY91Vj3WWfVs3779UGZuHvTrLjisDUNEPAZsBg4CF9Rb1yLic8DbMvPWbq8xOTmZhw8f7vawoXro2DRX3bAfgBuu2uJs0C6mpqbYtm1b0cVQH6yz6rHOqsc6q56IGEpYG9ZG7l1FxPqI+O6G2z8LfAf4d+BmYGft+BbgXOC2IsopSZJUpMWMWVuspwIfj4jVzE0sOAy8PDMzIt4OfDgi7gNOAlc6E1SSJC1FhYW1zPwG8P1t7nsQuGK0JVq4+qbtdW7eLkmSBqXIlrWx4KbtkiRpmAobszYuWm3aXufm7ZIkabFsWRug+qbtdW7eLkmSFsuwNkBu2i5JkgbNblBJkqQSM6xJkiSVmN2gC1RfrsNlOiRJ0jAZ1hbA5TokSdKo2A26AK2W63CZDkmSNAy2rC1SfbkOl+mQJEnDYFhbJJfrkCRJw2Q3qCRJUokZ1iRJkkrMsCZJklRijlnrg2urSZKkUTOs9ci11SRJUhHsBu2Ra6tJkqQi2LK2AK6tJkmSRsWwtgCurSZJkkbFblBJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUom5dEcb9a2l6txiSpIkFcGw1oJbS0mSpLKwG7SFVltL1bnFlCRJGiVb1rqoby1V5xZTkiRplAxrXbi1lCRJKpLdoJIkSSVmWJMkSSoxw5okSVKJLfkxa83rqYFrqkmSpPIYu7A2m8lDx6Z7euzMbPLmj9zJY6dmhlwqSZKkhRm7sHbsFFx1w/6BvJZrqkmSpKIVFtYiYhXwMeA5wKPAt4CrM/NARJwN7AEuAqZrx28bVllWL1/Gta+59LT101xTTZIkFa3olrXrgb/JzIyIX6vdvgK4Brg9M7dHxBbgloi4KDMf7/aC65bDDVdt6asQhjJJklRWhYW1zDwBfKrh0O3Ar9d+3gFcWHvc/oh4ELgcuLXb605EuIitJEkaG2VauuMtwCci4kxgIjMPN9x3ADivkFJJkiQVKDKz6DIQEe8Efgp4GbAaOJiZaxvuvxn4RGbuafHcXcCu+u01a9Zs2rt37/ALrYE5ceIEq1atKroY6oN1Vj3WWfVYZ9Wzffv2Q5m5edCvW3hYi4i3Ar8A/GhmPlw7dhy4oN66FhGfA96Wmbd2e73ly5fnOeecM7wCa+Cmp6dZudKu6yqxzqrHOqse66x6Dh06RGYOfBB8oWGt1ir2WuaC2pGG4x8EDmTme2oTDD4OPL2XCQaTk5N5+PDhbg9TiUxNTbFt27aii6E+WGfVY51Vj3VWPRExk5kDnw9Q5NIdm4H3AvcD+yICYDozfwB4O/DhiLgPOAlc2UtQkyRJGjdFzgZ9ICK2A7/H3ESH5cAf1u8GZht+dosBSZLUl1ZbSg7DsJcAK7JlLYCPAFsz8+6IuAD43xGxl0WssyZJksppVOGp/l6j2lLyhqu21JcNOzaM1y96UVyADbW/1wPfYW7HggWvsyZJkgZnUAFriezHPV5hrbZrwQ5gb23250bg54Cn4DprkiQNxGLC1jgErHZbSg7SsPcRL2w2aEScAXwaeHdmfrbW3fnfgRfgOmtLimsJVY91Vj3WWfV0qrPZTI6d6v4aswl/eu8MJ2e7P3ZUVkzArzx3GaPa5XHd8rndjUZhWOusFdkNegnw3Zn5WXiiu/PfmAtrRMRkQ+va+cDBVi+SmbuB3fXbk5OT6VTnanF6evVYZ9VjnZVfcwvYvn37+KEfemnLx/XT2rV63dxq84sxyNYp9+PuX5Fh7RvA5oj4nsz8UkQ8A7gI+DJwM7ATqK+zdi5wW3FFlSRpcJqDWasA9sjRGfYc2D+Q91ts2DJgFavIMWsPRsSvMjfTcxYI4E2ZeSgiXGdNklR6CxkPNqhxYP0EMMNWtRU6GzQzPwp8tMXxB4ErRl8iSZJa66U1bLEaA9i+ffvYunVL28cawJaOMizdIUlSobq1kA07mNU1BrD1K6K+dpeWOMOaJGlJm5lNdt54B4cefmxBz1/oeDBbxtQrw5okaWz1MqbsyPGTPQe1bq1h0jAY1iRJY6Ue0BbSdbl7x8VsXNt+gVODmYpgWJMkVUqn1rLFjC3btGE1T59cZxhT6RjWJEml1CqULSSM9TqmzFYzlZVhTZJUOoMc9G8IU9UZ1iRJhejUndlt0H+31jIDmsaJYU2SNDILGfzfatC/YUxLiWFNkjQUg1jx30H/kmFNkjRA/bac2Z0pdWdYkyQtymICmmFM6s6wJklakJnZ5KFj0x0Dmiv+S4tnWJMk9ayXVjRbzqTBMqxJklrqZ4KAAU0aHsOaJOkJCx1/dta6lQY0aUgMa5K0xDlBQCo3w5okLUG9BjQnCEjFM6xJ0hLS7wxOg5lUPMOaJC0RnTZHN6BJ5WVYk6Qx1DyT8+jJ5P7Dx+YFNQOaVA2GNUkaE53GoT1ydIanHrjridu7d1zsnptSRRQa1iJiJfBeYBtwErgzM38xIs4G9gAXAdPA1Zl5W3EllaRy69TF2czN0aVqKbpl7RpgFnhWZmZEfFfD8dszc3tEbAFuiYiLMvPxwkoqSSU1M3t6FyfM7+bct28fW7duAZzNKVVNYWEtItYCVwGbMzMBMvObtbt3ABfWju2PiAeBy4FbCyiqJJVWqxa13TsuZuPaFfNC2foVwVnrVhZVTEmLUGTL2kXAd4B3RcSPAo8B7wG+AExk5uGGxx4Azhtx+SSpVJonDQAcOX5yXlCzi1MaP1Fr1Br9G0d8H/B54HWZuSciLgY+AzwPuD8z1zY89mbgE5m5p8Xr7AJ21W+vWbNm0969e4defg3OiRMnWLVqVdHFUB+ss9GbzeT6e2f5zon2v7OvevYyzl0DE3F6ULPOqsc6q57t27cfyszNg37dIlvWvs7ceLUbATLzroj4GvBsgIiYbGhdOx842OpFMnM3sLt+e3JyMrdt2zbMcmvApqamsM6qxTobnXpr2pHjJ3n8vrt46orWj9u0YTW/9DOXtW1Rs86qxzpTXWFhLTMfioi/ZW4m6Kci4nzmxql9CbgZ2Am8pzbB4FzA2aCSlpR2MzzrY9IaOWlAGl9Fzwa9GvjziPgvwAzwxsz8ZkS8HfhwRNzH3JIeVzoTVNK4ax6T1jweDRyTJi1FhYa1zLwfeGmL4w8CV4y8QJJUkG7rpLWa4SlpaSi6ZU2SlrTGMWntgpqtadLSZliTpALMzCYPHZs+bVsoOH1Mmq1p0tJmWJOkEevU5WkrmqRmhjVJGpF2XZ6N20LZiiapmWFNkoaoHtBmZrNtl6ctaZI6WXBYi4jlwH8Eng78j8z864b7rs3MNw+gfJJUWd1meNrlKakXi2lZuxbYAOwH/iAiXpaZ/0/tvh9abMEkqao6zfC0y1NSvxYT1l4MXJKZGRF/DHwsIv44M68G/O0jacnpZYanAU1SvxYT1pZnbRf4zDweET8L3BQRfzqYoklSdTjDU9KwLCasHY6I52XmPQCZ+XhE7AD+EnjBQEonSSXnDE9Jw7aYsLYTONF4oCGwvWpRpZKkCui00botaZIGZWIRz/3NzPxK88HMnMnMjyzidSWpEo486kbrkoZvMS1r3zOwUkhSxTmBQNKwuCiuJPWoPj6t7sjxJ3/euHYFZ61bWUSxJI25xYS150fEt1scDyAz8+xFvLYklUq3BW4laVgWE9a+DPzEoAoiSWXUaYHbuk0bVrNxzYoRl0zSUrGYsDadmV8fWEkkqWQ6zfbcuPbJcOY4NUnDtJiw5m8mSWPN2Z6SymDBYS0zLx1kQSSpzJztKakozgaVJE6f6QnO9pRUDoY1SUueMz0lldlidjCQpMqbmU3uP3ysY1BztqekItmyJmnJatWi1jzTE5ztKalYpWhZi4h3R0RGxPNqt8+OiE9HxH0RcU9EXF50GSWNn+bZnvWZnmetWznvj0FNUpEKb1mLiMuAFwEHGw5fA9yemdsjYgtwS0RclJmPF1JISWOlcaHbut07LnZJDkmlVGhYi4iVwHXAa4B9DXftAC4EyMz9EfEgcDlw66jLKGm8tJtMsHGtXZ2SyqnolrXfBv4iM78WMfdLMiLOBCYy83DD4w4A542+eJLGRadto5xAIKnMIjOLeeOIFwO/C7wsMzMiDgAvB74JHMzMtQ2PvRn4RGbuafE6u4Bd9dtr1qzZtHfv3mEXXwN04sQJVq1aVXQx1Ieq1dlsJtffO8t3Tsz/fXfVs5exbjmsWw4TMd6talWrM1lnVbR9+/ZDmbl50K9bZMvaS4DvBeqtapuBKeANABEx2dC6dj7zx7Q9ITN3A7vrtycnJ3Pbtm1DLLYGbWpqCuusWqpSZ42taY/fdxdPbWg827RhNb/0M5ctma7PqtSZnmSdqa6wsJaZ1zA3kQCAestaZt5Ta0nbCbynNsHgXOC2QgoqqZK6bcLuchySqqLoMWvtvB34cETcB5wErnQmqKR+uAm7pHFRmrCWmRc0/PwgcEVxpZE0TmxNk1RlpQlrkjQsbsIuqcpKsYOBJEmSWrNlTdJYqM/8rGvcnUCSqsywJqny2s38lKRxYFiTVFmddiWoc3cCSVVnWJNUSd3WUatzBqikqjOsSaqUbnt8uo6apHFjWJNUGe5KIGkpMqxJqgx3JZC0FBnWJFXCzGzOW47D1jRJS4VhTVLpter+dFcCSUuFYU1SabWbTOByHJKWEsOapFLqNJnAMWqSlhL3BpVUSk4mkKQ5tqxJKj0nE0haygxrkkqh00bsTiaQtJQZ1iQVzo3YJak9w5qkwrgRuyR1Z1gbA83dR0UpYjxRWc69UT1YtCvXMK/TqK7H0ZPJQ8emge7n287MbPLmj9zJY6dm5h13I3ZJms+wVjHNX8btvvCKsHr5Mq59zaV9f7E2fvH3o0zn3mjFGXOTrE8+Ptvy/oVep25GeT0eOTrDngP7ge7n2w9ne0rS6QxrJdBra0hZw0ndY6dmeMOHPt/38xq/+MdBt9Cy0OtUVosNaY3h1VY0STqdYa1ggxpYPazWml4UHSKLPPdGzdehuVyjuk6juB779u3jh1/ywo7n2ysDmiR1Zlgbkl5byzoNrG6n1Zdi0V94H33jixY8Vmrfvn1s3bplwe9d9Lk3arwOrcq1mOvUq1Fcj/UrgnPWr+p6vpKkxSssrEXEKuBjwHOAR4FvAVdn5oGIOBvYA1wETNeO31ZUWeuG3V3ZPLC6nTJ+KS6biAWvg7V+xcKfWzbdrsNirlMZjdv5SFIZFd2ydj3wN5mZEfFrtdtXANcAt2fm9ojYAtwSERdl5uPdXnA2FzZYvZthd2E5sFqSJLVSWFjLzBPApxoO3Q78eu3nHcCFtcftj4gHgcuBW7u97rFTcNUN5Ris3s8YnjK2lkmSpOIV3bLW6C3AJyLiTGAiMw833HcAOK+QUjUxgEmSpFGKzCy6DETEO4GfAl4GrAYOZubahvtvBj6RmXtaPHcXsKt+e82atZs++LFbhlbWdcthIgxgg3TixAlWrVpVdDHUB+useqyz6rHOqmf79u2HMnPzoF+38LAWEW8FfgH40cx8uHbsOHBBvXUtIj4HvC0zb+32epOTk3n48OFuD1OJTE1NsW3btqKLoT5YZ9VjnVWPdVY9ETGUsDYx6BfsR61V7NXAj9WDWs3NwM7aY7YA5wKFzwaVJEkatSKX7tgMvBe4H9gXc12L05n5A8DbgQ9HxH3ASeDKXmaCSpIkjZvCu0EHbfny5XnOOecUXQz1YXp6mpUrXaurSqyz6rHOqsc6q55Dhw6RmQMf2D70lrWIeB/w08D5wPMz857a8bYL30bEGuADwBZgFnhHZu7t5f02bNjAAw88MPDz0PA4LqN6rLPqsc6qxzqrnogYymKsoxizdgtza6R9vel4feHbZwJXATdGRD08vpW5LtFnANuA90fExhGUVZIkqVSG3rKWmX8PEKcvd9Fp4dtXAa+v3fe1iPh74BXABwdVrl63jloM11mTJEmLVcgEgx4Wvj2P+S1xjfct2sxssvPGO/reQL1fmzas5rrXXmZgkyRpaTg2jBctcgeD5pkNzYkmO9z35B2nLYq7hqmpqY5vfPRk8sWDw9njs9EjRx9h7yenWL/CsNbJiRMnutaZysU6qx7rrHqss0oan7CWmd+JCCJisqF17XzgYO3ng8AFQON9n6KFzNwN7K7fnpyczG4DMh86Ns2eA3P7h+7ecTEb165Y4Jm0duT4SXbddBcAW7du4ax1zubpxEG01WOdVY91Vj3WmeqKbFmrL3z7nhYL39bve31EXAi8BLh6GIXYuHaFYUqSJJXW0GeDRsR1EfEAsBn4TER8pXbX24EfrC18+0HmL3z7B8Dq2mOngJ2Z+e/DLqskSVLZjGI26E5qW0c1HX8QuKLNc44zNyNUkiRpSSuyG3TJaF4mxCU9JElSrwxrQ9ZqmRCX9JAkSb0axQ4GS9qRR0+etp7boYcfG/qCvJIkaTwY1kboXT/57Cd+PnL8JA8dm37iz8xs87JzkiRJdoMO3SOPnnri56euWf7Ez/V12OrsGpUkSa3YsjZkv/PJf33i541rVrBpw+qWj7NrVJIktWLL2hDUQ1nzpIKz1q3kutdeNi+UNe52IEmS1MywNgTLJuK0UNa4XIc7JkiSpF4Z1oZk2UQYyiRJ0qI5Zk2SJKnEDGuSJEklZliTJEkqMcOaJElSiRnWJEmSSsywJkmSVGKGNUmSpBIzrEmSJJWYYU2SJKnEDGuSJEklZliTJEkqMcOaJElSiRnWJEmSSsywJkmSVGKGNUmSpBIzrEmSJJWYYU2SJKnEzii6AHrSkeMnAdi4ZgXLJqLg0kiSpDIwrJXIrpvuAmDThtVc99rLDGySJMlu0KJtXLOCTRtWzzt26OHHOPLoyYJKJEmSysSWtYItmwiue+1lHHn0JEeOn3yidU2SJAkMa6WwbCI4a93KooshSZJKyG5QSZKkEjOsldSR4yeZmc2iiyFJkgpmWCupXTfdxc4b7zCwSZK0xDlmrUTqM0MPPfwY8OSs0HEbzzYzm/Nmux49mTx0bHreY1xrTpKkOYa1EqnPDL3/8LGxnRU6M5vsvPGOJwIpwCNHZ9hzYP+8x7nWnCRJc+wGLZllE8HGtSuKLsbQHHn05Lyg1o5rzUmSNMeWNRVm946L2bh2Bfv27WPr1i0ArjUnSVKTRbWsRcSHBlUQjbeZ2blxafX9TwE2rl3BWetWsn7F3DpzZ61bOdatipIkLcRiW9a2LubJEXEAOFH7A/CfM/MvI+JsYA9wETANXJ2Zty3mvVSMekh780fu5LFTM0UXR5Kkyuka1iLi2+3uAjYMoAw/n5n3NB27Brg9M7dHxBbgloi4KDMfH8D7aURaTSao27RhNRvX2IomSVI3vbSsBfAy4JEWxz878BLN2QFcCJCZ+yPiQeBy4NYhvZ+GoHkywerly7j2NZfOTaJwaQ5JknrSS1j7Z+DMzLy7+Y6I+NYAynBjREwA/wv4T8AsMJGZhxsecwA4bwDvpYLs3nExT59c11dAq49vM9hJkpayyOy8Qn5ErAVOZuapiJgEHsvMYwN584jzMvNgRCwHfgd4PnAlcDAz1zY87mbgE5m5p8Vr7AJ21W+vWbNm0969ezu+79GTybV3z42fevMLlrF+RbmCQNnL181sJsdOwbFTcMO/dj+PEydOsGrVKmD+udeduSp443MnmIhqXYdx1lhnqgbrrHqss+rZvn37oczcPOjX7dqylpnHI+JNEfEu4FwgI+JeYFdmfiYiNmTmwwt588w8WPv7VET8V+DLmfmdiCAiJhta184HDrZ5jd3A7vrtycnJ3LZtW8f3fejY9BOLsG7duqV0OwQ0lu+S77/4tBmSZW5pah6n9tT1c8c7XeepqSnqdTYzm/ztw/PHuT0ObLm8fPW0lDXWmarBOqse60x1vUww+BXg14BfBv6pdvgHgfdGxG8A/xn4vn7fuNZit7wh6L0auLP2883ATuA9tQkG5wJLcjZoqzXHyry6f6tFb/uZTFDfxeHIoyfnrblml6gkaanqZczaW4Dt9Vawmk9FxBeBL9PQqtWnc4CPR8Qy5iYr3A/8Uu2+twMfjoj7gJPAlUtpJmjzHqHNqrJnaH3R234D1rKJOO3c6qGtzEFVkqRh6CWsTTQFNQAy80BEHMjMdyzkjTPzfuDSNvc9CFyxkNcdB42tS42qtrp/fdHbBT+/RWitSlCVJGlQeglrKyJiVWaeaDwYEatxb9GhadW6tNS06xIdZzOzOS+k2+0rSeolrO1lrkvyV+rjyyJiI3A98PEhlk1qGVqPHD85liGm1SLCdvtKknppGXsXcAp4ICLujIg7gG8wN0nvXcMsnNTKrpvuYueNdzAz23nZmaqob8l1/+Fjp41TPPTwYzx0bHren3E5b0lSb3pZuuMU8JqIuAi4rHb4zsz8ylBLpkqpd981btQ+SM3j18Zl7Fq7Lbne9ZPP5nc++a8AvOFDn593n61tkrS09LyRe2Z+FfjqEMuiiuq0B+ig1Mev3X/4WKXHrjWPSTtyvPVSJxectbb5qU8Yl6AqSepNz2FNamexa6v1atlEnLZAcBXUA9rMbPLmj9zJY6dmWj6ucakTYF5L4urly/itVzyXt90yt+tbpxbMcRzPJ0lLmWFNA7XQtdUWogoL5fba6rhpw+rT9k5tXL5l45oV81rkOrUu2k0qSePFsKaBWuzaav0o80K5jWP4moPa6uXLuPY1l84rb6vA2TwTtttiyXV2k0rSeDGsqVKqsFBuu9a0xbY6tlssua4qa9E1j9trVOZWUkkqimFNlVL2hXJnZrPlEhytujkXotfFkss6pq1bt3AZW0klqWiGNVVOWXd3aBVERjmGr1FZx7S1mozSqLmV1B0dJMmwpjHRqiVp1F/szUFkUK1pvaramLZ6kIX5Xbj1umw1e9aWN0lLkWFNY6FVS1KRX+y7d1w80qAGxY5p6zQOrbkMde0mo3QqY1mCpiSNkmFNfWu1sGsRurUkjeqLvdXuDRvXFtNdV0QX8SAWRe5Ul81rzEnSUmNYU19GsVtBr9q1JI1y4kGZrkc/elmjrtfxYt3GobXSvGhyp1bB5jXmjhw/6dg1SUuKYU196fTFPIxdC7operLBqHZvGLR6mG215hvA+lXLectH75x3bo2PPXpybvN5YN7G8o3j0DrpZV25TmVvLIvBTdK4M6xVVBlW72/+Yl7qX5pFzfzsVauuxsdOzZy2UTzAquUTnDg1O+9Y42MfOTrDngP7T3+PIS2K3Fz2xrI46UDSuDOsVVQZVu8f5W4FCzWsLrN249TKfD0auxq77VPaGNR+/+dfwLv/6t62jx2FetkfOjZ9WrmddCBp3BnWKqQKq/eXza6b7hp4oK3qODWY39X40Te+qKfxfpNPWXnaY/ft28cPv+SF84LTsLt/l00E56xf9URZyrgo8rC5+4O0NBnWKqTI1ftbtSSVVXOoHXSgreo4tWatxog1X7v6eTU/dv2K+cGp/txRhIWixykWxd0fpKXLsFYxVV2aYZTqofb+w8dOW2i110DRqQWjMbCWfZxav5pnZXY7r7IEpzKM4RyEdp+7+ozYbrs/3H/42MjX95M0fIY1dVXFlqRlEzFv8kM/Y/z6CadlH6e2EGUJYP3oNLu1KgGu0+du04bV/NYrnvvE7Xa7Pwyj219S8Qxr6kuVWpIWOsav13XDyh5Yx12vs1urEl46fe7qn9u6xv8kDLvbX1LxDGtjYJSLhFapJandGL9+usw6rRtWhcA6znqd3VrF8FL/3DV+bh959FTLx3bq9m/UuDaen93y6HXxaS1thrUxMKyujypNKminVZdeP12iVQqnS1Gn2a1Vni3a6nP3O5/817aPb9ft36hxbbyqtDaOu1Zd39aNWjGsVdSwuz6qNqmgm3Zdog8dmz7tl2KVw+lSVsWxdtD5P0WtPrftut+77ZXbqIqtjf3oNEGok1G3arXq+h5U3Sz0GrSzkGuzmDLYwjifYa2iWnV9DFIVJxV00q5LtNXq/Ro/ZZwtOjObLRf5bdRqz9R259Bpf1WYWxvvku+/eKC/LwYdCAah24LPnRTZqvWun3z2E62n9c9rY9d1PxZzDdppdW061f9iy7Bpw2re9+pLOXqidfd/oyL+XY+6+9qwVmHNXR/DUqVJBZ302/JS5XCq+cqw4wc8+Qu+0xdZq03ue/3cdnrs+hXzf18sdKxrL+dQVb22ag0qpDa2pj51zfInfn5inGKbbd2K0Hxtht37cujhx3jtn91+2rZ3rTT/ux72fyJaffZvuGrLUFuqDWvqatzGbTV3F7XbzLzq4XSpK9uOH52+3IrYmH7XTXf1/dmv0vCIdufWSj/jG4d1Dfrpxu5VP9egnXbXptdZ8/2WofH9eglqMP/fdZU+o/0wrGnJ6XfhV1XTIGYDD1KrL7f6F9lZ61aOZjZ3UyBotdRJY7maw2Oncyjbv6GF1m+3z0evIaUfmzas5qx1K0/rxt63bx9bt25Z8OsO+jPe2BLYanHwYZWh3eu3CpLDqJ92mv+dDJNhTUtSVQejqz+LnQ08LEUNLagH2G5j5RpDXOMX0jjv3lHXaYFl6D2k9KPxGjZv61am31PtWh+H3fvSy+vX62UY9dO2XCP87BvWJI29dl2i9x8+NpTA0WrMTOOXSJFDC5ZNnL6va12rsTjtWt/GaXhErwssn/a8MboG7XTrnh302N52+xN30ypIjlP9GNbGSBlnvEll0K5LdBitbFUZM9Oudbke4vqZBFF1vS6w3GjcrkE73WYZD/r7pp9hKp2C5LjVj2FtjJShe0cqq3o46dTKtpBN0Jtb0WZms2NQK/uXSKeFhuvG8T+EvZx3o3G8Bu2MethIr+/XKUiOW/0Y1iqubDPepLLr1MrW7390urWitRozU6UvkaU6tnOpnncVLZW6MqxVXLsvHknttWtlaxzH1mihMwPHacyMpOIY1sbAUvmfhTRorXYCafUfnnqLG3Da/qN1v//zL+Ddf3XvE2Odyt7dKak6DGsCTh934/6YWiqWTQRPn1zXccZbfR/Zd//VvW0fM/mUlfPGOlWpu1NSuRnWlrBx3jZG6ke7gcqNQwsOPHS86/IFtnJLGobShrWIeCbwIeAs4GHg9Zn5xUILNUZ6XV7ArhwtFd2CVn2TbTh94oCtaJKGqbRhDfgT4PrM/GBE/DzwAeDFBZdpbPS6bYxfQlrKWs223rRh9YKW+JCkhSplWIuIs4HLgCtqhz4O/FFEXJCZBzo9dzaTh45Nd3z9pTAeq9s5LoVtY6TFatU96r8TSaNWyrAGPA34t8x8HCAzMyIOAucBBzo98dgpuOqG/cMvYcn1s4SHywtI7TkOTVLRyhrWALLpdsv/ykbELmBX/fYZ6zbyyNFHenqDM1cF+2/bx0SMx/+SZzM54+Qs3znRfOnaK8M1OHHiBFNTU4W9v/pnnVWPdVY91pnqIrP3L/ZRqXWD3gecmZmPR0QA3wRe1K0b9MyzzsovHTjU0/uMY3dGqw2kOynDNZiammLbtm2FlkH9sc6qxzqrHuuseiLiUGZuHvTrlrJlLTO/HRF3Ar8IfBB4JXCgW1ADmIil3WVhl40kSeOllGGt5leBD0bEO4GjwOsKLo8kSdLIlTasZeaXcKkOSZK0xJU2rC3Uww8/zObNA+8u1hBNT0+zcqVdt1VinVWPdVY91lklbRrGiw49rEXE+4CfBs4Hnp+Z99SOnw3sAS4CpoGrM/O22n1rmFsEdwswC7wjM/f28n4bNmzggQceGPh5aHgcRFs91ln1WGfVY51VT0QMZd/GiWG8aJNbgMuBrzcdvwa4PTOfCVwF3BgR9fD4VmA6M58BbAPeHxEbR1BWSZKkUhl6y1pm/j1AnL6O1w7gwtpj9kfEg8yFuluBVwGvr933tYj4e+AVzM0MlVQx/S4po8E7erL77i4qF+usOoa9DFYhY9Yi4kxgIjMPNxw+wNwOBdT+/nqb+yRVyMxssvPGO07bi1aj9cjRGfYccHeXKrHOquOGq7bUl806NozXL3KCQbcdCrLDfU/e0bSDwZo1a1zxuWJcpbt6+qmzoyeTLx4cyjAO9SFns+fdXVQO1ll17Nu3j/UrAsYprGXmdyKCiJhsaF07HzhY+/kgcAHQeN+n2rzWbmB3/fbk5GQ6ILNaHERbPf3U2UPHpp9oHdi942I2rl0xzKKpjX379rF169aii6E+WGfVMZbdoDU3AzuB90TEFuBc4Lam+14fERcCLwGuLqSUkgZm49oV7rBRkPUr3N2kaqwz1Q19NmhEXBcRDwCbgc9ExFdqd70d+MGIuI+5iQNXZubjtfv+AFhde+wUsDMz/33YZZUkSSqbUcwG3clcK1nz8QeBK9o85zhzM0IlSZKWtFGssyZJkqQFMqxJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUol1DWsRsTwi3hER10fEy5vuu3Z4RZMkSVIvLWvXApcAXwL+ICL+sOG+H1rMm0fEgYj43xHxhdqfV9WOnx0Rn46I+yLinoi4fDHvI0mSVFVn9PCYFwOXZGZGxB8DH4uIP87Mq4EYQBl+PjPvaTp2DXB7Zm6PiC3ALRFxUWY+PoD3kyRJqoxeWtaWZ2YCZOZx4GeBsyPiT4dYrh3AdbX33A88CNi6JkmSlpxewtrhiHhe/UatdWsH8B+AFwygDDdGxL9ExJ9FxGREnAlMZObhhsccAM4bwHtJkiRVStQazdo/YC6oPZaZX42IydrPxyJiGfCqzPzIgt884rzMPBgRy4HfAZ4PXAkczMy1DY+7GfhEZu5p8Rq7gF3122vWrNm0d+/ehRZJBThx4gSrVq0quhjqQz91dvRkcu3dMwC8+QXLWL9iEKMn1C//nVWPdVY927dvP5SZmwf9ul3DGkBE7AR+EzgXSOBeYFdmfiYiNmTmw4suSMR3AV/OzKdExHHggnrrWkR8DnhbZt7a7XUmJyfz8OHD3R6mEpmammLbtm1FF0N96KfOHjo2zVU37Afghqu2cNa6lcMsmtrw31n1WGfVExFDCWu9LN3xK8BO4JeZ6/o8E3gH8N6IuAL424W8cUSsjYgNDYdeDdxZ+/nm2ntSm2BwLnDbQt5HkiSpynqZDfoWYHtmHmw49qmI+CJwH/DeBb73OcDHa92pAdwP/FLtvrcDH46I+4CTwJXOBJUkSUtRL2FtoimoAZCZByLia5n5joW8cWbeD1za5r4HgSsW8rqSJEnjpJfZoCsi4rQRjhGxusfnS5IkaYF6CVt7meuS3FA/EBEbgT3Ax4dULkmSJNFbWHsXcAp4ICLujIg7gG8Aj9fukyRJ0pB0HbOWmaeA10TERcBltcN3ZuZXhloySZIk9TTBAIDM/Crw1SGWRZIkSU2cICBJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSM6xJkiSVmGFNkiSpxAxrkiRJJWZYkyRJKjHDmiRJUokZ1iRJkkrMsCZJklRihjVJkqQSK21Yi4hnRsQ/RsSXI+JzEfGcosskSZI0aqUNa8CfANdn5rOA3wc+UHB5JEmSRu6MogvQSkScDVwGXFE79HHgjyLigsw80Om5s5k8dGx6yCXUIB09aZ1VTT91duT4ySGXRpLGWynDGvA04N8y83GAzMyIOAicBxzo9MRjp+CqG/YPv4QamEeOzrDngHVWJdaZJI1OWcMaQDbdjlYPiohdwK767TPWbeSRo48Ms1wasJxN66xiFlJnZ64K9t+2j4lo+U9ZQ3bixAmmpqaKLob6YJ2pLjKbM1Hxat2g9wFnZubjERHAN4EXdesGPfOss/JLBw6NoJQalH379rF169aii6E+LKTONq5ZwbIJg1pRpqam2LZtW9HFUB+ss+qJiEOZuXnQr1vKlrXM/HZE3An8IvBB4JXAgW5BDWAigrPWrRxuATVQ61dYZ1VjnUnS6JQyrNX8KvDBiHgncBR4XcHlkSRJGrnShrXM/BLw4qLLIUmSVKRSjllbjIh4HPhW0eVQX9YBx4ouhPpinVWPdVY91ln1nJuZA28IK23L2iJ8axiD+zQ8EfGAdVYt1ln1WGfVY51VT0Q8MIzXLfMOBpIkSUueYU2SJKnExjGs7S66AOqbdVY91ln1WGfVY51Vz1DqbOwmGEiSJI2TcWxZkyRJGhuGNUmSpBIbm7AWEc+MiH+MiC9HxOci4jlFl2mpi4hVEfHfa3XyhYj4dERcULvv7Nrt+yLinoi4vOF5ayLioxHxldpzf66wk1jCIuLdEZER8bzabeuspCJiZUT8Ua1u7o2Iv6gdt85KKiK2RcQ/R8Sdtbp5Xe24dVYSEfG+iDjQ+HuwdnxBdRQRExFxbUR8tXb/m3oty9iENeBPgOsz81nA7wMfKLg8mnM98D2ZeQnw17XbANcAt2fmM4GrgBsjor7u31uB6cx8BrANeH9EbBxtsZe2iLgMeBFwsOGwdVZe1wCzwLMy87nAbzQct85KJiIC+AhwVWZeCrwc+JOIeArWWZncAlwOfL3p+ELr6BeB5wDPAr4feFtEfG9PJcnMyv8BzgYeBs6o3Q7mdjG4oOiy+WdePb0Q+Ert52PAZMN9nwNeWvv5XmBLw303Aa8vuvxL5Q+wEvgn4ELgAPA866y8f4C1td9/61rcZ52V8E/tO+o7wA/Xbr8AOASssM7K96fx92Dt9oLqCPgk8H833Pf7wHt6KcO4tKw9Dfi3zHwcIOeuwkHgvEJLpWZvAT4REWcCE5l5uOG+AzxZX+cx/38yjfdp+H4b+IvM/Fr9gHVWahcx98X/roj4fET8Q0S8zDorr9p31A5gb0R8HbgNeB3wFKyzUlvkv6sF19+4hDWA5jVIopBSqKWIeCfwTOA3a4e61Vd2uE9DEhEvBrYA729xt3VWTsuBpwNfzMwXAr8GfIy57QStsxKqdZn9J+AVmXk+8DLgQ7W7rbPyW0wdLaj+xiWsfQPYXO8zro0HeBrzx9uoIBHxVuDngB/PzEcz8zu145MNDzufJ+vrIHBBm/s0XC8Bvhf4WkQcADYDU8yNr7DOyunrzI1XuxEgM+8CvgY8G6yzkroE+O7M/CxAZu4H/o257lDrrMQW+f214Pobi7CWmd8G7mRu8B7AK4EDmXmgsEIJgIjYBbwa+LHMfLjhrpuBnbXHbAHOZa4roPm+C5kLEP9jREVe0jLzmsz87sy8IDMvAB4AtmXm32CdlVJmPgT8LXODmYmI85kbb/glrLOyqjcwfA9ARDyDue7sL2OdVcFC6+hm4FcjYllE/AfgVcBf9vKGY7ODQe1D/0HgTOAo8LrMvLfQQi1xEbGZuV9K9wP/p3Z4OjN/ICLOAT7M3JfKSeBNmfl3teetBf4c+D7mWgzemZm3jLr8glrr2ssz8x7rrLwi4unMXf8zgRngtzLzv1ln5RURrwbeydy1D+D3MvNj1ll5RMR1wCuYC2MPAccy8xkLraOIWAa8D9hee4s/zMw/6qks4xLWJEmSxtFYdINKkiSNK8OaJElSiRnWJEmSSsywJkmSVGKGNUmSpBI7o/tDJGlxIuILtR9XMLeJ8T2121+q/bk3M3tab2gRZfgk8NuZ+b+ajl8NvIm5lcVXAv+cma8dZlm6iYgLgM9n5llFlkNSORjWJA1dZl4C80LIJaN8/4hYx9yK/p9rOv5C4K3A92fmv9d2P7l0lGWTpG7sBpVUqIj4YET8Wu3n90TERyPiryPiKxFxU0RcGhH/X0TcHxG7G553bu3+z0XE3RHx2x3e5seBT+fpC0s+DXiEuYW0yTl3NLzHltp7fz4i7oiIVzbc95MRsT8i7oqIL0TED9SOb6899u6I+LuIeE7t+Etrj3t/7Tn31sJi/fV21s75H4A3NByfjIj/GRH/UnvNG/q/ypKqzJY1SWXzwtqfY8AdwDXMha0zmNuz9I8z88vMbXz9u5n597V9gf86In42M/9bi9f8WeZ2OGk2BfxH4BsR8XfMbRlzY2YeiYgNwJ8AP5mZ34yIs4B/jojPAuuBDwA/nJlfjojlwJqIOBv4C2BrZv5LRLwWuAl4Xu39ngu8ITPfVOt+/V1gW0S8APhN4NLMfDAi3t9Qxl9kbvu8KwBq29RIWkJsWZNUNlOZ+UhmzgB3A/9vZk5n5nHmxrc9vbaly48A76uNh/s88AzmNqGfpxakfhDY13xfZj4K/F/ATwD/CPwccHctEP0g8HTgb2rv8RnmtgX6HuDHgE/VQiOZeSozHwF+APhCZv5L7fiNzO0B+V21t/xSZn6+9vM/MbcfJMBLgU9m5oO129c3FPN2YHtEvDcifho43sM1lDRGbFmTVDYnGn6eaXH7DOb+o5nAlsw81eX1fgT4bLvH1bpG7wTujIhrgS8yF56mgbsz84ebnxMRz2s+Vr+rVq7T3qb2d6tzqT+vpcz8p4i4BPhR4JXA70TEpbUwK2kJsGVNUuVk5v8B/gF4R/1YRHx3RGxu8fCfAVp1jRIR31vrgqx7GjAJ3M9cS9szI+JHGh5/SUSsYK779Mcj4lm148sj4qnMtZZdEhHPrh3/BeCBzPxWl1PaB/xErRsV4Jcb3vNC5jaQvgl4M3Ozadd1eT1JY8SWNUlV9Vpgd0T8S+32MeBq4IH6A2qzO7cBv9HmNdYAfxgR5wKPMdfC9Y7M/ELt+T8F/EFE/CGwHDgI/ExmfiUifhn4aK2bdQb41cz8XERcCdwYEcuAh4Ed3U4kM++OiN8D/jEivgV8suHulwK7ImIGWAb8Rq3LVdISEadPjpKk8RARLwLelZkvL7oskrRQhjVJkqQSc8yaJElSiRnWJEmSSsywJkmSVGKGNUmSpBIzrEmSJJWYYU2SJKnEDGuSJEklZliTJEkqsf8fYR9ujc7imqgAAAAASUVORK5CYII=\n",
"text/plain": [
" \n",
" \n",
" CC BY-SA 3.0\n",
" \n",
"Stepper motors are commonly used actuators in lab equipment and robotics. The position of the stepper motor would be manipulated variable. This is an example of a stepper motor with an integrated encoder that can be used to verify the motor's position.\n",
" \n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
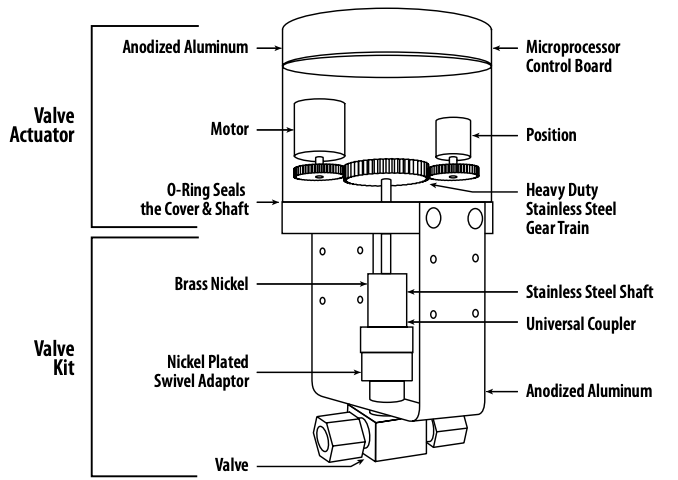
"Valve position feedback is a feature of control valves used in process applications, and should be regarded as a 'best practice' for industrial automation.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"This behavior also occurs in the Temperature Control Laboratory in which the manipulated power levels are constrained to the range 0% to 100%. This is demonstated in the following cell."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"TCLab version 0.4.9\n",
"Simulated TCLab\n",
"Q1 = 0\n",
"Q1 = 100\n",
"TCLab Model disconnected successfully.\n"
]
}
],
"source": [
"# show that inputs to the TCLab are constrained to the range 0 to 100%\n",
"\n",
"TCLab = setup(connected=False, speedup=20)\n",
"with TCLab() as lab:\n",
" print(f\"Q1 = {lab.Q1()}\")\n",
" lab.Q1(150)\n",
" print(f\"Q1 = {lab.Q1()}\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"To accomodate feedback of the manipulated variable, we first need to modify the event loop to incorporate the measurement of the manipulated variable, then send that value to the controller."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from tclab import TCLab, clock, Historian, Plotter, setup\n",
"\n",
"def experiment_2(controller, t_final=1000, t_step=5,\n",
" SP=lambda t: 40 if t >= 20 else 0, \n",
" DV=lambda t: 100 if t >= 420 else 0):\n",
" TCLab = setup(connected=False, speedup=60)\n",
" with TCLab() as lab:\n",
"\n",
" # set up historian and plotter\n",
" h = Historian(lab.sources)\n",
" p = Plotter(h, t_final)\n",
"\n",
" # initialize manipulated variable\n",
" lab.P1 = 200\n",
" next(controller)\n",
"\n",
" # event loop\n",
" for t in clock(t_final, t_step):\n",
" T1 = lab.T1\n",
" U1 = lab.Q1() # <==== new line\n",
" U1 = controller.send((t_step, SP(t), T1, U1)) # <==== send U1 to controller \n",
" lab.Q1(U1)\n",
" lab.Q2(DV(t))\n",
" p.update(t) "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"The next change is to the controller. The controller now accepts values for PV, SP, and, additionally, MV. To demonstrate the impact of these changes, this example will comment out the software limits placed on MV to show that feedback of manipulated variable is also an anti-reset windwup strategy."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmsAAAHYCAYAAAAS+q+iAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAxOAAAMTgF/d4wjAAA6VElEQVR4nO3df5TcZ133/+d7t9kk3ViSu02pZC39gb/41R8SBeV7a8W7iYoiyjf8qBV7ROyhlK/fiIDIOaBfvO3RQ/RQ61FQC8ECtg331xtB16/eqVi0NkBLbbmlhRJiosQW0sakyW66+/7+sTPpZDK7M7szs3N9Zp+Pc3Ky8/nMfOaaz/XZ3dde1+e6rshMJEmSVKaRQRdAkiRJ8zOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklSwMwZdgF5bvXp1bty4cdDF0CJMTU2xevXqQRdDi2CdVY91Vj3WWfUcOHBgOjN7XmlDF9Y2btzI/v37B10MLcLk5CRbtmwZdDG0CNZZ9Vhn1WOdVU9EPNKP49oNKkmSVLCha1lb6WZmk0NPTC/4nA1njjE6EstUIkmS1A3D2hCoB7SZ2eT6D9/DsRMzCz5/7apRbnzNZYyOhMFNkqTCGdYqbmY2ue6Wz3HgsWMdv+bYiRle98HPALBp/VpuuupyA5skSYUyrFXYzGzy8CNHTgtqjS1nzc9vbnk78NgxDj0xzTnrHHEkSVKJDGsV1apFbce2S9gwPrZg1+ZHXv9CDj0xzaGj02y/9fMAHDp66j1udo1KklQOw1pFHXpi+pSgtmn9Wi7auK5tyBodidNa0eqhrfFYdo1KklQGw1rF1AcTNLaG7dh2SUdBrdGGM8fYtH5ty3vd7BqVJKkchrUKmW8wwYbxxXdbjo4EN111+SnTfDR2jQ6jTqY1accuYknScjOsVUhz1yfMdVluOHNsScdr1SV68r1qLXdVDyeLndaknfkGb1T9PK0EzkEoqaqKCGsR8U7gXcDzMvP+iDgX2AlcDEwB12bmnQMsYnE6GUzQjXoLW5XvX1vKtCbtNE570qjK52kl6PRasB4llWjgYS0iLgdeCOxr2HwDcFdmbo2IzcDtEXFxZj45kEIWaMP4WM/vKWt1H9uBx47x8CNH2DA+dtpzS/uF1txycujo6S2R87WMdXLshVrmGs9TieemlW66hQ9PJ48emVrUa3p1XpZS7lbXQivzXe9LUZXrYLGaz/+wfs5uLfX7q34+Z2bzlO8zz3N3lnrdLlSPy1knAw1rEbEauAl4DbC7Ydc24EKAzNwTEQeBFwN3LHcZS9BqUEE/NN7H1nj/Wqv72Eppgei0m7MXLZH1aU8atTpP7QJhP7/BO/0F0W238OOHZ9i5d8+iXrPUoNyoF93Z9WuhUbvrfSk6+bzLGWCXErBbvU/z+e9FvQ6bbq7TtatG+d1XXcovfvRevvb1p77P+n2eG0Nit/f2lmap1227elzOa3/QLWu/DvxpZn4lYu7DRsTZwEhmNq5cvxc4f/mLN3j96MpbSP0+toVGi0IZI0YX07W12NGyrbS6x6/VeZqvq7SxPP0Iust9rSxWu/OyHOa7Ftpd70vRyeftxbXQab0vJWB3ooR6HSbHTszwCx/6bMvt/TzPm9av5b2vvow3feSeYn+G9FIvzudyXvuRmcvyRqe9ccSLgN8AXpKZGRF7gZcC/w7sy8zxhufeBnw8M3e2OM52YHv98fj4+KZdu3b1u/jL5vB0cuN9p6b6s9cEr3/OCCPR3zQ/m8mRE6duO3ICbv7fc+W5/vmjnDXWfRmOHz/OmjVrFl2exrLUjY3Azz9nlMbffetW0ddzVS/XbML7H5hherb9a675zlHWrequjJ2cj3Zana9OTE1NsXp1Z0F9MeelU0st90LnudX1vhSL/bzN18JidVrvOZtEj/5AGBuBn3v2KH/8hd7W67BZzHXa6rpZRfK6556xbOf5/3zWKLd9qbtBWCVb6nXbXI8LfY///TteeiAzJ3pT4qcMMqy9DXgTUG9vnQAOAq8DbgcuqLeuRcTdwFsy8452x52YmMj9+/f3pcyD8OiRKa65ee6v4X4PKlhKeXrRYjU5OcmWLVta7lvObs5eWKgLYaGpURbbnN7p+WhnqedroTprpdddK4Ou53bafd5+TZOzUL3v3r2bK664oifvM8xdZr202Ou0+XzuuXM3P7x1a1/P83zXYqc/Q6pkqddtq3qc7xgbv2lNX8LawLpBM/MG5gYSAFBvWauNBr0NuA54V22AwXnAih8N2o9BBd3Yfuvn+3rv2nJ3c/bCQtOhLNTV1svm9JLOR91C52UYtfu8/eh2bVfvZ431vg5WWr32W/P5rLcC9/M8t7oWS/wZ0ku9OJ/Lfe0P+p61+bwV+FBEPMRcy9vVjgQtQ/M3dj9GizYOqOhkNGfprSx1rSYi7vaG+Sqfj5Ws1bXQLetdS9HqWvRaKk8xYS0zL2j4+iBw5eBKo/nUv7EffuRIX0aLzteaVko3Z7da/TXWapRpp6p+PlYyW6VUCq/F8hUT1lQdoyPBRRvX9WW06HyrNNgkL0laqQxrWpL5unEab1ZdaF64+SZ+bF6gfhha0yRJ6oZhTUvWrkVoodFu80382Ki0ARWSJA2CYa0wrZZMqpJOR7nNN/FjXTcL1EuSNEwMawUpfQb6TrQb5dZq9OPYCPzRa1/giEZJklowrBWk1c31dVVqaWrXPdo8+nHPnbt5+lntVzCQJGklMqwVqnn26GFqaZpv4kdJknQ6w1qhvLlekiQBjAy6AJIkSZqfLWsFaFxeSZIkqZFhbcCGYQSoJEnqH7tBB2y+5ZWqMvJTkiT1ly1rBXF5JUmS1MywVhBHgEqSpGZ2g0qSJBXMsCZJklQww5okSVLBDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDCXm1pmM7PJoSemTz4+dHR6gWdLkqSVzrC2jGZmk+tu+RwHHjs26KJIkqSKsBt0GR16YnreoLZp/Vo2nDm2zCWSJEml60vLWkR8MDNf249jD4sd2y5hw/hT4WzDmWOMjsQASyRJkkrUr27QK/p03KGxYXyMc9atHnQxJElS4ZYc1iLiP+bbBaxf6nGHUX1QgYMJJEnSYnXTshbAS4DHW2z/dBfHHSoOKpAkSd3oJqx9Fjg7M+9r3hERX+viuEOl1aACBxNIkqROdRPWfgo40WpHZn5XF8cdWvVBBQ4mkCRJnepm6o4/ykxvwlqE+qACg5okSepUN2HtO3pWCkmSJLXUTVjLnpVCkiRJLXVzz9rz5pm+I4DMzHPbHSAi/ho4D5gF/hO4PjPvjYhzgZ3AxcAUcG1m3tlFWZed03VIkqRe6CasPQj8SJfvvy0zHwOIiJ8A/gS4HLgBuCszt0bEZuD2iLg4M5/s8v2WhdN1SJKkXukmrE1l5le7efN6UKt5GnMtbADbgAtrz9kTEQeBFwN3dPN+y8XpOiRJUq90Oylu1yJiJ08tT7U1Is4GRjLzkYan7QXO78X7LTen65AkSd2IzDLGCUTEa4FXAlcD+zJzvGHfbcDHM3Nni9dtB7bXH4+Pj2/atWvXMpR4foenkxvvmwHg+uePctaYIW0hx48fZ82aNYMuhhbBOqse66x6rLPq2bp164HMnOj1cYsJawARcQyYAPYBF9Rb1yLibuAtmXlHu2NMTEzk/v37+1rOdh49MsU1N+8B4OZrNrtgexuTk5Ns2bJl0MXQIlhn1WOdVY91Vj0R0Zew1s3UHV2JiLMi4hkNj18OfB34BnAbcF1t+2bmRoxWajSoJElSL3Rzz1q3ngbsioi1zA0seAR4aWZmRLwV+FBEPARMA1dXZSSoJElSLw0srGXmvwLfPc++g8CVy1ui7jm3miRJ6rVBtqwNFedWkyRJ/TCwe9aGjXOrSZKkfrBlrQ+cW02SJPWKYa0PNoyPOV2HJEnqCbtBJUmSCmZYkyRJKphhrQdmZtPpOiRJUl94z1qXnLJDkiT1ky1rXWqessPpOiRJUi/ZstZDO7ZdwkUb1zldhyRJ6hlb1npow7jzqkmSpN4yrEmSJBXMsCZJklQw71lbopnZ5NAT007ZIUmS+sqwtgRO1yFJkpaL3aBL0DxdBzhlhyRJ6g9b1rq0Y9slbBgfY8OZjgSVJEm9Z1jr0obxMc5Zt3rQxZAkSUPKblBJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKpjzrLVRXwO0keuBSpKk5WJYW4BrgEqSpEGzG3QBrdYAbeR6oJIkqd9sWetQfQ3QRq4HKkmS+s2wNo+Z2Tzl3jTXAJUkSYNgWGvBe9UkSVIpvGetheZ71bw3TZIkDYotaw3q03Q0dn/u2HYJF21c571pkiRpIIYurM0mPHpkatGvm5lNrv/wPRw7MXPK9g3jDiKQJEmDM3Rh7dDRaa65eU9PjmX3pyRJGrSBhbWIWAN8FHg28ATwNeDazNwbEecCO4GLgana9juXo1xrV41y42suY3QknJpDkiQN3KBb1t4H/GVmZkS8sfb4SuAG4K7M3BoRm4HbI+LizHyy3QE3jI9x8zWbl1wgA5okSSrJwMJaZh4HPtmw6S7gF2tfbwMurD1vT0QcBF4M3NHuuCOB86FJkqShUdLUHW8CPh4RZwMjmflIw769wPkDKZUkSdIARWYOugxExNuBHwNeAqwF9mXmeMP+24CPZ+bOFq/dDmyvPx4fH9+0a9eu/hdaPXP8+HHWrFkz6GJoEayz6rHOqsc6q56tW7ceyMyJXh934GEtIt4MvAr4ocx8rLbtKHBBvXUtIu4G3pKZd7Q73urVq3Pjxo39K7B6bmpqitWr7bquEuuseqyz6rHOqufAgQNkZs9vfB/oAINaq9iraQhqNbcB1wHvqg0wOA/oaDToxo0b2b9/f6+Lqj6anJxky5Ytgy6GFsE6qx7rrHqss+qJiJn2z1q8QU7dMQG8B3gY2B0RAFOZ+T3AW4EPRcRDwDRwdScjQSVJkobNIEeD7gdaNhVm5kHmpvCQJElaUH25yGE16HnWJEnSCtGPUDXfcpEDcqQfBzWsSZKkefUqYBUWqvrFsCZJktpbiQGrcbnIQdn4pv4c17AmSVLBFhu8Sg9Y/QpVw7xc5KCn7tgLHK/9A/jNzPyzQS7kLknSclkoiB2eTg4ePl5E8OplwBrmUNUvJbSsvSIz72/atuSF3CVJGrROWsPatYA9fniGnXs/s+QyGLCGRwlhrZUlL+QuSdJyaRXK+tENuZTgZcAaHiWEtVsiYgT4J+BXgFlcyF2SNCCd3iPWq1A2XxDbvXs3V1yxGTB4rXQDXRs0Is7PzH0RsQp4N/A84GpcyH1FcbHi6rHOqsc6a202kyMnGh/D+x+YYXq2+2OPjcDPP2eUdhlr3SoYidOfZJ1Vz9Au5F4XEd8MPJiZ39TNQu4TExPp2qDV4vp31WOdVc9KrbOFWsn63TLWbWvYSq2zKouIvoS1Qa4NOg6saljA/dXAPbWvl7yQuyRp5en1vWOLuUfMLkr12yDvWXs6sCsiRplbI/Rh4Gdq+1zIXZLUUnMw67aFrFUwM4CpJINcyP1h4LJ59rmQuyTppHpAW0owa9dKZjBT6UoYDSpJEtBdd2a/7h2TBs2wJkkaiG66M+261EpiWJMk9UWvR2I2BjSDmVYSw5okqWe6ubeszu5M6VSGNUnSkvRiVKbdmVJ7hjVJUscW23LmSEype4Y1SdKCuglohjGpe4Y1SdJJi+3atBtT6j/DmiStcLacSWUzrEnSCmRAk6rDsCZJK8zMbHLdLZ/jwGPHWu63a1Mqi2FNkobczGxyeDp59MgUAIeOTp8W1Gw5k8plWJOkIVZvRfvCvhl27t1z2v4d2y5hw/iYAU0qmGFNkoZQ/Z60Vq1odZvWr+WijesMaVLhDGuSNCTaDRqot6LV2ZomVYNhTZIqbmZ27n60hUZ1nr0mbEWTKsqwJkkV1MnUG42DBvbcudugJlWUYU2SKmahqTfmG9U5EgY1qaoMa5JUsObln2DhqTfOWbfaFjRpyBjWJKlQ7SavBafekFYCw5okFWhmNnn4kSMLBjWn3pBWBsOaJBWmVYta87Qb4NQb0kpRRFiLiHcC7wKel5n3R8S5wE7gYmAKuDYz7xxgESWpLzq5J80WNGllG3hYi4jLgRcC+xo23wDclZlbI2IzcHtEXJyZTw6kkJLUB53ek2ZQk1a2kUG+eUSsBm4C3gBkw65tte1k5h7gIPDiZS+gJPWJ96RJ6tSgW9Z+HfjTzPxK1OYAioizgZHMfKTheXuB85e/eJLUOwtNZOs9aZLmM7CwFhEvAjYDb2uxO5ufvsBxtgPb64/Hx8eZnJzsSRm1PI4fP26dVYx11rnZTI6cgNmE9z8ww/Ts6c85e03wpXs+3deJa62z6rHOVBeZzblomd444m3Am4D6nbUTzHV3vg64Hbig3roWEXcDb8nMO9odd2JiIvfv39+XMqs/Jicn2bJly6CLoUWwzjrT7p605ZzI1jqrHuuseiLiQGZO9Pq4A2tZy8wbmBtIAEBE7AVeWhsNehtwHfCu2gCD8wBHg0qqhHp350IrDTQvByVJ8xn0PWvzeSvwoYh4iLmWt6sdCSqpCuZrTXOlAUlLVUxYy8wLGr4+CFw5uNJI0tIceuL01jRHdUrqxpLDWkSsAn4JuAj4n5n5Fw37bszM63tQPkkqWvOktoeOPvW1rWmSeqGblrUbgfXAHuC3I+Ilmfl/1/Z9X7cFk6TStRtAsGF8jHPWrV7mUkkaNt1Mivsi4NWZ+R7gBcCzIuIPavv8E1LS0JqZTR49MrXgpLab1q9lw5ljLfdJ0mJ007K2KmvzfmTm0Yh4OXBrRLy/N0WTpPK0G0BQZ9enpF7pJqw9EhHPzcz7ATLzyYjYBvwZ8PyelE6SCrHQdBwOIJDUT92EteuA440bGgLbK7sqlSQVxOk4JA1SN/es/Wpmfql5Y2bOZOaHuziuJBVjvgXX661py7H6gKSVrZuWtW/vWSkkqUCtWtRsTZO03IqZFFeSSjHf/WnemyZpELoJa8+LiP9osT2AzMxzuzi2JA3EQvenGdQkDUI3Ye1B4Ed6VRBJGiRHe0oqVTdhbSozv9qzkkjSgDjaU1LJuglr/uSSNBRcfF1SyZYc1jLzsl4WRJJKYGuapNI4GlTSilO/P63u0NGnvnbxdUmlMaxJWlHmuz9NkkplWJO0Iiw02rNu0/q1bDhzrOU+SRoUw5qkoddutGed96lJKpFhTdLQc7SnpCozrElaURztKalqDGuSVhRHe0qqmoGGtYj4a+A8YBb4T+D6zLw3Is4FdgIXA1PAtZl55+BKKqlKFpqaQ5KqZtAta9sy8zGAiPgJ4E+Ay4EbgLsyc2tEbAZuj4iLM/PJgZVUUiU4NYekYTPQsFYPajVPY66FDWAbcGHtOXsi4iDwYuCO5SyfpOpwag5Jw2rQLWtExE7gitrDrRFxNjCSmY80PG0vcP5yl01SNTg1h6RhFpk56DIAEBGvBV4JXA3sy8zxhn23AR/PzJ0tXrcd2F5/PD4+vmnXrl3LUGL1yvHjx1mzZs2gi6FFKK3ODk8nN943c8q2s9cEr3/OCCNhOIPy6kztWWfVs3Xr1gOZOdHr4xYT1gAi4hgwAewDLqi3rkXE3cBbMvOOdseYmJjI/fv397Wc6q3JyUm2bNky6GJoEUqps8auz+23fh5wao75lFJn6px1Vj0R0ZewNrBu0Ig4C1iXmf9We/xy4OvAN4DbgOuAd9UGGJwHOBpU0smANjObXP/hezh24tQWNafmkDRsBnnP2tOAXRGxlrmBBY8AL83MjIi3Ah+KiIeAaeBqR4JKajfS0wEEkobRwMJaZv4r8N3z7DsIXLm8JZJUspnZ5OFHjpwW1NauGuXG11zG6EjY9SlpKA18NKgktdOqRc170yStFIY1ScVrXojdRdglrSSGNUmVsmPbJQY1SSvKyKALIEmLsWHcbk9JK4sta5KK0rwIO7gQu6SVzbAmqRguwi5Jp7MbVFIR5puao5HzqElaiWxZkzRwC03N0chpOiStRIY1SQPTuLanU3NIUmuGNUkDMd/9aU7NIUmnMqxJWlbztaaBLWqS1Iphbci0mvZgEEq5t6iU89FOq/M1X9k7Pbf9/OyHp5NHj0wt+nUzs8n1H76HYydmTtnu0lGSND/DWoU1/zKe7xfhIDQurt3OUn/xt1PS+Win+XwtVPZOzm2/P/vjh2fYuXdPT45la5okLcywVjH1gFZ6EDl2YobXffAzHT23l7/4q2ox52sxzy1VY+C0NU2SFmZYq4DFBrTFtGr1WokhcpDno51256ux7Es5t/367Lt37+aKKzYv+fUGNEnqnGGtMIvt2mz1y3jQvwg/8voXLupeqW5/8bcz6PPRzkLnq7nsiz23/frsZ40F56xb3fPjSpJOZ1grQDctZyUGkdGRxf0iX+m/+BdzvhZ7biVJ1WdYW2ZLHRRQekCTJEn9YVhbBr2458yAJknSymRY65Nh69qUJEmDYVhbooUmHK3ioABJklSmoQtrs0lfJlht1O0UCgYzSZLUqYGFtYhYA3wUeDbwBPA14NrM3BsR5wI7gYuBqdr2Ozs57qGj01xzcxkTrBrQJElStwbdsvY+4C8zMyPijbXHVwI3AHdl5taI2AzcHhEXZ+aTgyxss3YTjhrQJElStwYW1jLzOPDJhk13Ab9Y+3obcGHteXsi4iDwYuCOdsfdMD7Gzdf0b4LVU97LMCZJkvps0C1rjd4EfDwizgZGMvORhn17gfM7OchI4KShkiRpaERmDroMRMTbgR8DXgKsBfZl5njD/tuAj2fmzhav3Q5srz8eHx/ftGvXrv4XWj1z/Phx1qxZM+hiaBGss+qxzqrHOquerVu3HsjMiV4fd+BhLSLeDLwK+KHMfKy27ShwQb11LSLuBt6SmXe0O97ExETu37+/fwVWz01OTrJly5ZBF0OLYJ1Vj3VWPdZZ9UTE8IW1WqvYVcwFtUMN2z8A7M3Md9UGGOwCLupkgMHq1atz48aN/Sqy+mBqaorVq+26rhLrrHqss+qxzqrnwIEDZGbPb2bve1iLiPcCPw48E3heZt5f234JcC9wApgB9gPfyMzviYgLgH8EzgYS+H8y892dvJ8ta9XjX4/VY51Vj3VWPdZZ9UTETGb2fDzASK8P2MLtzI3k/GrT9v8L+LXMHAP+KzAGfF9t388Ak7V93wG8MSI2LENZJUmSitL30aCZ+SmAiNNaBReanuOVwM/W9n0lIj4FvAz4QK/Lt9CyUf3ilB+SJKlTA5m6o4PpOc7n1Ja4xn09MzObXHfL5zjw2LFeH3pBm9av5aarLjewSZI0XI7046CDnGet+Wa55uSSC+x7asfpU3cwOTnZUQEOTydf2Nf5+p698vjhx/nYJyY5a8ywBnPD0zutM5XBOqse66x6rLNKGp6wlplfjwgiYmND69ozgX21r/cBFwCN+z5JC5m5A9hRfzwxMZGd3pD56JEpdu6dW0d0x7ZL2DA+tshPsjiHjk6z/dbPA3Dpd5/6fiu5a9SbaKvHOqse66x6rDPVDbJl7TbgOqA+Pcd5wJ1N+342Ii4Evh+4tp+F2TA+tqwrH9RDW51do5IkqZW+jwaNiJsiYj8wAfxNRHyptuutwPdGxEPMDRy4umEetd8G1taeOwlcl5nf6HdZ+23DmWNsWr+25b4Djx1b9oEOkiSpfMsxGvQ65lrJmrcfBK6c5zVHmRsROlRGR4Kbrrr8lFDW2DUqSZLUrKSF3FeE0ZFwoXlJktSx5ZgUV5IkSUtkWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSrYGYMugJ5y6Og0ABvOHGN0JAZcGkmSVALDWkG23/p5ADatX8tNV11uYJMkSXaDDtqGM8fYtH7tKdsOPHaMQ09MD6hEkiSpJLasDdjoSHDTVZdz6IlpDh2dPtm6JkmSBIa1IoyOBOesWz3oYkiSpALZDSpJklQww5okSVLB7AYtVH0ajzqn85AkaWUyrBWqeaCB03lIkrQy2Q1akFbTeNQ5nYckSSuTLWsFaZzGo87pPCRJWtkMa4VxGg9JktTIblBJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSpYV2EtIj7Yq4JIkiTpdN0u5H5FNy+OiL3A8do/gN/MzD+LiHOBncDFwBRwbWbe2c17qUwzs8nh6eTRI1OnbN9w5hijIzGgUkmSVI62YS0i/mO+XcD6HpThFZl5f9O2G4C7MnNrRGwGbo+IizPzyR68nwoxM5tcd8vn+MK+GXbu3XPKvk3r13LTVZcb2CRJK14nLWsBvAR4vMX2T/e8RHO2ARcCZOaeiDgIvBi4o0/vpwE49MQ0Bx471nLfgceOceiJac5Zt3qZSyVJUlk6CWufBc7OzPuad0TE13pQhlsiYgT4J+BXgFlgJDMfaXjOXuD8HryXCjAzmxx6YppDR6dPbtux7RI2jI9x6Og022/9PMDJ/XaJSpJWssjMhZ8QMQ5MZ+aJiNgIHMvMIz1584jzM3NfRKwC3g08D7ga2JeZ4w3Puw34eGbubHGM7cD2+uPx8fFNu3bt6uj9D08nN943A8D1zx/lrLHyAkEVyjif2UyOnGjeBu9/YIbp2ae25WzypkvP4KyxOOXz1p29Jnj9c0YYiep89mF3/Phx1qxZM+hiaBGss+qxzqpn69atBzJzotfHbduylplHI+INEfEO4DwgI+IBYHtm/k1ErM/Mx5by5pm5r/b/iYj4XeDBzPx6RBARGxta154J7JvnGDuAHfXHExMTuWXLlo7e/9EjUyfvlbriis1FdrlVoYyt1O9Ha9XNuXYdrG14fMb0YX7yR7cwOhLMzCZ/+9ipr3sSeNZlcy1vtrKVYXJykk6/z1QG66x6rDPVdTLA4OeBNwI/B/xjbfP3Au+JiF8GfhP4rsW+ca3FblVD0Hs1cE/t69uA64B31QYYnAc4GrRCFrofDWDtqlFufM1ljI4Ee+7cfTKAjY4EN111+clu0nqXaP1/Bx5IklaaTu5ZexOwtd4KVvPJiPgC8CANrVqL9HRgV0SMMjdY4WHgZ2r73gp8KCIeAqaBqx0JWl31+9EaNbaQNXdvjo4E56xbzYYzx9i0fu0poe/AY8d4+JEjXLRxnYFNkrQidBLWRpqCGgCZuTci9mbm25byxpn5MHDZPPsOAlcu5bjDrKo33G8YH1tS9+1CrWy2sEmSVopOwtpYRKzJzOONGyNiLS5XtaxWYlfgfK1sTu0hSVopOglbH2OuS3J9fUNEbGBuhYHOhl1qyeohpVE9qKwk9Va2HdsuObnt0NFpHj0ydcq/mdmFRzdLklQ1nbSsvQP4ILC/dg9ZAt8GfLy2T300X1fgSjQ6Eqfc+9bqXKykVkdJ0srQydQdJ4DXRMTFwOW1zfdk5pf6WjKdVO8KrIqZ2TxlwtteajXooJHdo5KkYdPxQu6Z+WXgy30si4bAQvOr9UJjS2OjYWx1rK/00Kx5gEnz86o2AEWStLCOw5rUieb51TatX8uGM8cWeMXitWtpbG7Vq1J4qQevmdnk+g/fw7ETM6c9p97VC3OTJjc/z65gSRouhjX1zY5tlwxkPrTmFraqhJdOWyUPPHaMBw/+J+/88wdahjm7giVpuBjW1DcbxpevRWuhe9mqEl5arfrQuNJDY1fvW26/77Tn/drLnnNy+1LuGaxSC6QkrSSGtYqq6gS5/dLqXrYq38dWX/WhsX5bBdJ6mDtn3epTPvtSPndVWiAlaaUxrFXUSpwgt52F7mWrWrhttepDq0DaLswtRlVaICVppTGsVch8a2X6C7a9ksNtfVBBJ12XCwXS+UbKtlPlFkhJWgkMaxXiBLmLU2K4bZ5mY6FRn0vR7Zx8yz2Sdr7pSeZTlZZRSeolw1rFVG2C3EEqJdx2Mh1Ho35Md9Kp5nPUOMChm6DUKpQtJahuWr+W9776Mg4fP3FymwFO0rAzrGnJWv0C7tfKBUs16HDb6XQcvQpFS7HQvW7HTszwug9+5rQyHp5OHj0yddpxWpW7lxMlH3jsGFf90V0cPzF7cluJXduS1EuGNS1Jv1cqGBbtpuOoG2TrUKt73Vq1ejUGt8cPz7Bz755TjtPqc9WPtdB1Mt/rGjW2jDYGNRh813a/LdRVbKuitDIY1rQkrUJIo0F25bUzqBUOWk3HUYpWLZAfef0LF9V92xjm5lM/B42Wej7e8aPfybs/8b8X/bqqmJnNlitUNLJVUYvV6TJ2KothTV3r5S/g5dDPFQ6afxA2BsNW03GUrDHA1YNb3e7du7niis3A4u496+U5eNqZq05+3ar7veRrsFE39/MNe6uiemuhHhGDf9kMa+paFUJIuxUOHn7kSNetXsPcNdzc8nbW2KmPm8McnB44umltba6/5mO1GjxSWndzK0u5pxFO7Rbu9D7RVvcZzqe08zRIix2xvBjLfZ4X6hEpKfj365xX+bo2rA2BQ0enK30RLod2Kxz0Yh62hX4Qltwt3AvzDeRoDHHdXKPN9Vc/lwtNAtyqW3aQAzlaaXc7QeMKFfOVtdNRzq3uM5zPQt8H/Q4vQN+Ov1i9nlqn2SBbs+o9IksJ/v3Uz3NeP98w/zVW2jVYZ1gbAttv/fyyftPPzGYR39SL1Rwo5puHbbGtbK0mtW3uGi4hGAxCL0fjtjpWq0mAF/ph3xjgSuv2WcztBN2uVtHOfK0s/W49Pu9pawD42uPH+3L80vSjNWuhMN3utoxhn7vzwGPHePTIFO/88wfmvYZLvQYNaxXV/MN6uZqwh6mrb7552OZrZWv+IVj/C6zV+ahC1/Aw6KRFD1oHuF59z3TT0rTUexqXslpF432GC5VnoV/Y7VoCu1XaL8i6TkYsL8Zi533s9BpbSqtUv4P/UvXynJ/SetjmGi71GjSsVVT9h/XDjxxZ1r+Gmi/0qnfv1X/Zt2tla/VDcO2qUX7tZc857Ru/6udkGCw0urWTX5Stgnm/55BbrMW2WjbfZ9hOq9bzhVqPu9GqTnp5/G71s2W83W0s/bjGGn9GLXWZun7r1zl//ImnJtRuvMZ6dQ1ufFP3ZWzFsFZhoyMx0B9mO7ZdwkUb1xXTjdSNdq1srRw7McNbbr/v5OOSp+ZQ63DTahoXOL21dL57x3rV0lRiwG8XaPvderxSWqe33/r5eVuRZjOXdI21a5Vq/hk16MnDl1PjdD/trrGSrkHDmpZsw/hwhZKFWtnq1q4a5XdfdSm/+NF7T2ll27R+7dAE15Wk1TQurVpL6/e6tRqVWddNS1ApAb/TLrFeh8t2o32HTfPnnW+OwmNHZrjxkqdG8HZ6jZVyPZWi1XXdfI2Vfg0a1qQmC3UL1H8INt8T5Q/H6mg3jcveR4+efPxbr3g+7/zzB04G84Um/i3pr/Cl6rRLrNfXe6vRvsP8/VT/vO0mPZ6e5ZTW+2G4xgah1XXdqnWx5GvQsCa10K5bYCV1GwybdtO4NHaTbPym1Xzk9S/saCWBkv4K78agru2V9j01OhI8/aw1C85R+HjDtmG6xgahk+ur5GvQsCZpxelkGpf6L8eFfqk2vr6kv8JVHQuNaP7YJyZPjuD1GlvZDGuSVrxOu0lK/atbw2d0JBY9glfDy7AmSRjGJJXLsDZE6iPTbC6XJGl4GNaGSC/Wt2zUatbsKi4zJUlSlRnWKm6+mfe7XUZnmJaVkiSpygxrFTffzPtL1bgo+UJBzWHkkiQtD8PaEOjVjdHztaa1mjXb++IkSVoehjWd1GoNOpdRkiRpsAxraslFySVJKoNhTS25Bp0kSWUYGXQBJEmSND/DmiRJUsGKDWsR8a0R8Q8R8WBE3B0Rzx50mark0NFpHj0yxcxsnrJ9ZjZ59MjUyX/N+yVJUllKvmftD4H3ZeYHIuIVwB8DLxpwmSqj1WoGrabmWLtqlBtfcxmjI+HqBJIkFajIsBYR5wKXA1fWNu0Cfi8iLsjMvQu9djbh0SNTHb3PsIWT+VYzePiRI2wYH2s50e2xEzO87oOfWe6iSpKkDhUZ1oBvAf4tM58EyMyMiH3A+cDehV546Og019y8p/8lLNB8qxm0WtXgt17xfN755w9w7MTMaftcnUCSpHJEZnn3LEXEdwE7M/M5Ddv2AL+UmZ9qeu52YHv98RnrNmx60ds+tKj3O3tN8PrnjDASwzOf2Gwm73tglq8fP71+658X4MiJ01+7bhXLei6OHz/OmjVrlu391D3rrHqss+qxzqpn69atBzJzotfHLTWsnQs8BJydmU9GRAD/DrywXTfoMzZN5H1f/PKi3m9YJ36tr/PZrLTPOzk5yZYtWwZdDC2CdVY91ln1WGfVExF9CWtFdoNm5n9ExD3ATwMfAH4K2NsuqAGMBE7mWtOrNUMlSdLgFBnWan4B+EBEvB04DLx2wOWRJEladsWGtcz8Ik7VIUmSVrgi71nrxurVq3Pjxo2DLoYWYWpqitWr7a6tEuuseqyz6rHOqufAgQNkZs9vCu97y1pEvBf4ceCZwPMy8/7a9nOBncDFwBRwbWbeWdt3JnOT4G4GZoG3ZebHOnm/jRs3sn///p5/DvWPN9FWj3VWPdZZ9Vhn1RMRp8+H1QPLsdzU7cCLga82bb8BuCszvxW4BrglIurh8c3AVGY+C9gC/H5EbFiGskqSJBWl7y1r9XnR4vR5u7YBF9aesyciDjIX6u4AXgn8bG3fVyLiU8DLmBsZKqki5ps+Rsvv8HR2vLqLymCdqW4gAwwi4mxgJDMfadi8l7kVCqj9/9V59kmqgFZr0WpwHj88w869K3N1l6qyzirpSD8OOsjRoM0jG5qb3nKBfU/taFrBYHx8nMnJye5Lp2Vz/Phx66xiOqmzw9PJF/b15fYNLUHOJo8ffnzQxdAiWGeVNDxhLTO/HhFExMaG1rVnAvtqX+8DLgAa931ynmPtAHbUH09MTKQ3ZFaLN9FWTyd19uiRqZOtAju2XcKGcdebHaTdu3dzxRVXDLoYWgTrrHo2vqM/xx1ky9ptwHXAuyJiM3AecGfTvp+NiAuB7weuHUgpJXVtw/iYq2kM2FljrmhSNdaZ6vo+GjQiboqI/cAE8DcR8aXarrcC3xsRDzE3cODqzHyytu+3gbW1504C12XmN/pdVkmSpNIsx2jQ65hrJWvefhC4cp7XHGVuRKgkSdKKthzzrEmSJGmJDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklQww5okSVLBDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklQww5okSVLBDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklQww5okSVLBDGuSJEkFaxvWImJVRLwtIt4XES9t2ndj/4omSZKkTlrWbgQuBb4I/HZE/E7Dvu/r5s0jYm9E/EtE3Fv798ra9nMj4q8i4qGIuD8iXtzN+0iSJFXVGR0850XApZmZEfEHwEcj4g8y81ogelCGV2Tm/U3bbgDuysytEbEZuD0iLs7MJ3vwfpIkSZXRScvaqsxMgMw8CrwcODci3t/Hcm0Dbqq95x7gIGDrmiRJWnE6CWuPRMRz6w9qrVvbgP8CPL8HZbglIv45Iv4oIjZGxNnASGY+0vCcvcD5PXgvSZKkSolao9n8T5gLascy88sRsbH29ZGIGAVemZkfXvKbR5yfmfsiYhXwbuB5wNXAvswcb3jebcDHM3Nni2NsB7bXH4+Pj2/atWvXUoukATh+/Dhr1qwZdDG0CJ3U2eHp5Mb7ZgC4/vmjnDXWi7smtFR+n1WPdVY9W7duPZCZE70+btuwBhAR1wG/CpwHJPAAsD0z/yYi1mfmY10XJOKbgQcz85si4ihwQb11LSLuBt6SmXe0O87ExETu37+/2+JoGU1OTrJly5ZBF0OL0EmdPXpkimtu3gPAzdds5px1q5ejaJqH32fVY51VT0T0Jax1MnXHzwPXAT/HXNfn2cDbgPdExJXA3y7ljSNiPCLWN2x6NXBP7evbau9JbYDBecCdS3kfSZKkKutkNOibgK2Zua9h2ycj4gvAQ8B7lvjeTwd21bpTA3gY+JnavrcCH4qIh4Bp4GpHgkqSpJWok7A20hTUAMjMvRHxlcx821LeODMfBi6bZ99B4MqlHFeSJGmYdDIadCwiTrvDMSLWdvh6SZIkLVEnYetjzHVJrq9viIgNwE7AYZeSJEl91ElYewdwAtgfEfdExOeAfwWerO2TJElSn7S9Zy0zTwCviYiLgctrm+/JzC/1tWSSJEnqaIABAJn5ZeDLfSyLJEmSmjhAQJIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghUb1iLiWyPiHyLiwYi4OyKePegySZIkLbdiwxrwh8D7MvPbgN8C/njA5ZEkSVp2Zwy6AK1ExLnA5cCVtU27gN+LiAsyc+9Cr51NePTIVJ9LqF46PJ3WWcV0UmeHjk4vU2kkabgVGdaAbwH+LTOfBMjMjIh9wPnA3oVeeOjoNNfcvKf/JVTPPH54hp17rbMqsc4kafmUGtYAsulxtHpSRGwHttcfn7FuA48ffryf5VKP5WxaZxWzmDo7e02w587djETLb2Etk+PHjzM5OTnoYmgRrDPVRWZzJhq8WjfoQ8DZmflkRATw78AL23WDPmPTRN73xS8vQynVK7t37+aKK64YdDG0CIupsw1njjE6YlAbtMnJSbZs2TLoYmgRrLPqiYgDmTnR6+MW2bKWmf8REfcAPw18APgpYG+7oAYwEnDOutX9LaB66qyxsM4qxjqTpOVTZFir+QXgAxHxduAw8NoBl0eSJGnZFRvWMvOLwIsGXQ5JkqRBKvKetW5ExBTwyKDLoUVZBxwZdCG0KNZZ9Vhn1WOdVc95mdnzhrBiW9aWKjO9kaZiImJ/P27IVP9YZ9VjnVWPdVY9EbG/H8cteQUDSZKkFc+wJkmSVDDDmkqwY9AF0KJZZ9VjnVWPdVY9famzoRtgIEmSNExsWZMkSSqYYU2SJKlghjX1TUSsiYj/NyIejIh7I+KvIuKC2r5za48fioj7I+LFDa87MyI+EhFfqr32Jwf2IVawiHhnRGREPLf22DorVESsjojfq9XNAxHxp7Xt1lmhImJLRHw2Iu6p1c1ra9uts0JExHsjYm/jz8Ha9iXVUUSMRMSNEfHl2v43dFqWoZtnTcV5H/CXmZkR8cba4yuBG4C7MnNrRGwGbo+IizPzSeDNwFRmPisiLgT+MSJ2Z+ahgX2KFSYiLgdeCOxr2GydlesGYBb4ttr32jc3bLfOChMRAXwYuCIz76v9EfsvEfExrLOS3A78FnBn0/al1tFPA88Gvg14GvC5iPhfmfkv7Qpiy5r6JjOPZ+Yn86lRLHcBF9W+3gbcVHveHuAgUP/r5JUN+74CfAp42XKVe6WLiNXMnf83AI0jkKyzAkXEOHAN8Pb691pm/nttt3VWtvW1/88Cvg5MYZ0VIzM/lZmtJrldah29EviDzJzJzG8AtwKv6qQstqxpOb0J+HhEnA2MZGbjsmB7gfNrX58PfHWefeq/Xwf+NDO/MtcAANZZ0S5m7hf9OyLih4BjwLuAe7HOilRr/dwGfCwijgIbgJ8EvgnrrGhd/ixste8FnbyvLWtaFhHxduBbgV+tbWqeMyaaHucC+9QnEfEiYDPw+y12W2dlWsVci/UXMvMFwBuBjzL3x7h1VqCIOAP4FeBlmflM4CXAB2u7rbPydVNHS6o/w5r6LiLezNxfjT+cmU9k5tdr2zc2PO2ZPHV/1D7ggnn2qb++H/gO4CsRsReYACaB7wbrrFBfZe5+tVsAMvPzwFeA7wTrrFCXAs/IzE/Dya60fwOeD9ZZybr8/bXk+jOsqa8iYjvwauC/ZeZjDbtuA66rPWczcB5P3cTZuO9C5gLE/1ymIq9omXlDZj4jMy/IzAuA/cCWzPxLrLMiZeajwN8CWwAi4pnAhcAXsc5K9a/ARER8O0BEPIu57uwHsc6qYKl1dBvwCxExGhH/hbl72P6skzd0BQP1TURMMPdD6WHgP2ubpzLzeyLi6cCHmPulMg28ITP/rva6ceBPgO9irsXg7Zl5+3KXX1BrXXtpZt5vnZUrIi5i7vyfDcwAv5aZ/8M6K1dEvBp4O3PnPoD/npkftc7KERE3MTc44DzgUeBIbZTnkuooIkaB9wJba2/xO5n5ex2VxbAmSZJULrtBJUmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgrmclOS+i4i7q19OcbcIsb31x5/sfbvgczsaL6hLsrwCeDXM/OfmrZfy1ProK4GPpuZV/WzLO3UFvb+TGaeM8hySCqDYU1S32XmpXBKCLl0Od8/ItYxN6P/3U3bXwC8GfjuzPxGzC2Getlylk2S2rEbVNJARcQHIuKNta/fFREfiYi/iIgvRcStEXFZRPyviHg4InY0vO682v67I+K+iPj1Bd7mh4G/ytMnlvwW4HHgMMwtsJ2Zn2t4j8219/5MRHwuIn6qYd+PRsSeiPh8RNwbEd9T27619tz7IuLvIuLZte0/UHve79de80AtLNaPd13tM/898LqG7Rsj4q8j4p9rx7x58WdZUpXZsiapNC+o/TsCfA64gbmwdQZza5b+QWY+yNzC17+RmZ+qLYz9FxHx8sz8Hy2O+XLgAy22TwK/BPxrRPwdc0vG3JKZhyJiPfCHwI9m5r9HxDnAZyPi08BZwB8D/zUzH4yIVcCZEXEu8KfAFZn5zxFxFXAr8Nza+z0HeF1mvqHW/fobwJaIeD7wq8BlmXkwIn6/oYw/DezNzCsBasvUSFpBbFmTVJrJzHw8M2eA+4D/LzOnMvMoc/e3XVRb0uUHgffW7of7DPAs5hahP0UtSH0vsLt5X2Y+AfwfwI8A/wD8JHBfLRB9L3AR8Je19/gb5pYF+nbgvwGfrIVGMvNEZj4OfA9wb2b+c237LcytAfnNtbf8YmZ+pvb1PzK3HiTADwCfyMyDtcfvayjmXcDWiHhPRPw4cLSDcyhpiNiyJqk0xxu+nmnx+Azm/tBMYHNmnmhzvB8EPj3f82pdo/cA90TEjcAXmAtPU8B9mflfm18TEc9t3lbfVSvXaW9T+7/VZ6m/rqXM/MeIuBT4IeCngHdHxGW1MCtpBbBlTVLlZOZ/An8PvK2+LSKeERETLZ7+E0CrrlEi4jtqXZB13wJsBB5mrqXtWyPiBxuef2lEjDHXffrDEfFtte2rIuJpzLWWXRoR31nb/ipgf2Z+rc1H2g38SK0bFeDnGt7zQuYWkL4VuJ650bTr2hxP0hCxZU1SVV0F7IiIf649PgJcC+yvP6E2unML8MvzHONM4Hci4jzgGHMtXG/LzHtrr/8x4Lcj4neAVcA+4Ccy80sR8XPAR2rdrDPAL2Tm3RFxNXBLRIwCjwHb2n2QzLwvIv478A8R8TXgEw27fwDYHhEzwCjwy7UuV0krRJw+OEqShkNEvBB4R2a+dNBlkaSlMqxJkiQVzHvWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSC/f+TuozQJqhbtwAAAABJRU5ErkJggg==\n",
"text/plain": [
"
\n",
" \n",
" CC BY-SA 3.0\n",
" \n",
"Stepper motors are commonly used actuators in lab equipment and robotics. The position of the stepper motor would be manipulated variable. This is an example of a stepper motor with an integrated encoder that can be used to verify the motor's position.\n",
" \n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"Valve position feedback is a feature of control valves used in process applications, and should be regarded as a 'best practice' for industrial automation.\n",
"\n",
""
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"This behavior also occurs in the Temperature Control Laboratory in which the manipulated power levels are constrained to the range 0% to 100%. This is demonstated in the following cell."
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"TCLab version 0.4.9\n",
"Simulated TCLab\n",
"Q1 = 0\n",
"Q1 = 100\n",
"TCLab Model disconnected successfully.\n"
]
}
],
"source": [
"# show that inputs to the TCLab are constrained to the range 0 to 100%\n",
"\n",
"TCLab = setup(connected=False, speedup=20)\n",
"with TCLab() as lab:\n",
" print(f\"Q1 = {lab.Q1()}\")\n",
" lab.Q1(150)\n",
" print(f\"Q1 = {lab.Q1()}\")"
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"To accomodate feedback of the manipulated variable, we first need to modify the event loop to incorporate the measurement of the manipulated variable, then send that value to the controller."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"outputs": [],
"source": [
"%matplotlib inline\n",
"from tclab import TCLab, clock, Historian, Plotter, setup\n",
"\n",
"def experiment_2(controller, t_final=1000, t_step=5,\n",
" SP=lambda t: 40 if t >= 20 else 0, \n",
" DV=lambda t: 100 if t >= 420 else 0):\n",
" TCLab = setup(connected=False, speedup=60)\n",
" with TCLab() as lab:\n",
"\n",
" # set up historian and plotter\n",
" h = Historian(lab.sources)\n",
" p = Plotter(h, t_final)\n",
"\n",
" # initialize manipulated variable\n",
" lab.P1 = 200\n",
" next(controller)\n",
"\n",
" # event loop\n",
" for t in clock(t_final, t_step):\n",
" T1 = lab.T1\n",
" U1 = lab.Q1() # <==== new line\n",
" U1 = controller.send((t_step, SP(t), T1, U1)) # <==== send U1 to controller \n",
" lab.Q1(U1)\n",
" lab.Q2(DV(t))\n",
" p.update(t) "
]
},
{
"cell_type": "markdown",
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"source": [
"The next change is to the controller. The controller now accepts values for PV, SP, and, additionally, MV. To demonstrate the impact of these changes, this example will comment out the software limits placed on MV to show that feedback of manipulated variable is also an anti-reset windwup strategy."
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"nbpages": {
"level": 3,
"link": "[3.7.3.2 Anti-reset Windup - Version 2](https://jckantor.github.io/cbe30338-2021/03.07-Integral-Windup-and-Bumpless-Transfer.html#3.7.3.2-Anti-reset-Windup---Version-2)",
"section": "3.7.3.2 Anti-reset Windup - Version 2"
}
},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAmsAAAHYCAYAAAAS+q+iAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAxOAAAMTgF/d4wjAAA6VElEQVR4nO3df5TcZ133/+d7t9kk3ViSu02pZC39gb/41R8SBeV7a8W7iYoiyjf8qBV7ROyhlK/fiIDIOaBfvO3RQ/RQ61FQC8ECtg331xtB16/eqVi0NkBLbbmlhRJiosQW0sakyW66+/7+sTPpZDK7M7szs3N9Zp+Pc3Ky8/nMfOaaz/XZ3dde1+e6rshMJEmSVKaRQRdAkiRJ8zOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklSwMwZdgF5bvXp1bty4cdDF0CJMTU2xevXqQRdDi2CdVY91Vj3WWfUcOHBgOjN7XmlDF9Y2btzI/v37B10MLcLk5CRbtmwZdDG0CNZZ9Vhn1WOdVU9EPNKP49oNKkmSVLCha1lb6WZmk0NPTC/4nA1njjE6EstUIkmS1A3D2hCoB7SZ2eT6D9/DsRMzCz5/7apRbnzNZYyOhMFNkqTCGdYqbmY2ue6Wz3HgsWMdv+bYiRle98HPALBp/VpuuupyA5skSYUyrFXYzGzy8CNHTgtqjS1nzc9vbnk78NgxDj0xzTnrHHEkSVKJDGsV1apFbce2S9gwPrZg1+ZHXv9CDj0xzaGj02y/9fMAHDp66j1udo1KklQOw1pFHXpi+pSgtmn9Wi7auK5tyBodidNa0eqhrfFYdo1KklQGw1rF1AcTNLaG7dh2SUdBrdGGM8fYtH5ty3vd7BqVJKkchrUKmW8wwYbxxXdbjo4EN111+SnTfDR2jQ6jTqY1accuYknScjOsVUhz1yfMdVluOHNsScdr1SV68r1qLXdVDyeLndaknfkGb1T9PK0EzkEoqaqKCGsR8U7gXcDzMvP+iDgX2AlcDEwB12bmnQMsYnE6GUzQjXoLW5XvX1vKtCbtNE570qjK52kl6PRasB4llWjgYS0iLgdeCOxr2HwDcFdmbo2IzcDtEXFxZj45kEIWaMP4WM/vKWt1H9uBx47x8CNH2DA+dtpzS/uF1txycujo6S2R87WMdXLshVrmGs9TieemlW66hQ9PJ48emVrUa3p1XpZS7lbXQivzXe9LUZXrYLGaz/+wfs5uLfX7q34+Z2bzlO8zz3N3lnrdLlSPy1knAw1rEbEauAl4DbC7Ydc24EKAzNwTEQeBFwN3LHcZS9BqUEE/NN7H1nj/Wqv72Eppgei0m7MXLZH1aU8atTpP7QJhP7/BO/0F0W238OOHZ9i5d8+iXrPUoNyoF93Z9WuhUbvrfSk6+bzLGWCXErBbvU/z+e9FvQ6bbq7TtatG+d1XXcovfvRevvb1p77P+n2eG0Nit/f2lmap1227elzOa3/QLWu/DvxpZn4lYu7DRsTZwEhmNq5cvxc4f/mLN3j96MpbSP0+toVGi0IZI0YX07W12NGyrbS6x6/VeZqvq7SxPP0Iust9rSxWu/OyHOa7Ftpd70vRyeftxbXQab0vJWB3ooR6HSbHTszwCx/6bMvt/TzPm9av5b2vvow3feSeYn+G9FIvzudyXvuRmcvyRqe9ccSLgN8AXpKZGRF7gZcC/w7sy8zxhufeBnw8M3e2OM52YHv98fj4+KZdu3b1u/jL5vB0cuN9p6b6s9cEr3/OCCPR3zQ/m8mRE6duO3ICbv7fc+W5/vmjnDXWfRmOHz/OmjVrFl2exrLUjY3Azz9nlMbffetW0ddzVS/XbML7H5hherb9a675zlHWrequjJ2cj3Zana9OTE1NsXp1Z0F9MeelU0st90LnudX1vhSL/bzN18JidVrvOZtEj/5AGBuBn3v2KH/8hd7W67BZzHXa6rpZRfK6556xbOf5/3zWKLd9qbtBWCVb6nXbXI8LfY///TteeiAzJ3pT4qcMMqy9DXgTUG9vnQAOAq8DbgcuqLeuRcTdwFsy8452x52YmMj9+/f3pcyD8OiRKa65ee6v4X4PKlhKeXrRYjU5OcmWLVta7lvObs5eWKgLYaGpURbbnN7p+WhnqedroTprpdddK4Ou53bafd5+TZOzUL3v3r2bK664oifvM8xdZr202Ou0+XzuuXM3P7x1a1/P83zXYqc/Q6pkqddtq3qc7xgbv2lNX8LawLpBM/MG5gYSAFBvWauNBr0NuA54V22AwXnAih8N2o9BBd3Yfuvn+3rv2nJ3c/bCQtOhLNTV1svm9JLOR91C52UYtfu8/eh2bVfvZ431vg5WWr32W/P5rLcC9/M8t7oWS/wZ0ku9OJ/Lfe0P+p61+bwV+FBEPMRcy9vVjgQtQ/M3dj9GizYOqOhkNGfprSx1rSYi7vaG+Sqfj5Ws1bXQLetdS9HqWvRaKk8xYS0zL2j4+iBw5eBKo/nUv7EffuRIX0aLzteaVko3Z7da/TXWapRpp6p+PlYyW6VUCq/F8hUT1lQdoyPBRRvX9WW06HyrNNgkL0laqQxrWpL5unEab1ZdaF64+SZ+bF6gfhha0yRJ6oZhTUvWrkVoodFu80382Ki0ARWSJA2CYa0wrZZMqpJOR7nNN/FjXTcL1EuSNEwMawUpfQb6TrQb5dZq9OPYCPzRa1/giEZJklowrBWk1c31dVVqaWrXPdo8+nHPnbt5+lntVzCQJGklMqwVqnn26GFqaZpv4kdJknQ6w1qhvLlekiQBjAy6AJIkSZqfLWsFaFxeSZIkqZFhbcCGYQSoJEnqH7tBB2y+5ZWqMvJTkiT1ly1rBXF5JUmS1MywVhBHgEqSpGZ2g0qSJBXMsCZJklQww5okSVLBDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDCXm1pmM7PJoSemTz4+dHR6gWdLkqSVzrC2jGZmk+tu+RwHHjs26KJIkqSKsBt0GR16YnreoLZp/Vo2nDm2zCWSJEml60vLWkR8MDNf249jD4sd2y5hw/hT4WzDmWOMjsQASyRJkkrUr27QK/p03KGxYXyMc9atHnQxJElS4ZYc1iLiP+bbBaxf6nGHUX1QgYMJJEnSYnXTshbAS4DHW2z/dBfHHSoOKpAkSd3oJqx9Fjg7M+9r3hERX+viuEOl1aACBxNIkqROdRPWfgo40WpHZn5XF8cdWvVBBQ4mkCRJnepm6o4/ykxvwlqE+qACg5okSepUN2HtO3pWCkmSJLXUTVjLnpVCkiRJLXVzz9rz5pm+I4DMzHPbHSAi/ho4D5gF/hO4PjPvjYhzgZ3AxcAUcG1m3tlFWZed03VIkqRe6CasPQj8SJfvvy0zHwOIiJ8A/gS4HLgBuCszt0bEZuD2iLg4M5/s8v2WhdN1SJKkXukmrE1l5le7efN6UKt5GnMtbADbgAtrz9kTEQeBFwN3dPN+y8XpOiRJUq90Oylu1yJiJ08tT7U1Is4GRjLzkYan7QXO78X7LTen65AkSd2IzDLGCUTEa4FXAlcD+zJzvGHfbcDHM3Nni9dtB7bXH4+Pj2/atWvXMpR4foenkxvvmwHg+uePctaYIW0hx48fZ82aNYMuhhbBOqse66x6rLPq2bp164HMnOj1cYsJawARcQyYAPYBF9Rb1yLibuAtmXlHu2NMTEzk/v37+1rOdh49MsU1N+8B4OZrNrtgexuTk5Ns2bJl0MXQIlhn1WOdVY91Vj0R0Zew1s3UHV2JiLMi4hkNj18OfB34BnAbcF1t+2bmRoxWajSoJElSL3Rzz1q3ngbsioi1zA0seAR4aWZmRLwV+FBEPARMA1dXZSSoJElSLw0srGXmvwLfPc++g8CVy1ui7jm3miRJ6rVBtqwNFedWkyRJ/TCwe9aGjXOrSZKkfrBlrQ+cW02SJPWKYa0PNoyPOV2HJEnqCbtBJUmSCmZYkyRJKphhrQdmZtPpOiRJUl94z1qXnLJDkiT1ky1rXWqessPpOiRJUi/ZstZDO7ZdwkUb1zldhyRJ6hlb1npow7jzqkmSpN4yrEmSJBXMsCZJklQw71lbopnZ5NAT007ZIUmS+sqwtgRO1yFJkpaL3aBL0DxdBzhlhyRJ6g9b1rq0Y9slbBgfY8OZjgSVJEm9Z1jr0obxMc5Zt3rQxZAkSUPKblBJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKpjzrLVRXwO0keuBSpKk5WJYW4BrgEqSpEGzG3QBrdYAbeR6oJIkqd9sWetQfQ3QRq4HKkmS+s2wNo+Z2Tzl3jTXAJUkSYNgWGvBe9UkSVIpvGetheZ71bw3TZIkDYotaw3q03Q0dn/u2HYJF21c571pkiRpIIYurM0mPHpkatGvm5lNrv/wPRw7MXPK9g3jDiKQJEmDM3Rh7dDRaa65eU9PjmX3pyRJGrSBhbWIWAN8FHg28ATwNeDazNwbEecCO4GLgana9juXo1xrV41y42suY3QknJpDkiQN3KBb1t4H/GVmZkS8sfb4SuAG4K7M3BoRm4HbI+LizHyy3QE3jI9x8zWbl1wgA5okSSrJwMJaZh4HPtmw6S7gF2tfbwMurD1vT0QcBF4M3NHuuCOB86FJkqShUdLUHW8CPh4RZwMjmflIw769wPkDKZUkSdIARWYOugxExNuBHwNeAqwF9mXmeMP+24CPZ+bOFq/dDmyvPx4fH9+0a9eu/hdaPXP8+HHWrFkz6GJoEayz6rHOqsc6q56tW7ceyMyJXh934GEtIt4MvAr4ocx8rLbtKHBBvXUtIu4G3pKZd7Q73urVq3Pjxo39K7B6bmpqitWr7bquEuuseqyz6rHOqufAgQNkZs9vfB/oAINaq9iraQhqNbcB1wHvqg0wOA/oaDToxo0b2b9/f6+Lqj6anJxky5Ytgy6GFsE6qx7rrHqss+qJiJn2z1q8QU7dMQG8B3gY2B0RAFOZ+T3AW4EPRcRDwDRwdScjQSVJkobNIEeD7gdaNhVm5kHmpvCQJElaUH25yGE16HnWJEnSCtGPUDXfcpEDcqQfBzWsSZKkefUqYBUWqvrFsCZJktpbiQGrcbnIQdn4pv4c17AmSVLBFhu8Sg9Y/QpVw7xc5KCn7tgLHK/9A/jNzPyzQS7kLknSclkoiB2eTg4ePl5E8OplwBrmUNUvJbSsvSIz72/atuSF3CVJGrROWsPatYA9fniGnXs/s+QyGLCGRwlhrZUlL+QuSdJyaRXK+tENuZTgZcAaHiWEtVsiYgT4J+BXgFlcyF2SNCCd3iPWq1A2XxDbvXs3V1yxGTB4rXQDXRs0Is7PzH0RsQp4N/A84GpcyH1FcbHi6rHOqsc6a202kyMnGh/D+x+YYXq2+2OPjcDPP2eUdhlr3SoYidOfZJ1Vz9Au5F4XEd8MPJiZ39TNQu4TExPp2qDV4vp31WOdVc9KrbOFWsn63TLWbWvYSq2zKouIvoS1Qa4NOg6saljA/dXAPbWvl7yQuyRp5en1vWOLuUfMLkr12yDvWXs6sCsiRplbI/Rh4Gdq+1zIXZLUUnMw67aFrFUwM4CpJINcyP1h4LJ59rmQuyTppHpAW0owa9dKZjBT6UoYDSpJEtBdd2a/7h2TBs2wJkkaiG66M+261EpiWJMk9UWvR2I2BjSDmVYSw5okqWe6ubeszu5M6VSGNUnSkvRiVKbdmVJ7hjVJUscW23LmSEype4Y1SdKCuglohjGpe4Y1SdJJi+3atBtT6j/DmiStcLacSWUzrEnSCmRAk6rDsCZJK8zMbHLdLZ/jwGPHWu63a1Mqi2FNkobczGxyeDp59MgUAIeOTp8W1Gw5k8plWJOkIVZvRfvCvhl27t1z2v4d2y5hw/iYAU0qmGFNkoZQ/Z60Vq1odZvWr+WijesMaVLhDGuSNCTaDRqot6LV2ZomVYNhTZIqbmZ27n60hUZ1nr0mbEWTKsqwJkkV1MnUG42DBvbcudugJlWUYU2SKmahqTfmG9U5EgY1qaoMa5JUsObln2DhqTfOWbfaFjRpyBjWJKlQ7SavBafekFYCw5okFWhmNnn4kSMLBjWn3pBWBsOaJBWmVYta87Qb4NQb0kpRRFiLiHcC7wKel5n3R8S5wE7gYmAKuDYz7xxgESWpLzq5J80WNGllG3hYi4jLgRcC+xo23wDclZlbI2IzcHtEXJyZTw6kkJLUB53ek2ZQk1a2kUG+eUSsBm4C3gBkw65tte1k5h7gIPDiZS+gJPWJ96RJ6tSgW9Z+HfjTzPxK1OYAioizgZHMfKTheXuB85e/eJLUOwtNZOs9aZLmM7CwFhEvAjYDb2uxO5ufvsBxtgPb64/Hx8eZnJzsSRm1PI4fP26dVYx11rnZTI6cgNmE9z8ww/Ts6c85e03wpXs+3deJa62z6rHOVBeZzblomd444m3Am4D6nbUTzHV3vg64Hbig3roWEXcDb8nMO9odd2JiIvfv39+XMqs/Jicn2bJly6CLoUWwzjrT7p605ZzI1jqrHuuseiLiQGZO9Pq4A2tZy8wbmBtIAEBE7AVeWhsNehtwHfCu2gCD8wBHg0qqhHp350IrDTQvByVJ8xn0PWvzeSvwoYh4iLmWt6sdCSqpCuZrTXOlAUlLVUxYy8wLGr4+CFw5uNJI0tIceuL01jRHdUrqxpLDWkSsAn4JuAj4n5n5Fw37bszM63tQPkkqWvOktoeOPvW1rWmSeqGblrUbgfXAHuC3I+Ilmfl/1/Z9X7cFk6TStRtAsGF8jHPWrV7mUkkaNt1Mivsi4NWZ+R7gBcCzIuIPavv8E1LS0JqZTR49MrXgpLab1q9lw5ljLfdJ0mJ007K2KmvzfmTm0Yh4OXBrRLy/N0WTpPK0G0BQZ9enpF7pJqw9EhHPzcz7ATLzyYjYBvwZ8PyelE6SCrHQdBwOIJDUT92EteuA440bGgLbK7sqlSQVxOk4JA1SN/es/Wpmfql5Y2bOZOaHuziuJBVjvgXX661py7H6gKSVrZuWtW/vWSkkqUCtWtRsTZO03IqZFFeSSjHf/WnemyZpELoJa8+LiP9osT2AzMxzuzi2JA3EQvenGdQkDUI3Ye1B4Ed6VRBJGiRHe0oqVTdhbSozv9qzkkjSgDjaU1LJuglr/uSSNBRcfF1SyZYc1jLzsl4WRJJKYGuapNI4GlTSilO/P63u0NGnvnbxdUmlMaxJWlHmuz9NkkplWJO0Iiw02rNu0/q1bDhzrOU+SRoUw5qkoddutGed96lJKpFhTdLQc7SnpCozrElaURztKalqDGuSVhRHe0qqmoGGtYj4a+A8YBb4T+D6zLw3Is4FdgIXA1PAtZl55+BKKqlKFpqaQ5KqZtAta9sy8zGAiPgJ4E+Ay4EbgLsyc2tEbAZuj4iLM/PJgZVUUiU4NYekYTPQsFYPajVPY66FDWAbcGHtOXsi4iDwYuCO5SyfpOpwag5Jw2rQLWtExE7gitrDrRFxNjCSmY80PG0vcP5yl01SNTg1h6RhFpk56DIAEBGvBV4JXA3sy8zxhn23AR/PzJ0tXrcd2F5/PD4+vmnXrl3LUGL1yvHjx1mzZs2gi6FFKK3ODk8nN943c8q2s9cEr3/OCCNhOIPy6kztWWfVs3Xr1gOZOdHr4xYT1gAi4hgwAewDLqi3rkXE3cBbMvOOdseYmJjI/fv397Wc6q3JyUm2bNky6GJoEUqps8auz+23fh5wao75lFJn6px1Vj0R0ZewNrBu0Ig4C1iXmf9We/xy4OvAN4DbgOuAd9UGGJwHOBpU0smANjObXP/hezh24tQWNafmkDRsBnnP2tOAXRGxlrmBBY8AL83MjIi3Ah+KiIeAaeBqR4JKajfS0wEEkobRwMJaZv4r8N3z7DsIXLm8JZJUspnZ5OFHjpwW1NauGuXG11zG6EjY9SlpKA18NKgktdOqRc170yStFIY1ScVrXojdRdglrSSGNUmVsmPbJQY1SSvKyKALIEmLsWHcbk9JK4sta5KK0rwIO7gQu6SVzbAmqRguwi5Jp7MbVFIR5puao5HzqElaiWxZkzRwC03N0chpOiStRIY1SQPTuLanU3NIUmuGNUkDMd/9aU7NIUmnMqxJWlbztaaBLWqS1Iphbci0mvZgEEq5t6iU89FOq/M1X9k7Pbf9/OyHp5NHj0wt+nUzs8n1H76HYydmTtnu0lGSND/DWoU1/zKe7xfhIDQurt3OUn/xt1PS+Win+XwtVPZOzm2/P/vjh2fYuXdPT45la5okLcywVjH1gFZ6EDl2YobXffAzHT23l7/4q2ox52sxzy1VY+C0NU2SFmZYq4DFBrTFtGr1WokhcpDno51256ux7Es5t/367Lt37+aKKzYv+fUGNEnqnGGtMIvt2mz1y3jQvwg/8voXLupeqW5/8bcz6PPRzkLnq7nsiz23/frsZ40F56xb3fPjSpJOZ1grQDctZyUGkdGRxf0iX+m/+BdzvhZ7biVJ1WdYW2ZLHRRQekCTJEn9YVhbBr2458yAJknSymRY65Nh69qUJEmDYVhbooUmHK3ioABJklSmoQtrs0lfJlht1O0UCgYzSZLUqYGFtYhYA3wUeDbwBPA14NrM3BsR5wI7gYuBqdr2Ozs57qGj01xzcxkTrBrQJElStwbdsvY+4C8zMyPijbXHVwI3AHdl5taI2AzcHhEXZ+aTgyxss3YTjhrQJElStwYW1jLzOPDJhk13Ab9Y+3obcGHteXsi4iDwYuCOdsfdMD7Gzdf0b4LVU97LMCZJkvps0C1rjd4EfDwizgZGMvORhn17gfM7OchI4KShkiRpaERmDroMRMTbgR8DXgKsBfZl5njD/tuAj2fmzhav3Q5srz8eHx/ftGvXrv4XWj1z/Phx1qxZM+hiaBGss+qxzqrHOquerVu3HsjMiV4fd+BhLSLeDLwK+KHMfKy27ShwQb11LSLuBt6SmXe0O97ExETu37+/fwVWz01OTrJly5ZBF0OLYJ1Vj3VWPdZZ9UTE8IW1WqvYVcwFtUMN2z8A7M3Md9UGGOwCLupkgMHq1atz48aN/Sqy+mBqaorVq+26rhLrrHqss+qxzqrnwIEDZGbPb2bve1iLiPcCPw48E3heZt5f234JcC9wApgB9gPfyMzviYgLgH8EzgYS+H8y892dvJ8ta9XjX4/VY51Vj3VWPdZZ9UTETGb2fDzASK8P2MLtzI3k/GrT9v8L+LXMHAP+KzAGfF9t388Ak7V93wG8MSI2LENZJUmSitL30aCZ+SmAiNNaBReanuOVwM/W9n0lIj4FvAz4QK/Lt9CyUf3ilB+SJKlTA5m6o4PpOc7n1Ja4xn09MzObXHfL5zjw2LFeH3pBm9av5aarLjewSZI0XI7046CDnGet+Wa55uSSC+x7asfpU3cwOTnZUQEOTydf2Nf5+p698vjhx/nYJyY5a8ywBnPD0zutM5XBOqse66x6rLNKGp6wlplfjwgiYmND69ozgX21r/cBFwCN+z5JC5m5A9hRfzwxMZGd3pD56JEpdu6dW0d0x7ZL2DA+tshPsjiHjk6z/dbPA3Dpd5/6fiu5a9SbaKvHOqse66x6rDPVDbJl7TbgOqA+Pcd5wJ1N+342Ii4Evh+4tp+F2TA+tqwrH9RDW51do5IkqZW+jwaNiJsiYj8wAfxNRHyptuutwPdGxEPMDRy4umEetd8G1taeOwlcl5nf6HdZ+23DmWNsWr+25b4Djx1b9oEOkiSpfMsxGvQ65lrJmrcfBK6c5zVHmRsROlRGR4Kbrrr8lFDW2DUqSZLUrKSF3FeE0ZFwoXlJktSx5ZgUV5IkSUtkWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSrYGYMugJ5y6Og0ABvOHGN0JAZcGkmSVALDWkG23/p5ADatX8tNV11uYJMkSXaDDtqGM8fYtH7tKdsOPHaMQ09MD6hEkiSpJLasDdjoSHDTVZdz6IlpDh2dPtm6JkmSBIa1IoyOBOesWz3oYkiSpALZDSpJklQww5okSVLB7AYtVH0ajzqn85AkaWUyrBWqeaCB03lIkrQy2Q1akFbTeNQ5nYckSSuTLWsFaZzGo87pPCRJWtkMa4VxGg9JktTIblBJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSpYV2EtIj7Yq4JIkiTpdN0u5H5FNy+OiL3A8do/gN/MzD+LiHOBncDFwBRwbWbe2c17qUwzs8nh6eTRI1OnbN9w5hijIzGgUkmSVI62YS0i/mO+XcD6HpThFZl5f9O2G4C7MnNrRGwGbo+IizPzyR68nwoxM5tcd8vn+MK+GXbu3XPKvk3r13LTVZcb2CRJK14nLWsBvAR4vMX2T/e8RHO2ARcCZOaeiDgIvBi4o0/vpwE49MQ0Bx471nLfgceOceiJac5Zt3qZSyVJUlk6CWufBc7OzPuad0TE13pQhlsiYgT4J+BXgFlgJDMfaXjOXuD8HryXCjAzmxx6YppDR6dPbtux7RI2jI9x6Og022/9PMDJ/XaJSpJWssjMhZ8QMQ5MZ+aJiNgIHMvMIz1584jzM3NfRKwC3g08D7ga2JeZ4w3Puw34eGbubHGM7cD2+uPx8fFNu3bt6uj9D08nN943A8D1zx/lrLHyAkEVyjif2UyOnGjeBu9/YIbp2ae25WzypkvP4KyxOOXz1p29Jnj9c0YYiep89mF3/Phx1qxZM+hiaBGss+qxzqpn69atBzJzotfHbduylplHI+INEfEO4DwgI+IBYHtm/k1ErM/Mx5by5pm5r/b/iYj4XeDBzPx6RBARGxta154J7JvnGDuAHfXHExMTuWXLlo7e/9EjUyfvlbriis1FdrlVoYyt1O9Ha9XNuXYdrG14fMb0YX7yR7cwOhLMzCZ/+9ipr3sSeNZlcy1vtrKVYXJykk6/z1QG66x6rDPVdTLA4OeBNwI/B/xjbfP3Au+JiF8GfhP4rsW+ca3FblVD0Hs1cE/t69uA64B31QYYnAc4GrRCFrofDWDtqlFufM1ljI4Ee+7cfTKAjY4EN111+clu0nqXaP1/Bx5IklaaTu5ZexOwtd4KVvPJiPgC8CANrVqL9HRgV0SMMjdY4WHgZ2r73gp8KCIeAqaBqx0JWl31+9EaNbaQNXdvjo4E56xbzYYzx9i0fu0poe/AY8d4+JEjXLRxnYFNkrQidBLWRpqCGgCZuTci9mbm25byxpn5MHDZPPsOAlcu5bjDrKo33G8YH1tS9+1CrWy2sEmSVopOwtpYRKzJzOONGyNiLS5XtaxWYlfgfK1sTu0hSVopOglbH2OuS3J9fUNEbGBuhYHOhl1qyeohpVE9qKwk9Va2HdsuObnt0NFpHj0ydcq/mdmFRzdLklQ1nbSsvQP4ILC/dg9ZAt8GfLy2T300X1fgSjQ6Eqfc+9bqXKykVkdJ0srQydQdJ4DXRMTFwOW1zfdk5pf6WjKdVO8KrIqZ2TxlwtteajXooJHdo5KkYdPxQu6Z+WXgy30si4bAQvOr9UJjS2OjYWx1rK/00Kx5gEnz86o2AEWStLCOw5rUieb51TatX8uGM8cWeMXitWtpbG7Vq1J4qQevmdnk+g/fw7ETM6c9p97VC3OTJjc/z65gSRouhjX1zY5tlwxkPrTmFraqhJdOWyUPPHaMBw/+J+/88wdahjm7giVpuBjW1DcbxpevRWuhe9mqEl5arfrQuNJDY1fvW26/77Tn/drLnnNy+1LuGaxSC6QkrSSGtYqq6gS5/dLqXrYq38dWX/WhsX5bBdJ6mDtn3epTPvtSPndVWiAlaaUxrFXUSpwgt52F7mWrWrhttepDq0DaLswtRlVaICVppTGsVch8a2X6C7a9ksNtfVBBJ12XCwXS+UbKtlPlFkhJWgkMaxXiBLmLU2K4bZ5mY6FRn0vR7Zx8yz2Sdr7pSeZTlZZRSeolw1rFVG2C3EEqJdx2Mh1Ho35Md9Kp5nPUOMChm6DUKpQtJahuWr+W9776Mg4fP3FymwFO0rAzrGnJWv0C7tfKBUs16HDb6XQcvQpFS7HQvW7HTszwug9+5rQyHp5OHj0yddpxWpW7lxMlH3jsGFf90V0cPzF7cluJXduS1EuGNS1Jv1cqGBbtpuOoG2TrUKt73Vq1ejUGt8cPz7Bz755TjtPqc9WPtdB1Mt/rGjW2jDYGNRh813a/LdRVbKuitDIY1rQkrUJIo0F25bUzqBUOWk3HUYpWLZAfef0LF9V92xjm5lM/B42Wej7e8aPfybs/8b8X/bqqmJnNlitUNLJVUYvV6TJ2KothTV3r5S/g5dDPFQ6afxA2BsNW03GUrDHA1YNb3e7du7niis3A4u496+U5eNqZq05+3ar7veRrsFE39/MNe6uiemuhHhGDf9kMa+paFUJIuxUOHn7kSNetXsPcNdzc8nbW2KmPm8McnB44umltba6/5mO1GjxSWndzK0u5pxFO7Rbu9D7RVvcZzqe08zRIix2xvBjLfZ4X6hEpKfj365xX+bo2rA2BQ0enK30RLod2Kxz0Yh62hX4Qltwt3AvzDeRoDHHdXKPN9Vc/lwtNAtyqW3aQAzlaaXc7QeMKFfOVtdNRzq3uM5zPQt8H/Q4vQN+Ov1i9nlqn2SBbs+o9IksJ/v3Uz3NeP98w/zVW2jVYZ1gbAttv/fyyftPPzGYR39SL1Rwo5puHbbGtbK0mtW3uGi4hGAxCL0fjtjpWq0mAF/ph3xjgSuv2WcztBN2uVtHOfK0s/W49Pu9pawD42uPH+3L80vSjNWuhMN3utoxhn7vzwGPHePTIFO/88wfmvYZLvQYNaxXV/MN6uZqwh6mrb7552OZrZWv+IVj/C6zV+ahC1/Aw6KRFD1oHuF59z3TT0rTUexqXslpF432GC5VnoV/Y7VoCu1XaL8i6TkYsL8Zi533s9BpbSqtUv4P/UvXynJ/SetjmGi71GjSsVVT9h/XDjxxZ1r+Gmi/0qnfv1X/Zt2tla/VDcO2qUX7tZc857Ru/6udkGCw0urWTX5Stgnm/55BbrMW2WjbfZ9hOq9bzhVqPu9GqTnp5/G71s2W83W0s/bjGGn9GLXWZun7r1zl//ImnJtRuvMZ6dQ1ufFP3ZWzFsFZhoyMx0B9mO7ZdwkUb1xXTjdSNdq1srRw7McNbbr/v5OOSp+ZQ63DTahoXOL21dL57x3rV0lRiwG8XaPvderxSWqe33/r5eVuRZjOXdI21a5Vq/hk16MnDl1PjdD/trrGSrkHDmpZsw/hwhZKFWtnq1q4a5XdfdSm/+NF7T2ll27R+7dAE15Wk1TQurVpL6/e6tRqVWddNS1ApAb/TLrFeh8t2o32HTfPnnW+OwmNHZrjxkqdG8HZ6jZVyPZWi1XXdfI2Vfg0a1qQmC3UL1H8INt8T5Q/H6mg3jcveR4+efPxbr3g+7/zzB04G84Um/i3pr/Cl6rRLrNfXe6vRvsP8/VT/vO0mPZ6e5ZTW+2G4xgah1XXdqnWx5GvQsCa10K5bYCV1GwybdtO4NHaTbPym1Xzk9S/saCWBkv4K78agru2V9j01OhI8/aw1C85R+HjDtmG6xgahk+ur5GvQsCZpxelkGpf6L8eFfqk2vr6kv8JVHQuNaP7YJyZPjuD1GlvZDGuSVrxOu0lK/atbw2d0JBY9glfDy7AmSRjGJJXLsDZE6iPTbC6XJGl4GNaGSC/Wt2zUatbsKi4zJUlSlRnWKm6+mfe7XUZnmJaVkiSpygxrFTffzPtL1bgo+UJBzWHkkiQtD8PaEOjVjdHztaa1mjXb++IkSVoehjWd1GoNOpdRkiRpsAxraslFySVJKoNhTS25Bp0kSWUYGXQBJEmSND/DmiRJUsGKDWsR8a0R8Q8R8WBE3B0Rzx50mark0NFpHj0yxcxsnrJ9ZjZ59MjUyX/N+yVJUllKvmftD4H3ZeYHIuIVwB8DLxpwmSqj1WoGrabmWLtqlBtfcxmjI+HqBJIkFajIsBYR5wKXA1fWNu0Cfi8iLsjMvQu9djbh0SNTHb3PsIWT+VYzePiRI2wYH2s50e2xEzO87oOfWe6iSpKkDhUZ1oBvAf4tM58EyMyMiH3A+cDehV546Og019y8p/8lLNB8qxm0WtXgt17xfN755w9w7MTMaftcnUCSpHJEZnn3LEXEdwE7M/M5Ddv2AL+UmZ9qeu52YHv98RnrNmx60ds+tKj3O3tN8PrnjDASwzOf2Gwm73tglq8fP71+658X4MiJ01+7bhXLei6OHz/OmjVrlu391D3rrHqss+qxzqpn69atBzJzotfHLTWsnQs8BJydmU9GRAD/DrywXTfoMzZN5H1f/PKi3m9YJ36tr/PZrLTPOzk5yZYtWwZdDC2CdVY91ln1WGfVExF9CWtFdoNm5n9ExD3ATwMfAH4K2NsuqAGMBE7mWtOrNUMlSdLgFBnWan4B+EBEvB04DLx2wOWRJEladsWGtcz8Ik7VIUmSVrgi71nrxurVq3Pjxo2DLoYWYWpqitWr7a6tEuuseqyz6rHOqufAgQNkZs9vCu97y1pEvBf4ceCZwPMy8/7a9nOBncDFwBRwbWbeWdt3JnOT4G4GZoG3ZebHOnm/jRs3sn///p5/DvWPN9FWj3VWPdZZ9Vhn1RMRp8+H1QPLsdzU7cCLga82bb8BuCszvxW4BrglIurh8c3AVGY+C9gC/H5EbFiGskqSJBWl7y1r9XnR4vR5u7YBF9aesyciDjIX6u4AXgn8bG3fVyLiU8DLmBsZKqki5ps+Rsvv8HR2vLqLymCdqW4gAwwi4mxgJDMfadi8l7kVCqj9/9V59kmqgFZr0WpwHj88w869K3N1l6qyzirpSD8OOsjRoM0jG5qb3nKBfU/taFrBYHx8nMnJye5Lp2Vz/Phx66xiOqmzw9PJF/b15fYNLUHOJo8ffnzQxdAiWGeVNDxhLTO/HhFExMaG1rVnAvtqX+8DLgAa931ynmPtAHbUH09MTKQ3ZFaLN9FWTyd19uiRqZOtAju2XcKGcdebHaTdu3dzxRVXDLoYWgTrrHo2vqM/xx1ky9ptwHXAuyJiM3AecGfTvp+NiAuB7weuHUgpJXVtw/iYq2kM2FljrmhSNdaZ6vo+GjQiboqI/cAE8DcR8aXarrcC3xsRDzE3cODqzHyytu+3gbW1504C12XmN/pdVkmSpNIsx2jQ65hrJWvefhC4cp7XHGVuRKgkSdKKthzzrEmSJGmJDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklQww5okSVLBDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklQww5okSVLBDGuSJEkFM6xJkiQVzLAmSZJUMMOaJElSwQxrkiRJBTOsSZIkFcywJkmSVDDDmiRJUsEMa5IkSQUzrEmSJBXMsCZJklQww5okSVLBDGuSJEkFaxvWImJVRLwtIt4XES9t2ndj/4omSZKkTlrWbgQuBb4I/HZE/E7Dvu/r5s0jYm9E/EtE3Fv798ra9nMj4q8i4qGIuD8iXtzN+0iSJFXVGR0850XApZmZEfEHwEcj4g8y81ogelCGV2Tm/U3bbgDuysytEbEZuD0iLs7MJ3vwfpIkSZXRScvaqsxMgMw8CrwcODci3t/Hcm0Dbqq95x7gIGDrmiRJWnE6CWuPRMRz6w9qrVvbgP8CPL8HZbglIv45Iv4oIjZGxNnASGY+0vCcvcD5PXgvSZKkSolao9n8T5gLascy88sRsbH29ZGIGAVemZkfXvKbR5yfmfsiYhXwbuB5wNXAvswcb3jebcDHM3Nni2NsB7bXH4+Pj2/atWvXUoukATh+/Dhr1qwZdDG0CJ3U2eHp5Mb7ZgC4/vmjnDXWi7smtFR+n1WPdVY9W7duPZCZE70+btuwBhAR1wG/CpwHJPAAsD0z/yYi1mfmY10XJOKbgQcz85si4ihwQb11LSLuBt6SmXe0O87ExETu37+/2+JoGU1OTrJly5ZBF0OL0EmdPXpkimtu3gPAzdds5px1q5ejaJqH32fVY51VT0T0Jax1MnXHzwPXAT/HXNfn2cDbgPdExJXA3y7ljSNiPCLWN2x6NXBP7evbau9JbYDBecCdS3kfSZKkKutkNOibgK2Zua9h2ycj4gvAQ8B7lvjeTwd21bpTA3gY+JnavrcCH4qIh4Bp4GpHgkqSpJWok7A20hTUAMjMvRHxlcx821LeODMfBi6bZ99B4MqlHFeSJGmYdDIadCwiTrvDMSLWdvh6SZIkLVEnYetjzHVJrq9viIgNwE7AYZeSJEl91ElYewdwAtgfEfdExOeAfwWerO2TJElSn7S9Zy0zTwCviYiLgctrm+/JzC/1tWSSJEnqaIABAJn5ZeDLfSyLJEmSmjhAQJIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghnWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSCGdYkSZIKZliTJEkqmGFNkiSpYIY1SZKkghUb1iLiWyPiHyLiwYi4OyKePegySZIkLbdiwxrwh8D7MvPbgN8C/njA5ZEkSVp2Zwy6AK1ExLnA5cCVtU27gN+LiAsyc+9Cr51NePTIVJ9LqF46PJ3WWcV0UmeHjk4vU2kkabgVGdaAbwH+LTOfBMjMjIh9wPnA3oVeeOjoNNfcvKf/JVTPPH54hp17rbMqsc4kafmUGtYAsulxtHpSRGwHttcfn7FuA48ffryf5VKP5WxaZxWzmDo7e02w587djETLb2Etk+PHjzM5OTnoYmgRrDPVRWZzJhq8WjfoQ8DZmflkRATw78AL23WDPmPTRN73xS8vQynVK7t37+aKK64YdDG0CIupsw1njjE6YlAbtMnJSbZs2TLoYmgRrLPqiYgDmTnR6+MW2bKWmf8REfcAPw18APgpYG+7oAYwEnDOutX9LaB66qyxsM4qxjqTpOVTZFir+QXgAxHxduAw8NoBl0eSJGnZFRvWMvOLwIsGXQ5JkqRBKvKetW5ExBTwyKDLoUVZBxwZdCG0KNZZ9Vhn1WOdVc95mdnzhrBiW9aWKjO9kaZiImJ/P27IVP9YZ9VjnVWPdVY9EbG/H8cteQUDSZKkFc+wJkmSVDDDmkqwY9AF0KJZZ9VjnVWPdVY9famzoRtgIEmSNExsWZMkSSqYYU2SJKlghjX1TUSsiYj/NyIejIh7I+KvIuKC2r5za48fioj7I+LFDa87MyI+EhFfqr32Jwf2IVawiHhnRGREPLf22DorVESsjojfq9XNAxHxp7Xt1lmhImJLRHw2Iu6p1c1ra9uts0JExHsjYm/jz8Ha9iXVUUSMRMSNEfHl2v43dFqWoZtnTcV5H/CXmZkR8cba4yuBG4C7MnNrRGwGbo+IizPzSeDNwFRmPisiLgT+MSJ2Z+ahgX2KFSYiLgdeCOxr2GydlesGYBb4ttr32jc3bLfOChMRAXwYuCIz76v9EfsvEfExrLOS3A78FnBn0/al1tFPA88Gvg14GvC5iPhfmfkv7Qpiy5r6JjOPZ+Yn86lRLHcBF9W+3gbcVHveHuAgUP/r5JUN+74CfAp42XKVe6WLiNXMnf83AI0jkKyzAkXEOHAN8Pb691pm/nttt3VWtvW1/88Cvg5MYZ0VIzM/lZmtJrldah29EviDzJzJzG8AtwKv6qQstqxpOb0J+HhEnA2MZGbjsmB7gfNrX58PfHWefeq/Xwf+NDO/MtcAANZZ0S5m7hf9OyLih4BjwLuAe7HOilRr/dwGfCwijgIbgJ8EvgnrrGhd/ixste8FnbyvLWtaFhHxduBbgV+tbWqeMyaaHucC+9QnEfEiYDPw+y12W2dlWsVci/UXMvMFwBuBjzL3x7h1VqCIOAP4FeBlmflM4CXAB2u7rbPydVNHS6o/w5r6LiLezNxfjT+cmU9k5tdr2zc2PO2ZPHV/1D7ggnn2qb++H/gO4CsRsReYACaB7wbrrFBfZe5+tVsAMvPzwFeA7wTrrFCXAs/IzE/Dya60fwOeD9ZZybr8/bXk+jOsqa8iYjvwauC/ZeZjDbtuA66rPWczcB5P3cTZuO9C5gLE/1ymIq9omXlDZj4jMy/IzAuA/cCWzPxLrLMiZeajwN8CWwAi4pnAhcAXsc5K9a/ARER8O0BEPIu57uwHsc6qYKl1dBvwCxExGhH/hbl72P6skzd0BQP1TURMMPdD6WHgP2ubpzLzeyLi6cCHmPulMg28ITP/rva6ceBPgO9irsXg7Zl5+3KXX1BrXXtpZt5vnZUrIi5i7vyfDcwAv5aZ/8M6K1dEvBp4O3PnPoD/npkftc7KERE3MTc44DzgUeBIbZTnkuooIkaB9wJba2/xO5n5ex2VxbAmSZJULrtBJUmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgrmclOS+i4i7q19OcbcIsb31x5/sfbvgczsaL6hLsrwCeDXM/OfmrZfy1ProK4GPpuZV/WzLO3UFvb+TGaeM8hySCqDYU1S32XmpXBKCLl0Od8/ItYxN6P/3U3bXwC8GfjuzPxGzC2Getlylk2S2rEbVNJARcQHIuKNta/fFREfiYi/iIgvRcStEXFZRPyviHg4InY0vO682v67I+K+iPj1Bd7mh4G/ytMnlvwW4HHgMMwtsJ2Zn2t4j8219/5MRHwuIn6qYd+PRsSeiPh8RNwbEd9T27619tz7IuLvIuLZte0/UHve79de80AtLNaPd13tM/898LqG7Rsj4q8j4p9rx7x58WdZUpXZsiapNC+o/TsCfA64gbmwdQZza5b+QWY+yNzC17+RmZ+qLYz9FxHx8sz8Hy2O+XLgAy22TwK/BPxrRPwdc0vG3JKZhyJiPfCHwI9m5r9HxDnAZyPi08BZwB8D/zUzH4yIVcCZEXEu8KfAFZn5zxFxFXAr8Nza+z0HeF1mvqHW/fobwJaIeD7wq8BlmXkwIn6/oYw/DezNzCsBasvUSFpBbFmTVJrJzHw8M2eA+4D/LzOnMvMoc/e3XVRb0uUHgffW7of7DPAs5hahP0UtSH0vsLt5X2Y+AfwfwI8A/wD8JHBfLRB9L3AR8Je19/gb5pYF+nbgvwGfrIVGMvNEZj4OfA9wb2b+c237LcytAfnNtbf8YmZ+pvb1PzK3HiTADwCfyMyDtcfvayjmXcDWiHhPRPw4cLSDcyhpiNiyJqk0xxu+nmnx+Azm/tBMYHNmnmhzvB8EPj3f82pdo/cA90TEjcAXmAtPU8B9mflfm18TEc9t3lbfVSvXaW9T+7/VZ6m/rqXM/MeIuBT4IeCngHdHxGW1MCtpBbBlTVLlZOZ/An8PvK2+LSKeERETLZ7+E0CrrlEi4jtqXZB13wJsBB5mrqXtWyPiBxuef2lEjDHXffrDEfFtte2rIuJpzLWWXRoR31nb/ipgf2Z+rc1H2g38SK0bFeDnGt7zQuYWkL4VuJ650bTr2hxP0hCxZU1SVV0F7IiIf649PgJcC+yvP6E2unML8MvzHONM4Hci4jzgGHMtXG/LzHtrr/8x4Lcj4neAVcA+4Ccy80sR8XPAR2rdrDPAL2Tm3RFxNXBLRIwCjwHb2n2QzLwvIv478A8R8TXgEw27fwDYHhEzwCjwy7UuV0krRJw+OEqShkNEvBB4R2a+dNBlkaSlMqxJkiQVzHvWJEmSCmZYkyRJKphhTZIkqWCGNUmSpIIZ1iRJkgpmWJMkSSqYYU2SJKlghjVJkqSC/f+TuozQJqhbtwAAAABJRU5ErkJggg==\n",
"text/plain": [
"