{ "cells": [ { "cell_type": "markdown", "metadata": {}, "source": [ "\n", "*This notebook contains material from [cbe30338-2021](https://jckantor.github.io/cbe30338-2021);\n", "content is available [on Github](https://github.com/jckantor/cbe30338-2021.git).*\n" ] }, { "cell_type": "markdown", "metadata": {}, "source": [ "\n", "< [3.9 Lab Assignment 4: Solution](https://jckantor.github.io/cbe30338-2021/03.09-Lab-Assignment-Solution.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.1 Data/Process/Operational Historian](https://jckantor.github.io/cbe30338-2021/04.01-Process-Historians.html) >

\"Open

\"Download\"" ] }, { "cell_type": "markdown", "metadata": { "nbpages": { "level": 1, "link": "[4.0 Process Analytics](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0-Process-Analytics)", "section": "4.0 Process Analytics" } }, "source": [ "# 4.0 Process Analytics" ] }, { "cell_type": "markdown", "metadata": { "nbpages": { "level": 2, "link": "[4.0.1 Learning Goals](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0.1-Learning-Goals)", "section": "4.0.1 Learning Goals" } }, "source": [ "## 4.0.1 Learning Goals" ] }, { "cell_type": "markdown", "metadata": { "nbpages": { "level": 3, "link": "[4.0.1.1 Process Historians](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0.1.1-Process-Historians)", "section": "4.0.1.1 Process Historians" } }, "source": [ "### 4.0.1.1 Process Historians\n", "\n", "**Process historians** are widely used throughout the process industries. The core function is to record and provide access to **time series data** for **process tags**.\n", "\n", "The tclab library includes the basic functions of a process historian implemented using `SQLite`, a widely used database for web applications and internet connected devices.\n", "\n", "* An instance of the tclab historian requires a list of **data sources**. There is no limit on the number of data sources.\n", "* The default data sources record T1, T2, Q1, and Q2\n", "* Each data source consists of **(tag, function) pair**, where the **tag** is a string that uniquely identifies a time series, and **function**, with no arguments, returns the current value of the tag.\n", "* The tclab historian always records time with the tag \"Time\"\n", "* Data from the historian can be stored in .csv files, converted to Pandas data frames, or accessed directly from the historian data log.\n", "\n", "What you should be able to do:\n", "\n", "* Read a list of data sources, and describe what data is recorded.\n", "* Add a tag and a function to a list of data sources.\n", "* Save data from the historian to a .csv file, then load the saved data for analysis.\n", "\n", "

\n", "\n", "**Study Question.** The following list of data sources has been specified for the tclab historian. `lab.T1` and `lab.T1` are current values of temperatures T1 and T2.\n", "\n", " `sources = [[\"T1\", lambda: lab.T1], [\"T_ave\", lambda: (lab.T1 + lab.T1)/2], [\"T2\", lab.T2]]`\n", " \n", "* How many sources are specifiied?\n", "* One of these specification will result in an error. Which one. What is wrong? How would you fix it?\n", "* Explain what is being done with the second data source.\n", "* `lab.Q2` is a function defined so that executinig `lab.Q2()` returns a value. Specify a data source incorporating this function.\n", " \n", "**Study Question.** Suppose you've written a novel control algorithm. The algorithm generates a floating point value that is denoted by the Python variable `y_est`. Given a list of data sources `sources`, add a source for this quantity with the tag \"Y_EST\".\n", "\n", "**Study Question.** Suppose you have implemented a contrrol algorithm for a bioreactor application that utilizes a state space model. The state vector `x` has two elements representing temperature T and concentration C. Create a list of sources for the historian to record this data with tags \"T\" and \"C\".\n", "\n", "
" ] }, { "cell_type": "markdown", "metadata": { "nbpages": { "level": 3, "link": "[4.0.1.2 State-Space Models](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0.1.2-State-Space-Models)", "section": "4.0.1.2 State-Space Models" } }, "source": [ "### 4.0.1.2 State-Space Models\n", "\n", "A linear state-space model is written in the form\n", "\n", "\\begin{align}\n", "\\frac{dx}{dt} & = A x + B_u u + B_d d \\\\\n", "y & = C x\n", "\\end{align}\n", "\n", "where $x$ is the **state vector** with $n$ elements, $u$ is a vector of manipulable inputs, $d$ is a vector of disturbance inputs, and $y$ is a vector of process measurements. \n", "\n", "* A state-space system is stable if all eigenvalues have negative real parts. \n", "* If any eigenvalue has a positive real part, then the system is unstable.\n", "* Eigenvalues can be computed with `eigenvalues, _ = np.linalg.eig(A)`\n", "* The negative inverse of an eigenvalue corresponds to a system time constant.\n", "\n", "What you should be able to do:\n", "\n", "* Convert systems of linear differential equations into state-space form, identifying all relevant vectors and matrices.\n", "* For a given problem, determine if the vectors and matrices are of compatiable dimensions.\n", "* Compute eigenvalues and determine stability.\n", "* Simulate the response of a state-space model to inputs and disturbances.\n", "\n", "
\n", "\n", "**Study Question.** Suppose $x$ has five elements, $u$ has two elements, and $d$ has 1 element, and there is one process measurement. What are the dimensions of matrices $A$, $B_u$, $B_d$, and $C$?\n", "\n", "**Study Question.** Someone has proposed a different model a temperature control device that includes heat transfer to the surround assembly. The model is written\n", "\n", "\\begin{align}\n", "C_{p,1}\\frac{dT_1}{dt} & = U_a(T_2 - T_1) + Q_1 \\\\\n", "C_{p,2}\\frac{dT_2}{dt} & = U_a(T_1 - T_2) + U_b(T_{amb} - T_2)\n", "\\end{align}\n", "\n", "where $Q_1$ is the manipulable input, $T_2$ is measured, and $T_{amb}$ is an unmeasured external disturbance.\n", "\n", "* Rewrite this model in state space form. Identify the components of $x$, $u$, $d$, and $y$. Write out matrices $A$, $B_u$, $B_d$, and $C$ specifying all of the coefficients.\n", "* What are the units of $Q_1$ in this model?\n", "\n", "
" ] }, { "cell_type": "markdown", "metadata": { "nbpages": { "level": 3, "link": "[4.0.1.3 State Estimation](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0.1.3-State-Estimation)", "section": "4.0.1.3 State Estimation" } }, "source": [ "### 4.0.1.3 State Estimation\n", "\n", "State estimation is a form of real-time process analytics employed in control systems. State estimation combines process models with real-time process measurements to provide estimates of process variables that may not be directly measureable.\n", "\n", "At each time step $t_k$ there are two calculations to perform:\n", "\n", "* **Model Prediction:** Use the model to update the state to the next time step, i.e., $\\hat{x}_{k-1} \\rightarrow \\hat{x}_{k}^{pred}$ with the equation\n", "\n", "\\begin{align}\n", "\\hat{x}_k^{pred} & = \\hat{x}_{k-1} + (t_k - t_{k-1}) ( A \\hat{x}_{k-1} + B_u u_{k-1} + B_d \\hat{d}_{k-1}) \\\\\n", "\\hat{y}_k^{pred} & = C \\hat{x}_k^{pred}\n", "\\end{align}\n", "\n", "* **Measurement Correction:** Use measurement $y_k$ to update $\\hat{x}_{k}^{pred} \\rightarrow \\hat{x}_{k}$ with the equation\n", "\n", "$$\\hat{x}_{k} = \\hat{x}_{k}^{pred} - (t_k - t_{k-1})L (\\hat{y}_{k}^{pred} - y_k)$$ \n", "\n", "$L$ is a matrix of observer gains.\n", "\n", "The estimation error is given by $e = \\hat{x} - {x}$ which satisfies the differential equations\n", "\n", "\\begin{align}\n", "\\frac{de}{dt} & = (A - LC) e + B_d (\\hat{d}-d)\n", "\\end{align}\n", "\n", "where $d$ is the unmeasured disturbance, and $\\hat{d}$ is an apriori estimate of $d$. If the estimate is accurate, then $d = \\hat{d}$.\n", "\n", "
\n", "\n", "**Study Question.** For a system with 2 states and 1 measurement, what is the dimension of the matrix $L$? \n", "\n", "**Study Question.** For the same system, what is the dimension of the product $LC$?\n", "\n", "**Study Question.** Suppose you are given numerical values for $A$, $L$, and $C$, how could you determine if the observer will be stable?\n", "\n", "**Study Question.** The following charts test the performance of two different observers for the same system consisting of a single heater/sensor assembly. 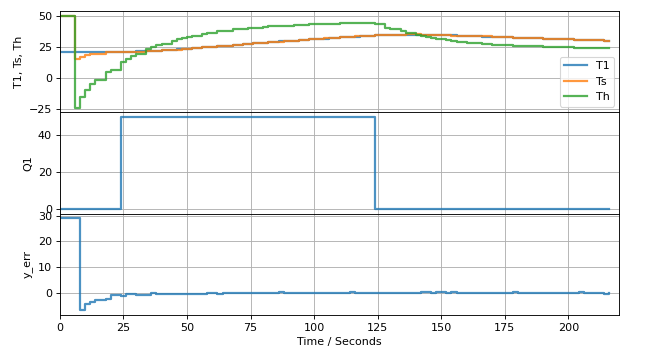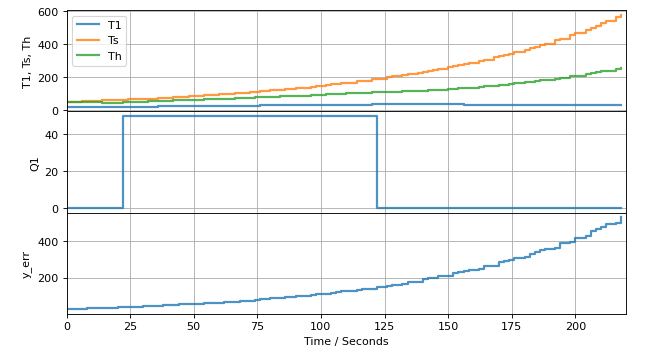T1 is the measured temperature, Ts is the estimated sensor temperature, Th is the estimated heater temperature.\n", "\n", "![](./figures/state_estimation_1.png)\n", "\n", "![](./figures/state_estimation_2.png)\n", "\n", "* Which of these is showing the useful result? Be sure you can explain why one is acceptable and one is not.\n", "* For the one that is not performing, what has gone wrong? How you propose to fix the problem?\n", "* Data for A, L, and C are available. What calculation would you perform to verify your analysis? What calculation would you perform to remedy the problem? Be sure you can write out the code (no more than five lines required) to do these calculations.\n", "\n", "
" ] }, { "cell_type": "code", "execution_count": null, "metadata": { "nbpages": { "level": 3, "link": "[4.0.1.3 State Estimation](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0.1.3-State-Estimation)", "section": "4.0.1.3 State Estimation" } }, "outputs": [], "source": [] }, { "cell_type": "code", "execution_count": null, "metadata": { "nbpages": { "level": 3, "link": "[4.0.1.3 State Estimation](https://jckantor.github.io/cbe30338-2021/04.00-Process-Analytics.html#4.0.1.3-State-Estimation)", "section": "4.0.1.3 State Estimation" } }, "outputs": [], "source": [] }, { "cell_type": "markdown", "metadata": {}, "source": [ "\n", "< [3.9 Lab Assignment 4: Solution](https://jckantor.github.io/cbe30338-2021/03.09-Lab-Assignment-Solution.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [4.1 Data/Process/Operational Historian](https://jckantor.github.io/cbe30338-2021/04.01-Process-Historians.html) >

\"Open

\"Download\"" ] } ], "metadata": { "kernelspec": { "display_name": "Python 3", "language": "python", "name": "python3" }, "language_info": { "codemirror_mode": { "name": "ipython", "version": 3 }, "file_extension": ".py", "mimetype": "text/x-python", "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", "version": "3.8.5" } }, "nbformat": 4, "nbformat_minor": 4 }