{
 "cells": [
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<!--NOTEBOOK_HEADER-->\n",
    "*This notebook contains material from [cbe30338-2021](https://jckantor.github.io/cbe30338-2021);\n",
    "content is available [on Github](https://github.com/jckantor/cbe30338-2021.git).*\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<!--NAVIGATION-->\n",
    "< [7.4 Batch Chemical Process](https://jckantor.github.io/cbe30338-2021/07.04-Project-Batch-Chemical-Process.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [8.0 Projects](https://jckantor.github.io/cbe30338-2021/08.00-Projects.html) ><p><a href=\"https://colab.research.google.com/github/jckantor/cbe30338-2021/blob/master/docs/07.05-Queuing-Systems-and-Poisson-Processes.ipynb\"> <img align=\"left\" src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open in Colab\" title=\"Open in Google Colaboratory\"></a><p><a href=\"https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.ipynb\"> <img align=\"left\" src=\"https://img.shields.io/badge/Github-Download-blue.svg\" alt=\"Download\" title=\"Download Notebook\"></a>"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 1,
     "link": "[7.5 Simulating Queuing Systems](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5-Simulating-Queuing-Systems)",
     "section": "7.5 Simulating Queuing Systems"
    }
   },
   "source": [
    "# 7.5 Simulating Queuing Systems\n",
    "\n",
    "Queuing theory is one of the foundations for the analysis of discrete-event systems. This notebook introduces the nomenclature and terminology of queuing theory that will be used in later applications."
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.1 Examples of Queues](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.1-Examples-of-Queues)",
     "section": "7.5.1 Examples of Queues"
    }
   },
   "source": [
    "## 7.5.1 Examples of Queues\n",
    "\n",
    "### Manufacturing Lines"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 109,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.1 Examples of Queues](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.1-Examples-of-Queues)",
     "section": "7.5.1 Examples of Queues"
    }
   },
   "outputs": [
    {
     "data": {
      "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wCEABALDBoYFhsaGRoeHRsfIicmIiIiIyctLScnLycxMC0nLS01PVBCNThLOS0tRWFFS1NWW1xbMkFlbWVYbFBZW1cBERISFxUXJRUVJVc2LTZXV2RXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV1dXV//AABEIAWgB4AMBIgACEQEDEQH/xAAbAAACAwEBAQAAAAAAAAAAAAAAAwECBAUGB//EAEcQAAEDAQUECAMFBgUCBgMAAAEAAhEDBBIhMUEFUWFxBhMigZGhsdEUMsFCUnLh8BUjM2KCshYkNHPxktJDY4Ois+JTVJP/xAAWAQEBAQAAAAAAAAAAAAAAAAAAAQL/xAAWEQEBAQAAAAAAAAAAAAAAAAAAARH/2gAMAwEAAhEDEQA/APn6EIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCEIQCFp+Bdvb5qfgX72+fsgyoWr4F+9vmo+Bfvb5oMyFqFhfvb5+yj4J28eaDMhaPg3cPNAsbt480GdC1fAP3t8/ZV+Cdvb5oM6Fo+Ddvb4lHwT+HigzoWoWB8Ey3DioFidMS3zQZkLSbC8GJHmg2F41b5oMyFp+Cdvb5q42c8tDpbBmMTp3IMaFqbYHkxLe8n2VjsyoDEt8T7IMaFrGz3kgS3Hn7J79iVWgS5mPE+yDmoW79lVInsx3+yodnP3t8/ZBkQtPwL5jDzQLE7ePFBmQtIsTjOLYGuMKosrt480CELU2wuJgFs9/spOznjVvn7IMiFtGzH44tw4n2Sn2NwOJCDOhbKWznuAxaJJAknGO5UNieM480GZC2s2VVcwOABBN0AZuOMwOEKKezKrgHAdkmL0OuzumEGNC2fs2pdLsLoN0mdeWap8E7ePNBmQtXwD97fNL+FdwQJQnCzHeEfDO4IEoTvhjvCn4V28IEIT/hXbwpFkO9vn7IM6Fp+Cdvb4qpsrt480CEJvw54Kxsrt4QIQtdLZ1R2QEbyr/smpMS3xPsgwoW87JqD7TPE+yS+xFubmdxPsgzIT2WVx1HmpdZHATLfP2QZ0JvUHgo6k8EC0JnUngjqTwQdaEsghSyomIIBCgncpjcgoJaoDU6lQmmXCM9+UZ/RLYoaqVSExwVYwVENKCEKQoFuGBS6WafUGBSMiBxQaWnsn1VC5WPyOKoDIlUMIkSn0rFVqtLmU3vaMy1sx4YrNTOH6/WafTr1WQab3MIzLSQfJRRRBa8OGbCHQRuM4rvjbNCpVY6rSplgvSHUs7xnS9MRhzXnqpJwxN4y9x1KGNLpw1CD0Nl+AqN7VIB/aiKlwglziMHEAwIVH2OibP1jnOa9rOzEEE3jDTE6EY4LgvY6TgVZ5h06YyiLWaneqjgnbQfevDRpAU7P7LXPdgACUp5kPMRLp/NAh7y0CCQqtruGOBUPaDqrOAIaBGA35nU/TuQW+KH2mDuV2U2PkhpCW2leIJmfVa5gIM9ayTEEgDRLNnMrV1hKgvmcUUuzUYM6prh2hyKyvqOBwUtruz3Ko0krJXwOAmVop2iTBEqsS+8RAbJ8MvNAuuQCG/c3b8z5plZgqN6xueThx3rNEklybZat1wzg4OGhCBthttWzva+mcWyRMESRBMHgtFj2i4GqwgXK2JY2Q1r5kOA4RH/AAstakWnAgtOXJFmBvskb/RBelaGll14/hlxZA+ZznAm8c4ACraK198nDcJJgSYEnHxS6rCIJEB0xxxiUs5YoJOOXmqkaqzslQEKCGiSqmnuTWBVeVQtzVUhdH9l17nWPY5lM5Oc1wB4TGZ0SalB7BeumJi9m08nDAoMwYftYD9aLTYnUDVb15eKepaJPcEgtJ4laqOyqj9IHHPwQVtjqV9xoXhTns3s44pLAX4Bt7kuzT2VTYP3hnh+QTusYwQxvj7IOU3ZxDb7hAGn5q1Gi28J7ytdZznjU+iy2hj2kAggkTxhBqqWprcgBzxKw1reSLwk80ohZw7shvmgmpVc4El0cEtjgAMMeKh7DCBuOaCTUJw9Fd/yJYzTKnyBAoHTeqwpDHboVnNGZM8kC1YAnIK16Mm+KA4kjFA9jZJ7lbEIoiHOHJMcEENdKkhLLYVm1EEt3K4EKAJUzjBQTEgpRwT2pdYZIFc1IhSW4DiFVwkhBZR1Y70BueKXiMioG1D2TujFKpxkJQ5x1UMInAGVQ2mBESpDiBpIwUCGuIOuERqh7ZEIBgfGvqtNnfDSX4Y6rO6icA2IHFOtUhoZTBN3IjNxxkqDVhAOEHI70m1vhsDMpdnvvbcdIIJu3siYyVKsEmN6K6LWjqQDkfRUuiIhJtFrIcxrJENEwcORTH9c1jKjm/u34NMNIPhiMkRQ2NuJBOPJLFmAOc9yeahIyA5KhdHNAPAj0hR1bjJGme4fmr02D5nuut1Op4BNfVaRDSIGgnDxQZ20zOWK0s2c92YgcVusNl+27PQbuK1q4a4NqsjmOIDXEaGOCylu8L1YZeBMYBecrV5qkwImAO9UIp0xu8Ew09xPenFgnDBQ6ZwjkoFmzuiS0kHW7gk9WP0VobXrN+VxA3A4eCv8dUM32tcB95qBNN4DS0ic44Sqsi+x0jiNxjMc08VaZEupQJjsujHkpbSpOOFRzcftNmPBBhMlw7MCVUjA/iWy0ULmT2uByIkSk90qBEYBQ3PgmuYDmpwAVCp3rRYq1Sm8PpDtDKWg9+OCtTswIkkAHuW+jZGAZz3oN9k6Q1nO6yuzrS0G4PlaD94j8tSq7SAtBvPa1pmcAG90D6kpBqNbgIHJZ6toAzIH63INDOqpiGMnicFV1qJwB7gsge57HvaAWsi8XOAzygTisT65cYmQNNEG+rXaPmcO7ErO63tGIZPMrHUEgKgIyOSBtW1vqGSYjKNFqtFoaWhxr1Hvu3cQctxMrnEQDzVQHaZcUGtjQSJN0ESCcjvCz2m7IuGd6ljAddMtO5UiNPFAkTOCeym9xAiSchEnwCgvn8lFOo5hvMcWne0kHxCBlagaZIe0tIiQQQfBRUm42FWpUc7FziScyTJPeprNN1sIEyTmpYNO9SJ1IVhGaBTippg3hhqrERlClklwQa2Uw3LVWIRKJQQquZKuiECgSMCmgyN6gtlUukZIGZKtR0wrMeCqVMEEvODeQVAMQrDRDcx+tFFQREqkJ7h6JJaqiCCimDeEhRcd+ir0w6ccuaAtDu0TE4ptKHEZDBLqOIcRBInOFag8EkGZjCMMVBor0m04F9r7wkFhvADwCReETOuversDSRJI0UOptjBBamZGaZZqN97tAFQUwBH6yKbZnXWE6uKBOLiTvKY2mM9d6GMAGGSHOnLL9ZIBx3K7acC84Z5N1PE8EXQwSfm0bu4lWsllqV3XWYuOJcTg0fecdAqBrC8xF5x8ANw3BbbBYYh7hhoN/FarJQptFxvab9qocL/Bu5vqn2mqRg0SgTUrFuWa5lfaTmmBJcuzsoCveIElpjvT39G62csM6GR6hVHO2fWqus4xMkmXYEn2WdlgFOo14JvNIcJjMGV0mbFtVPFrP+hwPlKXVo2hvzMqDmz8lFdmy2ttXC007OCci4Bs+Mp7tiWSoJFIf+m/815CpRcTi4zxVGWYtktMO3gwg9PW6JUT8tSozmAViq9EKo+Sqx3OQuXSttrpfLXqcrxPqt46VWmmMf3h4tAHkgz1ujNqb/4V4fykFYK9gqswfSe2N7SvTWDpVWqEB1mn8LvoV0H9IKLXAVCWHVuDo5xkg8Dd7L9YA7sVezGgboeQx0wXdozjmdF6bb9to17PWNNmLbnaugEy8d68JWPaKD0NZtlPZpk1Dq4uujzzWSpYW/eC41/irNqkaoNzrMB9r9ckVrP1cfvGmcolZm2x4wnDdA81ovhzZ1g4FAxlCu5pLWuc3Utx8YWV9MyZkHcfzWik+o0fu6jm6wCQtDbdaB8zg8bnAFBzbsODhEjKUszuK7fxNJwirZqZ/mYXNPlgoFkszwSKrqXBxafzQceoDdbjCrlvK11KGJh2SWaR4FAouwyVDz8U/qePckOZBhAMGeOihpgQRKvTMSYBjQ5HmqufJJgCdAgr1U5Hu1VT2d8qysXA/N46/mgqTlor2mYZyUPZkRiN6ZaPs8kGVrJUXSnAblQoIGI5K1MYqGjFXZmg1QoTFBagoFYFRCAgvCiFIKsFAp9MZ5JNRxjFay1ZqwQDTgrat5fRVbgFLXSWwirwcJBG7ik3TKeXEgAnIEBKzAREGZ8VLAZxwV61K64iMpShPFBPWdqArg4wEtjTemP1KYSNBiinU+2+DpPkFfqwMOycTkQVlbVId2dZC0CMImUFjERCkDwCjLEqILjAHdu4lEBJcYHcN6aW3BmC4+XJTgwQMXHM/RbNm7LdXN5xLaQMF0YuP3WjU+QVGew2B9odndY353nJvudwXWqFjWdTSBFKe1veR94/TILTbKrabBRpgNjQfZ346uOp9FyG03aNnkg1vrgQttlsTq9KWtknfpil2OxtewS5rXa3zCcNjm9LHUj+GpiiF/4frU8WMAx+y6PZT8PbWfK+0Dk696ytIsVrb8pq9zyfqpNS2NzdU/qaD6hFZ/2hbWfNUJ/3KTfoAmM29WGbKR5Xm+hV/wBpWludzvpkehCP2u4/PQpPPMj1BQX/AG6D89nnk5rv7goO0LC756Dxxuf9qSdp2bEVLNdPAg+gCw2m2WcA9XTeJ3nL1lB1alDZ7myHuZ3kf3Bc60WazMBu1i47gAfE4BcvrHPIOLtxIy5JtmswqvDXVLo8DyxQTaLULt0PLRubAWUOnstOH4QPNeib0fbdBptbO9xJJ70h3R6q04Mg6XXCfNBWz7IPVvY589ZdmBlBkQSuRaujNYEm5Uj8BPou9SZbaWAdVgb2h30Uja1rYZJpndepwfJB5Gpsao3OJ3EEJDtn1R9ieRBXuh0kqj+JRY/8LiPIpTukdmP8Wxxyuk+gVHhjZagzY4f0ld1lZrbB1AY4PvX3OMQc+E7l2xtXZb82VKZPB30JWW0VLA512nUqY4AASORkBQatmbSsHwtKnXuB7WgG9TOf4oWynsrZto/hPZP/AJdT6FeJtLgakBpAGEFZ2hB7S3dFqLAbtZzfxgEeOC87b7JTpgjraVT8Ek+iwyTMkkA4SVR54oL474Ul4VqVne8dlshOOz6gaXOgAc0CxTDwC3PJZK7cdxC02eoWP4HApm0aUgPGmBQc+Oy5KC1Na2DiUAMGQB5lBlTGMJyCbef9lrR3KDeOZhBTqXTOUKaovHdAUFmPzKpIB1KgsGtAzKRKcHn7qJO5FJawnIFXbqrk8VSVUa0SpQgJUwohEIJuohSCrAqKrKW/GFD3kOOoUBwdzCIsaQ3JbxiIwKdolsE47kFes0OBUN0VbUMAimQGiTjKo2bQcDVcRkTh4JDW9lx3e491Wq/tZyN/cmsxo1Md2n63KKreEDELO6S+ArMbJEJzacYjPXigsykAScymTCre8VLGTJOA1P0CIljC4/XQJpIaIb3neq9ZhAED9ZrtbJ2MSQ+q2dW0zu+8/hwzPLFAnZWyDVh9QG4flaMC/wBm8fCV1do28UAKdMjrIiRgGN+60afop20Le2h+7YZruHgNCd3ALyxrNLrznA49rGSqN1CmXEQDBOa69j2e6mSQwVA6JBe36FY7LtSysAAkDcabSP7lpG1LKdWf/wA6g/tRG51Aa2R39L3KjqNLWjXb5+oSWbQsv3qY76o9Qru2lQAkVcP5av0iUB1VGcHVW82j3V+sY0SLU9o5OHoVzLR0h7JDH1Qd7jMLPRZXtbTFaRORGfcEHTqbWLGki03+Un1XOqbWtNSboB4hgPmtdl2E26RUDidTD4z0AXQs1jFJt0Xbskw5tX2QcKwWGrXc6+67EfZkmVtbsao1zTccQDPy5rpllMfZpY/zvHqlvq026NH4a4+qAqUmuLS+lVBH3QPDJUdSs+vXt5hpWettxjCQ0VyN7aoIWC0dKKl2KTqgO95add0IOmbJZtKpHOn7KOupMMNt7WkaFz2rh1tt2pwkPBn/AMtkg7sly6t5ziXzeOJnNVXsxb6jQXNtVJ4G514+i5to6V2phhwpuBylpHoVzaGxLQGdaBcbEzjksxa+q66+cDjhlxUHSr9KHPEdRQB+8WyfNciraDUMnPwXqR0Sp9T1jTfkSMTiPdec/Z5a43nsaBqTmEGenSc49lpPIJpYaZh3ZK9h0XfZ3s6k3H1G4ggZj3Sek+yGgio1stOm535oPL1D1rb/ANtuDuI0cu7ZOiZeAb16QDM4HiFxmW9jT2aDRoZOK9X0c2ped1RjK9SjVureaDze19lGhULbv5jes9PZdRwnsgcSvd9ItnCvRvtEvYJHFuoXzuuwhxBngg9b0auNPUvLHuzbkeYXprTYadSk5l1oDhoF8vslZ1Oo17cHNxC+mbKt7a9Jrx9oZbjqEHzu10TZ6rmPYCWmMfJMp121RF27oQvS9MdmXmiu0YjB3LevFU6hY8Hx5IFVgabiCq9YSJkeS37Roh7LwzHouVc7MaoGB0ziSrABVpNhpxTSwxIKiqU3SYjBUN6dArURePJJMYoGnmqkDUqGjEKCqg7PEqZb93zVApQbFTrRMcYTrqQSL0Rr9EDUSie1HCVN1QSCpUQiECnjEqKXzFWfmq0z2igel1CGM4BXlVtDoYSDHdKDNVAqBsOAx1wHjoksa4ObeBGREjMbxvCvdFwai9hBjTSVFNkO1zwvCFQAg/8AKdTGBALgDnxSqFAziI/Wi2NbCCGtjAKcuakIbEiRI3KKsxmpmPMqCScPABbarbzgAIbHgunsPZwvXs3aO3fhG/j/AMionY2xywh9QTU0acmc97uGmu5bdq7XZZf3bCHV3Zzjcn7Tv5uCz7a222gOpoQagwLtG8t7vTmvLgT2nEknEk5nvQb6Dx1jqr3znJJxM7lhe0yYYInDGfFXJacwfFUcBoEEXTq3zV2ZjmpFMlxw3p9Cx1CcGk3cTAJjnGSBIcFakL056Zg711qPR2s513q4dF4AuAkcFpGyKVOm2pUrMDZ7bB2XAZHPUboQcAWd+notFKwueYBnPBoJJ8F27Ra9nUHsNMiuMnt7TuTgcp4JVs6U0xUY+zUCxzcMYAc3cQECDYKlnZeeyoxmPzGJMbgsJt7wezWfhucYWm39K7TWaWxTY06BsnxJXMFjcAe1nnARWk7Uqlv8Z5B3uKW22OLHXsYjTFUp2UGJJIAJUNALHAwMUR1X7CJsra9KpfB3acDuWnYWy7PaKb2Ejr2zhMzyWXYG1RZnXHS6i/B4iY0vLZtfZ7rLVbabPl8wIyPvxQZbG5lhtEVQS12BBbkJz5hdTpBsppAr0mhzSMIOGPHcdE22UGbRs3XMEVAO0NQY/XMLL0a2jdJsVo+U4Mnf932QM6L7aaT8LVAAdgzdxYVn6Q7NfQdepfIcYzkbjyWTpDsl1CqXtmJmR5OXodi28W+zmlVwqtGPHc8fVBh6LbZg9TUPZd8s/Zdu5FT0q2NI6xgz8ju5FcLaVhdZa5wN0nEDT9Zr2GxdoNtVE06mLgIP8w0cg+f2W0voVW1GGHsM+4K+l2S0U7bZg4YteII+6dR3Lxe3dlmz1w+CRIJ4jQrZ0Z2mKdVwypPOPA5AoOZtzZxo1TI5/Q96zbOtLmuaGmHA3mHc7d3r3u39nCtSLgJc0eI3LwNaxkRcBJB08ig+j7Ltra9Jrx9rMbnatXkelGyuqqlzR2XYt+oWjo7a306gDwQ2r838rxk7vXptp2MWmg5v2hiODgg+Yhq73RPaPVVepcYa/wCUnR4y8VzKtlcHlsY7vort2fUBBkAjHNB9JextVha4YOEEL5ltuwGhWcwjI4cRove7GtvWMF4i9k6PvRn3j0WLpds3rKXWtHaZnxag8dYawLbp/QWG0Uix5b4clqoNF7F92E7aFK80OaQS3UbkHMuujBqCxxTAJ3ouhAtjYyy1O9ZyIK1hg3IIA0UCWhUK1QNymFRharLWs9XNQaA1WYwKArtOComFKhSgmFMKAVIUCXiSqU29s8kxxxVaf8TuQOuJFsb+7d3eq0pFt/hO/WqDnP8A4Q/F9FNny70H+EPxIon1VDrCcDzWoLLY8nLSgs4Sr0acmNEvVbrIABioqXHq4Oe8cFvrbWDaFykSHH5nDAgHQFc7aF4gNDXRqYw4CVkslkv1mMMtLjdk8VUXIDaWgJ4SYHv9Ex1Z1JrYpFl4YE/MdCQ4jLkqCoKdU0Xi+0PLccMQYk+0rc19F2Lqci6SJJOWnkgx2agxzb76zKYByN4k8QAMloZ8G04uq1T/ACtDR5mU5tei2k5/VAQYgR4pmz7RTqPgsAwkHdCCrNphg/dWNojJzy55nfkl1ekNqMAPFOJgNZEA5jGcOCe/aTZ7LHOG9PfUD2gOYMRkcSEHGaa9fC+94bvfg0HDU4LdQ6MWki9FMTvd+S9DsCz0DMUx1oxkjTgtm09rWezQKjsdwEn8kHlv8K2kEGaZ5OPsuftHZtagR1jDdEi+MWnExivTs6ZWWYuVY5N/7l0rHtWzWqWscDIxY4QSNcDmqPnZpYgb11647Pel9Iuqp2vq6Mw0gOnIExgPJNq5KDFZqsvqNwkDfpqe7BOpFnVVGx2gBddObpzjlKo2zBrr7cHBZrG7sneiiDvXotgbSF34auZY75CfsncuGrNbJgCSojstnZ9ploJY7MTgRw+iftywU3htopAOBxwMRquZb75Yxzy48ycFzalrqNljaj2t+6CYx4Kj2VhtYttnNOrAqN138foVwGOqWWvLGtaWnCScd4KwWXaD6bOrYMScImZO6Eu3Cvfa+s14OEX5xjmqPcW5tO2We+0dsDI+beYXnLHWdQfevMD2mA3KQc1zjtZ4vloLC8aPIg71moV8y7tOccST670H0K0llrs8j5gJbO/Vp9F5F95ji11VrY0IEhRa6zhSD2Pc0EA9lxGnBcynNRxc8lxwxJk+Kg95sDa4ewUnPD3s1BGLd/cuV0hsYp1Q9jiym7UaHULzYphplsg7wSEy45wgvcRuLz6INwq0wcbSTIjMr1WxNqtqMHbDy0Q8jM/dK8FVst3MKLPg4iY70Hp+lNkaXis0ENd83A71wGspbyUu0PIb2SceMrJTqvvhpIg7kHoNlWxlJ5a0kB4unhuPcYXrW28Fl15a4xDjIg7187e1wzCqEG3aNkbSruGbDi0g+SpSqt+UTCyFbadgPZN8YwYhBgfSLHkfZ0VXMlPtbSCJzEjwKWw5IM14gmIhMDHZiMd8qQLriPBMQLh25viVOO4eKvKq45IKkFLdRJOabKEEBMbklgJjckEqUIQCkKFBqAZlBV+aqxvbngodVBdr3oc+BI3KDVA3jxVH0A4EF+axC0u4K9Ou4kDBBop2JgEXie8IGzqX3j4hZ3WlwJGCBaXSBhJQNfZ20wLusziqnIplY4NlLnA/rVUOpNBY86hzYPMH2Wux0wcMyfRZLP8AI/8AEz0culsgTV/od6KDTtWgKNBtUHtFwa4Ey0iCYLTh4JFhdRbXoXaYxfmHEgOJAyOS6HSmiDY2DL943+1y83TvNiHRDpGeeEclRo6Q0g11Q5EVT3zJRsmn1jBOJEjQGDhmVm2lbBUp4lxe50knXimbGrRLdw+qkGsbPqMvtcwuDso0xWeu2rSBqdW6m0y0EjeuvStMZiV07Lsx1dl4xcnBrphyo85TYHVadQkkCnTceLiI+hK2VLTTacXtHMhb7ZsB9QXQwAadW6IxwEHTErnU+h9RsuquuNGQaLzz3BEdLYFtp9f87PkdOI4cVz6tSy1yRVrPBLpLmtwBnLHPPRFp2GaNGrXJc5wAABaBAJgmBquHZcnu+60+P6Ko6O1bDTstQMcx7w4XmuD2gOG8dlLsNVnWNeyg4lhBB66CCPBdOmw2jZNMuaC+i+5MEkMJAwjm3wXAtdEseQRBG8R5IrdtKg+vWdWFO65zrzhfYRPCCpf17GgvoPDRqJjxSKO0sAPhbM6Mz1Zk84K00dpUSYdYqMn7jqjfqoIp1mvwEgxkfoVyrG6CZwjBdWqHGoDZab2k/YkvxGuXqug/ZVWuL9c06FVxiXQARxjD6/QOMHjeFenBmSBIIkzGI4LuWrojcogtrtNQHJwutPAZmVwKFmrOEii4tzvXCMOByQek6L2GKVoe664XYGoyKr0dsdnrWipN1zg115sGIviDiI4YLb0daW2GteEGTnyWHoS3/NWh38p83oFVLIaNsfVZTF1oLWgDUnPhAWuw0xaKpFohzLpgFowdO/NM2raKlC+epe6mSXF7CDHMaZLDW2j1bBVxhwaTvMqjDZ7CTbCAy60BxBc3sg3cM+JWq10atK7LmEOMSGNzP9K5lba1YvcWuhp+w4AjwIXrdkWOlUsrKr6bDUu3pDYxxIwHIIOS6xNrWo0iDcvOBaMBg2RiMsQmbb2FRstIOpggkn7RPqn7JeTa2/zmqXcYkBbOl77tJp559yg8YV6LZvR9tWmx/bkta7MRJnCI4LZUsNE03O6sS0HQaDkuzscf5elgB+7bgOSDwe2G3Khpj7LiJXNbmV3bVRbUtjmFs3nHUiMTuTbRsalTDnXXQASYedOYQYrBsc2mnIeWkuuiGzkAZOOGapb+jrrPFR1QHGIukaHivVdFGMFIlgcAXO+Yg4w3cEvpj/DpjifRB42rXa/Q4LpDYlQ5FvAOmcgfqk2bZlN2ItIEQSDTI7ple22NUFZjqktdJwIBGAwyKI8VaNjVmMLzdgCc/wAlendvNP2oHgvXdJoFkf3BeOsmz6ry17HtIBGBcAYGkFWB23bG1tI1ATJfMH+aJXBLoAPJek6TkiyMnMvE/wDSV5ZjiczqFFOIk3lZSQoQCq5WhVcghCEIJCm/ASTU3JbpOagZ8USJAaBxP0VPiHSNRGgVabAEy6FQphJHaxPEoDDv1nBNuhWAGqBUYpzMioN3cValkVBZvIKtKgGmVcCFZVUSo6sF06oIxVwERFbIJJyKbWOA5pN7mg12Q9ir/R6robEnrj/t1P7SubZT2av9P9y6Oxf4x/26n9hQdbpbe+DZdmesbl+Fy8vSdUgXr8a58M16rpX/AKQR/wDkb6FeSbeJG4cT7oFdXe0kNBTLFVNPFoEkY+KbYWNbUF7EEEeSqxohUPO1rp7TPRel6J7cD6nw7gReBczuzC8hVoyV1ujDbltpH8Q/9pUH0EAaSFBozqUk1FPX4Iht0tyAJ4mPNcna1gZaKRYKTW1NHAZc4gkLpNrb1Aqqjm7I2bVoMfSwAcwlrhjD+I757ly9sbItNctLmX3XBJJYC12onCRK9O61MZd6x7WXjDbxAk7gr2mrcZeulwBEgYnw1QeGsWxLfQqCpTpw4fzMPjiuwyptH/xLHSeON0H1XoRiA5hkHfl+SuyoDhkdxzQcptha1grMs7W1x9gOgY5ickupStFdpZUs9NrXa9bJG4xdx8V2oCIhFcKnsasWsbVqyKbpZd1GgdO7TFdVtMxdJF2Iu3dN2a0Krogk4BBmtf8ACeARF04Lg9CKbhUtDiCMG+pXZ2pLaFZwxhjjE8F5jovtenZusFVxF6IwJGE+GaBVv2zUpVqjPmEiMchEkLlW3aPWNDA260H9BNt1rvveBDgciRw3rnUaLqlRtNvzOMKBzquAEZZ8V9F2Oy7s6md9IHxavBiy08RfgyQS4a8Ny+g0RcsDBOVJonuCDj2WKTxUaMQHZz9oyVfar/i2ta4XY3Yz6JAOCmURmqWWpdcPiq0EEQQHZ969HsnaDHNbSaHSxgEmNBzXCruGE5LT0fc2/VIjBpyVHn7VbTStZqAXruMHWSVstG3utpPYaV0uaRIdMSOS49uLjWMHkJ4JEP0BUV73og0izAn7zvUeyzdM3dmn3/RbOiQIsbJzx/uK5/TR+NPkfUIPK9a4T2Qe9e86Kf6NnGT5rwXWDcvoHRoRZKfKUCuljosp4kLwfxABkOghe36Yn/LtG9y8Q+IKDrdJH/5SzzmYP/tK85Tz713ulTv3VBu4H6Lz9MDVUapQkkN+9HeVVzoBIfPCVBoVSlvqQJzUEv4IGIS77tW+BUdafulBRSFVSFBZChSqqUKFIxMDNQQUyioLQPmxO4K1N0lAyFKXfQXHFEMhWCW0lMCCtf5RzWfRaK/y96zhBosn2+Tf7gunsf8Aj/8Ap1f/AI3LlWU4v5D+4LrbH/1Dfw1P/jcqOp0oJNFjRq+fAH3XnG0TuXo9vGTTHM+i5rG8Qgw/Dncm0rNgZ1W4MwVwzAFEcvqoMQujsIAWlhIyn0KraGYXhpmkXtyo9p19M/eHci/TOT/EFeNFd4GD3DvKj46u3HrHd+KD2eGj2+Kkd3cV5Vm0apYXB0RngD4YLOOkFoaflYRxaR9UGjpX+8tFJjj2W0yRzLv/AKr1GwrT19kYXYkAsdxjCfCCvG7Qt/xJY9oh1245u7GQZ3Y+S7XRS0EUazQJLXAgc2/kg9FaGXmFoJBOo+oWKzWJzDjUc5v3TdhvFpGIWRu2K7mgmyPxGbHsd6kJ1K0Pe2erfT4OifIlB0LlYZVWEfzsx8QQPJUcauRrUB/Qf+9cytfOcrgbT2u+hVuXAcAZJQeuc93/AO0wfhYPqSppvaAb1Y1CRHaugeAAXgv8QVTkxvmV3tk2plSgx9atTY5xOEgakDCZQdjaT+so1Gkgy2BkAF5N2x5xAPcu1b6LnXXNc8tGYGDRAJk4SdM8E7Y9G+KhOgwQeSr2AjKcN4WCy1HNqBzCQ4TEcl62o8EkHzXmtmUf82GHe4eAKiorPF48969FT6WM+H6pzHDAAZEYRy3JVTZzTr4hZq2xvDgg6rTgFWkc880ptqpk3Q9sjCCYPgnBEVtNSIWnYVQXbQd1MlYLcYA71ko7TNBrwGkh7bpQYq7GuqHttGOTpHmrCyPIwF7ix49JWSqHOJcG5mUuSCMCPJFfTOjbC2y02kQbuIPMrhdNT+8b+H6rt7ArgUKbXSCKbcTrOOa4HS6vFoGAcABgdc0HmQV9L2C2LLSH8gXghXs5+ag5vFj/AKFfQ9mtAosAyDR9UHF6aPinTHGV4YmTC9l01Mmm0bivNUdk1i9pcwtbIMnLyQO6UOl1Ibmn6LkUsV0ekbprNG5g/XkuXTfBQNczPIrNUAOQhaH1JGSSUCSzigB2/wA05wUQgX1jxr6KfiHbh4K11F1BKkJNWoQYSxUO9Rca1MoYwkScArBwb8ue9BLaersB5qXVNG4BLJnMolAFXpFUAlMDIjHFBAdiVacUkOG9XacUDg9MaUqfRXaUE1/kKyhaq3yFZQqh1lOLuQ/uC6+yP9TT/q/sK5FjEvj+X6g/RdfZH+qpfi+hQdDbLpqMH8s+JPssTRwWnaJmqPwN9/qrUkCmHBOpCQVZ7AUUhCRC7qw1qdx0aaLpOGKVWpX24ZjJUYWtlMfZjC0UGBueaaXjciMlOlDY1V6bWVJaQJHDP2KcXcEk0TevDBFY69l6ozBu6p3R7bFOz1avWuIa8CDBOI/5W8uDgGvAOGv14Ln2rYjXGQAO5B36e3LABArRJmN0pNq23ZLpDLS0OjA3S4A8QF5epsNwyhZK+yqjMwg6VW1g57TfyFJ/usNcUHOl1rqPO/qzPmVm+CduUixOQXabI3Wu/wD6W+6fRt1Bp/d2Rrjvq1C7yACQLAm0rGAg9fStjq9CZgnQDD9eK3bJFylVJGn6xXndn1ixpaR2d69Psus3q3w4HDLXwQeUt1R0EtwM7pMLk2a+LQx4vTeEk8cD5L19eyNdmPBYGbL7YIxAxjLkiK9eb0Fdm02QtoB84c1xxRPWAEar0u1YbZGt4iEV5G07La+TAMrO2yVaeFOo5vAmQtxcQcDCltpOsFBgr1bQQ0PDTvIGibTcNVqNZp4JzKIcCYwWbGpWS43UBc21ViTDV2XWdsQFkNgaDI9VMXXOobSr04uVXAbpkeBRa7fUrkGoQTvAhbnWBu5Jfs3dK0ywsfBGOq95s7b9ESBVa4E4B3ZIwyxXinWJwSn0HDMIPSdMLUKjqbhlBjyXG2Za3NqBoJuuwIk+KwRC0bNbNenz+hQN27JtJETAA9Vz8NQte13TaanMegWQOKCcN6rdUzwCggcUEEKquBuKnHdKBaFMjcpgIMtc49yUHcE62Plw5LOHKNSujeJzRCq04KZREwrMYTkpp055K76oHZb4oJcQzAYnekl5ALkBVrjsO5IirGy47h6lNOYVLKZvc/omVBiFKpoChzTeDpMZRpzVwof8pVRer8hWQLZU+QrEFRp2eJqgbwfRdTZR/wA1R/3G+q5NidFRp4H0K6mzT/maH+6z+4INdod+8nPst/tCYx8KjhLj4eGC0MiMkEioTorEYIaUwNlBV/abegK9jpSSToltdm1FnqkPAB1xWkFamGnLAqABC3VaV5pC586KAKY2IS0AoM1rMPBGi02CuD2T4e3sslr+ZWsjMyg65s8iQZSnWcRBEhUoViMCe/Q8D7rWII9Qg41p2bqySN2v5rC6lGa9MWhZbRZWvnQ79/NBwg1Op050Ta1jLTl+fL9SmUhgICCAE+g5zZLXQY8UUqD3mGtkpt7qiW1GNdhBH5oFM2g4YOxHmtFjtbXnA47lzajm6BKoVSwkjUEeKDv3QTiAVv2hZ5oNF4nny0K89Qtj2EYyNxXaftAVKTZgRxQcSvZnN0wWYiF3JlJrUGOzGO8YIOM4SutZG3bFWOt5qzOsRGWPkfb0W2s8Cyim0EEmXAjE7ufcg4/xLhuKs2ve4LPUGKKYxRXbs9J12SA4cR9QsdpuzgC1ep2M39z/AFfQLyu0geueGjC8Y8UQkHiCh1MaqlBl5wBN2dc/RdapscBnZL3ujDANHuouuFWYzdKmwFjal6DglWtrmuIJS7GO0eSCu0i0vLmkEk4juCwl6dWxceaS4IIvovIhRCCbwU4aFUhRCC8lHcqSpvIMtqzCQE+1ZhIGaDe3IJ9KjqUUKYDQ47lWpWnDRRVqtWcBklwoClETKnPBUJVmZoEWMw8tP6hbH6LDaMKkrWwy0FKHtyQ7KN+CqwqzcXcvX9eqBtT5DyWFbqg7LuSwqh1j/is7x5FbrE8tr0eFRn9wXPspiqzmt1MxUadzgfNB1D87hxPqnUws/WdoninNeg0BWDktj1fCUFXHtSoq4Okc1L8uSU5ysZb2WqRoD3rHbiQbze/3S7ym9vVCWWgkqz6kLNWZcdHgqSitFZwcJkAhOo12BoGqwyrNcoN3xgE9lXo24CNNxiY4HeFz5Vm03HISg7ragdz9eIOoU4LlUb7BiJbnGoO8cVvo1r0YyDkd/A7ig20bLfzAu6ysdosgaeziPMe66FWuLgExhkEqhSvGScEGOy1DTJdmP1msNteXvLjqu3b7jouCHDC8NeB3rlVaJGYunjkeR+hQc9zTEqjc06o0gwoZTVFgE4vAbglvaQqlyB9lrlp4J7rY0OgyOKwB0GUqq+TKDuUu1iDI3hdC2UQ2gGmCJnyXmbI8hwgkcl3LXaopgEyFBzK1lB/PFJpWWHYgxwx/Na21Wu+Ug+vgmUvmBRXXslT91+7cDnOK8tb5LjJJ5r1z6VN1KSAHXfmGB8V5i1UZJyPkfZBnsVPtCF7Szva6mGzjdGB5FeQsjA1wvHDjgvV06jRTwwEfREeHt7e25Z7OIk8Fr2i2HmFjFTAoMj8ylkJhKoiqEKqZCrCCigqSqkKAQhQgRatFnC2W9oAaBxWNBva8lrRoAhVpHsjkrSoqyFEolAKW68lVWCIXWbMq1lebpEHBLfXgxAK00WETIAJ9kqrtdATaOAWbqHxi/wAArigNS496I1ucLp5LCmENGQAS1Rez/wARv4guuabc4XHo4Pb+Ieq7IEoGscnsSGhaKQ3IHAQmXJGaqxqsagGSBZEHPBVqCCrDFUqtLTikSqqzSN6mg0E46LUajJgtEcGY+a0jNXpX24ZjL2XLldxw3FpHDP0XMttKDeGRzhBnVgFSVqoMBGKKWFpp1GxBaOcIusGqqaU5AoGu54KtNxYZBkHMaFL+Dd96EtzLusqLjq0a4eJEkDOcxz3jittO03WR5rzjKhaQ5pgjVdOzWkPEZO1bv4t9kRupy4702pgC0gEHMZpVmtAZjE6JdSsXGUGWrZtwLhu+0OR15FKp0oEgyBnoRzC6lGiTicki1UQcQYeMLwnwIOYQc+o6SobSlS9hBhwDTofsn2PNMxbmIQZLRTumFnhaarpKpdQVpGCm165IhVLYSnoKh2PFdGyWt2AMO55+IXNAWizmCivSm0suQRBjDWTC5lSoMZwUVbSCwiFz+vI1kbnY+BzCDpUGCQRiF2vhKZZLOxh9nLLdkvP2W0NkYlvPLxC7VVwFMua7CNNUR5y30jJ+nt/yuVUpkT9F2LQZOCyuA1xQcdyot9azg5efusdSiW5iPTxRSlBKkhUKgCoKEIKlQrFVKBFqMws5Wivks6DXS+UJgS6PyhMUEqFKmEVACq54Gqr1ROZKtTs45ogs1EE3tBlzWwKAFIQDnxmqGqNxSrU+CEttSdEDL0rVZaWMkcgs1I6kLW2oTIEZKhQZL5n7U+a67M8VzrPQc4wBuXSt7mYBpEjOFAwOG9NbWGiwNqNDc8ValWaNfJUdGXO3IcxwE4JTKj8wEt9qdOg80Q11TDclmpvKpXbLZvY9ywxjiqOjStoacDmtjba45Md3g/Vcai+6ZC3tqPflkiHuLzmAOZ9kt7QRBe0ch+ajqScypFFozKKwudBwCi+d61WkMjshYjnCGttK0NAyxVxaXH5Quct1G1BrcsUDA17lLbPvKUbWTkjrHlBNZgASJTRTJzVuqjNBps1svG68w7R2juB4rUM4jEZhcVwWyzW2IbUJjR+o57wg7vWFtOJbPiua68Ti4qz3H23EbwrWcBzoIkILUgDg7EazikWqzhmFPtM1ZOXFp+hWmtRLNRyCzueg57matMjXePxDRDQtvUhxkG64ajP8wqWijdHbDRPyvGAn+bcis1QpJV6gIMOwVUEBqu2AhpUFBZ9TRIIMphf3JTjKI02d+I+i6NSAzDDD9YLlUTjIWipaOzH64IEVK41w8x7hUe4frFZqzln60tyMIraSllZ22oZHDliPBNvgjPDfogo+g08OSz1LK4ZQeS0kqJKg55H/AAqlb3AHAiUh9n+6e4oMyqr1GEZiPRUQIrnBKawlbXsbulVBjKByUEUWEDHLcmylyVKC8qS5LlF4IL3lsstjqPwa3HjAWWyNv1abd7gDynHyXsLQ+m2bgxJmfoOClqxwv2ZUHzQ3gc0VLFcaTemF1W9pYNogspuJ1SUcKvi/khoCA4xCsAtImVdriMiqAKwQMvE5klXCVKvKB4yTKYJSpwCdZqgB7x6qjS2q5qeKzXZjRWcxrxgs5pEKBlWkPsrC/BaBVIzSKxkyqKhy2UrTDYWEFMp5hEazaXFR2itLKTWiVJqtGSDO2zuKrWspatBtYEwkVLSTPJBkJQCocgIN9luxitHXtGi5TXkJjAXINjrWlOqkqzLOr9W0frVAgBDmwn9Y0LPVqSUDbLaur7Lsae77vELp03wA4EOacne40K4abZq7qbsMWn5mnI/miuvUqkpUglVAa5t9hvM1GreBClnkg0MonPAKlVxdg4yEypW7MArKXIhTqRaIaAW/cOX9J0SRTn5JwzacHD3HELWHjnyTHWXrREAHRxMEcoUVhaIzS3vT7RVdT7Fo7QjCq0f3BZ6rIg4FpycMiqKSiVBKEFwVV7lDkp7kC6hSHlMekuQLKgOIxHkpKoUDm2jf5eyc2oCN/L2WFEx+Sg3Xt3kqErO2sdfzUhodrPD8tUFzaNGi96eKUaE4kwdwGCYCAqOrDRBnJULJ8U7cEfFO3BBtChxWP4t24KPiXcEGooWX4l3BHxB3BB2NjtmsD90E/T6rtvqLyVm2k+lJaG47wfdNO2qp0Z4H3UsXXqG1Y1WHbFUlrROa4h2xV/lHcfdKqbRqOMugxkkha2QpXP8AjXbh5o+MduHmqjohSFzvjXbm+aPjn7m+aDpK0rmfHP3N8/dH7Qfub4H3Qdo5BAK5B2nU3N8D7oG1Km5vgfdB6GjWIIWunXBHH8vFeV/a1TczwPurDbNXczwPug9VXpAjDP8AJc+swgrkt2/WGQZ4H3UVNvVXZtp+B90HSlWaVxf2rU3N8D7o/atTc3wPug9D17jqpaCVwGbZqD7LDzB908dJKw+xS8He6qO62yuKa2xHVee/xNX0FMHfDvHNVPSOvuYOQPug9DUsYGRn8lidgVxztysdGeB90s7XqbmeB90V2pTaNSFwP2tU3M8D7o/a1TczwPug9IbUqGo4rgftmp91nOD7o/bNX7rPA+6D0HNSGrgDblUfZZ4H3Vv2/Wj5afg73Qd+6VR2C4v+Ia33afg73S3bcqn7LPA+6DvUK76brzDB13EbiujQqCqC5sB32qc+YXjv2zV+6zwPupbtuqCCA0EagH3UHsLx/wCURIxXl6nSau4zcpA6wHY88VX/ABHW+7T8He6I9hRZuC2VnAZYGdOS8OzpVXH2KXeHf9yKvSq0OOLaXcHe6D1FR17PFY+pdTk0ounNh+U+y8//AIkr/dp+DvdQekdfczwd7orvNDXns9l4zY4+h1REZgj8l5+pt6o4QadKdDDpHLFXHSSvdAcKbgPvA+6Dt1CszyuMdtVTozwPuqna1Tc3wPug6zkpy5h2pU3N8D7qv7Rfub4H3QdEqpXPNvfub4H3UfHP3N80G8qpWL4124eaj4x24eaDcoKxfGO3BHxjtw80GzzVSsvxbtw81HxTtwQIQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCAQhCD/9k=\n",
      "text/html": [
       "\n",
       "        <iframe\n",
       "            width=\"560\"\n",
       "            height=\"315\"\n",
       "            src=\"https://www.youtube.com/embed/yUVuiZUhbyA\"\n",
       "            frameborder=\"0\"\n",
       "            allowfullscreen\n",
       "        ></iframe>\n",
       "        "
      ],
      "text/plain": [
       "<IPython.lib.display.YouTubeVideo at 0x7fbe95f8cbd0>"
      ]
     },
     "execution_count": 109,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "from IPython.display import YouTubeVideo\n",
    "YouTubeVideo('yUVuiZUhbyA', width=560, height=315)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.1 Examples of Queues](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.1-Examples-of-Queues)",
     "section": "7.5.1 Examples of Queues"
    }
   },
   "source": [
    "\n",
    "[Tesla China - Shanghai Gigafactory production line](https://electrek.co/2020/08/31/tesla-video-production-gigafactory-shanghai-alien-dreadnought/?fbclid=IwAR2jHUZMQG4Gl77ugYHvm3DTq-zV5iOuN3bMNePzJswvfY_VVgYP3W7pSZQ).\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 3,
     "link": "[7.5.1.1 Service Lines](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.1.1-Service-Lines)",
     "section": "7.5.1.1 Service Lines"
    }
   },
   "source": [
    "### 7.5.1.1 Service Lines\n",
    "\n",
    "![mathworks queue](https://blogs.mathworks.com/images/seth/2015Q1/queues.png)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.2 Concepts](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.2-Concepts)",
     "section": "7.5.2 Concepts"
    }
   },
   "source": [
    "## 7.5.2 Concepts"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 3,
     "link": "[7.5.2.1 Nomenclature](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.2.1-Nomenclature)",
     "section": "7.5.2.1 Nomenclature"
    }
   },
   "source": [
    "### 7.5.2.1 Nomenclature\n",
    "\n",
    "\n",
    "* Servers\n",
    "* Arrival rate\n",
    "* Departure rate\n",
    "* Queuing area or waiting area"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 3,
     "link": "[7.5.2.2 Service Disciplines (of many possibilities)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.2.2-Service-Disciplines-(of-many-possibilities))",
     "section": "7.5.2.2 Service Disciplines (of many possibilities)"
    }
   },
   "source": [
    "### 7.5.2.2 Service Disciplines (of many possibilities)\n",
    "\n",
    "* First-in-first-out (FIFO or FCFS)\n",
    "* Last in first out (LIFO)\n",
    "* Shortest job first\n",
    "* Priority queue, no interruption\n",
    "* Priority queue with premption\n",
    "* Earliest due date"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.3 Poisson Process](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.3-Poisson-Process)",
     "section": "7.5.3 Poisson Process"
    }
   },
   "source": [
    "## 7.5.3 Poisson Process\n",
    "\n",
    "Poisson processes describe the occurance of independent random events. Examples:\n",
    "\n",
    "* Arrival of customers, orders, or other entities from totally independent sources.\n",
    "* Machine failures when characterized by a mean time between failures (MTBF)\n",
    "* Physical phenomena like molecules striking a surface, meteor strikes.\n",
    "\n",
    "Poisson processes are a useful approximation for many simulations, and also very easy to implement in practice. This section introduces some theory before describing a typical implementation.\n",
    "\n",
    "### Binomial distribution\n",
    "\n",
    "Suppose there is a probability $p$ of an event occurring in a short interval. We'll assume the interval is short enough that two or more events in the same interval would be extremely unlikely. Assuming each event is independent, the probability of seeing $k$ events in $n$ intervals is given by the binomial distribution\n",
    "\n",
    "$$\\text{Binomial}(k | n, p) = \\frac{n!}{k! (n-k)!} p^k (1 - p)^{n-k}$$\n",
    "\n",
    "The term $p^k (1 - p)^{n-k}$ is the probability of seeing a particular sequence of $k$ intervals with events and $n-k$ intervals with no events, assuming all of the events are independent of one another. The multiplier $\\frac{n!}{k! (n-k)!}$ is the number of different sequences that can be constructed from $k$ events occurring in $n$ intervals."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 110,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.3 Poisson Process](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.3-Poisson-Process)",
     "section": "7.5.3 Poisson Process"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "Text(0.5, 1.0, 'Binomial Distribution n=20, p=0.2')"
      ]
     },
     "execution_count": 110,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYgAAAEWCAYAAAB8LwAVAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3df5xcdX3v8dc7YQKuIRoIrRSQwIq0eIm/IrZea71FkRWVatcaNWm09u6lC/2Rxla8KCD+KLY3TW8NvZa7ojQRQdcfTTUr0qpXa4uyIERRA9kYJKgQAcPGqCzyuX98z8Iwe+bHZvec2Z15Px+PecyZ749zPnNm5nzmnO+ZM4oIzMzMai1odwBmZjY3OUGYmVkuJwgzM8vlBGFmZrmcIMzMLJcThJmZ5XKC6CKS3i/p7XN5uZK+KOkPZ7Cs35S042D758xvRNLabPoNkv59Fuf9ekmfm635mc02J4gOImm3pJ9K2i/pfkmfkXTcZH1EnBMR7yw7rtlarqSLJU1IGs9ut0naJOnoqmV9OSJObnFeW1qIvS8irpyF2JdLCkmHVM37wxFxxkznXRRJfyHpm9m6/q6kv6ipXy7pC5IOSPqOpBe1IcbTs2UfyGI5vk67X5L0EUnfl7RP0lckPbfseOcbJ4jO8/KIWAwcDdwNvK/N8cy2ayLicOAI4JXAk4Abq5PEbFDS7Z8PAb8PLAXOBM6TtKqq/iPA14EjgQuAYUlHlRactAz4BPB20vthFLimTvPFwA3As7O2VwKfkbS4hFDnr4jwrUNuwG7gRVWPXwrcVvX4Q8C7sukXAnuA9cA9wA+AN1a1fQLwT8Be4A7gbcCCrO4NwFeAjcCPgV3A87LyO7P5ra2z3KXAp7P53p9NH1vV9ovAH9Z5fhcDW2rKFgK3AP+r+nlV1b8FuAsYB3YAp5M2dg8CE8B+4JaqZb87e24/BZ5SHU/V894E7AO+A5zeYP0/Ei/wPSCy5e0HfiOb379XtX8eaSO2L7t/Xs16eWe2/HHgc8CyOuup4Ws7g/fX3wPvy6afCvwcOLyq/svAOdN4r74V+Fb2PvggcNg04xkA/qPq8eOz1+1XW+z/APDsdn9u5/Kt278hdSxJPcBrgOsbNHsSKREcA7wJuEzS0qzufVndicBvkb5JvrGq73OB7aRvj1cBVwPPIW1UVwOb6nw7W0DaGBwPPJn0gd40/WeYRMQvgH8GfrO2TtLJwHnAcyLtdbwE2B0RnwXeQ9obWRwRT6/qtoa04TmclBhrPRcYA5YBFwGfkHREC6G+ILt/YrbM/6yJ9QjgM6SN8JHA35K+4R5Z1ex1pNfgl4BFwJsbLK/uayvpfEk/rnfLm5kkkdbxrVnR04BdETFe1eyWrLxVrye9Jr2khPO2bFlPbhSfpNdVxXDL5Mwi4iek16ZpDJKeQVqHO6cRb9dxgug8n8o+5PuAFwN/06DtBHBJRExExDbSN9uTJS0EVgFvjYjxiNgNbCBtPCd9NyI+mG2grwGOy+b184j4HOkb+lNqFxgR90bExyPiQLZxeTcpAc3E90mHDWr9AjgUOEVSJSJ2R8RYk3l9KCJujYiHImIip/4e4O+ydXYNaa/krBlFn5wF3B4Rm7Nlf4S0h/LyqjYfjIjbIuKnwEeBZzSYX+5rCxARl0bEE+vd6szvYh5N7pAO2eyrabOPlFhbtSki7oyI+0jvg9dm8X2vUXwRcdVMYpC0BNgMvCMiavtbFSeIzvM72Yf8MNK35/8n6Ul12t4bEQ9VPT5A+tAtAyo89hv0HaRvo5Purpr+KUBE1JZN2YOQ1CPpHyXdIekB4EvAE7OkdLCOAe6rLYyIncCfkTZu90i6WtKvNJnXnU3q74qI6itc3gE0m2crfoWpeyy16/yHVdOTr1U99V7baZN0HmkP8qyI+HlWvB9YUtN0CenwV6uq1/XBrMdpxyDpccC/ANdHxF9Nc3ldxwmiQ0XELyLiE6Rv0c+fZvcfkb6BVp8R8mTSsfyZWk/6JvvciFjCo4dedDAzywaSX046/j1FRFwVEc8nPZcA3jtZVWeWzS5vfEx2uGXSk0l7MAA/AXqq6qoTc7P5fp/Hru/Jec/GOn8MSf8zO9Mt91bT9g+A80ljLXuqqm4FTpRU/W396Tx6CKoVx1VNP7Ies0NMdeOT9PqqGB45PCjp8aTDVbkxSDoU+BRpfOZ/TCPOruUE0aGys3DOJg0Kf3s6fbPDRh8F3i3p8OzUwT8Hmp4W2oLDSXsXP86Ou190MDORdIikXyOdSfMk0jH72jYnS/rtbMPws2y5D2fVdwPLD+JMpV8C/kRSRdKrgV8DtmV1NwOrsrqVQH9Vv73Zsk+sM99twFMlvS57bq8BTiEN4s+qiHhPNg6Se5tsl22I3wO8OCJ21czjNtLzvUjSYZJeCawAPp71faGkZknxXEnHZu+DC8jOQMoOMdWNLyI+nPX/JPBfJP2upMOAC4HtEfGd2gVJqgDDpPfA2oh4uLaNTeUE0Xn+JfsW+ADpuO7aiJjOt7pJf0z6RrwL+HfSQPQVsxDf3wGPI+2lXA98dpr9X5M9v33AVuBe0pko389peyhwabasH5I27m/N6j6W3d8r6aZpLP+rwEnZPN8N9EfEvVnd20nfYO8H3kFaZwBExIGs/VeygdZfr55pNo+Xkfaw7gX+EnhZRPxoGrHNtneRBsxvqPr2/v6q+lXAStLzvZS0LvZmdccB/9Fk/leRzsbaRRpcftd0gsuW9buk9Xo/6QSCR07DVfqB5mS8zyOt3zNIX04mn8+UkxvsUXrs4VQzs5mTNAR8LCKurVO/m3T68L+WGphNyyHNm5iZTU9EHPTlUmzu8CEmMzPL5UNMZmaWy3sQZmaWq2PGIJYtWxbLly9vdxhmZvPKjTfe+KOIyL3IYsckiOXLlzM6OtruMMzM5hVJedccA3yIyczM6nCCMDOzXE4QZmaWywmi24yNweAgLFkCCxak+8HBVG5mVsUJopuMjMCKFTA0BOPjEJHuh4ZS+chIuyM0sznECaJbjI1Bfz8cOAATNf+DMzGRyvv7vSdhZo9wgugWGzZMTQy1JiZg48Zy4jGzOc8Jolts2dJagti8uZx4zGzOc4LoFvv3N28znXZm1vGcILrF4hb/jrjVdmbW8ZwgusXq1VCpNG5TqcCaNeXEY2ZznhNEt1i/vrUEsW5dOfGY2ZznBNEtentheBh6eqYmikollQ8Pp3ZmZjhBdJe+Pti+HQYGGF/Uw8Mo/ZJ6YCCV9/W1O0Izm0M65nLf1qLeXti0iVMXp2Sw+9Kz2hyQmc1V3oOYb3wtJTMriRPEfOJrKZlZiZwg5gtfS8nMSuYEMV/4WkpmVjIniPnC11Iys5I5QcwXvpaSmZXMCWK+8LWUzKxkhSYISWdK2iFpp6Tzc+r/XNK3JG2X9G+Sjq+qWyvp9uy2tsg45wVfS8nMSlZYgpC0ELgM6ANOAV4r6ZSaZl8HVkbECmAY+Ous7xHARcBzgdOAiyQtLSrWecHXUjKzkhW5B3EasDMidkXEg8DVwNnVDSLiCxFxIHt4PXBsNv0S4LqIuC8i7geuA84sMNa5z9dSMrOSFZkgjgHurHq8Jyur503A5C+9WuoraUDSqKTRvXv3zjDcecDXUjKzEs2JazFJWg2sBH5rOv0i4nLgcoCVK1dGAaHNPb6WkpmVpMg9iLuA46oeH5uVPYakFwEXAK+IiJ9Pp6+ZmRWnyARxA3CSpBMkLQJWAVurG0h6JvCPpORwT1XVtcAZkpZmg9NnZGVmZlaSwg4xRcRDks4jbdgXAldExK2SLgFGI2Ir8DfAYuBjkgC+FxGviIj7JL2TlGQALomI+4qK1czMpip0DCIitgHbasourJp+UYO+VwBXFBedmZk14l9Sm5lZLicIMzPL5QRhZma5nCDMzCyXE4SZmeVygjAzs1xOEGZmlssJwszMcjlBmJlZLicIMzPL5QRhZma5nCDMzCyXE4S1bmwMBgfTv9gtWJDuBwdTuZl1HCcIa83ICKxYAUNDMD4OEel+aCiVj4w0n4eZzStOENbc2Bj098OBAzAx8di6iYlU3t/vPQmzDuMEYc1t2DA1MdSamICNG8uJx8xK4QRhzW3Z0lqC2Ly5nHjMrBROENbc/v2z287M5gUnCGtu8eLZbWdm84IThDW3ejVUKo3bVCqwZk058ZhZKZwgrLn161tLEOvWlROPmZXCCcKa6+2F4WHo6ZmaKCqVVD48nNqZWcdwgrDW9PXB9u0wMMD4oh4eRumX1AMDqbyvr90RmtksO6TdAdg80tsLmzZx6uKUDHZfelabAzKzInkPwszMcjlBmJlZLicIMzPL5QRhZma5nCDMzCyXE4SZmeVygjAzs1xOEGZmlssJwszMcjlBmJlZLicIMzPL5QRhZma5Ck0Qks6UtEPSTknn59S/QNJNkh6S1F9T9wtJN2e3rUXGaWZmUxV2NVdJC4HLgBcDe4AbJG2NiG9VNfse8AbgzTmz+GlEPKOo+MzMrLEiL/d9GrAzInYBSLoaOBt4JEFExO6s7uEC4zAzs4NQ5CGmY4A7qx7vycpadZikUUnXS/qdvAaSBrI2o3v37p1JrGZmVmMuD1IfHxErgdcBfydpyv9ZRsTlEbEyIlYeddRR5UdoZtbBikwQdwHHVT0+NitrSUTcld3vAr4IPHM2gzMzs8aKTBA3ACdJOkHSImAV0NLZSJKWSjo0m14G/Feqxi7MzKx4hSWIiHgIOA+4Fvg28NGIuFXSJZJeASDpOZL2AK8G/lHSrVn3XwNGJd0CfAG4tObsJzMzK1iRZzEREduAbTVlF1ZN30A69FTb7z+AU4uMzczMGpvLg9RmZtZGThDtMDYGg4OwZAksWJDuBwdTuZnZHOEEUbaREVixAoaGYHwcItL90FAqHxlpd4RmZoATRLnGxqC/Hw4cgImJx9ZNTKTy/n7vSZjZnOAEUaYNG6YmhloTE7BxYznxmJk14ARRpi1bWksQmzeXE4+ZWQNOEGXav39225mZFailBCHp5ZKcTGZq8eLZbWdmVqBWN/qvAW6X9NeSfrXIgDra6tVQqTRuU6nAmjXlxGNm1kBLCSIiVpMuljcGfEjSf2aX2j680Og6zfr1rSWIdevKicfMrIGWDxtFxAPAMHA1cDTwSuAmSX9cUGydp7cXhoehp2dqoqhUUvnwcGpnZtZmrY5BnC3pk6TLbleA0yKiD3g6sL648DpQXx9s3w4DA4wv6uFhlH5JPTCQyvv62h2hmRnQ+sX6XgVsjIgvVRdGxAFJb5r9sDpcby9s2sSpi1My2H3pWW0OyMxsqlYPMf2wNjlIei9ARPzbrEdlZmZt12qCeHFOmY+FmJl1sIaHmCT9ETAI9EraXlV1OPCVIgMzM7P2ajYGcRUwAvwVcH5V+XhE3FdYVGZm1nbNEkRExG5J59ZWSDrCScLMrHO1sgfxMuBGIABV1QVwYkFxmZlZmzVMEBHxsuz+hHLCMTOzuaLZIPWzGtVHxE2zG46Zmc0VzQ4xbWhQF8Bvz2IsZmY2hzQ7xPTfygrEzMzmlmaHmH47Ij4v6VV59RHxiWLCMjOzdmt2iOm3gM8DL8+pC8AJwsysQzU7xHRRdv/GcsIxM7O5otXLfR8p6e8l3STpRkn/W9KRRQdnHWRsDAYH06XNFyxI94ODqdzM5qRWL9Z3NbAX+F2gP5u+pqigrMOMjMCKFTA0BOPjEJHuh4ZS+chIuyM0sxytJoijI+KdEfHd7PYu4JeLDMw6xNgY9PfDgQMwMfHYuomJVN7f7z0Jszmo1QTxOUmrJC3Ibr8HXFtkYNYhNmyYmhhqTUzAxo3lxGNmLWuYICSNS3oA+O+k6zI9mN2uBgaKD8/mvS1bWksQmzeXE4+ZtazZWUyHlxWIdaj9+2e3nZmVptX/pEbSUuAk4LDJstq/ITWbYvHiNCDdSjszm1NaPc31D4EvkcYd3pHdX1xcWNYxVq+GSqVxm0oF1qwpJx4za1mrg9R/CjwHuCO7PtMzgR8XFpV1jvXrW0sQ69aVE4+ZtazVBPGziPgZgKRDI+I7wMnFhWUdo7cXhoehp2dqoqhUUvnwcGpnZnNKqwlij6QnAp8CrpP0z8AdzTpJOlPSDkk7JZ2fU/+C7NfZD0nqr6lbK+n27La2xThtLurrg+3bYWCA8UU9PIzSL6kHBlJ5X1+7IzSzHC0NUkfEK7PJiyV9AXgC8NlGfSQtBC4DXgzsAW6QtDUivlXV7HvAG4A31/Q9ArgIWEm6KOCNWd/7W4nX5qDeXti0iVMXp2Sw+9Kz2hyQmTUznbOYngU8n7TB/kpEPNiky2nAzojYlfW/GjgbeCRBRMTurO7hmr4vAa6LiPuy+uuAM4GPtBqvmZnNTKtnMV0IXAkcCSwDPijpbU26HQPcWfV4T1bWipb6ShqQNCppdO/evS3O2szMWtHqHsTrgadXDVRfCtwMvKuowFoREZcDlwOsXLky2hmLmVmnaXWQ+vtU/UAOOBS4q0mfu4Djqh4f20Kf2ehrZmazoNlfjr6PNOawD7g1GwsI0sDz15rM+wbgJEknkDbuq4DXtRjXtcB7sl9vA5wBvLXFvmZmNguaHWIaze5vBD5ZVf7FZjOOiIcknUfa2C8EroiIWyVdAoxGxFZJz8nmuxR4uaR3RMTTIuI+Se8kJRmASyYHrM3MrBzNLtZ35eS0pEXAU7OHOyKiySU6ISK2Adtqyi6smr6BdPgor+8VwBXNlmFmZsVoaZBa0gtJZzHtBgQcJ2mtL9ZnZta5Wj2LaQNwRkTsAJD0VNJvEp5dVGBmZtZerZ7FVJlMDgARcRvQ5ApsZmY2n7W6B3GjpCFgS/b49Tw6gG1mZh2o1QRxDnAu8CfZ4y8D/1BIRGZmNic0TRDZRfduiYhfBf62+JDMzGwuaDoGERG/AHZIenIJ8ZiZ2RzR6iGmpaRfUn8N+MlkYUS8opCozMys7VpNEG8vNAozM5tzml2L6TDSAPVTgG8AH4iIh8oIzMzM2qvZGMSVpH91+wbQR/rBnJmZdYFmh5hOiYhTASR9gOZXcDUzsw7RbA/ikQvy+dCSmVl3abYH8XRJD2TTAh6XPRYQEbGk0OjMzKxtml3ue2FZgZiZ2dzS6sX6zMysyzhBmJlZLicIMzPL5QRhZma5nCDMzCyXE4SZmeVygjAzs1xOEGZmlssJwszMcjlBmJlZLicIMzPL5QRhZma5nCDMzCyXE8TBGhuDwUFYsgQWLEj3g4Op3MysAzhBHIyREVixAoaGYHwcItL90FAqHxlpd4RmZjPmBDFdY2PQ3w8HDsDExGPrJiZSeX+/9yRmk/fWzNrCCWK6NmyYmhhqTUzAxo3lxNPpvLdm1jZOENO1ZUtrCWLz5nLi6WTeWzNrKyeI6dq/f3bbWX3eWzNrKyeI6Vq8eHbbWX3eWzNrKyeI6Vq9GiqVxm0qFVizppx4Opn31szaqtAEIelMSTsk7ZR0fk79oZKuyeq/Kml5Vr5c0k8l3Zzd3l9knNOyfn1rCWLdunLi6WTeWzNrq8IShKSFwGVAH3AK8FpJp9Q0exNwf0Q8BdgIvLeqbiwinpHdzikqzmnr7YXhYejpmZooKpVUPjyc2tnMeG/NrK2K3IM4DdgZEbsi4kHgauDsmjZnA1dm08PA6ZJUYEyzo68Ptm+HgQHGF/XwMErn5g8MpPK+vnZH2Bm8t2bWVocUOO9jgDurHu8BnluvTUQ8JGkfcGRWd4KkrwMPAG+LiC8XGOv09fbCpk2cujglg92XntXmgDrQ5N5af38ajK4esK5U0s17a2aFmauD1D8AnhwRzwT+HLhK0pLaRpIGJI1KGt27d2/pQVoJvLdm1jZF7kHcBRxX9fjYrCyvzR5JhwBPAO6NiAB+DhARN0oaA54KjFZ3jojLgcsBVq5cGUU8CZsDvLdm1hZF7kHcAJwk6QRJi4BVwNaaNluBtdl0P/D5iAhJR2WD3Eg6ETgJ2FVgrGZmVqOwPYhsTOE84FpgIXBFRNwq6RJgNCK2Ah8ANkvaCdxHSiIALwAukTQBPAycExH3FRWrmZlNVeQhJiJiG7CtpuzCqumfAa/O6fdx4ONFxmZmZo3N1UFqMzNrMycIMzPL5QRhZma5nCDMzCyXE4SZmeVygjAzs1xOEGZmlssJwszMcjlBmJlZLicIMzPL5QRhZma5nCDMzCyXE4SZmeVygjAzs1xOEGZmlssJwjrb2BgMDqb/sV6wIN0PDqZyM2vICcI618gIrFgBQ0MwPg4R6X5oKJWPjLQ7QrM5zQnCOtPYGPT3w4EDMDHx2LqJiVTe3+89CbMGnCCsM23YMDUx1JqYgI0by4nHbB5ygrDOtGVLawli8+Zy4jGbh5wgrDPt3z+77cy6kBOEdabFi2e3nVkXcoKwzrR6NVQqjdtUKrBmTTnxmM1DThDWmdavby1BrFtXTjxm81B3Jwj/iKpz9fbC8DD09ExNFJVKKh8eTu3MLFf3Jgj/iKrz9fXB9u0wMMD4oh4eRulLwMBAKu/ra3eEZnPaIe0OoC2qf0RVa2Ii3fr700bE3zDnt95e2LSJUxenZLD70rPaHJDZ/NGdexD+EZWZWVPdmSD8IyprlceprIt1Z4Lwj6isFR6nsi7XnQnCP6KyZnyxP7MuTRD+EZU143Eqsy5NEP4RlTXjcSqzLk0Q/hGVNTMb41Qe4LZ5rjsTBPhHVNbYTMepZjrA7eRic0D3Jgh49EdU6z7KiW/5F9i3DzZt8p6DzWycaqYD3O1OLjPp321953PcrYiIjrg9+9nPjoN1/Fs+Hce/5dNd07edy543fXfujOjpiUib5/xbT09qV+uP/iiiUmnct1KJOPfc2V1uRMS2bam+dvmVSirftq3x855J/27rO5/jrgKMRp3taqF7EJLOlLRD0k5J5+fUHyrpmqz+q5KWV9W9NSvfIeklRcZpNsVMxqlmMsA9k7OnZrrnMpP+3dZ3Psc9DYUlCEkLgcuAPuAU4LWSTqlp9ibg/oh4CrAReG/W9xRgFfA04EzgH7L5mZXnYMepZjLA3a7kMtP+3da3ncsu8RTsIvcgTgN2RsSuiHgQuBo4u6bN2cCV2fQwcLokZeVXR8TPI+K7wM5sfmblOphxqpkMcLcrucy0f7f1beeySzwFu8gEcQxwZ9XjPVlZbpuIeAjYBxzZYl8kDUgalTS6d+/eWQzdbAZmMsDdruQy0/7d1redyy7zUkH1BidmegP6gaGqx2uATTVtvgkcW/V4DFgGbAJWV5V/AOhvtLyZDFKbzap2DXAffnjjfpO3JUvy455J/27rO5/jrkGbBqnvAo6renxsVpbbRtIhwBOAe1vsazY3zWSAeya/8p/pJWRm0r/b+rZz2WVeKqhe5pjpjfRnRLuAE4BFwC3A02ranAu8P5teBXw0m35a1v7QrP8uYGGj5XkPwuacnTvTN/0lSyIWLEj3555b/xTVSQd7CuNMT5GdSf9u6zuf465Bgz2IwhJEWi4vBW4jHTq6ICu7BHhFNn0Y8DHSIPTXgBOr+l6Q9dsB9DVblhOEdZSyk8ts9O+2vvM57iptSxBl3pwgzDIHm1xmo3+39Z3PcWcaJQil+vlv5cqVMTo62u4wzMzmFUk3RsTKvLruvhaTmZnV5QRhZma5nCDMzCxXx4xBSNoL3DGDWSwDfjRL4cwmxzU9jmt6HNf0dGJcx0fEUXkVHZMgZkrSaL2BmnZyXNPjuKbHcU1Pt8XlQ0xmZpbLCcLMzHI5QTzq8nYHUIfjmh7HNT2Oa3q6Ki6PQZiZWS7vQZiZWS4nCDMzy9VVCULSmZJ2SNop6fyc+kMlXZPVf1XS8hJiOk7SFyR9S9Ktkv40p80LJe2TdHN2u7DouKqWvVvSN7LlTrnYlZK/z9bZdknPKiGmk6vWxc2SHpD0ZzVtSllnkq6QdI+kb1aVHSHpOkm3Z/dL6/Rdm7W5XdLaEuL6G0nfyV6nT0p6Yp2+DV/zAuK6WNJdVa/VS+v0bfj5LSCua6pi2i3p5jp9i1xfuduH0t5j9a7i12k3YCHp8uEn8uj/U5xS02aQx/4/xTUlxHU08Kxs+nDS5dFr43oh8Ok2rbfdwLIG9S8FRgABvw58tQ2v6w9JP/YpfZ0BLwCeBXyzquyvgfOz6fOB9+b0O4L0PydHAEuz6aUFx3UGcEg2/d68uFp5zQuI62LgzS28zg0/v7MdV039BuDCNqyv3O1DWe+xbtqDOA3YGRG7IuJB4Grg7Jo2ZwNXZtPDwOmSVGRQEfGDiLgpmx4Hvk3O/2/PYWcD/xTJ9cATJR1d4vJPB8YiYia/oj9oEfEl4L6a4ur30ZXA7+R0fQlwXUTcFxH3A9cBZxYZV0R8LtJ/vwNcT/qnxlLVWV+taOXzW0hc2Tbg94CPzNbyWtVg+1DKe6ybEsQxwJ1Vj/cwdUP8SJvsg7QPOLKU6IDskNYzga/mVP+GpFskjUh6WlkxAQF8TtKNkgZy6ltZr0VaRf0PbrvW2S9HxA+y6R8Cv5zTpt3r7Q9Ie355mr3mRTgvO/R1RZ3DJe1cX78J3B0Rt9epL2V91WwfSnmPdVOCmNMkLQY+DvxZRDxQU30T6RDK04H3AZ8qMbTnR8SzgD7gXEkvKHHZDUlaBLyC9K+Etdq5zh4RaV9/Tp1LLukC4CHgw3WalP2a/x+gF3gG8APS4Zy55LU03nsofH012j4U+R7rpgRxF3Bc1eNjs7LcNpIOAZ4A3Ft0YJIqpBf/wxHxidr6iHggIvZn09uAiqRlRceVLe+u7P4e4JOkXf1qrazXovQBN0XE3bUV7VxnwN2Th9my+3ty2rRlvUl6A/Ay4PXZhmWKFl7zWRURd0fELyLiYeD/1lleu9bXIcCrgGvqtSl6fdXZPpTyHuumBHEDcJKkE7JvnquArTVttgKTI/39wOfrfYhmS3Z88wPAtyPib+u0edLkWIik00ivWxmJ6/GSDp+cJg1yfrOm2Vbg95X8OrCvate3aHW/2bVrnWWq30drgX/OaXMtcIakpdkhlTOyssJIOhP4S9J/wh+o06aV13y246oes3plneW18vktwouA70TEnrzKotdXg+1DOe+xIkbe5+qNdMbNbaSzIS7Iyi4hfWAADiMdrtgJfA04sYSYnud9h6kAAAFzSURBVE/aPdwO3JzdXgqcA5yTtTkPuJV05sb1wPNKWl8nZsu8JVv+5Dqrjk3AZdk6/QawsqTYHk/a4D+hqqz0dUZKUD8AJkjHeN9EGrf6N+B24F+BI7K2K4Ghqr5/kL3XdgJvLCGunaRj0pPvs8kz9n4F2NboNS84rs3Ze2c7acN3dG1c2eMpn98i48rKPzT5nqpqW+b6qrd9KOU95kttmJlZrm46xGRmZtPgBGFmZrmcIMzMLJcThJmZ5XKCMDOzXE4QZgWStLz6CqFm84kThJmZ5XKCMCuJpBMlfV3Sc9odi1krDml3AGbdQNLJpEtUvyEibml3PGatcIIwK95RpGvlvCoivtXuYMxa5UNMZsXbB3yPdF0ds3nDexBmxXuQdJXSayXtj4ir2h2QWSucIMxKEBE/kfQy4LosSZRxqWqzGfHVXM3MLJfHIMzMLJcThJmZ5XKCMDOzXE4QZmaWywnCzMxyOUGYmVkuJwgzM8v1/wFhYUqWfjyoeQAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "%matplotlib inline\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "def factorial(n):\n",
    "    return 1 if n<=1 else n * factorial(n-1)\n",
    "\n",
    "def combination(n, k):\n",
    "    return factorial(n)/(factorial(k)*factorial(n-k))\n",
    "\n",
    "def binomial(k, n, p):\n",
    "    return combination(n, k) * p**k * (1-p)**(n-k)\n",
    "\n",
    "n = 20\n",
    "p = 0.20\n",
    "\n",
    "for k in range(0, n+1):\n",
    "    y = binomial(k, n, p)\n",
    "    plt.plot([k, k], [0, y], 'C0', lw=2)\n",
    "    plt.plot(k, y, 'r.', ms=20)\n",
    "plt.xlabel('k')\n",
    "plt.ylabel('Probability')\n",
    "plt.title(f\"Binomial Distribution n={n}, p={p}\")"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 3,
     "link": "[7.5.3.1 Poisson distribution](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.3.1-Poisson-distribution)",
     "section": "7.5.3.1 Poisson distribution"
    }
   },
   "source": [
    "### 7.5.3.1 Poisson distribution\n",
    "\n",
    "Now imagine the events are occuring at an average rate $r$ of events per unit time. In period $t$ there would be, on average, $r t$ events. If that period is broken into $n$ intervals then \n",
    "\n",
    "$$ p = \\frac{rt}{n}$$\n",
    "\n",
    "which leads to the Poisson distribution \n",
    "\n",
    "$$\\begin{align*}\n",
    "\\text{Poisson}(k | r, t) & = \n",
    "\\lim_{n\\rightarrow\\infty}\\text{Binomial}(k | n, \\frac{rt}{n}) \\\\\n",
    "& = \\lim_{n\\rightarrow\\infty} \\frac{n!}{k! (n-k)!} (\\frac{rt}{n})^k (1 - \\frac{rt}{n})^{n-k}\n",
    "\\end{align*}$$\n",
    "\n",
    "We're interested in the limit $n\\rightarrow\\infty$. Without detailing the math, the limit works out to be\n",
    "\n",
    "$$\\text{Poisson}(k | r, t) = \\frac{(rt)^k e^{-rt}}{k!}$$\n",
    "\n",
    "which is the probability of seeing $k$ events in an interval of length $t$ when the average rate is $r$ events per unit time."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 111,
   "metadata": {
    "nbpages": {
     "level": 3,
     "link": "[7.5.3.1 Poisson distribution](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.3.1-Poisson-distribution)",
     "section": "7.5.3.1 Poisson distribution"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<matplotlib.legend.Legend at 0x7fbe974ddf10>"
      ]
     },
     "execution_count": 111,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAY4AAAEWCAYAAABxMXBSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3df3hU5Zn/8fedOAQpRgHZrhUsGOlahQCSonaLtdJa4tWKulFRQd1qc7nRr9ayrei2omy//lgvSusXFZVWEFSQtChdm7JurbXd9QegEIhKYSwW0K4ILgSjMIT7+8c5wWGYTGbI/Ar5vK5rrpnznOc5c8+Q5OZ5zjnPY+6OiIhIukoKHYCIiHQtShwiIpIRJQ4REcmIEoeIiGREiUNERDKixCEiIhlR4hARkYwocYgUATMbamZLzex9Mzvg5ioz62tmi83sQzN728wuTdh/aVj+oZk9ZWZ98xe9dDdKHCLFIQY8CVzVzv77gN3Ap4HLgAfM7GSA8PlBYFK4vwW4P9cBS/dlunNcJDUz2wDMBC4HPgv8BrjC3T/OwXudAKxzd4sr+xTwATDU3f8Uls0DNrv7FDO7Axjk7peG+yqAN4B+7t6c7RhF1OMQSc9FwDhgMFAJXJmskpl9ycz+N8XjSwfx3p8D9rQljdAq4OTw9cnhNgDuHiXonXzuIN5LpEOHFToAkS7iXnd/B8DMfgWMSFbJ3f8IHJXl9+4N7Ego2w4cEbd/e4r9IlmlHodIev4a97qF4I91vuwEyhPKyoHmNPeLZJUSh0gWmdkYM9uZ4jHmIA77J+AwMxsSVzYcaApfN4XbbTEcD5SF7USyTkNVIlnk7n/gIHojZmYEf+x7hNs9g8P5Lnf/0Mx+CUwzs6sJhsnGA18Mmz8GvBgmpVeBacAvdWJcckU9DpHi8FngIz7pRXwErI3bXwccDrwHPAH8k7s3AYTP1xAkkPcIzm3U5Sds6Y50Oa6IiGREPQ4REcmIEoeIiGREiUNERDKixCEiIhnpFpfjHn300T5o0KBChyEi0qWsWLHifXfvn1jeLRLHoEGDWL58eaHDEBHpUszs7WTlGqoSEZGMKHGIiEhGlDhERCQj3eIch2QoGoXp02H+fNi5E3r3hokTYfJkqKgodHQiScViMTZt2sTHH2d9fa1DXs+ePRkwYACRSCSt+jmdcsTMxgE/BUqB2e5+V8L+7wJXA3uALcC33P3tcN8VwA/Cqj9y97lh+ShgDsG8Pb8GbvAOPkRVVZXr5HiaGhqgpgZiseDRJhIJHvX1UF1duPhE2vHnP/+ZI444gn79+hHMGSnpcHe2bt1Kc3MzgwcP3m+fma1w96rENjkbqjKzUoJ1kquBk4BLzOykhGqvAVXuXgnUA/8Wtu0LTAVOBUYDU82sT9jmAeDbwJDwMS5Xn6HLikahrg7Ky6GkJHiuqwvKO2pXUwMtLfsnDQi2W1qC/R0dR6QAPv74YyWNg2Bm9OvXL6OeWi7PcYwG1rv7W+6+G1hAMBX0Pu7+O3dvCTdfAgaEr78OPOvu29z9A+BZYJyZHQOUu/tLYS/jUeC8HH6GrqehASorYfZsaG4G9+B59uygvKGh/bbTpx+YMBLFYjBjRnZjFskSJY2Dk+n3lsvEcSywMW57U1jWnquAtr9q7bU9Nnyd7jG7l7DHEC1roe5rMcqnQMlUKJ8CdV+LES3roMcwfz7EYkT7QN057N/+HIj2IUgc8+bl9WOJZN3B9soFKJKrqsxsIlAF3JPFY9aa2XIzW75ly5ZsHba4TZ9Ow3G7qPwnmD0KmnuCW/A8exRU/hM0HLer/R7Dzp00nEDq9icE9US6rM70yjtQWlrKiBEjGD58OKeccgr//d//DcA777xDTU1Ntj5BUsuXL+f6669PWef555/nG9/4RqffK5eJYzMwMG57QFi2HzP7KvAvwLnuvquDtpv5ZDir3WMCuPtD7l7l7lX9+x9wx/whKfqrR6m5oJWWHhAr3X9frBRaekDNBa1El8xN3v7YXtRcROr2FwX1RLqkHJ/HO/zww1m5ciWrVq3izjvv5OabbwbgM5/5DPX19Z2NPqWqqiruvffenL5Hm1wmjmXAEDMbbGY9gAnAkvgKZjYSeJAgabwXt2spcLaZ9QlPip8NLHX3d4EdZnZauNTm5cDTOfwMXcr04R8e8Ac/UawUZgxL3mOYfumg9NpfOujgAhQptDyex9uxYwd9+gTX9GzYsIGhQ4cCMGfOHC644ALGjRvHkCFD+P73v7+vzRNPPMGwYcMYOnQoN910077y3r17873vfY+TTz6Zr371q7zyyiuceeaZHH/88SxZEvxZje9NvPLKK5x++umMHDmSL37xi6xdG7+YZOflLHG4+x7gOoIk8AbwpLs3mdk0Mzs3rHYPwfrMi8xspZktCdtuA/6VIPksA6aFZRAsiTkbWA9E+eS8SLc3v/LAnkKiWCnMG95O+yM3pNe+fMNBxSdScOF5vJQ6cR7vo48+YsSIEZx44olcffXV/PCHP0xab+XKlSxcuJDVq1ezcOFCNm7cyDvvvMNNN93Ec889x8qVK1m2bBlPPfUUAB9++CFnnXUWTU1NHHHEEfzgBz/g2WefZfHixdx6660HHP/EE0/kD3/4A6+99hrTpk3jlltuOajP056c3gDo7r8muNcivuzWuNdfTdH258DPk5QvB4ZmMcxDxs4enau3M9aSfEdivT3p1RMpOumenzvI83htQ1UAL774Ipdffjlr1qw5oN7YsWM58sgjATjppJN4++232bp1K2eeeSZtQ+uXXXYZL7zwAueddx49evRg3LjgzoNhw4ZRVlZGJBJh2LBhbNiw4YDjb9++nSuuuIJ169ZhZsQ6SpYZKoqT45IdvXt8Ks16vTMqP9h6IkWnd5o/u+nWS+H000/n/fffJ9nFOWVlZftel5aWsmfPnpTHikQi+y6ZLSkp2de+pKQkadsf/vCHfOUrX2HNmjX86le/yvrd9Eoch5CJwy8nQuqxpgilTBpxRfL2lROJlKSeciBSEmFS5aSDjlGkoCZODGZASCUSgUmd/xl/8803aW1tpV+/fmnVHz16NL///e95//33aW1t5YknnuDLX/7yQb339u3bOfbY4E6FOXPmHNQxUlHiOIRMPn0ykUhZyjqRSBk3nnZj++1LO0gcpZF224sUvcmT00scNx7cz3jbOY4RI0Zw8cUXM3fuXEpLOzhxGDrmmGO46667+MpXvsLw4cMZNWoU48eP77hhEt///ve5+eabGTlyZIe9mYOR07mqikV3mquqYV0DNYtqiLXGiO39ZFwzUhIhUhqh/sJ6qoe0P9dUZ9uLFMobb7zB5z//+Y4raj62pJJ9f3mfq0oKo3pINY3XNFI7qpbysnJKrITysnJqR9XSeE1jh3/0O9tepOhVV0NjI9TW7n/neG1tUN4Nk0am1OMQkUNC2j0OSUo9DhERyRklDhERyYgSh4iIZESJQ0S6nei2KHXP1FF+Zzklt5dQfmc5dc/UEd2madXTocQhIt1Kw7oGKmdVMvvV2TTvbsZxmnc3M/vV2VTOqqRhXeenVR86dCgXXnghLS3tT8+zZMkS7rrrrnb3FzMlDhHpNqLbotQsqqEl1rLffUoAsb0xWmIt1CyqOeieR9tcVWvWrKFHjx7MmjWr3brnnnsuU6ZMOaj3KTQlDhHpNqa/OJ1Ya+oJ/2KtMWa81Plp1ceMGcP69evZtm0b5513HpWVlZx22mk0NjYCwVQg1113HQCLFi1i6NChDB8+nDPOOAOApqYmRo8ezYgRI6isrGTdunUA/PjHP2bo0KEMHTqUn/zkJ0AwbfvnP/95vv3tb3PyySdz9tln89FHH3X6M7RHiUNEuo35jfMP6Gkkiu2NMa+xc8sj79mzh4aGBoYNG8bUqVMZOXIkjY2N3HHHHVx++eUH1J82bRpLly5l1apV+9bXmDVrFjfccAMrV65k+fLlDBgwgBUrVvDII4/w8ssv89JLL/Hwww/z2muvAbBu3TquvfZampqaOOqoo/jFL37Rqc+QihKHiHQbO3enN116uvUStc1VVVVVxXHHHcdVV13FH//4RyaFkyaeddZZbN26lR07duzX7u///u+58sorefjhh2ltbQWC2XXvuOMO7r77bt5++20OP/xw/vjHP3L++efzqU99it69e3PBBRfwhz/8AYDBgwczYsQIAEaNGpV0uvVsyel6HCIixaR3j940725Oq97BiF+PIxOzZs3i5Zdf5plnnmHUqFGsWLGCSy+9lFNPPZVnnnmGc845hwcffDDlMRKnau+yQ1VmNs7M1prZejM74CyQmZ1hZq+a2R4zq4kr/0q4ImDb42MzOy/cN8fM/hy3b0QuP4OIHDoKsXTAmDFjeOyxx4Bgedejjz6a8vLy/epEo1FOPfVUpk2bRv/+/dm4cSNvvfUWxx9/PNdffz3jx4+nsbGRMWPG8NRTT9HS0sKHH37I4sWLGTNmTNZiTVfOehxmVgrcB3wN2AQsM7Ml7v56XLW/AFcC/xzf1t1/B4wIj9OXYJnY/4ir8j13z+3K7yJyyJl8+mTmrpqb8jxHtpcOuO222/jWt75FZWUlvXr1Yu7cuQfU+d73vse6detwd8aOHcvw4cO5++67mTdvHpFIhL/927/llltuoW/fvlx55ZWMHj0agKuvvpqRI0fmdFgqmZxNcmhmpwO3ufvXw+2bAdz9ziR15wD/niwZmFkt8GV3v6yjuu3RJIcih750JznU0gHJFcskh8cCG+O2N4VlmZoAPJFQ9n/NrNHMZphZ0pWLzKzWzJab2fJkSzeKSPekpQM6r6hPjpvZMcAwYGlc8c3AX4EewEPATcC0xLbu/lC4n6qqqkN/7ngRSVtF3wpmnjOTmefMLHQoXVIuexybgYFx2wPCskxcBCx29339SXd/1wO7gEeA0Z2OVEQOCd1hfaFcyPR7y2XiWAYMMbPBZtaDYMhpSYbHuISEYaqwF4KZGXAesCYLsYpIF9ezZ0+2bt2q5JEhd2fr1q307Nkz7TY5G6py9z1mdh3BMFMp8HN3bzKzacByd19iZl8AFgN9gG+a2e3ufjKAmQ0i6LH8PuHQj5lZf8CAlcA1ufoMItJ1DBgwgE2bNqFzmpnr2bMnAwYMSLu+lo4VEZGktHSsiIhkhRKHiIhkRIlDREQyosQhIiIZUeIQEZGMKHFI9kWjUFcH5eVQUhI819UF5SLS5SlxSHY1NEBlJcyeDc3N4B48z54dlDc0FDpCEekkJQ7JnmgUamqgpQViCdNWx2JBeU2Neh4iXZwSh2TP9OkQixHtA3XnQPkUKJkaPNedA9E+BAlkxoxCRyoinaA7xyV7ystp+HQzNRdBrDR4tIm0Bo/6J6H6vXLYvr1wcYpIWnTnuORcNBIkjZYe+ycNCLZbekDNRUE9Eem6lDgka6aPiRyQMBLFSmHGmKJeBkZEOqDEIVkzf/iBPY1EsVKYV2n5CUhEckKJQ7JmZ8meNOvFOq4kIkVLiUOypneP3unVKzsix5GISC4pcUjWTKycSKQkkrJOpCTCpMpJeYpIRHIhp4nDzMaZ2VozW29mU5LsP8PMXjWzPWZWk7Cv1cxWho8lceWDzezl8JgLw2VppQhMPn0ykdIOEkdphBtPuzFPEYlILuQscZhZKXAfUA2cBFxiZiclVPsLcCXweJJDfOTuI8LHuXHldwMz3P0E4APgqqwHLwelom8F9RfW0yvS64CeR6QkQq9IL+ovrKeib0WBIhSRbMhlj2M0sN7d33L33cACYHx8BXff4O6NwN50DmhmBpwF1IdFc4HzshdycYhui1L3TB3ld5ZTcnsJ5XeWU/dMHdFtxT9VR/WQahqvaaR2VC3lZeWUWAnlZeXUjqql8ZpGqodUFzpEEemknN05Hg49jXP3q8PtScCp7n5dkrpzgH939/q4sj3ASmAPcJe7P2VmRwMvhb0NzGwg0ODuQ5McsxaoBTjuuONGvf3229n+iDnRsK6BmoX/QGzPx8Tsk3+biBuRw3pSf/Ev9MdXRPKiK945/tkw4EuBn5hZRuMb7v6Qu1e5e1X//v1zE2GWRbdFqVlwPi2tH+2XNABi5rS0fkTNgvO7RM9DRA5duUwcm4GBcdsDwrK0uPvm8Pkt4HlgJLAVOMrM2m49zuiYxW76b6YSi+1KWScW28WMpVPzFJGIyIFymTiWAUPCq6B6ABOAJR20AcDM+phZWfj6aODvgdc9GFf7HdB2BdYVwNNZj7xA5q99Mr07r99clJ+ARESSyFnicPc9wHXAUuAN4El3bzKzaWZ2LoCZfcHMNgEXAg+aWVPY/PPAcjNbRZAo7nL318N9NwHfNbP1QD/gZ7n6DPm209K7o3qn7c5xJCIi7cvpbHPu/mvg1wllt8a9XkYw3JTY7r+BYe0c8y2CK7YOOb13Q3NZGvVSj2aJiORUMZ8c73Ymvh4h0pq6TqQVJr2Z+iY7EZFcUuIoIpMHXphW4rhx4MX5CUhEJAkljiJS8Z1p1D9dRq/dHJBAIq3QazfUP11GxQ23FSQ+ERFQ4iguFRVU37OYxjk9qX3NKP8YSvZC+cdQ+5rROKcn1fcshgpN2SEihaM1x4tRNAozZsC8ebBzJ/TuDZMmwY03KmmISN60d+e4EoeIiCTVFaccERGRIqTEISIiGVHiEBGRjChxiIhIRpQ4REQkI0ocIiKSESUOERHJiBKHiIhkRIlDREQyosQhIiIZyWniMLNxZrbWzNab2ZQk+88ws1fNbI+Z1cSVjzCzF82sycwazeziuH1zzOzPZrYyfIzI5WcQEZH95WwFQDMrBe4DvgZsApaZ2ZK4JWAB/gJcCfxzQvMW4HJ3X2dmnwFWmNlSd//fcP/33L0+V7GLiEj7crl07GhgfbjUK2a2ABgP7Esc7r4h3Lc3vqG7/ynu9Ttm9h7QH/hfRESkoHI5VHUssDFue1NYlhEzGw30AKJxxf83HMKaYWZJV+k2s1ozW25my7ds2ZLp24qISDvSShxm9k0zy/uJdDM7BpgH/KO7t/VKbgZOBL4A9AVuStbW3R9y9yp3r+rfv39e4hUR6Q7STQYXA+vM7N/M7MQ022wGBsZtDwjL0mJm5cAzwL+4+0tt5e7+rgd2AY8QDImJiEiepJU43H0iMJJguGhOeMVTrZkdkaLZMmCImQ02sx7ABGBJOu8X1l8MPJp4EjzshWBmBpwHrEnnmCIikh1pDz+5+w6gHlgAHAOcD7xqZv+nnfp7gOuApcAbwJPu3mRm08zsXAAz+4KZbQIuBB40s6aw+UXAGcCVSS67fczMVgOrgaOBH2X2kUVEpDPSWjrWzMYTXDZ7AvAoMNfd3zOzXsDr7j4ol0F2lpaOFRHJXHtLx6Z7Oe4FwAx3fyG+0N1bzOyqbAQoIiJdQ7pDVX9NTBpmdjeAu/8261GJiEjRSjdxfC1JWXU2AxERka4h5VCVmf0TUAdUmFlj3K4jgP/KZWAiIlKcOjrH8TjQANwJxE9S2Ozu23IWlYiIFK2OEoe7+wYzuzZxh5n1VfIQEel+0ulxfANYAThgcfscOD5HcYmISJFKmTjc/Rvh8+D8hCMiIsWuo5Pjp6Ta7+6vZjccEREpdh0NVU1Psc+Bs7IYi0ggGoXp02H+fNi5E3r3hokTYfJkqKgodHQi3V5HQ1VfyVcgIgA0NBC9+gKmn7KL+dc6O8ug965mJq6ZxeQzHqFi9i+hWrcQiRRSyrmqzOwsd3/OzC5Itt/df5mzyLJIc1V1EdEoDeNPpmb8LmKlECv9ZFekNXjUP11G9dNN6nmI5MHBzlX1ZeA54JtJ9jnQJRKHdA3Rn9xKzfhdtPQ4cF9bIqkZv4vGn95Gxb3z8h+giAAdD1VNDZ//MT/hSHc2feMiYpWp68RKYcbGhcxEiUOkUNJdOrafmd1rZq+a2Qoz+6mZ9ct1cNK9zD8ptt/wVDKxUph3Yiw/AYlIUulOcrgA2AL8A1ATvl6Yq6Cke9qZZIgqab2y3MYhIqmlmziOcfd/dfc/h48fAZ/uqJGZjTOztWa23symJNl/RtiL2WNmNQn7rjCzdeHjirjyUWa2OjzmveESsnII6O2RNOulmWFEJCfSTRz/YWYTzKwkfFxEsCRsu8ysFLiPYPr1k4BLzOykhGp/IVhZ8PGEtn2BqcCpwGhgqpn1CXc/AHwbGBI+xqX5GaTITfy7i4i0pq4TaYVJJ16Yn4BEJKmUicPMms1sB8Ef6seB3eFjAVDbwbFHA+vd/S13b2szPr6Cu29w90Zgb0LbrwPPuvs2d/8AeBYYZ2bHAOXu/pIH1xE/CpyXzgeV4jd53O1EIqnHoSKRMm78+u15ikhEkkmZONz9CHcvD59L3P2w8FHi7uUdHPtYYGPc9qawLB3ttT02fN3hMc2s1syWm9nyLVu2pPm2UkgVfSuon7CYXqWHE/H9RyAjbvQqPZz6CYup6Kt7OEQKKd2hKsysj5mNDs9LnGFmZ+QysM5y94fcvcrdq/r371/ocCRN1UOqaaxbTe3oOsrLyimxEsrLyqkdXUdj3Wqqh+iucZFC6+gGQADM7GrgBmAAsBI4DXiR1HNVbQYGxm0PCMvSsRk4M6Ht82H5gIM8pnQRFX0rmHnOTGaeM7PQoYhIEun2OG4AvgC8Hc5fNRL43w7aLAOGmNlgM+sBTACWpPl+S4Gzw15OH+BsYKm7vwvsMLPTwqupLgeeTvOYIiKSBekmjo/d/WMAMytz9zeBv0vVwN33ANcRJIE3gCfdvcnMppnZueGxvmBmm4ALgQfNrClsuw34V4LkswyYFrfaYB0wG1gPRAmWthURkTxJOcnhvkpmi4F/BL5DMDz1ARBx93NyG152aJJDEZHMHewkhwC4+/nhy9vM7HfAkcBvshifiIh0EWklDti3GuCXCGbF/a/w3gwREelm0p3k8FZgLtAPOBp4xMx+kMvARESkOKXb47gMGB53gvwugstyf5SrwEREpDile1XVO0DPuO0ydP+EiEi3lLLHYWb/j+CcxnagycyeDbe/BryS+/BERKTYdDRU1XYN6wpgcVz58zmJRkREil5HS8fObXsd3v39uXBzrbtrGTYRkW4o3bmqziS4qmoDYMBAM7vC3V/IXWgiIlKM0r2qajpwtruvBTCzzwFPAKNyFZiIiBSndK+qirQlDQB3/xOQ3jqfIiJySEm3x7HCzGYD88Pty/jkxLmIiHQj6SaOa4BrgevD7T8A9+ckIhERKWodJg4zKwVWufuJwI9zH5KIiBSzDs9xuHsrsNbMjstDPCIiUuTSPTneh+DO8d+a2ZK2R0eNzGycma01s/VmNiXJ/jIzWxjuf9nMBoXll5nZyrjHXjMbEe57Pjxm276/Sf/j5kd0W5S6Z+oov7OckttLKL+znLpn6ohuixY6NBGRTkt3IacvJyt399+naFMK/IlgepJNBCv5XeLur8fVqQMq3f0aM5sAnO/uFyccZxjwlLtXhNvPA//s7mmfnM/nQk4N6xqoWVRDrDVGbO8n90hGSiJESiPUX1hP9ZDqvMQiItIZ7S3klLLHYWY9zew7BEu7nkiwDsfv2x4dvOdoYL27vxWu3bEAGJ9QZzzBjYUA9cDYcC3xeJeEbYtedFuUmkU1tMRa9ksaALG9MVpiLdQsqlHPQ0S6tI6GquYCVcBqoJrgRsB0HQtsjNveFJYlrROuUb6dYM2PeBcT3GwY75FwmOqHSRJNwUx/cTqx1tQzscRaY8x4aUaeIhIRyb6OEsdJ7j7R3R8EaoAxeYhpHzM7FWhx9zVxxZe5+7AwljHApHba1prZcjNbvmXLljxEC/Mb5x/Q00gU2xtjXuO8vMQjIpILHSWOfX8Fwx5BJjYDA+O2B3DgGh776pjZYQRrmW+N2z+BhN6Gu28On5uBxwmGxA7g7g+5e5W7V/Xv3z/D0A/Ozt0706u3qznHkYiI5E5HiWO4me0IH81AZdtrM9vRQdtlwBAzGxzOrDsBSLwSawlwRfi6BnjOw7P1ZlYCXETc+Q0zO8zMjg5fR4BvAGsoEr33pnc/Ze+9mq1FRLqujqZVLz3YA7v7HjO7DlgKlAI/d/cmM5sGLHf3JcDPgHlmth7YRpBc2pwBbHT3t+LKyoClYdIoBf4TePhgY8y2iatgdiXEUnxrkVaYtLrjK9lERIpVWpfjdnX5uhw32s+ovAZaerRfp9duaHzQqHh/b87jERHpjIO6HFcyUxE7gvong+QQad1/X6Q1KK9/MqgnItJVKXFk08SJVL8dofEBqF0B5R9Dyd7guXYFND4A1W9HYFLSC8FERLoEDVVlUzQKlZXQ0tJ+nV69oLERKipyH4+ISCdoqCofKiqgvj5IDpGEK6cikaC8vl5JQ0S6NCWObKuuDnoUtbVQXg4lJcFzbW1QXq15qkSka9NQlRxyotuiTH9xOvMb57Nz90569+jNxMqJTD59MhV91dsTSZeGqqRbaFjXQOX9w5i9bBbNu5txnObdzcxeNovK+4fRsK6h0CGKdHlKHHLIiG6LUrPgfFpaPyJm+/ekY+a0tH5EzYLzNTuxSCcpccghY/pvphKL7UpZJxbbxYylU/MUkcihSYlDDhnz1z6ZcroXCKaDmffmovwEJHKIUuKQQ8ZOSz2l/Sf1duc4EpFDmxKHHDJ6p5kPeqcezRKRDihxyCFj4uuRA+YISxRphUlvalp7kc5Q4pBDxuSBF6aVOG4ceHF+AhI5RClxyCGj4jvTqH+6LPXsxE+XUXHDbQWJT+RQocQhh46KCqrvWUzjnJ7Uvmb7z078mtE4pyfV9yzWXGEinZTTxGFm48xsrZmtN7MpSfaXmdnCcP/LZjYoLB9kZh+Z2crwMSuuzSgzWx22udfMLJefQbqY6moqXljDzM/Wsf3+clp/VML2+8uZ+dk6Kl5Yo7nCRLIgvUWyD4KZlQL3AV8DNgHLzGyJu78eV+0q4AN3P8HMJgB3A20D0FF3H5Hk0A8A3wZeBn4NjAM0j4R8oqICZs4MHiKSdbnscYwG1rv7W+6+G1gAjE+oMx6YG76uB8am6kGY2TFAubu/5MHsjI8C52U/dBERaU8uE8exwMa47U1hWdI67r4H2A70C/cNNrPXzOz3ZjYmrv6mDo4JgJnVmtlyM1u+ZWHSFZkAAA7JSURBVMuWzn0SERHZp1hPjr8LHOfuI4HvAo+bWXkmB3D3h9y9yt2r+vfvn5MgRUS6o1wmjs3AwLjtAWFZ0jpmdhhwJLDV3Xe5+1YAd18BRIHPhfUHdHBMERHJoVwmjmXAEDMbbGY9gAnAkoQ6S4Arwtc1wHPu7mbWPzy5jpkdDwwB3nL3d4EdZnZaeC7kcuDpHH4GERFJkLOrqtx9j5ldBywFSoGfu3uTmU0Dlrv7EuBnwDwzWw9sI0guAGcA08wsBuwFrnH3beG+OmAOcDjB1VS6okpEJI+0dKyIiCSlpWNFRCQrlDhERCQjShwiIpIRJQ4REcmIEoeIiGREiUNERDKixCEiIhlR4hARkYwocYiISEaUOEQSRLdFqXumjvI7yym5vYTyO8upe6aO6LZooUMTKQpKHCJxGtY1UDmrktmvzqZ5dzOO07y7mdmvzqZyViUN6zQ1mogSh0goui1KzaIaWmItxPbG9tsX2xujJdZCzaIa9Tyk21PiEAlNf3E6sdiulHVisV3MeGlGniISKU5KHCKh+aseJUZryjoxWpm3cm6eIhIpTkocIqGduz9Ms97OHEciUtyUOERCvXdnt57IoSqnicPMxpnZWjNbb2ZTkuwvM7OF4f6XzWxQWP41M1thZqvD57Pi2jwfHnNl+PibXH4G6T4mNkIk9UgVkVaYtCo/8YgUq5wljnDN8PuAauAk4BIzOymh2lXAB+5+AjADuDssfx/4prsPI1iTfF5Cu8vcfUT4eC9Xn0G6l8mrPpVW4rhxde/8BCRSpHLZ4xgNrHf3t9x9N7AAGJ9QZzzQdqaxHhhrZubur7n7O2F5E3C4mZXlMFYRKr55OfW/LKXX7gN7HpFW6LUb6n9ZSsW5VxQmQJEikcvEcSywMW57U1iWtI677wG2A/0S6vwD8Kq7x18n+Ug4TPVDM7Nkb25mtWa23MyWb9mypTOfQ7qLyZOp/ksZjQ9A7Qoo/xhK9gbPtSug8QGo/ksZ3HhjoSMVKajDCh1AKmZ2MsHw1dlxxZe5+2YzOwL4BTAJeDSxrbs/BDwEUFVV5XkIV7q6igqor6eipoaZz8aY+eu4mwAjkeBRXx/UE+nGctnj2AwMjNseEJYlrWNmhwFHAlvD7QHAYuByd993q667bw6fm4HHCYbEskpzFXVj1dXQ2Ai1tVBeDiUlwXNtbVBeXV3oCEUKztxz85/xMBH8CRhLkCCWAZe6e1NcnWuBYe5+jZlNAC5w94vM7Cjg98Dt7v7LhGMe5e7vm1kEeAL4T3eflSqWqqoqX758eVpxN6xroGbhPxDb8zEx++S7ibgROawn9Rf/guoh+uMhIoc+M1vh7lWJ5TnrcYTnLK4DlgJvAE+6e5OZTTOzc8NqPwP6mdl64LtA2yW71wEnALcmXHZbBiw1s0ZgJUFCejhbMUe3RalZcD4trR/tlzQAYua0tH5EzYLz1fMQkW4tZz2OYpJuj6Pu8YnMfvMxYqXt14m0Qu3nL2PmJfOzGKGISPHJe4+jK5q/9smUSQMgVgrz3lyUn4BERIqQEkecnRbruBKw0zTnhLRPF1fIoU6JI07acxWlnnlburGGdQ1U3j+M2ctm7b8Q1LJZVN4/TAtBySFBiSPOxNcj6c1V9GYkPwFJl6KLK6S7UOKIM3nghenNVTTw4vwEJF3K9N9MTW8hqKVT8xSRSG4occSp+M406p8uSz1X0dNlVNxwW0Hik+Kmiyuku1DiiFdRQfU9i2mc05Pa12z/uYpeMxrn9KT6nsWackKS0sUV0l0ocSSqrqbihTXM/Gwd2+8vp/VHJWy/v5yZn62j4oU1mnJC2qWLK6S7UOJIpqICZs6E7duhtTV4njlTPQ1JSRdXSHehxCGSJdm6uCK68jnqbhpK+S1GyW1G+S1G3U1Dia58LovRihw8JQ6RLMnGxRUNT0yjctFYZpc10VwGbtBcBrPLmqhcNJaGJ6bl9kOIpEGJQyRbOnlxRXTlc9SsmUpLDw64OitWCi09oGbNVPU8pOCUOESyqRMXV0x/4vq0LuedseCGlHU01CW5ptlxRYpE+S1Gc1ka9XbB9juS/942PDGNmjVTiZXu32uJtAaP+qG3U33JrSmPH135HNOfuJ75pU3s7BFcLTax9WQmX3IvFSPOyuQjSRen2XFFitzOHmnWa+eirGwMdWXjHEtnezxqX9j26VCPQ6RIdLbHUXfTUGaXNXW8nszuocy8a/UB+6Irn6Ny0VhaUiSwXruh8cLfttvz6GyPR+0L2z5RQXocZjbOzNaa2Xozm5Jkf5mZLQz3v2xmg+L23RyWrzWzr6d7TJGuamLryendB7J3aNJ980tTJw0IpzwpWZN0X2fPsXS2x6P2hW2fiZwlDjMrBe4DqoGTgEvM7KSEalcBH7j7CcAM4O6w7UnABOBkYBxwv5mVpnlMkS5p8iX3pncfyISfJt3X2aGuQicetS9s+0zksscxGljv7m+5+25gATA+oc54YG74uh4Ya2YWli9w913u/mdgfXi8dI4p0iVVjDiL+qG3p74PZOjt7Q4TpT3lSTtTahU68ah9YdtnIpeJ41hgY9z2prAsaR133wNsB/qlaJvOMQEws1ozW25my7ds2dKJjyGSP9WX3Erjhb+ldvdQyneF94HsCs5LNF7425Tj050d6ip04lH7wrbPxGGdP0RxcveHgIcgODle4HBE0lYx4ixmjljNzAzbTb7kXuYuGtvhyfH2hromtp7M7NaOT66nSjzpnNxvL/GofWHbZyKXPY7NwMC47QFhWdI6ZnYYcCSwNUXbdI4p0i11dqirs+dYOtvjUfvCts9ELhPHMmCImQ02sx4EJ7uXJNRZAlwRvq4BnvPg+uAlwITwqqvBwBDglTSPKdJtdWaoq9CJR+0L2z4TOUsc4TmL64ClwBvAk+7eZGbTzOzcsNrPgH5mth74LjAlbNsEPAm8DvwGuNbdW9s7Zq4+g0hXVDHiLGbetZrtdzittzvb73Bm3rU6rbu+C5l41L6w7TOhGwBFJKuiK59jxoIbmFeyhp2RYEx90t6h3Djhp2n90VL7wraP194NgEocIiKSlOaqEhGRrFDiEBGRjChxiIhIRrrFOQ4z2wK8fZDNjwbez2I42ab4OkfxdY7i65xij++z7t4/sbBbJI7OMLPlyU4OFQvF1zmKr3MUX+cUe3zt0VCViIhkRIlDREQyosTRsYcKHUAHFF/nKL7OUXydU+zxJaVzHCIikhH1OEREJCNKHCIikhEljpCZjTOztWa23symJNlfZmYLw/0vm9mgPMY20Mx+Z2avm1mTmR2waLCZnWlm281sZfhofxrT3MS4wcxWh+99wMRgFrg3/P4azeyUPMb2d3Hfy0oz22Fm30mok9fvz8x+bmbvmdmauLK+Zvasma0Ln/u00/aKsM46M7siWZ0cxXePmb0Z/vstNrOj2mmb8mchh/HdZmab4/4Nz2mnbcrf9RzGtzAutg1mtrKdtjn//jrN3bv9AygFosDxQA9gFXBSQp06YFb4egKwMI/xHQOcEr4+AvhTkvjOBP69gN/hBuDoFPvPARoAA04DXi7gv/VfCW5sKtj3B5wBnAKsiSv7N2BK+HoKcHeSdn2Bt8LnPuHrPnmK72zgsPD13cniS+dnIYfx3Qb8cxr//il/13MVX8L+6cCthfr+OvtQjyMwGljv7m+5+25gATA+oc54YG74uh4Ya2aWj+Dc/V13fzV83UywFknStdaL2HjgUQ+8BBxlZscUII6xQNTdD3Ymgaxw9xeAbQnF8T9jc4HzkjT9OvCsu29z9w+AZ4Fx+YjP3f/DgzVxAF4iWIGzINr5/tKRzu96p6WKL/y7cRHwRLbfN1+UOALHAhvjtjdx4B/mfXXCX57tQL+8RBcnHCIbCbycZPfpZrbKzBrM7OS8BgYO/IeZrTCz2iT70/mO82EC7f/CFvL7A/i0u78bvv4r8OkkdYrle/wWQQ8ymY5+FnLpunAo7eftDPUVw/c3Bvgfd1/Xzv5Cfn9pUeLoQsysN/AL4DvuviNh96sEwy/Dgf8HPJXn8L7k7qcA1cC1ZnZGnt+/Q+Fyw+cCi5LsLvT3tx8PxiyK8lp5M/sXYA/wWDtVCvWz8ABQAYwA3iUYDipGl5C6t1H0v0tKHIHNwMC47QFhWdI6ZnYYcCSwNS/RBe8ZIUgaj7n7LxP3u/sOd98Zvv41EDGzo/MVn7tvDp/fAxYTDAnES+c7zrVq4FV3/5/EHYX+/kL/0zZ8Fz6/l6ROQb9HM7sS+AZwWZjcDpDGz0JOuPv/eLDE9F7g4Xbet9Df32HABcDC9uoU6vvLhBJHYBkwxMwGh/8rnQAsSaizBGi7gqUGeK69X5xsC8dEfwa84e4/bqfO37adczGz0QT/tnlJbGb2KTM7ou01wUnUNQnVlgCXh1dXnQZsjxuWyZd2/6dXyO8vTvzP2BXA00nqLAXONrM+4VDM2WFZzpnZOOD7wLnu3tJOnXR+FnIVX/w5s/Pbed90ftdz6avAm+6+KdnOQn5/GSn02flieRBc9fMngisu/iUsm0bwSwLQk2CIYz3wCnB8HmP7EsGwRSOwMnycA1wDXBPWuQ5oIrhK5CXgi3mM7/jwfVeFMbR9f/HxGXBf+P2uBqry/O/7KYJEcGRcWcG+P4IE9i4QIxhnv4rgnNlvgXXAfwJ9w7pVwOy4tt8Kfw7XA/+Yx/jWE5wfaPsZbLvK8DPAr1P9LOQpvnnhz1YjQTI4JjG+cPuA3/V8xBeWz2n7mYurm/fvr7MPTTkiIiIZ0VCViIhkRIlDREQyosQhIiIZUeIQEZGMKHGIiEhGlDhECsDMBsXPnCrSlShxiIhIRpQ4RArMzI43s9fM7AuFjkUkHYcVOgCR7szM/o5gau8r3X1VoeMRSYcSh0jh9CeYj+oCd3+90MGIpEtDVSKFsx34C8FcZCJdhnocIoWzm2AW16VmttPdHy90QCLpUOIQKSB3/9DMvgE8GyaPfE7xLXJQNDuuiIhkROc4REQkI0ocIiKSESUOERHJiBKHiIhkRIlDREQyosQhIiIZUeIQEZGM/H96achQQS+MUAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "%matplotlib inline\n",
    "import matplotlib.pyplot as plt\n",
    "import numpy as np\n",
    "\n",
    "def factorial(n):\n",
    "    return 1 if n<=1 else n * factorial(n-1)\n",
    "\n",
    "def combination(n, k):\n",
    "    return factorial(n)/(factorial(k)*factorial(n-k))\n",
    "\n",
    "def binomial(k, n, p):\n",
    "    return combination(n, k) * p**k * (1-p)**(n-k)\n",
    "\n",
    "def poisson(k, r, t):\n",
    "    return (r*t)**k * np.exp(-r*t)/factorial(k)\n",
    "\n",
    "t = 2.0\n",
    "r = 2.0\n",
    "\n",
    "n = 100\n",
    "p = r*t/n\n",
    "\n",
    "k = range(0, 20)\n",
    "plt.plot(k, [binomial(k, n, p) for k in k], 'r.', ms=20, label=\"Binomial\")\n",
    "plt.plot(k, [poisson(k, r, t) for k in k], 'g.', ms=20, label=\"Poisson\")\n",
    "plt.xlabel(\"k\")\n",
    "plt.ylabel(\"Probability\")\n",
    "plt.title(f\"n = {n}\")\n",
    "plt.legend()\n"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 3,
     "link": "[7.5.3.2 Waiting time between events](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.3.2-Waiting-time-between-events)",
     "section": "7.5.3.2 Waiting time between events"
    }
   },
   "source": [
    "### 7.5.3.2 Waiting time between events\n",
    "\n",
    "Suppose an event has just occurred. What is the probability of no additional events in the next $t$ units of time? This is calculated with the Poisson distribution where $k=0$.\n",
    "\n",
    "$$\\text{Poisson}(0 | r, t) = e^{-r t}$$\n",
    "\n",
    "We can treat this as the probability distribution for the time period between events. We refer to this as the exponential distribution\n",
    "\n",
    "$$\\text{Exponential}(t | r) =  e^{-r t}$$\n",
    "\n",
    "This fact is useful in creating simulations of independent random events. For a given rate $r$, we sample values from an exponential distribution. "
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.4 Simulating a Poisson Process in SimPy](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.4-Simulating-a-Poisson-Process-in-SimPy)",
     "section": "7.5.4 Simulating a Poisson Process in SimPy"
    }
   },
   "source": [
    "## 7.5.4 Simulating a Poisson Process in SimPy\n",
    "\n",
    "Poisson processes are easy to implement in SimPy. A single parameter, commonly denoted as $r$ or $\\lambda$, is required to specify the average rate of occurance in units of number per unit time. For example, a value $\\lambda = 4.2 \\text{ min}^{-1}$ corresponds to an average of 4.2 events per minute.\n",
    "\n",
    "An alternative specification is so express the mean time between events. The rate of machine failures, for example, is typically specified as \"mean time between failures\" (MTBF). In these cases, $r = \\lambda = \\frac{1}{\\bar{\\tau}}$ where $\\bar{\\tau}$ is the mean time between events.\n",
    "\n",
    "Once the mean rate has been determined, the time between events can be simulated by drawing samples from an exponential distribution\n",
    "\n",
    "$$\\text{Exponential}(t | r) =  e^{-r t}$$\n",
    "\n",
    "The following cell demonstrates the simulation of a Poisson process with an average $r$ events per unit time."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 121,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.4 Simulating a Poisson Process in SimPy](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.4-Simulating-a-Poisson-Process-in-SimPy)",
     "section": "7.5.4 Simulating a Poisson Process in SimPy"
    }
   },
   "outputs": [],
   "source": [
    "%matplotlib inline\n",
    "import simpy\n",
    "import random\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "# average rate: events per unit time\n",
    "r = 2.0 \n",
    "\n",
    "def arrival(r):\n",
    "    while True:\n",
    "        yield env.timeout(random.expovariate(r))\n",
    "        data_log.append(env.now)\n",
    "\n",
    "data_log = []  \n",
    "env = simpy.Environment()\n",
    "env.process(arrival(r))\n",
    "env.run(10000)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.4 Simulating a Poisson Process in SimPy](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.4-Simulating-a-Poisson-Process-in-SimPy)",
     "section": "7.5.4 Simulating a Poisson Process in SimPy"
    }
   },
   "source": [
    "Visualization"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 122,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.4 Simulating a Poisson Process in SimPy](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.4-Simulating-a-Poisson-Process-in-SimPy)",
     "section": "7.5.4 Simulating a Poisson Process in SimPy"
    }
   },
   "outputs": [
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAA1gAAAHwCAYAAAC7T84CAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeXxeZZn/8c+3S9okXbK2TbN2Yyk7hBaVbWCEshYZQFEEFEEFlHFUEPUnDouDDg6KKA7KqqyiDqggorIMIyCt7EtpkjZNNxq6l3RLcv3+OCflIaQlbZ80Tft9v17P63nOfe5zn+s8OT3J1fs+91FEYGZmZmZmZluvX28HYGZmZmZmtqNwgmVmZmZmZpYlTrDMzMzMzMyyxAmWmZmZmZlZljjBMjMzMzMzyxInWGZmZmZmZlniBMvMzLJCUpWkVZL690Dbt0q6Mv18iKQZ2d5HN2IYKekJSSslfX9b79/MzPoGJ1hmZrZFJM2W9M8dyxExJyKGRERbT+43Iv43InbtyX1sxHnAW8CwiPhyL+z/PSTVSApJA3o7FjMzSzjBMjMz655q4NWIiN4OxMzMtl9OsMzMbLNJ+gVQBfwuHRZ4cefeFEmPSbpS0t/SOr+TVCzpDkkrJD0rqSajzd0kPSJpiaQZkk7byL4PlzQ3Y3m2pK9IelHSckn3SBqcsf54Sc9LWpbGsvcmjuuDaVzL0/cPpuW3AmcBF6fH8s9dbDtI0jWS5kh6U9JPJeWm616TdHxG3QGSmiXtny4flMa2TNILkg7PqPuYpCsk/V86PPFPkkrS1U+k78vSuD4gabykx9NjeEvSPRs7XjMzyz4nWGZmttki4pPAHOCEdFjg9zZS9WPAJ4FyYBzwFHALUAS8BlwGICkfeAS4ExiRbvcTSRO7GdJpwBRgDLA3cHba7n7AzcBngWLgv4EHJA3q3ICkIuAPwHVp3f8C/iCpOCLOBu4Avpce75+7iOFqYBdgX2B8eszfStfdBZyeUfdo4K2I+Iek8nS/V6bfy1eAX0sqzaj/ceBT6XeTk9YBODR9L0jjegq4AvgTUAhUAD/a6LdmZmZZ5wTLzMx60i0RUR8Ry4GHgPqI+HNEtAK/AvZL6x0PzI6IWyKiNSKeA34NnNrN/VwXEfMjYgnwO5IkB5L7pv47Ip6JiLaIuA1YCxzURRvHATMj4hdpDHcBrwMnvN/OJSnd15ciYklErAS+Q5IoQpI4nigpL13+OEnSBXAG8GBEPBgR7RHxCDANODZjF7dExBsRsRq4N+P4urKeZDjj6IhYExFPvl/8ZmaWPU6wzMysJ72Z8Xl1F8tD0s/VwOR0iNwyScuATwCjurmfhRmfWzq1++VO7VYCo7toYzTQ2KmskaQn6v2UAnnA9Iz9/DEtJyLqSHrsTkiTrBNJkq6OGE/tFOPBQFk3jq8rFwMC/i7pFUmf7kb8ZmaWJZ51yMzMtlQ2J3toAh6PiA9nsc2Odq+KiKu6UXc+SbKTqYokUXo/b5EkjHtExLyN1OkYJtiPZLKMuowYfxER53ZjP52952cQEQuBcwEkHQz8WdITGfszM7Me5B4sMzPbUm8CY7PU1u+BXSR9UtLA9HWgpN23st2fAZ+TNFmJfEnHSRraRd0H0xg+nk5C8VFgYhrbJkVEe7qvayWNAJBULunojGp3A0cBn+ed3iuAX5L0bB0tqb+kwelEHhXdOL5moJ2Mn4OkUzO2XUqShLV3oy0zM8sCJ1hmZral/gP4Zjqs7SvvW3sT0nuWjiK5Z2k+yZC47wLvmYxiM9udRtKbcz1JslFHOgFGF3UXk9wL9mVgMclQu+Mj4q1u7u6StP2nJa0A/gxseF5XRCwgmeTjg8A9GeVNwFTg6yQJUxPwVbrxOzoiWoCrgP9Lfw4HAQcCz0haBTwAXBQRDd08BjMz20ry4zzMzMzMzMyywz1YZmZmZmZmWeIEy8zMzMzMLEucYJmZmZmZmWWJEywzMzMzM7Ms2Smeg1VSUhI1NTW9HYaZmZmZme0gpk+f/lZElHYu3ykSrJqaGqZNm9bbYZiZmZmZ2Q5CUmNX5T02RFDSzZIWSXp5I+sl6TpJdZJelLR/xro2Sc+nrwcyysdIeibd5h5JOT0Vv5mZmZmZ2ebqyXuwbgWmbGL9McCE9HUecEPGutURsW/6OjGj/LvAtRExnuSBkedkN2QzMzMzM7Mt12MJVkQ8ASzZRJWpwO2ReBookFS2scqSBBwB3JcW3QaclK14zczMzMzMtlZvziJYDjRlLM9NywAGS5om6WlJHUlUMbAsIlq7qP8eks5L25jW3Nyc7djNzMzMzMzeY3ud5KI6IuZJGgv8VdJLwPLNaSAibgRuBKitrY0eiNHMzMzMzOxderMHax5QmbFckZYRER3vDcBjwH7AYpJhhAM61zczMzMzM9se9GaC9QBwZjqb4EHA8ohYIKlQ0iAASSXAh4BXIyKAR4FT0u3PAu7vjcDNzMzMzMy60mNDBCXdBRwOlEiaC1wGDASIiJ8CDwLHAnVAC/CpdNPdgf+W1E6SAF4dEa+m6y4B7pZ0JfAccFNPxW9mZmZmZra5eizBiojT32d9ABd0Uf43YK+NbNMATMpKgGZmZmZmZlnWm0MEzczMzMzMdihOsMzMzMzMzLLECZaZmZmZmVmWOMEyMzMzMzPLEidYZmZmZmZmWeIEy8zMzMzMLEucYJmZmZmZmWWJEywzMzMzM7MscYJlZmZmZmaWJU6wzMzMzMzMssQJlpmZmZmZWZY4wTIzMzMzM8sSJ1hmZmZmZmZZ4gTLzMzMzMwsS5xgmZmZmZmZZUmPJViSbpa0SNLLG1kvSddJqpP0oqT90/J9JT0l6ZW0/KMZ29wqaZak59PXvj0Vv5mZmZmZ2ebqyR6sW4Epm1h/DDAhfZ0H3JCWtwBnRsQe6fY/kFSQsd1XI2Lf9PV89sM2MzMzMzPbMgN6quGIeEJSzSaqTAVuj4gAnpZUIKksIt7IaGO+pEVAKbCsp2I1MzMzMzPLht68B6scaMpYnpuWbSBpEpAD1GcUX5UOHbxW0qCNNS7pPEnTJE1rbm7OZtxmZmZmZmZd2m4nuZBUBvwC+FREtKfFlwK7AQcCRcAlG9s+Im6MiNqIqC0tLe3xeM3MzMzMzHozwZoHVGYsV6RlSBoG/AH4RkQ83VEhIhZEYi1wCzBpG8ZrZmZmZma2Sb2ZYD0AnJnOJngQsDwiFkjKAX5Lcn/WfZkbpL1aSBJwEtDlDIVmZmZmZma9occmuZB0F3A4UCJpLnAZMBAgIn4KPAgcC9SRzBz4qXTT04BDgWJJZ6dlZ6czBt4hqRQQ8DzwuZ6K38zMzMzMbHMpmcRvx1ZbWxvTpk3r7TDMzMzMzGwHIWl6RNR2Lt9uJ7kwMzMzMzPra5xgmZmZmZmZZYkTLDMzMzMzsyxxgmVmZmZmZpYlTrDMzMzMzMyyxAmWmZmZmZlZljjBMjMzMzMzy5JuJViSxnSnzMzMzMzMbGfW3R6sX3dRdl82AzEzMzMzM+vrBmxqpaTdgD2A4ZJOzlg1DBjck4GZmZmZmZn1NZtMsIBdgeOBAuCEjPKVwLk9FZSZmZmZmVlftMkEKyLuB+6X9IGIeGobxWRmZmZmZtYnvV8PVoc6SV8HajK3iYhP90RQZmZmZmZmfVF3E6z7gf8F/gy09Vw4ZmZmZmZmfVd3E6y8iLikRyMxMzMzMzPr47o7TfvvJR27uY1LulnSIkkvb2S9JF0nqU7Si5L2z1h3lqSZ6eusjPIDJL2UbnOdJG1uXGZmZmZmZj2huwnWRSRJ1hpJKyStlLSiG9vdCkzZxPpjgAnp6zzgBgBJRcBlwGRgEnCZpMJ0mxtIZjDs2G5T7ZuZmZmZmW0z3RoiGBFDt6TxiHhCUs0mqkwFbo+IAJ6WVCCpDDgceCQilgBIegSYIukxYFhEPJ2W3w6cBDy0JfH1hj2/9UdWrfNtbGZmZmZmm+tzh47la8fu3tthbFK3erDSoXxnSPp/6XKlpElZ2H850JSxPDct21T53C7K+wQnV2ZmZmZmW+6nTzRw9YOv9XYYm9TdIYI/AT4AfDxdXgX8uEciyhJJ50maJmlac3Nzb4cD4OTKzMzMzGwr/fGVhb0dwiZ1N8GaHBEXAGsAImIpkJOF/c8DKjOWK9KyTZVXdFH+HhFxY0TURkRtaWlpFkLdekNy+vd2CGZmZmZmfdqUPUb1dgib1N0Ea72k/kAASCoF2rOw/weAM9MhiAcByyNiAfAwcJSkwnRyi6OAh9N1KyQdlM4eeCbJM7r6hJcvn+Iky8zMzMxsC/WFe7C6+xys64DfAiMkXQWcAnzz/TaSdBfJhBUlkuaSzAw4ECAifgo8CBwL1AEtwKfSdUskXQE8mzZ1eceEF8D5JLMT5pJMbtFnJriAJMkyMzMzM7Mdk5IJ/LpRUdoNOBIQ8JeI2L7vLstQW1sb06ZN6+0wzMzMzMxsByFpekTUdi7vVg+WpOuAuyNiu57YwszMzMzMrDd19x6s6cA3JdVLukbSezI1MzMzMzOznV23EqyIuC0ijgUOBGYA35U0s0cjMzMzMzMz62O624PVYTywG1ANvJ79cMzMzMzMzPqubiVYkr4n6Q3gcuAloDYiTujRyMzMzMzMzPqY7vZgzQauBP4WEbcCwyRN6qmgzMzMzMzM+qLuJlh7AZOB09PllYBnFDQzMzMzM8vQ3QcNT46I/SU9BxARSyXl9GBcZmZmZmZmfU53e7DWS+oPBICkUqC9x6IyMzMzMzPrg7qbYF0H/BYYIekq4EngOz0WlZmZmZmZWR/UrSGCEXGHpOnAkYCAkyLitR6NzMzMzMzMrI/p7j1YRMTr+NlXZmZmZmZmG7W5Dxo2MzMzMzOzjXCCZWZmZmZmliVOsMzMzMzMzLLECZaZmZmZmVmW9GiCJWmKpBmS6iR9rYv11ZL+IulFSY9JqkjL/0nS8xmvNZJOStfdKmlWxrp9e/IYzMzMzMzMuqvbswhurvTBxD8GPgzMBZ6V9EBEvJpR7Rrg9oi4TdIRwH8An4yIR4F903aKgDrgTxnbfTUi7uup2M3MzMzMzLZET/ZgTQLqIqIhItYBdwNTO9WZCPw1/fxoF+sBTgEeioiWHovUzMzMzMwsC3oywSoHmjKW56ZlmV4ATk4/fwQYKqm4U52PAXd1KrsqHVZ4raRBXe1c0nmSpkma1tzcvGVHYGZmZmZmthl6e5KLrwCHSXoOOAyYB7R1rJRUBuwFPJyxzaXAbsCBQBFwSVcNR8SNEVEbEbWlpaU9FL6ZmZmZmdk7euweLJJkqTJjuSIt2yAi5pP2YEkaAvxLRCzLqHIa8NuIWJ+xzYL041pJt5AkaWZmZmZmZr2uJ3uwngUmSBojKYdkqN8DmRUklUjqiOFS4OZObZxOp+GBaa8WkgScBLzcA7GbmZmZmZltth5LsCKiFbiQZHjfa8C9EfGKpMslnZhWOxyYIekNYCRwVcf2kmpIesAe79T0HZJeAl4CSoAre+oYzMzMzMzMNociordj6HG1tbUxbdq03g7DzMzMzMx2EJKmR0Rt5/LenuTCzMzMzMxsh+EEy8zMzMzMLEucYJmZmZmZmWWJEywzMzMzM7MscYJlZmZmZmaWJU6wzMzMzMzMssQJlpmZmZmZWZY4wTIzMzMzM8sSJ1hmZmZmZmZZ4gTLzMzMzMwsS5xgmZmZmZmZZYkTLDMzMzMzsyxxgmVmZmZmZpYlTrDMzMzMzMyyxAmWmZmZmZlZlvRogiVpiqQZkuokfa2L9dWS/iLpRUmPSarIWNcm6fn09UBG+RhJz6Rt3iMppyePwczMzMzMrLt6LMGS1B/4MXAMMBE4XdLETtWuAW6PiL2By4H/yFi3OiL2TV8nZpR/F7g2IsYDS4FzeuoYzMzMzMzMNkdP9mBNAuoioiEi1gF3A1M71ZkI/DX9/GgX699FkoAjgPvSotuAk7IWsZmZmZmZ2VboyQSrHGjKWJ6blmV6ATg5/fwRYKik4nR5sKRpkp6W1JFEFQPLIqJ1E20CIOm8dPtpzc3NW3ssZmZmZmZm76u3J7n4CnCYpOeAw4B5QFu6rjoiaoGPAz+QNG5zGo6IGyOiNiJqS0tLsxq0mZmZmZlZVwb0YNvzgMqM5Yq0bIOImE/agyVpCPAvEbEsXTcvfW+Q9BiwH/BroEDSgLQX6z1tmpmZmZmZ9Zae7MF6FpiQzvqXA3wMeCCzgqQSSR0xXArcnJYXShrUUQf4EPBqRATJvVqnpNucBdzfg8dgZmZmZmbWbT2WYKU9TBcCDwOvAfdGxCuSLpfUMSvg4cAMSW8AI4Gr0vLdgWmSXiBJqK6OiFfTdZcA/yapjuSerJt66hjMzMzMzMw2h5JOoR2bpGagsbfjyFACvNXbQVif5fPHtobPH9saPn9sa/j8sa21vZ1D1RHxnskedooEa3sjaVo6gYfZZvP5Y1vD549tDZ8/tjV8/tjW6ivnUG/PImhmZmZmZrbDcIJlZmZmZmaWJU6weseNvR2A9Wk+f2xr+PyxreHzx7aGzx/bWn3iHPI9WGZmZmZmZlniHiwzMzMzM7MscYJlZmZmZmaWJU6wtiFJUyTNkFQn6Wu9HY9tHyRVSnpU0quSXpF0UVpeJOkRSTPT98K0XJKuS8+jFyXtn9HWWWn9mZLO6q1jsm1PUn9Jz0n6fbo8RtIz6Xlyj6SctHxQulyXrq/JaOPStHyGpKN750isN0gqkHSfpNclvSbpA74GWXdJ+lL6++tlSXdJGuxrkG2MpJslLZL0ckZZ1q43kg6Q9FK6zXWStG2P0AnWNiOpP/Bj4BhgInC6pIm9G5VtJ1qBL0fEROAg4IL03Pga8JeImAD8JV2G5ByakL7OA26A5OIEXAZMBiYBl3VcoGyncBHwWsbyd4FrI2I8sBQ4Jy0/B1iall+b1iM95z4G7AFMAX6SXrds5/BD4I8RsRuwD8m55GuQvS9J5cAXgdqI2BPoT3It8TXINuZWkp9xpmxeb24Azs3YrvO+epwTrG1nElAXEQ0RsQ64G5jayzHZdiAiFkTEP9LPK0n+sCknOT9uS6vdBpyUfp4K3B6Jp4ECSWXA0cAjEbEkIpYCj9ALFxXb9iRVAMcBP0+XBRwB3JdW6Xz+dJxX9wFHpvWnAndHxNqImAXUkVy3bAcnaThwKHATQESsi4hl+Bpk3TcAyJU0AMgDFuBrkG1ERDwBLOlUnJXrTbpuWEQ8HclMfrdntLXNOMHadsqBpozluWmZ2QbpUIn9gGeAkRGxIF21EBiZft7YueRzbOf1A+BioD1dLgaWRURrupx5Lmw4T9L1y9P6Pn92XmOAZuCWdJjpzyXl42uQdUNEzAOuAeaQJFbLgen4GmSbJ1vXm/L0c+fybcoJltl2QtIQ4NfAv0bEisx16f/C+JkK9h6SjgcWRcT03o7F+qwBwP7ADRGxH/A27wzPAXwNso1Lh2VNJUnURwP5uOfStsKOcL1xgrXtzAMqM5Yr0jIzJA0kSa7uiIjfpMVvpl3dpO+L0vKNnUs+x3ZOHwJOlDSbZOjxEST30xSkw3Xg3efChvMkXT8cWIzPn53ZXGBuRDyTLt9HknD5GmTd8c/ArIhojoj1wG9Irku+BtnmyNb1Zl76uXP5NuUEa9t5FpiQzqqTQ3Ij5wO9HJNtB9Kx5zcBr0XEf2WsegDomBXnLOD+jPIz05l1DgKWp93qDwNHSSpM/0fxqLTMdmARcWlEVEREDcl15a8R8QngUeCUtFrn86fjvDolrR9p+cfSGb7GkNwY/PdtdBjWiyJiIdAkade06EjgVXwNsu6ZAxwkKS/9fdZx/vgaZJsjK9ebdN0KSQel5+OZGW1tMwPev4plQ0S0SrqQ5IToD9wcEa/0cli2ffgQ8EngJUnPp2VfB64G7pV0DtAInJauexA4luQG4BbgUwARsUTSFSTJPMDlEdH5JlLbeVwC3C3pSuA50gkM0vdfSKojucn4YwAR8Yqke0n+MGoFLoiItm0ftvWSLwB3pP8B2EByXemHr0H2PiLiGUn3Af8guXY8B9wI/AFfg6wLku4CDgdKJM0lmQ0wm3/znE8yU2Eu8FD62qaU/KeBmZmZmZmZbS0PETQzMzMzM8sSJ1hmZmZmZmZZ4gTLzMzMzMwsS5xgmZmZmZmZZYkTLDMzMzMzsyxxgmVmZjs0SQWSzk8/j06nlDYzM+sRnqbdzMx2aJJqgN9HxJ69HIqZme0E/KBhMzPb0V0NjEsf5D0T2D0i9pR0NnASkA9MAK4Bckge/L0WODZ9mOU44MdAKcmDLs+NiNe3/WGYmVlf4CGCZma2o/saUB8R+wJf7bRuT+Bk4EDgKqAlIvYDngLOTOvcCHwhIg4AvgL8ZJtEbWZmfZJ7sMzMbGf2aESsBFZKWg78Li1/Cdhb0hDgg8CvJHVsM2jbh2lmZn2FEywzM9uZrc343J6x3E7yO7IfsCzt/TIzM3tfHiJoZmY7upXA0C3ZMCJWALMknQqgxD7ZDM7MzHYsTrDMzGyHFhGLgf+T9DLwn1vQxCeAcyS9ALwCTM1mfGZmtmPxNO1mZmZmZmZZ4h4sMzMzMzOzLHGCZWZmZmZmliVOsMzMzMzMzLLECZaZmZmZmVmWOMEyMzMzMzPLEidYZmZmZmZmWeIEy8zMzMzMLEucYJmZmZmZmWWJEywzMzMzM7MscYJlZmZmZmaWJU6wzMzMzMzMssQJlpmZmZmZWZY4wTIzsx4j6WxJT27F9g9JOiubMW2vJH1EUpOkVZL26+14zMxsywzo7QDMzMwAJH0bGB8RZ3SURcQxvRfRNncNcGFE3N/bgXTo6mdiZmab5h4sMzOz7UM18EpvB2FmZlvHCZaZ2Q5KUqWk30hqlrRY0vVp+bcl/TKjXo2kkDQgXX5M0pWS/pYOV/udpGJJd0haIelZSTVdbZux/Wc2EtMP02FwKyRNl3RIWj4F+Drw0XSfL2S2JWmQpGWS9sxoq1TSakkj0uXjJT2f1vubpL03EoMkXStpURrHSx3tdo698xDH9FjPlzRT0kpJV0gal+5vhaR7JeVsZL/9JH1TUmO679slDU+PbRXQH3hBUv1Gtt9N0iOSlkiaIem0tHyypIWS+mfU/YikFzP2+zVJ9el5cK+kok4/v7MkzZH0lqRvvM/P5GxJDenxz5L0ia7iNTPbWTnBMjPbAaV/bP8eaARqgHLg7s1o4mPAJ9PtxgFPAbcARcBrwGVbGNqzwL5pO3cCv5I0OCL+CHwHuCcihkTEPpkbRcRa4DfA6RnFpwGPR8Si9J6lm4HPAsXAfwMPSBrURQxHAYcCuwDD03YWb8YxHA0cABwEXAzcCJwBVAJ7doox09np65+AscAQ4PqIWBsRQ9I6+0TEuM4bSsoHHiH5zkaQ/Hx+ImliRDwDvA0ckbHJx9O6AF8ATgIOA0YDS4Efd9rFwcCuwJHAtyTt3tXPJI3jOuCYiBgKfBB4fuNflZnZzscJlpnZjmkSyR/TX42ItyNiTURszmQTt0REfUQsBx4C6iPizxHRCvwK2KJJGCLilxGxOCJaI+L7wCCSP+y7406SxKJDZhJxHvDfEfFMRLRFxG3AWpIkqLP1wFBgN0AR8VpELNiMw/heRKyIiFeAl4E/RURDxne1se/mE8B/pXVXAZcCH8vs/duE44HZEXFL+t09B/waODVdfxdpYidpKHBsWgbwOeAbETE3TVS/DZzSab//HhGrI+IF4AXgXQluJ+3AnpJyI2JB+j2YmVnKCZaZ2Y6pEmhME6It8WbG59VdLA9hC0j6iqTXJC2XtIykB6mkm5s/CuSlQ+JqSHrCfpuuqwa+nA4PXJa2XUmSZL5LRPwVuJ6kF2eRpBslDduMw9jS72Y0SY9ih0aSyaZGdmOf1cDkTsf3CWBUuv5O4OS0x+5k4B8R0Zix7W8ztnsNaOu034UZn1s2dgwR8TbwUZKkbYGkP0jarRvxm5ntNJxgmZntmJqAqo30jrwN5GUsj+qiTne9nb6/b3vp/VYXkwzJK4yIAmA5oLRKbGpHEdEG3EvSU3M68PuIWJmubgKuioiCjFdeRNy1kbaui4gDgIkkQwW/mnE82fpuOptPkux0qAJaeXeCtjFNJMMhM49vSER8HiAiXiVJ2I7h3T17Hdse02nbwRExrxv7fc/PJCIejogPA2XA68DPutGOmdlOwwmWmdmO6e/AAuBqSfmSBkv6ULrueeBQSVWShpMMVdsiEdEMzAPOkNRf0qdJ7tnqylCShKIZGCDpW0Bmz9GbQI2kTf1uupOkB+UTvDuJ+BnwubR3S+kxH5cOl3sXSQem9QaSJFRrSIa9QfLdnCwpT9J44JxNfwOb5S7gS5LGSBrCO/c3daeX8ffALpI+KWlg+jpQ0u4Zde4ELiK5v+xXGeU/Ba6SVA0bJgeZ2s2Y3/UzkTRS0tT0Xqy1wCre+e7MzAwnWGZmO6S0t+cEYDwwB5hLkpgQEY8A9wAvAtNJ/njfGueS9AAtBvYA/raReg8DfwTeIOltWUPSu9KhIylYLOkfXTWQMaHDaJL7nTrKp6VxXE8yiUMdyYQSXRlGkpAtTeNYDPxnuu5aYB1JYnEbcMdG2tgSNwO/AJ4AZpEc/xe6s2HaU3cUyT1o80mG9H2X5B62DneRTGTx14h4K6P8h8ADwJ8krQSeBiZ3M+bOP5N+wL+lMSxJ9/f5brZlZrZTUMQmR2SYmZmZmZlZN7kHy8zMzMzMLEucYJmZmZmZmWWJEywzMzMzM7MscYJlZmZmZmaWJd15enyfV1JSEjU1Nb0dhpmZmZmZ7SCmT5/+VkSUdi7PaoIlqRK4neTp8AHcGBE/lFREMiVwDTAbOC0ilkoSyfSxx5I8Of7siPhH2tZZwDfTpq+MiNvS8gOAW4Fc4EHgonifqRBramqYNm1aFo/UzMzMzMx2ZpIauyrP9hDBVuDLETEROAi4QNJE4GvAXyJiAvCXdBmSJ85PSF/nATekwRYBl5E8p2MScJmkwnSbG0ieddKx3ZQsH4OZmZmZmdkWyWqCFRELOnqg0ocivgaUA1NJHthI+n5S+nkqcHskngYKJJUBRwOPRMSSiFgKPAJMSdcNi4in016r2zPaMjMzMzOzHU17O6xe3dtRdFuPTUZgC5gAACAASURBVHIhqQbYD3gGGBkRC9JVC0mGEEKSfDVlbDY3LdtU+dwuys3MzMzMrK9avRpefRXmzWP56vXMeOoFFh3+YZbWTGB9bh4PnXwuLzQt6+0ou6VHJrmQNAT4NfCvEbEiudUqEREhaZP3TGUphvNIhh1SVVXV07szMzMzM7ONiYDmZmhrY03JCOY1vUn+l/+NfrMayJ3byNDFiwC4/oizuObAUyldtZTbXqtnTsEoFu6/D/U1+3HM2tZePojuyXqCJWkgSXJ1R0T8Ji1+U1JZRCxIh/ktSsvnAZUZm1ekZfOAwzuVP5aWV3RR/z0i4kbgRoDa2toeT+jMzMzMzHZq69bBihVEcTFvrlhLXHIx7TPeIKdxFsPmNzFo7Wp+c+DxfPnIz6G2Nh579DEWDCtlTvk+LDuggjWV1azdr5av77UblYV5tF96Ah8ozGN43sDePrLNku1ZBAXcBLwWEf+VseoB4Czg6vT9/ozyCyXdTTKhxfI0CXsY+E7GxBZHAZdGxBJJKyQdRDL08EzgR9k8BjMzMzMz60IEtLRAfj7rWttZ/v0fsu7Zaaihgby5jQx7ayF/33USZ/3LZaxtbeeR+/6HQLxWOIrFB+zJ25XVrNxrfy6aPIGa4nzePP9VKgtyqR02mP799P777yOy3YP1IeCTwEuSnk/Lvk6SWN0r6RygETgtXfcgyRTtdSTTtH8KIE2krgCeTetdHhFL0s/n88407Q+lLzMzMzMz21rt7dAvmaah9be/ZdWj/8u6N+ro19BA/rw5NBeO4BNfvJF5S1dz1y9vYuzSeTQWlLGgbHdWHHA0y3fbizM/UE1VUR7zzn6WquJ8DinMZdCA/r18YNuO3ucRUjuE2tra8HOwzMzMzMwyPPMMbY89Tstrb7C+ro6Bs2bRb9VKLvjBH5n91tt86dbLOeb1J2kqGEnT8FEsKBnNspoJvPqRMxhTnEfN8BxqygoYU5xPYX5Obx/NNidpekTUdi7vkUkuzMzMzMysl9XVwRNPEPX1tMyYSdvMenLmzOYHP/0jM1fDP9/+Q05/9C7W5w5jTsFI5hTUsGBMGW8tfZs9Rg9n1pXXcP/oYsaMHMaeJfkclp9D5uR11jX3YJmZmZmZ9UXNzfDUU0RdHWveqGPdjJn0mz2L+791PS8MKWPP//klZ915Da3qx7zhI2gsKKOpYCQ/OuIsCipHM3FQK5WlQxldPZKa4nzGlORTOnSQk6hucg+WmZmZmVlf0tICzz1H1NXR8vpM1rwxE+obePzsL/Fs1V6MeOxhvvSjryJgfU4eTYVlzBk+klv+NpuVNQNYuPc/UVd7MPnjx1I1Yjg1JXkcUZLP6UMH028HmlRie+MEy8zMzMysN7S1JcP46utpr6/n7VdnsG5mPS9/+CT+ttehtE3/B9/81hkIyEUsG1rCnMJR/OqZRt5YWcqE8j24+rJb6T9hAsVVo6gqzmd8cR6/L8wjN2fnmVRie+MEy8zMzMysJ0TA4sVQXw8NDax/YyarX59J0561PH3YibzV0MQlZx0GQD+g/8BBNA8fxf8MnsgfVlYxPr+Ya7/0AwZOGMew3cZTWVZERWEuNxXmkpfjP+O3V/7JmJmZmZltqfXrYc6cd5KomXU0F5fxj+NPp7F5FecdszcD168FYCCwZEgRf5wb/GjleIbm9KffJ7+Jxoxh0G67UDq2kqqSfL5anM/3h3UM45vSq4dnm88JlpmZmZnZpixbBg0NUF9P1Nezpt8A6j5+Lk1LW/jAcQdT2NSwoWp7/4E8tdvBfHnFbgAsOuGLDB5RQr9x4xiy2wTKy4v5p+I8zi7Koyg/B8kJ1I7GCZaZmZmZ7dza2mDu3A29ULF8OfM+/XnmLl1N1dkfY/T//nlDVQEzyiZw0pLdAThlrxPJ3a8fq6tqGDB+HGW7j2OXsmE8WJxPVXEeQwYd10sHZb3FCZaZmZmZ7fhWrdrQC8Xs2bScfyH1zS0M/sYljL3zZvq3rt9QtSUnl4MX7QoSJw3fh5FHVNFSXgXjxjF41wmMLC/lp4V5VBblUll0FMMGD+zFA7PtjRMsMzMzM+v72tth4cJ3eqFOPpmF7QNo+eGPKf/Bdxm89K13VT+kYQSL8ws4Znkhe9VOZVFJOS0VVbSPHcuw8WO4anQB1UX5VBQeTkVhLgP69+ulA7O+xgmWmZmZmfUNq1fDrFlJT9TkyURJCSt++ztyLvkqOU2N9F+7dkPVU59cybTiMRzW0MLRVQcwb59RrBpdTfvYsQyYMI5PV45iTEk+40oPpbwwlyGD/GexZYfPJDMzMzPbPkRAc3PSC1VVBeXl8OKLtJ5/AVFXz8A3F2yoetW53+Husv0Z3zCTz/YrpnGfPWkqGMXb5dUM3GUce+86nqllBYwrmUxV8VcYNWywe6Fsm3CCZWZmZmbbzrp1MHs25OZCZWUyrO/znyfq64n6Bvq1vA3AfWdfzC9rTyRmzuTrjUuZU7oHcyYcQWNhGavLq4g99uAjlSOo+fAu5HzjDP65OJ+KwlwGDfADdq13OcEyMzMzs+yJgKVLYc0aGD06eU7U+edvmOKcuXNRezsvnH4e959+EQvnNXPx356jfthIGnc/kjkFo2gqLKO5bA+G5PSn+tD9+cdJ9zOmJI/jS4ZQXZzH4IFOomz75QTLzMzMzDZPayssXw7Fxcny5ZfDSy8lk0vU16Ply1l43Ee4/6v/SUPz23zxd39iyaAhzBw6jqaDPsScglG8kDeBeX+fQ3VxHt/9/q8ZW5rPhBFDOWjkUMaW5juJsj7LCZaZmZmZvdeaNTB4cPL51lvhmWc2zNBHYyOtkybz+r1/oHFxC7V3/ApWrqSpcBQzJhxKw9ARvDR8An9/6HVKhgyi7rK7qC7Oo6Y4n5riPA4vzqeqKI+CvIFI6tXDNMu2rCZYkm4GjgcWRcSeadm3gXOB5rTa1yPiwXTdpcA5QBvwxYh4OC2fAvwQ6A/8PCKuTsvHAHcDxcB04JMRsS6bx2BmZma2U4iAjuTmT3+CJ5545zlRDQ1Efj7NL73OnMUtlN/0SwpemM6bpeU0FdTwxgcn8VxBJb//0ZPJ9if9B+WFeYwbMYTxpUMYP2IIU0YOYZcRQxme52dE2c5FEZG9xqRDgVXA7Z0SrFURcU2nuhOBu4BJwGjgz8Au6eo3gA8Dc4FngdMj4lVJ9wK/iYi7Jf0UeCEibni/uGpra2PatGnZOEQzMzOzvue55+Cxx96VQDFvHmuaFzN/5ToGffFCyn71S5aXlLGgZDSzho3i5fwR3HDASQAMbFtP24CBVBTmUV2ct+G9uiiP6uJ8qovzyPc057aTkTQ9Imo7l2f1X0JEPCGpppvVpwJ3R8RaYJakOpJkC6AuIhoAJN0NTJX0GnAE8PG0zm3At4H3TbDMzMzMdmiNjUkPVEfyVF9PNDQw/5EnacorYOhNd7PHj7/Hmtx8FpWW01hQRv0+e/Pdr/+O1TmDGTLqONZ86SMMGJxDVVFe+srn34vTz8V5nqHPrJu21X81XCjpTGAa8OWIWAqUA09n1JmblgE0dSqfTDIscFlEtHZR/z0knQecB1BVVZWNYzAzMzPrHUuXwlNPJclTRgL19g0/Y/aY3Wm/4372/sZFtEssKRhBY8Eo6kr34tqfPMnCYSUM778f+uKdUFREWUEe5QWDGTFsMBcMH0zZ8Fyq0kRqxNBBvifKbCttiwTrBuAKINL37wOf7umdRsSNwI2QDBHs6f2ZmZmZbbE1a+DFF9/pgUqTqLf/9cvMnnQoLQ//lQM/fQoAa3MGM794NLOGjeT7P3+GV0YtZtiakZR85qcsGzmayrIixpXkU12cz78VDGb08FzKCgZTNnwweTkexmfW03r8X1lEvNnxWdLPgN+ni/OAyoyqFWkZGylfDBRIGpD2YmXWNzMzM9t+tbfDrFnvSaBaTpjKrKOmsuSFVznk2A9uqL54WDGNw0fyozum8+jT/chf286un/hPmkeUk1cxmoqiZMjeSYV5XFiYS2VRHuUFuZ6Vz2w70OMJlqSyiFiQLn4EeDn9/ABwp6T/IpnkYgLwd0DAhHTGwHnAx4CPR0RIehQ4hWQmwbOA+3s6fjMzM7NuWb78XfdA0dBA6z77Mve0M2mav5hD9hm/oeq6ATnMLRjJzatG8cvXixnQ1srhJ/8/FpWWw5gxlI4spKIwlw8W5nFaYS4VhUlC5QTKbPuX7Wna7wIOB0okzQUuAw6XtC/JEMHZwGcBIuKVdFbAV4FW4IKIaEvbuRB4mGSa9psj4pV0F5cAd0u6EngOuCmb8ZuZmZltVFsbzJ377pn4SktZdf4XaFrSwtg9xzFoyeIN1ZfmD+dXz7/Fd+Yk94KfeMJXWDy8lNaaMeTVVFJRPISqolx+kiZPFYXHUOgEyqzPy+o07dsrT9NuZmZm3bJq1buH8rW10XLRl1i4fA2lHz6coS9M31C1tV9/ntxlEmdP/QYAJ73yKKsHDGJpWQUDxo1jRHkpVekDdTteI4YOol8/J1BmO4JtMk27mZmZ2XatvR0WLtyQQLUvXEjz5y+iaUkLpReeR/Uffv2u6o1Fozls8UQAplYeTu6oDzC3cBRrqsYweEwVlSOGcXFRHtVF+VQVHUxVUZ4frGu2k3OCZWZmZjuW1auTXqh0MolVn/oMs5avZ9DVVzH2Z9cxYN3aDVXb1Y9Dm3dh7YAcjus/nupDz2TJqErWV9fAuHEMLRvBxcMGUTZ8MCOHTaa8IJfRBbkM7N+v947PzLZrTrDMzMysb4mA5uYNvVDrPnw09W05rLn1F0z4/hUMWfzmu6of//JgZheVc+TCwUze51gWlYxmTdUY+o0bS+6EMXxzZAEVRXlUFR1GeUEugwf6YbpmtuWcYJmZmdn2Z906aGxMeqH22ou1I0ay6A9/ZvjF/8bgpkZyVr+9oerZp3+Hv1XtzeQ5KzmlbC8W7zuF1RXVrKmqoW3MGE6tLmfciCFUFB5MRWEuw3M9kYSZ9RwnWGZmZtY7lixJEqgRI6CqivUz3qDtM+fCrFnkLJhHv/Z2AK467WvcNPZgdnlzFl9py2fOxCNZNqqSddU1aNw4Ju86gY+WFzJ+xMHUFH+F/EH+88bMeo+vQGZmZtYzWluhqQn694eqKtYtXsr6c84h6urJmTObnJUrALjzhPO4/gOn0bZgAT9pWERj4Xiaqg+meUQ562vG0DZxDy6sKWNsyb6MuuKTfLA0n7wc/wljZtsnX53MzMxsy61YkUxtPno0ra1trP7cBbS9PoP+jbPIWzCP/m2t/OmQj/DtYy6gednbPPjkNOYNG8Gc8YfQVFTG2+WVLN99Lz4wtoSy/SuoP/NPVBbmcfCIfEYMHdzbR2dmttmcYJmZmdnGtbfDsmVQVATA2u/+J2ue+TvUNzBozmwGL1vC83t/iH894wrmLVvN//zuEVr79WdOQRVNkyaxoqySxbvvzUHjiqksrOT5U/+PisI8jijKZdSwwQzwbHxmtoNxgmVmZrazW7cOcnIAWH/nXbT89XHa6uoZMHsWefPn8GZZDRdcfAtzlrTwk5/dzugVzTQWlNFUPYk3DxjN4l0mssfo4UzZs4yXT3qUisI89inM4+jhg8kZ4ATKzHYuTrDMzMx2dBHQMWve44+z7s9/peX1N4j6enLmNKK1a/n8D//EnCUt/NvNP+Ww+mnMLyxjzvCRzN1/X5orx5KX05+j9xjF87f/lreK8qgozOOowlyK83M8I5+ZWQYnWGZmZjuSV1+Fv/6VNTNmsnbGTDRrFoPnzuHfb/wzr68Kpt75Y8548j7eHlpCU8FIGkfvw5slo1m6soXdy4bS8L3rWTcqeS7UPkV5HDV0kIfxmZltBkVEb8fQ42pra2PatGm9HYaZmdnWmz8fHn+c9vp6Wl57IxnK1zibu678Oc/ljWTv39zOZ3/9Q1oGDmLO8FHMSXui7jrqTEqqytgtLygbMZyKskKqivKoLspneN7A3j4qM7M+R9L0iKjtXO4eLDMzs+3JypXw9NPJ86Hq61k7YyatM+t58sKv81TFXhQ98iBfvP5i+gEt+YU0FpQxp2RX7po2l9Zxg2k99DiuPm4qxWOrqCrJp7o4j4OL8viMpzU3M9smfLU1MzPbltavh5deShKohgairo61b9Qx57Qzee7AI2h56u986qJTAVjbfyBNw0cyp2AUN/6tidfHFrB7+Z4s+497yNt1HFUVI6guzmNSQS5Th3tGPjOz7YETLDMzs2yKSB6uW1+/IYlqr6tn2YcO46UppzD/jdmcfsKkDdWX5g2jcXgZP3/4df4wp5Sh7QN44XPX0j52HMPHVVFdOpRdRg7lxyOHMnLYIE8oYWa2nct6giXpZuB4YFFE7JmWFQH3ADXAbOC0iFiq5LfED4FjgRbg7Ij4R7rNWcA302avjIjb0vIDgFuBXOBB4KLYGW4kMzOz7ceqVRuSJxoaaJtZx4rKMbz20U8xf0kLJ31oAgPWrwOgtV9/5g0bwR2L8rhxfhVE8OS/fJO1VdUwZgxVNWWMHzGE04vyuKQoj/LCXPr3cxJlZtZX9UQP1q3A9cDtGWVfA/4SEVdL+lq6fAlwDDAhfU0GbgAmpwnZZUAtEMB0SQ9ExNK0zrnAMyQJ1hTgoR44DjMz21lFwIIFG+6DWjNjJsv65fDyxz9L09IWpp56GEULmjZUf3tQPg/tdghfXzERgMePuYi24hLaasaQO7aG8tKh1BTkcU9pPuNGDKE4/zj3RJmZ7aCynmBFxBOSajoVTwUOTz/fBjxGkmBNBW5Pe6CellQgqSyt+0hELAGQ9AgwRdJjwLCIeDotvx04CSdYZma2uVavhtmzob6eqK+nZclyZpzzBeoXreKAz57O2H/834aqA9WP2RUT+UzrAQC8PPl0hg8ZRGvNWPqNHUdhxUhGF+ZyZ0EuowtyKSuYwqAB/XvpwMzMrDdtq3uwRkbEgvTzQmBk+rkcaMqoNzct21T53C7K30PSecB5AFVVVVsZvpmZ9TkR8NZbG+6FWt8wi9mf+QJzl62h7P9dzG733bahqoDVecM5ec3+IHFi1SGMqaplbXUNA8aPZ/hu4ygfWcBvhw+msiiP4vxj3QNlZmZd2uaTXERESOrxe6Yi4kbgRkieg9XT+zMzs16wbh00Nm64F2r5KR+jca3Qddex6/XfJWd1y4aqA4FTm8eyLHcYR7VVsMehZ7C6spr2MePI2WU8xWPKuak4n5qSfGqKj/V9UGZmtkW2VYL1pqSyiFiQDgFclJbPAyoz6lWkZfN4Z0hhR/ljaXlFF/XNzGxHtWTJO7PxHXIoi/IKWH7PfVR8+1Jy35xPv/b2DVU//sw6Xhk1noMb+3HkxCNZXlZJa80YNH48+buO599HFVJRmEdl4ZGUDBlEPydRZmaWZdsqwXoAOAu4On2/P6P8Qkl3k0xysTxNwh4GviOpMK13FHBpRCyRtELSQSSTXJwJ/GgbHYOZmfWE1laYOzcZyjdhAmtHl7PosacouOgCcubMZtCqFRuqXnDqt3ho7CT2mb+IswvHM3/cIbxdUU1rTQ0DJkxg6thKvlAylLGlh1JVlMfggb4PyszMtq2emKb9LpLepxJJc0lmA7wauFfSOUAjcFpa/UGSKdrrSKZp/xRAmkhdATyb1ru8Y8IL4Hzemab9ITzBhZnZ9m/lyiSBGj4cxoxhRX0j+vSn0awGcufPpX9bKwDXnPAFfrzH0VQuWcDlqwcyZ8IhLCguY01VDYwZS83EXblidDFVRZOoKf4sJxbmeSifmZltV7QzPEKqtrY2pk2b1tthmJntuNrbYf58aGuD6mra16xlzRln0vb/2bvv8LiuMvHj3zOj3i3ZVrEsyZZ7TTFJSGLwOp00FrIsLARiErLABgIksNTd/RHYZRd2Q7IJgZBCKEkIsJBe7TikOrETO3YsF3XLtiTbKpYtWdLMnN8fc+94yr3TNJoZSe/nefLEGo1mbj33vOe855zGJjLbWsjp87aR/fH8T3LLuZ/G1dfPgw9/h/aSCtpLKugpr2a0bg6epcsoq5tFbVketWV51JTmM70gSyaUEEIIkXaUUlu01quCX0/6JBdCCCEmqMFB6OuDqioAXF//BsPvbIOWFrI72sgYGeH1sy7iO1d9k46eIf788mZ6covYV3sGHadUcKy6luNLlnP54kpqSus5eO1fmVeWx9rSPPKz5XEkhBBicpAnmhBCCC+tob8fSkq8P/7sZ4y88hqjexvJaG0l53AXzYtP45s33kH7kUHueOgJckeHaS+poO2U5XRNr6Jn4TIWzCzkgsXlbL1iAzWleZxbmk9VSQ4ZTkeKd1AIIYQYfxJgCSHEVDI6CpmZ3n8/9hieF19keE8jnsYmsttbOVZcyrf/+1Haewb5+v8+wPzOZm8aX+Vy2hdfwMGa+Xg8mrPnlfHqrx71pvGV5fG+0jzK8iWVTwghhJAASwghJhNzXK1SsGkTvPACrsYmRnbvRbW0kNlzmFse2kRr3zBX3f1Lzt/yPO0l5bSXVNK+7ELay2bRcHCAmtI81v/ol+ydUUBNaR4ry/K5rDSXvCx5bAghhBDhyJNSCCEmqsZGWL8ed2MTJ3btwdPcTHZbK7++72kaKGDVb+/lE4//kp78abSVVNJetoB99R/gyc1tlFdM44V//Cbvlf8XNWX51JblcWFpHlUluTIrnxBCCDEGMougEEKkq0OH4KWXoLkZ195GThi9UE9+51bemTmPOU/+kevv+z4jzgz2FVfQZszId+f7P4ajqpJFuTBregGVVWXUlOVRW5ZPTWke0/IyJZVPCCGEGCOZRVAIIdLN4KA3ja+5GZqa0E3NjOxtZNc/fo3XF52JXr+BL9xyPQD9uUXsK6mgraSO+97cT/ecAhYsej9ttz3BtHl11JUXU1uWx9rCHD5elC0L7AohhBApIgGWEEKMF7cbdu70C6CacO1t5OClf8uWD1zG0W0NfGbdhQC4HE72F8+krbiCX25o4uWWYuqyK2j+zq/IqK+nfPZM6mcUMG9GPn8qy5dpzYUQQog0JU9oIYQYiwMHfAEUzc14GhvpX3E6Oz/6afbtP8zH16zwvXUgO5+2kgp+ndHAHw7OJsPt4s11/8lo7Ryy5tRQNb2IurJ8vlxewP/OLKAkLyuFOyaEEEKIeEiAJYQQ4Zw4AS0t3iDKCKRcFRUcvP7L7Osd5LRVy8np6wHArRwcLJzOn1o93Nq7EICXP/pdhquqyJ4/j7KaSmpK8zi/NI/PTfeOh8rJvDKVeyeEEEKIBJMASwgxtWntnUzCL4DSwKEbv05bzyDzLv4g03bv8L19MCuH5+vP5Ma+5QB86IPX4y4owFFfT8HCeipnFFNVnMODZXnUleVTUfQhHDIrnxBCCDFlSIAlhJj8Rkagrc0XROnubg5/7Zvs7xti5nVXU/XcEwFv31U+l0uOnwbAhxZdRvaCixisrsUxr56S2llUluTxX0U5VJXkMm/meZQXZcusfEIIIYQAJMASQkwWvb2+cVA0NaFvuomeEc3It75Nxc9+ivJ4fG89kZHN2cdWMurM5KL8FVSdV0n3jGpGaurInj+X8opSvl+WR01pHrVla5hVkktWhiOFOyeEEEKIiUICLCHExOB2w759J1P5PvIRKC1l6O57yPrGzTj7+wPefsnBKnblTWdNZxGnnvUxOqZVMlo3h4x5cymaU8t3ZxQwqySX6tLVzCrJpTAnM0U7JoQQQojJRAIsIUT6GBg4GUC97314qmZx9Klnyf3SP5HZ0Y7D5fK99VvvDvFU2UIW7DnC5XPPpb2knPZplQzNqiV7QT1nzp7J35XlM2f6KmpKvRNKSC+UEEIIIcZbUgMspVQrMAC4AZfWepVSqhT4PVAHtAIf01r3Ku+AhtuADwGDwDVa67eNz/kM8F3jY3+gtX4gmfshhIiTx3NyWvPZs2HOHAa27cC5bh3Othaye4743vofn/g29885lzmdzXwpZxbtq06jraSSzrJKRmrnkD2nlsunFzB7TT2l067mtLJ86mcUkJslC+wKIYQQInVS0YP1N1rrw34/fxNYr7X+kVLqm8bP/wxcAsw3/jsTuAs40wjI/hVYBWhgi1LqMa11bzJ3QghhY3DQO615Tg7U13P0YDeOq69GtbSQ09GGc2QEgAcuu57/Pv0jZB/u5taeUdpnr6J9eSWHZlQxUjsHtXAB66pnUFW8mOybruIDxTnMKsmlJC9TJpQQQgghRNpKhxTBK4E1xr8fADbiDbCuBH6ttdbAG0qpEqVUpfHe57XWPQBKqeeBi4GHkrvZQkxRWkNXF5w4gbumlu6jQzg/9zlU417y9rWRf6QbgCfO+TDfOv/zDA4O85cdTXQUl9N+ynIOlFYyNLuWE4uXceWcWdSUzmfgH89nRWkeH5qWS3GuBFBCCCGEmLiSHWBp4DmllAZ+obW+GyjXWh80ft8JlBv/ngXs8/vbDuM1u9cDKKWuB64HqKmpSeQ+CDH5DQ9DTw9UVuJyezj+vX/D9eZmHC3N5O9vJ2t4iNcWv59Pf/i7uDya/3ttCyPOTNqrVtC1ooqBqloGFi/lw0tnUT0tl9ZP/pXqabmsmpbH9IIsCaCEEEIIMWklO8A6V2u9Xyk1E3heKbXL/5daa20EX2NmBG93A6xatSohnynEpKG1d0KJoiJOjLo5+vN74OWXcbQ0k72vjfzug+yrnsfVN/yC/X1D3P/QE8w81sO+kgoOrFzM8dm1nFi8nOvPmcusabkcv/ZlakvzOaUom5xMGQMlhBBCiKkrqQGW1nq/8f9updSfgTOALqVUpdb6oJEC2G28fT8w2+/Pq43X9nMypdB8feM4b7oQE4/LBRkZaK3pefRJhp9+Dt3URGZbK4X723E5HJz3rT/RPTDM7Y89yFnt22ktqaBt+kK6F62lf848VlQXc/nKSg7+7V/IKM1j+fQCzpdFdYUQQgghbCUtwFJK5QMO9xPM+wAAIABJREFUrfWA8e8Lge8DjwGfAX5k/P9R408eA25QSj2Md5KLfiMIexb4d6XUNON9FwLfStZ+CJGO3G+/w8BjT3Ji115oaSZnXxuF3Qe46t+fYteAh688dz/XbHmMjuIK9pSUc2jleQxV17JmXhnV0wtwffTX7CnJZ3phFheU5FIka0IJIYQQQsQlmT1Y5cCfjZbvDOBBrfUzSqm3gEeUUtcCbcDHjPc/hXeK9ka807SvA9Ba9yilbgHeMt73fXPCCyEmrfZ2Rp99joH3djO8pxFnSzMFHW189+u/YFPWDC5a/wj/8sIv6Mktor2kgn0lc+hb/AEq852curiawvN+yBvldzKrLJ8zS3LJy0qH+W2EEEIIISYf5Z2kb3JbtWqV3rx5c6o3Qwh7vb3ol15iaPdeBhv24GlqJrOtlT9c921eqlpKzUvP8R+//VdGHU72F82kvaSC7umVPH/5NeQumEddlofZJdlU1lQwuzSPiuIcMp2yqK4QQgghxHhRSm3RWq8Kfl2asYVIhuFheOstPI1NHNu5mxN7GnG0NLPpik+xfvka1OYt/PePryMPcGXn01ZSQXtJJa/uP87xMjf6vPO478JzmL54HrXlxawsy6c4L5OrUr1fQgghhBAigARYQiSCxwO7d0NzMyN7GjnesBvX3iYaTv8Az55zBf0t+7jjpktxAAUojhZNp72kksfeO8T2vCPU19Rz148fpmDxfMrrqqgpy2PNtDwuzZZbVAghhBBiIpHamxDROnQImpuhqQl3YxODDbvZX13Psxd9irZDR/nPT7+fTNcoWcBoZg6dJRVscNbxZNFBZpcU8r9fv52s+fMoXjSPmsppzJqWy21FOTKtuRBCCCHEJCIBlhCm0VFoa4OmJmhu5sSuPfRm5rHpk1+k9chxPvXJtUzv3g+AEzheUMprC8/lpxlnUFWcy+3X/4CcqkpyFs5jev1sasry+er0Av4tz5yRb3XKdk0IIYQQQiSHBFhiaunt9fZCNTfj2tvIsd6jbL3uq+zrGeSDn/97at590/dW5cxkV+0KvpJxNkpB9wWfo6QkHz13Dtn19VRXT+e0mQXsLC8kN8sJrE3dfgkhhBBCiLQgAZaYXFwu6OjwpfKdaG5l9xdupq13iPpvf4WlT/3B99YMYKC4nGsc54BSXDLvAmYtXIOnbg7ZC+ZROq+OupmFPF+Wx+zSPHIyL03dfgkhhBBCiAlBAiwx8QwMeHugGhs59t5uGj/yKTpGncz8+W2cee+tON0u31sdjgyuHlrB0ZwC1uYuZsXF1zNcU4eqryd34TwqZs3gD9PzqS3NY3rBh3A4VAp3TAghhBBCTHQSYIn04/HAwYPoxkaON+xh1ynn0OQsIO+xP/M3t/8/Co72At6LtwT4XmshDTPncnZ/MTvP+ghHZ9Xgqp2DY149JfPn8uOZhdSW5VFTepEssCuEEEIIIcaV1DZFagwNoZubGdy1l45Zc2kpmMnwq69z9g9uprhrP1mjwyigALjro99j/bwzOaXTg3vB+zk2q4bRujlkzK8nb+ECvlVTQVVJLpXFF5Ev05oLIYQQQogUktqoGB9aQ3c3uqmJ3vwSWkoq6NzRyMp//iIFB9op6T2EAvKB31zwBX572qXU9h4mr6CS/vlnMDS7FubOJXvhfD69bAH/VjWNiuJLyHR+NdV7JoQQQgghhC0JsET8hofRra30nXDTOq2Szq4+Fn/tenL3tVHc2UHO8BAKePisq/ivD15DwfAg9xwd5kj96QxV16Dn1pM5fx4fXLGUj9dWUD0tl+Lc61BKxkEJIYQQQoiJSQIsYU9r6OnB03+Ug6UVNB86Rvl3vk7ungby9++j5EgnDq3ZuGQNX738ZtCavzS101JYSu+ZKxms9vZCTT91JfcvmU9tWR7VP/4oWRmOVO+ZEEIIIYQQ40ICrKnO5cLTfYiu/BJaDh0n947byNvyFnkdbZR2dZA/dIzNNcv42Cd+BMCDm94hyz3KoeolHDvzElT9XJynnsovzzid6mm5zPp/OyjKyYzwpUIIIYQQQkxOEmBNBcePcywjm/29Q4w8/DDZL20ko7WFgv3tlB05yIGimaz+x3sAuPupF6g/0sH+GVU0nHkRx2fXMrRgMbect5R5Mwup/sbrVBTnkOmUXighhBBCCCGCSYA1CWi3m74hF/v6hhh8YSM5G57D2dpK/v52yro6yD0xyPKb/oRWDv79mT9x0Z7X6ZhWQXv1QobOvgjX3Hnc8uFlzJ2eT8031lNZnEO9BFBCCCGEEELEbEIGWEqpi4HbACdwj9b6RynepHE34vKwv2+Iw29tRT3zDDQ3k9PeSsnBfczs6eSCL9zH4fxpfOnVP3Ljqw9xoGQmh2ZU0/a+tQzX1PHN8+qpLC9h1ud+g2tGIcsLsmVRXSGEEEIIIRJMaa1TvQ0xUUo5gT3ABUAH8BbwCa31Tru/WbVqld68eXOStjA+WmuOHB/hQEMzrmeew7V3L87WVgoOtDO9q4N1H/0X3q2Yz1XbX+AnT/2Ugew8OqfPoq9yNsM1dbRd83lmzJ1NdY6manoRxUV5MhufEEIIIYQQ40QptUVrvSr49YnYg3UG0Ki1bgZQSj0MXAnYBljppLH5IEPrNzK0aw+exiZvL1RnB//5wc/wdN0qzm7dyoO//y4eFF3FMzgycxaNqz7AR1cv5DOnLKfuU8vovvNmps+uZL5fGt+5KdwnIYQQQgghhNdEDLBmAfv8fu4AzkzRtsTsm//7LH/86ToAjmfm0DW9it7K2Zy5ooYzPriEupzFtH75EsqXL6KyMI9K4+8mzA4KIYQQQggxhU3EACsqSqnrgesBampqUrw1J335ugvZufoZypYvZGZ9DXMd3l6oU1O8XUIIIYQQQoixm4gB1n5gtt/P1cZrAbTWdwN3g3cMVnI2LbIPLK2CpVWp3gwhhBBCCCHEOJiIc3G/BcxXSs1RSmUBHwceS/E2CSGEEEIIIcTE68HSWruUUjcAz+Kdpv0+rfV7Kd4sIYQQQgghhJh407THQyl1CGhL9Xb4mQ4cTvVGiAlLrh8xFnL9iLGQ60eMhVw/YqzS7Rqq1VrPCH5xSgRY6UYptdlqznwhoiHXjxgLuX7EWMj1I8ZCrh8xVhPlGpqIY7CEEEIIIYQQIi1JgCWEEEIIIYQQCSIBVmrcneoNEBOaXD9iLOT6EWMh148YC7l+xFhNiGtIxmAJIYQQQgghRIJID5YQQgghhBBCJIgEWEIIIYQQQgiRIBJgJZFS6mKl1G6lVKNS6pup3h6RHpRSs5VSLyqldiql3lNK3Wi8XqqUel4ptdf4/zTjdaWUut24jt5VSp3m91mfMd6/Vyn1mVTtk0g+pZRTKfWOUuoJ4+c5SqlNxnXye6VUlvF6tvFzo/H7Or/P+Jbx+m6l1EWp2RORCkqpEqXUH5VSu5RSDUqp90sZJKKllPqq8fzaoZR6SCmVI2WQsKOUuk8p1a2U2uH3WsLKG6XU6Uqp7cbf3K6UUsndQwmwkkYp5QTuBC4BlgCfUEotSe1WiTThAm7SWi8BzgL+ybg2vgms11rPB9YbP4P3Gppv/Hc9cBd4CyfgX4EzgTOAfzULKDEl3Ag0+P38n8CtWut5QC9wrfH6tUCv8fqtxvswrrmPA0uBi4GfGeWWmBpuA57RWi8CVuK9lqQMEhEppWYBXwZWaa2XAU68ZYmUQcLOr/CeY3+JLG/uAj7n93fB3zXuJMBKnjOARq11s9Z6BHgYuDLF2yTSgNb6oNb6bePfA3grNrPwXh8PGG97APiw8e8rgV9rrzeAEqVUJXAR8LzWukdr3Qs8TwoKFZF8Sqlq4FLgHuNnBawF/mi8Jfj6Ma+rPwLnGe+/EnhYaz2stW4BGvGWW2KSU0oVAx8A7gXQWo9orfuQMkhELwPIVUplAHnAQaQMEja01n8FeoJeTkh5Y/yuSGv9hvbO5Pdrv89KGgmwkmcWsM/v5w7jNSF8jFSJU4FNQLnW+qDxq06g3Pi33bUk19jU9VPgG4DH+LkM6NNau4yf/a8F33Vi/L7feL9cP1PXHOAQcL+RZnqPUiofKYNEFLTW+4GfAO14A6t+YAtSBonYJKq8mWX8O/j1pJIAS4g0oZQqAP4EfEVrfdT/d0YrjKypIEIopS4DurXWW1K9LWLCygBOA+7SWp8KHOdkeg4gZZCwZ6RlXYk3UK8C8pGeSzEGk6G8kQArefYDs/1+rjZeEwKlVCbe4Op3Wuv/M17uMrq6Mf7fbbxudy3JNTY1nQNcoZRqxZt6vBbveJoSI10HAq8F33Vi/L4YOIJcP1NZB9Chtd5k/PxHvAGXlEEiGucDLVrrQ1rrUeD/8JZLUgaJWCSqvNlv/Dv49aSSACt53gLmG7PqZOEdyPlYirdJpAEj9/xeoEFr/T9+v3oMMGfF+QzwqN/rnzZm1jkL6De61Z8FLlRKTTNaFC80XhOTmNb6W1rraq11Hd5yZYPW+pPAi8BVxtuCrx/zurrKeL82Xv+4McPXHLwDg99M0m6IFNJadwL7lFILjZfOA3YiZZCITjtwllIqz3iemdePlEEiFgkpb4zfHVVKnWVcj5/2+6ykyYj8FpEIWmuXUuoGvBeEE7hPa/1eijdLpIdzgKuB7UqprcZr3wZ+BDyilLoWaAM+ZvzuKeBDeAcADwLrALTWPUqpW/AG8wDf11oHDyIVU8c/Aw8rpX4AvIMxgYHx/98opRrxDjL+OIDW+j2l1CN4K0Yu4J+01u7kb7ZIkS8BvzMaAJvxlisOpAwSEWitNyml/gi8jbfseAe4G3gSKYOEBaXUQ8AaYLpSqgPvbICJrPN8Ee9MhbnA08Z/SaW8jQZCCCGEEEIIIcZKUgSFEEIIIYQQIkEkwBJCCCGEEEKIBJEASwghhBBCCCESRAIsIYQQQgghhEgQCbCEEEIIIYQQIkEkwBJCCDGpKaVKlFJfNP5dZUwpLYQQQowLmaZdCCHEpKaUqgOe0FovS/GmCCGEmAJkoWEhhBCT3Y+AemMh773AYq31MqXUNcCHgXxgPvATIAvvwt/DwIeMxSzrgTuBGXgXuvyc1npX8ndDCCHERCApgkIIISa7bwJNWutTgK8H/W4Z8BHgfcAPgUGt9anA68CnjffcDXxJa306cDPws6RstRBCiAlJerCEEEJMZS9qrQeAAaVUP/C48fp2YIVSqgA4G/iDUsr8m+zkb6YQQoiJQgIsIYQQU9mw3789fj978D4jHUCf0fslhBBCRCQpgkIIISa7AaAwnj/UWh8FWpRSfwegvFYmcuOEEEJMLhJgCSGEmNS01keAV5VSO4Afx/ERnwSuVUptA94Drkzk9gkhhJhcZJp2IYQQQgghhEgQ6cESQgghhBBCiASRAEsIIYQQQgghEkQCLCGEEEIIIYRIEAmwhBBCCCGEECJBJMASQgghhBBCiASRAEsIIYQQQgghEkQCLCGEEEIIIYRIEAmwhBBCCCGEECJBJMASQgghhBBCiASRAEsIIYQQQgghEkQCLCGEEEIIIYRIEAmwhBBCCCGEECJBJMASQggxJkqpGqXUMaWUM9XbIoQQQqSaBFhCCCFiopRqVUqdb/6stW7XWhdord1J+O6NSqnrxvt7YqWU0kqpeanejmDB50oIIcT4kwBLCCGEEEIIIRJEAiwhhBBRU0r9BqgBHjfSAr+hlKozenAyjPdsVEr9QCn1mvGex5VSZUqp3ymljiql3lJK1fl95iKl1PNKqR6l1G6l1MdsvvuHwGrgDuNz7zBeP9v4zH7j/2eH2f5WpdTNSql3jff/XimV4/f7y5RSW5VSfcb2rzBe/3ulVItSqsj4+RKlVKdSaoZS6q/Gn28ztuvvbb77s0qpBqVUr1LqWaVUrfH6XUqpnwS991Gl1NeMf1cppf6klDpkbMOX/d73b0qpR5RSv1ZKDSil3lNKrbI7V3bHRQghROJIgCWEECJqWuurgXbgciMt8L9s3vpx4GpgFlAPvA7cD5QCDcC/Aiil8oHngQeBmcbf/UwptcTiu78DvAzcYHz3DUqpUuBJ4HagDPgf4EmlVFmY3fgYcDEwB1gBXGNsy6nAfcA/Gp/1C+AxpVS21vr3wGvA7cZn3wtcp7U+pLX+gPG5K43t+n3wFyqlrgS+DXwEmGHsx0PGrx8C/l4ppYz3TgMuBB5WSjmAx4FtxrE8D/iKUuoiv4+/AngYKAEeA+4wjle050oIIUQCSYAlhBBiPNyvtW7SWvcDTwNNWusXtNYu4A/Aqcb7LgNatdb3a61dWut3gD8Bfxfl91wK7NVa/8b4+4eAXcDlYf7mdq31Aa11D97g5RTj9euBX2itN2mt3VrrB4Bh4Czj9/8ErAU2Ao9rrZ+IchsBPg/8h9a6wTgG/w6cYvRivQxovL1zAFcBr2utDwDvA2Zorb+vtR7RWjcDv8QbiJpe0Vo/ZYyB+w2wMobtEkIIkWASYAkhhBgPXX7/HrL4ucD4dy1wppGS16eU6gM+CVRE+T1VQFvQa214e3vsdPr9ezBoW24K2pbZxnegte7DGxwuA/47yu0z1QK3+X1uD6CAWVprjbcH6hPGe/8B+J3f31UFbdO3gfIw+5NjpmsKIYRIPimAhRBCxEon8LP2AS9prS+I87sP4A1C/NUAz8S5LT/UWv/Q6pdKqVOAz+JN6bsdb5phrJ/9O5vfPwQ8p5T6EXAm8Ld+f9eitZ4fw3f5S+S5EkIIEQXpwRJCCBGrLmBugj7rCWCBUupqpVSm8d/7lFKLo/zup4y//welVIYxwcQS43Nj9Uvg80qpM5VXvlLqUqVUoTERxm/x9h6tA2Yppb4YZruC/Rz4llJqKYBSqlgp5UuDNFIjDwP3AM8avWUAbwIDSql/VkrlKqWcSqllSqn3RblPiTxXQgghoiABlhBCiFj9B/BdI2Xt5rF8kNZ6AO+EDh/H2xvVCfwnkG3zJ7cBVxkz8d2utT6CdxzXTcAR4BvAZVrrw3Fsy2bgc3gniegFGjEmwMC7z/u01ndprYeBTwE/UEqZPUv/BjxgHJOQWRC11n829uthpdRRYAdwSdDbHgTON/5v/p3b2L9TgBZOBmHFUe5Wws6VEEKI6Chv6rcQQgghhBBCiLGSHiwhhBBCCCGESBAJsIQQQgghhBAiQSTAEkIIIYQQQogEkQBLCCGEEEIIIRJkSqyDNX36dF1XV5fqzRBCCCGEEEJMElu2bDmstZ4R/PqUCLDq6urYvHlzqjdDCCGEEEIIMUkopdqsXp8SAZZIP26PZuPubt47cJSlVUWsWTgTp0OlerOEEEIIIYQYEwmwRNK5PZqr793E1n19DI24yc1ycsrsEn5z7ZkSZAkhhBBCiAlNJrkQSbdxdzdb9/UxOOJGA4Mjbrbu62Pj7u5Ub5oQQgghhBBjIgGWSLr3DhxlaMQd8NrQiJudB46maIuEEEIIIYRIDAmwRNItrSoiN8sZ8FpulpMlVUUp2iIhhBBCCCESQwIskXRrFs7klNkl5GU5UUCeMQZrzcKZqd40IYQQQgghxkQmuRBJ53QofnPtmWzc3c3OA0dZIrMICiGEEEKISUICLJESTofivMXlnLe4PNWbIoQQQgghRMJIiqAQQgghhBBCJIj0YAkhRBiyKLYQQgghYiEBlhBC2JBFsYUQQggRK0kRFEIIG7IothBCCCFiJQGWEFOU26NZ39DF7ev3sr6hC7dHp3qT0o4sii2EECJR5Lk7dUiKoBBTkKS+RcdcFHvQL8iSRbGFEELESp67U4v0YAkxBUnqW3RkUWwhxFQmPS6JI8/dqUV6sISYgsKlvsnaZCfJothCiKlKelwSS567U4sEWEJMQZL6Fj1ZFFsIMRX597hAYI+LlIexk+fu1CIpgiKEpARMfpL6JoQQIhyZ5Cex5Lk7tUgPlgggKQFTg6S+CSEmK1kcPDGkxyWx5Lk7tUzYAEsp5QQ2A/u11pelensmC0kJmDok9U0IMdlII2HimD0uwcdSelziJ8/dqWPCBljAjUADIE0pCSSDMFNrorW8TrTtFUJMbtJImDjS4yJE/CZkgKWUqgYuBX4IfC3FmzOpSEpA6ky0lteJtr1CjDdpcEg9aSRMLOlxESI+EzLAAn4KfAMotHuDUup64HqAmpqaJG3WxDdVUgLSsSI00VpeJ9r2CjGepMEhPUgjoZiq0rFeM5VNuABLKXUZ0K213qKUWmP3Pq313cDdAKtWrZJp8KI0FVIC0rUiNNFaXifa9goxnqTBIT1MlUbCeEgFfPJK13rNVDbhAizgHOAKpdSHgBygSCn1W631p1K8XZPGZE8JSNeK0ERreZ1o2yvEeJIGh/QwFRoJ4zHZKuASLAZK13rNVDbhAiyt9beAbwEYPVg3S3AlYpGuFaGJ1vI60bZXiPEkDQ7pY7I3EsZjMlXAJ1uwmAjpWq+ZyiZcgCXEWKVrRWiitbxOtO0VYjxJg4NIZ5OpAj6ZgsVESdd6zVQ2oQMsrfVGYGOKN0NMMMmoCMWbvjDRWl4n2vYKMV6kwUFEKxXpbZOpAj6ZgsVEkQae9DOhAywh4jHeFSFJXzhJ8uTFVCINDiKSVD0fJlMFfDIFi/GyerZKA096kQBrApBKauKNZ0VoqqUv2F2f6RZoyn0khEi1VD0fJlMP62QKFuMR7tkqDTzpQwKsNJduldSxirWSOxErxVMpfSHc9ZlOgeZku4+EEBNTKp8Pk6WHdTIFi/FI9rN1ItbD0oEEWGkunSqpYxVrJXeiVoqnUvpCuOsznQLNyXQfCSEmrkQ8H6TCO3mCxXgk89k6Ueth6cCR6g0Q4YW7kRLJ7dGsb+ji9vV7Wd/QhduT+LWZ/Su5Gm8ld0tbLxsauqJ+v1kpTtU+RMNMX8jLcqKAvEmcvhDu+jQrEv5SFWhOpvsoXa5zIcbTZL3Ox/p8MCu8X3roHW59fg9feugdrr5306Q5Pqkw0a61ZD5bY62HiZOkByvNJaM3JFktFO8dOBqwHwDDLg+3PLGTtYvLQ74rllaadGplmUrpC+Guz9XzZ1BbmkfjoWO43DqlefKT5T5Kp+tciPEy1us8nXt4xvp8kN74xJqIZWoyx6ClUybKRCMBVppLxo2UrAJ7aVUR2RkOhl2egNe7BoYtvyuWSnG6PXSmSvqC3fW5ev4Mrrn/TVqPHGfUrcl0KmpK8/jVujNS8tCaLPdRul3nQoyHcNf5moUzwwZPE6HCPJbnw2Sp8KZLEDwRy9RkNuJOpSEPiSYBVppLxo2UrAJ7zcKZzCzMZl/vUMDrIy6P5XfFUimeLA+dicbu+jQfWkOj3mB61K1p7xnk5b2HUhbwTob7aLJc5+lSuRLpye4637G/n3tfaQkbPCWqwpyu12g8Fd5025d0CoInSplqdQ7DBemJOudTfcbGsZAAawIY796QZLVQOB2Kf7l8CTc8+E5AL5bdd8VSKZZWltSxuj4T8dBKdKVgMtxHk+E6T6fKlUhPdte526MjBk+JKnuScY3GU8bFWuFNx/stnXqNJkKZmsoJwqbSkIdEkwBLJLWFYu2ick6vnRb1d0VbKZZWltSxqiSM9aGVykpBvIFdMq7B4O/IyXRQU5rH9v39vt+n+4MvnspVqlrgrb7X3Id06Q2YjOzuJYdDRQyeElFhTkYAEG8ZF2uFN5nBTLT3aTr1GkUqt9Oh9y/Wc5joc56MIQ/pcJwTTQIskdQWivH6LvNzNzR08eT2gwBcuqIyEZucluIpjMajALOrJPxq3RljCjZS1cI5lsAukde23bny/44d+/t5ZkcnbT2D3PbC3rRomY5GrJUr/3MyOOImO8PBzMJs/uXyJaxdFDo5TqJYXQsrq4tRSqWsN2AyVkKshEs9jhQ8JaKhIxkBwFjKuFgqvMkKZmIpO9Op1yhcuZ0uvX+xnsN0CmCjkS7HOdEkwBJAcidlGM/vuv+1Vt9N+tzOrklxkwaLpzAarwLMrpLw8t5DYwo2UvWAGGtgl4hrO9K5Mr8D4Bd/bU6LNJtYxFq5Cj4nwy4P+3qHuOHBdzi9dtq43d9W18Lb7X2+bTBf27qvjw0NXTgcalwDn8laCbFjdS9FEzxFauiIJkhNRgCQrDIuWcFMLGVnumWc2JXb6ZLKGOs5TNQ5T1aDTroc50STAEtMGpP1Jg0Wz36O17GJVEmIN9hIVQun1f4Mjri595UWIDkpeNGeq4nWSmmKtXJltZ/gDXLG8/62+t7gGVDBe35ueWInh4+PWPawQWJSCidj+RZrBS6aXuJwnxltb2gyAoBEl3F2+52sYCaW8miijOtJlzI21nOYiHOezAaddDnOiSYBVhqYKmkfiRZ83Lbv75+UN2mweAqj8SrAxisQsnpArKwuxqM1t6/fO273idX+ALzWdIQtbb2cVlPCb687K+rvjefejvZcpVOaTSxirVzZnRMIPS6JLEutvjc7wwEEBlrZGQ66BoZ9r/n3sJ1WU5KwlMJ4UivT+bkyljFI5y0u96UM3vliY8D4uHCfGW1vaDICgEQGPpGOZTKCmVjLo4mwlEm6lLHx9MqO9Zwns0EnXY5zokmAlWJTLe0jUayOW01p3qS8SYPFUxglMxBKROto8ANlUUUh97/Wyo0Pb/VN7lBbls/FyypYPqs4IGd+LJVK//2xWhR7U0sPGxq6uGBpRcTPivfejvZcJTPNJpUzOq6eP4NMp/V3+R8Xt0fzqXve4O32PoZdHrIzHDEHxP7sgvzggKksP4uOoKUnwHu92KUUxlNJieUeTufninktPb7tAFvaeuM6Nnb7t+6curCVwlh6Q8c7AEhk4BOpMpyMYCbd0v4SYSz7lKwyM9y9PpZznsxepcl47YAEWCk3GdM+ksHquDUfOsbcGQW09wxOqps0WDyF0Xj1CI1n66j/A2V9Q1fA+R4a9bCrc4DdnQMBE2tcc/+bY6pU+u/Pj5/dza7OgYDfezQ88e6BqAKseO/taM9vslqmU11Zf3nvIUYsUvOh1w6eAAAgAElEQVSyMxwBx2VDQxebWnrwaO/vYw2Ig9kdXyDgNY/W3PjwVsseNquUwngrKbHc9+n6XAlO0QsW7bGx278n3z0YtlIYS29oMsQT+FhV3NMhxWqipP3FIt59SmaZaXUvvNPey20v7CHD6Yj72Z7MXqXJeO1AigMspdQC4C6gXGu9TCm1ArhCa/2DVG5XMqVDwTgRvXfgaMhDcsStOX5ilNs+fgq7Dg5Mmps0WDyFUaQeobGukxFtJSHeVj27lmfNycrVHRv2JqRSae7P49sOhARYAK82HcHt0Zbb7b9/zYeOxXVvh6vYr2/oCjl2490ynerK+nsHjnJiNDRQuWRZBf/9sVN85+HJ7Qd9wZXJo72vxxNggf217f+a26M5ZXZJQG+MySqlMN5KSiz3fSqfK+Hu8eBrKVi0x8Zu/8zPsKsUmkGq1bmaCNkO4XruxrosRiJ6WyZC2l+s4tmnZJaZlvfCqIe7XmrC5dZxP9vj7VVKlxmO00Gqe7B+CXwd+AWA1vpdpdSDwJQJsOJtJYj2gpysF+7SqiKyMxwhD8nuYyM4lOJL581P0ZYlRzyFfrgeoWRUmsfSqheu5Rm8lavNbb0JrVReuqKSR7ceIKjOzsAJl+VxCt6/rAwHSoH2+4DcLCeLKgotAyUr2u+zx9I7N5ZyINWNQFbnPi/LyeUrq6LaB62Dz2BimYHPhoYubnliJ10Dw4y4PGGndY+3Vz3a+z5VYxoi3eN2DSXgPafRHhu7/bt0eSXdA8O2xzvcuUpEtsN4PW/DpVW+1drDaTUlY0plS9d00okqmWWm3bNx1O0t92J9tvtfw+vOrgNF1A3W6TTDcTpIdYCVp7V+U6mAg+hK1cakQjytBNFekMm8cJMdyK2eP4PCnAyGj40EvD7i8sRUiKVDAJqKbUhFpTmeVj3z2Gzf309taR5tPYOWQVZulpNVxgLWiZyatqwgi8NhrjH/97rcnpAB9A7l7cXwr3D7LyVgdU/ajS9s99v3RIxXifTQM/drxOUNFhPRCxOPaMtIu4B4d9cx2x7HRHE6FBcsrWDt4vKIKYXJuL9TNabB6h7f0tbLTY9s5fKVVSyuLLScOOSSZRVcvrIq6mNjt39rF5dbngP/zwx3rsZyXsbreRsprXLUrfnFX5tZVTstruyNVPdQR5IOz+hYxdPAEe9+rp4/g9rSPBoPHcPl1mQ4lS+4MkX7bB/rNZxOMxyng1QHWIeVUvUYDbVKqauAg6ndpOSKJ90r2gsyWRduslsgzNb8o0OjIb+LNS0i1S0nqdqGcA+A8XqgjWWBWf+JLS5aWsFz73kX2PU/Zjesnc/mtt6ETk2b6VQoCKi0+x8n//daPdg82pvKVj+jwHK8jtU9aXXfNhkPz2iPnb9Yy4HgCl3w/jsUSR3bGG0ZuXZROQsrCkPSOtt7BpP2sI4mpTAZwh2z8ayw2k1t/5etB3huZxcrq4sDJpHJznAwoyCL6tJctu/vB6JfCmHd2XUBi8r7T7MezfFOdDpbPGNhojkXkdIqwRtkbevojyt7Y7wb28ZyvY24PFx5xyu+4GGi9G7E2sARbz3ArAu1HjnOqFuT6VSUF+bQMzgSV0PjWOuMiZ7h2JwpdCIF1/5SHWD9E3A3sEgptR9oAT6V2k1KvlgL+mgv4ngu9ngKw2S3QJjfNxJU4Qwe9B7t56Sy5SSabYi0rks8BZDdA2D1/Bm2Bb25vfEWdmNdYHZo1EN7zyArqov58nnzLSuPiZ6adsStcSjIcjpCUomC3xscXMHJVDbzXN6+fm/Ye9Lt0Ty+7YBlukdmUAA31vEqduVA8H4F71Wm08G6s+vietDFe71GU0Y6HYqLl1Wwu3MgYJun6phWq2M23g064VJ5B0fcbOvo57a/PwWAW57YSefRE3T0neCODU3AyTTBWFOKugeGfWuOjUUs12dUy4SEGQsT7bkIl1YZ8F1xXufjmU46luvN7dFccccrAQ0m8TyjU9EDFulZFLxNHq3jqouYZfWQMUZ11K05cnyYurL8kAbIaOpFYw22EznD8aKKwpQ3gI9VSgMsrXUzcL5SKh9waK1DR5SLENH2Prjcnpgu9ngLw2Snm1k9yCB00Lu/dJ15KdI2hDsnEH7Nl3DsHgB2Ad+Ghq6IqW2RBA8wz3IqakrzbFuu41nEeKyt0lbf6dEwZ3o+iyoKA1rK7So+mU4VUKHyf7BFunevvncTW9p6Qz4zN9MR90MzmodepMk5/I24vDM4xjpxRLSLvI7F8lnFKRl7NFGMtUEnknDLHID3/t3V6U1hO3x8JKSRLJUpRVY95jWleSysKMShVMC9H+0yIWA/Fiba/Yg0/tQU73U+numkYzlXG3d303ToWMjrkbIe/K/d1fNnjHlm2XjZPYusrp2y/Kyo6iLRBPUnRj1cvKyCZbOKY25oHGuwnagZjk+ZXQKKlDeAj1WqZxEsAT4N1AEZ5lgsrfWXU7hZac9qXZhMp+Ls+ukhD4isDAd5Wc6QXgqrQfbxFobJHFDt9mie2dEZ0qoebtD7eM28lAiRjl24cwJjK4CsHgB2Qc2T2w9ajq2IdQps/wkHRt2aPV0np1pfWV3MZ8+dQ8PBAZZWFVmO1xjv82NXmdndOUB7z2BAS7nluct08LnVc8l0OiwfbOEeQOa5tpqJ7tSaafxq3Rm8vPdQzA/NSA+9aCbn8BfvOQi+lu0WeR0Lu7Jx9fwZY/rcsUpFK3o8jUqRGnQi7YN/w83j2w7w9I5Oy7F74XplxpJSFK7SvX1/Px6PxuFQLJ9VzOr5M3h57yHbXoShUQ+7u46xu8tbyX9s2wHOmlvm27/g8rDtyPGARpBIY2Gs9mNwxM3j2w4EBAgej6YsP4sR1wlcwdNkAso4rvEGRf7nbMf+ftzGMdq4u3vM1+lYGjHfO3DUMisgw6miXvutZlouLUcGE7IOXaJYXTtuz3DEca6xrP25bFZxXA2N0QZIduVZImY4Nv/mzhcbbe+PiZIqmOoUwaeAN4DtQOg8vMKS1bowIy4Pd21sDHlAAAEVPv8WneBW5HgLw/Gq1FjdxBt3d9N25HjIe2tL8wIqjNF0v6OJWPFMVKXI7rPWLJzJyurigMVRV1YX+7Yh3EO4bnp+wnvg7AI+83v9Dbs83PLETtYujq73YePubrZ19PseIpqTlfjBETdvNPfwdntfwIQQyR6ob9cC7z8dvPlwtnsY3Xj+AtvjEe4BZFfpPHV2CWfMKeXlvYdYs3BmzOc20kPPKvAxJ+cw/w3eczWWcxDLIq+xCO61tyobX957aMxrDUF8KbKpGGcZT6OS26O57YU9vNXaE9LrYtWDHdwg4l/JMu+P7oHAHsuy/Cw8Wls2ngRvj514Flx+p73X9zwEb0NIVoaDUbcO24vgz6NhS1uv7xqwSgdcUF7A1y5cwK6DA4y6PdzzSovtdlrth0PB0zs6GXF5fA2ko27N4Ijb9lo5u76Mz547Z0zPJ/NZdO8rLQm9Tq32MSvDQdOhY6xv6Aq7zUurisjNdAScN4D6GQWW5Y9V4LK761hIY+xYnpGJqBPYjVOsmZbL4eMjts+6aIL6sT4jnQ7Fr9adwR0b9rK5rZdVtdO4Ye38mCZPiyeLxOpv7Bo7n97RSffApgmRKpjqACtHa/21FG/DhGKO0QgudE6MeiynqT4x6iHT6fANfA2entu/FXnO9Py4egzsAr5YKzXB+2l1E58xp9RyTZyLl1WEpG6YD/XsDIdlILKrcyDsQPBEVYqCH/KZTkX9jAIeu+FcnA5F0CyaAT+HK2TiPV/h2AUNl66oDGmNBugaGI46vSjSWAINAS2N5ngNh0MlbQY2/2Dk3ldaeL3piO14nnjHfNk9gOwqXO/s62NTS09U12C4lkW7h55dWqQ5OceCmQVsP9jP2219lg/caI3HIq/RTDRyYjT2mUWD73276dajKQ/imWRkrJU4u++0a1Qyx176B1cmux7sTS2BDSJWPV3rzq7DozU/fLKBroFhOnqHuPHhrb7Gk+DAJ5qp2mNJQwoeo+Lbp1FPwGt2vQjBho0ZRO2u5Wfe6+LQsRHfcQg36U7wfniDKY/v+4O30W3Re5WX5eSz584Je21Hup7CTQE/1t6e4AYrh4JRt4dHjUlPwt1DZuPjGy0nU6YVMC0v0/K7rMoxq074rAxH1JM5+b9nsbF2ZPCkSxcvq2D5rOIxpeHlZTn53mVLAO9C9l1Hh5lRmM2GXV1hU9LHkg5oJXg5kK37+tjc1htwjpI1dj14SIFprA1yyZTqAOs3SqnPAU8Aw+aLWuue1G1S+go7RiMrummqw7Uix9saYrUQaKyVmmB2N/Gq2mmWhdOyWcWWfzfs8lg+MM3jYlfxDDcWyWEUdrFMAuJfkRh1a3Z1DrD2Jxv53mVLAtLChl0e3mnv5dbnd9PRO4TWmprSPFoOHw8pZBLdegXhF7mdWZjNvt6hgPcHT1keLiiNdiyByQyCv3Te/ITPehnuwWpeE0DE+8ls+QXvfQDRz4IWLFKFK5qKeTSNAiMuT0AL5dKq0HFLZsrtmoUzAz7T6oEb6/692dITkuoUa8OAXaXQKqXIHDAd7dpjVvf+2+19QGADQKQZ4kyxZAYkqmHH7jvtGpXMfbY7fubf+/NoQq5Nq56umtI8Dh8fsWw8ufbcOb60NKfDwbJZ0ZWp4WYQjGU8oT//XgS7MirDoVhUUeibGntP9wBuT+Bn+N+j4RpggsvapkPHeHTrgYjbGW6MZ7BI11OkKeDHmhERLmU0mop531Dgqj0a2NbRb/k30T5fyguzw07m5H8dBadOj7o9vsXMh0a9Y1HNFPdo71O7BoIPLpzJZ+7bxKaWHt93PO6XlmrXcxtvOqCVaIKnZI1dN6+dmx7Zyl+C7otkj5WPV6oDrBHgx8B3ONnYoIG5KduiNBZujMbK6mKWVhVRlp+F22O/eGK4QshsDVlSWRTw8IrE6jO9LcmeqNafiWWsgNOhAlo1gmcOjGbGpWhaSe1S8255YmdAN75dmkzIZ1n0unX0DfGdv2y3TDW588Um3w2hgLKCrJA1vxLdemWyCzr/5fIl3PDgO7Z54pEK5+DWzODpv4PFWjGORiwV2GhaymP5vGgCu0gVruAHS7h1uKwejiMuD+/74fP0GxWX15qOUJTjZGV1Cds6Qns1rFLGIo29C7efWuuQhX9jWWA2+JjbVab8K6HRrD3mzy6FJ1i4GeL8xZLSlqjW4XDfGe3YS/AeR7MH+7mdXWErr3Y9XY3dx0IC6sERN/e/1sq1586JqUc03AyCbo9mQ0MX339iJ93GAsKRxhP6M3sRHA7Fjv39PL39YEiKmUdr7nu1hftfa6X1yPGA4Mr/OPj3coer/Pr/fn1DV8RjHGmMZ7BI11Pw70O+L46MCKv73xxzFpzpEq6iHOskF3YNVP6XXnaGg+9dtoSX9x6KeJ9ZNdZasUofDyfcBFNvt/cFbK+ZlrqhoQuA0rxMRlweXB4dMpwgEaIJnpI55t7pUFy+sirkvpgoExelOsC6CZintT6c4u1IuWi6q987cNSyICzMcgKKrz6yzZcWV12ay79cFjo7l123K5wMiu5/rdXX4/Lk9oO+dLasDIfldpuDcF3uE75ZoUbdmnteaYnY2h3rWIFF5YU8vf0gLo/H9/f7egZ5YWcnDoei+dCxsGkeDgU1pXn8at0ZYR9MS6uKyAnK/1bA/v4TvlQNM01mS1svI8Y02lbHamlVUcgU26bewRHL7dVB/+4bHPWNifE/Hksqi0LeP1Z21+LaReWcbvSS+geYHq25ff1ey9bicCl1wy43d/+1OWQmMfBWdmKtGEcjlgpspBTAcGNWgj8v2kAsUoUrK8PBoopCy8+MZoHJOzbs9QVXpqMn3JxeW8J1q+f49vPs+ulceccr7O4aIKhuHHbsXbj93LCrK6B1Frz31GfPreOr5y+M+pxGrBQGVUJdbs2XH34n6pZzqwpEtnE/B9+n0QSe0Y5RtZuiP57W2lhn87La50yn4gsfrOfG8xcARKy82vV0WU3MAPB60xG27utLyEKmZs+ZVTqRQ0GWUwWUM7lB45vM8WEofAHBDWvnc+vzu7nrpWZfme/RhPRmBrOanCCalM/gc5ZjMU4s0hjPYJEqzOEaJGNt+DD31Sq99rPnzqH50DEyg85DTqbDtqIc6yQXweX1oqCUPvP4rV1cHtUECtv390edbQGx3ad2jRxW15RZ3h46NhzSUBs8vGCsogmeYpkIY0NDl6+x/pJlFTgcKmxjtJXxnOVyvKU6wGoEBlO8DSkXbeVraVVRSCUboO+Ei7fbewPSzI4cG8GhlO0sTxsaunzrkPgHRT9/qTnggWims115xys88eXVtoMdB0fcZDgCF2X1r8iYLTTRzlxoNVZgZXUxt67fy66uk61aLo9mX+8Qn//t2yjlfQA6FLa9Ix7tXXg00viw1fNnkJURGGBpQvPgPZqA42em/m24eY0vyFqzcCb1MwpCFkD1HkOYVZzt6xWzqiSb+1lVnBPSezaWACS4ALx0RSUfXDAz7LS2Vg+wGx/e6qt0BbcWW6XUmQ8Wt0fzQkN3yHHJdCquO3cOy6uLIy7KG41IKUPhHozBD0K3R7O+oYvt+/t5dkcnjYeORQxqIL6eCXMMgn9QYjaArDVan4NTT4MFDyjfbJFeDPBOex83X7TId14uve2vAfdZsOCxd9Hs55PvHgwJ1jTQ0TNkmd4Vtkc4QqXQrIS6PZo1P34xpMwMd86tHujmGCzzeDuMssafXeAZzRjVSOnfsbbWxjo+MJoJW6KpvEbT02WK1PIfS2aD2XNmVUH1aPjQ8krmTM8PSEVcPX8GL+3u5pYndgaMD/Mv77IynHiCTnS4MVrBQYnbo/nUPW8ETGJ0Wk0Jv73uLNtns/85M2c6jGexaLdH43J7Qp4pkSbayM5wcMmyCl+KcLTfB9b3vzlWz+q4ZWU4bCfDspvkYp7NJBfmMfQvr81yMvj4RTOBQvB5jyRcsBgNu/pdhkPRNTAc8vqwyxPXTL7hRBvM+KfomoHTnS82BkwI9Kl73gh4dv1l6wEcKnCyJHNm3GhnJk3WWOxESXWAdRzYqpR6kcAxWFNmmvZIreD+gcniikLLcTAuj7ZMwTBbYyB09qsLllawdnE5t72wh7teavJ9t11rY+OhYyEPweDC1Opvh0bc7Njfbzs7kdU6Dmb6yLqz60DBroPedVM8WvPF371tuX3+M9J5tLfFsig3k97B0ZCgKJqWppf3HrKssEajo2+ItT/ZyFWrqn2DXx+74VzW/mQjHX2B5y44LaWx+xhPbg+tiJqpDf4TPni0DglA3mrt4bYX9kRs5Rxxebjif18OSIF5bNsBFpQX0t4zaBsIBPewBKdQOIzZ58xZsMKtc+V0WC8MO+rWtPcMWk7aEksrYbQpQ9FWYKNJTbP7vHCzQdo9LJwOxWfPnRNQOfFofOdj+/5+y9RTs7fUakD5abUlvNZ0JORvTq+d5vv3hoYu39TUdvzH3vmzXGzVOGeRxNLQFNy7DDCjIIt//8jygF77jbu76R4YJpg50N2K3QPd7dFceccrlkG1ySrwjGaMarj077FMvx3t2IxoKjHRVF4hsGHMrsHIn9U9HWtmg/k5VoIX+/bncKiQ8WH+5Z1l+rvD23Dpf66sghLw3kv+lcxhl4dNLT22lWKrcxb8c6T15Mzv/f4TO+k6eiLg+Gcaaw+aQU1wRkt2hoPTa6cFrCcZSxq03YQ5dkHpqFuHNHb6T6tfV5ZP65HjAZNDPWpMDhUNu3sgmgkUHDFW4MMFi3aCJ9E4raYk4HpxKKgszqEjqM7nv72xzOQbzbacMaeUVbXTLMdEWq0V9+Lu7pBe1nXn1IWkO8LJRilzDOuVd7wSMobcLr1+mzH+d9TtYfX8GRJgReEvxn9RU0rNBn4NlOOtV9+ttb5tHLZt3I24PLZpOHaBSc203JBWDrvemifePcjm1h4KcjJpt7mIM5yOqAIJl1uz88DRgIAvmgHEuVlO3B7radI3NHRZrmkF3rEhwekjt6/fG3XQM+rWXH1WLW6PDgggzW2KVKGOZiyXGUhYbVFH3xC3vbA3MEXq5jW+Cpr/uI21Rq/BT57dzR6LawHg1Brv+/y3z+r4j7q9+xsuNXPE5bEM9jwa9nYfC2m5swtq3u0ITaEwZ5+bMz2fZ3Z00tYzGHIc/LfJamFYh8JyxkKIPRiySxkyz10s6QaRUtPg5JiV4M+zazF9avtBdnUO2M5E1XBwwHbcgl0L68VLvTNqWg0o/8xZtRTnZgSkCRblOFlaVczt6/eytKqIx949EDHl1Oo82K1RZ753UUUhj207EHB9OxRcutw7zjPaXr41C2dSW5Yf0vN5fMQd0mtvl3aTk+HAo7XtGFGzYmaWd3e+2IjL7aGtZzBsGWQVeEZKu7FLDYSTi6cDCR2LaMWuMhrrzJT+gZrVVOXBgo9FuBntgjMbzEYcj9aWqdaRAlS7ho8d+/t95z+4F9nt0eQZQZ1dUGKyaizzaO/r8fY6WI0NMmcCPq2mBKWU5RAAONl4dc39b/pmOgweExn8s9V9addzEs9ERsFjSoMr8LVl+VyyrNKysh/vbJvRTKCwfFYxORmKE67o6xyxzJxsl0551ydP4+kdncDJMfD+DanB7LIJYmEXRH9hTX3AMbZaKy54Ns6t+/p48t2DYXt6zb/1b6wKLu/N87uto497Xj5ZhrzWdIQHXm/lre9cYDlsJZ2kNMDSWj8Qx5+5gJu01m8rpQqBLUqp57XWOxO8eePK7dFccccrlmljYB+Y7O0+xrS8LDx6FJfb+1AJroCZXB5NR98J4ITvNasWugyHsu25MmU6FcMuN2t+/GLY3gCHgkxnYOXV4VC2aR1Wa1qF21arlAE7iyoKOX9JRdipcu1EelA4FNSV5QHYtvZbpcA88eXVlq2+4a4FgL7jI4y4PHzkZ6/6AjS7Adyjbh027eaKO14JCa78fx88XsyqMj3i8vDLl5tC/t5sLQb4xV+bA67dN1t6+Nrvt3LFKSdbeSPNnGdSxLYGk12PAAROQW7VUm/34I4UdPuPWbGbMCO44jNipJXazUQVbgIZu/z7eTMLUYqQcmFwxM3T73XyxrfO566NjWxp6+XUmhK2tPXx1Ue2+u6PjDCVFLvzYPbEN3aHXsOleVls39/P0soizpxTGpIuZTYcWI0xterls+v5tKqsjbisJ1PpP+EKSQcLFs0Yt2AOB7zaeJhFlYW+nrRwaTfhUgP976XxWEcreDbJG9bOD6mwmI2AZkUouLckXHBqVpL8y9+cTIfxLNEh6/5FM6Od/yyIO/b3+xpxdnUO4FD4UjfNDIZz5k3nMr+JmoLv7cWVhZa9oc/s6PRNvhHci6yBgROugH0PDkpiEWugEG4m4Ldaey1T2f2ZAdJNj2ylpjQvYG3CYZcnZJY+q/vSrufEnF3R/xkVPFYv2ILyAt+/g4O5oVEP7T2DLJtVFNeY1nDsJlAw06oXzCwgO9PJCZcrzKecFOtYSavAdVtHPxlOBz/9+KkB+2q1pIHJLpsgFlbbYtXDFGmtOPNvd3UORKxXmhMR+TOPof/stVZlQf+Qizs27OVrFy6MY2+TJyUBllLqEa31x5RS2wl99mmt9Uq7v9VaHwQOGv8eUEo1ALOACRVg2c2QA95KjF1g4tZw+Lh3NrlMp6IwJ4MjQbPLReJfEKxZOJO8LCdHT4QvRJRS/PLllrADiDOdirnT8/naBQvZ0zUQMDuOXVqH1ZpW4bb11JppvN3WE7FVSQO3vrCX85dUhF3ryu7BZlaK7L7LHMs1e1pu2O0I3gerVt/1DV2214Kp8dAxLviflwICo3AtRGYPKBCyUHO478oy0jD80zL8U0pMd2zYy+BI6PdPy8vEozX3v9oaUjC6PJpHtx3g+YaT659AYD63Bh6zmKo43GKa0Y7VMIVLGQqXfhNucVTzfcuri223ya7F1Nxvqx4b8zoMHmv1s41NlORmhvRme5cs8AbD9mMMhn0VkfUNXdznd64GR9zY1U/OqCth9fyZlpN9XH3vJmP69dC/6xo44evFXFldzB3/cKov7df/cxZXFFqObTLHRfjn63s8OmKv0NX3bmJza49tb5wZ9N/6/G5Wzi4JGXwdXOmIpvfc7YE3Wnp4s7XHN71yuPQ7M802XM9LomYW9Gc1m+Q9rzTzudX1rPCbmSy44ce/t+T02mkh614Fl6P+Y36f3H4QrTW7u47Rcvhkw5rZUBCph9hsWAB8++3fiOPR3uN28dJy9nQdo/XIcR7deoCnjIma/vzFc7j2gbdCegysekPbegZ9x9dq9jvNyZR4q6DEdOmKSuteWyPoiyZQsAoK7cqhSA2lpmGXh79sPWA5+VLws8Pl9liODTrQfyKgF8tcQ6n1yHFGjfpAXVkepfnZbOuwPq/+z2m7RqzBETf3vtICYHtvmgFBNMsm+Aue2dY/rdpc8DladpNv2AmXNm6ea3MMnpm213LkOM/s6Aw4Z+Z9YY7rtLoPIwXxdgtnB/cwRbNWHMCuzgGsjrz/GKya0ryA4QhwsgyPJlvEqlEq3aSqB+tG4/8NwNf9XlfAf0X7IUqpOuBUYJPF764HrgeoqamJczPHj90MOeB9KK07uw6HQ4XtRRl1awZOuKK64P35V0ScDsXVZ9Vy58bQ3giT2aJt1xtQlJtJ/5C3R21f7xAPvN4a8ICwa8GNZkC0f6FlPqyDx43ZafIbNxYuj93qweZfKXq3o49ndnSG9FQNjXrY223fA2eKtHJ9uGvB5PLA/n7rXicrmU7FMzs6+flLTb5Aae70fBaWF9l+lwJW1ZVy72feF9BT5p9SYgamz+3ssvyMg/0n+OLv3g67P8EzfwWnwAZfz+EW04xlrAZ4r+UVs4p8Mx8GP2wipd9YpScNjrjpDlpENXhRWnMmLcCysmIKbgV1OhS/WncGX/39Ozy5vdP3PpdH+3cornwAACAASURBVBpa/Jmz0zkdyrLHzBwYfdMjW7l8ZZXlmCm7OtqqulIWVRaGrPdlTrZhV7nzf0C/3d7HZzW+hc8D2NSFhl0eNjUf4ez/WE//CW85Y86wlpfltOyZNrfJaoZKfy6P5s4Xm3w9wf7lQDRpwnY82lsBCK50m1tjVnjufaXF8jvM1MBwlU7/ipjdWFu7CqbVbJKDIx5uW7/XN1HDunPqbBtjzPX6rO5hq54E/5lpgz/HDBYjHe/gmWnDTadvNhCZf7erc4AL/uclegZHAirl2zr6uWBxeUhvqJkmuGbhTNs0dn92vRdrF5Vz1tyykDFO5rTyVuOv/cfRQmjvpblIs10aYCysyumcTAfP7OjkF39t9pVzVlweHdCLZZad/sd9X+8QN1+4EIdDcc/LzbzeHLrE6Z6uAd/+2mWOBM84aRcQRFo2wa7hy0xL9U+rjvXY1ttMvhH8nWbQZDfj8ZPvHsTl0ZazSK6sLuZ9daUhDW6/fLmZB15vDXnvNWfX8dT2g7zadISBE66QRcHDZUpY9TANuzwU53rDBnOctf9snP403gbb02qmUVGcw0VLynmv86hvwfovrJnna/Dwn8nTo3VUZa//uOF0lZIAy+iFAu8U7W3+v1NKLYrmM5RSBcCfgK9orUNGUGut7wbuBli1alX8/fcJ5H+jjbjsLx63x/tA+OLfzDMW5jxi2TIM3gt+ekEWLovJHIIFp/eMuDzcvn4Pv369Jez7y/KzbAdZZmc4GDjhCnhAWLUk+ad1uD3aO4DUL5/eLsgyCy3/Y9ceYRyEadStfbn0wTbs6mJza4+vAmZut3+FyEzvAWg7MkjrkcGAwtDpwHIdlLxMJyjvZyq8BdFfjBYxq/SaaFMfY8lCKc7JDKlk7O46ZpvOWJSTwY+vWsn5S7wD1/3HmgRPunL1vZto7Lb+HI8GTxTnxn/mL/8KT/DMdQp8ha7/eJlwYzXeae/ltJqSkKUDwNuC1tA54Jv5MPhhEy79xlwc1WqiEf/v39LmTdPxP35vNPfwZmtvxHs0OBgHuOb+N9nUEt3a6/6z09n1mJmt18/t7KKmNC/qMRM/f6n5/7d35+FxVffBx7/n3lk02iVL8r6vOAEbcIgTAgEDCZC9yZOGbizZE0pI27xPur1P3z7t27dL0tCkSZqELUkTaNLSQFgawCGAwRgbCxvjRbYWL1qtfZ/lnvePe+94pLkzGkmjGY39+zyPQL6a5cy5d8496+8AKRoiGU7bTbco+3DbYMprPHHkHuzKlNaaGzYvons4HJ/i5r5mqgAgXhID5CRe65muJ3E7Hbw+a+J0F7e8MRQU+c34+03mjrCmq/y46xTdCpNXoz7dlKlXm1NfT4nrKNKVs6MRi6/96ihNCeWi1+ja5GiXXu9374tNnpvIuz3eOuGxiefHa3rfrhPdnu/V2j+adH2NhGN0DIylnCa4aVE5jR6NzMnTTlN1onlFXkXBN3c2pIxCmriO9vYrV3lOI7vnt7dy+ztXJUUCninTUPFR4RXVxbQkjCyMRix8BpjK/h4mSlz/k6oj4PGDbXzt41t5/VSfZwPL0sQ/7wO3X+FZJ0gc4d95uMMzOqKbd+777mvp5ZlD7fh8RjyIRKrOgFQjlamUF5kMjE38rGcHx/mj/6jn/QkbX7sdgO717zMg4Dv33ffq/og4ZYnX+qa9Lb189uo1XLq8ku8+f277AK/H7m7sYXdj8gh+upkSEzo7PUaYwJ6e5zPs2VN/8M6VfPGa9bx04qxnAzoS01y5roYvXLtuwsyQfS29PLL/DH/xvou49R0r+dvHD0+I5DnVfak4YHLnDo9OunkmX1MEPw98AVijlDqQ8KcyYFcGz/djN67+XWv9X3OTyuxKms+fZm2eG+HKLZzvfmg/jx1oS/n4sxlMEVxaUcS2VdUoZ3pCOGqx/e+eSerFBLsg/dzVaylyRromR6tz+QwVb2AlStWTdM3GuqSgHVuWVXDPJ7byZutA0saOCnvKmTv1IHGdTqrAHpMlzqVPjE70o5ebk25KoxFrQoNs8nQxd46/1jhrCQzPqZVj0Rjr60rpHgpPqBR6Ta9xG3GXrqiKF8KmAlMpYmhiFhmtkZts+5oFPHYw9TXjMg3F+rqJe3el6zF3GzTTTc9kAZ+B1qkjf7k0TBhB+vGntgOkX6sRsfi35xuJxHTS9ywc04QTrvnEm/ZU+6iNhGMcah3g7hs2xKdu3b+rOekzeFV2ploXAfa15TbG3f3nvnz9BupP9U35XFdidDrTUJ5TlBI/T0v3MKsWlNB4dnjKHtvE15hc0U21z5vXlL9Ui7Knu0B+LKp56lA7UWfNoVtBe6Ghi90ekRIzNRKO8YMXGrnjytVTdgAFfUZ8T77JDGX3zt/98P4JkRst7d2wSrW+bap1ivaox8S1N1NNI6wpDabNg9FwDK31lOWsVyh/d4qZZWked4K4TNXYfflEN/tP9sZHJd3y1uu6dUeLvnDtOs/pfQOjEc/nWhrP63RPUw9eyxmPdQzylZ+/7vl9XlYVotMJna1IjtaZ2LBNDJiSSRRSsCum+1p6qS0Neq5fPtI+yB9etz4eCfibO49ndD9MdT4VsLSqiA9fupR9zb0caZ88vdv+HJNbqInrf1J9fx87YF8DN2xOPZ3VXTf8QkNXvEF674tNvHyiO2lk8U9+/joj41ESLymvTo7xqMVdD9djKPueYBpgWRMb63uaurn7of2srSv1nHbslV9Bn8Hvv30VP9g1ccnE2eEwv6hv5dH6VravqebHn9qe1LkQtSA6qeE4HfZWOicwDWPKe0K6v46EY3z/+UYOnumPB1fy2iLArXd5TfcfGIvy/eebeK2ljwduv4J/fOpI0vsoBZsWl6WcGXLXQ/WsrilJiuTp3pcaPDYpB/j0VavnfYALyN8UwZ8ATwJ/B3w14fig1jptV62yJ2zfCxzWWn997pKYXUnz+dPcbxIjXAEYM9hMzu1tMhQsLi9iWXUxTx2yh7+ffKOd2tKAZ+MK7BtRUcCMT+NxF1m66Q+YKr7nVKq1W4k9SXub7XUOp3tHk0YbXj/dj6EUd+5YTyRm0dA1HP/cGnj9dD//8uyxCc+bztB9Q+cgdz+0n5U1xfz3/taksLWTJRZaO490THjfyXP8U02fcaPxpeJOr0kMff7A7VfEF5xftqKSvS297D/ZR8zyjlI4lddO9absWU/0gUsW8w8f28ILDV0cdCpFzd3DSY0Mt8d8tlNSXGFnqlqmFerE8MaGoaaspJzbdmDqtIyEY3zpYXsUKmbplGuQwJ52mmm49ulYVhmic3AsaU+1P3vkwLSmqYUCJpsWlcUjzoWjsbQjn2MRixvfuoims8Oea8PScSu6n333WhaWFSUFTvEbyT3eMLFSlrgXm9ba7j1PGHmdyuSRc3dR9mzPy8uN9t49taUB7njXKvY09bCnKXnOf7rvg6VJ2zE22aZFZWxcVMZNb13EziMdE9aEJVZ+TnQN8YtJ5yrVFhle4c+fO9pJ11By6PpEoYDJ8upizyA6UynyGzxxsI1vPNOQcdmlIX7OP33VGk72jPDEwTbPxo07xT1VsJNUozmGgpDfROvYhPyy3ARMEktxf/MbYGkdb1inGgGdvPfj5AhsUxmPWjx+sBVj0kyJxM3G3UjAmTauPnvNan76yqmke3/U0pzpHeM7zzWmvGco0gdAciMuvto8sQPOnZHTOTCWstEMEwMcANSVBT07u7zqLanSnPhcr9kmUevcd9RU4DOM+NS4UMDkkqXl9I5EOJbQ8RuOWjy871TK774Gdjfa96rDGXQuTFfUImWnznTsbuphd1NPPPz9I1+4ErDTb1ma3xw7F7L91eZedjd2J11n7hTfb+1soPFs8nIJS8MvX29DKe9OpfGoxXGPRtRoxGJdbTGdg+N0T5oKXxwwuWRZ5aw+e67ka4pgP9AP3DKDp18J/D5wUClV7xz7M631E9lK31yYznz+ASfClTvtYyaL+dwy0NLQNjDGmf5zkQTHo5YTXdCb1+awiTf48WiMbz93Im1koEThmL3OwevhieHoX23uSSooR8Ix7tvVnFHF3mukJ7EAzYRp2L0iMUvz14+96bm5n7tIO920jKnyJnG0bPII3T5nrwf3NTIdvUh0Js35dflNxbKqELfdvycpmIfi3Ghdqsh+s6GxQ9kX+834mqSpesstDfe+2MT2tQtSfpdmMtoHEwv/dE9v6Bhg55GOtFOeZqK0yMfpvuQ37h6OZPR8hV2xXV4V4v8k7H/jzMRN/TxlV+y9okdOxW3M3Xb/Hs4OTbzeDJW6E8nvLMr+xjPHeOpgG8c6hybk+bLKEMuqQlhas/9UX8Zpmrwoe7bccvLbvz6RanlY1iigoWOQw+2D/Hd9a/y74K7ZcWcAgN3Iz2Td7eRyfPJ0pVQMZU/d9plGxmW8K+iMQE21j5r7PpNf314varCmtjRl+bqyujieF17bPKSSrkNwOiydvnx1R0D/6X+OTjsC22RepzgctbhvVzPv3lgXX8uTruHiUgp8KvW2LFONskctqCk9t7ekVwh8pVTK8qZnJH1Z5jMVmxaVec4ameWEiYzENMScVpih7Kn+t1+5BoC7Hto/IYrkVLOGNHYo/g9sWTLtctUVMM+twc9WmebF7cy7/G+eBiYGOnIjchb5TIwUHbYj4Rg/2XMy5ff1F6+3EjBTl6Cp7tePHfRe5534/Z/v8r0P1rRprV8k5XLo+Ws601803tM+Zmo6TzcNUgYBcANF3P3Q/mkXeKkeHgqYRGKW06hIfpTCu+fD63F+Z2RtpoVR0GfEI7Cl2qAUSBtOfToeP9jKic5BWgfGeK3l3KZ8mTZkFHDF6mr2tky9tseLvTi2yXMvL+3854NblqAUaUc3TAUVIf+UN1AvI5EYppHwnlN4pbmH072jSd8ld2RxX0tfyhD02XC0Y5j/8+ihrPdKrq0pSeqJn46yoEnAZyY1/Ke6LLSGrz99jKazwxO+N5PXvrjH3Oe4U9lQ9sbHiY1zQ4GBMzLgQSmVdm+k032jnO4btSsYfoNoLJZRvphG8qLsbMhF5U4DicFK3V/Hoxa7G7t55s12Hny5JV7xVKSe7gXnKoj29FDNjk0Lk9adpkyLhlvfsRKfaaQNyDJZ0LRnXmTSKVAcMFleWcSxzuGka2zTojIMQ+EzvBsY128+NzJ00aIyti6vzOhzZUsmbzN5LcpIOMZoeHTG3+9EGni5sZsdX3su3pGSSYXIDbwy08AtMLFhEY5aE8LTu7N0ZlpfWVtbGi9PEiNDBkxFnccI+VyytD3l766H9lNXFpxWNMFE12ysY21t6bTqDInTNQ2laOwc4vGD6QOtGMruXJzNdyBVJ2M4pgnH0ndMTNXgzOZ38z3OPo+FoOAaWIXKHT5399MImIoiv8lYJEY4pj2nYqRq2We6/mgmTKWSggC40Wjcze/a+qceHcnUiqoQv6hv9byJpwoi4SVxislMGMqOSnPV+lqePdzBvS82ZXXExsuxjmGOdUwdhRBSj8y8c+0C+kcjM270pfuMGjjaMcj1F9Wl7UWM6al7J9PJ9ByD/R053TeK31QTNgvesqyC5QuK4+He54rGDk/sxW+o+ALl6Xoig0hl6QyMx2B8+hUn+xwnBxb53LvXsGVZJU8cbKNjYJyFFUXc6ESB2tfcS01pkDW1pTx+oC2poWTpNI0r5/+ZdJrYN/ZYxj3AlpVcjrr7IQ2ORef8+zxXLA3372rmwJlzG3tPlRtuBfEX9a38or6VjXWltGUYDEFjh87+4xs2UFcW5FSKAEeTjWf4Ra4pDfCJty3n6Tc7vD+Hsu+Xi8pDnpXqR/a3cu+LzUlR9fY0z++wzdm+ZycGnsr0tWOWzmg/t0xo4NXmcxsOzybqprve+o0zya8RjmnaBqbXuHI7XGdbsR+PWpxx7jfTeS03FL9pKH7+uXdy+d88PWX5YxrwtpXV3H7lKh58uYX7nGvcZ2T2fVdzWjOcP2JZmB6ZK9LAyimF5dz9NbB5cTmfvGo1R9oGM9rx3jWXXyGvIACpotFkw8ZFZTx1KHkoWAFrFpTQ0JVZA2QmJgf+ePeGOm6975UJm0rmk1sZTRXRJ+AzaDo7zJevW88/P9vAsY7BrPe2H2kfpLFrKCe9+NPhBrBYVh3iL26+iAdfbuHfftOY0Zqr2UqZFyr5n14PNZ3GauLfMs1e9y3m8nRoYF9zL/Wn+ieEpH/uaCfhqDWrjgzN9MMfZ1oZ1Nj5k9jw3rq8Mh744vvPN7I7w2iM803faGRWIw9H06wJ9XKkfZAvPVzPiqpQRms5p+PsUJjvPd/oHQxGw5G2QW7YvIiPXr6Me55tSHpM4jpaN6y535z5gvdsVEsXlATYsLB0zu6T2bK3pTdpT66gMwV8JmVn1NL82X8d5FCb9950mdLYI1enekY88286nXAK+ODWJaDt6WmzZenpj8BsWFgWD8X/se++NGWZZyhYX1fGDz/5dl5o6Mp4vX6iTDs4Ct1/7z/Dl2/YWBCjWNLAypGdRzp4pak7XrhFYpo9zT188qrV/OF16yfseJ+thfPZMlc3jKDP4GjHkGfho2HOGlcKKAv6uHxlNe/fci6k6tOH2nmlqSfjxoQ7Le1I2wBHM9gPa7oMp0frk1et5t0b6iZE9EkM//7Y661zWtjkaurNdEUtTfdQmEOtA9SnWKsTMO2Rv2w2EH2GsiP+pQgR7Er1ljPNzuKE0eSvP30so3UuM/VKc++EiufkMMDzlaXtPaTW1pZO2ND3mo11hMMx9p30norsUsDi8iCtA+mDQOTadRvrPEMmz6WRcIyWnhEWl2d/elbKQBQGbKgrtcvixu6kxp3X3jyzXfT/gUsWsetEd8brHb2MRmL0jkQ8w73PJ16RFUcj1qzWXHQNh7nnmYb4nkgzXQc7Gkm/NjxTGli1oJj/3Hdm1q81m1TsPNKBZaUPeOWyNJzsGeHW+16htjSYlzqggROwJefvPD1n+iZucD2fzf84h+eJXx5o8yzcfulGsHECSXzzlkt5++rcbqA2i86/WQlHraytZ5oODQyMR3n0QCuf+eE+3vcvLxCOWjx+MPkcpVPkN/h/H93CDW9ZNCeLAmMW7DvZy/27muORBj/1rtVsXFga/xxgV9jDsew2IrLBbYjMpZFwjKcOtXvekPymYmF5UVbzxVDwtlVVrKktzd6LZmD76mq+ecul/PhT23nvWxezYIow29kwm2wzgAXF/mwlJWNBn8H7Ll7MH163Ph6hMxy1eN89z/P5n+6f0LgqCyb3L2qYd40rBVyy3J4GVxwwc/reYxGLj1y2JGfvG7Pg7v+o57M/3sfupolBj4oDJmtrSwllMS1Bn8GKBSWzbhSNhGM0dQ3iN5JvpgXQ0T7rSrU7RT8ctfjM1avxzeBDZyubFPCf+85kvVNgOh/pSPsQn/nhPu56aH/Go7/ubKFHpxGUK5ss5n/jCs4FECkE0sDKkY4U6zbc42644kfrz9DQMXWjI5tldrqR5ZkUlJmaD19mjT0dZsc/Pcd0O0HHIzE+8u1dfOc3jXP2WSIxzatOmPvb7t/DD15smrBX2HTN9GxO93nlRT7+9XcuZfuaBXNeOTuWYiRn9YISPnTpkmmN7oX8BhvqSjyve0PB569ey48/tZ0b35q73rOKkI8fOpthAjx7uANrvrWmJynymwyOzz5i23SFoxb3v9Qcr9TELM0Hv/Wi535N+UjfVEyPLTk08DePH+ayFZV87WNb2LQod417n6loPjsy69cxVOZlyGjESuoUMQ3FHVeu4svXr2dBSSDj73R1iZ+a0gDbVlUS8tg3Zzxq8eBLLdMaMbhiVWU8TPqE14rZHXeTWdoO7X4hGI1YBH0mX7x23bSfm60SzTCgYzB768RdQZ85rfrQTKZDZ7NUV4CvABr35zOZIpgjC8u9e5zrygLELM3v/WC35y7nqeSqelVXGqBraDzjecCF6nTfKFpP70OORXVORuAiMc23nzuRFNVtJqZ6vqmgstifNF1mSUWQzsHMr4MlFUVcu2khhlLxzUanyqt0kedm4ljnEM2/Gbb3Y8rghQ0Fm5eU0TcS9ZziYml4+NWTXLK8kuazw1lPbyp1ZUH+5Gf1LKsO8Wh925R7uc0Ho5HMIv9lmwb2n+zlnmeO4TMNojF7n5VCoVPk2qneUb6Vg3Dxk0VimifeaJ/VGqyyoI9Ni0o4eGZgQrTJ6YhZmkfrW7lvVzMjzsL/TPQ45Vi6KGfTbWgfafee1p5KccDk9nes4nsvNM44CE4hefKNdv74PRsIZCHIxEzELJiL0mc0Mr+WbqSjgA0LS6ko9vNqU++86MzOFjeASCFQerq7CBagbdu26b179+Y1DU8faufTP9qXdHxphR2O8zu/yXxfKSHyIVXYZC8Ku/fb0nZ0t4ATeEAu8eyb6ZqH85kb9dLdcF0UvtlE6cwnn4ItKyrZ19KX76TkhAI+f+0aHnixhZECapScb87X+0LIb/DaX74nq1OFZ0sptU9rvS3puDSwciNmad53z/OeU1WEEEIIIc4H2Y48KUSiixaV8cu7rpo3kQRTNbAukJnB+WcaihsvLoxhzWyYP30L2VVeJLNqxfmvpiRAwJwfNy8xN/zKDgQjRLbNdePKNGa2nlgu9/PD0Y5Bdh5O3t5nvpEGVg69ZXF5vpOQM5lMDMhX9MLZuGpdTb6TIMScCvoMQgFz3obnF9kR0ZnvMSbEfHLZ8kqWVoam/Ty53M8Ploa//uWb836UtACruIWrEOePz6VCu/h8wLEMIjwKUcjGoxadg+PzZvqFEEIkerWlj7b+7IZhF4WlfWCM54525jsZaRVaHbdghaMWX364Pt/JmFcKLTJhlLnb/FiI+WQ8al0woaWFEBOZyp5COp/JaNSFLRLTvNk6kO9kpCULSnLkWzsbpr0nghBC5MtMQ2oLIQpbTGc2zV+IfNpQl7s9AWdC+ihzZG9Lb76TIIQQQgghRME72Naf7ySkJQ2sHNm2sirfSRBCCCGEEKLg7Z/ne8tJAytH7tyxnpAsahBCCCGEEGJWLllWme8kpCU1/hwxDcWCkmC+kyGEEEIIIURBazk7v6M6SwMrR3Ye6eB0n4QVFUIIIYQQYjZelSmCAuCx+jP5ToIQQgghhBAFrzI0vwOhSwMrRw7LBrVCCCGEEELM2rqF5flOQlrSwMqR0XHZVUIIIYQQQojZ6h2O5DsJaUkDK0eWVIXynQQhhBBCCCEKXtSa3wMX0sDKkdu3r8p3EoQQQgghhCh4g6MygiUAn+yBJYQQQgghxKwV+1W+k5CW1Ppz5FDrQL6TIIQQQgghRMHbf2aIcNTKdzJSkgZWjkTm8UUghBBCCCFEIfnWzoZ8JyElaWDlyN7mnnwnQQghhBBCiPPCvpbefCchJWlg5Uj/WDTfSRBCCCGEEOK8cPnKqnwnISVpYOXIjk21+U6CEEIIIYQQBc9UcOeO9flORkrSwMqRi5dU5jsJQgghhBBCFLzLllcQ8M3fZsz8TVkaSqkblVJHlVLHlVJfzXd6MvHkobZ8J0EIIYQQQoiCp5Ew7VmllDKBfwVuAjYDtyilNuc3VVPrHBjPdxKEEEIIIYQoeK39o/lOQloF18ACrgCOa60btdZh4CHgQ3lO05TqyoP5ToIQQgghhBAFb3Aslu8kpFWIDaylwKmEf592jk2glPqMUmqvUmpvV1dXzhKXygcuWZLvJAghhBBCCFHwyot8+U5CWoXYwMqI1vp7WuttWutttbX5j+C346KFvGNNdb6TIYQQQgghREH78KVJYyvzSiE2sM4AyxP+vcw5Nq+ZhuLHn9rOd265NN9JEUIIIaZUiBUEIcT5r7zIx5eu35DvZKQ1v8fXvL0KrFdKrcZuWH0C+J38JikzpqG4acsSDl+0kK/8rJ6XT5wlpjVKKRSKmtIg6+tKaBsY5XjHCD4DVi4opmsoAsCHti7hzh3reenEWQ6c7qOxa5izg+PUlAVZW1vKxcsquGp9Lc8eaufrzxzlVO8oplKUFweoCPm5ZlMN45EYP3n5JOMW+AyoKQmwrKoY01CMh8O80TpMFPtvlyyr4O2rF9DaNwZollaHONk1zL6TvfSNRikO+Pity5YSMA32n+ylqthP59A4rb1jlBT52LiwjMVVQX59uIuOgXHqygKsqyujqWsYFGxcVM77Ll6EYSgOnO7j5eNnOdo+hFKKjYvKuGR5OU++0UHfSISLFpdyy7YVfP2ZY3QPR6gq9rFlWSVNXcMMhaMYymBJZRGXrqhk/8k+zvSOEgoYoBQjY1EwFKUBk7KQj8GRKEPhKApFKGCgDAMdizEcsRgai7KwPMimRRX4TMVNb10EwOMHWjncNsDZoTDhqAWAUgq/qQgFfJSH/Oy4qJaLF1fy5ButHGkfZCRsxdP0WksvjWdHCPlNbrp4Iae7R9jV2IOJprIkQPdQJH6+OwfDDI2FiWoYj1iYhsJvKPx+gyKfgQbCUY3WesJ7v2VhBT96pYX+0QhXbVzA6bOjvNLUjQWE/CYlQR9VJUEWVxRx81vtfD/SNsiGulIOtvXzWnMvlSEfDWeH6R0Ks6q2hG0rq9nb1M3h1gEiFvhMqAgFMA2DrcsreM/mRfxkz0l6hsaIAb1DYbSC4oCPJRVF1JYGOd45xFA4Chq0AlMZLK0Kcds7VhGNxvjbJ9+kYzCCAspDJiG/CUphOuf0bauqMQxFU9cQDR1DWNoiEovR2hcmYmkqikzqykNUhnzUlAZpPDtCeZFJbVkRvSMRLltZyVsWV/DkG60c7bCvL/dcPXWojba+UfrGoqA15cV+DA09I2F6hsLEtEVMKxSwrqaYwXCMjoFxSot8LK0oon8sysh4jOKgSWVxAOVcFwvLg6xYUIxC0dg5yP6TfQyMRfGbCp/S9I7EiAJ+A1ZUF1NVEmDASYN7jQ6MhRkat4haFlXFAZZW2u83NBphNBpjPKoJ+U3e4ulI5QAADUxJREFUvmYB6+tKiVoW+1r6GBiNcN3mOu7asQHTUOw83MHjB9uwLIuo1hxrHaBtcJxw1MJvKooCPkI+k63LK1ldW0JL9wid/aN0O3mglX39FAdMNNA9OM5YxEIZiiXlQSpLgrT3jxIwoXMoykg4ht8A0zAo8husrilheDxGzIoxGI7RNxxGofCbEI7BeEzjNxRlRT5W1YQwlUFr31j8+zs6Hot/T02luHrjAk51jfDiiW6smIXfbxKJxtBANKqJabAADfgMRUXIz8e3LefLN2wg4DOIWZpnDrVz364mTveOUhw0qQj5GRiLooC1dSUYQEPnMDj/NpWic2AcS2t6R8J0D4WJxDQBn8GCkgAVxX56h8dp7x8nYmnKivx87PJlbKgp4S8fe4ORiAagyFRUlwa5bEUlK2qKOdNjl63LFxTjN0w2Ly4jGrO4f1cTDZ1D8fdw7w0dQ+O0942xuKKIurIgx7vsNK5bWMrK6mL2NHZzrGOYgM/go5cvY+uySp44eIa9Lb30OPleXORnTXUIDbT0jFIZMikPBWjsHGQsBoZSbF5axgO3vZ3SIh89Q2Fuuuc5Ogcj+E3F725fgc9Q/HzvaYbGowRMg5KgyWhEoxRcuaaaFTWlPH+si7Kg/T3sGQ6zoDSA1hb1pwcYi8RYXVvCO9fUsn5BMd94roHmsyMU+RSLK4vxmQbXbKpBacWvj3QSsyy0UgyPRhiLWcQsWFge5JqNddSf7OV45xBRCypCfj6wZTGXLD1XDg8738+qkiC1JT6Odg7T0T/GwvIgGxeWc3bIPq99oxFGnTL7bauq8ZkGWmtMw4iflwdeauZk97BnGk50DaOUYl1tKbe9cxWgeeClZk71jKAVGCiK/IqhcIz+kQg+w6CuLMBQOErvcARQLCgNsLwqhFIqfo9xyxJTGcQsi+auIfadtM+ntkAZCqWgqjjAMue5SilqS/209o/S0D4cv6desbqagM/krUvL43WFf372GG39Y5QW+VheVcyiiiKWVBXxWvPE+2hi3i+qKOLu6zfw3rfY98edhzt47PUzHGkfZGgsGv+8br4vKg/GX7O1b4wllUVcvrKKU93D7D/dz3jU4m2rKllWVcLjr7cyMBYl6DdZ7VynjV1DjMcsolGNBkxTURnyUxI06RmOEI5aaK0Zi2osp75lABcvrWA8alER8rF1RSX1p/oZGI1w7UW1XFRbzjefa4h/drc8Hw1bLK0KcceVq7l2Ux2/OdrJLw+00t4/hqU1/QnlhM8wMJTifZcs5t0b6nihoYs3WwdYV1PCY2+08mqTXS+67qJFFPlNNi0s5fXWPp4+2EbrgF0G+wwwTRNDKa5aV8P//a1L+P4LJ3jmzQ4srSkr8nGmb5S+kQgGEAz4MA3FFauruHHzYn68u5njXcPx+kDIBz2jUYbGopQETWpKggyNRxgcixGOWQR9JosrQ2xcWEpMWxw4NcBIOEqR38Q0DBZXBKktDXKs3b5PRC2oLvFz88WLeePMQDz/Eus6w+MxSop8rKsp5mjnEKd7RjCNc/eWLcsq8PnO5dWOTQvj1417b7LrDxG2rqhAa/j1kU40sK62hPbBMZo6h8FQ1JYGueEtC7lrx4Z5HaIdQGmt852GaVNK3Qx8AzCB+7TWf5vu8du2bdN79+7NSdqEEEIIIYQQ5z+l1D6t9bak44XYwJoupVQX0JLvdCSoAc7mOxEXAMnn3JG8zg3J59yRvM4NyefckbzODcnn3JkPeb1Sa50U7OGCaGDNN0qpvV6tXZFdks+5I3mdG5LPuSN5nRuSz7kjeZ0bks+5M5/zen5PYBRCCCGEEEKIAiINLCGEEEIIIYTIEmlg5cf38p2AC4Tkc+5IXueG5HPuSF7nhuRz7khe54bkc+7M27yWNVhCCCGEEEIIkSUygiWEEEIIIYQQWSINLCGEEEIIIYTIEmlg5ZBS6kal1FGl1HGl1FfznZ5Co5RarpT6tVLqTaXUIaXUl5zjf6WUOqOUqnd+bk54zp86+X1UKfXehONyLqaglGpWSh108nSvc6xaKfW0UqrB+X+Vc1wppf7Fyc8DSqnLEl7nVufxDUqpW/P1eeYjpdTGhOu2Xik1oJS6W67p7FBK3aeU6lRKvZFwLGvXsFLqcuc7ctx5rsrtJ5w/UuT1Pyqljjj5+YhSqtI5vkopNZpwfX834TmeeZrqvF1oUuRz1soLpdRqpdQrzvGHlVKB3H26+SVFXj+ckM/NSql657hc0zOkUtftCrus1lrLTw5+ABM4AawBAsDrwOZ8p6uQfoDFwGXO72XAMWAz8FfAn3g8frOTz0FgtZP/ppyLjPO7GaiZdOwfgK86v38V+Hvn95uBJwEFbAdecY5XA43O/6uc36vy/dnm449zXbYDK+WazlqeXg1cBryRcCxr1zCwx3mscp57U74/8zzL6/cAPuf3v0/I61WJj5v0Op55muq8XWg/KfI5a+UF8B/AJ5zfvwt8Pt+feT7l9aS/fw34387vck3PPJ9T1e0KuqyWEazcuQI4rrVu1FqHgYeAD+U5TQVFa92mtX7N+X0QOAwsTfOUDwEPaa3HtdZNwHHs8yDnYuY+BDzo/P4g8OGE4z/Utt1ApVJqMfBe4GmtdY/Wuhd4Grgx14kuENcBJ7TWLWkeI9f0NGitnwd6Jh3OyjXs/K1ca71b23fwHya81gXHK6+11r/SWkedf+4GlqV7jSnyNNV5u6CkuKZTmVZ54fTq7wB+7jz/gs1nSJ/XTl59HPhputeQa3pqaep2BV1WSwMrd5YCpxL+fZr0jQORhlJqFXAp8Ipz6E5nqPi+hGH2VHku5yIzGviVUmqfUuozzrGFWus25/d2YKHzu+T17H2CiTdruabnRrau4aXO75OPC293YPccu1YrpfYrpX6jlLrKOZYuT1OdN2HLRnmxAOhLaBTLNZ3aVUCH1roh4Zhc07M0qW5X0GW1NLBEwVFKlQL/CdyttR4AvgOsBbYCbdjD9mL23qW1vgy4CfiiUurqxD86PUGyz0MWOOscPgj8zDkk13QOyDWcG0qpPweiwL87h9qAFVrrS4E/An6ilCrP9PXkvCWR8iL3bmFih5hc07PkUbeLK8T8kQZW7pwBlif8e5lzTEyDUsqP/QX8d631fwForTu01jGttQV8H3v6A6TOczkXGdBan3H+3wk8gp2vHc5wuzv1odN5uOT17NwEvKa17gC5pudYtq7hM0yc8iZ57kEpdRvwfuB3nUoSzpS1buf3fdjrgTaQPk9TnbcLXhbLi27s6Va+ScdFAid/fgt42D0m1/TseNXtKPCyWhpYufMqsN6J0BPAng70aJ7TVFCcOc/3Aoe11l9POL444WEfAdyIP48Cn1BKBZVSq4H12Asd5VxMQSlVopQqc3/HXqz+BnY+uZF5bgV+4fz+KPAHTnSf7UC/M7T/P8B7lFJVzrSV9zjHxEQTekPlmp5TWbmGnb8NKKW2O2XTHyS8lsCOVAf8L+CDWuuRhOO1SinT+X0N9nXcOEWepjpvF7xslRdOA/jXwMec50s+e7seOKK1jk87k2t65lLV7Sj0sno6ETHkZ9aRUm7Gjo5yAvjzfKen0H6Ad2EPER8A6p2fm4EfAQed448CixOe8+dOfh8lIWqMnIsp83oNdmSp14FDbh5hz9F/FmgAngGqneMK+FcnPw8C2xJe6w7sxdXHgdvz/dnm2w9Qgt1zXJFwTK7p7OTtT7Gn7kSw591/MpvXMLANuzJ7AvgWoPL9medZXh/HXhPhltffdR77UadcqQdeAz4wVZ6mOm8X2k+KfM5aeeGU/Xucc/czIJjvzzyf8to5/gDwuUmPlWt65vmcqm5X0GW1e5KFEEIIIYQQQsySTBEUQgghhBBCiCyRBpYQQgghhBBCZIk0sIQQQgghhBAiS6SBJYQQQgghhBBZIg0sIYQQQgghhMgSaWAJIYQQM6CU+rBSanO+0yGEEGJ+kQaWEEIIMTMfBqSBJYQQYgLZB0sIIcR5Syn1e8BdQAB4BXszy1Va6684f78Ne6PKOz0e+wWtdUwpNQTcA7wfGAU+BKwFfgn0Oz8f1VqfyOVnE0IIMT/JCJYQQojzklLqIuC3gSu11luBGDAEfCThYb8NPJTisb/rPKYE2K213gI8D3xaa/0S8CjwFa31VmlcCSGEcPnynQAhhBBijlwHXA68qpQCCAGdQKNSajvQAGwCdgFfTPFYgDD2aBXAPuCGHKVfCCFEAZIGlhBCiPOVAh7UWv/phINK3QF8HDgCPKK11spuVSU91hHR5+bTx5B7pxBCiDRkiqAQQojz1bPAx5RSdQBKqWql1ErgEex1VLcAD03x2HQGgbI5SbkQQoiCJQ0sIYQQ5yWt9ZvAXwC/UkodAJ4GFmute4HDwEqt9Z50j53iLR4CvqKU2q+UWjtXn0MIIURhkSiCQgghhBBCCJElMoIlhBBCCCGEEFkiDSwhhBBCCCGEyBJpYAkhhBBCCCFElkgDSwghhBBCCCGyRBpYQgghhBBCCJEl0sASQgghhBBCiCyRBpYQQgghhBBCZMn/B6QCWC98nQYBAAAAAElFTkSuQmCC\n",
      "text/plain": [
       "<Figure size 864x504 with 3 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD4CAYAAAD8Zh1EAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAPdElEQVR4nO3df6xfd13H8eeLbhPl1wy9mqUt3CV2xokgcB0kI1IVtFtJqxFlVUDMoP8wgoEoJeqG459NEoLGwayjWUBdMwGxYYVBZLggDHoLY6yrW5pR2a0kvWyIDqKz8vaP+y1e7u7t9/T2fO9393Ofj+Sm33POO+e8v7np637yOb9SVUiSVr8njbsBSVI/DHRJaoSBLkmNMNAlqREGuiQ14pxxHXj9+vU1OTk5rsNL0qp06NChb1bVxGLbxhbok5OTTE9Pj+vwkrQqJfnXpbY55SJJjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0Y252iZ2Ny922da49dt22EnUjSE4cjdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktSIoYGeZG+SE0nuPU3NliR3Jzmc5J/6bVGS1EWXEfrNwNalNiY5H3gvsL2qfhr4jX5akySdiaGBXlV3Ao+cpuS3gI9U1dcH9Sd66k2SdAb6mEO/CPjRJJ9JcijJa5cqTLIryXSS6dnZ2R4OLUk6pY9APwd4IbAN+BXgj5NctFhhVe2pqqmqmpqYWPSl1ZKkZerjWS4zwMNV9R3gO0nuBJ4HPNDDviVJHfUxQv8H4CVJzknyI8CLgCM97FeSdAaGjtCT3AJsAdYnmQGuAc4FqKobq+pIkk8A9wDfA26qqiUvcZQkjcbQQK+qnR1q3gW8q5eOJEnL4p2iktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNWJooCfZm+REktO+tCLJzyU5meSV/bUnSeqqywj9ZmDr6QqSrAOuBz7ZQ0+SpGUYGuhVdSfwyJCyNwEfBk700ZQk6cyd9Rx6kg3ArwHvO/t2JEnL1cdJ0fcAb6uq7w0rTLIryXSS6dnZ2R4OLUk6ZehLojuYAvYlAVgPXJ7kZFV9dGFhVe0B9gBMTU1VD8eWJA2cdaBX1YWnPie5GfjYYmEuSRqtoYGe5BZgC7A+yQxwDXAuQFXdONLuJEmdDQ30qtrZdWdV9bqz6kaStGzeKSpJjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJasTQQE+yN8mJJPcusf23k9yT5KtJPpfkef23KUkapssI/WZg62m2fw14aVX9DPBOBi+BliStrC6voLszyeRptn9u3uJdwMazb6s/k7tv61R37LptI+5Ekkar7zn0K4GPL7Uxya4k00mmZ2dnez60JK1tvQV6kl9gLtDftlRNVe2pqqmqmpqYmOjr0JIkOky5dJHkucBNwGVV9XAf+5QknZmzHqEneRbwEeA1VfXA2bckSVqOoSP0JLcAW4D1SWaAa4BzAarqRuBq4JnAe5MAnKyqqVE1LElaXJerXHYO2f564PW9dSRJWhbvFJWkRhjoktQIA12SGmGgS1IjDHRJaoSBLkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNWJooCfZm+REknuX2J4kf57kaJJ7kryg/zYlScN0GaHfDGw9zfbLgM2Dn13A+86+LUnSmRoa6FV1J/DIaUp2AB+oOXcB5ye5oK8GJUnd9DGHvgF4aN7yzGDd4yTZlWQ6yfTs7GwPh5YknbKiJ0Wrak9VTVXV1MTExEoeWpKa10egHwc2zVveOFgnSVpBfQT6fuC1g6tdXgx8u6q+0cN+JUln4JxhBUluAbYA65PMANcA5wJU1Y3AAeBy4CjwXeB3R9WsJGlpQwO9qnYO2V7AG3vrSJK0LN4pKkmNMNAlqREGuiQ1wkCXpEYY6JLUCANdkhphoEtSI4Zeh75WTO6+rVPdseu2jbgTSVoeR+iS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDWiU6An2Zrk/iRHk+xeZPuzktyR5MtJ7klyef+tSpJOZ2igJ1kH3ABcBlwM7Exy8YKyPwJurarnA1cA7+27UUnS6XUZoV8CHK2qB6vqMWAfsGNBTQFPH3x+BvBv/bUoSeqiS6BvAB6atzwzWDffO4BXD945egB402I7SrIryXSS6dnZ2WW0K0laSl8nRXcCN1fVRuZeGP3BJI/bd1XtqaqpqpqamJjo6dCSJOgW6MeBTfOWNw7WzXclcCtAVX0eeDKwvo8GJUnddAn0g8DmJBcmOY+5k577F9R8HfglgCQ/xVygO6ciSStoaKBX1UngKuB24AhzV7McTnJtku2DsrcCb0jyFeAW4HVVVaNqWpL0eJ2eh15VB5g72Tl/3dXzPt8HXNpva5KkM+GdopLUCANdkhphoEtSIwx0SWqEgS5JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDWi0/PQ9f8md9/Wqe7YddtG3Ikk/aBOI/QkW5Pcn+Rokt1L1PxmkvuSHE7yt/22KUkaZugIPck64Abg5cAMcDDJ/sFbik7VbAbeDlxaVd9K8mOjaliStLguI/RLgKNV9WBVPQbsA3YsqHkDcENVfQugqk7026YkaZgugb4BeGje8sxg3XwXARcl+eckdyXZutiOkuxKMp1kenZ2dnkdS5IW1ddVLucAm4EtwE7gr5Kcv7CoqvZU1VRVTU1MTPR0aEkSdAv048CmecsbB+vmmwH2V9X/VNXXgAeYC3hJ0grpEugHgc1JLkxyHnAFsH9BzUeZG52TZD1zUzAP9tinJGmIoYFeVSeBq4DbgSPArVV1OMm1SbYPym4HHk5yH3AH8PtV9fCompYkPV6nG4uq6gBwYMG6q+d9LuAtgx9J0hh4678kNcJAl6RGGOiS1AgDXZIaYaBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjOj1tUWducvdtneqOXbdtxJ1IWiscoUtSIzoFepKtSe5PcjTJ7tPU/XqSSjLVX4uSpC6GBnqSdcANwGXAxcDOJBcvUvc04M3AF/puUpI0XJcR+iXA0ap6sKoeA/YBOxapeydwPfBfPfYnSeqoS6BvAB6atzwzWPd9SV4AbKqqbmcCJUm9O+uTokmeBLwbeGuH2l1JppNMz87Onu2hJUnzdAn048CmecsbB+tOeRrwHOAzSY4BLwb2L3ZitKr2VNVUVU1NTEwsv2tJ0uN0CfSDwOYkFyY5D7gC2H9qY1V9u6rWV9VkVU0CdwHbq2p6JB1LkhY1NNCr6iRwFXA7cAS4taoOJ7k2yfZRNyhJ6qbTnaJVdQA4sGDd1UvUbjn7tiRJZ8o7RSWpEQa6JDXCQJekRhjoktQIH587Zj5mV1JfHKFLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRhjoktQIA12SGmGgS1IjDHRJaoS3/q8SPiJA0jCdRuhJtia5P8nRJLsX2f6WJPcluSfJPyZ5dv+tSpJOZ2igJ1kH3ABcBlwM7Exy8YKyLwNTVfVc4EPAn/bdqCTp9LqM0C8BjlbVg1X1GLAP2DG/oKruqKrvDhbvAjb226YkaZgugb4BeGje8sxg3VKuBD6+2IYku5JMJ5menZ3t3qUkaaher3JJ8mpgCnjXYturak9VTVXV1MTERJ+HlqQ1r8tVLseBTfOWNw7W/YAkLwP+EHhpVf13P+1JkrrqMkI/CGxOcmGS84ArgP3zC5I8H/hLYHtVnei/TUnSMENH6FV1MslVwO3AOmBvVR1Oci0wXVX7mZtieSrwd0kAvl5V20fYt5bQ9Xp18Jp1qTWdbiyqqgPAgQXrrp73+WU99yVJOkPe+i9JjTDQJakRBrokNcJAl6RGGOiS1AgDXZIa4fPQ1zCfsS61xRG6JDXCEbqGciQvrQ6O0CWpEY7Q1RtH8tJ4OUKXpEYY6JLUCANdkhrhHLpWnHPt0mgY6HrCMvilM9Mp0JNsBf6MuTcW3VRV1y3Y/kPAB4AXAg8Dr6qqY/22Ki3O4JfmDA30JOuAG4CXAzPAwST7q+q+eWVXAt+qqp9IcgVwPfCqUTQsLdeZvJ6vK/9I6Imkywj9EuBoVT0IkGQfsAOYH+g7gHcMPn8I+IskqarqsVfpCWcUfyTGwT9MbegS6BuAh+YtzwAvWqpm8FLpbwPPBL45vyjJLmDXYPHRJPcvp2lg/cJ9rwF+57VhLN8516/0EX+Av+cz8+ylNqzoSdGq2gPsOdv9JJmuqqkeWlo1/M5rg995bRjVd+5yHfpxYNO85Y2DdYvWJDkHeAZzJ0clSSukS6AfBDYnuTDJecAVwP4FNfuB3xl8fiXwaefPJWllDZ1yGcyJXwXcztxli3ur6nCSa4HpqtoPvB/4YJKjwCPMhf4onfW0zSrkd14b/M5rw0i+cxxIS1IbfJaLJDXCQJekRqy6QE+yNcn9SY4m2T3ufkYtyd4kJ5LcO+5eVkqSTUnuSHJfksNJ3jzunkYtyZOTfDHJVwbf+U/G3dNKSLIuyZeTfGzcvayUJMeSfDXJ3Umme933appDHzyG4AHmPYYA2LngMQRNSfLzwKPAB6rqOePuZyUkuQC4oKq+lORpwCHgVxv/PQd4SlU9muRc4LPAm6vqrjG3NlJJ3gJMAU+vqleMu5+VkOQYMFVVvd9MtdpG6N9/DEFVPQacegxBs6rqTuauHFozquobVfWlwef/BI4wdzdys2rOo4PFcwc/q2e0tQxJNgLbgJvG3UsrVlugL/YYgqb/o691SSaB5wNfGG8nozeYfrgbOAF8qqpa/87vAf4A+N64G1lhBXwyyaHB41B6s9oCXWtIkqcCHwZ+r6r+Y9z9jFpV/W9V/Sxzd2NfkqTZKbYkrwBOVNWhcfcyBi+pqhcAlwFvHEyr9mK1BXqXxxCoAYN55A8Df1NVHxl3Pyupqv4duAPYOu5eRuhSYPtgPnkf8ItJ/nq8La2Mqjo++PcE8PfMTSX3YrUFepfHEGiVG5wgfD9wpKrePe5+VkKSiSTnDz7/MHMn/v9lvF2NTlW9vao2VtUkc/+PP11Vrx5zWyOX5CmDE/0keQrwy0BvV7CtqkCvqpPAqccQHAFurarD4+1qtJLcAnwe+MkkM0muHHdPK+BS4DXMjdruHvxcPu6mRuwC4I4k9zA3cPlUVa2ZS/nWkB8HPpvkK8AXgduq6hN97XxVXbYoSVraqhqhS5KWZqBLUiMMdElqhIEuSY0w0CWpEQa6JDXCQJekRvwfow0OELIg7tEAAAAASUVORK5CYII=\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "fig, ax = plt.subplots(3, 1, figsize=(12, 7))\n",
    "ax[0].plot(data_log, np.ones((len(data_log), 1)), '.')\n",
    "ax[0].set_xlabel('time')\n",
    "ax[0].set_ylabel('event')\n",
    "ax[0].set_title('timeline of events')\n",
    "\n",
    "ax[1].plot(data_log, range(1, len(data_log)+1))\n",
    "ax[1].plot(data_log, r*np.array(data_log), 'r--')\n",
    "ax[1].set_xlabel(\"time\")\n",
    "ax[1].set_title(\"cumulative sum of events\")\n",
    "\n",
    "ax[2].plot(np.diff(data_log), '.', ms=10)\n",
    "ax[2].set_xlabel(\"event\")\n",
    "ax[2].set_ylabel(\"time\")\n",
    "ax[2].set_title(\"time to next event\")\n",
    "\n",
    "plt.tight_layout()\n",
    "\n",
    "fig, ax = plt.subplots(1, 1)\n",
    "ax.hist(np.diff(data_log), bins=30, density=True);"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.5 Kendall notation for queues](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.5-Kendall-notation-for-queues)",
     "section": "7.5.5 Kendall notation for queues"
    }
   },
   "source": [
    "## 7.5.5 Kendall notation for queues\n",
    "\n",
    "Kendall notation is a standardized methods to describe and classify queues. The notation consists of three factors written as A/S/c where where A describes the arrival process, S the service process, and c is the number of servers attending the queue.\n",
    "\n",
    "* $A/S/c$\n",
    "    * $A$: statistical nature of the arrival process \n",
    "    * $S$: Statistical nature of the service process \n",
    "    * $c$: Number of servers at the queue node\n",
    "    \n",
    "* Typical Statistics\n",
    "    * D: Deterministic (average arrival rate $\\lambda$)\n",
    "    * M: Markov or memoryless (average arrival rate $r$)\n",
    "    * G: General or arbitrary distribution (mean $\\mu$ and standard deviation $\\simga$ or variance $\\sigma^2$)\n",
    "    \n",
    "Example: M/D/1\n",
    "\n",
    "![Aircraft queue](https://i0.wp.com/nats.aero/blog/wp-content/uploads/2013/08/aircraft-queue-e1377251576844.jpg?ssl=1)\n",
    "\n",
    "Example: M/M/8\n",
    "\n",
    "![Call Center](https://upload.wikimedia.org/wikipedia/commons/thumb/b/b1/Emergency_Call_Center_112.jpg/640px-Emergency_Call_Center_112.jpg)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.6 Example: Simulation of an Order Processing Queue](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.6-Example:-Simulation-of-an-Order-Processing-Queue)",
     "section": "7.5.6 Example: Simulation of an Order Processing Queue"
    }
   },
   "source": [
    "## 7.5.6 Example: Simulation of an Order Processing Queue\n",
    "\n",
    "A chemical storeroom processes orders for a large research campus. At peak loads it is expected to receive an average of one order every 12 minutes. The time required to process each order is a fixed 10 minutes. \n",
    "\n",
    "1. Describe the process using the Kendall notation: M/D/1\n",
    "\n",
    "2. Create a simulation of the order queue that operates for 8 hours. Determine the average time between the arrival and completion of an order, and determine the average queue length. "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 107,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.6 Example: Simulation of an Order Processing Queue](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.6-Example:-Simulation-of-an-Order-Processing-Queue)",
     "section": "7.5.6 Example: Simulation of an Order Processing Queue"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[<matplotlib.lines.Line2D at 0x7fbe974dd250>]"
      ]
     },
     "execution_count": 107,
     "metadata": {},
     "output_type": "execute_result"
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAtEAAAF1CAYAAAAurLZiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeZwcdZ3/8fenu2cmN0lIQMhBAgEhiMI6BhBWuUU8YFdXg4rg4mZVWFHk5wIeKN4nrrvqmuUUuREBOeW+c8yQQEhCIOQgE3IyOSaZzNHdn98fVd3TM5mje9LX9Lyej0cyXfe3u75d9alvf+pb5u4CAAAAkL1IqQsAAAAADDQE0QAAAECOCKIBAACAHBFEAwAAADkiiAYAAAByRBANAAAA5IggGgAqiJmdZ2bPlmjb15vZD0uxbQAoNoJoAEDOShmsA0A5IIgGAAAAckQQDQBZMrOjzOxFM2sys9vM7NZU+kJ3LbNm5mY2LXxdY2a/NLM3zWyDmf2vmQ3d02WzKPOhZvaImTWa2TIz+1TGtOvN7Hdmdn/4nuaa2UEZ008Ll9lmZr83s6fM7Itmdpik/5V0rJntMLOtGZsc09P6AKCSEEQDQBbMrFrS3ZJulDRW0h2SPpHDKn4q6RBJR0qaJmmCpO8WclkzGy7pEUk3S9pH0kxJvzez6RmzzZT0fUljJC2X9KNw2XGS7pR0maS9JS2T9H5Jcvelkr4k6QV3H+Huo/taHwBUGoJoAMjOMZKqJP3G3dvd/U5J87NZ0MxM0ixJX3f3RndvkvRjBQFnwZaV9FFJq9z9OnePu/sCSX+R9C8Z8/zV3ee5e1zSTQoCdUk6Q9Jid78rnPZbSeuz2GZP6wOAihIrdQEAYIDYX9Jad/eMcauzXHa8pGGS6oOYWJJkkqIFXvYASUd3SbeIKWhNT8kMjJsljQhf7y9pTWqCu7uZNWSxzZ7WBwAVhSAaALKzTtIEM7OMQHqypDfC1zsVBLuSJDN7R8aymyXtknS4u6/tZt17smxv1kh6yt1PzXE5KXi/EzPKZJnDkny3JQBgECGdAwCy84KkuKSvmlmVmf2zpBkZ01+SdLiZHWlmQyR9LzXB3ZOS/k/SVWa2jySZ2QQz+1Aelu3NfZIOMbNzwjJXmdn7whsD+3K/pCPM7Cwzi0m6QFJmcL9B0sQwVxwABh2CaADIgru3SfpnSedJapT0aUl3ZUx/TdKVkh6V9Lqkrn0o/6eCG+3mmNn2cL537umyfZS5SdJpCvKn31KQavEzSTVZLLtZQe70zyW9LWm6pDpJreEsj0taLGm9mW3ua30AUGmsc3ofACBbZna9pAZ3/3apy1JoZhaR1CDps+7+RKnLAwClRks0AKBbZvYhMxttZjWSLldwQ+OcEhcLAMoCQTQAoCfHKrhxcrOkj0k6y913lbZIAFAeSOcAAAAAckRLNAAAAJAjgmgAAAAgR2X3sJVx48b5lClTSl0MAAAAVLj6+vrN7j6+P8uWXRA9ZcoU1dXVlboYAAAAqHBmtrq/y5LOAQAAAOSo7FqiAQAY6NY0Nutbd7+i1vaEJOnkw/bRrA8cVOJSAcgnWqIBAMizF9/coqdf26SW9oRe37hDd9Y3lLpIAPKMIBoAgAL5zcyjdMyBY8UjGYDKQxANAECeJcOoOWKSmaWHAVQOgmgAAPIsmQz+RswUMaMlGqhABNEAAORZZsuzdRkGUBkIogEAyLNUzByJmCImJYmhgYpDEA0AQJ5l5kRHyIkGKhJBNAAAeZZqeY6YyciJBioSQTQAAHnmCqJms6A12omigYpDEA0AQJ5ltkQH6RylLQ+A/COIBgAgzzydE22KROidA6hEBNEAAORZMmx6tvB/WqKBykMQDQBAnnVO5yAnGqhEBNEAAORZKn3DInRxB1SqogXRZhY1swVmdl+xtgkAQCl4l5Zo0jmAylPMluiLJC0t4vYAACiJVBd3EVPYTzRRNFBpYsXYiJlNlPQRST+SdHExtgkAQKb61Vv09o7WTuNiUdP7DxqnIVXRrNezYXuLXlqztdd5Xl3fJKmji7u2RFJ/X7w+621EI6ZjDtxbw2uKcpoG0A/F+nb+RtI3JY3sbqKZzZI0S5ImT55cpCIBAAaLTU2t+sQfnu922g/OPFznHDsl63V966+v6NGlG/qcb1h1VLGIafSwKrW0JzXrxvqstyFJ3zz9nfrKCdNyWgZA8RQ8iDazj0ra6O71ZnZCd/O4+2xJsyWptraW37wAAHm1qy0hSfr6KYfo5MP2kSS1xhP6xB9e0M5wWraa2+Kavt8o/fyT7+51vvEjaxSLRvSVEw7SKYftm9PNhR/7n2fV3JpbuQAUVzFaoo+T9HEzO0PSEEmjzOzP7v65ImwbAIB0jvKksUP1rgl7SZJa2oMgNdd0ZXdpxJBYej19iUUjmr7/qJy2ETVLlxlAeSr4jYXufpm7T3T3KZJmSnqcABoAUEyZ/TanpF7m2v1c0l0R63u+PcGjwoHyRz/RAICKl+63OSP4TQXUufac4d45GC8EMx4VDpS7ot726+5PSnqymNsEAMDTQXRH8JsKhHNt8U26d1pPIZjlnmYCoLhoiQYAVLyOdI6OcZE9SucobBAdMVOSfA6grBFEAwAqXipQ7pwT3d+WaBW8JZqcaKD8EUQDACpeMhn87XpDYJA2kWtOdOFvLCQnGih/BNEAgIqX6i6uawtyxCz3Lu5U+BsLC71+AHuOIBoAUPG8my7uguFy7eKOlmig3BFEAwAqXkdOdOfx1o/c4yA1pBg50QTRQDkjiAYAVLxUoNw1SyLSj5zoYrREBznRhd0GgD1DEA0AqHjJbvqJlvrX4luch61YzsE9gOIiiAYAVDzvpou71HB/HrYSKfDZM2IdPYoAKE8E0QCAitfdw1ak/nUlV4wnFpITDZQ/gmgAQMXruXeO8u3ijhAaKG+xUhcAAIB827arXZ+9eo627WqXJLW0B7kR3d1YeGd9gx57dUPW617TuEsHjR+Rt7J2x0x6YNE6zV35dtbLjBpSpZu+eLRGD6suYMkApBBEAwAqTsOWZr2ydruOnjpWE0YPlSQNq4nq3RNHd5rvopMP1ssN27Je75uNzVrTuEubmlrzWt6uLjxxmuatbMx6/re27dKcFY1q2LKLIBooEoJoAEDFSaVonH/8VJ12+Dt6nO+846bmtN57Fq5V3eote1K0rMycMVkzZ0zOev5Hl2zQnBWN5FEDRURONACg4vSUA72nCn1DYX+legshhgaKhyAaAFBx0k8ozPNZLtW7R7nF0qngnpZooHgIogEAFaenh6vsqUL3ytFfkXQQXeKCAIMIQTQAoOKkH/Od5/WWZwjdUS6ecggUD0E0AKDi9PSEwj2Vatkut1iVlmig+AiiAQAVJ1mgGwu7PvGwXKTKRU40UDwE0QCAitPREp3f9ZZrTjQ3FgLFRxANAKg46ZzofLdEl+lZM32xQAwNFE2ZHg4AAOi/QrVEl28/0eREA8VGEA0AqDjpnOg8R9Hlms5BTjRQfATRAICKk+4nOs/rTa2v/GJpcqKBYiOIBgBUnEI/bKXcYtVUS3S5lQuoZAUPos1skpk9YWZLzGyxmV1U6G0CAAa3VCyZ/9458ru+fInQOwdQdLEibCMu6Rvu/qKZjZRUb2aPuPuSImwbADAIFfphK+WGh60AxVfwINrd10laF75uMrOlkiZIIogGAOyRxW9t0/yVjenh900dq8P330vLN+6QNHgetpJ6m48t3aC1W5qzXu5dE/ZS7ZSxBSoVMrXFk7p7wVo1t8V3m/beA8bqiIl7pYc372jVg4vWKdHDVVE0YvrIu/fX2OHVBSsv+laMlug0M5si6ShJc7uMnyVpliRNnjy5mEUCAAxg3793ieat6giij546Vrf9+7F65vXNkqS9R+Q3yNhn1BBJ0off9Y68rndPjR9Zo+pYRLfOX5PTclP2HqYn/9+JBSoVMs1b2ahv/uXlbqcdOWm07r7guPTwLXPf1K8eea3X9e1oTejLJxyU1zIiN0ULos1shKS/SPqau2/PnObusyXNlqTa2lp+jAIAZKU1kdT7D9pbv/vMP+jLN9WrNZ6UJFVHI5q2zwjtP3poXrc3ddxwvfqD0zWkKprX9e6pfUcN0UvfPU0t7Ymsl/ne3xZ3asVHYbUlgn1z4/kz9K79O1qdL7ptoTY3tXaZN6jHC75z6m7rSbir9oePqi2s6yidogTRZlalIIC+yd3vKsY2AQCVz91VE4tozPBqVcei2tUeBBZJdw0tUKBbbgF0ytDqqIZWZ1+2IbEoOdRFlAxj3r2GVmlMRhpGTSyy2w2hSXdFI9ZpvpRUvj83kZZeMXrnMEnXSFrq7r8u9PYAAINH0j2d9xwxpft4c5Vv/nK5iEQk5znhRdPRY0znitldPXXvuf6mbm5lz5VeMfqJPk7SOZJOMrOF4b8zirBdAECFSyY7goqIWbplNenl25NGubCMzwuF19F3eefxQb3t2hLde/2NWEeLNEqnGL1zPKv8PzQKAIBOLc4R6whU3J2W6D4QiBVXT90uRrq5mOmr/nYXeKP4eGIhAGDA8ox0DuvUEu15796u0nQXvKFwUp9113pptnt+c1/1l31XHgiiAQADVtI9/fN4kBId3nSVzH8f0ZXGxM1pxZRMt0R3Hm9muz2uPel9/ITfTeCN4iOIBgAMWElXxo2FHT9xJ72vKARmpiTNmUWT+qi75jpH+tUSrd0CbxQfQTQAYMDKbImORDoCld56N0Ag0k0LKArHe2iJ7i6/2X33GxB3W4YLoJIjiAYADFie0RId/Cye6uKOnOi+RIxu0orJe8mJ7nox4+6K9HIVGDFj35UBgmgAwICVzOjFILNlNTPNA92LROjhoZh66+Kuu5zo3upvdzcjovgIogEAA1bXh61k5kQTQ/eOQKy4euqdo+ec6J7XRSpOeSCIBgAMWMmk0jcQBr1NhONpie6TiW7SiqmnluhgP+z+sJXe7ozlAqg8EEQDAAYs79QS3RGMOC3RfeJhK8XV48NWMm6IzZyXh62UP4JoAMCAlczohcM65URzY2FfeGBHcfX8sBXb7WImmy7u2HelRxANABiwesyJTtLFXV+6y8VF4fT0sJXuAuLMi8PudBd4o/hipS4A8iORdJ161VNa/XazTnznPrr63NpSF6moHly0ThfdulAJd5mkH5z1Lp09Y3KpiyVJak8kdfC3HtSP/uld+uzRB5SsHJfc8ZL+umCtJOncY6foux+bXrKyoPx9++5FumXemh6nn3/8VF1+xmG9ruOehWt1yR0vKenBMUqSojlEtu8YNUSPfeODGlIV7TT+iVc36kt/rlc86UokPb3OWNS0bluLDrr8ASWSrkljh2a9rcEoGonIXTro8geyXqbcjq8DxcW3L0wff7t+B2KRiBp3tnXaD33V31jEdMu8Nbq9riHrMoweWqVHL/6gxgyvzrH06AlBdIVoTyS1YtNOSdKr67eXuDTF9/rGHWpLJPWVEw7S1c+s1GsbmkpdpLTm1oQk6WcPvlrSIHrpuu2aPHaYWtoTWrZh8NUR5Gbpuibtt9cQnXXkhN2m3VG/Rq+u7/s79tqGJsWTrvPeP0XXPbdKkvTlDx6U1fYXrd2mp17bpKaW+G5B9Bubdqg1ntSsDxyomlhEZx65vyTpX4+bqnEjatIpHacdvm9W2xqsPvHeCUq45/TQjtnPrCir4+tAsXRdk6bsPVz/etwU7T2iptO0c449QCOHxHbrbePISaN7XN/3P364Xm7YlvX2l2/coYcWr9fGplaC6DwiiK4QmT/JDcZfeFLv/5LT3qk/z1k9KD+DviRdmrbPCG1rbg96NAB6kXTX1HHDdcmH3rnbtOff2JzVT8lJD1rMvnLCtHQQ3d36uvPnOav11Gubut1O6vt+0ckHa3hNx2ns4H1H6hunZbd+SBPHDNPFpx6S0zI3cnztF3fXwfuM0DnHTtlt2kHjR+Rcb087/B067fB3ZD3/Q6+s00OL15O+k2fkRFeIzIaEwfglSb1/s/J9gECpS5S625uukZCNpAd5l93JtmeAoK9m61ducirPubtG0p5u0ELhkUfdP6W+0dXS3yf2XT4RRFeIzC/GYPySpLqzCk7Y5RlEl1rqIE4n/chGb11sRcyy+jXDw5uj+hM8pLbd3Xe5p/52UXgcX/sn6UFXdqWS+g6y6/KLILpCZH4xBuOXxDMerBD0fVriAmXwsA261Of71GcU9ElaRh8QylLmd6ors4563fs6Oi7ccpU+6fdQtsx5UDzGRXi/ePirTKmkLkrZd/lFEF0hvFNLdAkLUiKZj0i1Muv7tFwOWqnHINOShGz09tjhbPsXTj010PpxpknFG93d9Nbx0Irc14s9Q//E/dPbRWkxREjnKAiC6AqR7NQSPfi+JJn5m+X2FK5yOWilDuJmVvL8bJS/XnOiI9l9xzIv3HLV28/P5ESXToT+ifult4vSYrBe0qPQfwTRFSIzR3Awfkk87B9akkzl1dJaLq02qYDGVD5lQvnK/E51FXzHsllHUN/6Ezv0dtInJ7p0Bus5Zk8lvbQpfR03FpawEBWIILpCpA5q0TJLZSiW3Z9aVuICZUi12pS6SKmf1sutpR7lqbfeBLINpJLuikT2LCe6+yA6VQ6i6GLjUeH9U+reOTpyotl5+UQQXSFS34tomXbvVmiZj0i1Msv5LZcTDjnRyEVvvQlknxPtYQpR7tvvaInefVpvPYegsGiJ7h/vJT2qGHrrMhL9RxBdIVIHtVhkcN453aklOlI+N/NJ5XPCycyJ5mEr6Euqj+fuZPtrRurids9yortP5yAfujToIrN/yImuTATRFSKzJXow/lwTXOUHr8vtxpdUSUp9yk+13vGwBGSll94Esg2kUq1ve/KwlZ66uCOILg3Swfqn1HWWfqILgyC6QqRboqORQflzjYe5l1L55ex110VXKXTkRNOShL711nKWbcpUx4Vbvh+2wk2FpVJux9eBIrg/oHTb7+2XHfQfQXSFICe64yBRbjl75VKU9COYedgKspDstSU6u9zKPcuJDnM4u0k9ctI5Sqbcjq8DRW9dRhZDx0VpyYpQkYoSRJvZ6Wa2zMyWm9mlxdjmYJPZO8dgPL4lO3VxVz6Bq9Sxb0pdpFTrXbl1AYjylPmd6spyyIk29S946KuLO2Lo0uCJhf3TW5eRxUBOdGEUPIg2s6ik30n6sKTpks42s+mF3u5gk6QlOuNhK+X1GZRLWVI/rVuZPRYd5am33gSy/Y71dnNiX/p62Aot0aXBPRX9U+qbYTv6iWbf5VOsCNuYIWm5u6+QJDO7VdKZkpYUYdtZ+/2Ty7W1ub3Uxei3rc1tkoIgOp50/fiBpSUuUXEteHNL+ueqiJmWrtteNp9Bat80tcRLWqYdrfF0TvTmHa1l8/mgPG1tbuv1sd8bm/quQy83bOt3Hmhq29c+t1LjR9Z0mjZ35du0RJdIuR1fB4qdbYmS9s6RCuBvnbdGz7/xdukK0ouPvXt/HTFxr1IXIyfFCKInSFqTMdwg6ejMGcxslqRZkjR58uQiFGl3dy9YqzWNu0qy7XwZPaxKHz7iHbppzpu68YXVpS5O0R03bW9J0hET99L9L68ry8+glGWKRkyH7TdKTS3temTJhrL8fFA+zKTp+4/qdtrhE0bp8Vc3ZlWHTjp0H0nSeybupcP263593Tlg72Hae3i1HnplfbfT33vAmKzXhfw5YsJeuq9Mj6/lLBYef0tl/9FDtM/IGj312qaSlaEvh+8/asAF0VboOzXN7JOSTnf3L4bD50g62t0v7G7+2tpar6urK2iZAAAAADOrd/fa/ixbjBsL10qalDE8MRwHAAAADEjFCKLnSzrYzKaaWbWkmZLuLcJ2AQAAgIIoeE60u8fN7EJJD0uKSrrW3RcXersAAABAoRQ8JzpXZrZJUqnuWBgnaXOJto3SYt8PXuz7wYn9Pnix7wev7vb9Ae4+vj8rK7sgupTMrK6/yeUY2Nj3gxf7fnBivw9e7PvBK9/7nsd+AwAAADkiiAYAAAByRBDd2exSFwAlw74fvNj3gxP7ffBi3w9eed335EQDAAAAOaIlGgAAAMgRQbQkMzvdzJaZ2XIzu7TU5UF+mdm1ZrbRzF7JGDfWzB4xs9fDv2PC8WZmvw3rwstm9g+lKzn2lJlNMrMnzGyJmS02s4vC8ez/CmdmQ8xsnpm9FO7774fjp5rZ3HAf3xY+BExmVhMOLw+nTyll+bFnzCxqZgvM7L5wmP0+CJjZKjNbZGYLzawuHFew4/2gD6LNLCrpd5I+LGm6pLPNbHppS4U8u17S6V3GXSrpMXc/WNJj4bAU1IODw3+zJP2hSGVEYcQlfcPdp0s6RtIF4feb/V/5WiWd5O7vkXSkpNPN7BhJP5N0lbtPk7RF0vnh/OdL2hKOvyqcDwPXRZKWZgyz3wePE939yIyu7Ap2vB/0QbSkGZKWu/sKd2+TdKukM0tcJuSRuz8tqbHL6DMl3RC+vkHSWRnj/+SBOZJGm9l+xSkp8s3d17n7i+HrJgUn1Qli/1e8cB/uCAerwn8u6SRJd4bju+77VJ24U9LJZmZFKi7yyMwmSvqIpKvDYRP7fTAr2PGeIDo4oa7JGG4Ix6Gy7evu68LX6yXtG76mPlSo8GfaoyTNFft/UAh/0l8oaaOkRyS9IWmru8fDWTL3b3rfh9O3Sdq7uCVGnvxG0jclJcPhvcV+Hyxc0t/NrN7MZoXjCna8j+1JSYFK4O5uZnRTU8HMbISkv0j6mrtvz2xoYv9XLndPSDrSzEZL+qukQ0tcJBSYmX1U0kZ3rzezE0pdHhTd8e6+1sz2kfSImb2aOTHfx3taoqW1kiZlDE8Mx6GybUj9bBP+3RiOpz5UGDOrUhBA3+Tud4Wj2f+DiLtvlfSEpGMV/GSbakDK3L/pfR9O30vS20UuKvbccZI+bmarFKRnniTpv8R+HxTcfW34d6OCC+cZKuDxniBami/p4PDO3WpJMyXdW+IyofDulXRu+PpcSfdkjP98eNfuMZK2ZfwMhAEmzG28RtJSd/91xiT2f4Uzs/FhC7TMbKikUxXkxD8h6ZPhbF33fapOfFLS486DFAYcd7/M3Se6+xQF5/PH3f2zYr9XPDMbbmYjU68lnSbpFRXweM/DViSZ2RkKcqiikq519x+VuEjIIzO7RdIJksZJ2iDpCkl3S7pd0mRJqyV9yt0bw6DrfxT05tEs6QvuXleKcmPPmdnxkp6RtEgd+ZGXK8iLZv9XMDN7t4KbiKIKGoxud/crzexABS2UYyUtkPQ5d281syGSblSQN98oaaa7ryhN6ZEPYTrHJe7+UfZ75Qv38V/DwZikm939R2a2twp0vCeIBgAAAHJEOgcAAACQI4JoAAAAIEcE0QAAAECOyq6f6HHjxvmUKVNKXQwAAABUuPr6+s3uPr4/y5ZdED1lyhTV1XEzPAAAAArLzFb3d1nSOQAAAIAcEUQDAACg6DZsb9Hvn1yugdrdMkE0AAAAiu7Cm1/Uzx9apmUbmkpdlH4hiAYAAEDRNbXEJUnJZB8zlimCaAAAAJSMWalL0D8E0QAAACi6VCo0QbQkM4ua2QIzuy8cnmpmc81suZndZmbV+dweAAAABhZ313PLNysRRtGRARpF57sl+iJJSzOGfybpKnefJmmLpPPzvD0AAAAMIPcvWqfPXj1XyzfukCQNzBA6j0G0mU2U9BFJV4fDJukkSXeGs9wg6ax8bQ8AAAADz/ptLZ2GB2hDdF5bon8j6ZuSUvdY7i1pq7vHw+EGSRPyuD0AAAAMMDWxyrglLy/vwsw+Kmmju9f3c/lZZlZnZnWbNm3KR5EAAABQhqq7BNHJgfmslby1RB8n6eNmtkrSrQrSOP5L0mgzi4XzTJS0truF3X22u9e6e+348ePzVCQAAACUm643EiYH8xML3f0yd5/o7lMkzZT0uLt/VtITkj4ZznaupHvysT0AAAAMTF1D5sQAbYoudFLKf0q62MyWK8iRvqbA2wMAAEAZ8y4tzwO0IVqxvmfJjbs/KenJ8PUKSTPyvQ0AAAAMTF2D5kGdzgEAAABko2v2xgDN5iCIBgAAQPF0bXmmJRoAAADoQ9eQOTlAm6IJogEAAFA0XW8sHKAxNEE0AAAAiocbCwEAAIAckRMNAAAA5KhrzDxAY2iCaAAAABRP15ZnnlgIAAAA5Ih0DgAAAKAPXYPmARpDE0QDAACgeHZ/YuHAjKIJogEAAFA0XWNmcqIBAACAPuzexV2JCrKHCKIBAABQMl2fYDhQEEQDAACgaJJJWqIBAACAnHSNmbmxEAAAAOgDj/0GAAAAckQXdwAAAECOut5ImEyWqCB7iCAaAAAARdO15TlBSzQAAADQOx62AgAAAOSoa8zcnhiY+RwE0QAAACiarjnRbXGCaAAAAKBXXXOi2xOkcwAAAAC96pq9QToHAAAA0IfdW6IJogEAAIBedQ2i//vx5Xp48foSlab/CKIBAABQNN11adfSnihBSfYMQTQAAACKprtuoaMRK35B9hBBNAAAAIom2U0UHSOIBgAAAHrWNSdakmKRgReSDrwSAwAAYMBKdBNER6ODuCXazCaZ2RNmtsTMFpvZReH4sWb2iJm9Hv4dk69tAgAAYGDpJoYe9OkccUnfcPfpko6RdIGZTZd0qaTH3P1gSY+FwwAAABiEUr1z1MQ6wtBBfWOhu69z9xfD102SlkqaIOlMSTeEs90g6ax8bRMAAAADSyon+tGLP5geR050yMymSDpK0lxJ+7r7unDSekn7FmKbAAAAKH9Jd03bZ4QmjR2WHjcQW6Jj+V6hmY2Q9BdJX3P37WYdH4q7u5ntlgljZrMkzZKkyZMn57tIAAAAKAPf/9tiPbBo96cTVg3mGwslycyqFATQN7n7XeHoDWa2Xzh9P0kbuy7n7rPdvdbda8ePH5/PIgEAAKBMXPfcqm7HD8SW6Hz2zmGSrpG01N1/nTHpXknnhq/PlXRPvrYJAACAgW8g5kTnM53jOEnnSFpkZgvDcZdL+qmk283sfEmrJX0qj9sEAADAANC4s63HaQOxJTpvQbS7Pyupp0/g5HxtBwAAAAPPtl3tPU4b7P1EAwAAAN3y7p6yEo7hZWAAACAASURBVBqILdEE0QAAACi4nkNoKTbYe+cAAAAAutNbS/RAvLFw4JUYAAAAA057orcgmpZoAAAAYDe93VgYJZ0DAAAA2N36bS09TqMlGgAAAOhGIknvHAAAAEBOktxYCAAAAOSmtyCalmgAAACgG5nZHJd9+NDSFSRPCKIBAABQcJk50REbeC3PXRFEAwAAoOAy0zkqIIYmiAYAAEDhJWmJBgAAAHKT+cDCAXgf4W4IogEAAFBw3imdY+BH0bFSFwAAAACVL3Vj4T8ePE7HHzxOknT152u1vaXnx4GXM4JoAAAAFFwqJXr2ObUaWh2VJJ0yfd8SlmjPkM4BAACAgkv1zjEAH07YrQp5GwAAAChnqXSOaAXkQ0sE0QAAACiCdEs0QTQAAACQnVQ/0ZFK6N9OBNEAAAAogqRXRv/QKQTRAAAAKLiEu6IVFEUTRAMAAKDgku4V8ZCVFIJoAAAAFFwy6RXTM4dEEA0AAIAiSCTJiQYAAAByknSvmJ45JIJoACiotnhSX7t1gZau217qogBASSXdK6aPaIkgGgNMeyKZ7mcSg1tbPKnmtnjRtre9pV0t7QlJ0ryVjapfvSWr5eaufFt3L3xLP7x/SSGLhwJwdz25bCPHnAqwtblN7YlkqYsx6CXpnQOF5N7zwfq1DU06/mePa+3WXQUvx87WuG54fpXa4vk/6KzYtKPfJ6WDv/Wg/vMvL+e5RANbIuna2Vq8YDIfNjW16op7XtH2lvbdpu1ojWvKpffrxhdW9bqOT89+QdO/+3BhCtiNd3/v75o5e44k6VN/fEGf+MPz3c63+u2dmnLp/Xrm9U2SpDc27pAkTR47bI+Dsa/cVK/v3P2KJOnO+gb992Ov97lMIul6bUPTHm230JZvbOq2LmRje0t7QY5TaxqbNfvpFTrvuvn689zVvc7bFk8q3kOA1tTL+2ppTxSk7Jn+vni9Nu9o7deyyaSrYUtzv7d9Z32Dlof1vzebmlq1+K1tOa27pT2hHVke9+56sUFHXvmIfnT/0m7Xs3Lzzpy23Ztk0tXSntDyjU16+rVNu01/ctnGgu/z/tjZGk83EhQSOdEV7O+L1+vnD73a4/Rk0nsNciXpD0++oSv/1r8Wp2272jX1sgd014sN6XGpE8v3/7ZYp131tBq27NLfF6/vdvnGnW2acun9+vEDwYHC3fW3l95S4862nMvyP08s1xX3Ltbjr25Mj+v63tc0NneaduOc1WpqaVci6T0GC2u37tJJv3pKP35gaXrelJfWbO31813UEBxk76hv6Hb61uY2rdi0Q1t2tqk1nuhxXfFEUlt2tu1RQPP2jtbdDuArNu3o9eC4tbktq33xxKsb9aGrnt6t1STzAJdIBvv2Jw8u1UGXP6DDr3hYX71lgZJJ7zaozjzBtyeS+qffP6cpl96vjU0t3ZahpT2hh15Zp7Z4UhfftlBL123Xkrd6TkfI5YQmSb98eJlueGG1nnltsx5dsiG9rxJJ130vvSVJ+sXDy3pdx4I3t/a5nY3bW/TXBQ3p/XL9cys15dL79YP7lujWeW92mnfeykbN+NGjqlvVqNc2NHUK4q97bqUkaeGarbulZcQTnQOoPz69QpJ0zjXzdP/L6/TGpuAE/Y5RQ3XudfP0uavn9ljeT//xBV1820JJHcebXW0Jfe7qubpn4Vo9sGi9bpwTBHSX3PGSfvXIa+llk0nX125doOeWb9Y518zVlEvvV8OWZv3w/iU67aqn0xff1zwbfAaFPmFua27XaxuadNldL6e/cw8sWqeW9oReXb9dzy/fLCk4dpzy66f1mf+b02n59dtatCX8viSTrtZ49+U94RdPaubsF9LLbGraPWBc/fZO/fdjr6t+daN+eN+SdH1rbovr8Vc36DP/N0cL3tySLncy6frHnz+hnzwYnA96a7j4w5Nv6JBvP6jT/+uZ9Li6VY16YtlGLVvfpCO+93fdvWBtt8sedeUjOvN3z0mStoTH73Ou2b1+NLfF+zz3dKd+9RbNurFeX79toeKJZKfve0/B/bOvb9Yt4Xfjl39fpuN/9oQ2bO98nHh7R2unY3cy6Xrhjbc7Hf9Wbt6pS+54SV/+c72eem2T7lnY8RmsaWzW2ztatWx9kx5ctE7fvecVfeS3z+q5sE5IQVDX3T5fum57cIz8zdM64nsPa2NTS6dz0Wf+b06nz3BXW0IX3/6SJOn651eppT3R6Vh28e0LdeIvn9Qfn3pDLzdszeoYvXTddp35P8/qlbW7B/4HXv6ADv3OQzrl10/r89fO63QBM29lo867br5+/tCrWv12R+D+5tvNql/dqG3N/buQfOq1TXq9jwvlppb2Ho/R7q7Dr3hYJ//qqfS459/Y3Gmf5YtXWDpHrNQFKCezbqyXJB0xYS99+Ij9dNPc1dra3K6aWESNO9v0+yffSM/77H+eqJ2tCe1si6s6GtG7JuwlSfpZGIR/92PT9fRrm3TIviMVjZiS7hpeE9Oihm0aVh1Vw5ZdOmTfERoxJKZh1TFtamrVyw1BUDD76RVa9Xazjpo8Wl+4br5u/rejdd1zq9Lbro4F1z5rGpv1T79/Tt847Z1atHabnn19c3r5y884TPNXbdF/3LJAkrTyJ2fo3pfe0j9MHqM/PPWGLvvwoVq6rkl/e+ktnXTYPmpuTehXf1+mFV2uyL/053rNu/xkbW9p1ym/flo3f/FovbWtRfWrG3XLvDWKRUyfft8kvWfSaH3n7le04M0tuuvFtao9YIzu/PL7tXxjkyTTn+es1vXPr9J7Jo2WJF33/Cpd/exKTR47TC3tCU0dN1xzVzbqqMmj9ad/naHn33hbLe0JvfeAMdp31BB97uq5mruyMXj/0YiuuOcVrW5s1vVfmJEu65FXPrLbPv3BWe9SMum6s75B67bt0oypY/XAouAi5MDxw3X2+ybryMmjNbQqqkP2HanqWCT42b4toRWbd2rm7Dn661fery9cP19bm9t1zIFj9ZtPH6UzfvuMIibVfftUSdL518/XY+EFx0/++QjtNbRK37j9Je1qT+joqWN1xccO16dnv6Cmlriu/nytTpm+b7qMb+9o1Xt/+Kj+++yj9LH37K8vXD9fUtDqfvMXj9b7p43T/FWN+pf/DQKFB776j3rm9U3pE3zKvS+9pXvDAFSSHrzoH3X3grXpoO6w/Ubpn4+aoB890NEa84uHlulT75uk796zWONH1uiac2u1oyWuG15Ypd88+rrGjajR5h2tuisMAr560jRddMoh2ryjVUf/+DFJ0qs/OF0n/+oprd26S++bMkZ3fOn9cndNvewBSdKL3zlVY4dXp7cZTyTTLT8X3PxiUM8+eJA+M2OyPvCLJ9LzbW8JDvg3zlmtm+e+qRu+8D7tM2qI7n85OOmmPLFso6oiER1/8DhJ0ssNWzV9v1GKRSOaEZbx67e9pBcuO0nfCy9wr3k2CIrPPHKCDvvuQ53rzP1L9dKa4Lv48fdM0KihMX0/48L4W39dlH79w/uW6OpnV+rQd4zUcdPG6fzjp+rmuR3B+QU3v6hY2Oxy1aMdAe/1z63U3iNqdNy0cTrhF0/oio8drqnjh6fr+KnT99WXb3pR5x8/Ve+euJeeXb5Zz2YEGPNXNaZft7QnVBOL6J9+/5xeatimuxd21IHjf9bxee5sDQKxH9wXvJcLb35Rs8+p1eK3tusdew3RXkOrtG1Xu8aNqFY86aqKRvTGph065ddPyV165psn6s76Br1vyli9b+oYJcN46eZ5b+qcYw7Q9pZ2vf+njwcXXqceol9nBPi3zFuj7tzxpWM1Ze/hkqRX1m5XIunavKNVY4ZV65ifBPvuW2cclq6zK358hv778eU64Z3jdcSEvbRmS7MadwYXpys27dBJYRCw9MrTdd518/Ttj0zXERP30szZc7RuW4t+FR4i7qhv0IUnTuv0Xbj8r6/osg8fqs9fO2+3cv7xqRX6VO0k1cQiun3+Gn3tlEP04CvrdeV9i7VhexAkpVpct+1q1yfD72rK125bqD/PWa0TD91HF5w4TTtb42rYsku72hPpi7LUdp95fbN++9jrOu+4KWpuTchMOvrHjykaMd14/gxNGz9CjyzdoLPfN1mRiOn5NzbrSzfW61O1k/Taxh3607/OCC6+2hN6YNG69DqnfetBSdJvPn2kvhZeqEnSrz/1nnSQedMXj9bnwgB02j4jdNv8YL/dUbdG1zy7UhecOE0nHrqPTv7VUzpw/HD9+wcO1JlHTtDXb1uoB19ZrwPHDdfjl5ygR5Zs0L/9qU6S9PrGHTo3fG8X3bpQvz37KH31lgUaUhVRS3vnhoJZf6rT4itP19qtu3TcTx/XIfuO0K2zjtUV9y7WsvXb9dqG3Vu1Z/woqCdPXnKCnlm+Wc+/8XZ62opNO/Q/jy/vNP/Fty/UA4vW6ysnHBQE5MuC1uLU8XTy2GF6+psnaltzu8783bP61afeo89ePVct7Uldd977NHdlo/73qSAWuLO+QUOqIvrpg8t01lH7d/uL4Bsbd+jPc1brSx88KH0xfvWzK3X1syt1+RmH6scP7N5wd/7xUzVuRI1+/8RyNbXG9fDXPqBb5r2pXW0JXfKhd6qmKqJdbQkd/ePH9H+fr01/1qt++hFJQYPUkKqoqmMRnfjLJzV9v1FaEtazC048SP/vQ4cqnkiqPeF6aPG6dFC7dusu7WpL6Jt/eVl/C88lp07fV8Oq8xcqJpKVlc5h/bm6zXkjZqdL+i9JUUlXu/tPe5q3trbW6+rqCl6mru6sb9Ald7zU7+W/97HpSrp05X3lmff4T0dN0F97aA3JxbDqqJrbsmvBOvPI/XVPxgk9WyNrYmrKoVXzX947UYfvPyodIPXX0Kqo/u0DB+q3WfxEnvKeiXupOhbR/FW958eOHlalrRmtDP9x0jQl3TWsOqaHF6/Xy2Er+/c+Nn2399HduEL5+imHdAr2snH2jEmdgqQJo4dq6rjh6aDvnfuO1NkzJqWn9/RezKS+Dkf//oED0xcFXX3+2ANkkm54IWip/ezRk3XT3De7nXcwOuWwffXo0g2dxk3bZ8RuP7cf+o6RenV9k/75Hyborhfz3xLV1adrJ+m2uqD+HL7/KC3u5RePlFFDYjpk35GqyyIv/ZLTDtEv/55bne7Ll084SH/IaFRJ6e939RunHtLpV4Vsdbe973x0um6Z92ZWaRT5kLrQLjfdBen59q4Jo/TK2uxvGB4zrEpb+tnanK3PHTNZf57T+3FvwuihOaWF1sQi+tIHD9KYYVV7Wjz9deFb2tzUqucuPWmP15UvZlbv7rX9WrbQQbSZRSW9JulUSQ2S5ks62927PdKUKoj+x58/rjWNhc81LoVsghMAQXCWagHvauSQmJrCabM+cKBufGG1dhUhh7C/xo+s6Ta1AdnL9YIe5ek9k0brux89TJ/4wwvdTj9o/PB02hUKb8aUsbr9S8eWuhhp5R5EHyvpe+7+oXD4Mkly9590N3+pguhtze2SSSNqYnJ37WxLKBYxRSOmmlhE7QlXWyKpRMJVHYuopT2hIVVRtSeDcSmxqCmZlFwuk8kV9IkYi1iQK+xB/lhVLCJTcKdqPOGKRk3uQUtvWzyphLs8XI+7NGpoldoTSUXMtLM1LjMpEjFFzNQeT8pMGlYdUyxi2rarXamUo+E1MbW0JxRPuIZURdXSHvw8GKSYBAn+Lili1inZP2LB+5aCnyelYP2pbVdFI4onXJGIlHRJrvTnMmJILPzpuCOAT5U3akGZW+MJVcciSoQ/G7eFOaWeTD0WVIpFI4pFTK3tSVXFUvsiqu0t7TJJZkGaTObnXxWLKBF+ntFweuoxoxELbgAaVh2TmbSrPaGImSzcb82tQUCUen9Jd9XEotrVlpAs+KwSyWBdqbqxK2yVr45F0u8rqAfB8imJRJAHVh2LqC2eTL9HU1DGodXBvnEPPqcRNcHPZ9t3dbRaVMciimfk5Y8cUpXuLiieTCqZTM0T/EwXTyQVi0bkHuRJRyKWzgMfUhVVVTSippZ2uUvRqHWUM6yvVdGImtviGlIVVVsiqapIJP3+TCaLKL1/olFTdTSi9kRSFtbJWNQUi0R2y71N7dsRNbGgbrkkC74X1bGIEu4aUR1TWyKplvZEUNfC9536vIbVRJVMBvstqJMd7y0atfTnbREpasG+ao0nNaw6ms7lDL4LQT0fUhXs5+pYRDta4+n9m9onsWiwT7bviqsqZhpWHXyvWtoTCmpQx2fYHk9qdNhi09yWUMJdQ2JRtcQTqopE5PL0T5pt8WT6u5R014ghsaAeWpC2lPrsUsea6mhQz5rb4ho5pErxZFLxRHAMqamKqCoa0c62uEbWxNSecLUngulVMVN7IvgMIxHTyJqYdrYl1B5Pqir8nscTSUUilj7GtYXHlepYJF3WpAc5jbFoRPFEMl0PImaKJ4L3kvrcUvUtVW8lqSoSrDcWtdRuD76TNVHFE662eFLDa2Lp40Hq84xFg+Onh8eZtnhQ1mgk+F63x4P33xrv6L0n1RdtMumKRYPvXms8qZpYRM2tCUWjphHVMcWTwXdxR0tcsWhqGWlYTfAdaWlPKBox7QgvoFLHtNQ64+HxJzMfePSwKrXGk0okXUOrotrRFk9/Fm3xpIZURdPrao0n08es4dUx7WiNqyYW/FwfjQaf4bDqmFriiXRdjidd7RnbS33WqbqfWrckjRpSpR1twTqDGyCDcqSOP63xhGpiUSXC40R1NDiGuILjcSp1oCoWSR9vh1ZH1RpPyt3Tx49hVVHtbE2oKhbuq3DbLe3BudQVHD+b2xLheTJ4XxGTmtsTGl4d0/bw3GWy9HtJevC+hsSC45ApOGRURyNqiSfS56mW9rC+hseL9oz6Wx2NKBbuy9T3PHXPiZlpr6FVam6LKxqxdN1wV3o/ZJ4zzYLx1dGItjYH5U3tz9TxOJUeEU8m03U/tV9GDImpuS2h6miwP1Lpme3J4Bibql+ujtzh1Gc9vCY4t1aFy6Y+o8xzQ2p/dK0H0fCYnno/qUdvp5YZXhOTy9XSnlTEgvNLWzyZPufnM1QcOSSmWLR8bskr9yD6k5JOd/cvhsPnSDra3S/MmGeWpFmSNHny5PeuXt37ndAAAADAntqTILosLgXcfba717p77fjx40tdHAAAAKBXxQii10qalDE8MRwHAAAADEjFSOeIKbix8GQFwfN8SZ9x98U9zL9JUqnyOcZJ2tznXEAH6gxyRZ1BrqgzyAX1JTcHuHu/0iAK3k+0u8fN7EJJDyvo4u7angLocP6S5XOYWV1/82IwOFFnkCvqDHJFnUEuqC/FU5SHrbj7A5IeKMa2AAAAgEIrixsLAQAAgIGEILqz2aUuAAYc6gxyRZ1BrqgzyAX1pUiK8thvAAAAoJLQEg0AAADkiCBakpmdbmbLzGy5mV1a6vKgdMzsWjPbaGavZIwba2aPmNnr4d8x4Xgzs9+G9eZlM/uHjGXODed/3czOLcV7QXGY2SQze8LMlpjZYjO7KBxPvUG3zGyImc0zs5fCOvP9cPxUM5sb1o3bzKw6HF8TDi8Pp0/JWNdl4fhlZvah0rwjFIOZRc1sgZndFw5TX0ps0AfRZhaV9DtJH5Y0XdLZZja9tKVCCV0v6fQu4y6V9Ji7HyzpsXBYCurMweG/WZL+IAXBk6QrJB0taYakK1IBFCpSXNI33H26pGMkXRAeQ6g36EmrpJPc/T2SjpR0upkdI+lnkq5y92mStkg6P5z/fElbwvFXhfMprGczJR2u4Lj1+/Cchsp0kaSlGcPUlxIb9EG0gpPVcndf4e5tkm6VdGaJy4QScfenJTV2GX2mpBvC1zdIOitj/J88MEfSaDPbT9KHJD3i7o3uvkXSI9o9MEeFcPd17v5i+LpJwUlugqg36EG473eEg1XhP5d0kqQ7w/Fd60yqLt0p6WQzs3D8re7e6u4rJS1XcE5DhTGziZI+IunqcNhEfSk5gujgZLcmY7ghHAek7Ovu68LX6yXtG77uqe5Qpwap8GfToyTNFfUGvQh/ml8oaaOCC6Y3JG1193g4S+b+T9eNcPo2SXuLOjOY/EbSNyUlw+G9RX0pOYJoIAcedGdDlzbYjZmNkPQXSV9z9+2Z06g36MrdE+5+pKSJCloDDy1xkVCmzOyjkja6e32py4LOCKKltZImZQxPDMcBKRvCn9sV/t0Yju+p7lCnBhkzq1IQQN/k7neFo6k36JO7b5X0hKRjFaT2pJ4knLn/03UjnL6XpLdFnRksjpP0cTNbpSDl9CRJ/yXqS8kRREvzJR0c3uVarSDp/t4Slwnl5V5JqZ4SzpV0T8b4z4e9LRwjaVv48/3Dkk4zszHhjWGnheNQgcJcw2skLXX3X2dMot6gW2Y23sxGh6+HSjpVQS79E5I+Gc7Wtc6k6tInJT0e/rpxr6SZYW8MUxXcrDqvOO8CxeLul7n7RHefoiBGedzdPyvqS8nF+p6lsrl73MwuVHCyikq61t0Xl7hYKBEzu0XSCZLGmVmDgt4SfirpdjM7X9JqSZ8KZ39A0hkKbs5olvQFSXL3RjP7gYILNEm60t273qyIynGcpHMkLQpzXCXpclFv0LP9JN0Q9owQkXS7u99nZksk3WpmP5S0QMHFmcK/N5rZcgU3Ps+UJHdfbGa3S1qioJeYC9w9UeT3gtL5T1FfSqrPJxaa2bWSUvk47+pmuin4WeEMBSeE81J3qof9nH47nPWH7n5D1+UBAACAgSabdI7r1Xs3S/R5CgAAgEGlzyC6h35zM9HnKQAAAAaVfNxYSJ+nAAAAGFTK4sZCM5ulIBVEw4cPf++hh9JdJgAAAAqrvr5+s7uP78+y+Qiie+vz9IQu45/sbgXuPlvSbEmqra31urq6PBQLAAAA6JmZre7vsvlI56DPUwAAAAwqfbZE99BvbpUkufv/ij5PAQAAMMj0GUS7+9l9THdJF/Qw7VpJ1/avaAAAAEB54rHfAAAAQI4IogEAAIAcEUQDAAAAOSKIBgAAAHJEEA0AAADkiCAaAAAAyBFBNAAAAJAjgmgAAAAgRwTRAAAAQI4IogEAAIAcEUQDAAAAOSKIBgAAAHJEEA0AAADkiCAaAAAAyBFBNAAAAJCjrIJoMzvdzJaZ2XIzu7Sb6VeZ2cLw32tmtjVjWiJj2r35LDwAAABQCrG+ZjCzqKTfSTpVUoOk+WZ2r7svSc3j7l/PmP8/JB2VsYpd7n5k/ooMAAAAlFY2LdEzJC139xXu3ibpVkln9jL/2ZJuyUfhAAAAgHKUTRA9QdKajOGGcNxuzOwASVMlPZ4xeoiZ1ZnZHDM7q98lBQAAAMpEn+kcOZop6U53T2SMO8Dd15rZgZIeN7NF7v5G5kJmNkvSLEmaPHlynosEAAAA5Fc2LdFrJU3KGJ4YjuvOTHVJ5XD3teHfFZKeVOd86dQ8s9291t1rx48fn0WRAAAAgNLJJoieL+lgM5tqZtUKAuXdetkws0MljZH0Qsa4MWZWE74eJ+k4SUu6LgsAAAAMJH2mc7h73MwulPSwpKika919sZldKanO3VMB9UxJt7q7Zyx+mKQ/mllSQcD+08xePQAAAICByDrHvKVXW1vrdXV1pS4GAAAAKpyZ1bt7bX+W5YmFAAAAQI4IogEAAIAcEUQDAAAAOSKIBgAAAHJEEA0AAADkiCAaAAAAyBFBNAAAAJAjgmgAAAAgRwTRAAAAQI4IogEAAIAcEUQDAAAAOSKIBgAAAHJEEA0AAADkiCAaAAAAyBFBNAAAAJCjrIJoMzvdzJaZ2XIzu7Sb6eeZ2SYzWxj++2LGtHPN7PXw37n5LDwAAABQCrG+ZjCzqKTfSTpVUoOk+WZ2r7sv6TLrbe5+YZdlx0q6QlKtJJdUHy67JS+lBwAAAEogm5boGZKWu/sKd2+TdKukM7Nc/4ckPeLujWHg/Iik0/tXVAAAAKA8ZBNET5C0JmO4IRzX1SfM7GUzu9PMJuW4LAAAADBg5OvGwr9JmuLu71bQ2nxDLgub2SwzqzOzuk2bNuWpSAAAAEBhZBNEr5U0KWN4Yjguzd3fdvfWcPBqSe/Ndtlw+dnuXuvutePHj8+27AAAAEBJZBNEz5d0sJlNNbNqSTMl3Zs5g5ntlzH4cUlLw9cPSzrNzMaY2RhJp4XjAAAAgAGrz9453D1uZhcqCH6jkq5198VmdqWkOne/V9JXzezjkuKSGiWdFy7baGY/UBCIS9KV7t5YgPcBAAAAFI25e6nL0Eltba3X1dWVuhgAAACocGZW7+61/VmWJxYCAAAAOSKIBgAAAHJEEA0AAADkiCAaAAAAyBFBNAAAAJAjgmgAAAAgRwTRAAAAQI4IogEAAIAcEUQDAAAAOSKIBgAAAHJEEA0AAADkiCAaAAAAyBFBNAAAAJAjgmgAAAAgRwTRAAAAQI6yCqLN7HQzW2Zmy83s0m6mX2xmS8zsZTN7zMwOyJiWMLOF4b9781l4AAAAoBRifc1gZlFJv5N0qqQGSfPN7F53X5Ix2wJJte7ebGZflvRzSZ8Op+1y9yPzXG4AAACgZLJpiZ4habm7r3D3Nkm3SjozcwZ3f8Ldm8PBOZIm5reYAAAAQPnIJoieIGlNxnBDOK4n50t6MGN4iJnVmdkcMzurH2UEAAAAykqf6Ry5MLPPSaqV9MGM0Qe4+1ozO1DS42a2yN3f6LLcLEmzJGny5Mn5LBIAAACQd9m0RK+VNCljeGI4rhMzO0XStyR93N1bU+PdfW34d4WkJyUd1XVZd5/t7rXuXjt+/Pic3gAAAABQbNkE0fMlHWxmU82sWtJMSZ162TCzoyT9UUEAvTFj/Bgzqwlfj5N0nKTMGxIBAACAAafPdA53j5vZhZIelhSVdK27LzazKyXVufu9kn4haYSkO8xMkt50949LOkzSH80sqSBg/2mXXj0AAACAAcfcvdRl6KS2ttbr6upKXQwAAABUODOrd/fa/izLEwsBH6KBqwAABX9JREFUAACAHBFEAwAAADkiiAYAAAByRBANAAAA5IggGgAAAMgRQTQAAACQI4JoAAAAIEcE0QAAAECOCKIBAACAHBFEAwAAADkiiAYAAAByRBANAAAA5IggGgAAAMgRQTQAAACQI4JoAAAAIEdZBdFmdrqZLTOz5WZ2aTfTa8zstnD6XDObkjHtsnD8MjP7UP6KDgAAAJRGn0G0mUUl/U7ShyVNl3S2mU3vMtv5kra4+zRJV0n6WbjsdEkzJR0u6XRJvw/XBwAAAAxY2bREz5C03N1XuHubpFslndllnjMl3RC+vlPSyWZm4fhb3b3V3VdKWh6uDwAAABiwsgmiJ0hakzHcEI7rdh53j0vaJmnvLJcFAAAABpRYqQsgSWY2S9Ks/9/e3YPYUYZRHP8fjWJhjMU2gtGk2IgYhcgWEQsFRTTFWviBQtBIsFLRKBaiqChpFC0Ev1YMQUEhNrJgJIVGAmLUhUAwW0hQCatC/EwTEkw8FjNFWG5y39klM9fZ86vuvTszPBcOc5+deed967fHJX3XZT0xksaA37suIkZOchGDJBcxSHIRg1yx0B1LmuifgZWnvL+0/mzQNnOSlgErgD8K98X2FDAFIGnG9kTpF4ilIbmIQZKLGCS5iEGSixhE0sxC9y0ZzvEtMC5ptaTzqR4UnJ63zTRwf/36TuBz264/v6eevWM1MA58s9BiIyIiIiJGwdAr0bZPSHoY2AWcC2yzfUDSC8CM7WngXeB9SQeBP6kabertdgCzwAngIdsnz9J3iYiIiIhoRdGYaNs7gZ3zPnv2lNfHgLtOs+9WYGuDmqYabBtLR3IRgyQXMUhyEYMkFzHIgnOhatRFRERERESUyrLfERERERENddZEL2Yp8eivglw8LmlW0n5Jn0m6vIs6o13DcnHKdndIsqQ8gb8ElORC0t31OeOApA/arjHaV/A7cpmk3ZL21b8lG7qoM9ojaZukw6ebQlmV1+rM7Jd0bclxO2miF7OUePRXYS72ARO2r6FaHfOldquMthXmAknLgUeBr9utMLpQkgtJ48BTwPW2rwIea73QaFXh+eIZYIftdVQTIbzRbpXRge3ArWf4+21UM8iNU61b8mbJQbu6Er2YpcSjv4bmwvZu20frt3up5h6Pfis5XwC8SPXP9rE2i4vOlOTiQeB1238B2D7cco3RvpJcGLiofr0C+KXF+qIDtvdQzR53OrcD77myF7hY0iXDjttVE72YpcSjv5ouE78Z+PSsVhSjYGgu6ltvK21/0mZh0amS88UaYI2kLyXtlXSmK1HRDyW5eB7YKGmOauaxR9opLUZY0/4DGJFlvyOakrQRmABu6LqW6Jakc4BXgU0dlxKjZxnV7dkbqe5a7ZF0te2/O60qunYvsN32K5Kuo1rnYq3tf7suLP5furoS3WQpceYtJR79VbRMvKSbgaeBSdvHW6otujMsF8uBtcAXkn4C1gPTebiw90rOF3PAtO1/bP8IfE/VVEd/leRiM7ADwPZXwAXAWCvVxagq6j/m66qJXsxS4tFfQ3MhaR3wNlUDnfGNS8MZc2H7iO0x26tsr6IaKz9pe6abcqMlJb8jH1NdhUbSGNXwjh/aLDJaV5KLQ8BNAJKupGqif2u1yhg108B99Swd64Ejtn8dtlMnwzkWs5R49FdhLl4GLgQ+qp8zPWR7srOi46wrzEUsMYW52AXcImkWOAk8aTt3NHusMBdPAO9I2kL1kOGmXKTrN0kfUv1DPVaPhX8OOA/A9ltUY+M3AAeBo8ADRcdNbiIiIiIimsmKhRERERERDaWJjoiIiIhoKE10RERERERDaaIjIiIiIhpKEx0RERER0VCa6IiIiIiIhtJER0REREQ0lCY6IiIiIqKh/wBBRpoMXdgZWQAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 864x432 with 3 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "%matplotlib inline\n",
    "import matplotlib.pyplot as plt\n",
    "import numpy as np\n",
    "import random\n",
    "import simpy\n",
    "import pandas as pd\n",
    "\n",
    "# time unit = minutes\n",
    "\n",
    "order_log = []    # log data on order processing\n",
    "queue_log = []    # log data on queue length\n",
    "\n",
    "# log time and queue_length at regular time steps\n",
    "def queue_logger(t_step=1.0):\n",
    "    while True:\n",
    "        queue_log.append([env.now, len(queue.items)])\n",
    "        yield env.timeout(t_step)\n",
    "\n",
    "# generate and place orders on the queue at a specified rate\n",
    "def order_generator(order_rate):\n",
    "    order_id = 1\n",
    "    while True:\n",
    "        yield env.timeout(random.expovariate(order_rate))\n",
    "        yield queue.put([order_id, env.now])\n",
    "        order_id += 1\n",
    "    \n",
    "# process orders from the queue with a specified processing time\n",
    "def server(t_process):\n",
    "    while True:\n",
    "        order_id, time_placed = yield queue.get()\n",
    "        yield env.timeout(t_process)\n",
    "        log.append([order_id, time_placed, env.now])\n",
    "        \n",
    "env = simpy.Environment()\n",
    "queue = simpy.Store(env)\n",
    "\n",
    "env.process(queue_logger(0.1))\n",
    "env.process(order_generator(1/12.0))\n",
    "env.process(server(10.0))\n",
    "\n",
    "env.run(until=8*60)\n",
    "\n",
    "queue_df = pd.DataFrame(queue_log, columns=[\"time\", \"queue length\"])\n",
    "order_df = pd.DataFrame(order_log, columns=[\"order id\", \"start\", \"finish\"])\n",
    "\n",
    "fig, ax = plt.subplots(3, 1, figsize=(12, 6))\n",
    "\n",
    "ax[0].plot(queue_df[\"time\"], queue_df[\"queue length\"])\n",
    "ax[0].set_xlabel(\"time / min\")\n",
    "ax[0].set_title(\"queue length\")\n",
    "\n",
    "order_df[\"elapsed\"] = order_df[\"finish\"] - order_df[\"start\"]\n",
    "ax[1].plot(df_orders[\"elapsed\"])\n",
    "#ax[1].hist(df_orders[\"elapsed\"], bins=int(np.sqrt(len(df_orders.index))));\n",
    "#ax[1].set_xlim((0,ax[1].get_xlim()[1]))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    }
   },
   "source": [
    "## 7.5.7 Batch Processing Example  (NEEDS REWORK)\n",
    "\n",
    "**Note that this model is incorrect! Update expected soon.**\n",
    "\n",
    "Schultheisz, Daniel, and Jude T. Sommerfeld. \"Discrete-Event Simulation in Chemical Engineering.\" Chemical Engineering Education 22.2 (1988): 98-102.\n",
    "\n",
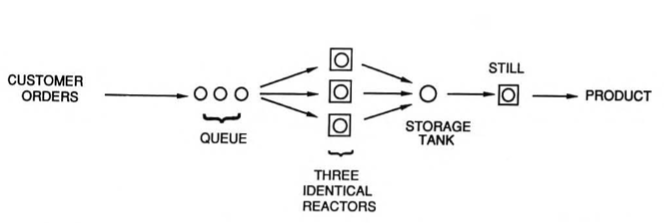    "![Batch Process](figures/BatchProcess.png)\n",
    "\n",
    "    \"... a small, single-product batch chemical plant has three identical reactors in parallel, followed by a single storage tank and a batch still. Customer orders (batches) to be filled (which begin with processing in the reactor) occur every 115 ± 30 minutes, uniformly distributed. The reaction time in a given reactor is 335 ± 60 minutes, and the distillation time in the still is 110 ± 25 minutes, both times uniformly distributed. The holding capacity of the storage tank is exactly one batch. Hence, the storage tank must be empty for a given reactor to discharge its batch; if not, the reactor cannot begin processing a new batch until the storage tank becomes empty. The simulation is to be run for 100 batches. The model should have the capability to collect waiting line statistics for the queue im- mediately upstream of the reactor.\"\"\n",
    "    \n",
    "    G/G/3"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 32,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [],
   "source": [
    "%matplotlib inline\n",
    "import matplotlib.pyplot as plt\n",
    "\n",
    "import random\n",
    "import simpy"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "The first step in any SimPy simulation is to setup the simulation environment and define any shared resources that may be used in the course of the simulation."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 33,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [],
   "source": [
    "env = simpy.Environment()"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "In this application, the batch process is conceptually modeled as a sequence of components that process individual orders. Here we use the SimPy [Store](http://simpy.readthedocs.io/en/latest/api_reference/simpy.resources.html) primative to describe the reactor queue and storage tank. These components will accept orders corresponding to batches, and process them on a first-in, first-out (FIFO) basis.  We'll put no upper limit on the orders that can be stored in the reactor queue, but we will establish the storage tank so that it can accept only one batch at a time."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 34,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [],
   "source": [
    "customer_order_queue = simpy.Store(env)"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "Next we turn to the process that will generate the customer orders. The function `order_generator` begins by initializing a counter that will be used to assigned a consecutive order numbers, after which `order_generator` enters a loop that will create a total of 100 orders for the simulation.\n",
    "\n",
    "At the start of each loop, `order_generator` issues a yield statement that will return control back to the simulation for a simulated period extending into the future. The period is given by a random number uniformly distributed in the range 115 +/- 30 minutes. \n",
    "\n",
    "Technically speaking, the `yield` statement defines the function as a generator of events, and provides the means for `order_generator` to communicate with other processes and to be controlled by the simulation environment. At least one `yield` statement is needed in every function that will simulate a SimPy process.\n",
    "\n",
    "Once control returns to `order_generator`, the order counter is incremented and a second yield used to request the simuation environment put the order into the reactor queue. On return the order_generator completes the loop by writing an entry into the simulation log.\n",
    "\n",
    "The `env.process()` creates order generator within the simulation environment. The actual simulation, however, happens later when we use `env.run()` after creating the other needed processes for this application. "
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 36,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<Process(order_generator) object at 0x7fa83184c6d0>"
      ]
     },
     "execution_count": 36,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "def order_generator(env, customer_order_queue):\n",
    "    orderID = 1\n",
    "    while orderID <= 100:\n",
    "        yield env.timeout(random.uniform(115-30,115+30))\n",
    "        yield customer_order_queue.put(orderID)\n",
    "        writeLog(env, orderID, 'Stage 0', 'Queue')\n",
    "        orderID += 1\n",
    "        \n",
    "env.process(order_generator(env, customer_order_queue))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "The user is responsible for managing the logging of simulation events.  A simple but useful approach is to initialize a Python list, then append data containing a description of the event and time at which it occurred. Later we'll see how to process this log to get the desired process performance indicators."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 37,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [],
   "source": [
    "log = []\n",
    "def writeLog(env, orderID, stage, event):\n",
    "    log.append([orderID, stage, event, env.now])"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 38,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    }
   },
   "outputs": [],
   "source": [
    "env.run()"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 39,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    }
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "[[1, 'Stage 0', 'Queue', 139.7912689063472],\n",
       " [2, 'Stage 0', 'Queue', 281.90183364963775],\n",
       " [3, 'Stage 0', 'Queue', 383.9453070616212],\n",
       " [4, 'Stage 0', 'Queue', 473.3172502050613],\n",
       " [5, 'Stage 0', 'Queue', 579.7437399430546],\n",
       " [6, 'Stage 0', 'Queue', 700.9082069695478],\n",
       " [7, 'Stage 0', 'Queue', 797.3263526092184],\n",
       " [8, 'Stage 0', 'Queue', 938.8568078270348],\n",
       " [9, 'Stage 0', 'Queue', 1055.831373019922],\n",
       " [10, 'Stage 0', 'Queue', 1158.4320187228143],\n",
       " [11, 'Stage 0', 'Queue', 1284.9471277131183],\n",
       " [12, 'Stage 0', 'Queue', 1373.0125904139793],\n",
       " [13, 'Stage 0', 'Queue', 1469.363988086261],\n",
       " [14, 'Stage 0', 'Queue', 1571.3833209362244],\n",
       " [15, 'Stage 0', 'Queue', 1699.2527666939222],\n",
       " [16, 'Stage 0', 'Queue', 1822.6510441755897],\n",
       " [17, 'Stage 0', 'Queue', 1915.304591044007],\n",
       " [18, 'Stage 0', 'Queue', 2041.8743538454528],\n",
       " [19, 'Stage 0', 'Queue', 2155.278139269896],\n",
       " [20, 'Stage 0', 'Queue', 2290.0547002600742],\n",
       " [21, 'Stage 0', 'Queue', 2393.5362204948715],\n",
       " [22, 'Stage 0', 'Queue', 2506.2849727620733],\n",
       " [23, 'Stage 0', 'Queue', 2642.6189836453086],\n",
       " [24, 'Stage 0', 'Queue', 2729.8169921354465],\n",
       " [25, 'Stage 0', 'Queue', 2832.19696545759],\n",
       " [26, 'Stage 0', 'Queue', 2929.6045375554263],\n",
       " [27, 'Stage 0', 'Queue', 3070.3439449353186],\n",
       " [28, 'Stage 0', 'Queue', 3211.7279498110393],\n",
       " [29, 'Stage 0', 'Queue', 3336.40988792481],\n",
       " [30, 'Stage 0', 'Queue', 3463.380538361207],\n",
       " [31, 'Stage 0', 'Queue', 3603.2230123608497],\n",
       " [32, 'Stage 0', 'Queue', 3711.035428144933],\n",
       " [33, 'Stage 0', 'Queue', 3846.174135049626],\n",
       " [34, 'Stage 0', 'Queue', 3941.908203577261],\n",
       " [35, 'Stage 0', 'Queue', 4059.7083248328127],\n",
       " [36, 'Stage 0', 'Queue', 4170.078647909729],\n",
       " [37, 'Stage 0', 'Queue', 4305.77360484569],\n",
       " [38, 'Stage 0', 'Queue', 4395.53096517807],\n",
       " [39, 'Stage 0', 'Queue', 4536.0827433731665],\n",
       " [40, 'Stage 0', 'Queue', 4660.549148301049],\n",
       " [41, 'Stage 0', 'Queue', 4771.915112790694],\n",
       " [42, 'Stage 0', 'Queue', 4908.858514856362],\n",
       " [43, 'Stage 0', 'Queue', 5007.856696350772],\n",
       " [44, 'Stage 0', 'Queue', 5125.895058131786],\n",
       " [45, 'Stage 0', 'Queue', 5259.66045952376],\n",
       " [46, 'Stage 0', 'Queue', 5354.399130237207],\n",
       " [47, 'Stage 0', 'Queue', 5483.216083813942],\n",
       " [48, 'Stage 0', 'Queue', 5597.939751736744],\n",
       " [49, 'Stage 0', 'Queue', 5711.070472200441],\n",
       " [50, 'Stage 0', 'Queue', 5847.5720533883505],\n",
       " [51, 'Stage 0', 'Queue', 5938.885193496104],\n",
       " [52, 'Stage 0', 'Queue', 6074.379038858271],\n",
       " [53, 'Stage 0', 'Queue', 6170.097868087694],\n",
       " [54, 'Stage 0', 'Queue', 6296.965828425611],\n",
       " [55, 'Stage 0', 'Queue', 6386.230592889007],\n",
       " [56, 'Stage 0', 'Queue', 6501.134880674207],\n",
       " [57, 'Stage 0', 'Queue', 6639.365892028055],\n",
       " [58, 'Stage 0', 'Queue', 6750.043874352989],\n",
       " [59, 'Stage 0', 'Queue', 6886.445488191414],\n",
       " [60, 'Stage 0', 'Queue', 6985.649225657926],\n",
       " [61, 'Stage 0', 'Queue', 7100.921676185798],\n",
       " [62, 'Stage 0', 'Queue', 7194.905104793235],\n",
       " [63, 'Stage 0', 'Queue', 7291.21004031581],\n",
       " [64, 'Stage 0', 'Queue', 7411.807271603546],\n",
       " [65, 'Stage 0', 'Queue', 7541.9225706988345],\n",
       " [66, 'Stage 0', 'Queue', 7663.532255909225],\n",
       " [67, 'Stage 0', 'Queue', 7808.497271428981],\n",
       " [68, 'Stage 0', 'Queue', 7893.914423491529],\n",
       " [69, 'Stage 0', 'Queue', 7988.467184947141],\n",
       " [70, 'Stage 0', 'Queue', 8133.331587205895],\n",
       " [71, 'Stage 0', 'Queue', 8250.26166814278],\n",
       " [72, 'Stage 0', 'Queue', 8352.826517833395],\n",
       " [73, 'Stage 0', 'Queue', 8449.030320608046],\n",
       " [74, 'Stage 0', 'Queue', 8565.33638606168],\n",
       " [75, 'Stage 0', 'Queue', 8697.03378742154],\n",
       " [76, 'Stage 0', 'Queue', 8834.792708239542],\n",
       " [77, 'Stage 0', 'Queue', 8956.134435889602],\n",
       " [78, 'Stage 0', 'Queue', 9051.059534162901],\n",
       " [79, 'Stage 0', 'Queue', 9156.387991246875],\n",
       " [80, 'Stage 0', 'Queue', 9298.27282815946],\n",
       " [81, 'Stage 0', 'Queue', 9432.612966261526],\n",
       " [82, 'Stage 0', 'Queue', 9518.958039574118],\n",
       " [83, 'Stage 0', 'Queue', 9622.244858766759],\n",
       " [84, 'Stage 0', 'Queue', 9738.571191914454],\n",
       " [85, 'Stage 0', 'Queue', 9881.187052184567],\n",
       " [86, 'Stage 0', 'Queue', 9968.89003070113],\n",
       " [87, 'Stage 0', 'Queue', 10085.847687786474],\n",
       " [88, 'Stage 0', 'Queue', 10172.446830735656],\n",
       " [89, 'Stage 0', 'Queue', 10281.001833155075],\n",
       " [90, 'Stage 0', 'Queue', 10408.338121229022],\n",
       " [91, 'Stage 0', 'Queue', 10507.247153761977],\n",
       " [92, 'Stage 0', 'Queue', 10640.706199960125],\n",
       " [93, 'Stage 0', 'Queue', 10784.663646773472],\n",
       " [94, 'Stage 0', 'Queue', 10873.007758668453],\n",
       " [95, 'Stage 0', 'Queue', 10970.584783893359],\n",
       " [96, 'Stage 0', 'Queue', 11087.107698691347],\n",
       " [97, 'Stage 0', 'Queue', 11203.466699373446],\n",
       " [98, 'Stage 0', 'Queue', 11300.12551313884],\n",
       " [99, 'Stage 0', 'Queue', 11405.146524051328],\n",
       " [100, 'Stage 0', 'Queue', 11544.512786337717]]"
      ]
     },
     "execution_count": 39,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "log"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "Next we create a function `batch_reactor` that will be use to create processes corresponding to each of the three batch reactors. Each reactor is assigned a unique name so they can be distinguished in the simulation log.\n",
    "\n",
    "The batch reactors have three interactions with the simulation environment. The first is to get an orderID from the reactor_queue. The batch_reactor yields to the simulation environment until an order is ready for processing. Once the processing can start, and suitable event is written to the log, the process waits a period of time corresponding the length of the reaction, and the order put into the storage_tank.  The reactor will wait until the storage tank is ready to accept a new batch.\n",
    "\n",
    "`env.process()` is called three times to put three copies of the batch_reactor process into the simulation environment."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 19,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<Process(batch_reactor) object at 0x7fa8312b8f10>"
      ]
     },
     "execution_count": 19,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "def batch_reactor(name, env, reactor_queue, storage_tank):\n",
    "    while True:\n",
    "        orderID = yield reactor_queue.get()\n",
    "        writeLog(env, orderID, 'Stage 1', name)\n",
    "        yield env.timeout(random.uniform(335-60,335+60))\n",
    "        writeLog(env, orderID, 'Stage 2', name)\n",
    "        yield storage_tank.put(orderID)\n",
    "        writeLog(env, orderID, 'Stage 3', 'Storage')\n",
    "        \n",
    "env.process(batch_reactor('Reactor A', env, reactor_queue, storage_tank))\n",
    "env.process(batch_reactor('Reactor B', env, reactor_queue, storage_tank))\n",
    "env.process(batch_reactor('Reactor C', env, reactor_queue, storage_tank))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "The last process to model is the batch still. Similar to the reactor model, `batch_still` yields control while waiting for an orderID to be retrieved from a preceding unit. Once an order has been received from the storage_tank, a message is written to the simulation log, time is yielded to the simulation environment corresponding to the time required for distillation, and then a final completion message is written to the log."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 20,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [
    {
     "data": {
      "text/plain": [
       "<Process(batch_still) object at 0x7fa8312b83d0>"
      ]
     },
     "execution_count": 20,
     "metadata": {},
     "output_type": "execute_result"
    }
   ],
   "source": [
    "def batch_still(name, env, storage_tank):\n",
    "    while True:\n",
    "        orderID = yield storage_tank.get()\n",
    "        writeLog(env, orderID, 'Stage 4', name)\n",
    "        yield env.timeout(random.uniform(110-25,110+25))\n",
    "        writeLog(env, orderID, 'Stage 5', 'complete')\n",
    "\n",
    "env.process(batch_still('Still A', env, storage_tank))"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "source": [
    "We're now ready to run the the simulation.  In this case the simulation is limited to the 100 orders generated in the `order_generator` process. Simulation is complete once all of the resulting events have been processed."
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 21,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.7 Batch Processing Example  (NEEDS REWORK)](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.7-Batch-Processing-Example-(NEEDS-REWORK))",
     "section": "7.5.7 Batch Processing Example  (NEEDS REWORK)"
    },
    "pycharm": {}
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Simulation complete.\n",
      "600  messages have been logged.\n"
     ]
    }
   ],
   "source": [
    "env.run()\n",
    "\n",
    "print('Simulation complete.')\n",
    "print(len(log), ' messages have been logged.')"
   ]
  },
  {
   "cell_type": "markdown",
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.8 Processing the Simulation Log](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.8-Processing-the-Simulation-Log)",
     "section": "7.5.8 Processing the Simulation Log"
    },
    "pycharm": {}
   },
   "source": [
    "## 7.5.8 Processing the Simulation Log"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 22,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.8 Processing the Simulation Log](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.8-Processing-the-Simulation-Log)",
     "section": "7.5.8 Processing the Simulation Log"
    },
    "pycharm": {},
    "scrolled": true
   },
   "outputs": [],
   "source": [
    "def process_log(log):\n",
    "\n",
    "    df = pd.DataFrame([[a,b,c,t] for (a,b,c,t) in log])\n",
    "    df = df.pivot(index=0,columns=1,values=3).reset_index()\n",
    "    df = df.set_index([0]).dropna()\n",
    "    df.index.rename('OrderID',inplace=True)\n",
    "\n",
    "    stage1 = df['Stage 1']-df['Stage 0']\n",
    "    stage2 = df['Stage 2']-df['Stage 1']\n",
    "    stage3 = df['Stage 3']-df['Stage 2']\n",
    "    stage4 = df['Stage 4']-df['Stage 3']\n",
    "    stage5 = df['Stage 5']-df['Stage 4']\n",
    "\n",
    "    print('Mean Order Completion = {0:6.1f} min.\\n'.format((df['Stage 5'] - df['Stage 0']).mean()))\n",
    "\n",
    "    print('Mean Time in Process Stages:\\n')\n",
    "    print('     Reactor Queue = {0:6.1f} min.'.format(stage1.mean()))\n",
    "    print('          Reactors = {0:6.1f} min.'.format(stage2.mean()))\n",
    "    print('    Reactor Holdup = {0:6.1f} min.'.format(stage3.mean()))\n",
    "    print('           Storage = {0:6.1f} min.'.format(stage4.mean()))\n",
    "    print('             Still = {0:6.1f} min.'.format(stage5.mean()))\n",
    "\n",
    "    print('\\nUtilization\\n')\n",
    "    print('Reactor Utilization = {0:5.3f}'.format(stage2.sum()/3.0/(df['Stage 2'].max()-df['Stage 2'].min())))\n",
    "    print('  Still Utilization = {0:5.3f}'.format(stage5.sum()/(df['Stage 5'].max()-df['Stage 5'].min())))\n",
    "    \n",
    "    stage1.hist(bins=30)\n",
    "    plt.title('Distribution of Reactor Queue Times')\n",
    "    plt.ylabel('Count')\n",
    "    plt.xlabel('Minutes')"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": 23,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.8 Processing the Simulation Log](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.8-Processing-the-Simulation-Log)",
     "section": "7.5.8 Processing the Simulation Log"
    },
    "pycharm": {}
   },
   "outputs": [
    {
     "name": "stdout",
     "output_type": "stream",
     "text": [
      "Mean Order Completion =  501.3 min.\n",
      "\n",
      "Mean Time in Process Stages:\n",
      "\n",
      "     Reactor Queue =   22.9 min.\n",
      "          Reactors =  335.2 min.\n",
      "    Reactor Holdup =    0.2 min.\n",
      "           Storage =   34.1 min.\n",
      "             Still =  109.0 min.\n",
      "\n",
      "Utilization\n",
      "\n",
      "Reactor Utilization = 0.960\n",
      "  Still Utilization = 0.932\n"
     ]
    },
    {
     "data": {
      "image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEWCAYAAABhffzLAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAbEElEQVR4nO3de5jcZX338fcHwnkhAUO3IRwCD9SKICIrglibALYgx7aUQlMNNTaPV6uCYCsI7SWtVqiCAp6aAg8RKQtEMBGFFjDRKhAkoIRjOYUzCYEkZsMx8H3+uO+VYbLHyf5mZnN/Xte1187v/J3fzH7mnvt3WEUEZmZWjg1aXYCZmTWXg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4RyFJ35H0jyO0rh0l9UjaMA/Pl/TxkVh3Xt91kqaN1PqGsd0vSlom6dlmb9uGL78Hd2l1HaVw8LcZSYslvSRplaQVkm6W9AlJv32tIuITEfEvQ1zXwQPNExGPR0RHRLw+ArV/QdL36tZ/aETMWtd1D7OOHYFTgN0j4nf7mD5Z0hs5bFZJekDSX1dc0yRJIWnMCK93nKRvS3pW0ouSFrXig3YgNY2L3p+QtLpm+A/ye/CRVtdaihF9E9qIOSIibpQ0FvhD4DzgfcCIhpOkMRGxZiTX2SZ2BJ6PiKUDzPN0RGwvScChwFxJN0fEA80pcXj6eq0kbQzcCCwF9geeBA4CZkkaGxHnN7/StUXE40BH77CkAPaKiIdaV1XhIsI/bfQDLAYOrhu3L/AGsEcevgT4Yn48HrgWWAG8APwP6ZvcpXmZl4Ae4B+ASUAA04HHgZ/VjBuT1zcf+DJwG/AbYA6wTZ42GXiyr3qBQ4BXgdfy9n5ds76P58cbAGcAj5HC6rvA2Dytt45pubZlwOkD7Kexefnn8vrOyOs/OD/nN3Idl/SxbF/PYynw5zV1ngo8DDwPXNm7D/L0q4BngZV5H76zZtpmwDm5ppXAz/O4x/Pz68k/+w9xf/z2terjeUzPy21RN/4v8mvXkYcD2LVm+iXk908ePhz4Fek9dDPwrpppDS87wGv3lnXWj8vb+BZwXd5XvwB+F/g6sBy4H9i7ZtntgO/n98KjwKfr/nZuz/tjCXBuq//G2+HHXT2jQETcRmrN/UEfk0/J07YFOoHPp0XiI6TAOCLS1+h/q1nmD4F3AH/czyY/CnwMmACsAQZtOUbE9cC/Alfk7e3Vx2wn5J8pwC6kVuA36ub5APB2Usv1nyS9o59NXkAK/13y8/ko8NcRcSOpBf90ruOEgeqWtIGkI0kfoL0t0E8BR+f1bkcKm2/WLHYdsBvwO8AdwGU1074K7AO8H9iG9IH7BvDBPH1cruuWIe6PgV6rDwHXRcTquvHfBzYnfbgMSNLewMXA/wXeBvw76dvPJlUuOwTHkj4UxwOvALeQ9vV4YDZwbq5hA+CHwK+BiaT3zUmSevfXecB5EbEV8H9IH+LFc/CPHk+TgqTea6SA3ikiXouI/4nc1BnAFyJidUS81M/0SyPi7hwo/wgc23vwdx1NJbW4HomIHuA04Li6fu8zI+KliPg16Y95rQ+QXMtxwGkRsSoiFpNa2R8ZRi3bSVpB+nZwDXByRNyZp32C9G3jyYh4BfgCcExvnRFxcd5u77S9JI3NIfQx4MSIeCoiXo+Im/N8je6PgV6r8cAz9SMjdQktIzUGBjMD+PeIWJDrnUUK2v0qXnYw10TEwoh4mfT6vBwR3410LOoKYO8833uBbSPinyPi1UjHCf6D9P6A9Pexq6TxEdETEbeOQG2jnoN/9JhI6sqp9xVSS/W/JT0i6dQhrOuJYUx/DNiIFDLraru8vtp1jyF9U+lVexbOi9T0DdcYn2uqX9fEYdTydESMA7YifaM5sGbaTsA1+eD6CuA+4HWgU9KGks6S9LCk35C6unprGg9sSuoiGoqh7I+BXqtlpA/9t8gfHOPz9MHsBJzS+1zz890h11blsoNZUvP4pT6Ge98XO5E/xGtq+Dxv7sPpwO8B90v6paTDR6C2Uc/BPwpIei8p1H5ePy23PE+JiF2AI4GTJR3UO7mfVQ72jWCHmsc7klpNy4DVpC6E3ro25K2tysHW+zTpD7V23Wt46x/1UCzLNdWv66lhrofcGv8csKeko/PoJ4BDI2Jczc+mEfEU8JfAUaRjCWNJffEAynW9TOpSWGtTfYwbyv4YaJ/eCBwqaYu68X9GOt6yIA+/SM3rRuov7/UE8KW657p5RFw+Ass2wxPAo3U1bBkRHwaIiAcj4nhSt9zZwOw+9ldxHPxtTNJWuYXSDXwvIhb1Mc/hknbNZ6esJLVM38iTl5D6jofrryTtLmlz4J+B2fkr9v8Cm0o6TNJGpD7Y2v7cJcCk2lNP61wOfEbSzpI6ePOYwLDOLMq1XAl8SdKWknYCTga+N/CS/a7vVVJX0T/lUd/J694JQNK2ko7K07YkdWc8TwrEf61ZzxukPu9zJW2Xvx3sn/u8nyO9LrWvx7ruj0tJx3euyqeLbpT7ts8HvhIRK/N8vwL+MtdzCOm4Qa//AD4h6X1Ktsiv75YjsGwz3AaskvQ5SZvlOvfIjSUk/ZWkbfNrsyIv80a/ayuEg789/VDSKlJr5nTSgaz+TuXcjdTy6yEdAPtWRMzL074MnJG/An92GNu/lHRmxbOkrotPA+Qg+VvgQlLrejUpeHpdlX8/L+mOPtZ7cV73z0hnX7xMOpDaiE/l7T9C+ib0n3n9jboY2FHSEaQDgnNJ3WergFtJp9NCOvPmMdLzvzdPq/VZYBHwS1LX3NnABhHxIvAl4Bf59diPddwf+dvKwaT3yQJSF8j1pLNfzqyZ9UTgCFLwTQV+ULOO24G/IR1UXk7qNjxhhJatXG4EHA68m7QPl5Hen2PzLIcA90jqIb2uxw1wbKsYGvw4oJmNBvlb2HWkD6UThnCQ3wrlFr/ZeiIiXiP17z9MOiXWrE9u8ZuZFabSWzZIWgysIh1wXBMRXZK2IZ2HO4l0KtyxEbG8yjrMzOxNlbb4c/B3RcSymnH/BrwQEWflc863jojPDbSe8ePHx6RJkxqqYfXq1Wyxxeg8e8u1t4Zrbw3XPvIWLly4LCLWvpBvOPd3GO4PqUU/vm7cA8CE/HgC8MBg69lnn32iUfPmzWt42VZz7a3h2lvDtY884PboI1OrbvE/SjrNK0iXds+UtCLSFZPkc8+X9w7XLTuDdEk4nZ2d+3R3dzdUQ09PDx0dfV382f5ce2u49tZw7SNvypQpCyOia60JfX0ajNQPMDH//h3SfVc+CKyom2f5YOtxi3/0ce2t4dpbo11rp58Wf6Wnc0a6xJ1I90W/hnSL1CWSJgDk3wPdM93MzEZYZcGfL9/esvcx8EfA3aQrInv/Q9A00v3ezcysSao8nbOTdIfD3u38Z0RcL+mXwJWSppMufT+2whrMzKxOZcEf6b7Ya91LPSKeJ/2zBDMzawHfssHMrDAOfjOzwjj4zcwKU+m9etrBoqdWcsKpPxp0vsVnHdaEaszMWs8tfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwK4+A3MyuMg9/MrDAOfjOzwjj4zcwKU3nwS9pQ0p2Srs3DO0taIOkhSVdI2rjqGszM7E3NaPGfCNxXM3w28LWI2BVYDkxvQg1mZpZVGvyStgcOAy7MwwIOBGbnWWYBR1dZg5mZvZUiorqVS7OBLwNbAp8FTgBuza19JO0AXBcRe/Sx7AxgBkBnZ+c+3d3dDdWw9IWVLHlp8Pn2nDi2ofVXqaenh46OjlaX0RDX3hquvTXatfYpU6YsjIiu+vFjqtqgpMOBpRGxUNLk4S4fETOBmQBdXV0xefKwVwHABZfN4ZxFgz/NxVMbW3+V5s+fT6PPu9Vce2u49tYYbbVXFvzAAcCRkj4MbApsBZwHjJM0JiLWANsDT1VYg5mZ1amsjz8iTouI7SNiEnAc8JOImArMA47Js00D5lRVg5mZra0V5/F/DjhZ0kPA24CLWlCDmVmxquzq+a2ImA/Mz48fAfZtxnbNzGxtvnLXzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8JUFvySNpV0m6RfS7pH0pl5/M6SFkh6SNIVkjauqgYzM1tblS3+V4ADI2Iv4N3AIZL2A84GvhYRuwLLgekV1mBmZnUqC/5IevLgRvkngAOB2Xn8LODoqmowM7O1KSKqW7m0IbAQ2BX4JvAV4Nbc2kfSDsB1EbFHH8vOAGYAdHZ27tPd3d1QDUtfWMmSlwafb8+JYxtaf5V6enro6OhodRkNce2t4dpbo11rnzJlysKI6KofP6bKjUbE68C7JY0DrgF+fxjLzgRmAnR1dcXkyZMbquGCy+ZwzqLBn+biqY2tv0rz58+n0efdaq69NVx7a4y22ptyVk9ErADmAfsD4yT1JvH2wFPNqMHMzJIqz+rZNrf0kbQZ8CHgPtIHwDF5tmnAnKpqMDOztVXZ1TMBmJX7+TcAroyIayXdC3RL+iJwJ3BRhTWYmVmdyoI/Iu4C9u5j/CPAvlVt18zMBuYrd83MCuPgNzMrjIPfzKwwQwp+SQcMZZyZmbW/obb4LxjiODMza3MDntUjaX/g/cC2kk6umbQVsGGVhZmZWTUGO51zY6Ajz7dlzfjf8OZFWGZmNooMGPwR8VPgp5IuiYjHmlSTmZlVaKgXcG0iaSYwqXaZiDiwiqLMzKw6Qw3+q4DvABcCr1dXjpmZVW2owb8mIr5daSVmZtYUQz2d84eS/lbSBEnb9P5UWpmZmVViqC3+afn339eMC2CXkS3HzMyqNqTgj4idqy7EzMyaY0jBL+mjfY2PiO+ObDlmZla1oXb1vLfm8abAQcAdgIPfzGyUGWpXz6dqh/O/VOyupCIzM6tUo7dlXg2439/MbBQaah//D0ln8UC6Ods7gCurKsrMzKoz1D7+r9Y8XgM8FhFPVlCPmZlVbEhdPflmbfeT7tC5NfBqlUWZmVl1hvofuI4FbgP+HDgWWCDJt2U2MxuFhtrVczrw3ohYCiBpW+BGYHZVhZmZWTWGelbPBr2hnz0/jGXNzKyNDLXFf72k/wIuz8N/Afy4mpLMzKxKg/3P3V2Bzoj4e0l/CnwgT7oFuKzq4szMbOQN1uL/OnAaQERcDVwNIGnPPO2ISqszM7MRN1g/fWdELKofmcdNqqQiMzOr1GDBP26AaZuNZCFmZtYcgwX/7ZL+pn6kpI8DC6spyczMqjRYH/9JwDWSpvJm0HcBGwN/UmVhZmZWjQGDPyKWAO+XNAXYI4/+UUT8pPLKzMysEkO9H/88YF7FtZiZWRP46lszs8JUFvySdpA0T9K9ku6RdGIev42kGyQ9mH9vXVUNZma2tipb/GuAUyJid2A/4O8k7Q6cCtwUEbsBN+VhMzNrksqCPyKeiYg78uNVwH3AROAoYFaebRZwdFU1mJnZ2prSxy9pErA3sIB0NfAzedKzQGczajAzs0QRMfhc67IBqQP4KfCliLha0oqIGFczfXlErNXPL2kGMAOgs7Nzn+7u7oa2v/SFlSx5afD59pw4tqH1V6mnp4eOjo5Wl9EQ194arr012rX2KVOmLIyIrvrxQ70tc0MkbQR8H7gs3+QNYImkCRHxjKQJwNK+lo2ImcBMgK6urpg8eXJDNVxw2RzOWTT401w8tbH1V2n+/Pk0+rxbzbW3hmtvjdFWe5Vn9Qi4CLgvIs6tmTQXmJYfTwPmVFWDmZmtrcoW/wHAR4BFkn6Vx30eOAu4UtJ04DHS//A1M7MmqSz4I+LngPqZfFBV2zUzs4H5yl0zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MCuPgNzMrjIPfzKwwDn4zs8I4+M3MClNZ8Eu6WNJSSXfXjNtG0g2SHsy/t65q+2Zm1rcqW/yXAIfUjTsVuCkidgNuysNmZtZElQV/RPwMeKFu9FHArPx4FnB0Vds3M7O+NbuPvzMinsmPnwU6m7x9M7PiKSKqW7k0Cbg2IvbIwysiYlzN9OUR0Wc/v6QZwAyAzs7Ofbq7uxuqYekLK1ny0uDz7TlxbEPrr1JPTw8dHR2tLqMhrr01XHtrtGvtU6ZMWRgRXfXjxzS5jiWSJkTEM5ImAEv7mzEiZgIzAbq6umLy5MkNbfCCy+ZwzqLBn+biqY2tv0rz58+n0efdaq69NVx7a4y22pvd1TMXmJYfTwPmNHn7ZmbFq/J0zsuBW4C3S3pS0nTgLOBDkh4EDs7DZmbWRJV19UTE8f1MOqiqbZqZ2eB85a6ZWWEc/GZmhXHwm5kVxsFvZlYYB7+ZWWEc/GZmhXHwm5kVxsFvZlYYB7+ZWWEc/GZmhXHwm5kVxsFvZlaYZt+P3/ow6dQf9Tn+lD3XcELNtMVnHdasksxsPeYWv5lZYRz8ZmaFcfCbmRXGffxZf/3s9Ybazz7U9ZmZNZtb/GZmhXHwm5kVxsFvZlYYB7+ZWWF8cNfWCyN9cN5sfeYWv5lZYRz8ZmaFcfCbmRXGffzDtD5dmNWqfvHh7MNWbPuUPdcweUS32trnbFbPLX4zs8I4+M3MCuPgNzMrjPv410MjfRyixHPkS3zOQzXS768S92GrucVvZlYYB7+ZWWEc/GZmhXEf/yjS7tcQ1NZX/4/i11dVvCY+vtC/9eX4QqtfY7f4zcwK05Lgl3SIpAckPSTp1FbUYGZWqqYHv6QNgW8ChwK7A8dL2r3ZdZiZlaoVLf59gYci4pGIeBXoBo5qQR1mZkVSRDR3g9IxwCER8fE8/BHgfRHxybr5ZgAz8uDbgQca3OR4YFmDy7aaa28N194arn3k7RQR29aPbNuzeiJiJjBzXdcj6faI6BqBkprOtbeGa28N1948rejqeQrYoWZ4+zzOzMyaoBXB/0tgN0k7S9oYOA6Y24I6zMyK1PSunohYI+mTwH8BGwIXR8Q9FW5ynbuLWsi1t4Zrbw3X3iRNP7hrZmat5St3zcwK4+A3MyvMeh38o+XWEJJ2kDRP0r2S7pF0Yh6/jaQbJD2Yf2/d6lr7I2lDSXdKujYP7yxpQd73V+QD+W1H0jhJsyXdL+k+SfuPlv0u6TP5/XK3pMslbdqu+13SxZKWSrq7Zlyf+1nJ+fk53CXpPa2rvN/av5LfM3dJukbSuJppp+XaH5D0x62pemDrbfCPsltDrAFOiYjdgf2Av8u1ngrcFBG7ATfl4XZ1InBfzfDZwNciYldgOTC9JVUN7jzg+oj4fWAv0nNo+/0uaSLwaaArIvYgnShxHO273y8BDqkb199+PhTYLf/MAL7dpBr7cwlr134DsEdEvAv4X+A0gPx3exzwzrzMt3IWtZX1NvgZRbeGiIhnIuKO/HgVKXwmkuqdlWebBRzdmgoHJml74DDgwjws4EBgdp6lLWuXNBb4IHARQES8GhErGCX7nXRW3maSxgCbA8/Qpvs9In4GvFA3ur/9fBTw3UhuBcZJmtCcStfWV+0R8d8RsSYP3kq6HglS7d0R8UpEPAo8RMqitrI+B/9E4Ima4SfzuLYmaRKwN7AA6IyIZ/KkZ4HOFpU1mK8D/wC8kYffBqyo+cNo132/M/Ac8P9yN9WFkrZgFOz3iHgK+CrwOCnwVwILGR37vVd/+3m0/e1+DLguPx4Vta/PwT/qSOoAvg+cFBG/qZ0W6bzbtjv3VtLhwNKIWNjqWhowBngP8O2I2BtYTV23Thvv961Jrcudge2ALVi7O2LUaNf9PBhJp5O6ai9rdS3DsT4H/6i6NYSkjUihf1lEXJ1HL+n9ipt/L21VfQM4ADhS0mJSd9qBpH7zcbkLAtp33z8JPBkRC/LwbNIHwWjY7wcDj0bEcxHxGnA16bUYDfu9V3/7eVT87Uo6ATgcmBpvXhA1Kmpfn4N/1NwaIveJXwTcFxHn1kyaC0zLj6cBc5pd22Ai4rSI2D4iJpH28U8iYiowDzgmz9autT8LPCHp7XnUQcC9jIL9Turi2U/S5vn901t72+/3Gv3t57nAR/PZPfsBK2u6hNqCpENI3ZtHRsSLNZPmAsdJ2kTSzqQD1Le1osYBRcR6+wN8mHTE/WHg9FbXM0CdHyB9zb0L+FX++TCpr/wm4EHgRmCbVtc6yPOYDFybH+9CesM/BFwFbNLq+vqp+d3A7Xnf/wDYerTsd+BM4H7gbuBSYJN23e/A5aRjEa+RvmlN728/AyKdkfcwsIh05lK71f4QqS+/9+/1OzXzn55rfwA4tNX7vq8f37LBzKww63NXj5mZ9cHBb2ZWGAe/mVlhHPxmZoVx8JuZFcbBb8WRFJK+VzM8RtJzNXcWPXJd7uYq6SRJm49ErWZVcPBbiVYDe0jaLA9/iJqrKyNibkSctQ7rP4l00zSztuTgt1L9mHRHUYDjSRfpAOlSfEnfyI8vyfeGv1nSI5KOyeMn935DyMPfyMt9mnTvnHmS5uVpfyTpFkl3SLoq35MJSWcp/Q+GuyR9tSnP2gwHv5Wrm3Rp/abAu0h3Q+3PBNLV1YcDA34TiIjzgaeBKRExRdJ44Azg4Ih4D+kq4ZMlvQ34E+Cdke7p/sV1fUJmQzVm8FnM1j8RcVe+BfbxpNb/QH4QEW8A90oa7i2a9yP9I6BfpFvqsDFwC+k2yi8DF+VvDtf2uwazEebgt5LNJd3TfjLpvjH9eaXmsfLvNbz1G/Om/Swr4IaIOH6tCdK+pJurHQN8knRnU7PKuavHSnYxcGZELGpg2ceA3fNdGMeRArzXKmDL/PhW4ABJuwJI2kLS7+V+/rER8WPgM6R/+2jWFG7xW7Ei4kng/AaXfULSlaQ7Yz4K3FkzeSZwvaSncz//CcDlkjbJ088gfTjMyccYBJzc4NMwGzbfndPMrDDu6jEzK4yD38ysMA5+M7PCOPjNzArj4DczK4yD38ysMA5+M7PC/H/qdZQxzEoNuAAAAABJRU5ErkJggg==\n",
      "text/plain": [
       "<Figure size 432x288 with 1 Axes>"
      ]
     },
     "metadata": {
      "needs_background": "light"
     },
     "output_type": "display_data"
    }
   ],
   "source": [
    "process_log(log)"
   ]
  },
  {
   "cell_type": "code",
   "execution_count": null,
   "metadata": {
    "nbpages": {
     "level": 2,
     "link": "[7.5.8 Processing the Simulation Log](https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.html#7.5.8-Processing-the-Simulation-Log)",
     "section": "7.5.8 Processing the Simulation Log"
    }
   },
   "outputs": [],
   "source": []
  },
  {
   "cell_type": "markdown",
   "metadata": {},
   "source": [
    "<!--NAVIGATION-->\n",
    "< [7.4 Batch Chemical Process](https://jckantor.github.io/cbe30338-2021/07.04-Project-Batch-Chemical-Process.html) | [Contents](toc.html) | [Tag Index](tag_index.html) | [8.0 Projects](https://jckantor.github.io/cbe30338-2021/08.00-Projects.html) ><p><a href=\"https://colab.research.google.com/github/jckantor/cbe30338-2021/blob/master/docs/07.05-Queuing-Systems-and-Poisson-Processes.ipynb\"> <img align=\"left\" src=\"https://colab.research.google.com/assets/colab-badge.svg\" alt=\"Open in Colab\" title=\"Open in Google Colaboratory\"></a><p><a href=\"https://jckantor.github.io/cbe30338-2021/07.05-Queuing-Systems-and-Poisson-Processes.ipynb\"> <img align=\"left\" src=\"https://img.shields.io/badge/Github-Download-blue.svg\" alt=\"Download\" title=\"Download Notebook\"></a>"
   ]
  }
 ],
 "metadata": {
  "kernelspec": {
   "display_name": "Python 3",
   "language": "python",
   "name": "python3"
  },
  "language_info": {
   "codemirror_mode": {
    "name": "ipython",
    "version": 3
   },
   "file_extension": ".py",
   "mimetype": "text/x-python",
   "name": "python",
   "nbconvert_exporter": "python",
   "pygments_lexer": "ipython3",
   "version": "3.8.5"
  }
 },
 "nbformat": 4,
 "nbformat_minor": 4
}