ESTM60203

Introduction to Applied Operations Research

View the Project on GitHub jckantor/ESTM60203

Introduction to Applied Operations Research

ESTM 60203: Introduction to Applied Operations Research is a 1.5 credit, 14 class session introduction to selected concepts and analytical tools of Operations Research with broad application in business.

0. Getting Started Guides

1. Maximizing Profits

Your alt text

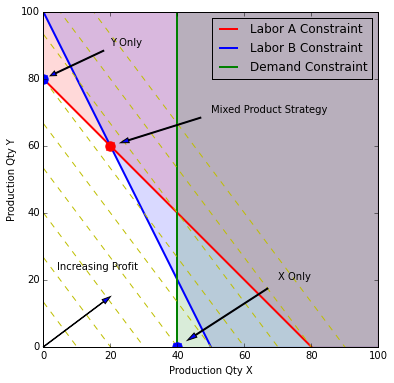
If you have ever needed to fit one more task into an overbooked calendar, or one more item into an overtaxed budget, then you understand the difficult decisions one makes when working in tightly constrained situations. Working against constraints requires tradeoffs between good alternatives, that you understand the penalties imposed on an objective by the constraints and the relationships between decisions and objectives.

In this unit we examine the problem of maximizing profits subject to linear relationships between resources, constraints, and objectives. We will see that maximizing profits means operating against constraints. When operating at conditions for maximum profit, we can calculate the value of additional resources (i.e., the 'shadow prices'), the cost of changing the product mix (i.e, the 'opportunity' or 'reduced' costs), and thereby gain important insights on how profits could be increased.

The unit will comprise two class sessions, the first outlining concepts and how to specify linear programming problems in a mathematical programming language MathProg. Students will work in teams to apply these techniques to a wine blending operation. The second class session will review the results, and discuss the business implications.

Notebooks
Reading
  1. Jonathan Eckstein. "Note on Linear Programming," 12 pages, HBS Case 191085-PDF-ENG, revised Nov 4, 1992.
  2. Robert Fourer, David M. Gay, and Brian W. Kernighan. "Chapter 1: Production Models: Maximizing Profits," pages 1-25 in AMPL: A Modeling Language for Mathematical Programming, Second Edition, Cengage Learning, 2002. (Available on-line for free download.)
Case Study
  1. Owen Hall and Kenneth Ko. "Landhills Winery: Developing an Optimal Blending Plan," 3 pages, HBS Case W14167-PDF-ENG, published May 21, 2014.

2. Modeling Business Decisions

Many logistical and production problems can be formulated and solved as linear programs. This unit will extend the skills learned in the earlier unit to several categories of operational problems that arise in business applications. The text used for this unit is the latest edition of a classic reference on the formulation of mathematical programs for practical applications. (See here for background on the book and author).

The unit will comprise two class sessions. In the first we will survey several broad categories of applications, including blending, transportation, and assignment problems, with solved examples. Working in teams, students will then formulate and solve a model for the DHL Supply Chain case study. The second class session will review student solutions, discuss alternative formulations, and analyze the solutions for insights about logistical operations with multiple objectives.

Notebooks
Reading
  1. H. Paul Williams. Model Building in Mathematical Programming, 5th Edition, 432 pages, Wiley, 2013. (Available from Amazon.)
Case Study
  1. Singfat Chu and David Ringrose. "DHL Supply Chain," 3 pages, HBS Case W12888-PDF-ENG, published Apr 19, 2014.

3. Planning and Scheduling

This unit looks into the problems of organizing tasks to meet deadlines, allocating services to meet customer demand in a flow shop, optimal scheduling for a limiting resource, and creating and managing schedules for complex projects. The unit focuses on simple, practical techniques for handling common situations arising in business and professional life.

The first class session will be devoted to an in-class simulation of a car wash business. The challenge is to allocate limited resources to meet demand during periods of steady customer flow, and during periods of peak demand. The second session will be based on a discussion on project management methods demonstrated in a short novel by Andreas Scherer, and introduce critical path and critical chain methods for project management. Students will break into teams to apply those methods to a project management case study. The third class session introduces empirical and optimization based methods of scheduling for process bottlenecks.

Notebooks
Reading
  1. Andreas Scherer. Be Fast or Be Gone: Racing the Clock with Critical Chain Project Management, 234 pages, Prochain Solutions Inc, 2011. (Available from Amazon.)
  2. Willy Herroelen and Roel Leus. "On the merits and pitfalls of critical chain scheduling," Journal of Operations Management, Vol. 19, 559-577, 2001. (Available here to Notre Dame students and faculty through Hesburgh Library.)
  3. Kenneth R. Baker. "Sequencing: The Shortest Processing Time Rule," pages 1-17 in Building Intuition: Insights From Basic Operations Management Models and Principles, ed. Dilip Chhajed and Timothy J. Lowe, Springer, 2008. (Available here to Notre Dame students and faculty through Hesburgh Library.)
Case Study/Simulation
  1. Ricardo Ernst. "Operations Management Exercise: Balancing Process Capacity," Online Simulation Exercise, HBS Product Number 4301-HTM-ENG, published Jun 21, 2012.
  2. Carol Prahinski and Thomas Kwan-Ho Yeung. "Multiple Sclerosis Society of Canada: London-Grand Bend Bicycle Tour," 7 pages, HBS Case Study 905D14-PDF-ENG, revised Sep 28, 2009

4. Supply Chains and Dynamics

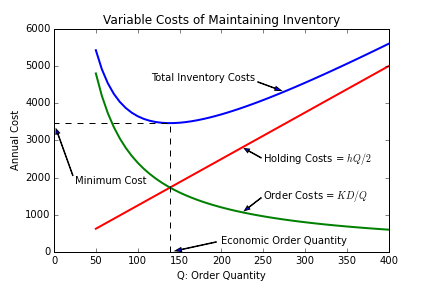
Supply chains refers to system of suppliers, distribution channels, and logistical operations that allow a business to produce goods and deliver them to market. Maintaing flexible and efficient supply chains are critical to modern operations. This unit will introduce basic concepts in inventory management, the causes of unstable dynamical behavior in supply chains, and tools for simulating the performance of complex operations.

The unit will comprise three class sessions. The first will basic economic concepts of inventory management, and how they lead to economic order quantity, replenishment strategies, the determination of safety stocks, and economy of scale associated with large warehouse operations. The second session is devoted to an in-class simulation to illustrate the potential for unstable dynamics in a manufacturer - distributor - retailer - customer supply chain and the critical role of information flow. The third class session will review the results of the simulation exercise, and demonstrate methods for simulating the behavior of discrete logistical operations.

Notebooks
Reading
  1. Leroy B. Schwarz. "The Economic Order-Quantity (EOQ) Model," pages 135-154 in Building Intuition: Insights From Basic Operations Management Models and Principles, ed. Dilip Chhajed and Timothy J. Lowe, Springer, 2008. (Available here to Notre Dame students and faculty through Hesburgh Library.)
  2. Hau L. Lee, V. Padmandbhan, and Seungjin Wang. "The Bullwhip Effect in Supply Chains," Sloan Management Review, Vol. 38, 93-102, 1997. (Available here to Notre Dame students and faculty through Hesburgh Library.)
Simulation
  1. Harvard Business School Press. "Supply Chain Management Simulation: Root Beer Game V2," Online Simulation Exercise, HBS Product Number 6619-HTM-ENG, published Jul 5, 2012.

5. Uncertainty, Risk, and Diversification

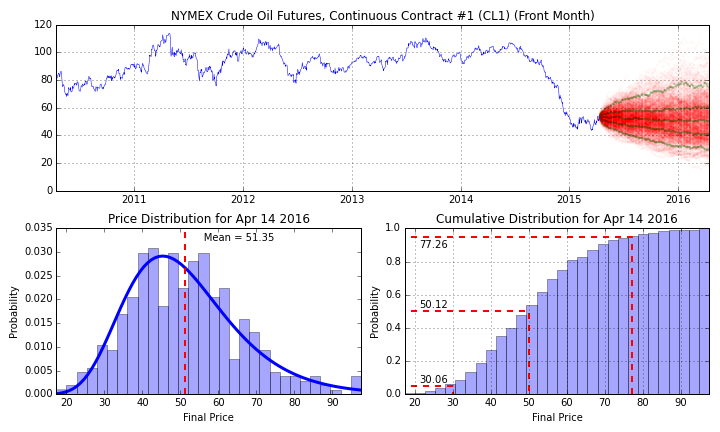
The final unit of the course focuses on making operational decisions in the face of financial uncertainties. The topics address issues of information, the critical distinction between 'here-and-now' decisions versus 'wait-and-see' decisions, measuring financial risk, and balancing risk and return when making operational decisions. Basic concepts of probability, expected value, and economic utility will be used to demonstrate the profound difference between optimzing for average wealth versus growth. The concepts will be applied to analyzing the 'real options' present in many business situations.

Four sessions are allocated to this unit in order to introduce a range of economic, finance, and statistical concepts. The first session will discuss two-stage decision making under uncertainty in the context of the newsvendor problem. The second session will show how to model multi-stage problems with decision trees, and how to quantify risk and return with the economic concept of utility. For the third class session, students will be asked to read the book length Fortune's Formula to establish a context for discussing the theoretical advantage of managing for growth versus average outcome. We will then show how these concepts can be applied to hedge risk in a portfolio of assets. The final class session will show how to appropriately apply these concepts to find value in the 'real options' common in many multi-stage business decisions.

Following the last session, students will be asked to use these concepts to prepare a critical review of a paper on valuation of an early-stage biotechnology investment.

Notebooks
Reading
  1. Evan V. Porteus. "The Newsvendor Problem," pages 115-134 in Building Intuition: Insights From Basic Operations Management Models and Principles, ed. Dilip Chhajed and Timothy J. Lowe, Springer, 2008. (Available here to Notre Dame students and faculty through Hesburgh Library.)
  2. Frank K. Crundwell. "Decision Tree Analysis and Utility Theory," pages 427-456 in Finance for Engineers: Evaluation and Funding of Capital Projects, Springer, 2008. (Available here to Notre Dame students and faculty through Hesburgh Library.)
  3. William Poundstone. Fortune's Formula: The Untold Story of the Scientific Betting System That Beat the Casinos and Wall Street, Hill and Wang, 2008. (Available from Amazon)
  4. Frank K. Crundwell. "Real Options Analysis," pages 427-456 in Finance for Engineers: Evaluation and Funding of Capital Projects, Springer, 2008. (Available here to Notre Dame students and faculty through Hesburgh Library.)
  5. Tom Copeland and Peter Tufano. "Real-World Way to Manage Real Options," Harvard Business Review, 82(3), 90-99, 2004. Available as Harvard Business School Case R0403G-PDF-ENG, 11 pages, published Mar 1, 2004.
Case Study
  1. Andrew G. Sutherland and Jeffrey R. Williams. "Valuing Real Options: Insights from Competitive Strategy," pages 334-366 in The Valuation Handbook: Valuation Techniques from Today's Top Practitioners, ed. Rawley Thomas and Benten E. Gup, Wiley, 2010. (Available as a teaching preprint from Research Showcase @ CMU at the Tepper School of Business, Carnegie-Mellon University.)
  2. Richard L. Shockley. "The Option Value of an Early-Stage Biotechnology Investment," Journal of Applied Corporate Finance, Vol. 15, 44-55, 2003. (Available here to Notre Dame students and faculty through Hesburgh Library.)