4.5. Scheduling Multipurpose Batch Processes using State-Task Networks#
Keywords: cbc usage, state-task networks, gdp, disjunctive programming, batch processes
The State-Task Network (STN) is an approach to modeling multipurpose batch process for the purpose of short term scheduling. It was first developed by Kondili, et al., in 1993, and subsequently developed and extended by others.
4.5.1. Imports#
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from IPython.display import display, HTML
import shutil
import sys
import os.path
if not shutil.which("pyomo"):
!pip install -q pyomo
assert(shutil.which("pyomo"))
if not (shutil.which("cbc") or os.path.isfile("cbc")):
if "google.colab" in sys.modules:
!apt-get install -y -qq coinor-cbc
else:
try:
!conda install -c conda-forge coincbc
except:
pass
assert(shutil.which("cbc") or os.path.isfile("cbc"))
from pyomo.environ import *
4.5.2. References#
Floudas, C. A., & Lin, X. (2005). Mixed integer linear programming in process scheduling: Modeling, algorithms, and applications. Annals of Operations Research, 139(1), 131-162.
Harjunkoski, I., Maravelias, C. T., Bongers, P., Castro, P. M., Engell, S., Grossmann, I. E., … & Wassick, J. (2014). Scope for industrial applications of production scheduling models and solution methods. Computers & Chemical Engineering, 62, 161-193.
Kondili, E., Pantelides, C. C., & Sargent, R. W. H. (1993). A general algorithm for short-term scheduling of batch operations—I. MILP formulation. Computers & Chemical Engineering, 17(2), 211-227.
Méndez, C. A., Cerdá, J., Grossmann, I. E., Harjunkoski, I., & Fahl, M. (2006). State-of-the-art review of optimization methods for short-term scheduling of batch processes. Computers & Chemical Engineering, 30(6), 913-946.
Shah, N., Pantelides, C. C., & Sargent, R. W. H. (1993). A general algorithm for short-term scheduling of batch operations—II. Computational issues. Computers & Chemical Engineering, 17(2), 229-244.
Wassick, J. M., & Ferrio, J. (2011). Extending the resource task network for industrial applications. Computers & chemical engineering, 35(10), 2124-2140.
4.5.3. Example (Kondili, et al., 1993)#
A state-task network is a graphical representation of the activities in a multi-product batch process. The representation includes the minimum details needed for short term scheduling of batch operations.
A well-studied example due to Kondili (1993) is shown below. Other examples are available in the references cited above.
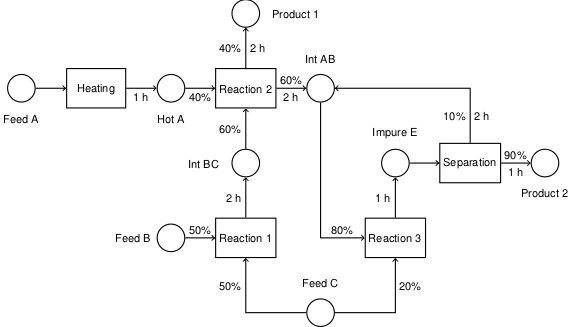
Each circular node in the diagram designates material in a particular state. The materials are generally held in suitable vessels with a known capacity. The relevant information for each state is the initial inventory, storage capacity, and the unit price of the material in each state. The price of materials in intermediate states may be assigned penalties in order to minimize the amount of work in progress.
The rectangular nodes denote process tasks. When scheduled for execution, each task is assigned an appropriate piece of equipment, and assigned a batch of material according to the incoming arcs. Each incoming arc begins at a state where the associated label indicates the mass fraction of the batch coming from that particular state. Outgoing arcs indicate the disposition of the batch to product states. The outgoing are labels indicate the fraction of the batch assigned to each product state, and the time necessary to produce that product.
Not shown in the diagram is the process equipment used to execute the tasks. A separate list of process units is available, each characterized by a capacity and list of tasks which can be performed in that unit.
4.5.3.1. Exercise#
Read this recipe for Hollandaise Sauce: http://www.foodnetwork.com/recipes/tyler-florence/hollandaise-sauce-recipe-1910043. Assume the available equipment consists of one sauce pan and a double-boiler on a stove. Draw a state-task network outlining the basic steps in the recipe.
4.5.4. Encoding the STN data#
The basic data structure specifies the states, tasks, and units comprising a state-task network. The intention is for all relevant problem data to be contained in a single JSON-like structure.
# planning horizon
H = 10
Kondili = {
# time grid
'TIME': range(0, H+1),
# states
'STATES': {
'Feed_A' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_B' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_C' : {'capacity': 500, 'initial': 500, 'price': 0},
'Hot_A' : {'capacity': 100, 'initial': 0, 'price': -100},
'Int_AB' : {'capacity': 200, 'initial': 0, 'price': -100},
'Int_BC' : {'capacity': 150, 'initial': 0, 'price': -100},
'Impure_E' : {'capacity': 100, 'initial': 0, 'price': -100},
'Product_1': {'capacity': 500, 'initial': 0, 'price': 10},
'Product_2': {'capacity': 500, 'initial': 0, 'price': 10},
},
# state-to-task arcs indexed by (state, task)
'ST_ARCS': {
('Feed_A', 'Heating') : {'rho': 1.0},
('Feed_B', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_3'): {'rho': 0.2},
('Hot_A', 'Reaction_2'): {'rho': 0.4},
('Int_AB', 'Reaction_3'): {'rho': 0.8},
('Int_BC', 'Reaction_2'): {'rho': 0.6},
('Impure_E', 'Separation'): {'rho': 1.0},
},
# task-to-state arcs indexed by (task, state)
'TS_ARCS': {
('Heating', 'Hot_A') : {'dur': 1, 'rho': 1.0},
('Reaction_2', 'Product_1'): {'dur': 2, 'rho': 0.4},
('Reaction_2', 'Int_AB') : {'dur': 2, 'rho': 0.6},
('Reaction_1', 'Int_BC') : {'dur': 2, 'rho': 1.0},
('Reaction_3', 'Impure_E') : {'dur': 1, 'rho': 1.0},
('Separation', 'Int_AB') : {'dur': 2, 'rho': 0.1},
('Separation', 'Product_2'): {'dur': 1, 'rho': 0.9},
},
# unit data indexed by (unit, task)
'UNIT_TASKS': {
('Heater', 'Heating') : {'Bmin': 0, 'Bmax': 100, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Still', 'Separation'): {'Bmin': 0, 'Bmax': 200, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
},
}
STN = Kondili
H = 16
Hydrolubes = {
# time grid
'TIME': range(0, H+1),
# states
'STATES': {
'Feed_A' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_B' : {'capacity': 500, 'initial': 500, 'price': 0},
'Feed_C' : {'capacity': 500, 'initial': 500, 'price': 0},
'Hot_A' : {'capacity': 100, 'initial': 0, 'price': -100},
'Int_AB' : {'capacity': 200, 'initial': 0, 'price': -100},
'Int_BC' : {'capacity': 150, 'initial': 0, 'price': -100},
'Impure_E' : {'capacity': 100, 'initial': 0, 'price': -100},
'Product_1': {'capacity': 500, 'initial': 0, 'price': 10},
'Product_2': {'capacity': 500, 'initial': 0, 'price': 10},
},
# state-to-task arcs indexed by (state, task)
'ST_ARCS': {
('Feed_A', 'Heating') : {'rho': 1.0},
('Feed_B', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_1'): {'rho': 0.5},
('Feed_C', 'Reaction_3'): {'rho': 0.2},
('Hot_A', 'Reaction_2'): {'rho': 0.4},
('Int_AB', 'Reaction_3'): {'rho': 0.8},
('Int_BC', 'Reaction_2'): {'rho': 0.6},
('Impure_E', 'Separation'): {'rho': 1.0},
},
# task-to-state arcs indexed by (task, state)
'TS_ARCS': {
('Heating', 'Hot_A') : {'dur': 1, 'rho': 1.0},
('Reaction_2', 'Product_1'): {'dur': 2, 'rho': 0.4},
('Reaction_2', 'Int_AB') : {'dur': 2, 'rho': 0.6},
('Reaction_1', 'Int_BC') : {'dur': 2, 'rho': 1.0},
('Reaction_3', 'Impure_E') : {'dur': 1, 'rho': 1.0},
('Separation', 'Int_AB') : {'dur': 2, 'rho': 0.1},
('Separation', 'Product_2'): {'dur': 1, 'rho': 0.9},
},
# unit data indexed by (unit, task)
'UNIT_TASKS': {
('Heater', 'Heating') : {'Bmin': 0, 'Bmax': 100, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_1', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_1'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_2'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Reactor_2', 'Reaction_3'): {'Bmin': 0, 'Bmax': 80, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
('Still', 'Separation'): {'Bmin': 0, 'Bmax': 200, 'Cost': 1, 'vCost': 0, 'Tclean': 0},
},
}
STN = Hydrolubes
4.5.4.1. Setting a time grid#
The following computations can be done on any time grid, including real-valued time points. TIME is a list of time points commencing at 0.
4.5.5. Creating a Pyomo model#
The following Pyomo model closely follows the development in Kondili, et al. (1993). In particular, the first step in the model is to process the STN data to create sets as given in Kondili.
One important difference from Kondili is the adoption of a more natural time scale that starts at \(t = 0\) and extends to \(t = H\) (rather than from 1 to H+1).
A second difference is the introduction of an additional decision variable denoted by \(Q_{j,t}\) indicating the amount of material in unit \(j\) at time \(t\). A material balance then reads
Following Kondili’s notation, \(I_j\) is the set of tasks that can be performed in unit \(j\), and \(\bar{S}_i\) is the set of states fed by task \(j\). We assume the units are empty at the beginning and end of production period, i.e.,
The unit allocation constraints are written the full backward aggregation method described by Shah (1993). The allocation constraint reads
Each processing unit \(j\) is tagged with a minimum and maximum capacity, \(B_{ij}^{min}\) and \(B_{ij}^{max}\), respectively, denoting the minimum and maximum batch sizes for each task \(i\). A minimum capacity may be needed to cover heat exchange coils in a reactor or mixing blades in a blender, for example. The capacity may depend on the nature of the task being performed. These constraints are written
4.5.5.1. Characterization of tasks#
STATES = STN['STATES']
ST_ARCS = STN['ST_ARCS']
TS_ARCS = STN['TS_ARCS']
UNIT_TASKS = STN['UNIT_TASKS']
TIME = STN['TIME']
H = max(TIME)
# set of tasks
TASKS = set([i for (j,i) in UNIT_TASKS])
# S[i] input set of states which feed task i
S = {i: set() for i in TASKS}
for (s,i) in ST_ARCS:
S[i].add(s)
# S_[i] output set of states fed by task i
S_ = {i: set() for i in TASKS}
for (i,s) in TS_ARCS:
S_[i].add(s)
# rho[(i,s)] input fraction of task i from state s
rho = {(i,s): ST_ARCS[(s,i)]['rho'] for (s,i) in ST_ARCS}
# rho_[(i,s)] output fraction of task i to state s
rho_ = {(i,s): TS_ARCS[(i,s)]['rho'] for (i,s) in TS_ARCS}
# P[(i,s)] time for task i output to state s
P = {(i,s): TS_ARCS[(i,s)]['dur'] for (i,s) in TS_ARCS}
# p[i] completion time for task i
p = {i: max([P[(i,s)] for s in S_[i]]) for i in TASKS}
# K[i] set of units capable of task i
K = {i: set() for i in TASKS}
for (j,i) in UNIT_TASKS:
K[i].add(j)
4.5.5.2. Characterization of states#
# T[s] set of tasks receiving material from state s
T = {s: set() for s in STATES}
for (s,i) in ST_ARCS:
T[s].add(i)
# set of tasks producing material for state s
T_ = {s: set() for s in STATES}
for (i,s) in TS_ARCS:
T_[s].add(i)
# C[s] storage capacity for state s
C = {s: STATES[s]['capacity'] for s in STATES}
4.5.5.3. Characterization of units#
UNITS = set([j for (j,i) in UNIT_TASKS])
# I[j] set of tasks performed with unit j
I = {j: set() for j in UNITS}
for (j,i) in UNIT_TASKS:
I[j].add(i)
# Bmax[(i,j)] maximum capacity of unit j for task i
Bmax = {(i,j):UNIT_TASKS[(j,i)]['Bmax'] for (j,i) in UNIT_TASKS}
# Bmin[(i,j)] minimum capacity of unit j for task i
Bmin = {(i,j):UNIT_TASKS[(j,i)]['Bmin'] for (j,i) in UNIT_TASKS}
4.5.5.4. Pyomo model#
TIME = np.array(TIME)
model = ConcreteModel()
# W[i,j,t] 1 if task i starts in unit j at time t
model.W = Var(TASKS, UNITS, TIME, domain=Boolean)
# B[i,j,t,] size of batch assigned to task i in unit j at time t
model.B = Var(TASKS, UNITS, TIME, domain=NonNegativeReals)
# S[s,t] inventory of state s at time t
model.S = Var(STATES.keys(), TIME, domain=NonNegativeReals)
# Q[j,t] inventory of unit j at time t
model.Q = Var(UNITS, TIME, domain=NonNegativeReals)
# Objective function
# project value
model.Value = Var(domain=NonNegativeReals)
model.valuec = Constraint(expr = model.Value == sum([STATES[s]['price']*model.S[s,H] for s in STATES]))
# project cost
model.Cost = Var(domain=NonNegativeReals)
model.costc = Constraint(expr = model.Cost == sum([UNIT_TASKS[(j,i)]['Cost']*model.W[i,j,t] +
UNIT_TASKS[(j,i)]['vCost']*model.B[i,j,t] for i in TASKS for j in K[i] for t in TIME]))
model.obj = Objective(expr = model.Value - model.Cost, sense = maximize)
# Constraints
model.cons = ConstraintList()
# a unit can only be allocated to one task
for j in UNITS:
for t in TIME:
lhs = 0
for i in I[j]:
for tprime in TIME:
if tprime >= (t-p[i]+1-UNIT_TASKS[(j,i)]['Tclean']) and tprime <= t:
lhs += model.W[i,j,tprime]
model.cons.add(lhs <= 1)
# state capacity constraint
model.sc = Constraint(STATES.keys(), TIME, rule = lambda model, s, t: model.S[s,t] <= C[s])
# state mass balances
for s in STATES.keys():
rhs = STATES[s]['initial']
for t in TIME:
for i in T_[s]:
for j in K[i]:
if t >= P[(i,s)]:
rhs += rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t-P[(i,s)]])]
for i in T[s]:
rhs -= rho[(i,s)]*sum([model.B[i,j,t] for j in K[i]])
model.cons.add(model.S[s,t] == rhs)
rhs = model.S[s,t]
# unit capacity constraints
for t in TIME:
for j in UNITS:
for i in I[j]:
model.cons.add(model.W[i,j,t]*Bmin[i,j] <= model.B[i,j,t])
model.cons.add(model.B[i,j,t] <= model.W[i,j,t]*Bmax[i,j])
# unit mass balances
for j in UNITS:
rhs = 0
for t in TIME:
rhs += sum([model.B[i,j,t] for i in I[j]])
for i in I[j]:
for s in S_[i]:
if t >= P[(i,s)]:
rhs -= rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t-P[(i,s)]])]
model.cons.add(model.Q[j,t] == rhs)
rhs = model.Q[j,t]
# unit terminal condition
model.tc = Constraint(UNITS, rule = lambda model, j: model.Q[j,H] == 0)
SolverFactory('cbc').solve(model).write()
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Name: unknown
Lower bound: -4870.33333333
Upper bound: -4870.33333333
Number of objectives: 1
Number of constraints: 252
Number of variables: 332
Number of binary variables: 136
Number of integer variables: 136
Number of nonzeros: 136
Sense: maximize
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
User time: -1.0
System time: 2.22
Wallclock time: 2.28
Termination condition: optimal
Termination message: Model was solved to optimality (subject to tolerances), and an optimal solution is available.
Statistics:
Branch and bound:
Number of bounded subproblems: 1476
Number of created subproblems: 1476
Black box:
Number of iterations: 17777
Error rc: 0
Time: 2.296165943145752
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
4.5.6. Analysis#
4.5.6.1. Profitability#
print("Value of State Inventories = {0:12.2f}".format(model.Value()))
print(" Cost of Unit Assignments = {0:12.2f}".format(model.Cost()))
print(" Net Objective = {0:12.2f}".format(model.Value() - model.Cost()))
Value of State Inventories = 4893.33
Cost of Unit Assignments = 23.00
Net Objective = 4870.33
4.5.6.2. Unit assignment#
UnitAssignment = pd.DataFrame({j:[None for t in TIME] for j in UNITS}, index=TIME)
for t in TIME:
for j in UNITS:
for i in I[j]:
for s in S_[i]:
if t-p[i] >= 0:
if model.W[i,j,max(TIME[TIME <= t-p[i]])]() > 0:
UnitAssignment.loc[t,j] = None
for i in I[j]:
if model.W[i,j,t]() > 0:
UnitAssignment.loc[t,j] = (i,model.B[i,j,t]())
UnitAssignment
| Heater | Reactor_1 | Reactor_2 | Still | |
|---|---|---|---|---|
| 0 | None | (Reaction_1, 80.0) | (Reaction_1, 80.0) | None |
| 1 | (Heating, 100.0) | None | None | None |
| 2 | None | (Reaction_1, 80.0) | (Reaction_2, 80.0) | None |
| 3 | None | None | None | None |
| 4 | None | (Reaction_2, 80.0) | (Reaction_2, 80.0) | None |
| 5 | (Heating, 60.0) | None | None | None |
| 6 | None | (Reaction_3, 80.0) | (Reaction_2, 80.0) | None |
| 7 | None | (Reaction_3, 80.0) | None | None |
| 8 | None | (Reaction_3, 80.0) | (Reaction_2, 80.0) | (Separation, 160.0) |
| 9 | (Heating, 53.333333) | (Reaction_1, 80.0) | None | None |
| 10 | None | None | (Reaction_3, 80.0) | None |
| 11 | None | (Reaction_2, 53.333333) | (Reaction_2, 80.0) | (Separation, 160.0) |
| 12 | None | None | None | None |
| 13 | None | (Reaction_3, 40.0) | (Reaction_3, 80.0) | None |
| 14 | None | None | None | (Separation, 120.0) |
| 15 | None | None | None | None |
| 16 | None | None | None | None |
4.5.6.3. State inventories#
pd.DataFrame([[model.S[s,t]() for s in STATES.keys()] for t in TIME], columns = STATES.keys(), index = TIME)
| Feed_A | Feed_B | Feed_C | Hot_A | Int_AB | Int_BC | Impure_E | Product_1 | Product_2 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 500.00000 | 420.0 | 420.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 0.00000 | 0.0 |
| 1 | 400.00000 | 420.0 | 420.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 0.00000 | 0.0 |
| 2 | 400.00000 | 380.0 | 380.0 | 68.000000 | 0.000000e+00 | 112.0 | 0.0 | 0.00000 | 0.0 |
| 3 | 400.00000 | 380.0 | 380.0 | 68.000000 | 0.000000e+00 | 112.0 | 0.0 | 0.00000 | 0.0 |
| 4 | 400.00000 | 380.0 | 380.0 | 4.000000 | 4.800000e+01 | 96.0 | 0.0 | 32.00000 | 0.0 |
| 5 | 340.00000 | 380.0 | 380.0 | 4.000000 | 4.800000e+01 | 96.0 | 0.0 | 32.00000 | 0.0 |
| 6 | 340.00000 | 380.0 | 364.0 | 32.000000 | 8.000000e+01 | 48.0 | 0.0 | 96.00000 | 0.0 |
| 7 | 340.00000 | 380.0 | 348.0 | 32.000000 | 1.600000e+01 | 48.0 | 80.0 | 96.00000 | 0.0 |
| 8 | 340.00000 | 380.0 | 332.0 | 0.000000 | 3.182357e-14 | 0.0 | 0.0 | 128.00000 | 0.0 |
| 9 | 286.66667 | 340.0 | 292.0 | 0.000000 | 6.364715e-14 | 0.0 | 80.0 | 128.00000 | 144.0 |
| 10 | 286.66667 | 340.0 | 276.0 | 53.333333 | 0.000000e+00 | 0.0 | 80.0 | 160.00000 | 144.0 |
| 11 | 286.66667 | 340.0 | 276.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 160.00000 | 144.0 |
| 12 | 286.66667 | 340.0 | 276.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 160.00000 | 288.0 |
| 13 | 286.66667 | 340.0 | 252.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 213.33333 | 288.0 |
| 14 | 286.66667 | 340.0 | 252.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 213.33333 | 288.0 |
| 15 | 286.66667 | 340.0 | 252.0 | 0.000000 | 0.000000e+00 | 0.0 | 0.0 | 213.33333 | 396.0 |
| 16 | 286.66667 | 340.0 | 252.0 | 0.000000 | 1.200000e+01 | 0.0 | 0.0 | 213.33333 | 396.0 |
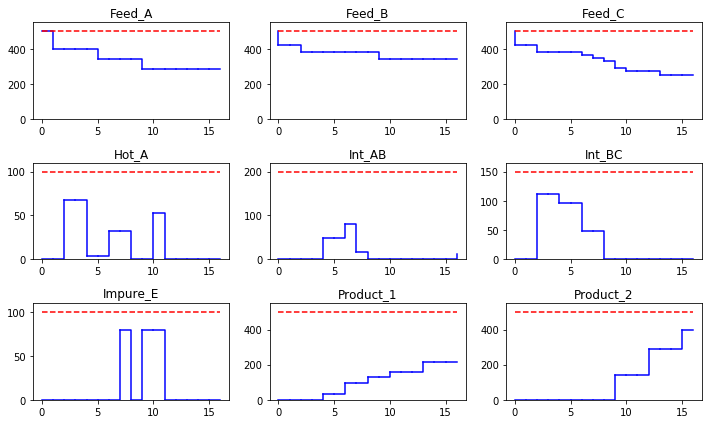
plt.figure(figsize=(10,6))
for (s,idx) in zip(STATES.keys(),range(0,len(STATES.keys()))):
plt.subplot(ceil(len(STATES.keys())/3),3,idx+1)
tlast,ylast = 0,STATES[s]['initial']
for (t,y) in zip(list(TIME),[model.S[s,t]() for t in TIME]):
plt.plot([tlast,t,t],[ylast,ylast,y],'b')
#plt.plot([tlast,t],[ylast,y],'b.',ms=10)
tlast,ylast = t,y
plt.ylim(0,1.1*C[s])
plt.plot([0,H],[C[s],C[s]],'r--')
plt.title(s)
plt.tight_layout()
4.5.6.4. Unit batch inventories#
pd.DataFrame([[model.Q[j,t]() for j in UNITS] for t in TIME], columns = UNITS, index = TIME)
| Heater | Reactor_1 | Reactor_2 | Still | |
|---|---|---|---|---|
| 0 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 1 | 100.000000 | 80.000000 | 80.0 | 0.0 |
| 2 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 3 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 4 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 5 | 60.000000 | 80.000000 | 80.0 | 0.0 |
| 6 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 7 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 8 | 0.000000 | 80.000000 | 80.0 | 160.0 |
| 9 | 53.333333 | 80.000000 | 80.0 | 16.0 |
| 10 | 0.000000 | 80.000000 | 80.0 | 0.0 |
| 11 | 0.000000 | 53.333333 | 80.0 | 160.0 |
| 12 | 0.000000 | 53.333333 | 80.0 | 16.0 |
| 13 | 0.000000 | 40.000000 | 80.0 | 0.0 |
| 14 | 0.000000 | 0.000000 | 0.0 | 120.0 |
| 15 | 0.000000 | 0.000000 | 0.0 | 12.0 |
| 16 | 0.000000 | 0.000000 | 0.0 | 0.0 |
4.5.6.5. Gannt chart#
plt.figure(figsize=(12,6))
gap = H/500
idx = 1
lbls = []
ticks = []
for j in sorted(UNITS):
idx -= 1
for i in sorted(I[j]):
idx -= 1
ticks.append(idx)
lbls.append("{0:s} -> {1:s}".format(j,i))
plt.plot([0,H],[idx,idx],lw=20,alpha=.3,color='y')
for t in TIME:
if model.W[i,j,t]() > 0:
plt.plot([t+gap,t+p[i]-gap], [idx,idx],'b', lw=20, solid_capstyle='butt')
txt = "{0:.2f}".format(model.B[i,j,t]())
plt.text(t+p[i]/2, idx, txt, color='white', weight='bold', ha='center', va='center')
plt.xlim(0,H)
plt.gca().set_yticks(ticks)
plt.gca().set_yticklabels(lbls);

4.5.7. Trace of events and states#
sep = '\n--------------------------------------------------------------------------------------------\n'
print(sep)
print("Starting Conditions")
print(" Initial Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,STATES[s]['initial']))
units = {j:{'assignment':'None', 't':0} for j in UNITS}
for t in TIME:
print(sep)
print("Time =",t,"hr")
print(" Instructions:")
for j in UNITS:
units[j]['t'] += 1
# transfer from unit to states
for i in I[j]:
for s in S_[i]:
if t-P[(i,s)] >= 0:
amt = rho_[(i,s)]*model.B[i,j,max(TIME[TIME <= t - P[(i,s)]])]()
if amt > 0:
print(" Transfer", amt, "kg from", j, "to", s)
for j in UNITS:
# release units from tasks
for i in I[j]:
if t-p[i] >= 0:
if model.W[i,j,max(TIME[TIME <= t-p[i]])]() > 0:
print(" Release", j, "from", i)
units[j]['assignment'] = 'None'
units[j]['t'] = 0
# assign units to tasks
for i in I[j]:
if model.W[i,j,t]() > 0:
print(" Assign", j, "with capacity", Bmax[(i,j)], "kg to task",i,"for",p[i],"hours")
units[j]['assignment'] = i
units[j]['t'] = 1
# transfer from states to starting tasks
for i in I[j]:
for s in S[i]:
amt = rho[(i,s)]*model.B[i,j,t]()
if amt > 0:
print(" Transfer", amt,"kg from", s, "to", j)
print("\n Inventories are now:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,model.S[s,t]()))
print("\n Unit Assignments are now:")
for j in UNITS:
if units[j]['assignment'] != 'None':
fmt = " {0:s} performs the {1:s} task with a {2:.2f} kg batch for hour {3:f} of {4:f}"
i = units[j]['assignment']
print(fmt.format(j,i,model.Q[j,t](),units[j]['t'],p[i]))
print(sep)
print('Final Conditions')
print(" Final Inventories:")
for s in STATES.keys():
print(" {0:10s} {1:6.1f} kg".format(s,model.S[s,H]()))
--------------------------------------------------------------------------------------------
Starting Conditions
Initial Inventories:
Feed_A 500.0 kg
Feed_B 500.0 kg
Feed_C 500.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
--------------------------------------------------------------------------------------------
Time = 0 hr
Instructions:
Assign Reactor_2 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 40.0 kg from Feed_C to Reactor_2
Transfer 40.0 kg from Feed_B to Reactor_2
Assign Reactor_1 with capacity 80 kg to task Reaction_1 for 2 hours
Transfer 40.0 kg from Feed_C to Reactor_1
Transfer 40.0 kg from Feed_B to Reactor_1
Assign Heater with capacity 100 kg to task Heating for 1 hours
Transfer 6.6666667 kg from Feed_A to Heater
Inventories are now:
Feed_A 493.3 kg
Feed_B 420.0 kg
Feed_C 420.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_1 performs the Reaction_1 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Heater performs the Heating task with a 6.67 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 1 hr
Instructions:
Transfer 6.6666667 kg from Heater to Hot_A
Release Heater from Heating
Assign Heater with capacity 100 kg to task Heating for 1 hours
Transfer 100.0 kg from Feed_A to Heater
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 420.0 kg
Hot_A 6.7 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_1 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Reactor_1 performs the Reaction_1 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Heater performs the Heating task with a 100.00 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 2 hr
Instructions:
Transfer 80.0 kg from Reactor_2 to Int_BC
Transfer 80.0 kg from Reactor_1 to Int_BC
Transfer 100.0 kg from Heater to Hot_A
Release Reactor_2 from Reaction_1
Assign Reactor_2 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 48.0 kg from Int_BC to Reactor_2
Transfer 32.0 kg from Hot_A to Reactor_2
Release Reactor_1 from Reaction_1
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 48.0 kg from Int_BC to Reactor_1
Transfer 32.0 kg from Hot_A to Reactor_1
Release Heater from Heating
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 420.0 kg
Hot_A 42.7 kg
Int_AB 0.0 kg
Int_BC 64.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 3 hr
Instructions:
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 420.0 kg
Hot_A 42.7 kg
Int_AB 0.0 kg
Int_BC 64.0 kg
Impure_E 0.0 kg
Product_1 0.0 kg
Product_2 0.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Reactor_1 performs the Reaction_2 task with a 80.00 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 4 hr
Instructions:
Transfer 48.0 kg from Reactor_2 to Int_AB
Transfer 32.0 kg from Reactor_2 to Product_1
Transfer 48.0 kg from Reactor_1 to Int_AB
Transfer 32.0 kg from Reactor_1 to Product_1
Release Reactor_2 from Reaction_2
Assign Reactor_2 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 32.0 kg from Int_AB to Reactor_2
Transfer 8.0 kg from Feed_C to Reactor_2
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 64.0 kg from Int_AB to Reactor_1
Transfer 16.0 kg from Feed_C to Reactor_1
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 396.0 kg
Hot_A 42.7 kg
Int_AB 0.0 kg
Int_BC 64.0 kg
Impure_E 0.0 kg
Product_1 64.0 kg
Product_2 0.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_3 task with a 40.00 kg batch for hour 1.000000 of 1.000000
Reactor_1 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 5 hr
Instructions:
Transfer 40.0 kg from Reactor_2 to Impure_E
Transfer 80.0 kg from Reactor_1 to Impure_E
Release Reactor_2 from Reaction_3
Assign Reactor_2 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 48.0 kg from Int_BC to Reactor_2
Transfer 32.0 kg from Hot_A to Reactor_2
Assign Still with capacity 200 kg to task Separation for 2 hours
Transfer 120.0 kg from Impure_E to Still
Release Reactor_1 from Reaction_3
Assign Reactor_1 with capacity 80 kg to task Reaction_2 for 2 hours
Transfer 16.0000002 kg from Int_BC to Reactor_1
Transfer 10.666666800000002 kg from Hot_A to Reactor_1
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 396.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 64.0 kg
Product_2 0.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 1.000000 of 2.000000
Still performs the Separation task with a 120.00 kg batch for hour 1.000000 of 2.000000
Reactor_1 performs the Reaction_2 task with a 26.67 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 6 hr
Instructions:
Transfer 108.0 kg from Still to Product_2
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 396.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 64.0 kg
Product_2 108.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_2 task with a 80.00 kg batch for hour 2.000000 of 2.000000
Still performs the Separation task with a 12.00 kg batch for hour 2.000000 of 2.000000
Reactor_1 performs the Reaction_2 task with a 26.67 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 7 hr
Instructions:
Transfer 48.0 kg from Reactor_2 to Int_AB
Transfer 32.0 kg from Reactor_2 to Product_1
Transfer 12.0 kg from Still to Int_AB
Transfer 16.0000002 kg from Reactor_1 to Int_AB
Transfer 10.666666800000002 kg from Reactor_1 to Product_1
Release Reactor_2 from Reaction_2
Assign Reactor_2 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 64.0 kg from Int_AB to Reactor_2
Transfer 16.0 kg from Feed_C to Reactor_2
Release Still from Separation
Release Reactor_1 from Reaction_2
Assign Reactor_1 with capacity 80 kg to task Reaction_3 for 1 hours
Transfer 12.0 kg from Int_AB to Reactor_1
Transfer 3.0 kg from Feed_C to Reactor_1
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 377.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 106.7 kg
Product_2 108.0 kg
Unit Assignments are now:
Reactor_2 performs the Reaction_3 task with a 80.00 kg batch for hour 1.000000 of 1.000000
Reactor_1 performs the Reaction_3 task with a 15.00 kg batch for hour 1.000000 of 1.000000
--------------------------------------------------------------------------------------------
Time = 8 hr
Instructions:
Transfer 80.0 kg from Reactor_2 to Impure_E
Transfer 15.0 kg from Reactor_1 to Impure_E
Release Reactor_2 from Reaction_3
Assign Still with capacity 200 kg to task Separation for 2 hours
Transfer 95.0 kg from Impure_E to Still
Release Reactor_1 from Reaction_3
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 377.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 106.7 kg
Product_2 108.0 kg
Unit Assignments are now:
Still performs the Separation task with a 95.00 kg batch for hour 1.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 9 hr
Instructions:
Transfer 85.5 kg from Still to Product_2
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 377.0 kg
Hot_A 0.0 kg
Int_AB 0.0 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 106.7 kg
Product_2 193.5 kg
Unit Assignments are now:
Still performs the Separation task with a 9.50 kg batch for hour 2.000000 of 2.000000
--------------------------------------------------------------------------------------------
Time = 10 hr
Instructions:
Transfer 9.5 kg from Still to Int_AB
Release Still from Separation
Inventories are now:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 377.0 kg
Hot_A 0.0 kg
Int_AB 9.5 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 106.7 kg
Product_2 193.5 kg
Unit Assignments are now:
--------------------------------------------------------------------------------------------
Final Conditions
Final Inventories:
Feed_A 393.3 kg
Feed_B 420.0 kg
Feed_C 377.0 kg
Hot_A 0.0 kg
Int_AB 9.5 kg
Int_BC 0.0 kg
Impure_E 0.0 kg
Product_1 106.7 kg
Product_2 193.5 kg