5.1. Response of a First Order System to Step and Square Wave Inputs#
Keywords: Simulator, ipopt usage
This notebook demonstrates simulation of a linear first-order system in Pyomo using the Simulator class from Pyomo. The notebook also demonstrates the construction and use of analytical approximations to step functions and square wave inputs.
5.1.1. Imports#
import matplotlib.pyplot as plt
from math import pi
import shutil
import sys
import os.path
if not shutil.which("pyomo"):
!pip install -q pyomo
assert(shutil.which("pyomo"))
if not (shutil.which("ipopt") or os.path.isfile("ipopt")):
if "google.colab" in sys.modules:
!wget -N -q "https://ampl.com/dl/open/ipopt/ipopt-linux64.zip"
!unzip -o -q ipopt-linux64
else:
try:
!conda install -c conda-forge ipopt
except:
pass
assert(shutil.which("ipopt") or os.path.isfile("ipopt"))
from pyomo.environ import *
from pyomo.dae import *
5.1.2. First-order differential equation with constant input#
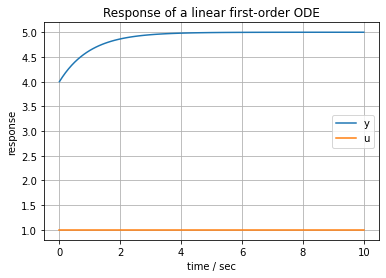
The following cell simulates the response of a first-order linear model in the form
where \(\tau\) and \(K\) are model parameters, and \(u(t)=1\) is an external process input.
tfinal = 10
tau = 1
K = 5
# define u(t)
def u(t):
return 1.0
# create a model object
model = ConcreteModel()
# define the independent variable
model.t = ContinuousSet(bounds=(0, tfinal))
# define the dependent variables
model.y = Var(model.t)
model.dydt = DerivativeVar(model.y)
# fix the initial value of y
model.y[0].fix(4)
# define the differential equation as a constraint
@model.Constraint(model.t)
def ode(m, t):
return tau*model.dydt[t] + model.y[t] == K*u(t)
model.y.display()
y : Size=2, Index=t
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : None : 4 : None : True : False : Reals
10 : None : None : None : False : True : Reals
# simulation using scipy integrators
tsim, profiles = Simulator(model, package='scipy').simulate(numpoints=101)
tsim
profiles
array([[4. ],
[4.09516518],
[4.18126635],
[4.25917761],
[4.32967597],
[4.39346666],
[4.45118776],
[4.50341441],
[4.55067095],
[4.5934305 ],
[4.63212104],
[4.66713048],
[4.69880924],
[4.72747142],
[4.75340218],
[4.77686354],
[4.79809743],
[4.81731337],
[4.83469911],
[4.85042886],
[4.86466192],
[4.87754068],
[4.88919421],
[4.89973902],
[4.90928022],
[4.91791317],
[4.92572462],
[4.93279283],
[4.93918842],
[4.9449753 ],
[4.95021132],
[4.95494926],
[4.95923631],
[4.96311531],
[4.9666254 ],
[4.96980139],
[4.97267511],
[4.97527546],
[4.97762825],
[4.97975715],
[4.98168354],
[4.98342653],
[4.9850037 ],
[4.9864308 ],
[4.98772205],
[4.98889045],
[4.98994758],
[4.99090399],
[4.99176946],
[4.99255276],
[4.99326147],
[4.99390272],
[4.99448304],
[4.99500813],
[4.99548319],
[4.99591304],
[4.99630201],
[4.99665391],
[4.99697229],
[4.99726045],
[4.99752118],
[4.99775709],
[4.99797055],
[4.99816375],
[4.99833848],
[4.99849659],
[4.99863967],
[4.9987691 ],
[4.99888618],
[4.99899214],
[4.99908806],
[4.99917492],
[4.99925359],
[4.99932482],
[4.99938923],
[4.99944739],
[4.99950001],
[4.99954764],
[4.99959071],
[4.99962961],
[4.99966475],
[4.99969657],
[4.99972537],
[4.99975145],
[4.99977533],
[4.99979649],
[4.99981579],
[4.99983331],
[4.99984916],
[4.99986348],
[4.99987643],
[4.99988812],
[4.99989869],
[4.99990825],
[4.99991692],
[4.99992473],
[4.99993178],
[4.99993818],
[4.999944 ],
[4.99994935],
[4.99995422]])
fig, ax = plt.subplots(1, 1)
ax.plot(tsim, profiles, label='y')
ax.plot(tsim, [u(t) for t in tsim], label='u')
ax.set_xlabel('time / sec')
ax.set_ylabel('response')
ax.set_title('Response of a linear first-order ODE')
ax.legend()
ax.grid(True)
5.1.3. Encapsulating into a function#
In following cells we would like to explore the response of a first order system to changes in parameters and input functions. To facilitate this study, the next cell encapsulates the simulation into a function that can be called with different parameter values and input functions.
def first_order(K=1, tau=1, tfinal=1, u=lambda t: 1):
model = ConcreteModel()
model.t = ContinuousSet(bounds=(0, tfinal))
model.y = Var(model.t)
model.dydt = DerivativeVar(model.y)
model.y[0].fix(0)
@model.Constraint(model.t)
def ode(m, t):
return tau*model.dydt[t] + model.y[t] == K*u(t)
tsim, profiles = Simulator(model, package='scipy').simulate(numpoints=1000)
fig, ax = plt.subplots(1, 1)
ax.plot(tsim, profiles, label='y')
ax.plot(tsim, [u(t) for t in tsim], label='u')
ax.set_xlabel('time / sec')
ax.set_ylabel('response')
ax.set_title('Response of a linear first-order ODE')
ax.legend()
ax.grid(True)
first_order(5, 1, 30, sin)
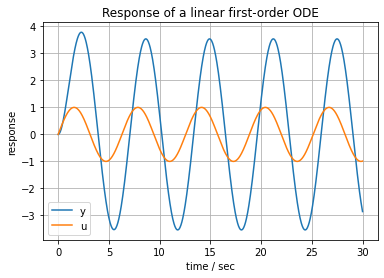
5.1.4. Analytical approximation to a step input#
The math functions supported by Pyomo are limited to that are imported to the standard arithmetic operations of Python (*, /, *, *=, /=, *=) and a particular set of nonlinear functions from the Python math library. Simulating the response of a system to a discontinuous step input, for example, requires an approximate.
An infinitely differentiable approximation to a step change is given by the Butterworth function \(b_n(t)\)
where \(n\) is the order of a approximation, and \(c\) is value of \(t\) where the step change occurs.
u = lambda t: 1/(1 + (t/10)**100)
first_order(5, 1, 30, u)
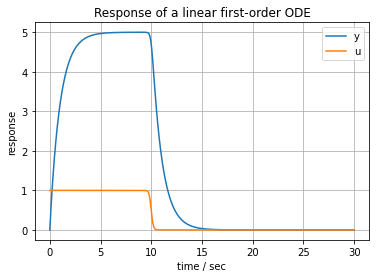
u = lambda t: 1 - 1/(1 + (t/10)**100)
first_order(5, 1, 30, u)
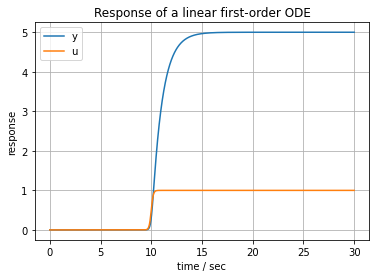
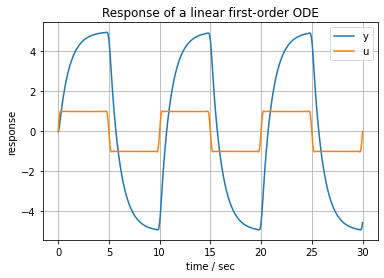
5.1.5. Analytical approximation to a square wave input#
An analytical approximation to a square wave with frequency \(f\) is given by
where the first term is the Lanczos sigma factor designed to suppress the Gibb’s phenomenon associated with Fourier series approximations.
def square(t, f=1, N=31):
return (4/pi)*sum((N*sin(k*pi/N)/k/pi)*sin(2*k*f*pi*t)/k for k in range(1, N+1,2))
u = lambda t: square(t, 0.1)
first_order(5, 1, 30, u)