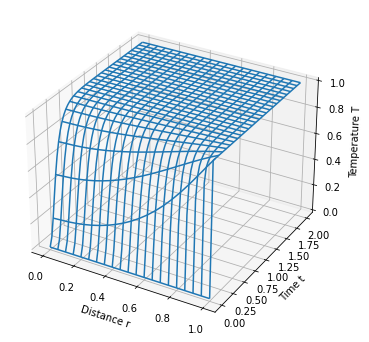
5.3. Transient Heat Conduction in Various Geometries#
Keywords: ipopt usage, dae, differential-algebraic equations, pde, partial differential equations
5.3.1. Imports#
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
import shutil
import sys
import os.path
if not shutil.which("pyomo"):
!pip install -q pyomo
assert(shutil.which("pyomo"))
if not (shutil.which("ipopt") or os.path.isfile("ipopt")):
if "google.colab" in sys.modules:
!wget -N -q "https://ampl.com/dl/open/ipopt/ipopt-linux64.zip"
!unzip -o -q ipopt-linux64
else:
try:
!conda install -c conda-forge ipopt
except:
pass
assert(shutil.which("ipopt") or os.path.isfile("ipopt"))
from pyomo.environ import *
from pyomo.dae import *
5.3.2. Rescaling the heat equation#
Transport of heat in a solid is described by the familiar thermal diffusion model
\[
\begin{align*}
\rho C_p\frac{\partial T}{\partial t} & = \nabla\cdot(k\nabla T)
\end{align*}
\]
We’ll assume the thermal conductivity \(k\) is a constant, and define thermal diffusivity in the conventional way
\[
\begin{align*}
\alpha & = \frac{k}{\rho C_p}
\end{align*}
\]
We will further assume symmetry with respect to all spatial coordinates except \(r\) where \(r\) extends from \(-R\) to \(+R\). The boundary conditions are
\[\begin{split}
\begin{align*}
T(t,R) & = T_{\infty} & \forall t > 0 \\
\nabla T(t,0) & = 0 & \forall t \geq 0
\end{align*}
\end{split}\]
where we have assumed symmetry with respect to \(r\) and uniform initial conditions \(T(0, r) = T_0\) for all \(0 \leq r \leq R\). Following standard scaling procedures, we introduce the dimensionless variables
\[\begin{split}
\begin{align*}
T' & = \frac{T - T_0}{T_\infty - T_0} \\
r' & = \frac{r}{R} \\
t' & = t \frac{\alpha}{R^2}
\end{align*}
\end{split}\]
5.3.3. Dimensionless model#
Under these conditions the problem reduces to
\[
\begin{align*}
\frac{\partial T'}{\partial t'} & = \nabla^2 T'
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T'(0, r') & = 0 & \forall 0 \leq r' \leq 1\\
T'(t', 1) & = 1 & \forall t' > 0\\
\nabla T'(t', 0) & = 0 & \forall t' \geq 0 \\
\end{align*}
\end{split}\]
which we can specialize to specific geometries.
5.3.4. Preliminary code#
def model_plot(m):
r = sorted(m.r)
t = sorted(m.t)
rgrid = np.zeros((len(t), len(r)))
tgrid = np.zeros((len(t), len(r)))
Tgrid = np.zeros((len(t), len(r)))
for i in range(0, len(t)):
for j in range(0, len(r)):
rgrid[i,j] = r[j]
tgrid[i,j] = t[i]
Tgrid[i,j] = m.T[t[i], r[j]].value
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(1, 1, 1, projection='3d')
ax.set_xlabel('Distance r')
ax.set_ylabel('Time t')
ax.set_zlabel('Temperature T')
p = ax.plot_wireframe(rgrid, tgrid, Tgrid)
5.3.5. Planar coordinates#
Suppressing the prime notation, for a slab geometry the model specializes to
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{\partial^2 T}{\partial r^2}
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T(0, r) & = 0 & \forall 0 \leq r \leq 1 \\
T(t, 1) & = 1 & \forall t > 0\\
\frac{\partial T}{\partial r} (t, 0) & = 0 & \forall t \geq 0 \\
\end{align*}
\end{split}\]
m = ConcreteModel()
m.r = ContinuousSet(bounds=(0,1))
m.t = ContinuousSet(bounds=(0,2))
m.T = Var(m.t, m.r)
m.dTdt = DerivativeVar(m.T, wrt=m.t)
m.dTdr = DerivativeVar(m.T, wrt=m.r)
m.d2Tdr2 = DerivativeVar(m.T, wrt=(m.r, m.r))
@m.Constraint(m.t, m.r)
def pde(m, t, r):
if t == 0:
return Constraint.Skip
if r == 0 or r == 1:
return Constraint.Skip
return m.dTdt[t,r] == m.d2Tdr2[t,r]
m.obj = Objective(expr=1)
m.ic = Constraint(m.r, rule=lambda m, r: m.T[0,r] == 0 if r > 0 and r < 1 else Constraint.Skip)
m.bc1 = Constraint(m.t, rule=lambda m, t: m.T[t,1] == 1)
m.bc2 = Constraint(m.t, rule=lambda m, t: m.dTdr[t,0] == 0)
TransformationFactory('dae.finite_difference').apply_to(m, nfe=50, scheme='FORWARD', wrt=m.r)
TransformationFactory('dae.finite_difference').apply_to(m, nfe=50, scheme='FORWARD', wrt=m.t)
SolverFactory('ipopt').solve(m, tee=True).write()
model_plot(m)
Ipopt 3.13.4:
******************************************************************************
This program contains Ipopt, a library for large-scale nonlinear optimization.
Ipopt is released as open source code under the Eclipse Public License (EPL).
For more information visit https://github.com/coin-or/Ipopt
******************************************************************************
This is Ipopt version 3.13.4, running with linear solver mumps.
NOTE: Other linear solvers might be more efficient (see Ipopt documentation).
Number of nonzeros in equality constraint Jacobian...: 30347
Number of nonzeros in inequality constraint Jacobian.: 0
Number of nonzeros in Lagrangian Hessian.............: 0
Total number of variables............................: 10299
variables with only lower bounds: 0
variables with lower and upper bounds: 0
variables with only upper bounds: 0
Total number of equality constraints.................: 10200
Total number of inequality constraints...............: 0
inequality constraints with only lower bounds: 0
inequality constraints with lower and upper bounds: 0
inequality constraints with only upper bounds: 0
iter objective inf_pr inf_du lg(mu) ||d|| lg(rg) alpha_du alpha_pr ls
0 1.0000000e+00 1.00e+00 0.00e+00 -1.0 0.00e+00 - 0.00e+00 0.00e+00 0
1 1.0000000e+00 1.48e-12 2.50e+01 -1.7 2.50e+03 -2.0 1.00e+00 1.00e+00h 1
2 1.0000000e+00 1.56e-12 8.30e-11 -1.7 2.26e-11 -2.5 1.00e+00 1.00e+00h 1
Number of Iterations....: 2
(scaled) (unscaled)
Objective...............: 1.0000000000000000e+00 1.0000000000000000e+00
Dual infeasibility......: 8.3006480378414195e-11 8.3006480378414195e-11
Constraint violation....: 3.1190328098062865e-14 1.5595164049031494e-12
Complementarity.........: 0.0000000000000000e+00 0.0000000000000000e+00
Overall NLP error.......: 8.3006480378414195e-11 8.3006480378414195e-11
Number of objective function evaluations = 3
Number of objective gradient evaluations = 3
Number of equality constraint evaluations = 3
Number of inequality constraint evaluations = 0
Number of equality constraint Jacobian evaluations = 3
Number of inequality constraint Jacobian evaluations = 0
Number of Lagrangian Hessian evaluations = 2
Total CPU secs in IPOPT (w/o function evaluations) = 1.430
Total CPU secs in NLP function evaluations = 0.006
EXIT: Optimal Solution Found.
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Lower bound: -inf
Upper bound: inf
Number of objectives: 1
Number of constraints: 10200
Number of variables: 10299
Sense: unknown
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
Message: Ipopt 3.13.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 1.0381290912628174
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
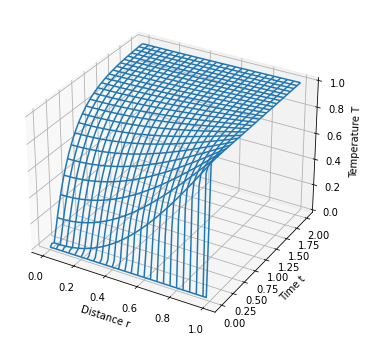
5.3.6. Cylindrical coordinates#
Suppressing the prime notation, for a cylindrical geometry the model specializes to
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{1}{r}\frac{\partial}{\partial r}\left(r\frac{\partial T}{\partial r}\right)
\end{align*}
\]
Expanding,
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{\partial^2 T}{\partial t^2} + \frac{1}{r}\frac{\partial T}{\partial r}
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T(0, r) & = 0 & \forall 0 \leq r \leq 1\\
T(t, 1) & = 1 & \forall t > 0\\
\frac{\partial T}{\partial r} (t, 0) & = 0 & \forall t \geq 0 \\
\end{align*}
\end{split}\]
m = ConcreteModel()
m.r = ContinuousSet(bounds=(0,1))
m.t = ContinuousSet(bounds=(0,2))
m.T = Var(m.t, m.r)
m.dTdt = DerivativeVar(m.T, wrt=m.t)
m.dTdr = DerivativeVar(m.T, wrt=m.r)
m.d2Tdr2 = DerivativeVar(m.T, wrt=(m.r, m.r))
m.pde = Constraint(m.t, m.r, rule=lambda m, t, r: m.dTdt[t,r] == m.d2Tdr2[t,r] + (1/r)*m.dTdr[t,r]
if r > 0 and r < 1 and t > 0 else Constraint.Skip)
m.ic = Constraint(m.r, rule=lambda m, r: m.T[0,r] == 0)
m.bc1 = Constraint(m.t, rule=lambda m, t: m.T[t,1] == 1 if t > 0 else Constraint.Skip)
m.bc2 = Constraint(m.t, rule=lambda m, t: m.dTdr[t,0] == 0)
TransformationFactory('dae.finite_difference').apply_to(m, nfe=20, wrt=m.r, scheme='CENTRAL')
TransformationFactory('dae.finite_difference').apply_to(m, nfe=50, wrt=m.t, scheme='BACKWARD')
SolverFactory('ipopt').solve(m).write()
model_plot(m)
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Lower bound: -inf
Upper bound: inf
Number of objectives: 1
Number of constraints: 4060
Number of variables: 4110
Sense: unknown
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
Message: Ipopt 3.13.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.4122738838195801
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
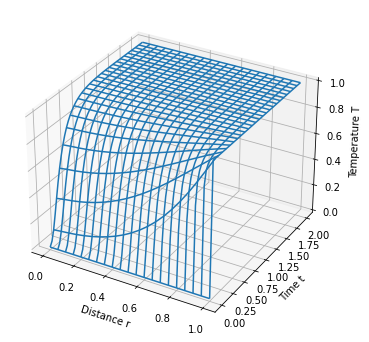
5.3.7. Spherical coordinates#
Suppressing the prime notation, for a cylindrical geometry the model specializes to
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial T}{\partial r}\right)
\end{align*}
\]
Expanding,
\[
\begin{align*}
\frac{\partial T}{\partial t} & = \frac{\partial^2 T}{\partial t^2} + \frac{2}{r}\frac{\partial T}{\partial r}
\end{align*}
\]
with auxiliary conditions
\[\begin{split}
\begin{align*}
T(0, r) & = 0 & \forall 0 \leq r \leq 1\\
T(t, 1) & = 1 & \forall t > 0\\
\frac{\partial T}{\partial r} (t, 0) & = 0 & \forall t \geq 0 \\
\end{align*}
\end{split}\]
m = ConcreteModel()
m.r = ContinuousSet(bounds=(0,1))
m.t = ContinuousSet(bounds=(0,2))
m.T = Var(m.t, m.r)
m.dTdt = DerivativeVar(m.T, wrt=m.t)
m.dTdr = DerivativeVar(m.T, wrt=m.r)
m.d2Tdr2 = DerivativeVar(m.T, wrt=(m.r, m.r))
m.pde = Constraint(m.t, m.r, rule=lambda m, t, r: m.dTdt[t,r] == m.d2Tdr2[t,r] + (2/r)*m.dTdr[t,r]
if r > 0 and r < 1 and t > 0 else Constraint.Skip)
m.ic = Constraint(m.r, rule=lambda m, r: m.T[0,r] == 0)
m.bc1 = Constraint(m.t, rule=lambda m, t: m.T[t,1] == 1 if t > 0 else Constraint.Skip)
m.bc2 = Constraint(m.t, rule=lambda m, t: m.dTdr[t,0] == 0)
TransformationFactory('dae.finite_difference').apply_to(m, nfe=20, wrt=m.r, scheme='CENTRAL')
TransformationFactory('dae.finite_difference').apply_to(m, nfe=50, wrt=m.t, scheme='BACKWARD')
SolverFactory('ipopt').solve(m).write()
model_plot(m)
# ==========================================================
# = Solver Results =
# ==========================================================
# ----------------------------------------------------------
# Problem Information
# ----------------------------------------------------------
Problem:
- Lower bound: -inf
Upper bound: inf
Number of objectives: 1
Number of constraints: 4060
Number of variables: 4110
Sense: unknown
# ----------------------------------------------------------
# Solver Information
# ----------------------------------------------------------
Solver:
- Status: ok
Message: Ipopt 3.13.4\x3a Optimal Solution Found
Termination condition: optimal
Id: 0
Error rc: 0
Time: 0.40662384033203125
# ----------------------------------------------------------
# Solution Information
# ----------------------------------------------------------
Solution:
- number of solutions: 0
number of solutions displayed: 0
