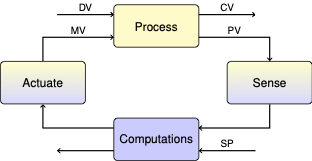
3.7. Integral Windup and Bumpless Transfer

“the devil is in the details” – anonymous

“and everything is detail” – military expression

3.7.1. Learning Goals

Up to this point we have been giving a “textbook” introduction to proportional-integral (PI) control. There is a world of difference between “textbook” and “practical”.

• Explain the purpose of each of the following enhancements of ‘textbook’ PI control:

  • Anti-reset windup

    • What is reset windup?

    • Fix 1: Insert limits on the manipulated variable (MV)

    • Fix 2: If possible, get field measurements of the manipulated variable (MV)

  • Bumpless Transfer

    • What is bumpless transfer?

    • Manual to Auto transition

3.7.2. Glossary of terms

Process control is full of specialized jargon for describing control systems and their performance. Here are some terms relevant to PID control.

P&ID

Piping and Instrumentation Diagrams showing type and placement of sensors, controllers, actuators, and other instruments used in process control. A typical encoding is given XY where

X	Variable
F	Flow
L	Level
P	Pressure
T	Temperature

Y	Instrument Type
T	Transmitter
G	Gauge
I	Indicator
IC	Indicating Controller

PID

Proportional-Integral-Derivative Control

PV

Process Variable. Generally a variable that is measured and used for feedback control. Typical examples are flow, level, pressure, and temperature, but may include composition, displacement, and many other variable types.

MV

Manipulated Variable. The variable being manipulated by the controller. Typically a flowrate using a control valve.

SP

Setpoint Variable. A desired value for process variable (PV). The job of the controller is change MV to cause PV to become equal to SP.

Reset-windup (also call Integral windup)

Reset-Windup refers to changes in the manipulated variable (MV) caused by specifying an infeasible setpoint. An example would be a setpoint of 120 degrees C for a heater that can reach a maximum temperature of only 100 deg C, or a setpoint of 10 deg C below ambient temperature when no cooling is available. In these situation the error signal (PV - SP) can never return to zero which causes the integration of the error signal to “wind-up”.

Anti-reset-windup

A modification to the standard PI and PID control algorithms to (1) avoid out-of range values of the manipulated variables (MV), and (2) incorporate field measurements of the manipulated variable. Anti-reset-windup avoids infeasible values of the manipulated variable due to infeasible setpoints or situations where the actuator is not responding to inputs.

Bumpless transfer

A modification to the standard PI and PID control algorithms to avoid sudden jumps in manipulated variable when switching from manual to automatic control.

3.7.3. Typical P&ID Diagram for PI and PID control.

---

Study Question: Carefully review the following P&ID diagrams. Locate the control loops, identify the sensors, controls, and actuators.

• Example Notice the sensors are not clearly shown. Modify this diagram to show the sensors and transmitters.

• Distillation Unit

• A complete unit operation

---

3.7.4. PI Control

Proportional-Integral (PI) Control in velocity form is given by

(3.10)\[\begin{align} MV_k & = MV_{k-1} - K_P (e_{k} - e_{k-1}) - \delta t K_I e_k \end{align}\]

where \(MV_0= \bar{MV}\) is the initial value, and the error \(e_k\) is the difference between the process variable and setpoint, and \(\delta t\) is the time step.

(3.11)\[\begin{align} e_k & = PV_k - SP_k \\ \end{align}\]

and \(\delta t\) is the time step.

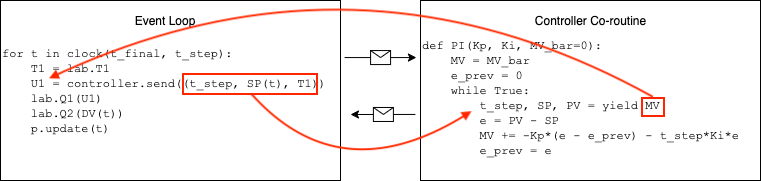
We encode the controller using the Python yield' statement. The implementation has added t_step` to facilitate use of this code for situations where we may change the time step or have a variable time step.

# caution: this is not a final version of our PI controller
def PI(Kp, Ki, MV_bar=0):
    MV = MV_bar
    e_prev = 0
    while True:
        t_step, SP, PV = yield MV
        e = PV - SP
        MV -= Kp*(e - e_prev) + t_step*Ki*e
        MV = max(0, min(100, MV))
        e_prev = e
        

from tclab import TCLab, clock, Historian, Plotter, setup

def SP(t):
    return 40 if t >= 20 else 20

def DV(t):
    return 100 if t >= 420 else 0

TCLab = setup(connected=False, speedup=60)

t_final = 1000
t_step = 5

controller = PI(5, 0.2)

with TCLab() as lab:
    sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
               ("U1", lambda: U1), ("Q1", lab.Q1))
    h = Historian(sources)
    p = Plotter(h, t_final, layout=[("T1", "SP"), ("Q1", "U1")])

    # initialize manipulated variable
    lab.P1 = 200
    lab.P2 = 200
    lab.Q1(next(controller))

    # event loop
    for t in clock(t_final, t_step):
        T1 = lab.T1
        U1 = controller.send((t_step, SP(t), T1))
        lab.Q1(U1)
        lab.Q2(DV(t))                        # <= disturbance
        p.update(t)

TCLab Model disconnected successfully.

Sequence diagram

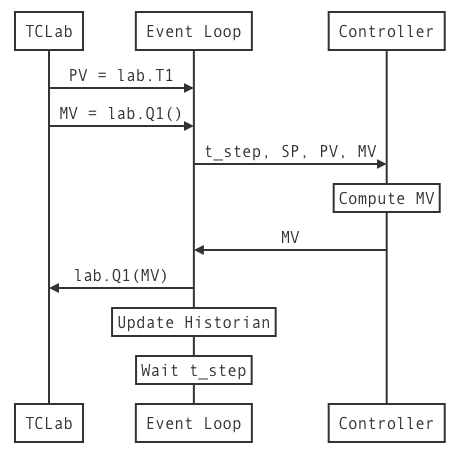
The benefits of using the yield statement is that we can use the same code to create multiple instances of controller, each with it’s own parameters and state. The communication between the main event loop and a controller instance is illustrated in this diagram:

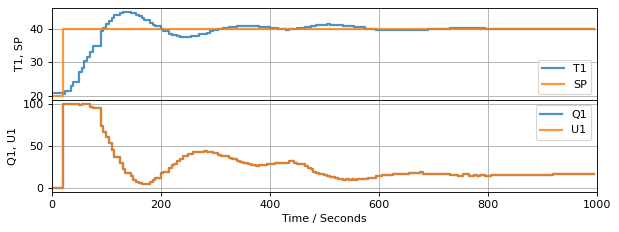
The following cells demonstrate performance of the controller when subject to a step change in setpoint and a disturbance input.

3.7.5. What is Integral/Reset Windup?

Let’s increase the magnitude of the control gains to see if we an acheive even better control performance.

controller = PI(10, 0.5)

with TCLab() as lab:
    sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
               ("U1", lambda: U1), ("Q1", lab.Q1))
    h = Historian(sources)
    p = Plotter(h, t_final, layout=[("T1", "SP"), ("Q1", "U1")])

    # initialize manipulated variable
    lab.P1 = 200
    lab.P2 = 200
    lab.Q1(next(controller))

    # event loop
    for t in clock(t_final, t_step):
        T1 = lab.T1
        U1 = controller.send((t_step, SP(t), T1))
        lab.Q1(U1)
        lab.Q2(DV(t))                        # <= disturbance
        p.update(t)

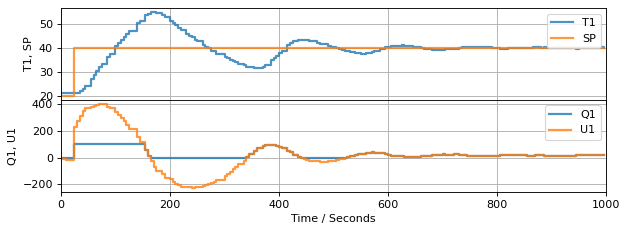
TCLab Model disconnected successfully.

---

Study Question: Examine the results of this experiment. The PI velocity algorithm is given by an equation

(3.12)\[\begin{align} MV_{k} & = MV_{k-1} - K_p(e_{k} - e_{k-1}) - \delta t K_i e_{k} \end{align}\]

Looking at the period from 0 to 100 seconds, is this equation describing what is actually happening? Is it possible for \(MV\) to be different from the actual input applied to the device?

---

Integral (also called Reset) windup is a consequence the controller computing values for the manipulable input that are outside the range of feasible values. The difference is due to the presence of upper and lower bounds on the manipulated variable.

3.7.5.1. Anti-reset windup - Type 1

There several common strategies for avoiding integral (reset) windup. The first of these should be part of any practical implementation. The technique is to limit computed values of manipulated variable to the range of values that can be implemented. This will avoid \(MV\) ‘winding up’ due to range limits.

\[ \begin{align} \hat{MV}_{k} & = MV_{k-1} - K_p(e_{k} - e_{k-1}) - \delta t K_i e_{k} \end{align} \]

\[\begin{split} \begin{align} MV_k & = \begin{cases} MV^{min} & \text{if } \hat{MV}_k \leq MV^{min}\\ \hat{MV}_k & \text{if } MV^{min} \leq \hat{MV}_k \leq MV^{max}\\ MV^{max} & \text{if} \hat{MV_k} \geq MV^{max} \end{cases} \end{align} \end{split}\]

The logic in the if statement can be conveniently coded with a single line of Python

MV = max(MV_min, min(MV_max, MV))

Let’s see how this works when applied to a simulation of the temperature control lab.

# add anti-integral windup feature. Not yet final.
def PI_antiwindup_1(Kp, Ki, MV_bar=0, MV_min=0, MV_max=100):
    MV = MV_bar
    e_prev = 0
    while True:
        t_step, SP, PV = yield MV
        e = PV - SP
        MV = MV - Kp*(e - e_prev) - t_step*Ki*e
        MV = max(MV_min, min(MV_max, MV))
        e_prev = e
        
controller = PI_antiwindup_1(10, 0.5)

with TCLab() as lab:
    sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
               ("U1", lambda: U1), ("Q1", lab.Q1))
    h = Historian(sources)
    p = Plotter(h, t_final, layout=[("T1", "SP"), ("Q1", "U1")])

    # initialize manipulated variable
    lab.P1 = 200
    lab.P2 = 200
    lab.Q1(next(controller))

    # event loop
    for t in clock(t_final, t_step):
        T1 = lab.T1
        U1 = controller.send((t_step, SP(t), T1))
        lab.Q1(U1)
        lab.Q2(DV(t))                        # <= disturbance
        p.update(t)
        

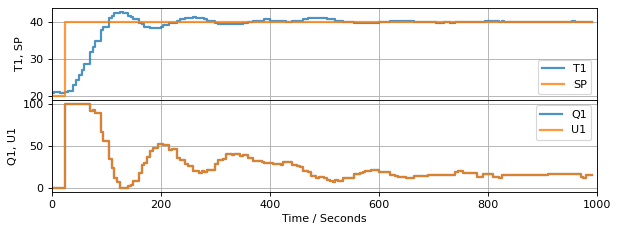
TCLab Model disconnected successfully.

3.7.5.2. Anti-reset Windup - Type 2

Another form of windup occurs when the manipulated variable is subject to external interventions. This can occur when a valve stem in a process application gets stuck, an operator or user intervenes and resets a mechanical actuator, or there is some sort of system failure.

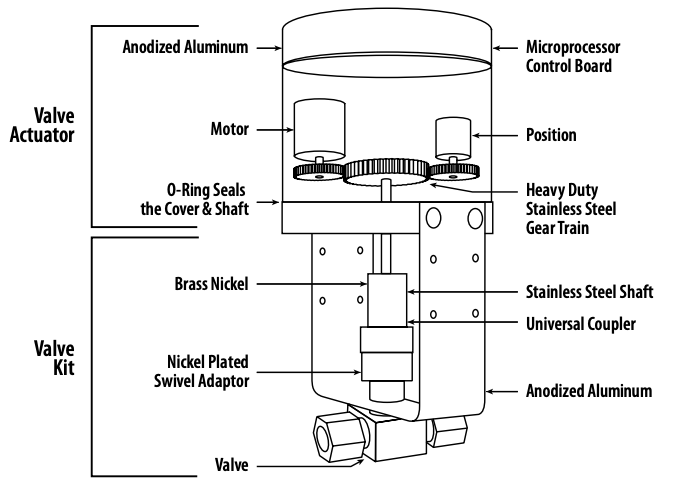
For these reasons, practical control systems often include a field measurement of the manipulated variable. The following image, for example, shows a pneumatically operated globe valve with a positioner, and with feedback of position to the central control system.

CC BY-SA 3.0

Stepper motors are commonly used actuators in lab equipment and robotics. The position of the stepper motor would be manipulated variable. This is an example of a stepper motor with an integrated encoder that can be used to verify the motor’s position.

Valve position feedback is a feature of control valves used in process applications, and should be regarded as a ‘best practice’ for industrial automation.

This behavior also occurs in the Temperature Control Laboratory in which the manipulated power levels are constrained to the range 0% to 100%. This is demonstated in the following cell.

# show that inputs to the TCLab are constrained to the range 0 to 100%
TCLab = setup(connected=False, speedup=20)
with TCLab() as lab:
    print(f"Q1 = {lab.Q1()}")
    lab.Q1(150)
    print(f"Q1 = {lab.Q1()}")

TCLab version 0.4.10dev
Simulated TCLab
Q1 = 0
Q1 = 100
TCLab Model disconnected successfully.

To accommodate feedback of the manipulated variable, we first need to modify the event loop to incorporate the measurement of the manipulated variable, then send that value to the controller.

# add anti-integral windup feature. Not yet final.

def PI_antiwindup_2(Kp, Ki, MV_bar=0, MV_min=0, MV_max=100):
    MV = MV_bar
    e_prev = 0
    while True:
        t_step, SP, PV, MV = yield MV   # <==== now gets MV from experiment
        e = PV - SP
        MV = MV - Kp*(e - e_prev) - t_step*Ki*e 
        # MV = max(MV_min, min(MV_max, MV)) # <=== turn this off for demo
        e_prev = e

from tclab import TCLab, clock, Historian, Plotter, setup

TCLab = setup(connected=False, speedup=60)

controller = PI_antiwindup_2(10, 0.5)

with TCLab() as lab:

    # set up historian and plotter
    sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
               ("U1", lambda: U1), ("Q1", lab.Q1))
    h = Historian(sources)
    p = Plotter(h, t_final, layout=[("T1", "SP"), ("Q1", "U1")])

    # initialize manipulated variable
    lab.P1 = 200
    next(controller)

    # event loop
    for t in clock(t_final, t_step):
        T1 = lab.T1
        U1 = lab.Q1()                            # <==== new line
        U1 = controller.send((t_step, SP(t), T1, U1))    # <==== send U1 to controller 
        lab.Q1(U1)
        lab.Q2(DV(t))
        p.update(t)     

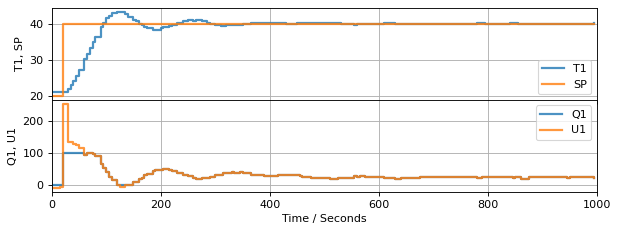
TCLab Model disconnected successfully.

The next change is to the controller. The controller now accepts values for PV, SP, and, additionally, MV. To demonstrate the impact of these changes, this example will comment out the software limits placed on MV to show that feedback of manipulated variable is also an anti-reset windwup strategy.

3.7.5.3. Anti-reset Windup - Complete

With these considerations in place, the following cell presents a version of the PI control algorithm incorporating both range limits and direct feedback of the manipulated variables.

# add anti-integral windup feature.

def PI_antiwindup(Kp, Ki, MV_bar=0, MV_min=0, MV_max=100):
    MV = MV_bar
    e_prev = 0
    while True:
        t_step, SP, PV, MV = yield MV       # <= now gets MV from experiment
        e = PV - SP
        MV = MV - Kp*(e - e_prev) - t_step*Ki*e 
        MV = max(MV_min, min(MV_max, MV))   # <= range limits
        e_prev = e
        

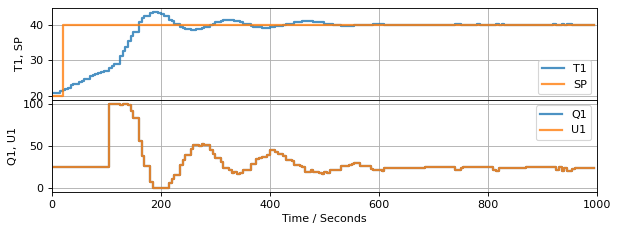
3.7.6. Manual to Auto Transition: Bumpless Transfer

Manual operation can be implemented by specifying the manipulated variable. We will implement this by specifying a function that specifies values of manipulated variable whenever manual conteol is in effect.

from tclab import TCLab, clock, Historian, Plotter, setup

def MV(t):
    return 25 if t <= 100 else None   # <== manipulated variable. Return none for auto
    
TCLab = setup(connected=False, speedup=60)

controller = PI_antiwindup(10, 0.5)

with TCLab() as lab:

    # set up historian and plotter
    sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
               ("U1", lambda: U1), ("Q1", lab.Q1))
    h = Historian(sources)
    p = Plotter(h, t_final, layout=[("T1", "SP"), ("Q1", "U1")])

    # initialize manipulated variable
    lab.P1 = 200
    lab.Q1(next(controller))

    # event loop
    for t in clock(t_final, t_step):
        T1 = lab.T1
        U1 = lab.Q1()
        if MV(t) is None:           
            U1 = controller.send((t_step, SP(t), T1, U1))    # automatic control
        else:
            U1 = MV(t)                                       # manual control
        lab.Q1(U1)
        lab.Q2(DV(t))
        p.update(t)  

TCLab Model disconnected successfully.

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/var/folders/cm/z3t28j296f98jdp1vqyplkz00000gn/T/ipykernel_39778/3602164331.py in <module>
     32         p.update(t)
     33 
---> 34 experiment_3(PI_antiwindup(10, 0.5))

NameError: name 'experiment_3' is not defined

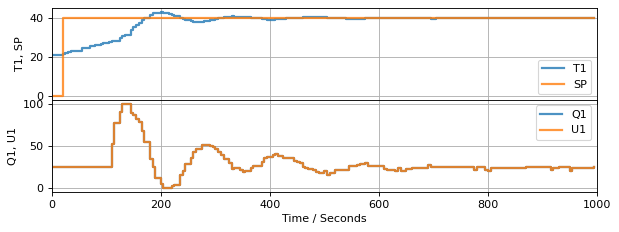
3.7.7. Bumpless Transfer

• Remove setpoint from proportional term

• Only the integral control term incorporates the setpoint.

3.7.7.1. Bumpless Transfer

(3.13)\[\begin{align} e_k & = PV_k - SP_k \\ \hat{MV}_{k} & = MV_{k-1} - K_p(PV_{k} - PV_{k-1}) - \delta t K_i e_{k} \end{align}\]

(3.14)\[\begin{align} MV_k & = \max(MV^{min}, \min(MV^{max}, \hat{MV}_k) \end{align}\]

# add anti-integral windup feature.

def PI_bumpless(Kp, Ki, MV_bar=0, MV_min=0, MV_max=100):
    MV = MV_bar
    PV_prev = None
    while True:
        t_step, SP, PV, MV = yield MV 
        e = PV - SP
        if PV_prev is not None:
            MV += -Kp*(PV - PV_prev) - t_step*Ki*e 
            MV = max(MV_min, min(MV_max, MV))
        PV_prev = PV
        
experiment_3(PI_bumpless(10, 0.5))

TCLab Model disconnected successfully.