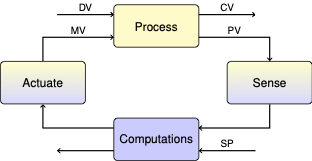
3.8. Controller Tuning#

3.8.1. Learning Goals#

Up to this point we have been discussing the theory and implementation of Proportional and Proportional-Integral control. The controllers have been specified with several parameters \(K_p\), \(K_I\), and the sampling time step. The purpose of this notebook is to describe methods for the practical determination of these parameters.

3.8.2. Versions of P, PI, and PID Control#

3.8.2.1. Error Signal#

The error signal measures the difference

\[e(t) = SP(t) - PV(t)\]

3.8.2.2. Idealized (Textbook) PID control#

Textbook equations, Position Form

\[MV = \bar{MV} + \underbrace{K_P (SP - PV)}_{\text{proportional}} + \underbrace{K_I \int^t (SP - PV) dt}_{\text{integral}} + \underbrace{K_D \frac{d}{dt}(SP-PV)}_{\text{derivative}}\]

Expressed with error signal

\[MV = \bar{MV} + \underbrace{K_P e(t)}_{\text{proportional}} + \underbrace{K_I \int^t e(t) dt}_{\text{integral}} + \underbrace{K_D \frac{d}{dt}e(t)}_{\text{derivative}}\]

Discrete-time Version for TCLab

\[MV_k = \bar{MV} + \underbrace{K_P(SP_k - PV_k)}_{\text{proportional}} + \underbrace{\delta t K_I \sum^k (SP_k - PV_k)}_{\text{integral}}\]

  • Proportional Control: Reduces system time constants. Too much leads to overshoot and excessive control action.

  • Integral Control: Eliminates steady-state offset. Tends to slow-down and destablize control.

  • Derivative Control: Mitigates fast changes in PV. Not as important as P and PI for most process control applications.

3.8.2.3. Practical PI Control#

Problems with textbook control:

  1. Position Form: How to choose \(\bar{MV}\)?

  2. Reset (also called Integral) windup due to limits on manipulated variable.

  3. Abrupt changes (“Bumps”) on transition from manual to automatic control.

Three changes to the textbook control rule:

  • Velocity form. Compute updates to \(MV\)

  • Anti-reset windup. Limit MV to feasible limits. Use measured MV if available.

  • Bumpless transfer. Leave SP out of the proportional control term.

Given parameters \(\delta t\), \(K_P\), \(K_I\), \(MV_{min}\), \(MV_{out}\)

At each time step \( t + \delta t\)

Using

  • prior values \(PV_{k-1}\)

  • current values for \(PV_k\), \(SP_k\), \(MV_k\) (if available)

Compute

\[\begin{align*} \\ E_k & = SP_k - PV_k & \text{error} \\ \\ \hat{MV}_{k} & = MV_{k-1} - K_p(PV_{k} - PV_{k-1}) - \delta t K_i E_{k} & \text{proposed update to MV}\\ \\ MV_k & = \max(MV^{min}, \min(MV^{max}, \hat{MV}_k)) & \text{limit MV to feasible values} \end{align*}\]

3.8.3. PI Control for Temperature Control Lab#

The following sequence diagram shows the flow of information for one measure-compute-act-record cycle of the control system is shown in the following sequence diagram

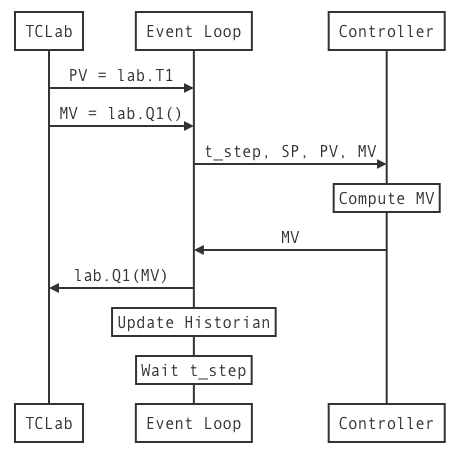
3.8.4. PI Control with anti-reset windup and bumpless transfer#

# add anti-integral windup feature.
def PI_bumpless(Kp, Ki, MV_bar=0, MV_min=0, MV_max=100):
    MV = MV_bar
    PV_prev = None
    while True:
        t_step, SP, PV, MV = yield MV 
        e = PV - SP
        if PV_prev is not None:
            MV += -Kp*(PV - PV_prev) - t_step*Ki*e 
            MV = max(MV_min, min(MV_max, MV))
        PV_prev = PV

3.8.5. Event Loop with Disturbance Variable and Manual Control#

from tclab import TCLab, clock, Historian, Plotter, setup

def experiment_3(controller, t_final=1000, t_step=5,
               SP=lambda t: 40 if t >= 20 else 0, 
               DV=lambda t: 100 if t >= 420 else 0,
               MV=lambda t: 25 if t <= 100 else None):   # <== manipulated variable. Return none for auto
    TCLab = setup(connected=False, speedup=60)
    with TCLab() as lab:

        # set up historian and plotter
        sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
                   ("U1", lambda: U1), ("Q1", lab.Q1))
        h = Historian(sources)
        p = Plotter(h, t_final, layout=[("T1", "SP"), ("Q1", "U1")])

        # initialize manipulated variable
        lab.P1 = 200
        lab.Q1(next(controller))

        # event loop
        for t in clock(t_final, t_step):
            T1 = lab.T1
            U1 = lab.Q1()
            if MV(t) is None:           
                U1 = controller.send((t_step, SP(t), T1, U1))    # automatic control
            else:
                U1 = MV(t)                                       # manual control
            lab.Q1(U1)
            lab.Q2(DV(t))
            p.update(t)  
        h.to_csv("data.csv")

experiment_3(PI_bumpless(2, 0.1))
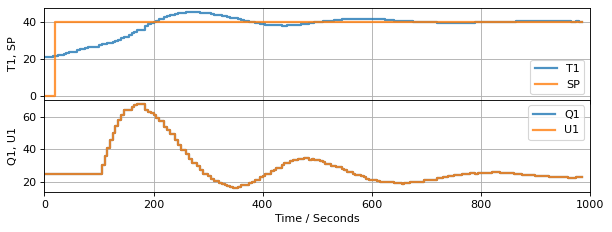
../_images/2448500a977f8faf3c1ff725b7af8ec72fac3953ba5fe2dbc5ca40f32371bcdb.png 
TCLab Model disconnected successfully.
../_images/2448500a977f8faf3c1ff725b7af8ec72fac3953ba5fe2dbc5ca40f32371bcdb.png

3.8.6. Empirical Tuning Rules#

There are a number of tuning rules in the literature that provide recommended values for the proportional gain \(K_P\). These rules require process information obtained from testing.

3.8.6.1. Tuning Rules Based on Step Test Experiments#

3.8.6.1.1. Step Test Procedure#

  1. Initialize experiment at a steady state. Confirm the process variable \(PV\) is at a constant value \(PV_1\). Eliminate any disturbances that might affect the test outcome.

  2. Make a step change in the manipulated variable \(MV_1 \rightarrow MV_2\)

\[ \Delta MV = MV_2 - MV_1\]

  1. Record the process variable \(PV(t)\) until a new steady state \(PV_2\) is reached.

\[ \Delta PV = PV_2 - PV_1 \]

3.8.6.1.2. Control Parameters#

Using \(PV(t)\) and the following chart, compute values for a first-order plus dead-time model parameters for gain (\(K\)), process time constant (\(\tau\)), and dead-time (\(\theta\)).

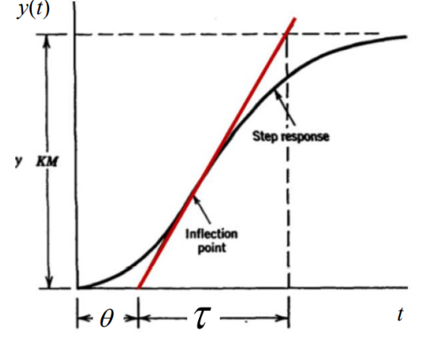
\[\begin{align*} \\ K & = \frac{\Delta PV}{\Delta MV} & \text{gain} \\ \tau & & \text{first-order time constant} \\ \theta & & \text{dead time} \end{align*}\]

The Ziegler-Nichols estimates for the proportional and integral gain are then computed from the following tuning rules. Astrom and Hagglunc (200\6) provide an updated “improved” formula for these parameters.

Type

\(K_P\)

\(K_I\)

P (Ziegler-Nichols)

\(\frac{\tau}{K\theta}\)

PI (Ziegler-Nichols)

\(\frac{0.9 \tau}{K\theta}\)

\(\frac{0.3\tau}{K\theta^2}\)

PI (Astrom and Hagglund, 2006)

\(\frac{0.15\theta + 0.35\tau}{K\theta}\)

\(\frac{0.46\theta + 0.02\tau}{K\theta^2}\)

3.8.6.1.3. Evaluate Control Performance#

Tuning rules are developed based on acheiving some performance criteria. Typical criteria include measures liks

(3.15)#\[\begin{align} \text{IAE} & = \int_0^{\infty} |e(t)|dt \qquad \text{Integral Absolute Error}\\ \text{ISE} & = \int_0^{\infty} |e(t)|^2dt \qquad \text{Integral Square Error}\\ \text{ITAE} & = \int_0^{\infty} t|e(t)|dt \qquad \text{Integral Time Absolute Error}\\ \end{align}\]

Among the best known and commonly used tuning rules are listed in the following table (also see Astrom and Murray, Chapter 11):

3.8.6.2. Tuning Rules based on Closed Loop Testing#

For strong theoretical and practical reasons, closed-loop experiments can provide superior results for tuning P, PI, and PID controllers. The easiest closed-loop tuning experiment is to implement simple relay control. The following code cells demonstrate relay control suitable for the identification experiment.

Experimental requirements:

  1. Conduct the experiment long enough to ensure steady cycling about a constant setpoint.

  2. Choose MV_min and/or MV_max to so the MV is “on” approximately 50% of the time.

\[\Delta MV = MV_{max} - MV_{min}\]

  1. Determine \(\Delta PV\) from peak-to-peak amplitude of the oscillation in \(PV\). The “critical gain” is

\[K_c = (\frac{4}{\pi}) \frac{\Delta MV}{\Delta PV}\]

  1. Determine the “critical period” \(T_c\) by measuring the period of oscillation.

Type

\(K_P\)

\(K_I\)

P (Ziegler-Nichols)

\(0.5 K_c\)

PI (Ziegler-Nichols)

\(0.4 K_c\)

\(0.5\frac{K_c}{T_c}\)

  1. Implement and test the resulting controller.

from tclab import TCLab, clock, Historian, Plotter, setup

def experiment_4(controller, t_final=1000, t_step=5, SP=lambda t: 40 if t >= 20 else 0):
    TCLab = setup(connected=False, speedup=60)
    with TCLab() as lab:

        # set up historian and plotter
        sources = (("T1", lambda: lab.T1), ("SP", lambda: SP(t)), 
                   ("U1", lambda: U1), ("Q1", lab.Q1))
        h = Historian(sources)
        p = Plotter(h, 200, layout=[("T1", "SP"), ("Q1", "U1")])

        # initialize manipulated variable
        lab.P1 = 200
        lab.Q1(next(controller))

        # event loop
        for t in clock(t_final, t_step):
            T1 = lab.T1
            U1 = lab.Q1()
            U1 = controller.send((t_step, SP(t), T1, U1))    # automatic control
            lab.Q1(U1)
            p.update(t)  

def Relay(MV_bar=0, MV_min=0, MV_max=60):
    MV = MV_bar
    while True:
        t_step, SP, PV, MV = yield MV 
        e = PV - SP
        if PV < SP:
            MV = MV_max
        else:
            MV = MV_min  
            
experiment_4(Relay())
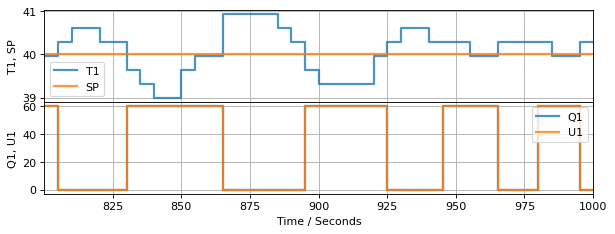
../_images/5b2cede3f531d063988fd649b143e0d0ac51fc8e6185f91e618ad8229c5a6a73.png 
TCLab Model disconnected successfully.
../_images/5b2cede3f531d063988fd649b143e0d0ac51fc8e6185f91e618ad8229c5a6a73.png

3.8.7. Lab Assignment 5#

You will test PI controllers tuned using Step Test experiment and a closed-loop Relay experiment. For testing, use the Chocolate tempering setpoint profile you developed for Lab Assignment 5.

  1. Perform the Step Test experiment desribed above. Report the following results.

    • The code used to perform the experiment.

    • Calculations of \(K\), \(\tau\), and \(\theta\).

    • PI Parameter \(K_P\) and \(K_I\) determined using the “improved” tuning rules.

    • The code and results of applying this controller to the Chocolate tempering setpoint used in Lab Assignment 4. This time, leave heater 2 off.

  2. Repeat the previous steps using closed-loop relay control to determine critical gain \(K_c\) and critical period \(T_c\). Report the PI Control parameters and experimental verification for the Chocolate tempering setpoint.