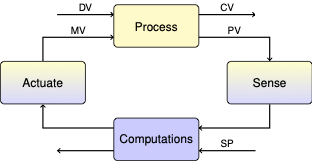
6.2. Static Operability#

Static operability refers to the ability to operate a system under steady-state conditions. We are primarily interested in determining values for the manipulable inputs that acheive a desired process target, subject to all relevant operating constraints.

6.2.1. State Space Model#

The state-space model for the Temperature Control Laboratory is given by

\[\begin{split} \begin{align} \frac{dx}{dt} & = A x + B_u u + B_d d \\ y & = C x \end{align} \end{split}\]

where the structure of the matrix parameters and vector variables is given by

\[\begin{split} \begin{align} \frac{d}{dt}\underbrace{\left[\begin{array}{c} T_{H,1} \\ T_{S,1} \\ T_{H,2} \\ T_{S,2} \end{array}\right]}_x & = \underbrace{\left[\begin{array}{cccc} -(\frac{U_a+U_b+U_c}{C^H_p}) & \frac{U_b}{C^H_p} & \frac{U_c}{C^H_p} & 0 \\ \frac{U_b}{C^S_p} & -\frac{U_b}{C^S_p} & 0 & 0 \\ \frac{U_c}{C^H_p} & 0 & -(\frac{U_a+U_b+U_c}{C^H_p}) & \frac{U_b}{C^H_p} \\ 0 & 0 & \frac{U_b}{C^S_p} & -\frac{U_b}{C^S_p} \end{array}\right]}_A \underbrace{\left[\begin{array}{c}T_{H,1} \\ T_{S,1} \\ T_{H,2} \\ T_{S,2}\end{array}\right]}_x + \underbrace{\left[\begin{array}{cc}\frac{\alpha P_1}{C_p} & 0 \\ 0 & 0 \\ 0 & \frac{\alpha P_2}{C_p} \\ 0 & 0 \end{array}\right]}_{B_u} \underbrace{\left[\begin{array}{c}u_1 \\ u_2\end{array}\right]}_u + \underbrace{\left[\begin{array}{c}\frac{U_a}{C^H_p} \\ 0 \\ \frac{U_a}{C^H_p} \\ 0 \end{array}\right]}_{B_d} \underbrace{\left[\begin{array}{c}T_{amb}\end{array}\right]}_{d} \end{align} \end{split}\]
\[\begin{split} \begin{align} \underbrace{\left[\begin{array}{c} T_1 \\ T_2 \end{array}\right]}_y & = \underbrace{\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right]}_C \underbrace{\left[\begin{array}{c}T_{H,1} \\ T_{S,1} \\ T_{H,2} \\ T_{S,2}\end{array}\right]}_x \end{align} \end{split}\]

6.2.2. Steady State Operability#

6.2.3. Steady State Model#

At steady-state our becomes

\[\begin{split} \begin{align} 0 & = A \bar{x} + B_u\bar{u} + B_d\bar{d} \\ \bar{y} & = C \bar{x} \\ \end{align} \end{split}\]

where the overbar \(\bar{u}\), \(\bar{x}\), and \(\bar{y}\) denote the steady-state value of \(u\), \(x\), and \(y\), respectively. We assume \(\bar{d}\) is known.

6.2.3.1. Steady-State input constraints#

The constraints on \(\bar{u}\) are given by upper and lower bounds

\[\begin{split} \begin{align} 0 & \leq \bar{u}_1 \leq 100 \\ 0 & \leq \bar{u}_2 \leq 100 \end{align} \end{split}\]

when the values of \(u_1\) and \(u_2\) correspond to percentage of maximum power.

6.2.3.2. Steady-State output constraints#

We will assume there are upper limits for each of the temperature outputs

\[\begin{split} \begin{align} \bar{y}_1 & \leq \bar{y}_1^{max} \\ \bar{y}_2 & \leq \bar{y}_2^{max} \end{align} \end{split}\]

when the values of \(u_1\) and \(u_2\) correspond to percentage of maximum power.

6.2.3.3. Steady-State setpoint targets or ranges#

The purpose of control is to find inputs \(\bar{u}_1\) and \(\bar{u}_2\) that cause the outputs to take on desired values. Those values could be specified as specific setpoints \(\bar{r}_1^{SP}\) and \(\bar{r}_2^{SP}\) in the form

\[\begin{split} \begin{align} \bar{y}_1 & = \bar{r}_1^{SP} \\ \bar{y}_2 & = \bar{r}_2^{SP} \end{align} \end{split}\]

Alternatively, the desired operation could be specified by a range of values

\[\begin{split} \begin{align} \bar{r}_1^{min} & \leq \bar{y}_1 \leq \bar{r}_1^{max} \\ \bar{r}_2^{min} & \leq \bar{y}_2 \leq \bar{r}_2^{max} \end{align} \end{split}\]

6.2.4. CVXPY Solution#

6.2.4.1. Imports#

import numpy as np
import cvxpy as cp

6.2.4.2. Model Parameters#

# parameter estimates.
alpha = 0.00016       # watts / (units P * percent U1)
P1 = 200              # P units
P2 = 100              # P units
CpH = 4.46            # heat capacity of the heater (J/deg C)
CpS = 0.819           # heat capacity of the sensor (J/deg C)
Ua = 0.050            # heat transfer coefficient from heater to environment
Ub = 0.021            # heat transfer coefficient from heater to sensor
Uc = 0.0335           # heat transfer coefficient between heaters
Tamb = 21             # ambient room temperature

# state space model
A = np.array([[-(Ua + Ub + Uc)/CpH, Ub/CpH, Uc/CpH, 0], 
              [Ub/CpS, -Ub/CpS, 0, 0],
              [Uc/CpH, 0, -(Ua + Ub + Uc)/CpH, Ub/CpH],
              [0, 0, Ub/CpS, -Ub/CpS]])

Bu = np.array([[alpha*P1/CpH, 0], [0, 0], [0, alpha*P2/CpH], [0, 0]])

Bd = np.array([[Ua/CpH], [0], [Ua/CpH], [0]])

C = np.array([[0, 1, 0, 0], [0, 0, 0, 1]])

# initial values for states and inputs
u_initial = np.array([0, 0])
d_initial = np.array([Tamb])
x_initial = np.array([Tamb, Tamb, Tamb, Tamb])

6.2.4.3. CVXPY Model#

The following cell implements some, but not all, elements of the steady state analysis as a CVXPY optimization model.

# knowns
d = d_initial            # disturbance
r = np.array([30, 40])   # setpoints

# unknowns to be computed
u = cp.Variable(2)
x = cp.Variable(4)
y = cp.Variable(2)

# objective
objective = cp.Minimize(0)

# model constraints
model_constraints = [
    0 == A@x + Bu@u + Bd@d,
    y == C@x]

# input constraints

input_constraints = [
    0 <= u, 
    u <= 100]

# output constraints
output_constraints = []

# setpoints
r = np.array([70, 40])
setpoints = []
objective = cp.Minimize(0)

# solve problem
constraints = model_constraints + input_constraints + output_constraints + setpoints
problem = cp.Problem(objective, constraints)
problem.solve()

# display solution
print(f"u = {u.value}")
print(f"x = {x.value}")
print(f"y = {y.value}")

u = [1.00000000e+02 6.51901705e-08]
x = [66.67521368 66.67521368 39.32478634 39.32478634]
y = [66.67521368 39.32478634]

6.2.5. Lab Assigment 7#

6.2.5.1. Exercise 1.#

  1. In the cells below, cut and paste the parameter values for matriix coefficients \(A\), \(B_d\), \(B_u\) and \(C\) to match those you previously identified for your copy of the Temperature Control Lab.

  2. Using the CVXPY outline provided above, write a Python function named feedforward that accepts an estimate of \(T_{amb}\), and setpoints for \(T1\) and \(T2\), and returns values for inputs \(U1\) and \(U2\). The function should constrain inputs U1 and U2 to values between 0 and 100%, constrain all temperatures to values no greater than 60 deg C. Use the the power settings required to set \(T1 = 45\) and \(T2 = 40\). Then create a simple event loop, and test these values on your hardware. How close was your result to the predicted value?

  3. Write an optimization model to find the greatest temperature differential between \(T1\) and \(T2\) while limiting both to temperatures less than 60 deg C. Verify this prediction using your hardware.