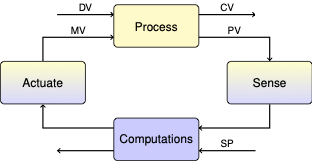
4.4. Lab Assignment 5: State Estimation#
Using the notes for Secion 4.2, the goal of this lab assignment is to build a state estimator for the Temperature Control Laboratory, then use it to achieve independent control of the two heater temperatures. The project will require updating the four state model your developed for Lab Assignment 2 described in Section 2.4.
4.4.1. Step 1. Estimate model parameters#
Refer to exercise 3 from Lab Assignment 2. Write our the four state model of the Temperature Control Lab. If needed, perform the experiment described in the assignment to gather the data needed to fit all model parameters. Report the parameter values.
4.4.2. Step 2. Create state-space model#
Using the matrix and vector formulation described in notebook 4.2, rewrite the equations for the four state model in state-space form. In a new python notebook, use the parameter values from Step 1 to numerically evaluate matrices \(A\), \(B_u\), \(B_d\) and \(d\). Compute the eigenvalues (they should all be negative real numbers) of \(A\) and report the negative inverse of the eigenvalues as time constants.
4.4.3. Step 3. Implement a state estimator#
Implement a state estimate utilizing measurements T1 and T2, and inputs Q1 and Q2, to estimate the state. As an initial choice for matrix \(L\) use
4.4.4. Step 4. Implement relay control for the heater temperatures T1H and T2H#
Using constant setpoints of 45 and 40 degrees, respectively, for temperatures \(T_{1}\) and \(T_{2}\). At time t = 300, have the setpoints switch to 40 and 45 degrees, respectiviely. Show control performance over total of 600 seconds when using sensor measurements for relay control. Replace the sensor measurements with observer estimates for heater temperatures \(T_{H,1}\) and \(T_{H,2}\) and repeat the test. What do you observe?