Low-Level Measurement#

References#

Limits to Measurements#

Sources of noise

White noise:

  • Shot noise from the discrete nature of charge carriers

  • Johnson noise caused by thermal fluctuations

Other noise:

  • Flicker 1/f noise from a variety of sources

  • …. and many more!

Shot Noise#

Shot noise is the noise due to descrete nature of electric charge. Shot noise can be modeled as a Poisson process. A fundamental consideration in electrical and optical devices including photography.

In a Poisson process:

  • Poisson processes model the occurrence of independent events that occur one at a time.

  • The probability of exactly one event in a sufficiently short interval \(h\) is \(P = \nu h\) where the constant \(\nu\) is the average rate of events.

  • Each interval is a Bernoulli trial. The number of events in a time period is given by

\[P(k) = \frac{(\nu h)^k}{k!} e^{-\nu h}\]

  • \(\mu = \nu h\) is the expected number of events in the interval \(h\)

  • \(\sigma^2 = \nu h\) is also the variance in the number of events in interval \(h\).

  • The waiting time between events follows an exponential distribution. The probability of waiting longer than \(t\) is

\[P(t > h) = e^{-\nu h}\]

or less that \(t\)

\[P(t \leq h) = 1 - e^{-\nu h}\]

This last expression is the cumulative distribution function. The probably density function is the derivative

\[f(h) = \nu e ^ {-\nu h}\]

Frequency domain

A frequency-domain derivation of shot noise

\[i_{noise} = \sqrt{2 q I_{dc}}\]

where \(q = 1/C\) is the electron charge \(1.60\times 10^{-19}\) C.

Signal to Noise Ratio

Signal to noise ratio is normally expressed as the power of the signal divided by the power of the noise.

\[\text{SNR} = \frac{\mu^2}{\sigma^2}\]

If the interval is \(\delta t\) the current is \(I\), rate of charge carriers is \(C I h\) where \(C\) is Coulomb constant. The SNR is then

\[\text{SNR} = \frac{(C I \delta t)^2}{C I \delta t} = C I \delta t\]

Question: Suppose you need 5 sigma accuracy (i.e, \(\frac{\mu}{\sigma} > 5\)) and are measuring a 1 nA signal, what is the fastest sampling rate you can expect?

Simulated Photon Noise

A sequence of images in which the average number of photons captured per pixel increases by factors of 10x between images. source

Question:

  1. Which image has the most noise?

  2. Which image has the lower signal to noise ratio?

# Demonstration
# 
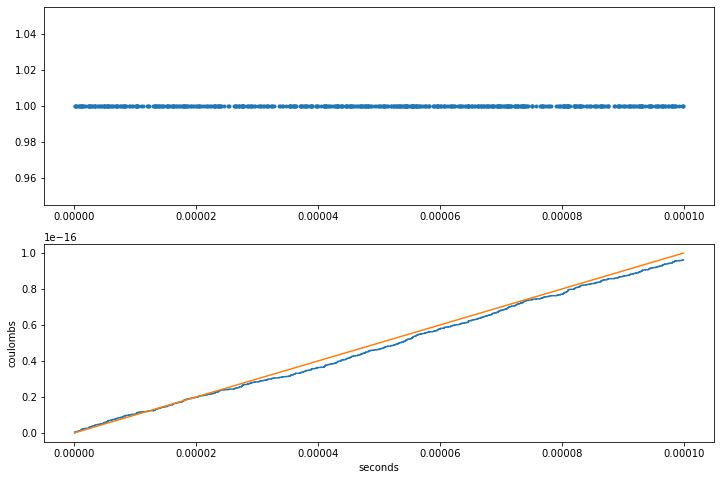
# Simulate shot noise for a 1 pA current

%matplotlib inline

import random
import math
import numpy as np
import matplotlib.pyplot as plt

# constants
C = 6.241509074e18     # number of electrons in a Coulomb
I = 1e-12              # 1 pA of current
h = 1e-6               # 1 microsecond

nu = C*I
print("nu =", nu, "electrons per second") 
print("expected number of electrons per step nu*h =", nu*h)

K = 600

# simulate arrival of K charge carriers
dt = np.random.exponential(1/nu, size=(K))
t = np.cumsum(dt)

# plot results
y = np.array([1]*len(t))

fig, ax = plt.subplots(2, 1, figsize=(12, 8))
ax[0].plot(t, y, '.')

ax[1].step(t, np.cumsum(y)/C, where="pre")
ax[1].plot(t, I*t)
ax[1].set_ylabel('coulombs')
ax[1].set_xlabel('seconds')

nu = 6241509.074 electrons per second
expected number of electrons per step nu*h = 6.241509074

Text(0.5, 0, 'seconds')
../../_images/03.01-Low-Level-Measurment_4_2.png

Johnson-Nyquist Noise#

  • Discovered and measured by John B. Johnson, Bell Labs, 1926

  • Explained by Harry Nyquist, Bell Labs, 1928.

Johnson noise has the same origins as black-body radiation. The average (root mean square) voltage due to thermal noise in a resistor is

\[v_{noise} = \sqrt{4kTRB}\]

where \(k\) is Boltzmann’s constant, T is absolute temperature, R is resistance, and B is bandwidth in Hertz. At 20 deg C

\begin{align*} 4kT & = 1.62 \times 10^{-20} & V^2/Hz-\Omega \ \sqrt{4ktR} & = 1.27\times 10^{-10}\sqrt{R} & V/Hz^{1/2} \end{align*}

The short-circuit current noise is

\[i_{noise} = v_{noise}/R = \sqrt{\frac{4kTB}{R}}\]

Question: What is the RMS voltage of 10k ohm resistor?

  • High resistances results in noisy voltage signals

  • Low resistance results in noisy currrent signals

\[P_{noise} = v_{noise}i_{noise} = 4kTB\]

Chemical Applications#

  • Electrochemical Measurements

    • Ion-selective electrodes

    • pH measurements

    • Conductivity cells

    • Potientiostat/Galvanostat